Amaliy mashgʻulot yechish bosqichlari

1.   Географик ва осмон координаталари орасидаги ўзаро боғлиқлик.

2.   Экваториал координата тизимидан горизонтал кордината тизимига ўтиш.

Географик ва осмон координаталари орасидаги ўзаро боғлиқлик қуйидаги теоремалар билан белгиланади

1-теорема. Шимолий ярим шарда турган кузатувчи учун кузатиш жойининг географик кенглиги j дунё қутбини горизонтдан баландилиги h_p га ҳамда зенитнинг оғиши d_Z га тенгдир, яъни

                                  j = h_p = d_Z                                                      (9)

Жанубий кенглик ва жанубий ярим шардаги зенит оғиши салбий бўлгани сабабли, жанубий ярим шарда турган кузатувчи учун (9) формула қуйидагича ифодаланади:

                                -j = h_p = -d_Z                                                  (10)

Оқибат шимолий ярим шарда қутб ва зенит орасидаги меридиан ёйи кенгликни 90° га тўлдирувчисига тенгдир, яъни

                                È PZ=90°- j                                     (11)

Жанубий яримшарда эса жанубии қутб ва зенит орасидаги меридиан ёйи кенгликка 90°ни қўшилганига тенгдир яъни:

                               È P'Z=90°+ j                                    (12)

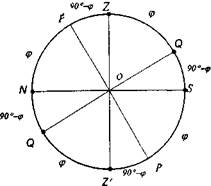
(11) ва (12) тенгликлар осмон сферасини осмон меридиани билан кесишини тасвирловчи 14-шаклдан келиб чиқади.  È NZ =90 ° ва NP =j бўлгани учун È PZ = 90° бўлади.

2-теорема. Ер сиртининг икки нуқтасида бир моментда кузатилган ёритқич соат бурчакларининг фарқи қийматан ушбу кузатиш нуқталарининг географик узоқликларини фарқига тенгдир.

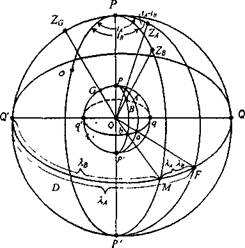
Ушбу теоремани исботлаш учун ер сиртидаги А ва В нуқталари ҳамда G (Гринвич) нуқтасини шовун чизиғи йўналишида осмон сферасидаги проекцияларини кўрамиз (15-шакл). Узоқликни ҳисоблашда Гринвич осмон меридиани саноқ боши тарзида олинади. Шаклдаги Z_A , Z_B ва Z_G нуқталари ер сиртидаги А, В ва G нуқталарининг зенитлари, PZ_AP', PZ_BP' ва PZ_GP' катта доиралари эса ушбу нуқталарнинг осмон меридианлари бўлади.

Гринвичдан шарқда жойлашган А ва В нуқталарида бир вақт моментида s ёритқичи кузатилган РsР' катта доира s ёритқичининг оғиш доирасидир. А ва В нуқталарининг географик узоқликлари осмон экваторининг Q'F ва Q'M ёйларига тенг бўлиб, мос тарзда l_А ва l_В белгилари билан ифодаланади. Ёритқични А нуқтада кузатилган соат бурчагини t_A билан, В нуқтада кузатилган соат бурчагини t_B билан белгилаймиз. Демак

                              t_A – t_B = l_А – l_В                                   (13)

эканлигини исботлаш керак бўлади.

А ва В нуқтада бир вақт моментида кузатилган s ёритқичнинг соат бурчаклари sPZ_A ва sPZ_B сферик бурчаклари билан ўлчанади. Уларнинг фарқи қуйидагича аниқланади:

            t_A – t_B  = ÐsPZ_A – ÐsPZ_B = ÐZ_APZ_B

Демак, бир вақтни ўзида ер сиртидаги иккита нуқта А ва B дан кузатилган ёритқичнинг соат бурчакларини фарқи ушбу кузатиш нуқталарининг осмон меридианлари орасидаги сферик бурчак орқали  яъни ÐZ_APZ_B орқали, ёки осмон экваторининг ейи ÈFM орқали, ёки кузатиш нуқталарининг осмон меридианлари текисликлари орасидаги икки қиррали бурчак Z_APР'Z_B орқали, ёки марказий бурчак FOM орқали аниқланиши мумкин. 20-шаклдан кўриниб турибдики

                l_А – l_В  = ÈQ'F – ÈQ'M = ÈМF

А ва В нуқталарининг географик узоқликларини фарқи ҳам Z_APZ_B сферик бурчаги орқали, ёки марказий бурчак MOF орқали, ёки ушбу кузатиш нуқталарининг осмон меридиани текисликлари орасидаги икки қиррали бурчак Z_APP'Z_B орқали ўлчаниши мумкин.

Шундай қилиб, биз (13) тенгликни шимолий ярим шар учун ҳам, жанубий ярим шар учун ҳам ўринли эканлигини исботладик.

Агар А ва В кузатиш нуқталари гринвич меридианидан ғарбда жойлашган бўлса, тенглик қуйидаги кўринишни олади:

                              t_А – t_В = l_А – l_В                                   (14)

2. Астрономик йилномалар ва юлдуз каталогларида ёритқичнинг экваториал координаталари эълон қилинади Ер сиртидаги нуқтанинг жойлашиш ҳолатини астрономик аниқлаш учун ушбу мақсадда, кузатилаётган ёритқичнинг горизонтал координаталарини билиш зарур. Шу сабабдан горизонтал координата тизими ва экваториал координата тизимлари орасидаги муносабатни аниқлаб, a ва d дан z ва А га ўтиш формуласини чиқарамиз. Ушбу мақсадда қирралари дунё қутби Р, кузатиш жойининг зенити Z ва ёритқич s бўлган сферик учбурчак PZs ни (16-шакл) кўриб чиқамиз. Ушбу сферик учбурчак параллактик учбурчак деб аталади.

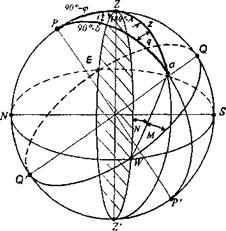
Параллактик учбурчакнинг томонлари қуйидагилардир: дунё шимолий қутби ва зенит орасидаги осмон меридианининг ёйи (қийматан ÈPZ = 90°- j, оғиш доирасининг ёйи (қийматан ÈPs =90°- d  ва s ёритқичининг зенит масофасига тенг вертикал ейи ÈZs = z.

Агар ёритқич осмон сферасининг ғарбий ярмида жойлашган бўлса дунё шимолий қутбидаги бурчак соат бурчаги t га тенг бўлади, зенитдаги бурчак эса азимутни 180°гача тўлдирувчи қийматга яъни (180°-А) га тенг бўлади. Агар ёритқич осмон сферасининг шарқий яримида турган бўлса дунё қутбидаги бурчак (360°-t) га. тенг, зенитдаги бурчак эса (А-180°) га тенг бўлади. Ёритқичдаги бурчак параллактик бурчак деб аталади ва q ҳарфи билан белгиланади.

Кенглиги j бўлган кузатиш нуқтасидаги белгиланган юлдуз вақт моменти s да s ёритқичининг экваториал координаталари a ва d маълум бўлиб, ушбу ёритқичнинг зенит масофаси z ва азимути А ларни ҳисоблаш зарур бўлсин. Сферик тригонометриядан маълум бўлган томонлар косинуси, синуслар теоремаси ва бешта элемент формулаларини PZs учбурчагининг z томони ва (180°-А) бурчагига қўллаймиз. Ушбу қўллашда сфер ик учбурчак томонларини a=z, b=90°-d ва с=90°-j орқали, бурчакларни эса A=t ва B=180⁰-A орқали белгилаймиз.

Натижада:

cos z = sin j sin d + cos j cos d cos t

sin z cos(180°-A) = sin(90°-j) cos(90°-d) -

                            - cos(90°-j) sin(90°-d) cos t

ёки

cos z = sin j sin d + cos j cos d cos t

sin z sin A = cos d sin t                                                 (16)

sin z cos A = cos d sin j cos t – sin d cosj

Бу ерда t = s – a.

Ушбу формулалар горизонтал ва экваториал координата тизимлари орасидаги боғлиқликни ифодалайди. Биринчи қатордаги формула зенит масофасини аниқласа, қолган иккитаси орқали азимут аниқланиши мумкин. Агар кузатиш нуқтасининг кенглиги j, ёритқич соат бурчаги t ва оғиши d маълум бўлса, z ва А нинг қийматларини  (16) формулалардан исталган иккитаси орқали "тригонометрик функциянинг натурал қийматлари жадвали" ёрдамида аниқлаш мумкин. Иккинчи қатордаги формулани учинчи қаторга қатнашувчилари бўйича тақсимлаб қуйидагига эга бўламиз:

                                         (17)

A бурчаги бевосита тангенс орқали бир қийматда аниқланмайди. Бунга сабаб тангенс мусбат ишорага эга бўлганда бурчак биринчи ёки учинчи чоракда, манфий ишорага эга бўлганда эса иккинчи ёки тўртинчи чоракда бўлиши мумкин. Аммо, иккинчи ва учинчи формулаларнинг ўнг томондаги ифодаларини ишораси А бурчакни бир қийматда аниқлаш имкониятини беради.

Аслида tg А мусбат ишорага эга десак, иккинчи ва учинчи формулаларнинг ўнг томонидаги ифодаларини ишораси бир хил бўлиши керак. Агар улар мусбат ишорали бўлса sinz доимо мусбатлигини инобатга олган холда А бурчаги биринчи чоракда ётади. Аксинча улар манфий ишорага эга бўлса, бурчак учинчи чоракда ётади. Бундай таҳлил tgA манфий бўлганда ҳам ўринлидир.

Кўраётган параллактик учбурчагимизда параллактик бурчак q ни ҳам аниқлаш мумкин. Бунинг учун юқоридаги иккинчи ва ва учинчи сферик тригонометрия формулаларини қўллаймиз ва a=z, b=90°-j, A=t ва B=q белгилашларини киритиш билан қуйидагига эга бўламиз:

sin z cos q = sinj cos d – cosj sind cos t.

Натижада

                                         (19)

q бурчаги ётувчи квадрат ҳам aзимyт А ни ҳисоблашдаги каби аниқланади.

Горизонтал координата тизимидан экваториал координата тизимига ўтиш. Бунинг учун сферик тригонометриянинг учта асосий формулаларини яна бир карра параллактик учбурчак PZs га қўллаймиз. Ушбу қўллашда сферик учбурчак томонларни a = 90 °-5, b = z, ва с = 90°- j орқали, бурчакларни эса А=180°-А ва B = t орқали белгилаймиз.

У ҳолда қуйидагига эга бўламиз:

cos d = sin j cos z – cos j cos z cos А

sin d sin t =sin z  sin A                                                  (20)

sin d cos t  = cos z cos j + sin z sin j cos А

Биринчи катордаги формуладан фойдаланган ҳолда, ёритқичнинг берилган горизонтал координаталари z ва А, ҳамда кузатиш жойининг кенлиги j орқали ёритқичнинг оғиши d ни аниқлаймиз. Иккинчи ва учинчи формулалар орқали соат бурчак t ни аниқлаймиз:

                                       (21)

Соат бурчаги t нинг квадратини аниқлаш ҳақида юқорида айтдик.

Юқорида келтирилган формулалар билан кичик электрон ҳисоблаш машиналарида ҳисоб бажариш қулайдир. Агар ҳисоблашларни логарифмлар орқали бажариш зарурияти туғилиб қолса, ушбу формулалар ёрдамчи қийматлар киритилиши натижасида логарифмик кўринишга келтирилади. Масалан: М ва N ёрдамчи сферик бурчаклари. Уларнинг қийматлари қуйидагига тенгдир:

                                                                       (22)

                                                                   (23)

Азимут ва зенит масофасини логарифмик аниқлаш формулалари қуйидаги кўринишда бўлади:

                                   (24)

Горизонтал координата тизимидан экваториал координата тизимига ўтиш формуласининг логарифмик кўриниши куйидагичадир:

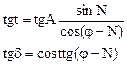                                                           (25)