
AMALIY MATEMATIKA INFORMATIKAYO’NALISHI
204 - guruh talabasi
Xo’jamurodov Sh
MALAKAYIY AMALIYOT HISOBOTI
MAVZU: 1- Topshiriq
“Oddiy matematik modellarning sinteziga doir misollar. Matematik model va o’rganilayotgan obyekt orasidagi muvofiqligi. Real hodisa va jarayonlarning matematik modellariga misollar.”
HISOBOT
Tekshirdi:RO’ZIYEVA. M
Bajardi:Xo’jamurodov Sh
SAMARQAND
– 2022
Mavzu: Oddiy matematik modellarning sinteziga doir misollar. Matematik model va o’rganilayotgan obyekt orasidagi muvofiqligi. Real hodisa va jarayonlarning matematik modellariga misollar
1. Energiya va materiyaning saqlanish qonunlaridan foydalanish. Modellarni qurishning eng ko’p qo’llaniladigan usuli tabiatning fundamental qonunlarini aniq holatlarda qo’llashdir. Bu qonunlar bir qancha tajribalar asosida tasdiqlangan, umumtanolingan qonunlar bo’lib, ilmiy-texnikaviy yutuqlar to’plamining poydevori hisoblanadi.
a) Energiyaning saqlanish qonuni. Bu qonun deyarli 200 yildan beri ma’lum bo’lib, tabiatning barcha qonunlari ichida muhim ahamiyat kasb etadi. Bu qonunni sodda ko’rinishdagi quyidagi masalada qo’llanilishini qaraymiz: yaqin joyda maxsus laboratoriya bo’lmasa, revolverdan otilgan o’qning tezligini kanday aniqlash mumkin.
Buni
aniqlashda erkin aylanuvchi ![]() uzunlikdagi sterjenli mayatnik
tipidagi uskunadan foydalanish mumkin. Bu sterjenga ma’lum
uzunlikdagi sterjenli mayatnik
tipidagi uskunadan foydalanish mumkin. Bu sterjenga ma’lum ![]() og’irlikka ega bo’lgan yuk osilib,
unga rivolverdan
og’irlikka ega bo’lgan yuk osilib,
unga rivolverdan ![]() og’irlikdagi o’q kelib
urilsin. Natijada
og’irlikdagi o’q kelib
urilsin. Natijada ![]() tezlikga ega bo’lgan
o’qning kinetik energiyasi
tezlikga ega bo’lgan
o’qning kinetik energiyasi ![]() miqdorga teng
bo’ladi. Bu energiya natijasida sterjenga osilgan yuk
miqdorga teng
bo’ladi. Bu energiya natijasida sterjenga osilgan yuk
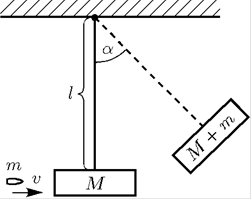
potensial energiyasi miqdori esa ![]() ga teng bo’ladi, bunda
ga teng bo’ladi, bunda ![]() – o’q ta’sir etgandagi yukning
tebranma harakat tezligi. Shunday qilib, energiyaning saqlanish qonuniga ko’ra bu
energiyalar teng bo’lishi lozim:
– o’q ta’sir etgandagi yukning
tebranma harakat tezligi. Shunday qilib, energiyaning saqlanish qonuniga ko’ra bu
energiyalar teng bo’lishi lozim:
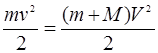 . (1)
. (1)
Mexanika kursidan ma’lumki, burchak tezlik
![]()
miqdorga teng bo’ladi, bunda ![]() – erkin tushish tezlanishi,
– erkin tushish tezlanishi, ![]() –
yukning eng katta og’ish burchagi. Bu
tenglikni (1) formulaga qo’ysak, ushbu
–
yukning eng katta og’ish burchagi. Bu
tenglikni (1) formulaga qo’ysak, ushbu
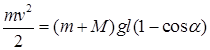
tenglikka ega bo’lamiz. Bu tenglikdan revolver o’qining tezligi
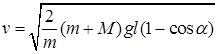
formula bilan aniqlanishi kelib chiqadi.
O’q va mayatnik orasida ro’y
berayotgan hodisa sof mexanik jarayon bo’la olmaydi. Shuning uchun ![]() mikdorni
hisoblash uchun mexanik energiyaning saqlanish qonunidan foydalanish noto’g’ri.
Chunki mexanik energiya o’zgarib, to’la energiya saqlanadi. Bu o’q tezligini
aniqlashning quyi chegarasinigina beradi.
mikdorni
hisoblash uchun mexanik energiyaning saqlanish qonunidan foydalanish noto’g’ri.
Chunki mexanik energiya o’zgarib, to’la energiya saqlanadi. Bu o’q tezligini
aniqlashning quyi chegarasinigina beradi.
b) Materiyaning
saqlanish qonuni. Yana bir oddiy ko’rinishdagi hayotiy masalani
qaraymiz: ![]() og’irlikdagi ho’l mevani quritganda,
undan qancha miqdorda quruq meva tayyorlanadi. Buni aniqlash uchun mevadagi suv
miqdorini aniqlash kifoya. Chunki materiyaning saqlanish qonuniga ko’ra
og’irlikdagi ho’l mevani quritganda,
undan qancha miqdorda quruq meva tayyorlanadi. Buni aniqlash uchun mevadagi suv
miqdorini aniqlash kifoya. Chunki materiyaning saqlanish qonuniga ko’ra ![]() , bunda
, bunda ![]() va
va ![]() mos holda
mos holda ![]() og’irlikdagi ho’l mevada
suv va quruq meva (qolgan moddalar) og’irliklari. Bu tenglikdan esa
og’irlikdagi ho’l mevada
suv va quruq meva (qolgan moddalar) og’irliklari. Bu tenglikdan esa ![]() bo’lishi tabiiydir.
bo’lishi tabiiydir.
Materiyaning saklanish konunini modellashtirishda qo’llash sohasi nihoyatga keng hisoblanadi.
1-amaliy mashg’ulot
Turli modellar tuzishga doir misollar yechish
Jismga yerda uning sirtiga α burchak
ostida yo‘nalgan ![]() boshlang‘ich tezlik
berildi. Jismning harakat trayektoriyasini toping va uning boshlang‘ich va
oxirgi nuqtalari orasidagi masofani aniqlang.
boshlang‘ich tezlik
berildi. Jismning harakat trayektoriyasini toping va uning boshlang‘ich va
oxirgi nuqtalari orasidagi masofani aniqlang.
Masalani yanada konkretlashtirish uchun gap katapulta yordamida tashlab yuborilgan tosh ustida boryapti deb qaraymiz. Bu bizga jismning xarakterli o‘lchamlarini, uning massasini hamda mumkin bo’lgan boshlang’ich tezligini aniqlashda yordam beradi. Endi berilgan holda quyidagi farazlarga asoslangan matematik modelni quramiz;
1) Yer — inersial sanoq sistemasi;
2) Erkin tushish tezlanishi ![]() – o‘zgarmas;
– o‘zgarmas;
3) Yerning egriligini e’tiborga olmasdan, uni yassi deb qarash mumkin;
4) Harakatdagi toshga havoning qarshilik kuchi ta’sirini e’tiborga olmaslik mumkin.
Koordinatalar sistemasini kiritamiz.
Koordinatalar boshini katapulta bilan ustma-ust tushiramiz, ![]() o‘qini toshning harakat yo‘nalishi
bo‘yicha gorizontal,
o‘qini toshning harakat yo‘nalishi
bo‘yicha gorizontal, ![]() o‘qini esa yuqoriga
vertikal yo‘naltiramiz. Bu farazlarga ko‘ra toshning
o‘qini esa yuqoriga
vertikal yo‘naltiramiz. Bu farazlarga ko‘ra toshning ![]() o‘qiga
proeksiyasi
o‘qiga
proeksiyasi ![]() tezlik bilan tekis harakatlanadi.
Toshning
tezlik bilan tekis harakatlanadi.
Toshning ![]() o‘qiga proeksiyasi esa
o‘qiga proeksiyasi esa ![]() tezlanish va
tezlanish va ![]() boshlang‘ich tezlik bilan tekis
tezlanuvchan harakat qiladi. Shunday qilib tosh harakatining xarakteri ushbu
boshlang‘ich tezlik bilan tekis
tezlanuvchan harakat qiladi. Shunday qilib tosh harakatining xarakteri ushbu
![]() (1)
(1)
![]() (1)
(1)
formulalar bilan aniqlanadi. Bu formulalar (1)–(4) shartlar bajarilganda masalaning matematik modelini beradi. Hosil qilingan model g‘oyatda sodda va qo‘yilgan savolga javob osonlik bilan olinishi mumkin. (1) dan t vaqtni x koordinata orqali ifodalaymiz:
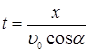
va uni (2) ga qo’yamiz. Natijada tosh trayektoriyasining parabolani (1-chizma) ifodalovchi.
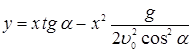 (3)
(3)
tenglamasiga ega bo’lamiz. Bu parabola x o’qini x=0 va x=l nuqtada kesib o’tadi, bunda
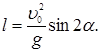 (4)
(4)
Birinchi nuqta traektoriyaning boshi bo‘lib, unda tosh katapultadan otilib chiqadi. Ikkinchi nuqta toshning yerga tushgan joyiga mos keladi. (4) formula qabul qilingan model doirasida izlangan masofa l ni aniqlaydi.
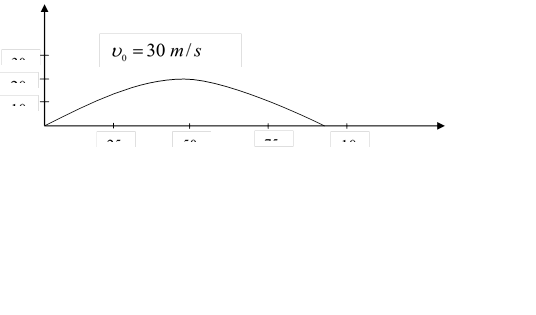 |
Tajriba ko‘rsatadiki, ko‘p hollarda modelning to‘g‘ri tanlanishi – muammoning yarmidan ko‘pini hal qilish demakdir. Bu bosqichning qiyinligi shundan iboratki.u matematika va sotsial bilimlarning uyg‘unlashishini talab etadi. O‘rta maktab fizika kursiga doir masalalar yechishda siz bir vaqtda ham fizik, ham matematik xizmatini o‘taysiz. Ammo amaliy matematikada qaraladigan katta muammolar uchun mutaxassisliklarning bunday uyg‘unlashishi tipik emas. Odatda matematik model ustida matematiklar hamda o‘rganilayotgan ob'ekt tegishli bo‘lgan sohaning mutaxassislari birgalikda ishlaydilar. Ularning faoliyati muvaffaqiyatli bo‘lishi uchun bir-birini tushunishi g‘oyatda muhim. Bunga matematiklar ob'ekt haqida maxsus bilimlarga ega bo‘lganda, ularning sheriklari esa ma'lum darajada matematik bilimga, o‘z sohasida tadqiqotning matematik metodlarini qo‘llanish tajribasiga ega bo‘lgandagina erishish mumkin.
O’tgan mavzuda qarab chiqilgan gorizontga burchak ostida otilgan jism harakatini modellashtirishda ko’tarilish balandligi, uchish uzoqligi, va trayektoriya uzunliklari topilgan edi. Endi boshlang’ich tezlik va otilish burchagi berilgan holda bu uchta parametrni topishni kompyuterli modellashtiramiz. Yuqori darajali dasturlash tillaridan C++ tilida quyidagi dasturni tuzamiz.
#include <iostream>
#include <math.h>
using namespace std;
double funk(double v0, double alpha, double x)
{
double y;
y=sqrt(pow(tan(alpha)-(2*x*9.81)/(2*v0*v0*pow(cos(alpha),2)),2)+1.0);
return y;
}
int main()
{
double v0,x,alpha,L,l,h;
cout<<"Dastlabki tezlikni kiriting: "<<endl;
cin>>v0;
cout<<"Otilish burchagini kiriting: "<<endl;
cin>>alpha;
alpha=(alpha*M_PI)/180;
if (floor(alpha-M_PI/2.0)==0)
l=0;
else
l=(v0*v0*sin(2*alpha))/9.81;
h=(v0*v0*pow(sin(alpha),2))/(2.0*9.81);
int n;
cout<<"Trayektoriya uzunligini hisoblash uchun qadamlar sonini kiriting: "<<endl;
cin>>n;
x=0; L=0;
double dx=l/n;
cout<<endl;
cout<<"Qadam uzunligi = "<<dx<<endl;
while (x<l)
{
if (x==0 || x==l)
L+=funk(v0,alpha,x);
else
L+=2*funk(v0,alpha,x);
x+=dx;
}
L*=dx/2;
cout << "Ko'tarilish balandligi: " << h << endl;
cout << "Uchish uzoqligi: " << l << endl;
cout << "Trayektoriya uzunligi: " << L << endl;
return 0;
}
Dastur ishlashi natijasida quyidagi natijalarni olamiz.
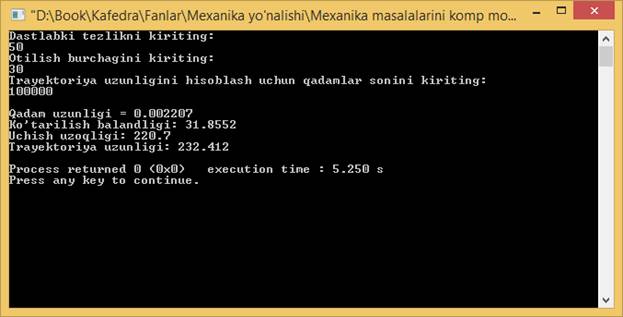
Ya’ni ![]() bo’lganda
jismning ko’tarilish balandligi h=31,8552, uchish uzoqligi hamda l=220,7
trayektoriya uzunligi L=232,412 topilgan.
bo’lganda
jismning ko’tarilish balandligi h=31,8552, uchish uzoqligi hamda l=220,7
trayektoriya uzunligi L=232,412 topilgan.
Maktabda matematik modellarni yaratish uchun ko'proq narsa bor
Siz fizikadan masalalarni yechish jarayonida uchrashgansiz. Ba'zi hududlarda odatda jismoniy tizim taqdim etiladi
uning holatini tasvirlab bering. Siz ushbu tizimning mumkin bo'lgan idealizatsiyasi haqida gapiryapsiz
(masalan, haqiqiy ob'ektni moddiy nuqta sifatida ko'rib chiqing)
O'ylab ko'ring, u o'rganishda hisobga olinadi
fizika qonunlarini aniqlang va ularni matematik jihatdan qo'llang
tenglamalar orqali ifodalanishi kerak. Bu ko'rib chiqilayotgan jismoniy tizimning matematik modeli.
Misol tariqasida mexanikaning ushbu muammosini ko'rib chiqing
Qani ketdik Tana Yer yuzasiga burchak ostida joylashgan
boshlang'ich s a ga boshlang'ich tezlik berildi. Tananing harakati
Traektoriyani va uning boshlang‘ich va yakuniy yo‘nalishini toping
Nuqtalar orasidagi masofani aniqlang.
Masalaga oydinlik kiritish uchun u katapulta yordamida tashlangan tosh haqida gapirayotganini aytdi.
Ko'raylikchi. Bu bizga tananing xarakterli o'lchamlarini beradi,
shuningdek, gvineya cho'chqasining massasini imkon qadar tezroq aniqlashga yordam beradi. Endi, berilgan holatda, quyidagi 12 ga teng
dagi taxminlar asosida matematik modelni qurish
1) Yer - inertial sanoq sistemasi;
2) erkin tushishning tezlashishi d - o'zgarmaydi;
3) Yerning egriligidan qat'iy nazar, u tekis
deb hisoblash mumkin;
4) harakatlanuvchi jinsga havo qarshiligining ta'sirini e'tiborsiz qoldirish mumkin.
Koordinatalar tizimi bilan tanishtiring. Koordinatalar
Biz katapult bilan boshni tushiramiz, eksa x
toshning harakat yo'nalishi bo'yicha gorizontal, u o'qi
va vertikal yuqoriga. Ushbu taxminlarga ko'ra
toshning x o'qidagi proyeksiyasi v=v0cos@, tezlik bilan
silliq harakat qiladi. Ushbu o'qdagi toshning proyeksiyasi
ay = —g tezlanish va vy =v0 dastlabki tezlik
bir xil tezlanish bilan harakat qiladi. Shunday qilib,
bu tosh harakatining tabiati
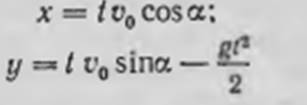
formulalar bilan aniqlanadi.
Ushbu formulalar 1) -4) shartlar bajarilganda masalaning matematik modeli
beradi. Olingan model juda oddiy va yotqizilgan Savolga javobni osongina olish mumkin. (1) dan ^Vaqtni x koordinatalarida ifodalaymiz:
![]()
va uni qo'ying (2). Natijada toshning traektoriyasi parabolani tasvirlash (1-rasm)
![]()
tenglamamiz bor Bu x parabolaning o'qi ikkita x = O ga teng va x I nuqtada kesishadi, bu erda
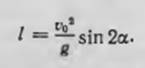
Birinchi nuqta - traektoriyaning boshlanishi, keyin tosh katapult. Ikkinchi nuqta - tosh
erga tushadigan joyga mos keladi. (4) Formula qabul qilingan model doirasida men izlagan masofani l aniqlaydi.
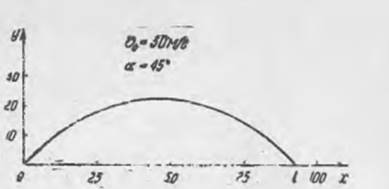
Bu formula sizga tanish: u 8-sinf fizika darsida taqdim etiladi va to‘liq tahlil qilinadi.
Amaliy masalalarda matematik model qurish ustida ishlasheng murakkab va mas’uliyatli bosqichlardan biridir.Tajriba shuni ko'rsatadiki, ko'p hollarda modelning to'g'ri tan olinishi muammoning yarmini hal qilishini anglatadi. Ushbu bosqichning qiyinligi shundaki, u mavzuli va ijtimoiy bilimlarni uyg'unlashtirishni talab qiladi. Siz bir vaqtning o'zida o'rta maktab fizikasi va matematika muammolarini hal qila olasiz. Biroq, amaliy matematikaning katta muammolari uchun bunday mutaxassisliklar kombinatsiyasitipik emas. Odatda matematiklar matematik model bo'yicha va tadqiqot ob'ekti tegishli bo'lgan soha
mutaxassislar birgalikda ishlaydi. Muvaffaqiyatlari uchun bir-birlarini tushunish
nihoyatda muhim. Matematiklar ushbu ob'ekt haqida alohida ahamiyatga ega
va ularning sheriklari bilimga ega bo'lganda ma'lum bo'ladi matematika darajasi, o'z sohangizda tadqiqot
Bunga matematik usullarni qo'llashda tajribangiz bo'lsagina erishish mumkin.
2-§. Matematik model o'rganilmoqda
ob'ekt bilan muvofiqligi. Operatsion mezonlari
Hech qachon hisobga olinmaydigan ob'ektga ega matematik model
u bir xil emas, u o'zining barcha xususiyatlarini va xususiyatlarini bera olmaydi. Oddiylashtirish va ideallashtirishga asoslangan model ob'ektning taxminiy tavsifidan iborat. Shuning uchun modelni tahlil qilish natijasida olingan natijalar ob'ekt uchun har doim taxminan bo'ladiega bo'ladi. Ularning aniqligi model va ob'ektga mos keladi, -yetarlilik darajasiga bog‘liq. Aniqlik haqiqati va natijalarning ishonchliligi masalasi barcha matematikaning eng nozik muammolaridan biridir.Ob'ektning holati va xususiyatlarini tartibga soluvchi qonunlar yaxshi ma'lum va ularning qo'llanilishi juda keng.Ko'p tajribaga ega bo'lsangiz, aniqlik muammosi osonbilan hal qiladi. Natijalar ko‘rib chiqilmoqdaapriori (eksperimental, a) model tomonidan taqdim etilgan aniqlikbu erda - matematik muammo hal qilinmaguncha).
Mana bir misol. SSSRda 1959 yil 2 yanvarLuna-1 avtomatik stansiyasi ishga tushirildi, bu insoniyat uchunsayyoralararo parvozlar davrini ochdi. Sayyoralararomexanika qonunlari va tortishish qonunidan foydalangan holda stansiyaning fazodagi traektoriyasini hisoblab chiqadi
matematik modelga asoslangan. Quyosh sistemasidagi samoviy jismlarni kuzatish bo‘yicha ko‘p asrlik tajriba shuni ko‘rsatdiki, bu model ularning harakatining juda to‘g‘ri tavsifini beradi. Tabiat qonunlarining universalligi shundaki, model inson tomonidan yaratilgan makondirqurilmaga qo'llanilishi mumkin.O'rganilayotgan ob'ekt haqida etarli ma'lumot bo'lmasa, vaziyat yanada murakkablashadi. Ushbu holatdaGipotetik xarakterdagi qo'shimcha farazlar haqiqatdir. Tadqiqot ob'ekti uchun ushbu faraziy modelni o'rganish natijalarishartli xarakterga ega. Ularning ahamiyati boshlanaditaxminlarning qanchalik to'g'riligiga bog'liq. Ularni sinab ko'rish uchun modelni o'rganish natijalarini o'rganilayotgan ob'ekt haqidagi barcha ma'lumotlar bilan solishtirish kerak. Hisoblangan va eksperimental ma'lumotlarning yaqinligi Gipotetik modelning sifati
dastlabki taxminlarning to'g'riligi yoki xatosi haqidahaqida fikr yuritishga imkon beradi. Shunday qilib, qon matematik model tomonidan ko'rib chiqilayotgan ob'ektni o'rganishga tayyorQo'llash muammosi oddiy matematik masala emas va shundaydirmatematik usullar bilan yechish mumkin emas. Haqiqatning asosiy mezoni keng ma'noda eksperimentdir,
operatsiya. Harakat mezoni barcha faraziy modellarni solishtirish va ulardan eng oddiyini topish,bir vaqtning o'zida kerakli aniqlikda o'rganilmoqda ob'ekt xususiyatlarini to'g'ri aks ettirishni farqlash imkonini beradi.
Mapleda yunon alifbosidan ham foydalanish mumkin. Buning uchun satrga yunoncha harfning nomi yoziladi, bosh harf bilan yozish uchun yunoncha harfning nomi bosh harf bilan yozilishi kerak.Masalan.
|
|
|
|
|
|
ε-epsilon |
ζ-zeta |
η-eta |
θ-teta |
|
ι-ita |
κ-kappa |
Κ-Kappa |
λ-lambda |
|
μ-mu |
ν-nu |
ξ-xi |
ο-omikron |
|
π-pi |
ρ-rho |
Σ-Sigma |
σ-sigma |
|
τ-tau |
υ-uosilon |
φ-phi |
χ-chi |
|
ψ-psi |
ω-omega |
Γ-Gamma |
Ω-Omega |
Matematik ifodalar shaklini o'zgartirish.
Айрим кўп учрайдиган командалар ва уларга доир мисоллар келтирамиз.
|
|
Команда |
Маъноси |
Параметрланинг маъноси |
|
1 |
expand(eq) |
Қавсларни очиб ёйиш |
еq-ифода |
|
2 |
faсtor(eq) |
Кўпҳадни кўпайтувчиларга ажратиш |
|
|
3 |
normal(eq) |
Касрни нормал кўринишга келтириш |
|
|
4 |
collect(eq, var) |
Ўхшаш ҳадларни ихчамлаш |
var-ўзгарувчи |
|
5 |
simplify(eq {,option}) |
Ифодаларни соддалаштириш |
option-параметр |
|
6 |
combine(eq, param) |
Даражаларни бирлаштириш ёки тригонометрик ифодаларни даражаларини пасайтириш |
param=trig, param=power,
|
|
7 |
radnormal(eq) |
Илдиз, даражали ифодаларни соддалаштириш |
|
|
8 |
convert(eq,param) |
Ифода param типли ифодага алмаштирилади |
param- тип параметр param=sincos, param=tan, param=vector, param=string, param=termin |
|
9 |
subs(g(x)=t, f) |
f(x) да g(x)=t деб ўзгарувчини алмаштириш |
|
Mustaqil ishlash uchun misollar
1-misol
> 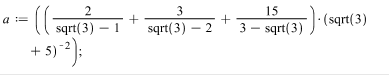
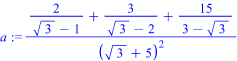
> ![]()
![]()
2-misol
> 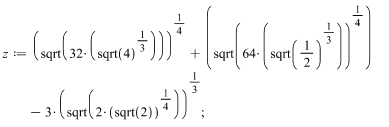
![]()
> ![]()
![]()
> ![]()
3-misol
> ![]()
![]()
> ![]()
![]()
> ![]()
![]()
4-misol
> ![]()
![]()
5-misol
> ![]()
![]()
> ![]()
![]()
6-misol
> 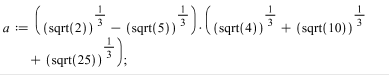
![]()
> ![]()
![]()
7-misol
> ![]()
![]()
8-misol
> ![]()
![]()
Xulosa:
Men bu amaliy mashg’ulot tufayli Maple12 dasturida sodda matematik amallarni hisoblarni ,arifmetik amallarni hisoblashni kurib chiqdim .Maple12 dasturi hech qachon matematik ifodalarni xato hisoblamaydi,lekin o’zimiz hisoblab chiqsak xato ishlashimiz mumkin.Birmuncha oson hisoblanadi Maple12 dasturida va vaqtimizni tejashga sabab bo’ladi.
Foydalanilgan adabiyotlar
1. Матросов А. Решение задач математики и механики в среде Maple 6. СПб.: Питер, 2000.
2. В.З. АЛАДЬЕВ. Основы программирования в Maple. Таллинн, 2006.
3. Основы использования математического пакета Maple в моделировании: Учебное пособие / Международный институт компьютерных технологий. Липецк, 2006. 119с.
4. Дьяконов В. Maple 6. Учебный курс СПб.: Питер, 2001.
5. Аладьев В.З., Лиопо В.А., Никитин А.В. Математический пакет Maple в физическом моделировании.- Гродно: Гродненский госу-дарственный университет им. Янки Купалы, 2002, 416 с.
6. O’runbayev E., Murodov F. Kompyuter algebrasi tizimlarining amaliy tadbiqlari. –SamDU nashri – Samarqand, 2003, 96 s.
7. Аладьев В.З., Богдявичюс М.А. Решение физико-технических и математических задач с пакетом Maple V.- Вильнюс: Изд-во Техника, 1999, 686 c., ISBN 9986-05-398-6.
8. Аладьев В.З., Богдявичюс М.А. Maple 6: Решение математичес-ких, статистических и инженерно-физических задач.- Москва: Лаборатория Базовых Знаний, 2001, 850 с. + CD-ROM, ISBN 5-93308-085-X.
9. Математика на компьютере: Maple 8. — М.: СОЛО
O’ZBEKISTON RESPUBLIKASI
OLIY VA O’RTA-MAXSUS TA’LIM VAZIRLIGI
SAMARQAND DAVLAT UNIVERSITETI
RAQAMLI TEXNOLOGIYALAR FAKULTETI
AMALIY MATEMATIKA INFORMATIKAYO’NALISHI
204- guruh talabasi
Xo’jamurodov Sh
Kompyuter algebrasining MALAKAYIY AMALIYOT HISOBOTI
“CHIZIQLI TENGLAMALAR SISITEMASINI YECHISH” amaliyoti bo’yicha
HISOBOTI
Tekshirdi:RO’ZIYEVA.M
Bajardi: Xo’jamurodov Sh
2-Mavzu:Chiziqli tenglamalarsistemasini yechishga keltiriluvchi amaliy masalalar va ularni matematik tizimlardan foydalanib yechish.
Reja:
Kirish.
1.Chiziqli tenglamalar sistemasini Gauss usulida hisoblash
2.Chiziqli tenglamalar sistemasini Kramer usulida hisoblash
3.Matritsa tenglamasini teskari matritsa toppish usulida hisoblash
Xulosa .
Foydalanilgan adabiyotlar.
18-variant
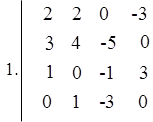
![]()
2.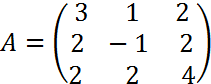 ,
, 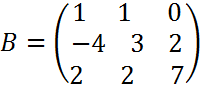 ,
, ![]()
3. a)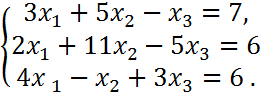 , b)
, b)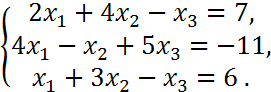
4.a)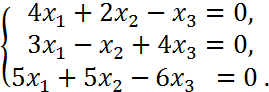 , b)
, b)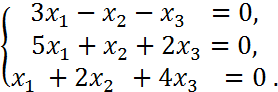
Maple 12 da savolning javobi
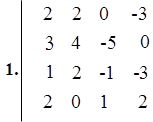
![]()
> A:=array(1..4,1..4,[[2,2,0,-3],[3,4,-5,0],[1,0,-1,3],[0,1,-3,0]]);
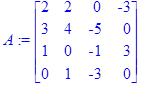
2-misol
2.A 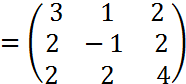 ,
, 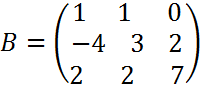 ,
, ![]()
> A:=matrix([[3,1,2],[2,-1,2],[2,2,4]]);
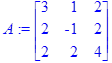
> B:=matrix([[1,1,0],[-4,3,2],[2,2,7]]);
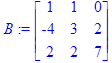
3. a)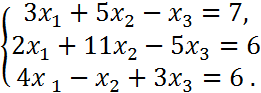
chiziqli tenglamalar sistemasini umumiy va bitta xususiy yechimini topish:
> eq:={3*x1+5*x2-x3=7,2*x1+11*x2-5*x3=6,4*x1-x2+3*x3=6}:
> s:=solve(eq,{x1,x2,x3});
![]()
Xususiy yechimini topish uchun subs komandasidan foydalanib bitta uzgaruvchi qiymatini umumiy yechimga qo’yish kerak
> subs({x1=10,x2=1,x3=18},s);
![]()
b) )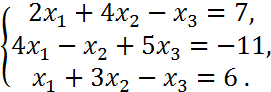
chiziqli tenglamalar sistemasini umumiy va bitta xususiy yechimini topish:
> eq:={2*x1+4*x2-x3=7,4*x1-x2+5*x3=-11,x1+3*x2-x3=6}:
s:=solve(eq,{x1,x2,x3});
![]()
Xususiy yechimini topish uchun subs komandasidan foydalanib bitta uzgaruvchi qiymatini umumiy yechimga qo’yish kerak
> subs({x1=-1,x2=2,x3=-1},s);
![]()
4.a)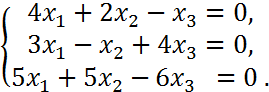
chiziqli tenglamalar sistemasini umumiy va bitta xususiy yechimini topish:
> eq:={4*x1+2*x2-x3=0,3*x1-x+4*x3=0,5*x1+5*x2-6*x3=0}:
s:=solve(eq,{x1,x2,x3});
![]()
Xususiy yechimini topish uchun subs komandasidan foydalanib bitta uzgaruvchi qiymatini umumiy yechimga qo’yish kerak
> subs({x1=0,x2=0,x3=0},s);
![]()
b)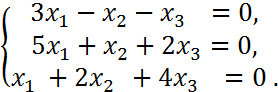
chiziqli tenglamalar sistemasini umumiy va bitta xususiy yechimini topish:
> eq:={3*x1-x2-x3=0,5*x1+x2+2*x3=0,x1+2*x2+4*x3=0}:
s:=solve(eq,{x1,x2,x3});
![]()
Xususiy yechimini topish uchun subs komandasidan foydalanib bitta uzgaruvchi qiymatini umumiy yechimga qo’yish kerak
> subs({x1=-0x2=0,x3=-0},s);
![]()
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.