
Аналитическая
и геометрическая модели
числового промежутка
Цели: ввести понятие числового промежутка как геометрической модели числового неравенства; рассмотреть различные виды числовых промежутков; формировать умения изображать на координатной прямой числовой промежуток и множество чисел, удовлетворяющих неравенству.
Ход урока
I. Организационный момент.
II. Устная работа.
1. Назовите верное неравенство, которое получится, если:
а) к обеим частям неравенства –1 < 3 прибавить число 4; число –2;
б) из обеих частей неравенства –15 < –2 вычесть число 3; число –5;
в) обе части неравенства 6 > –1 умножить на 8; на –5;
г) обе части неравенства 9 < 27 разделить на 9; на –3; на –1.
2. Заполните пустые квадратики:
а) 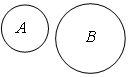 б)
б)
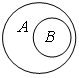 в)
в)
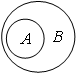
А ![]() В =
В = ![]() А
А
![]() В =
В = ![]() А
А
![]() В =
В = ![]()
III. Объяснение нового материала.
1. А к т у а л и з а ц и я з н а н и й.
Напоминаем учащимся, что алгебра, в частности, занимается тем, что описывает различные реальные ситуации на математическом языке в виде математических моделей, а затем имеет дело уже не с реальными ситуациями, а с этими моделями, используя разные правила, свойства, законы, выработанные в алгебре.
Математические модели бывают не только алгебраические (в виде числового равенства, уравнения, неравенства), но и словесные (в виде словесного описания реальной ситуации), графические (в виде схемы, графика, чертежа). Учащиеся уже знакомы со всеми этими видами моделей. Напоминаем, что алгебраическую модель ещё называют аналитической, а графическую – геометрической. Чтобы свободно оперировать любыми видами математических моделей, нужно учиться переходить от одного из них к другому.
Н а п р и м е р:
|
Словесная модель № 1 |
Аналитическая |
Геометрическая |
Словесная модель № 2 |
|
b больше а |
b > a |
|
Точка с координатой b |
2. В в е д е н и е н о в о г о п о н я т и я.
Работаем с представленными выше моделями, причём идём в обратном порядке: от словесной модели № 2 к словесной модели № 1.
Возьмём произвольную точку х на координатной прямой, причём эта точка лежит между точками a и b. Это означает, что ей соответствует число х, которое больше a и меньше b, то есть a < x < b. Верно и обратное: для любой точки, лежащей между точками a и b, будет выполняться это неравенство.
О п р е д е л е н и е: Множество чисел,
удовлетворяющих условию
a < x < b, называют интервалом и
обозначают так: (a; b).
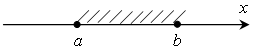
На рисунке (геометрическая модель) это множество изображают в виде:
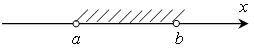
Светлые кружочки означают, что числа a и b не принадлежат этому множеству.
Аналогично вводим определения отрезка, полуинтервала, числового луча, открытого числового луча и числовой прямой.
О п р е д е л е н и е: Числовые отрезки, интервалы, полуинтервалы, числовые лучи, открытые числовые лучи и числовая прямая называются числовыми промежутками.
3. О п е р а ц и и с р а з л и ч н ы м и м о д е л я м и.
Рассматриваем на с. 173 учебника таблицу, в которой представлены такие модели числовых промежутков, как:
– аналитическая (неравенство, задающее числовой промежуток), например: a ≤ x ≤ b;
– словесная (обозначение и название числового промежутка), например: [a; b] – числовой промежуток от a до b;
– геометрическая (изображение числового промежутка на координатной прямой), например:
IV. Формирование умений и навыков.
Все упражнения, решаемые на этом уроке,
можно разбить на т р и
г р у п п ы:
1) Изобразить на координатной прямой числовой промежуток по его обозначению (создание геометрической модели).
2) Назвать числовой промежуток, изображённый на координатной прямой, и обозначить его (создание словесной модели).
3) Изобразить на координатной прямой множество чисел, удовлетворяющих неравенству, и записать неравенство, соответствующее изображенному или обозначенному числовому промежутку (переход от аналитической к геометрической модели и наоборот).
О с о б о е в н и м а н и е уделяем:
– правильным формулировкам;
– верному использованию круглых и квадратных скобок при обозначении числового промежутка;
– верному использованию светлых кружков («выколотых» точек) и тёмных при изображении числовых промежутков на координатной прямой.
1. № 812 (а, б, д, е), № 813, № 814.
2. № 815 (а, г), № 816 (в, г).
Р е ш е н и е
№ 815.
а) х ≥ –2; ![]() ; [–2;
+∞).
; [–2;
+∞).
г) х < –5; ![]() ; (–∞;
–5).
; (–∞;
–5).
№ 816.
в) –5 ≤ х ≤
–3![]() ;
; 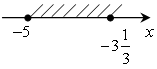 ;
; 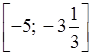 .
.
г) 2 < х ≤
6,1; ![]() ; (–2; 6,1].
; (–2; 6,1].
3. № 817 (а) – устно, № 819 (а, в).
Р е ш е н и е
№ 819.
а) ![]() ≈
1,4,
≈
1,4, ![]()
![]() (1,5; 2,4).
(1,5; 2,4).
в) ![]() ≈
2,2,
≈
2,2, ![]()
![]() (1,5; 2,4).
(1,5; 2,4).
4. Задайте неравенством числовой промежуток:
а) 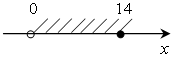 ж)
х
ж)
х ![]() [2;7,3];
[2;7,3];
б) 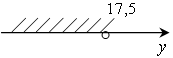 з)
y
з)
y ![]() (–∞; 100);
(–∞; 100);
в) 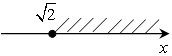 и)
х
и)
х ![]() (–8,3; 0];
(–8,3; 0];
г) 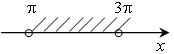 к)
y
к)
y ![]() (0; +∞);
(0; +∞);
д) 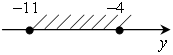 л)
х
л)
х ![]() (–15; –4);
(–15; –4);
е) 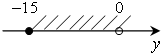 м)
y
м)
y ![]() [–60; 100).
[–60; 100).
Р е ш е н и е
а) 0 < x ≤ 14; ж) 2 ≤ х ≤ 7,3;
б) y < 17,5; з) у < 100;
в) x ≥![]() ; и)
–8,3 < x ≤ 0;
; и)
–8,3 < x ≤ 0;
г) π < x < 3π; к) у > 0;
д) –11 ≤ у ≤ –4; л) –15 < x < –4;
е) –15 ≤ у < 0; м) –60 ≤ у < 100.
V. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Что называется числовым промежутком?
– Какие виды числовых промежутков существуют?
– Как выглядит геометрическая модель числового промежутка?
– Как записать аналитическую модель числового промежутка с помощью неравенства?
Домашнее задание: № 812 (в, г, ж, з), № 815 (б, в), № 816 (а, б), № 817 (б), № 819 (б, г).
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.