
Содержание
Введение…………………………………………………………………………………...2
Анализ особенностей вероятностно-статистического метода прогнозирования …….3
Исследование и модернизация экстраполяционного метода прогнозирования……...6
Разработка причинно-следственного метода прогнозирования……………………...27
Системная организация мониторинга технического состояния оборудования……..72
Заключение……………………………………………………………………………….74
Список используемых источников……………………………………………………..77
Введение
Возможность заглянуть в будущее всегда являлась не только абстрактной мечтой человечества, но и предпосылкой эффективного принятия решений в самых разных направлениях практической деятельности. Вряд ли стоит объяснять, что для рассматриваемой задачи малопригодны пришедшие из глубокой древности заведомо ненаучные и псевдонаучные подходы – гадание по дыму жертвенного костра, по полёту птиц, по кофейной гуще, прогнозы с использованием методов астрологии и нумералистики, ясновидение и прочая чепуха, основанная на человеческом невежестве и глупости. Научный подход заключается в применении фактографических методов прогнозирования, ориентированных на обработку совокупности измеренных параметров и харак- теристик объекта.
Вероятностно-статистический метод предусматривает использование в качестве прогнозной базы статистических характеристик накопленных массивов наблюдений за поведением объекта Применение этой концепции в задаче прогнозирования обусловле- но развитием теории вероятностей и математической статистики. Информационную базу составляют оценки результатов ускоренных ресурсных испытаний, обобщение опыта эксплуатации (и в том числе, статистика отказов, аварий и рекламаций) и предремонтной дефектации судового оборудования.
Собственно прогнозированию предшествует предварительная статистическая об- работка результатов наблюдений – оценка однородности выборки и отбрасывание край- них членов, подбор закона распределения, вычисление основных статистических пара- метров (математического ожидания, дисперсии, среднеквадратичного отклонения, мо- ментов), построение функций распределения и плотности вероятностей. Эти функции могут быть использованы для решения прогнозных задач, которые могут быть сформу- лированы следующим образом:
− какова вероятность того, что данный агрегат проработает без отказа
|
заданный период времени, т.е.: |
1- |
Pотк A< X <B |
= ? |
− какой период времени проработает данный агрегат при заданной вероятности безот- казной работы?
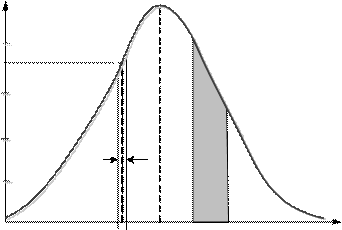
Для решения первой задачи целесообразно использовать плотность вероятностей (рис. 6.1) и применить выражение 6.1, а для решения второй задачи – функцию распреде- ления (рис. 6.2) и выражение 6.2:
 f(x)т
f(x)т
0 , 004
f(t)
0,003
0,002
dX
0,001
B
P отк =
A<X <B ò
A
f (x) dX
|
(15.1)
![]()
![]()
![]() 0 М Наработка, ч
0 М Наработка, ч
Рисунок 6.1− Пример применения плотности вероятностей для оценки вероятности отказа оборудования при заданной наработке
 1,0
1,0
F(t2 )
F(t1 )
0 t1 t2
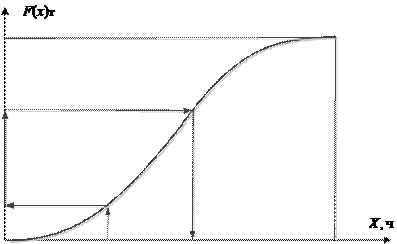
Рисунок 6.2− Пример применения функции распределения для оценки наработки при заданной вероятности безотказной работы оборудования
При заданной вероятности безотказной работы оборудования на временном интер- вале t1 ÷ t2 нетрудно найти вероятность отказа на этом же интервале:
Ротк =1 - Рботк (6.2)
Из определения функции распределения (Рt – это вероятность того, что событие случит- ся ранее момента t) следует, что при t1<t<t2 Ротк = F(t2) – F(t1) (6.3)
Нетрудно видеть, что наличие функции распределения и совместное использование выражений 6.2 и 6.3 позволяет достаточно просто решить поставленную задачу:
− с помощью выражения 6.2 найти вероятность отказа Ротк на интервале t1 - t2;
− для заданного начала эксплуатационного периода оборудования (например, начала рейса судна) с помощью функции распределения (рис. 6.2) найти значение F(t1);
− используя выражение 15.3 найти значение F(t2) = F(t1) + Ротк ; (6.4)
− для определённого значения F(t2) с помощью функции распределения найти время окончания эксплуатационного периода t2 .
Понятно, что ключевыми моментами применимости рассмотренного метода явля- ется наличие достаточно представительной выборки параметра, характеризующего фак- тическую эксплуатационную надёжность оборудования, например, наработки на отказ, и соответствующего программного обеспечения, предназначенного для статистической обработки этой выборки с целью определения вида закона распределения.
Автором разработана специальная компьютерная программа, обеспечивающая решение этой задачи в режиме диалогового общения с персональным компьютером [405]. Пример применения этой программы приведён в Приложении 6.
Программа позволяет подтвердить соответствие статистических данных о нара- ботках на отказ партии судовых насосов заданному закону распределения и определить основные параметры распределения, которые могут быть использованы для статистиче- ских оценок надёжности (например, прогнозирования долговечности) соответствующе- го оборудования в процессе эксплуатации.
Вместе с тем, следует заметить, что вероятностно-статистический метод прогно- зирования достаточно эффективен в тех случаях, когда анализируемое изделие выпуска- ется в массовом количестве и срок его службы сравнительно невелик, благодаря чему возможно в приемлемые сроки накопить представительную выборку статистических данных об отказах оборудования.
Для большинства видов судостроительного оборудования характерны мелкосе- рийное (а иногда и уникальное) производство и большие сроки службы. В связи с этим статистические данные в большинстве случаев оказываются либо недостаточно пред- ставительными, либо уже сильно устаревшими: к моменту завершения сбора статисти- ческих данных наблюдаемое оборудование уже выработало бóльшую часть своего ре- сурса и подлежит замене, а для новых типов оборудования статистика, относящаяся к устаревшему оборудованию, оказывается уже малопригодной.
Кроме того, вероятностный характер прогнозов, отягощенных, как правило, су- щественной дисперсией из-за значимых для судового оборудования коэффициентов ва- риации ресурса, ограничивает область применения этих методов оценками групповых осреднённых эксплуатационных показателей долговечности оборудования (например, парка однотипных изделий). Достоверный индивидуальный прогноз изменений техни- ческого состояния конкретного механизма или агрегата этим методом получить сложно.
Этот метод приспособлен для индивидуальных прогнозов, поскольку в качестве базы прогнозирования используется временной ряд наблюдений за изменением пара- метра (совокупности параметров) конкретного объекта.
Исходной предпосылкой является предположение о том, что изменение контро- лируемого параметра во времени подчиняется некоторому детерминированному закону, который сохраняется неизменным как на интервале наблюдений за объектом (базовом прогнозном периоде), так и на интервале прогнозирования. Располагая аналитическим описанием этого закона, можно, в принципе, оценить ожидаемые изменения параметра (характеристики технического состояния оборудования) путём обычной экстраполяции. При этом предполагается, что неизбежные случайные флуктуации временнóго ряда можно довести до приемлемого уровня дисперсии известными статистическими мето- дами сглаживания [106] .
В соответствие с этой концепцией прогноз изменения состояния объекта предусматрива- ет последовательное выполнение ряда этапов:
− выбор контролируемой характеристики состояния объекта;
− накопление результатов измерения выбранного параметра на заданном временном интервале (периоде основания прогноза), т.е. формирование временного ряда;
− аппроксимация временного ряда с целью выявления детерминированного
закона изменения параметра во времени и оценка статистических характеристик слу- чайных отклонений, обусловленных флуктуациями процесса и погрешностями изме- рений;
− экстраполяция – применение установленного закона для определения прогнозируемо- го значения параметра при заданном приращении времени;
− оценка ожидаемой случайной погрешности прогноза на основании статистических характеристик временного ряда.
Следует отметить, что способы математической обработки временного ряда могут быть различными: экспоненциальное сглаживание, выявление тренда (оценка первой
производной), аппроксимация с помощью L-интегрирования и метода наименьших квадратов и т.п.
Последний способ пригоден как для квазилинейных, так и для существенно нели- нейных законов.
Аппроксимации временнóго ряда включает три процедуры:
− выбор типа аппроксимирующей функции;
− вычисление численных значений её коэффициентов (например, методом наименьших квадратов);
− оценка адекватности аппроксимации.
При выборе типа аппроксимирующей зависимости современные компьютерные программы часто используют библиотеки типовых функций. Последовательно переби- рая типовые функции, вычисляя для них соответствующие числовые коэффициенты ме- тодом наименьших квадратов и оценивая погрешности аппроксимации, программа вы- бирает наиболее пригодную аппроксимирующую функцию. Более рациональным пред- ставляется применение программ, обеспечивающих поиск аппроксимирующих функций с помощью специальных преобразований временного ряда наблюдений, например, пе- реходом в фазовую плоскость в результате L- или I-преобразований [107].
На рис. 6.3 показано, каким образом экстраполяция такой функции может быть использована для оценки интервала времени до наступления предельного значения кон- тролируемого параметра объекта.

![]() Момент формирования прогноза Время эксплуатации Т
Момент формирования прогноза Время эксплуатации Т
Рисунок 6.3 − Экстраполяционный метод оценки остаточного ресурса оборудования
Применение анализа временных рядов внешних (выходных) характеристик объ- екта придаёт этим методам свойства универсальности, поскольку применяемые алго- ритмы абстрагированы от физической природы объекта, не требуют знаний его внут- ренней структуры и функциональных связей между входными и выходными параметра- ми.
В данном разделе анализируются особенности применения метода, в основе кото- рого лежит обработка результатов мониторинга диагностического параметра, характе- ризующего техническое состояние контролируемого узла [107].
Реализация этого метода предусматривает последовательное выполнение ряда этапов:
- выбор главного диагностического параметра y, в наибольшей степени характеризу- ющего техническое состояние объекта и его работоспособность;
- организация измерений этого параметра через заданные временные интервалы Δt и накопление результатов в процессе эксплуатации объекта;
- сглаживание полученной последовательности результатов измерений - временного ряда y(t) с целью подавления влияния случайных отклонений параметра, не связан- ных с изменением технического состояния объекта;
- аппроксимация сглаженного временного ряда, т.е. формирование его аналитического описания с помощью функции Y(t), аргументом которой является время;
- экстраполяция аппроксимирующей функции на предстоящий период эксплуатации с целью прогнозирования интервала времени до наступления предельного состояния объекта (т.е. остаточного ресурса);
- корректировка аппроксимирующей функции и уточнение прогноза по мере накопле- ния результатов измерения определяющего параметра.
В течение времени τ формирование ряда наблюдений может происходить путём периодических измерений контролируемого параметра y через интервалы времени Δt. В этом случае количество результатов измерений n= τ/Δt. Обычно достаточно иметь объём выборки временного ряда: n = 10÷15 (условие Δt = idem не является обязательным).
Как правило, полученный таким образом временной ряд y(t), представленный множеством пар {yi; ti} при i = 1,2,…, n, имеет на плоскости (y, t) существенный разброс
точек, обусловленный неучтёнными изменениями режимов и условий эксплуатации объекта, а также случайными погрешностями измерений. Это обстоятельство суще- ственно затрудняет выдвижение гипотезы о подходящем типе аппроксимирующей функции (функции тренда) Y(t).
Выполнение операции последовательного интегрального сглаживания временного ряда обеспечивает получение двух дополнительных множеств: {xi; ti} и {zi; ti}, где xi и zi
– результаты применения, соответственно, I- или L-операторов. Дополнительные мно- жества позволяют принять к рассмотрению фазовые плоскости (y – x) и (y – z), на кото- рых будут располагаться точки, соответственно, с координатами yi, xi и yi, zi. Во многих случаях расположение точек в фазовых плоскостях можно достаточно точно описать линейной зависимостью:
y(t) = a0+a1I[y(t)]k (6.7)
или y(t) = a0+a1L[y(t)]k , (6.8)
где оценки коэффициентов a0 и a1 вычисляются методом наименьших квадратов. Зави- симости (6.17) и (6.18) являются интегральными уравнениями, решения которых имеют при k = 1, соответственно, следующий вид:
Y(t) = a0 exp(a1t) (6.9)
или Y(t) = a0/(1 – a1t)2 (6.10)
Полученные выражения можно использовать в качестве аппроксимирующих функ- ций. Их коэффициенты имеют следующий физический смысл:
a0 – величина начального дефекта, выполняющего роль инициатора процесса дегра- дации работоспособности объекта;
a1 – параметр тренда, характеризует интенсивность процесса.
При известном допустимом значении контролируемого параметра можно с помощью аппроксимирующей функции вычислить момент наступления предельного состояния
объекта (разумеется, если на прогнозируемом периоде сохраняется неизменным пара- метр тренда a1).
В тех случаях, когда расположение точек на фазовой плоскости может быть описа- но несколькими аппроксимирующими функциями, выбирают ту из них, которая имеет наибольшее значение коэффициента парной корреляции ρ при наименьшем значении среднеквадратичного отклонения σ аппроксимирующей функции. Граничным значени- ем коэффициента корреляции, ниже которого аппроксимирующая функция не принима- ется к рассмотрению, можно принять ρ = 0,707. Данному значению соответствует равен- ство мощностей измеряемого сигнала и случайных погрешностей (шума).
Если ни на одной из рассмотренных фазовых плоскостей не удаётся обеспечить выполнение этого условия, выполняется операция повторного сглаживания временного ряда, т.е. двукратное интегрирование.
Повторное сглаживание временного ряда увеличивает коэффициент корреляции с сохранением содержательности аппроксимирующей функции, правда при этом сама функция несколько усложняется.
В рассматриваемом примере объектом мониторинга являлись подшипники качения и скольжения с начальными дефектами – выбоинами на контактной поверхности [108] (рис. 6.4 и 6.5).
Испытания проводились на стенде АР7000 (рис.6.5).
 |
Рисунок 6.5 − Стенд АР7000 для виброиспытаний подшипников
1−электродвигатель; 2−преобразователь частоты; 3−блок управления; 4−блок АЦП; 5−вихретоковые датчики; 6−упругая муфта; 7−опоры с подшипниками; 8,9−кронштейны с вихретоковыми датчиками; 10−съёмный маховик; 11−кронштейн для закрепления вихретоковых датчиков фазы и биения.
Режим нагружения подшипников задавался частотой вращения, радиальными и осевыми усилиями на подшипниках. Кроме того, конструкция стенда обеспечивала нагружение подшипников в условиях перекоса и дисбаланса валов.
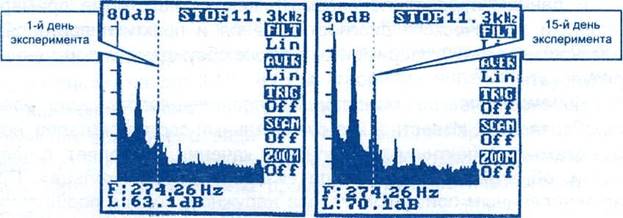 |
Рисунок 6.6 − Изменение уровня вибрации подшипника на характерной частоте спектра, вызванное износом подшипника
При испытаниях подшипника качения электродвигатель стенда работал в течение 20 суток в повторно-кратковременном режиме (по 1,5 ч в сутки).
На 20-й день эксперимента произошёл отказ подшипника. На рис. 6.6 показано из- менение спектра вибрации, видимое на дисплее прибора, а в табл.6.1 представлены ре- зультаты измерений.
|
№ замера |
1 |
2 |
3 |
4 |
5 |
|
Наработка t, ч |
1,5 |
3,0 |
4,5 |
6,0 |
7,5 |
|
Уровень вибрации y, дБ |
67,6 |
68,0 |
68,2 |
67,5 |
68,0 |
|
№ замера |
6 |
7 |
8 |
9 |
10 |
|
Наработка t, ч |
9,0 |
10,5 |
12,0 |
13,5 |
15,0 |
|
Уровень вибрации y, дБ |
68,8 |
70,0 |
70,2 |
70,8 |
71,0 |
|
№ замера |
11 |
12 |
13 |
14 |
15 |
|
Наработка t, ч |
16,5 |
18,0 |
19,5 |
21,0 |
22,5 |
|
Уровень вибрации y, дБ |
72,0 |
71,2 |
73,4 |
73,0 |
74,4 |
|
№ замера |
16 |
17 |
18 |
19 |
20 |
|
Наработка t, ч |
24,0 |
25,5 |
27,0 |
28,5 |
30,0 |
|
Уровень вибрации y, дБ |
74,0 |
75,0 |
76,0 |
76,1 |
76,0 |
В рассматриваемой задаче целью мониторинга является прогнозирование работо- способности объекта, поэтому на основе результатов эксперимента была выполнена следующая операция: из исходного временнóго ряда y(t) были взяты 10 первых резуль- татов и эту выборку отнесли к периоду предварительных наблюдений. На основании выборки на 10-й день эксперимента (при фактической наработке подшипника t = 15 ч) была сделана попытка спрогнозировать дальнейшее развитие событий и оценить оста- точный ресурс подшипника.
Сглаживание временнóго ряда из 10 наблюдений при k = 1 и k = 2 наблюдений при показало, что линейная аппроксимация в фазовой плоскости обеспечила наиболь- шее значение коэффициента линейной корреляции ρ = 0,9309 при наименьшем средне- квадратичном отклонении σ = 0,98. При этом была получена следующая аппроксимиру- ющая функция:
Y(t) = 66,7/(1 – 0,002t) (6.14)
Вычисленный с помощью этой функции прогноз математического ожидания оставшейся до отказа наработки составил 31,5 часов. Как видно, ошибка прогноза соста- вила Δt = 1,5 часа в сторону запаздывания. Правда, если учесть ширину зоны разброса прогнозных оценок, обусловленную среднеквадратическим отклонением аппроксими- рующей функции σY = 0,48, то запаздывание окажется меньше. Задача прогнозирования может быть сформулирована и другим образом: какое значение будет иметь контроли- руемый параметр через заданный временной период эксплуатации объекта? Применение аппроксимирующей функции (6.14) для наработки t = 30 часов даёт результат Y(30)
=75,5 дБ (расхождение с экспериментальными данными – 0,5дБ). Такая точность вполне достаточна для вынесения достоверного прогноза об изменении состояния контролиру- емого узла.
Отмечая сравнительную простоту реализации алгоритма прогнозирования, преду- сматривающего мониторинг только одного диагностического параметра, нельзя не от- метить и его существенный недостаток: неприспособленность к мониторингу многоре- жимных объектов. А между тем режим работы объекта (например, частота вращения ротора) в моменты очередных замеров диагностического параметра (например, уровня вибрации) может существенно влиять на результаты измерений. Это обстоятельство де- лает актуальной рассматриваемую далее доработку экстраполяционного алгоритма с це- лью обеспечения его универсальности [376].
Корректировка алгоритма однопараметрического экстраполяционного прогнозирования методом Эйлера
Рассмотренный выше алгоритм однопараметрического прогнозирования преду- сматривает в процессе формирования временного ряда автоматическое вычисление вре- мени проведения следующего измерения (см. рис. 6.15). Реальные технические объекты в назначенный момент измерения могут находиться, как минимум, в двух состояниях:
«включён» - «выключен». Поскольку контроль режима однопараметрическим алгорит- мом не предусматривается, диагностическая система будет автоматически проводить измерения и на неработающем механизме. Полученные при этом близкие к нулевым значения вибрации приведут к сильному искажению экспериментального временного ряда наблюдений, показанного на рис. 6.10 (он получен при сохранении постоянного режима работы стенда).
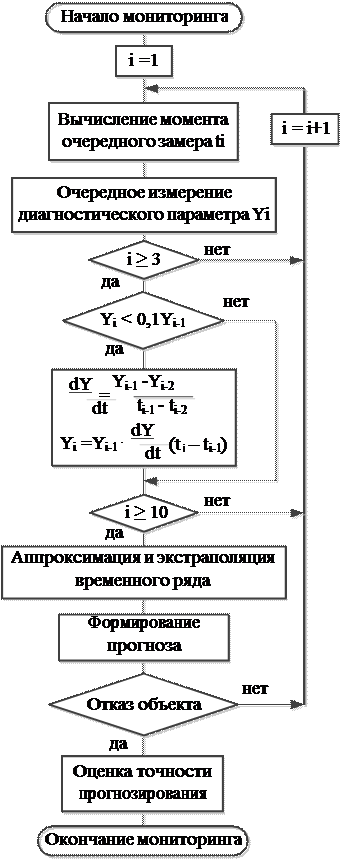
Для устранения этого эффекта предложено использовать откорректированный ал- горитм, показанный на рис. 6.12
 Рисунок
6.12 (слева) – Алгоритм однопараметрического экстраполяци- онного прогнозирования, откорректиро-
Рисунок
6.12 (слева) – Алгоритм однопараметрического экстраполяци- онного прогнозирования, откорректиро-
Алгоритм предусматривает выяв- ление заведомо ложных результатов измерений, выполненных на неработа- ющем объекте, путём их сравнения с
предыдущими полноценными измере-
ниями, и замену их на значения, вычис- ленные по методу Эйлера (т.е. с исполь- зованием тренда, вычисленного по предыдущим замерам).
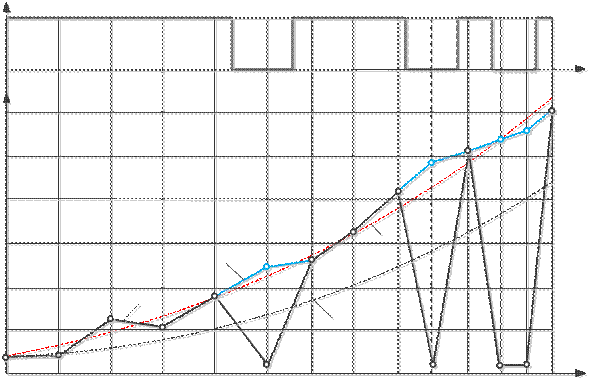
На рис. 6.13 показан пример примене- ния откорректированного алгоритма.
 100
100
0
12,0
n, %
![]()
Режимы работы механизма
t, час
10,0
Aк
8,0
Yк
6,0
Yи![]()
4,0
2,0
t, час
1 2 3 4 5 6 7 8 9 10 11 12 13 14
Номера замеров диагностического параметра
Рисунок 6.13 – Результаты применения алгоритма однопараметрического экстраполяционного прогнозирования, откорректированого по методу Эйлера
Yи и Yк измеренный и откорректированный временные ряды;
Аи и Ак аппроксимация измеренного и откорректированного рядов.
На рисунке 6.13 результаты 6-го измерения откорректированы по тренду на участке 4-5, 10-го измерения по тренду на участке 8-9 и 12, 13 по тренду на участке 10-11.
|
№ изм. |
Измеренный ряд (дБ) |
Откорректированный ряд (дБ) |
||||||
|
Yи |
Aи |
Δи =Yи -Aи |
(Δи)2 |
Yк |
Aк |
Δк =Yк -Aк |
(Δк)2 |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1 |
0,8 |
0,8 |
0,0 |
0,00 |
0,8 |
0,8 |
0,0 |
0,00 |
|
2 |
0,9 |
0,9 |
0,0 |
0,00 |
0,9 |
1,2 |
-0,3 |
0,09 |
|
3 |
2,5 |
1,2 |
1,3 |
1,69 |
2,5 |
1,9 |
0,6 |
0,36 |
|
4 |
2,1 |
1,5 |
0,6 |
0,36 |
2,1 |
2,7 |
-0,6 |
0,36 |
|
5 |
3,5 |
2,0 |
1,5 |
2,25 |
3,5 |
3,5 |
0,0 |
0,00 |
|
6 |
0,5 |
2,8 |
-2,3 |
5,29 |
5,0 |
4,4 |
0,6 |
0,36 |
|
7 |
5,2 |
3,4 |
1,8 |
3,24 |
5,2 |
5,3 |
-0,1 |
0,01 |
Окончание таблицы 6.2
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
8 |
6,5 |
4,1 |
2,4 |
5,76 |
6,5 |
6,4 |
0,1 |
0,01 |
|
9 |
8,5 |
5,0 |
3,5 |
12,25 |
8,5 |
7,5 |
1,0 |
1,00 |
|
10 |
0,5 |
5,7 |
-5,2 |
27,04 |
9,5 |
8,6 |
0,9 |
0,81 |
|
11 |
10,3 |
6,5 |
3,8 |
14,44 |
10,3 |
9,5 |
0,8 |
0,64 |
|
12 |
0,5 |
7,2 |
-6,7 |
44,89 |
10,8 |
10,8 |
0,0 |
0,00 |
|
13 |
0,5 |
8,0 |
-7,5 |
56,25 |
11,2 |
11,7 |
-0,5 |
0,25 |
|
14 |
12,2 |
8,8 |
3,4 |
11,56 |
12,2 |
12,6 |
-0,4 |
0,16 |
|
Σ(Δи)2 (дБ)2 |
185 |
Σ(Δк)2 (дБ)2 |
4 |
|||||
|
Dи =[Σ(Δи)2]/13 (дБ)2 |
14,23 |
Dк =[Σ(Δк)2]/13 (дБ)2 |
0,34 |
|||||
|
СКОи =√ дБ |
3,77 |
СКОк =√ дБ |
0,58 |
|||||
Сравнительная оценка результатов аппроксимации исходного и откорректирован- ного временных рядов, приведённая в табл. 6.2, свидетельствует о том, что применён- ный алгоритм позволил в 6,5 раз уменьшить среднеквадратическую ошибку аппрокси- мации. Кроме того, значительно изменилось и расположение аппроксимирующей функ- ции (а значит, и прогноз, который получается в результате её экстраполяции).
Принципиальным отличием предлагаемой адаптивной методики от однопа- раметрической экстраполяции является использование диагностической модели, харак- теризующей зависимость значений диагностического параметра от степени деградации технического состояния контролируемого узла оборудования. Наиболее надёжным и до- стоверным способом получения такой зависимости является проведение экспериментов, предусматривающих замеры диагностического параметра при различной степени износа диагностируемого узла. Такие измерения можно проводить, например, в процессе дли- тельных ресурсных испытаний соответствующего узла оборудования. Далее в качестве примера рассматривается методика и результаты подобных испытаний подшипников качения судового конденсатного насоса на специальном стенде, показанном на рис.6.14.
Методика проведения экспериментов на данном стенде отличалась от ранее из- ложенной тем, что для сокращения времени длительных испытаний ускорение износа подшипника достигалась не предварительным нанесением начальных дефектов дорожек и тел качения, а интенсификацией эксплуатационных нагрузок:
− увеличением с помощью винтовых упоров 2 и динамометров 3 и 9 радиальных и осевых усилий, воспринимаемых подшипником;
− увеличением частоты вращения вала;
− ухудшением качества смазки путём уменьшения количества масла в ванне, увеличе- ния его температуры и заполнения ванны загрязнённым отработанным маслом.
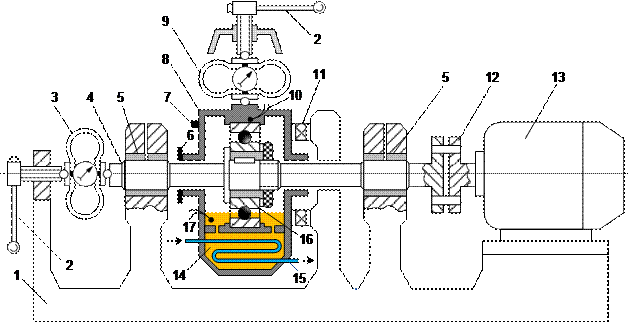 |
1 – фундамент; 2 – горизонтальный и вертикальный винтовые упоры; 3,9 – горизон- тальный и вертикальный динамометры; 4 – вал; 5 – опорные металлофторопластовые подшипники с водяной смазкой; 6 – четыре индуктивных датчика для измерения отно- сительных смещений корпуса 8 и вала 4; 7 – вибродатчик (акселерометр); 8 – «плаваю- щий» разъёмный корпус; 10,17 – термопары для измерения температуры наружного кольца подшипника и масла; 11 – амортизаторы; 12 – муфта с резиновыми пальцами; 13
– электродвигатель; 14 – масляная ванна; 15 – змеевик охлаждающей воды; 16 – испы- тываемый подшипник.
В качестве диагностического признака использовался сигнал вибродатчика 7, уста- новленного на «плавающем» корпусе 8. Измерения проводились в октавной полосе 250÷500 Гц. Результаты представлены на рис. 6.15. Кривая, показанная на графике, яв- ляется результатом аппроксимации результатов вибромониторинга в процессе длитель- ных испытаний подшипника судового конденсатного насоса. Резкое возрастание уровня вибрации при радиальном зазоре выше 20 мкм объясняется большим количеством накопленных дефектов на беговых дорожках колец и шариках.
S, дБ 80
75
70
65
60
10 15 20 25 t, 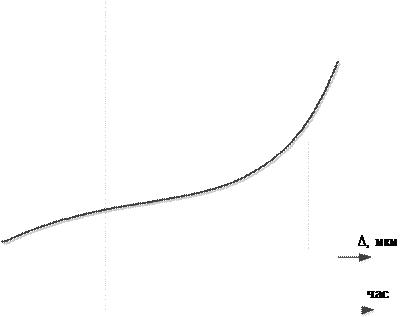
100
Рисунок 6.15 (слева) – За- висимость уровня вибра- ции на корпусе подшип- никового узла от времени испытаний t и радиально- го зазора в подшипнике Δ
.
![]()
![]() Монотонный характер аппроксимирующей
функции, так же, как и в рассмотрен- ном
ранее примере, делает возможным её экстраполяцию для решения прогнозных за- дач, правда, только для однорежимных
объектов, поскольку эта зависимость, как и вре- менной ряд, показанный на рис. 6.14, получены при неизменном
режиме работы соот- ветствующих стендовых
установок.
Монотонный характер аппроксимирующей
функции, так же, как и в рассмотрен- ном
ранее примере, делает возможным её экстраполяцию для решения прогнозных за- дач, правда, только для однорежимных
объектов, поскольку эта зависимость, как и вре- менной ряд, показанный на рис. 6.14, получены при неизменном
режиме работы соот- ветствующих стендовых
установок.
Отсутствие непосредственного учёта влияния изменчивости условий эксплуата- ции и режимов работы оборудования весьма существенно ограничивает возможности практического применения однопараметрических экстраполяционных алгоритмов про- гнозирования, поскольку большинство реально используемых диагностических пара- метров судового энергетического оборудования не являются инвариантными по отно- шению к режимам использования оборудования. Это противоречие становится явным даже для бинарных объектов, которые в моменты очередных замеров диагностического параметра, вычисленные рассмотренной выше программой, могут находиться как во включённом, так и в выключенном состоянии. Понятно, что результаты измерений, про- ведённых на выключенном объекте, приведут только к увеличению дисперсии и поста- вят под сомнение возможность получения аппроксимирующей функции с достаточно большим коэффициентом корреляции.
Для бинарных объектов устранение этих ложных замеров требует добавления в алгоритм и реализующую его программу функции дискретного контроля режимного со- стояния объекта («включён» −«выключен») и соответствующей блокировки возможно- сти измерений параметра на неработающем объекте. Для объектов с плавным изменени- ем режима от нулевого до номинального простая блокировка делу не поможет: требует-
ся аналоговая процедура компенсации влияния режима объекта на результаты измере- ний определяющего параметра, например, путём введения в результаты измерений по- правок, учитывающих отклонение режима от номинального. Для формирования таких поправок необходимо располагать математической моделью диагностического объекта, описывающей влияние на контролируемый диагностический параметр не только техни- ческого состояния диагностируемого узла, но и режима функционирования объекта.
Правда, задачу можно упростить, если в первом приближении принять допуще- ние, что зависимость диагностического параметра от режима объекта носит линейный характер. Это допущение позволяет построить номограмму (рис. 6.16), позволяющую в процессе мониторинга оборудования определять текущее значение структурного пара- метра (в рассматриваемом примере зазора в подшипнике) по измеренному диагностиче- скому параметру (уровню вибрации) и показателю режима (частоте вращения ротора механизма).
Например, если в результате измерения на режиме 50% от номинального получен уровень вибрации около 69дБ (красные стрелки на номограмме), то временной ряд наблюдений должен быть дополнен точкой, соответствующей степени износа подшип- ника, при которой зазор равен 25 мкм.
S, дБ

![]() 80
80
S, дБ
75
70
65
0 25 50 75 100 5
Режим работы механизма, %
10 15 20 25
Зазор в подшипнике Δ, мкм
Рисунок 6.15 – Номограмма для определения значения структурного параметра по пока- зателю режима и измеренному значению диагностического параметра
Применение предложенной методики позволяет в процессе мониторинга меха- низма формировать временной ряд наблюдений не в координатной плоскости «диагно- стический параметр – время», а в плоскости «структурный параметр – время». Это дела-
ет последующую аппроксимацию временного ряда и формирование прогноза о техниче- ском состоянии диагностируемого узла инвариантными по отношению к режимам, на которых производились замеры, а значит, открывает возможность применения экстра- поляционного метода для прогнозирования состояния узлов многорежимного оборудо- вания.
Преимуществом предлагаемой методики является возможность использования ре- зультатов длительных ресурсных испытаний, выполненных на номинальном режиме ра- боты механизма (рис. 6.15). Недостаток заключается в методической погрешности, вно- симой допущением о линейном характере зависимости диагностического параметра от режима работы механизма. Для более точной оценки требуется, очевидно, использова- ние нелинейных многофакторных зависимостей.
Точное аналитическое решение такой задачи обычно затруднено сложностью, многосвязностью и недостаточной изученностью соответствующих процессов, свойств объектов и характера их взаимодействия. В этой связи целесообразно использовать экс- периментальные исследования, позволяющие в приемлемые сроки получить достаточно достоверные результаты.
В качестве примера реализации этой концепции рассмотрим методику и результа- ты экспериментальных исследований судового центробежного насоса как объекта диа- гностирования. Приводной электродвигатель насоса снабжён преобразователем частоты питающего тока, обеспечивающим плавное изменение частоты вращения. Диа- гностируемый узел – подшипник скольжения ротора насоса. В качестве диагностическо- го параметра контролировался уровень вибрации на лапе насоса.
Исследования проводились методом активного эксперимента (условия опытов за- давались экспериментатором в соответствие с планом эксперимента). Типовая программа таких экспериментов предполагает выполнение следующих этапов:
· выбор номенклатуры варьируемых факторов и контролируемого параметра и опре- деление цели эксперимента;
· выбор типа математической модели;
· подготовка плана и матрицы эксперимента;
· выбор условий проведения опытов и их выполнение;
· предварительная статистическая обработка результатов;
· выявление грубых промахов;
· вычисление коэффициентов регрессии;
· оценкa знaчимости коэффициентов регрессии;
· оценка aдеквaтности модели и анализ её свойств;
· графическое представление и физическая трактовка результатов.
· применение модели для определения поправок.
Варьируемые факторы:
X1 – частота вращения рабочего колеса (об/мин);
X2 – степень износа подшипника скольжения, т.е. зазор (мкм); X3 – давление смазки подшипника (бар).
Изучаемый отклик: Y – уровень сигнала диагностического вибродатчика в задан- ной частотной полосе (дБ).
Цель эксперимента: определение регрессионной математической модели объекта, характеризующей зависимость диагностического параметра от степени износа подшип- ника и указанных выше режимных факторов.
Обычно в теории планирования рекомендуется выбирать модель в виде полинома, т.е. в виде алгебраической суммы факторов и их произведений, помноженных на коэф- фициенты регрессии. Поскольку нет априорной уверенности в том, что влияние рас- сматриваемых факторов на сигнал диагностического вибродатчика может быть описано чисто линейной зависимостью, выбираем модель 2-го порядка.
Таблица 6.3. Состав квадратичной модели
|
2 2 Y=B0 + B1X1+ B2X2 + B3X3 + B12X1X2 + B13X1X3 + B23X2X3 + B11X12 + B22X2 + B33X3 |
||
|
линейная часть |
эффекты взаимодействия факторов |
квадратичные члены |
Для экспериментального определения коэффициентов квадратичной модели тре- буются планы, предусматривающие реализацию более двух уровней варьирования фак- торов. Пригодны планы полного факторного эксперимента с варьированием на 3-х уровнях (ПФЭ 3к), либо центрально-композиционные планы (варьирование на 5 уров- нях). Сопоставление данных о необходимом количестве опытов при использовании ука- занных планов для трёхфакторной задачи (27 опытов для ПФЭ 3к и 15 опытов для ЦКП) позволяет сделать выбор в пользу центрально-композиционного планирования, обеспе-
чивающего большее количество уровней варьирования факторов при меньшем количе- стве опытов.
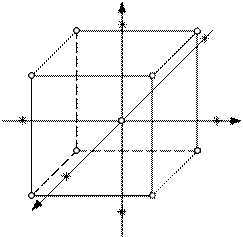 Графическое представление ЦКП для
3-х факторов и соответствующая матрица планирования приведены
на рис. 6.6 и в табл. 6.4.
Графическое представление ЦКП для
3-х факторов и соответствующая матрица планирования приведены
на рис. 6.6 и в табл. 6.4.
|
X2 5 11 4
14 3 6 10 15 9 X 1
1 8 13 7 12 2 X3 |
Рисунок 6.16 (слева) – Центрально- композиционный план α – «звёздное плечо» - расстояние «звёзд- ных точек» от центра плана По условию ортогональности матрицы планирования для 3-х факторов α =1,215 |
|
№ |
X0 |
X1 |
X2 |
X3 |
X1∙X2 |
X1∙X3 |
X2∙X3 |
X 2 1 |
X 2 2 |
X 2 3 |
Части ЦКП |
|
1 |
+1 |
-1 |
-1 |
-1 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
Ядро Nя = 2к |
|
2 |
+1 |
+1 |
-1 |
+1 |
-1 |
+1 |
-1 |
+1 |
+1 |
+1 |
|
|
3 |
+1 |
-1 |
+1 |
+1 |
-1 |
-1 |
+1 |
+1 |
+1 |
+1 |
|
|
4 |
+1 |
+1 |
+1 |
-1 |
+1 |
-1 |
-1 |
+1 |
+1 |
+1 |
|
|
5 |
+1 |
-1 |
+1 |
-1 |
-1 |
+1 |
-1 |
+1 |
+1 |
+1 |
|
|
6 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
|
|
7 |
+1 |
-1 |
-1 |
+1 |
+1 |
-1 |
-1 |
+1 |
+1 |
+1 |
|
|
8 |
+1 |
+1 |
-1 |
-1 |
-1 |
-1 |
+1 |
+1 |
+1 |
+1 |
|
|
9 |
+1 |
+α |
0 |
0 |
0 |
0 |
0 |
α2 |
0 |
0 |
Звёздные точки N* = 2к |
|
10 |
+1 |
-α |
0 |
0 |
0 |
0 |
0 |
α2 |
0 |
0 |
|
|
11 |
+1 |
0 |
+α |
0 |
0 |
0 |
0 |
0 |
α2 |
0 |
|
|
12 |
+1 |
0 |
-α |
0 |
0 |
0 |
0 |
0 |
α2 |
0 |
|
|
13 |
+1 |
0 |
0 |
+α |
0 |
0 |
0 |
0 |
0 |
α2 |
|
|
14 |
+1 |
0 |
0 |
-α |
0 |
0 |
0 |
0 |
0 |
α2 |
|
|
15 |
+1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Центр |
Важным свойством матрицы планирования является её ортогональность, которая обеспечивает возможность независимой оценки всех коэффициентов математической модели объекта и обеспечивает простой алгоритм вычисления коэффициентов регрес- сии. Правило проверки ортогональности матрицы: сумма почленных произведений лю- бых двух столбцов должна равняться нулю. Нетрудно видеть, что для матрицы, приве-
дённой в табл.6.8, это условие не соблюдается. Этот недостаток можно устранить сле- дующим образом:
·
j
вместо квадратичных переменных x2
введём в матрицу новые переменные
j j j
XН = x2 - x)2 , (6.15)
где
x)2 = 1 åN x2
![]()
- среднее значение квадратичного столбца исходной матрицы.
N i=1 i, j
· зададим значение звёздного плеча α = 1,215 .
В результате получим матрицу, представленную в табл.6.4
Таблица 6.4. Ортогональная матрица ЦКП для 3-х факторов
|
№ |
X0 |
X1 |
X2 |
X3 |
X1∙X2 |
X1∙X3 |
X2∙X3 |
XН 1 |
XН 2 |
XН 3 |
|
1 |
+1 |
-1 |
-1 |
-1 |
+1 |
+1 |
+1 |
0,27 |
0,27 |
0,27 |
|
2 |
+1 |
+1 |
-1 |
+1 |
-1 |
+1 |
-1 |
0,27 |
0,27 |
0,27 |
|
3 |
+1 |
-1 |
+1 |
+1 |
-1 |
-1 |
+1 |
0,27 |
0,27 |
0,27 |
|
4 |
+1 |
+1 |
+1 |
-1 |
+1 |
-1 |
-1 |
0,27 |
0,27 |
0,27 |
|
5 |
+1 |
-1 |
+1 |
-1 |
-1 |
+1 |
-1 |
0,27 |
0,27 |
0,27 |
|
6 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
0,27 |
0,27 |
0,27 |
|
7 |
+1 |
-1 |
-1 |
+1 |
+1 |
-1 |
-1 |
0,27 |
0,27 |
0,27 |
|
8 |
+1 |
+1 |
-1 |
-1 |
-1 |
-1 |
+1 |
0,27 |
0,27 |
0,27 |
|
9 |
+1 |
+α |
0 |
0 |
0 |
0 |
0 |
0,746 |
-0,73 |
-0,73 |
|
10 |
+1 |
-α |
0 |
0 |
0 |
0 |
0 |
0,746 |
-0,73 |
-0,73 |
|
11 |
+1 |
0 |
+α |
0 |
0 |
0 |
0 |
-0,73 |
0,746 |
-0,73 |
|
12 |
+1 |
0 |
-α |
0 |
0 |
0 |
0 |
-0,73 |
0,746 |
-0,73 |
|
13 |
+1 |
0 |
0 |
+α |
0 |
0 |
0 |
-0,73 |
-0,73 |
0,746 |
|
14 |
+1 |
0 |
0 |
-α |
0 |
0 |
0 |
-0,73 |
-0,73 |
0,746 |
|
15 |
+1 |
0 |
0 |
0 |
0 |
0 |
0 |
-0,73 |
-0,73 |
-0,73 |
Исходя из заданного диапазона изменения факторов в процессе эксперимента, определим координаты центра плана и интервалы варьирования для рассматриваемых факторов (табл. 6.5).
Значения нижнего и верхнего уровня получены вычитаются или прибавляются к координате центра соответствующих интервалов варьирования. Для получения коорди- нат звёздных точек вычитается или прибавляется звёздное плечо, полученное умноже- нием интервала варьирования на α = 1,215.
.
Таблица 6.5. Значения факторов на пяти уровнях варьирования
|
Факторы |
Размерность |
Интервалы варьирования Δj |
Звёздное плечо αj = 1,215Δj |
Нижняя звёздная точка «-α» |
Нижний уровень «-1» |
Центр плана «0» |
Верхний уровень «+1» |
Верхняя звёздная точка «+α» |
|
X1 |
об/мин |
100 |
122 |
578 |
600 |
700 |
800 |
822 |
|
X2 |
мкм |
20 |
24,3 |
45,7 |
50 |
70 |
90 |
94,3 |
|
X3 |
бар |
1 |
1,22 |
3,78 |
4 |
5 |
6 |
6,22 |
Сопоставляя столбцы плана (они выделены жирными линиями в табл.6.4) и соот- ветствующие им фактические значения факторов (табл.6.5), получим условия проведе- ния опытов. При проведении каждого опыта замер сигнала Y производился трижды (столбцы Ya , Yb и Yc в табл.6.6).
Таблица 6.6. Условия и результаты опытов
|
№ оп. |
Заданные значения факторов |
Сигнал датчика, дБ |
Обработка |
|||||
|
X1 об/мин |
X2 мкм |
X3 бар |
Ya |
Yb |
Yc |
Yср. |
D |
|
|
1 |
600 |
50 |
4 |
25,518 |
24,736 |
25,166 |
25,14 |
0,153 |
|
2 |
800 |
50 |
8 |
29,955 |
28,843 |
28,139 |
28,98 |
0,838 |
|
3 |
600 |
90 |
8 |
25,688 |
25,279 |
24,873 |
25,28 |
0,166 |
|
4 |
800 |
90 |
4 |
41,655 |
40,793 |
41,152 |
41,20 |
0,187 |
|
5 |
600 |
90 |
4 |
29,683 |
28,462 |
29,515 |
29,22 |
0,438 |
|
6 |
800 |
90 |
8 |
37,082 |
36,877 |
37,461 |
37,14 |
0,088 |
|
7 |
600 |
50 |
8 |
20,821 |
20,943 |
21,356 |
21,04 |
0,079 |
|
8 |
800 |
50 |
4 |
32,843 |
33,406 |
33,351 |
33,20 |
0,096 |
|
9 |
822 |
70 |
6 |
35,456 |
35,552 |
34,712 |
35,24 |
0,211 |
|
10 |
578 |
70 |
6 |
22,893 |
22,809 |
23,718 |
23,14 |
0,252 |
|
11 |
700 |
94,3 |
6 |
34,091 |
34,393 |
34,536 |
34,34 |
0,052 |
|
12 |
700 |
45,7 |
6 |
26,237 |
26,828 |
27,635 |
26,90 |
0,492 |
|
13 |
700 |
70 |
8,43 |
27,908 |
27,595 |
28,437 |
27,98 |
0,181 |
|
14 |
700 |
70 |
3,56 |
33,163 |
32,233 |
33,424 |
32,94 |
0,392 |
|
15 |
700 |
70 |
6 |
30,551 |
29,427 |
30,112 |
30,03 |
0,321 |
Результаты измерений несколько отличаются друг от друга из-за случайной по- грешности измерений. Предварительная статистическая обработка результатов заключа- ется в вычислении среднего значения Yср. и дисперсии D:
Yср.= (Ya + Yb + Yc)/3 (6.16)
D = [(Ya -Yср.)2 + (Yb -Yср.)2 + (Yc -Yср.)2]/2 (6.17)
![]() Проверка выполняется путем оценки
однородности дисперсий с помощью крите- рия
Кохрэна (G - критерия). Экспериментальное
значение критерия определяется по формуле (6.18):
Проверка выполняется путем оценки
однородности дисперсий с помощью крите- рия
Кохрэна (G - критерия). Экспериментальное
значение критерия определяется по формуле (6.18):
|
G = Dmax экс N å Di i=1 |
где: в числителе – максимальная из дисперсий (0,838); в знаменателе – сумма всех дисперсий (3,946). |
Gэкс. = 0,838/3,946 = 0,21
Для определения табличного значение критерия задают следующие координаты:
§ уровень значимости a = 1 – 0,95 = 0,05;
§ степень свободы f1 = 2 (на единицу меньше числа замеров);
§ степень свободы f2 = 15 (количество опытов). Пользуясь справочной таблицей, находим: Gтабл. = 0,36.
Поскольку Gэкс. < Gтабл. – сделан вывод об однородности дисперсий и отсутствии гру-
бых промахов.
Для вычисления коэффициентов регрессии ортогональной матрицы достаточно столбец матрицы с одноимённым индексом факторов (табл. 6.6) почленно перемножить со столбцом средних результатов, произведения сложить и сумму разделить на число опытов (15). Применение этого алгоритма даёт результаты, приведённые в табл. 6.7.
Таблица 6.7. Коэффициенты регрессии
|
B0 |
B1 |
B2 |
B3 |
B12 |
B13 |
B23 |
B11 |
B22 |
B33 |
|
30,03 |
4,98 |
3,06 |
-2,04 |
0,98 |
-0,03 |
0,04 |
-0,51 |
0,40 |
0,29 |
Эта процедура выполняется с целью упрощения модели с использованием крите- рия Стьюдента. Сначала вычислим дисперсию коэффициентов и среднеквадратичное отклонение (6.19):
![]()
S
å Di
2 = i=1
B N 2 n(n -1)
= 0,00293
SB = = 0,054
|
Затем зададим координаты: |
Р = 0,95 – доверительная вероятность; f = N(n-1) = 15(3-1) =30 – степень свободы |
![]() и находим
табличное значения критерия Стьюдента: tтабл. = 2,042
и находим
табличное значения критерия Стьюдента: tтабл. = 2,042
После этого вычислим доверительный интервал коэффициентов регрессии:
|
Оценка значимости коэффициента выполняется в соответствии с правилом: |
|Bj| ≥ ΔB → коэффициент значимый. |
После сравнения по абсолютной величине с доверительным интервалом признаны зна- чимыми 8 коэффициентов. Модель после упрощения имеет вид (6.20):
|
Адекватность модели – это её способность достоверно описывать реальные свой- ства объекта. Оценка адекватности модели заключается в статистическом сопоставле- нии результатов, полученных опытным путем (Y), и результатов, вычисленных для тех же условий с помощью модели (Yмод). Для оценки используем критерий Фишера.
N i i![]()
0,5nå(Y - Y мод )2
Дисперсия адекватности:
где: i – номер опыта;
Dадекв = i=1
L
= 0,186 (6.21)
å Di
S
Дисперсия эксперимента:
2 = i=1
N (n -1)
= 0,132 (6.22)
F =
S2
Экспериментальное значение критерия Фишера:
ад
Э S2
= 1,40 (6.23)
Зададим доверительную вероятность p = 0.95 и степени свободы:
f1 = L = 2; f2 = N(n-1) = 30 и найдём табличное значение критерия Фишера:
Условие адекватности Fэ < Fтабл. соблюдается, следовательно полученная экспе- риментальным путём математическая модель объекта адекватна.
Наличие в модели значимых коэффициентов при эффектах взаимодействия фак- торов и квадратичных элементах подтвердило справедливость принятой при выборе ти- па модели и плана эксперимента гипотезы о нелинейном характере влияния рассматри- ваемых факторов на сигнал вибродатчика. Отсутствие резкого превышения свободного члена B0 над коэффициентами регрессии B1 B2 и B3 является признаком достаточной чувствительности модели.
Графическое отображение функции 3-х переменных представляет собой некую гиперповерхность в четырёхмерном пространстве. Находясь в трёхмерном простран- стве, мы можем изобразить только различные сечения этой поверхности, характеризу- ющие зависимость отклика от двух факторов при зафиксированном третьем факторе.
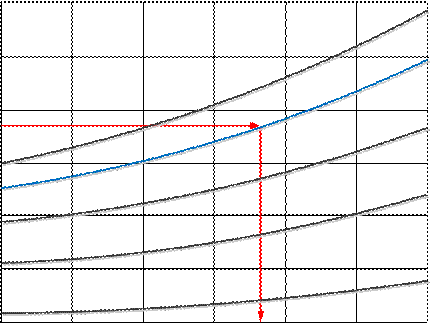
Например, в табл. 6.8 и на рис.6.17 показано влияние зазора в подшипнике и ча- стоты вращения рабочего колеса на уровень сигнала вибродатчика при постоянном дав- лении смазки 6 бар.
Таблица 6.8. Зависимость сигнала вибродатчика (Y, дБ) от режима насоса и технического состояния подшипника
|
Зазор, мкм |
Частота вращения, об/мин |
||||
|
500 |
600 |
700 |
800 |
900 |
|
|
40 |
15,53 |
20,57 |
24,59 |
27,59 |
29,57 |
|
50 |
15,58 |
21,11 |
25,62 |
29,11 |
31,58 |
|
60 |
15,83 |
21,85 |
26,85 |
30,83 |
33,79 |
|
70 |
16,28 |
22,79 |
28,28 |
32,75 |
36,20 |
|
80 |
16,93 |
23,93 |
29,91 |
34,87 |
38,81 |
|
90 |
17,78 |
25,27 |
31,74 |
37,19 |
41,62 |
|
100 |
18,83 |
26,81 |
33,77 |
39,71 |
44,63 |
Наличие такой модели позволяет по результатам вибромониторинга насоса оце- нивать фактическое техническое состояние подшипника и прогнозировать его измене- ние экстраполяционным методом, не внося в результаты прогноза ошибок, обусловлен- ных тем, что насос в моменты проведения измерений может эксплуатироваться на раз- личных режимах (при различных частотах вращения вала).Так, если очередное измере- ние в процессе вибромониторинга насоса проводится при частоте вращения 800 об/мин, то уровень сигнала вибродатчика Y=33дБ будет соответствовать зазору в подшипнике насоса Δ = 77мкм.
![]() 45
45
![]()
![]() 40
40
![]() 35
35
![]() 30
30
![]() 25
25
20
15
50 60
70 80
90 100
Зазор в подшипнике Х2, мкм
Рисунок 6.17 – Зависимость сигнала диагностического датчика от зазора в подшипнике и частоты вращения вала насоса
Предложенные варианты модернизации алгоритма обработки временного ряда, полученного в процессе мониторинга объекта, расширяет функциональные возможно- сти экстраполяционного метода прогнозирования, делая возможным его применение и для многорежимных объектов. Правда, для этого требуется предварительное исследова- ние свойств соответствующего оборудования с целью получения его диагностической модели (функциональной связи диагностического параметра со структурным парамет- ром, определяющим техническое состояние контролируемого узла) и возможность пе- риодического измерения во время эксплуатации этого диагностического параметра.
Слабым местом всех экстраполяционных методов является предположение о том, что характер накопления эксплуатационных повреждений контролируемого узла на про- гнозируемом периоде будет таким же, как и на периоде формирования временного ряда. Понятно, что одним из важных условий корректности такого предположения является неизменность условий и режимов эксплуатации объекта.
Если прямое измерение диагностического параметра во время эксплуатации объ- екта невозможно, а также в тех случаях, когда планируется изменение графика режимов объекта на прогнозируемом периоде, есть смысл обратиться к методикам прогнозирова-
ния, допускающим возможность учёта влияния переменных режимов на интенсивность накопления эксплуатационных повреждений. Именно эта концепция лежит в основе причинно-следственного метода (термин предложен автором), который можно считать антиподом экстраполяционного, поскольку он предусматривает регистрацию индивиду- альной истории нагружений, т.е. не следствий, а причин, определяющих темп накопле- ния эксплуатационных повреждений оборудования.
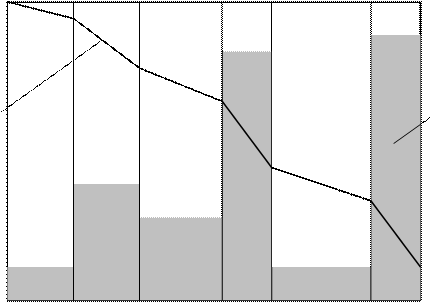
Теоретическая основа метода – гипотеза линейного суммирования повреждений. Предполагается, что каждому уровню нагружения оборудования соответствует свой темп расходования ресурса, а накопление эксплуатационных повреждений много- режимного оборудования подчиняется принципу суперпозиции, т.е. можно подсчитать расходование ресурса на отдельных режимах эксплуатации и затем их сложить (рис. 6.18).
![]()
![]() Соответствующий
алгоритм может быть реализован в штатной системе контроля параметров и в автономных приборах - счетчиках
наработки ресурса и регистраторах эксплуатационных нагружений.
Соответствующий
алгоритм может быть реализован в штатной системе контроля параметров и в автономных приборах - счетчиках
наработки ресурса и регистраторах эксплуатационных нагружений.
 |
Время эксплуатации агрегата
Рисунок 6.18 − Оценка предполагаемой выработки ресурса оборудования при заданном графике режимов его эксплуатации
Достоинства метода: детерминированный характер прогноза, возможность оценки темпов расходования ресурса многорежимных объектов и минимизации количества контролируемых параметров за счет использования комплексных характеристик. Прав- да, при этом следует иметь в виду и определённые условия применимости этого метода:
- для его использования необходимо располагать предельными характеристиками дол- говечности оборудования, получение которых расчетно-экспериментальным путем является трудоёмкой и дорогостоящей задачей;
- регистрацию нагружений необходимо вести с момента начала эксплуатации объекта, поэтому эффективное использование метода возможно для вновь устанавливаемого оборудования;
- метод не является универсальным, поскольку далеко не для всех видов эксплуатаци- онных разрушающих процессов доказана возможность корректного применения ли- нейного суммирования повреждений.
Тем не менее, ориентация метода на контроль, прежде всего, режимов использо- вания оборудования, как основного фактора, определяющего интенсивность процессов эксплуатационного повреждения наиболее напряженных узлов и деталей, создаёт опре- делённые предпосылки для его успешного применения в качестве информационной ба- зы для индивидуального прогноза долговечности и упреждающего обслуживания обо- рудования, особенно в тех случаях, когда периодическое измерение и экстраполяция ди- агностических параметров, характеризующих фактическое техническое состояние обо- рудования, по тем или иным причинам невозможно или нецелесообразно.
Реализация этого метода предусматривает последовательное выполнение ряда этапов:
· анализ физико-химических процессов, вызывающих во время эксплуатации объекта деградацию его технического состояния, и выделение режимных параметров, опреде- ляющих интенсивность этой деградации;
· экспериментальное определение регрессионной математической модели, связываю- щей темп накопления эксплуатационных повреждений с режимными параметрами;
· задание предполагаемого на прогнозируемый период графика изменения во времени режимов эксплуатации объекта;
· вычисление с помощью регрессионной модели накоплений эксплуатационных по- вреждений на каждом из планируемых режимов, и оценка суммарного повреждения в течение прогнозного периода;
· оценка остаточного ресурса путём сопоставления, вычисленного и предельно допустимого изменений технического состояния.
Конкретные методики применения этого метода существенным образом зависят от конструктивных особенностей контролируемого объекта, условий его эксплуатации и ре- жимов использования, характера эксплуатационных нагрузок и типичных разрушающих процессов, интенсивность которых лимитирует долговечность наиболее ответственных и
нагруженных узлов, возможности непосредственного контроля или косвенного определе- ния интенсивности эксплуатационных нагружений и других специфических особенностей контролируемого оборудования. Ниже приводятся примеры практической реализации причинно-следственного метода прогнозирования судового оборудования.
Сильфон - гибкий металлический патрубок, имеющий гофрированную поверхность, который обычно изготавливают из одного или нескольких тонких слоев легированной ста- ли методом гидропрессования (рис. 6.19).

Рисунок 6.19 – Внешний вид металлических сильфонов
Сильфоны являются основным элементом сильфонных компенсаторов – гибких вставок, которые устанавливают в тех участках трубопроводов, где нужно компенсировать взаимное осевое, сдвиговое или угловое смещение труб, возникающее вследствие неточ- ности монтажа, тепловых деформаций и механических перемещений одних участков тру- бопровода относительно других. Кроме того, сильфоны используют в качестве гибких уплотнительных элементов в запорной трубопроводной арматуре и в устройствах гидро- и пневмоавтоматики.
В судовых энергетических установках сильфоны и сильфонные компенсаторы при- меняют для решения трёх основных задач:
- герметическое уплотнение перемещаемых деталей запорной трубопроводной арматуры;
- гибкое соединение участков трубопроводов, подверженных значительным температур- ным деформациям (например, главных паропроводов);
-  гибкое соединение участков трубопроводов, подверженных относительным смещениям вследствие нежёсткой установки на
фундаментах механизмов и агрегатов (например,
гибкая вставка в циркуляционной трассе, по которой подаётся забортная
вода на охла- ждение главного
конденсатора паротурбинной установки).
гибкое соединение участков трубопроводов, подверженных относительным смещениям вследствие нежёсткой установки на
фундаментах механизмов и агрегатов (например,
гибкая вставка в циркуляционной трассе, по которой подаётся забортная
вода на охла- ждение главного
конденсатора паротурбинной установки).
Рисунок 6.20 (слева). Типовые конструкции сильфонных компенсаторов для стыковки трубопроводов
В данном разделе рассматриваются технические предложения по организации мо- ниторинга третьей из вышеуказанных групп корабельных сильфонных компенсаторов. Сильфонные компенсаторы на циркуляционной трассе главного конденсатора имеют са- мые большие габаритные размеры из всех корабельных компенсаторов (диаметр до 1200 мм). Основным фактором, определяющим условия их эксплуатационных нагружений, яв- ляется установка главного турбозубчатого агрегата (паровая турбина + редуктор + глав- ный конденсатор) на гибких амортизаторах. Это делается для уменьшения вибраций, пе- редаваемых от ГТЗА на корпус корабля, благодаря чему снижается шумность корабля и повышается его скрытность. При качке корабля гибко подвешенный ГТЗА смещается в поперечном и вертикальном направлениях, в связи с чем сильфонный компенсатор под- вергается осевым и сдвиговым циклическим деформациям. Особенно опасны сдвиговые деформации. При сильной бортовой качке их амплитуда может достигать 30 мм. Кроме того, сдвиговые деформации вызывают наиболее неблагоприятное распределение напря- жений в гофрах сильфона.
Ожидаемый во время эксплуатации спектр циклических деформаций компенсатора может быть, в принципе, очень приблизительно оценён путём анализа ожидаемых режи- мов использования корабля, погодных условий в районе плавания корабля, изучения ха- рактерных для разных времен года спектров волнения моря в этих районах и мореходных качеств корабля (зависимости периода и амплитуды качки от волнения моря и курса ко- рабля относительно волны). Нетрудно представить, что достоверность таких прогнозов
будет весьма невелика, поэтому и фактическая наработка компенсатора во время эксплуа- тации может существенно отличаться от расчётной.
Основным видом эксплуатационных изменений технического состояния сильфонов является накопление усталостных повреждений металла под действием переменных де- формаций. В результате длительного воздействия эксплуатационных нагрузок на много- слойные сильфоны может произойти их расслоение, в результате которого нарушается равномерность распределения напряжений между отдельными слоями оболочки, развитие усталостных микротрещин, перерастающих в макротрещины и сквозные трещины отдель- ных слоев оболочки сильфона. Последней стадией этого процесса является повреждение всех слоёв и разгерметизация сильфона.
Экспериментальная проверка достоверности этой гипотезы о характере эксплуата- ционных повреждений выполнялась для партии сильфонов во время их ресурсных испы- таний. Испытания проводились на специальном стенде, обеспечивающем циклическую деформацию сильфонов и параллельное измерение сигналов акустической эмиссии [75]. Регистрировалась следующие параметры:
- амплитуда импульсов А (mV);
- частота импульсов Z (имп/с).
Характеристики и условия экспериментов по циклическим ресурсным испытаниям сильфонов приведены в табл. 6.9. На рис. 6.19 показан характер изменения сигналов АЭ, генерируемых многослойным сильфоном в ходе непрерывных циклических ресурсных ис- пытаний.
На графике достаточно отчетливо выделяются три этапа:
· период начального акустического молчания (ПНАМ);
· период активной акустической эмиссии (ПААЭ);
· период конечного акустического молчания (ПКАМ).
Таблица 6.9. Результаты ресурсных испытаний сильфонов с контролем сигналов акустической эмиссии
|
Тип силь- фонов |
Колич., шт. |
Жесткость С, кН/м |
Частотный диапазон канала АЭ, Δf, кГц |
Гарантийная наработка Nг, цикл |
Фактическая нара- ботка при испыта- ниях Nэкс, цикл |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
НС 27-10- 0,16*3 |
18 |
50 - 75 |
750 и выше |
3000 |
8300 - 18000 |
|
НС 27-9- 0,16*6 |
6 |
- |
750 и выше |
3000 |
3500 - 1850 |
Окончание таблицы 6.9
|
1 |
2 |
3 |
4 |
5 |
6 |
|
НС 22-9- 0,16*5 |
4 |
94 - 129 |
30 и выше |
4000 |
5500 - 10600 |
|
НС 28-10- 0,16*3 |
12 |
41 - 77 |
30 и выше |
5000 |
11860 - 31120 |
|
НС 28-10- 0,16*3 |
15 |
50 - 79 |
60 и выше |
5000 |
16420 - 48700 |
|
НС 38-13- 0,2*6 |
29 |
125 - 175 |
60 и выше |
3000 |
1467 - 5242 |
|
НС 38-16- 0,2*6 |
12 |
98 - 136 |
60 и выше |
3000 |
3800 - 12700 |

|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Аотн, Zотн
0,8
0,6
0,4
0,2
0,2 0,4 0,6 0,8 N/Nном
Рисунок 6.19 – Зависимость интенсивности сигналов АЭ от наработки сильфона
На первом этапе (ПНАМ) межслойного трения (и сигналов АЭ) нет вследствие от- сутствия расслоения сильфона. Второй этап (ПААЭ) сопровождается активным межслой- ным трением, которое и является источником интенсивных сигналов АЭ. На третьем этапе (ПКАМ) межслойное трение отсутствует, поскольку герметичным остался только один внешний слой. Остальные слои разгерметизированы, и рабочая жидкость заполнила зазо- ры между слоями. На третьем этапе (ПКАМ) межслойное трение отсутствует, поскольку герметичным остался только один внешний слой. Остальные слои разгерметизированы, и рабочая жидкость заполнила зазоры между слоями. Этот этап заканчивается разрушением последней оболочки и разгерметизацией сильфона.
Своевременное обнаружение этих процессов во время эксплуатации судна затруд- нено тем, что разрушение может начаться с внутренних слоев, невидимых для персонала, причём, вплоть до полной разгерметизации сильфона рабочие характеристики техниче- ской системы, снабжённой сильфонным компенсатором, не изменяются. Следствием не- контролируемого накопления эксплуатационных повреждений сильфонных компенсато- ров могут быть внезапные отказы корабельных энергетических систем. Необходимость предотвращения таких отказов делает актуальной организацию мониторинга и прогнози- рования технического состояния сильфонных компенсаторов. Наступление этапа конечно- го акустического молчания могло бы служить признаком предотказного состояния силь- фона при наличии измерительного канала, непрерывно отслеживающего во время эксплу- атации сигналы акустической эмиссии, генерируемые сильфоном в процессе его цикличе- ских деформаций.
Если такой возможности нет, можно воспользоваться тем обстоятельством, что, как показывают результаты рассмотренных выше длительных стендовых испытаний с парти- ями однотипных сильфонов, количество циклов деформаций сильфона, приводящих к раз- герметизации, зависит от амплитуды этих циклов: чем больше амплитуда цикла, тем быст- рее наступает усталостное разрушение оболочек сильфона. Это обстоятельство создаёт предпосылки для применения причинно-следственного метода прогнозирования.
![]() Суть
его заключается в том, что во время эксплуатации контролируют параметры, характеризующие интенсивность
эксплуатационных нагрузок, от которых зависит ско- рость накопления и развития эксплуатационных повреждений объекта:
Суть
его заключается в том, что во время эксплуатации контролируют параметры, характеризующие интенсивность
эксплуатационных нагрузок, от которых зависит ско- рость накопления и развития эксплуатационных повреждений объекта:
![]() Количество циклов до разрушения N
Количество циклов до разрушения N
Методика регистрации истории нагружения контролируемого объекта во многом определяется характером испытываемых им эксплуатационных нагрузок.
Наиболее простыми с точки зрения методического обеспечения являются объекты с несущественным изменением уровня нагружения во времени. Для них не требуется каких- либо приборных средств измерения и регистрации эксплуатационных нагрузок. Прогнози- рование остаточного ресурса таких объектов производится путем сопоставления их фак- тической наработки, зарегистрированной в формуляре, с назначенным ресурсом.
Достаточно распространены объекты, которые во время эксплуатации могут нахо- диться в одном из двух дискретных состояний: «включен – выключен», «работает – не ра- ботает», «нагружен – не нагружен». Регистрация фактической истории нагружения таких объектов сводится к подсчету «чистого» времени нахождения их в рабочем состоянии (так называемых моточасов). Простота данного метода обеспечивает достаточно широкое его применение в различных отраслях техники.
В принципе, так же решается задача и для более сложных объектов, которые во время эксплуатации могут находиться в нескольких дискретно переключаемых режимах, каждому из которых соответствует свой темп расходования ресурса. В этом случае доста- точно установить несколько счётчиков моточасов и отдельно подсчитывать время нара- ботки объекта на каждом из режимов. Иногда необходимо учитывать количество пере- ключений (запусков, реверсов, и т.п.). Эта особенность не вносит существенных измене- ний в методику регистрации истории нагружения, поскольку может быть учтена добавле- нием соответствующих счётчиков.
Регистрация истории нагружения всережимных объектов, темп расходования ресур- са которых определяется некоторым аналоговым показателем (мощностью, частотой вра- щения, силой тока и т.п.), может быть выполнена в соответствии с ранее изложенным спо- собом, если весь диапазон изменения характерного показателя режима разбить на ряд под- диапазонов, и отдельно подсчитывать время работы в каждом из них.
В случае, когда целью контроля является прогнозирование остаточного ресурса, может быть рекомендован и иной алгоритм, связанный с концепцией эквивалентного ре- сурса. Подсчёт эквивалентного ресурса связан с нелинейным преобразованием сигнала датчика, либо с использованием цифровой обработки информации.
Более сложными для решения рассматриваемой задачи являются объекты, расходо- вание ресурса которых обусловлено циклическими эксплуатационными нагрузками, осо- бенно в том случае, когда изменение параметров нагружения (частоты, амплитуды, асим- метрии циклов) во времени носит стохастический характер. К таким объектам относятся и судовые сильфонные компенсаторы. Существует два принципиальных подхода к реализа- ции контроля истории нагружения подобных объектов.
Первый основан на допущении стационарного характера нагружения в достаточно больших промежутках времени, что позволяет использовать методы анализа случайных процессов, в частности, спектральный анализ, либо оценку среднеквадратичного отклоне- ния показателя нагружения. Реализация такого алгоритма связана с использованием до- вольно сложной и дорогостоящей аппаратуры, применение которой оправдано в составе испытательных стендов для достаточно сложных объектов и систем, однако не может быть рекомендовано для эксплуатационного контроля истории нагружения отдельных элементов и узлов энергетического оборудования в судовых условиях.
Второй подход предполагает измерение амплитуды каждого из циклов и накопле- ние информации об истории нагружения путём суммирования числа циклов в заданных амплитудных поддиапазонах, либо приведения каждого из циклов к эквивалентному ре- жиму. Этот подход представляется более перспективным, поскольку, избавляя от необхо- димости фиксации и обработки данных достаточно длительного процесса случайного нагружения, позволяет использовать более простые аппаратурные средства.
Для сильфонного компенсатора циркуляционной трассы (СКЦ) главными эксплуа- тационными факторами, определяющими долговечность, следует считать количество и амплитуду циклов сдвиговой деформации под действием поперечной качки судна, по- скольку эта компонента характеризуется максимальным количеством и размахом циклов и неблагоприятным характером распределения напряжений. Исходные допущения, прини- маемые для разработки алгоритмов регистрации наработки:
− симметричность циклических смещений при качке судна, поскольку наличие постоян- ных составляющих крена не свойственно нормальной эксплуатации судна, монтажные перекосы исключены;
− использование в качестве показателя деформации сильфона сдвигового смещения по- движного фланца компенсатора;
− изменение амплитуды смещений во времени считается близким по периодичности среднему периоду качки судна и монотонным, то есть не содержащим высокочастотных составляющих, способных оказать влияние на усталостную долговечность СКЦ, по- скольку подвижная опорная поверхность СКЦ соединена с агрегатом, обладающим су- щественной массой.
Алгоритм регистрации истории нагружения СКЦ с разделением на амплитудные диапазоны должен содержать следующие последовательно выполняемые процедуры:
· измерение деформаций (преобразование относительных смещений подвижного фланца компенсатора в электрический сигнал);
· выделение амплитуды цикла;
· сортировка (сопоставление сигнала об амплитуде с граничными уставками поддиа- пазонов);
· адресация (направление сигнала о наличии цикла нагружения в канал соответству- ющего диапазона);
· суммирование (прибавление единицы к значению количества циклов, ранее накоп- ленных в данном поддиапазоне амплитуд);
· запоминание информации и длительное её хранение с защитой от стирания при по- терях электропитания;
· представление информации (непрерывная или по требованию индикация результа- та).
Преимуществом диапазонного учета наработки является сравнительная простота его реализации. Однако, принцип суммирования наработки по диапазонам имеет и ряд не- достатков:
− отсутствует автоматизированное приведение результатов суммирования к единому по- казателю, определяющему степень расходования ресурса, например, в процентах или долях от назначенного ресурса;
− существенна величина методической погрешности, обусловленной искусственно вво- димой нивелировкой всех режимов внутри каждого из диапазонов.
Погрешность может быть снижена путем увеличения количества диапазонов. Одна- ко это усложняет схему регистратора, поскольку для каждого диапазона требуется отдель- ный счётчик. В связи с этим представляет интерес исследование возможности реализации принципа эквивалентной оценки ресурса.
![]() Алгоритм
регистрации эквивалентной наработки
отличается от вышеприведенного тем, что вместо процедур сортировки и адресации выполняется нелинейное преобразова- ние амплитуды в соответствии с заданной кривой
разрушения (см. рис. 6.20.) В основу этого
алгоритма положена гипотеза линейного суммирования повреждений, выражаемая формулой:
Алгоритм
регистрации эквивалентной наработки
отличается от вышеприведенного тем, что вместо процедур сортировки и адресации выполняется нелинейное преобразова- ние амплитуды в соответствии с заданной кривой
разрушения (см. рис. 6.20.) В основу этого
алгоритма положена гипотеза линейного суммирования повреждений, выражаемая формулой:
|
ån Ni = 1 i=1 [Ni ] |
(6.24) |
где i =1,2,……n – номер режима нагружения;
Ni – количество циклов на i-ом режиме;
[Ni] – допустимое кол-во циклов на i-ом режиме.
Если, например, кривой разрушения определено, что при амплитуде А1 допускается 5000 циклов нагружения, а при амплитуде А2 – 1000 циклов, то одному циклу с амплиту-
дой А1 соответствует «порция» наработки эквивалентного ресурса (1/5000) ∙100% = 0,02%, а с амплитудой А2 – (1/1000) ∙100% = 0,1% .
Поскольку функциональная зависимость величины этих «порций» от амплитуды имеет существенно нелинейный характер, а именно, с увеличением амплитуды темп рас- ходования ресурса быстро возрастает, в алгоритме должно быть предусмотрено формиро- вание нелинейной статической характеристики. Форма статической характеристики опре- деляется формой кривой разрушения, индивидуальной для каждого типа сильфона, по- этому подбор стандартного датчика деформации, имеющего достаточно близкую нели- нейную характеристику, не представляется возможным. Использование же специального нелинейного преобразователя неприемлемо ввиду жестких требований к стоимости, габа- ритам и надёжности регистратора наработки. Эти обстоятельства делают целесообразной аппроксимацию исходной статической характеристики либо ступенчатой, либо кусочно- линейной функцией (рис.6.21).
— ![]() зависимость израсходованного за один цикл ресурса Ri от амплитуды цикла Ai;
зависимость израсходованного за один цикл ресурса Ri от амплитуды цикла Ai;
— аппроксимация характеристики ступенчатой функцией;
— аппроксимация характеристики кусочно-линейной функцией.
Рисунок 6.21 (слева) – Статические ха- рактеристики регистратора наработки эквивалентного ресурса.
Сопоставление графиков свидетельствует о том, что кусочно-линейная аппроксима- ция обеспечивает более точное воспроизведение заданной функции при том же числе диа- пазонов. Реализация её предполагает, очевидно, что при изменении амплитуды цикла в пределах одного диапазона единичная прибавка наработки, вносимая этим циклом, будет изменяться пропорционально его амплитуде, причем коэффициент пропорциональности должен соответствовать углу наклона данного линейного участка аппроксимирующей функции. В том случае, если амплитуда цикла превышает ширину одного диапазона,
«прибавка» должна формироваться сначала в соответствии с законом первого диапазона, затем второго и т.д. При этом на границе диапазонов необходимо переключать коэффици- ент пропорциональности, то есть дискретно изменять темп накопления наработки. После
достижения амплитудного значения накопление наработки, соответствующее циклу, должно заканчиваться и возобновляться с началом нового цикла.
Аппроксимация ступенчатой функции предполагает упрощённый вариант изложен- ного алгоритма, в котором исключено накопление внутри диапазонов и предусмотрено дискретное прибавление «порций» наработки на их границах. Оба подхода, очевидно, обеспечивают индивидуальное масштабирование каждого из циклов, что весьма важно для случайного характера нагружения в эксплуатационных условиях. Основные требования к регистратору: простота, надежность, низкая стоимость, стабильность результатов, высокая ремонтопригодность, отсутствие дефицитных материалов и дорогостоящих комплектую- щих изделий. Для выбора типа регистратора необходимо предварительно выбрать способы обработки информации в процессе измерения сдвиговых перемещений фланца сильфон- ного компенсатора, регистрации истории нагружений и представления результатов. Воз- можны следующие варианты:
· аналоговое измерение – аналоговая регистрации – аналоговая индикация;
· аналоговое измерение - дискретная регистрации – цифровая индикация;
· дискретное измерение - дискретная регистрации – цифровая индикация;
· дискретное измерение - аналоговая регистрации – аналоговая индикация. Рассмотрим сначала особенности реализации первого из указанных вариантов аппа-
ратурного обеспечения регистратора с полностью аналоговым способом обработки и представления информации.
Прежде всего, следует выбрать датчик линейных перемещений. Все предлагаемые на рынке датчики линейных перемещений принято разделять по диапазонам измерений на датчики микроперемещений (до 1 мм), датчики средних перемещений (от 0 до 50 мм), дат- чики больших перемещений (более 50 мм).
По характеру взаимодействия с контролируемым объектом имеются контактные и бесконтактные датчики. По принципу действия различают потенциометрические, оптиче- ские, вихретоковые, индукционные и другие типы датчиков.
Кроме того, при выборе датчика учитывают такие характеристики, как точность, линейность характеристики, характер выходного сигнала, массогабаритные характеристи- ки, допустимые условия эксплуатации, показатели надёжности, цена. С учётом требующе- гося диапазона измерений может быть использован, например, индуктивный датчик фир- мы «BAUMER» (модификация IWRM30), обеспечивающий бесконтактное измерение пе- ремещения стальной детали в диапазоне от 0 до 16 мм (рис.6.22). Датчик имеет погреш- ность ±1% и линейность характеристики в указанном диапазоне измерений.
Конструктивное исполнение и уровень защиты датчика позволяют использовать его в су- довых условиях.
Рисунок 6.22 – Внешний вид, габаритный чертёж и схема подключения датчика перемещений
С учётом требований к максимальной простоте и дешевизне разрабатываемого при- бора, в качестве аналогового регистрирующего устройства выбран капиллярный интегра- тор (НПО «Квант», Москва). Общий вид и электрическая схема интегратора показаны на рисунках 6.22 и 6.23.
Рисунок 6.23 – Капиллярный интегратор
Основным элементом капиллярного интегратора (КИ) является тонкая стеклянная трубка - капилляр, внутри которого находятся два столбика ртути, разделённые пузырьком электролита. На лицевой панели под трубкой находится шкала, которая может быть раз- мечена, например, от 0 до 100%. Пузырёк электролита у нового интегратора находится в начале шкалы у отметки «0%».
R,%
![]()
Рисунок 6.24 – Электрическая схема капиллярного интегратора
В оба конца трубки впаяны электроды, касающиеся ртути и соединённые проводами с делителем напряжений, состоящим из двух резисторов R1 и R2. Дополнительный регули- руемый резистор R2 служит для точной настройки характеристики прибора. Диод Д предотвращает обратное прохождение тока через капилляр. Резисторы, диод и провода находятся внутри корпуса прибора.
Если к прибору подвести постоянное напряжение в соответствии с полярностью, показанной на рисунке, на границах пузырька электролита возникнет напряжение, вели- чина которого может быть задана подбором сопротивлений резисторов R1 и R2 и R3. При этом в пузырьке будет происходить процесс электролиза: положительно заряженные ионы ртути с правого положительно заряженного столбика ртути (анода) будут переходить в раствор электролита, двигаться в нём влево и оседать на левом, отрицательно заряженном столбике ртути (катоде).
В результате проходящего таким образом по капилляру электрического тока правый столбик ртути будет уменьшаться, а левый столбик – увеличиваться на ту же величину, т.е. пузырёк электролита будет перемещаться слева направо. Величина перемещения будет зависеть от массы перенесённой в процессе электролиза ртути, которая, в соответствии с законом электролиза Фарадея, пропорциональна электрическому заряду, перенесённому в процессе электролиза.
При подаче на вход устройства постоянного напряжения U через капилляр будет идти постоянный ток i, и величина заряда будет определяться произведением тока на вре- мя: q = i∙t . Перемещение пузырька, как уже было сказано, будет пропорционально заряду: X=K∙q = K∙i∙t (6.24)
Если на вход устройства подавать изменяющееся во времени напряжение U(t), через капилляр будет идти ток i(t), пропорциональный напряжению U(t). Перемещение пузырька будет определяться выражением:
|
T x = K × ò i(t)dt 0 |
(6.25) |
Поэтому это устройство и называется интегратором. Если на него подавать импуль- сы напряжения, величина которых соответствует амплитуде перемещений фланца силь- фонного компенсатора, то пузырёк электролита будет перемещаться вдоль шкалы тем быстрее, чем больше будет амплитуда и частота циклов деформации сильфонного компен- сатора. Подключение капиллярного интегратора (КИ) к датчику перемещений (ДП), ди- станционно измеряющего перемещения фланца сильфонного компенсатора (ФСК), пока- зано на рис. 6.26.
![]()
![]()
Uпит.
Рисунок 6.26 – Схема измерения перемещений фланца сильфонного компенсатора
![]() Для
исключения прохождения тока через капиллярный интегратор при статичном состоянии сильфонного компенсатора (т.е.
при отсутствии циклов деформации), датчик линейных
перемещений фланца компенсатора можно подключить к регистратору через дифференцирующую R-C цепочку. На рис. 6.27 показаны временные
диаграммы, поясня- ющие действие схемы измерений.
Для
исключения прохождения тока через капиллярный интегратор при статичном состоянии сильфонного компенсатора (т.е.
при отсутствии циклов деформации), датчик линейных
перемещений фланца компенсатора можно подключить к регистратору через дифференцирующую R-C цепочку. На рис. 6.27 показаны временные
диаграммы, поясня- ющие действие схемы измерений.
|
X, мм
t, с
Uвх. В
t, с
R, %
t, с |
Рисунок 6.27 – Временные диаграммы работы измерительной схемы Верхняя диаграмма показывает линейные перемещения Х фланца сильфонного компенса- тора циркуляционного контура главного кон- денсатора. Сдвиговые деформации вызваны перемещениями главно- го конденсатора, уста- новленного на гибких амортизаторах, в про- цессе качки судна. |
На второй диаграмме показан продифференцированный сигнал датчика, подавае- мый на вход капиллярного интегратора. Отрицательная зона сигнала выделена пунктиром, поскольку соответствующий ей обратный ток через капилляр не пропускается встроенным диодом. На нижней диаграмме показано перемещение вдоль капилляра пузырька электро-
![]() лита, вызванное
импульсами тока. Амплитуды импульсов, а значит, и соответствующие перемещения пузырька вдоль шкалы, связаны с величиной деформаций сильфона.
лита, вызванное
импульсами тока. Амплитуды импульсов, а значит, и соответствующие перемещения пузырька вдоль шкалы, связаны с величиной деформаций сильфона.
Важно отметить, что предложенная схема регистрации истории эксплуатационных нагружений сильфонного компенсатора позволяет совместить в одном устройстве – ка- пиллярном интеграторе, функции обработки и представления информации и надёжного хранения результатов в течение неограниченного срока, т.к. отключение от схемы элек- трического питания и даже её полный демонтаж не стирают показания на шкале прибора.
Рассмотренный аналоговый вариант счётчика наработки ресурса сильфонного ком- пенсатора достаточно прост, надёжен и дёшев, полностью скомпонован из серийно выпус- каемых элементов. Однако в том случае, когда требуется вывод информации в систему централизованного контроля оборудования, предпочтительнее использовать варианты с цифровым представлением результатов.
![]() Для реализации дискретного
способа обработки информации выберем наиболее простой в реализации метод регистрации истории эксплуатационных
нагружений – ре- гистрацию количества
и амплитуды циклов с разбивкой амплитуды на дискретные диа- пазоны. Для упрощения регистрирующего
устройства возложим функцию распределе- ния
измеряемого перемещения по амплитудным диапазонам непосредственно на изме- рительное
устройство. Для этого на подвижном
фланце сильфонного компенсатора установим малогабаритный магнит, а в качестве измерительного
устройства применим сборку из
нескольких герконов, расстояние между которыми выбрано таким образом, что каждый из герконов срабатывает при
перемещении магнита на величину соответ- ствующего амплитудного диапазона (рис. 6.28).
Для реализации дискретного
способа обработки информации выберем наиболее простой в реализации метод регистрации истории эксплуатационных
нагружений – ре- гистрацию количества
и амплитуды циклов с разбивкой амплитуды на дискретные диа- пазоны. Для упрощения регистрирующего
устройства возложим функцию распределе- ния
измеряемого перемещения по амплитудным диапазонам непосредственно на изме- рительное
устройство. Для этого на подвижном
фланце сильфонного компенсатора установим малогабаритный магнит, а в качестве измерительного
устройства применим сборку из
нескольких герконов, расстояние между которыми выбрано таким образом, что каждый из герконов срабатывает при
перемещении магнита на величину соответ- ствующего амплитудного диапазона (рис. 6.28).
|
Фланец сильфонного компенсатора
Магнит
Сборка герконов |
Рисунок 6.28 (слева) − Схема измерения перемещений фланца сильфонного компенсато- ра с помощью сборки герконов Преимущества применения геркона: высокая надежность (до 106 циклов срабатыва- ния), защищенность контактов от внешней сре- ды, низкая стоимость, простота замены; геркон является элементом с «сухими контак- тами», т.е. при подключении его к какой-либо схеме не надо заботиться о гальванической раз- вязке. |
Цифровой способ накопления и хранения информации о количестве циклов нагружения и распределения циклов по амплитуде предполагает использование специ- альных микросхем, выполняющих функции счётчиков.
Проведенный анализ типовых счетчиков показывает, что функциональные воз- можности специализированных микросхем обеспечивают несколько вариантов органи- зации счетчика, соответствующего следующим требованиям:
· тип счетчика – двоично-десятичный, реверсивный;
· количество десятичных разрядов – 6.
Обозначим такой счетчик аббревиатурой РС (реверсивный счетчик) и будем рас- сматривать его в качестве средства учета количества циклов нагружения компенсатора, соответствующего одному из заданных диапазонов амплитуды деформации сильфона. Диапазонный учет наработки можно организовать, подключив дискретные датчики (герконы) к счетчикам в соответствии с функциональной схемой, показанной на рис. 6.29.
Обозначим символом «+» вход счетчика, который обеспечивает при подаче на не- го импульсного сигнала увеличение хранящегося кодового слова на единицу (операцию
- РС4 ФИ4 + - РС3 ФИ3 + - РС2 ФИ2 + - РС1 ФИ1 +
«инкремент»). Символом «-»
обозначим вход счетчика, который обеспечивает при по- даче на него импульсного сигнала уменьшение хранящегося кодового
слова на единицу (операцию «декремент»).
![]() Рисунок 6.29 (слева) − Функциональная схема диапазонного учета циклических деформаций сильфонного компенсатора
Рисунок 6.29 (слева) − Функциональная схема диапазонного учета циклических деформаций сильфонного компенсатора
![]() Условные
обозначения на схеме: Д1, Д2, Д3,
Д4 – дискретные датчики деформации
сильфона (герконы);
Условные
обозначения на схеме: Д1, Д2, Д3,
Д4 – дискретные датчики деформации
сильфона (герконы);
![]() Ф1, Ф2, Ф3, Ф4 – формирователи импульсов;
Ф1, Ф2, Ф3, Ф4 – формирователи импульсов;
При деформации сильфона закрепленный на одном из его фланцев магнит прохо- дит мимо герконов и вызывает замыкание их контактов (рис. 6.28).
При этом подаётся напряжение на соответствующие формирователи импульсов, которые по переднему фронту сигналов от герконов формируют короткие прямоуголь- ные импульсы, поступающие на входы счетчиков. Формирование счетных импульсов требуется для того, чтобы устранить влияние гистерезиса герконов. Если деформация сильфона в данном цикле нагружения соответствует первому амплитудному диапазону (самому малому), то срабатывает только счетчик РС1, который, получив сигнал на входе
«+», увеличивает хранящееся в нём число на 1. Если деформация сильфона в данном цикле нагружения соответствует второму амплитудному диапазону (который больше первого), то сначала срабатывает первый датчик и первый счетчик РС1, который, полу- чив сигнал на входе «+», увеличивает хранящееся в нем число на 1. Затем срабатывает второй датчик, посылающий через формирователь импульсов сигнал на вход «-» перво- го счетчика РС1 и на вход «+» второго счетчика РС2. В результате счетчик РС1 умень- шает хранящееся в нём число на 1 (т.е. возвращается в исходное положение), а счетчик РС2 увеличивает хранящееся в нем число на 1. Аналогичным образом действует схема при любой амплитуде деформации сильфона, благодаря чему осуществляется сортиров- ка по амплитуде и раздельный подсчёт циклов нагружения сильфонных компенсаторов.
Каждый из предложенных вариантов аппаратурного обеспечения регистрации ис- тории эксплуатационных нагружений судовых сильфонных компенсаторов имеет как специфические преимущества, так и определённые недостатки.
Первый вариант с капиллярным интегратором прост, надёжен и дёшев, полностью скомпонован из серийно выпускаемых элементов, однако не позволяет выводить ре- зультаты в цифровой форме в систему централизованного контроля оборудования.
Вариант с герконами и счётчиками допускает подключение счётчиков к централи- зованной системе для дистанционного снятия текущей информации об остаточном ре- сурсе сильфонного компенсатора. Однако он менее точен, чем аналоговый вариант, по- скольку предусматривает разбивку гладкой кривой длительной прочности сильфона на несколько дискретных диапазонов.
В качестве контролируемого объекта рассмотрим трубопровод внешнего контура системы охлаждения оборудования морского судна. Основным разрушающим
![]()
![]() процессом
является химическая и электрохимическая коррозия внутренней поверхности труб в результате их длительного
контакта с потоком морской воды (рис. 6.30).
процессом
является химическая и электрохимическая коррозия внутренней поверхности труб в результате их длительного
контакта с потоком морской воды (рис. 6.30).
Рисунок 6.30 – Новые медные трубы и коррозия внутренней поверхности трубы Повышенная агрессивность морской воды связана с наличием в ней ионов хлора и
Рисунок 6.31 – Схема стендовой установки для коррозионных испытаний
1 – расходная цистерна; 2 – дроссельный клапан; 3 – дроссельная шайба; 4 – дифмано- метр; 5 – кассета с образцами; 6 – цистерна запаса; 7 - электронагреватель; 8- ре- гулятор температуры; 9 – датчик температуры (термометр сопротивления);
10 – датчик давления; 11 – регулятор давления; 12 - преобразователь частоты тока;
13 – асинхронный электродвигатель центробежного насоса; 14 – центробежный насос; 15 – напорный трубопровод; 16 – сливной трубопровод; 17 – запорный поплав- ковый клапан; 18 – трубопровод с воронкой для пополнения запаса воды.
Исследования проводились для ряда конструкционных материалов, применяемых в судостроении для изготовления деталей систем охлаждения, контактирующих с морской водой:
· медно-никелевый сплав – МНЖ5-1 (ГОСТ 492-73);
· медь – М3Р (ГОСТ 859-78).
Методика проведение эксперимента заключалась в следующем.
Расходная цистерна 1 и цистерна запаса 6 заполнялась искусственно приготов- ленной морской водой. Образцы при закрытых клапанах 2 помещались в кассеты, после чего открытием клапанов 2 вода подавалась в кассеты с образцами. Скорость потока воды через кассеты в первом приближении определялась высотой уровня воды в рас- ходной цистерне над соответствующей линией подачи воды в кассеты: чем выше линия подачи воды в кассету, тем меньше напор в этой линии, а значит и скорость потока во- ды. Точная настройка скоростей потока выполнялась степенью открытия дросселирую- щих клапанов и контролировалась с помощью дифманометров 4, измеряющих перепа- ды давления на дроссельных шайбах 3.
Для стабильного поддержания скоростей потока в кассетах, в расходной цистерне поддерживался постоянный уровень воды с помощью контура регулирования, состоя- щего из датчика давления 10, ПИ-регулятора 11и преобразователя частоты тока 12, под- ключённого к электродвигателю 13 насоса 14. Нужное значение температуры воды под- держивалось с помощью контура регулирования, состоящего из датчика температуры 9, ПИ-регулятора 8 и электронагревателя 7. Защита расходной цистерны 1 от перелива обеспечивалась сливным трубопроводом 16. Расходная цистерна 6 поплавковым запор- ным клапаном 17 защищалась от перелива (при отказе контура управления насосом или несанкционированном отключении питающего напряжения).
Скорость коррозионного процесса оценивалась весовым методом путём периоди- ческого взвешивания образцов и вычисления скорости потери массы: i (г/м2·час).
Перед основным этапом длительных испытаний выполнялась экспериментальная оценка времени стабилизации коррозионного процесса.
Из литературных источников и анализа опыта эксплуатации и дефектации обору- дования судовых систем известно, что скорость коррозии на разных стадиях развития процесса существенно изменяется: сначала она растёт, после достижения максимума уменьшается, и затем стабилизируется, приобретая характер очень пологой, медленно возрастающей кривой. Поэтому на первом этапе исследований ставилась задача опреде- ления периода стабилизации процесса коррозии с тем, чтобы задать необходимую дли- тельность выдержки в воде образцов при проведении основного этапа испытаний. Ис- пытания проводились при скорости потока Vср. = 3,5 м/сек и температуре воды Т=90°С. Результаты проведения первого этапа применительно к образцам из МНЖ5- 1представлены на рис. 6.32.
![]()
i, г/м2·час
0,6
![]()
![]() 0,5
0,5
0,4
0,3
0,2
0,1
0 40
80 120
160 200 240 280 320 360 Т, час
![]() Наработка образца
Наработка образца
Рисунок 6.32 – Зависимость скорости коррозии от наработки
Как показал анализ полученных данных, зависимость скорости коррозии от вре- мени на интервале 0÷150 часов отличается сильной нестабильностью. Поэтому для по- строения математической модели процесса коррозии было принято использовать изме- ренные скорости коррозии при наработке 300 часов и более.
Основной целью эксперимента являлось определение численных значений коэф- фициентов регрессионной модели, описывающей зависимость скорости коррозии от температуры морской воды и скорости потока. На основании анализа литературных данных было установлено, что в общем случае эта зависимость нелинейна. Поэтому план эксперимента должен быть нацелен на построение модели второго порядка, вклю-
чающей линейную часть, эффекты взаимодействия факторов (их произведения) и квад- ратичные элементы:
где: Х1 – скорость потока;
Х2 – температура воды.
![]()
![]() Выбор плана эксперимента был предопределён видом регрессионной модели (6.29):
наличие квадратичных элементов требует применения плана, предусматриваю- щего не менее трёх уровней
варьирования факторов. Был выбран центрально- композиционный план. В общем виде такой план для двух факторов
графически выгля- дит следующим
образом (см. рис. 6.33 слева). Однако обеспечение ортогональности плана накладывает определённые требования
на величину звёздного плеча α:
для двух факторов звёздное
плечо должно равняться 1.
Выбор плана эксперимента был предопределён видом регрессионной модели (6.29):
наличие квадратичных элементов требует применения плана, предусматриваю- щего не менее трёх уровней
варьирования факторов. Был выбран центрально- композиционный план. В общем виде такой план для двух факторов
графически выгля- дит следующим
образом (см. рис. 6.33 слева). Однако обеспечение ортогональности плана накладывает определённые требования
на величину звёздного плеча α:
для двух факторов звёздное
плечо должно равняться 1.
|
X2
2 7 1 α 6 9 α X1 α 5 α 3 8 4 |
2 X2 1 7
6 9 5 X1
8 3 4 Рисунок 6.33 – Планы ЦКП |
Соответствующий ортогональный ЦКП показан на рис. 6.33 (справа).
При диапазоне изменения фактора Х1 (скорости потока) от 1 до 6 м/с в центре плана Х1 будет иметь значение 3,5 м/с, а интервал варьирования ΔХ1 будет равен 2,5 м/с. При диапазоне изменения фактора Х2 (температуры воды) от 21 до 89°С в центре плана Х2 будет иметь значение 55°С, а интервал варьирования ΔХ2 будет равен 34°С (рис. 6.34). Вторым условием получения ортогональной матрицы является специальная под-
X
Н
становка переменных. После введения новых переменных 1 и
Н
X
2 матрица планиро-
вания приобрела следующий вид, представленный в табл. 6.10.
1 2 3 4 5 Х 9 8 6 7 ![]()
Х1 (V, м/с)
![]()
![]()
![]() 6,0
6,0
![]()
![]() 5,0
5,0
4,0
![]()
3,0
2,0
1,0
Рисунок 6.41 (слева) -
План эксперимента
с натуральными значениями факторов
![]()
![]() 10 20 30 40 50
10 20 30 40 50
![]() 60 70 80 90
60 70 80 90
2 (t,°C)
![]()
Таблица 6.10. Матрица планирования
|
|
B0 |
B1 |
B2 |
B12 |
B11 |
B22 |
|
|
№ |
X0 |
X1 |
X2 |
X1∙X2 |
XН 1 |
XН 2 |
iср., г/м2·час |
|
1 |
+1 |
+1 |
-1 |
-1 |
+1/3 |
+1/3 |
0,5 |
|
2 |
+1 |
+1 |
0 |
0 |
+1/3 |
-2/3 |
1,5 |
|
3 |
+1 |
+1 |
+1 |
+1 |
+1/3 |
+1/3 |
1,0 |
|
4 |
+1 |
0 |
+1 |
0 |
-2/3 |
+1/3 |
0,75 |
|
5 |
+1 |
-1 |
+1 |
-1 |
+1/3 |
+1/3 |
0,5 |
|
6 |
+1 |
-1 |
0 |
0 |
+1/3 |
-2/3 |
0,9 |
|
7 |
+1 |
-1 |
-1 |
+1 |
+1/3 |
+1/3 |
0,05 |
|
8 |
+1 |
0 |
-1 |
-0 |
-2/3 |
+1/3 |
0.25 |
|
9 |
+1 |
0 |
0 |
0 |
-2/3 |
-2/3 |
1,25 |
После подготовки плана и матрицы выполнялся сам эксперимент с образцами. Для обеспечения заданной наработки выдержка образцов при заданных условиях долж- на была составлять 300 часов. При одиночном проведении опытов общая продолжи- тельность эксперимента составила бы 300·9=2700 часов. Однако схема стендовой уста- новки, показанной на рис. 6.38, позволила проводить одновременно 3 опыта с одной температурой воды, но разными скоростями потока. Т.е. опыты 7 – 8 – 1, затем опыты 6
– 9 – 2 и опыты 5 – 4 – 3. Это позволило сократить общее время эксперимента в три ра- за, т.е. до 900 часов.
Правый столбец матрицы заполнен после проведения опытов с образцами из ме- ди и вычисления средней для образцов каждой кассеты скорости коррозии. Поскольку матрица ортогональна, для вычисления коэффициентов можно было применить доста- точно простой алгоритм.
После пересчёта коэффициентов с учётом произведённой подстановки перемен- ных и подстановки их в исходное выражение получено следующее выражение для ре- грессионной модели процесса коррозии меди в морской воде:
|
где Х1 = (V- 3,5)/2,5 – относительное значение скорости потока;
Х2 = (t- 55)/34 – относительное значение температуры воды.
Абсолютные значения коэффициентов характеризуют силу влияния соответству- ющего элемента модели на отклик (скорость коррозии). Применение оценки значимости коэффициентов с помощью критерия Стьюдента позволило упростить модель, прирав- няв нулю малозначимые коэффициенты (четвёртый и пятый). После упрощения модель получила следующий вид:
|
Полученные результаты в графическом виде представлены на рис. 6.42.
iВ, г/м2·час
![]() 2,0
2,0
1,8
1,6
1,4
1,2
1,0
0,8
0,6
0,4
0,2
10 20 30 40 50 60 70 80 90
6 м/с
![]() 3,5 м/с 1м/с
3,5 м/с 1м/с
t,°C
![]()
Рисунок 6.42 (слева) –
Зависимость скорости корро- зии от температуры морской воды для меди М3Р при нара- ботке 300 часов и скорости воды 1, 3,5 и 6 м/с
(«жирные» точки – резуль- таты опытов, штриховая ли- ния – аппроксимация)
Адекватность, т.е. соответствие полученной математической модели реальным свойствам исследуемого процесса, проверялась путём сопоставления опытных результа- тов и результатов, вычисленных с помощью модели (при подстановке в неё тех же отно- сительных значений факторов. Результаты сопоставления приведены в табл. 6.11.
Таблица 6.11. Оценка расхождения опытных и модельных результатов
|
№ |
X1 |
X2 |
iоп. , г/м2·час |
iмод. , г/м2·час |
Δi |
(Δi)2 |
|
1 |
+1 |
-1 |
0,5 |
0,568 |
0,068 |
0,0046 |
|
2 |
+1 |
0 |
1,5 |
1,508 |
0,008 |
0 |
|
3 |
+1 |
+1 |
1,0 |
1.048 |
0,048 |
0,0023 |
|
4 |
0 |
+1 |
0,75 |
0,790 |
0,040 |
0,0016 |
|
5 |
-1 |
+1 |
0,5 |
0,532 |
0,032 |
0,0010 |
|
6 |
-1 |
0 |
0,9 |
0,920 |
0,020 |
0,0004 |
|
7 |
-1 |
-1 |
0,05 |
0,052 |
0,002 |
0 |
|
8 |
0 |
-1 |
0.25 |
0,310 |
0,060 |
0.0036 |
|
9 |
0 |
0 |
1,25 |
1,250 |
0 |
0 |
Средняя дисперсия результатов: Dср. = [Σ(Δi)2]/9=0,0015 Среднеквадратичное отклонение: СКО = (Dср.)1/2 = 0,0387 Средняя для эксперимента скорость коррозии: i = (Σiоп.)/9 = 0,74 Относительная погрешность модели: δ = СКО/ i = 0.052 = 5,2%
Полученное значение средней погрешности модели можно считать вполне удо- влетворительным, а модель – адекватной. Применение критерия Фишера подтвердило вывод об адекватности модели.
Чувствительность модели (т.е. её способность реагировать на изменения факто- ров) оценивалась путём сопоставления абсолютное значения свободного члена (коэф- фициента b0) с абсолютными значениями остальных коэффициентов (чем меньше коэф- фициент b0 , тем чувствительнее модель). В полученной модели коэффициенты имеют достаточно близкие значения:
Это позволяет сделать предположение о достаточной чувствительности модели к изменению факторов. Действительно, сопоставление модельной оценки скорости корро- зии в опытах 7 и 3 (см. табл. 6.18.), показывает, что при изменении относительных зна-
чений обоих факторов на противоположные вычисленный результат изменяется при- мерно в 20 раз.
Линейность модели определяют по наличию или отсутствию эффектов взаимо- действия факторов и квадратичных элементов. В исходной модели (выражение 6.26) ко- эффициенты при квадрате фактора Х1 и произведении Х1·Х2 оказались мало значимыми, и в упрощённой модели соответствующие элементы отсутствуют. Поэтому она имеет смешанный характер: линейна по отношению к фактору Х1 и нелинейна по отношению к Х2 .
Силу влияния факторов на результат оценивают, сопоставляя абсолютные значе- ния коэффициентов. В полученной модели коэффициенты b1 и b2 имеют достаточно близкие значения. Правда, фактор Х2 имеет ещё и квадратичный элемент с достаточно весомым коэффициентом, однако отрицательное значение этого коэффициента умень- шает значение линейного элемента, имеющего положительный знак. Поэтому в целом можно сделать вывод о том, что в исследованной области эксперимента фактор Х1 (ско- рость потока) оказывает более существенное влияние на скорость коррозии, чем фактор Х2 (температура).
Направление влияния факторов на результат оценивают, сопоставляя знаки коэф- фициентов. Фактор Х1 имеет положительный коэффициент при линейном элементе, по- этому можно однозначно утверждать, что в исследованной области эксперимента уве- личение скорости потока будет способствовать увеличению скорости коррозии.
Фактор Х2 имеет положительный коэффициент при линейном элементе, но отри- цательный элемент при квадратичном элементе. Это приводит к тому, что увеличение температуры воды сначала приводит к увеличению скорости коррозии, однако при дальнейшем росте температуры процесс коррозии замедляется (см. рис. 6.42). Физиче- ски это можно объяснить тем, что повышение температуры реагентов всегда увеличива- ет скорость протекания химических реакций, в том числе и химическую коррозию. Од- нако последующее замедление темпа коррозии объясняется, видимо, тем, что с увеличе- нием температуры воды уменьшается количество растворённого в ней кислорода, кото- рый играет важную роль в коррозионном разрушении поверхности металла, контакти- рующего с водой.
По полученным многофакторным регрессионным зависимостям были построены и проанализированы для разных материалов частные характеристики.
Зависимости скорости коррозии от температуры при постоянной скорости потока пока- заны на рис. 6.43.
![]()
![]() iВ,
г/м2·час iВ, г/м2·час
iВ,
г/м2·час iВ, г/м2·час
0 10 20 30 40 50 60 70 80 90
0 10 20 30 40 50 60 70 80 90
Рисунок 6.43 – Зависимость скорости коррозии меди М3Р (слева) и медно-никелевого сплава МНЖ5-1(справа) от температуры морской воды
Из рисунков видно, что для разных материалов температура воды по-разному вли- яет на скорость коррозии. Например для меди М3Р в районе 60°С наблюдается точка максимума. Её координата на температурной оси может быть получена так-же диффе- ренцированием регрессионного уравнения для меди:
X2 = 0,24/1,4 = 0,172 = (tmax. - 55)/34 tmax.=34·0,172+55=61°C
Скорость коррозии сплава МНЖ5-1 в области эксперимента максимума не имеет. (рис. 6.44).
V
![]()
1,6
1,4
1,2
1,0
0,8
0
iВ, г/м2·час
1 2 3 4 5 6 7
, м/с
![]()
![]()
0,9
0,8
0,7
0,6
0,5
0,4
0
iВ, г/м2·час
V
1 2 3 4 5 6 7
, м/с
![]()
Рисунок 6.44 – Зависимость скорости коррозии меди М3Р (слева) и медно-никелевого сплава МНЖ5-1 (справа) от скорости потока морской воды
Полученная регрессионная модель и частные характеристики могут быть исполь- зованы для многорежимного прогнозирования степени коррозионных повреждений тру- бопровода во время эксплуатации судна при различных сочетаниях рассмотренных ре- жимных факторов (скорости и температуры морской воды). Для этого на каждом из ре- жимов достаточно вычислить скорость коррозии и, умножив её на запланированную длительность режима, получить прогнозируемую степень износа трубопровода на дан- ном режиме. Просуммировав предполагаемые степени износа на всех ожидаемых режи- мах, можно оценить итоговую степень износа. Обязательные условия применимости та- кого алгоритма:
− наличие запланированного на прогнозный период спектра режимов использования энергетической установки судна и связанного с ним временного графика режимов си- стемы охлаждения;
− наличие предварительно определённой регрессионной модели (и частных характери- стик), позволяющих для каждого режима, заданного сочетанием значений рассмот- ренных факторов (скорости потока и температуры морской воды), определить пред- полагаемую скорость коррозии трубопровода;
− справедливость гипотезы о возможности линейного суммирования повреждений, по- лученных на разных режимах эксплуатации.
Для оценки работоспособности рассмотренного алгоритма были проведены дли- тельные испытания коррозионной стойкости в морской воде образцов из меди М3Р и сплава МНЖ5-1. В процессе испытаний чередовали различные спецификационные ре- жимы с соответствующими изменениями температуры воды и скорости потока, и изме- ряли скорости коррозии на каждом из режимов, итоговую потерю массы в конце каждо- го режима и накопленную потерю массы (табл.6.12).
Таблица 6.12. Результаты испытаний коррозионной стойкости образцов на заданных спецификационных режимах
|
Материал |
Параметры режимов |
Длитель- ность режима ΔТ, час. |
Потери массы образцов за время ΔТ, мг |
||||||
|
1 пара |
2 пара |
3 пара |
|||||||
|
t, °С |
V, м/с |
Обра- зец 1.1 |
Обра- зец 1.2 |
Обра- зец 2.1 |
Обра- зец 2.2 |
Обра- зец 3.1 |
Обра- зец 3.2 |
||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Медь М3Р |
20 |
1,5 |
510 |
55,6 |
61,7 |
52,2 |
52,7 |
75,6 |
65,9 |
|
22 |
1,5 |
1300 |
101,7 |
108,7 |
108,2 |
120,1 |
100,7 |
94,9 |
|
|
89 |
3,5 |
545 |
186,5 |
182,1 |
152,1 |
141,8 |
123,7 |
139,9 |
|
|
55 |
6,0 |
400 |
294,1 |
304,3 |
311,5 |
342,8 |
295,3 |
324,4 |
|
Окончание таблицы 6.12
|
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
||||
|
55 |
3,5 |
330 |
180,4 |
200,6 |
190,1 |
201,9 |
190,7 |
185,7 |
|||||
|
21 |
3,5 |
420 |
61,2 |
62,9 |
62,5 |
60,0 |
41,6 |
31,7 |
|||||
|
55 |
1,0 |
276 |
111,9 |
114,4 |
110,0 |
112,3 |
86,6 |
63,0 |
|||||
|
Итого: |
3781 |
991,4 |
1034,7 |
986,6 |
1031,6 |
914,2 |
905,5 |
||||||
|
2026,1 |
2018,2 |
1819,7 |
|||||||||||
|
Сплав МНЖ 5-1 |
20 |
1,5 |
510 |
59,7 |
47,5 |
47,3 |
46,8 |
14,0 |
26,3 |
||||
|
20 |
1,5 |
1300 |
84,4 |
76,7 |
77,0 |
72,9 |
32,8 |
37,0 |
|||||
|
89 |
3,5 |
545 |
183,6 |
169,5 |
187,3 |
175 |
61,4 |
81,9 |
|||||
|
55 |
6,0 |
400 |
269,1 |
315,7 |
278,3 |
319,7 |
170,0 |
167,3 |
|||||
|
55 |
3,5 |
330 |
174,5 |
183,5 |
133,6 |
137,6 |
100,7 |
77,7 |
|||||
|
21 |
3,5 |
420 |
44,9 |
44,7 |
44,5 |
45,0 |
26,0 |
27,5 |
|||||
|
55 |
1,0 |
276 |
87,7 |
77,3 |
85,2 |
78,8 |
60,7 |
54,4 |
|||||
|
Итого: |
3781 |
903,9 |
914,9 |
853,2 |
875,8 |
465,6 |
472,1 |
||||||
|
1818,8 |
1728,2 |
937,7 |
|||||||||||
По результатам, приведённым в табл. 6.12, вычисляли накопленную потерю массы путём суммирования потерь на отдельных режимах (табл.6.13).
Таблица 6.13. Результаты вычислений суммарного коррозионного повреждения образцов за время длительных испытаний
|
Материал |
Параметры режимов |
Время Т, час |
Потери массы образцов М, мг |
||||||
|
1 пара |
2 пара |
3 пара |
|||||||
|
t, °С |
V, м/с |
Потеря за ΔТ |
Потеря за Т |
Потеря за ΔТ |
Потеря за Т |
Потеря за ΔТ |
Потеря за Т |
||
|
Медь М3Р |
20 |
1,5 |
510 |
117.3 |
117.3 |
104,9 |
104,9 |
141,5 |
141,5 |
|
22 |
1,5 |
1810 |
210,4 |
327,7 |
228,3 |
333,2 |
194,6 |
336.1 |
|
|
89 |
3,5 |
2355 |
368,6 |
696,3 |
293,9 |
627,1 |
264,5 |
600,6 |
|
|
55 |
6,0 |
2755 |
598,4 |
1294,7 |
654,3 |
1281,4 |
619,7 |
1220,3 |
|
|
55 |
3,5 |
3085 |
381 |
1675,7 |
392 |
1673,4 |
376,4 |
1596,7 |
|
|
21 |
3,5 |
3505 |
124,1 |
1799,8 |
122,5 |
1795,7 |
73,3 |
1670 |
|
|
55 |
1,0 |
3781 |
226,3 |
2026,1 |
222,3 |
2018,2 |
149,6 |
1819,7 |
|
|
Сплав МНЖ 5-1 |
20 |
1,5 |
510 |
107,2 |
107,2 |
94,1 |
94,1 |
40,3 |
40,3 |
|
20 |
1,5 |
1810 |
161,1 |
268,3 |
149,9 |
243,2 |
69,8 |
110,1 |
|
|
89 |
3,5 |
2355 |
353,1 |
621,4 |
362,3 |
605,5 |
143,3 |
253,4 |
|
|
55 |
6,0 |
2755 |
584,8 |
1206,2 |
598 |
1203,5 |
337,3 |
590,7 |
|
|
55 |
3,5 |
3085 |
358 |
1564,2 |
271,2 |
1474,7 |
178,4 |
769,1 |
|
|
21 |
3,5 |
3505 |
89,6 |
1653,8 |
89,5 |
1564,2 |
53,5 |
822,6 |
|
|
55 |
1,0 |
3781 |
165 |
1818,8 |
164 |
1728,2 |
115,1 |
937,7 |
|
![]() 2000
2000
1800
1600
1400
1200
1000
800
600
400
200
0 200
400
600
800
1000
1200
1400 1600 1800 2000 2200 2400 2600 2800 3000 3200 3400
Т, час.
Рисунок 6.45 – Результаты длительных коррозионных испытаний на спецификационных режимах образцов меди М3Р и сплава МНЖ 5-1 (сплошные линии – прогноз, штриховые линии – экспериментальные данные)
Параллельно экспериментально контролировали фактическую накопленную по- терю массы путём периодического взвешивания образцов. Сопоставление расчётных и экспериментальных данных подтвердило справедливость для данного процесса гипоте- зы о линейном суммировании повреждений и работоспособность алгоритма прогнози- рования, основанного на определении долевых повреждений на отдельных режимах пу- тём умножения средней для данного режима скорости повреждения на длительность режима и последующего суммирования долевых повреждений.
На основании полученных расчётно-экспериментальных данных для заданного графика изменения во времени режимов эксплуатации системы охлаждения можно по- строить зависимость М = f(t) (рис. 6.45).
Эта зависимость позволяет либо спрогнозировать ожидаемую степень поврежде- ния трубопровода при заданной наработке, либо оценить остаточный ресурс трубопро- вода при заданной предельной степени коррозионного повреждения. Аналогичным спо- собом можно получить эту расчётную зависимость для любого временного графика из- менения режимных параметров, причём при изменении этого графика во время эксплуа- тации нетрудно изменить и прогнозные оценки. При этом точность прогнозов будет определяться степенью адекватности математической модели и точностью измерения (или косвенного определения) режимных параметров во время эксплуатации объекта.
Газотурбинные установки (ГТУ) нашли широкое применение в качестве главных двигателей на надводных военных кораблях и судах с динамическими принципами под- держания благодаря ряду существенных достоинств: компактность и высокая мощность, широкий диапазон единичных мощностей газотурбинных двигателей (5÷20 МВт) и воз- можность компоновки их в агрегаты из нескольких двигателей, высокая маневренность (запуск и вывод на полную мощность за 2÷3 минуты), хорошая приспособленность к ав- томатизации и управлению, относительно небольшое число вспомогательных механиз- мов и систем, малошумность, экологичность, возможность быстрой агрегатной замены при аварийном повреждении или исчерпании назначенного ресурса. Основным пре- имуществом ГТУ является самая большая из всех применяемых в судостроении энерге- тических установок удельная мощность, которая достигается за счёт высокого уровня интенсивности рабочих процессов и эксплуатационных нагрузок основных узлов и де- талей газотурбинного двигателя (ГТД). Тяжёлые условия эксплуатации характерны для
многих компонентов ГТД, и в первую очередь, для рабочих лопаток газовых турбин, находящихся во время работы ГТД в сложном напряжённом состоянии в связи с сово- купным воздействием высоких температур и центробежных сил. Способность материала лопаток длительное время выдерживать это сложное напряжённое состояние без разру- шения принято называть жаропрочностью конструкционного материала. Значительный вклад в сокращение долговечности лопаток газовых турбин вносят и процессы высоко- температурной коррозии и разупрочнения поверхностного слоя металла, вызванные воздействием высокоскоростного и высокотемпературного газового потока, содержаще- го кислород и некоторые агрессивные компоненты, образующиеся при сгорании топли- ва (например, соединения серы и ванадия). Способность поверхностного слоя материала лопаток длительное время противостоять высокотемпературной коррозии принято называть жаростойкостью. В ряде исследований экспериментально показано наличие взаимовлияния этих процессов эксплуатационной деградации газотурбинных лопаток.
Несмотря на достигнутый к настоящему времени прогресс в разработке и приме- нении методов и средств технической диагностики, безразборный инструментальный контроль степени эксплуатационной деградации газотурбинных лопаток (особенно накопления внутренних изменений структуры металла) в судовых условиях не возмо- жен. В этой связи практически значимыми являются методы оценки фактической нара- ботки и остаточного ресурса ГТД, в основе которых лежит регистрация истории эксплу- атационных нагружений путём мониторинга во время работы двигателя режимных па- раметров, характеризующих интенсивность разрушающих процессов, и времени работы двигателя на каждом из режимов. Совместная обработка указанных режимных пара- метров и временных интервалов, характеризующих продолжительность работы ГТД на различных режимах, может выполняться либо с помощью автономных приборов (их принято называть счётчиками наработки ресурса – СНР) либо средствами централизо- ванной системы контроля и диагностики.
В любом из отмеченных аппаратурных вариантов обработка информации выпол- няется в соответствии с алгоритмом, структура которого определяется принятой мето- дикой оценки фактической доли израсходованного ресурса.
Регистрация наработки ГТД в единицах времени не отражает интенсивность фак- тического нагружения и темп расходования ресурса двигателя и его основных деталей в эксплуатации, так как двигатели, даже одного типа, эксплуатируются с различной сте- пенью напряженности в зависимости от задаваемых скоростей корабля во время рейса и
необходимых для обеспечения этих скоростей мощностей главного двигателя, атмо- сферных условий и прочих факторов. Поэтому очевидна необходимость объективной оценки степени выработки ресурса путем приведения режимов работы двигателя к од- ному в каких-то единицах эквивалентной наработки. В основу рассматриваемого ниже способа приведения режимов работы двигателя и вычисления эквивалентной наработки положен закон линейного суммирования повреждения, преобразованный к виду, удоб- ному для использования в реальной эксплуатации.
![]()
![]() Исходя из того, что подсчет эквивалентной наработки будет производиться в условиях
эксплуатации, очевидно, что вычисление её должно базироваться на парамет- рах, характеризующих работу авиадвигателя,
по которым можно бы было оценивать накопление
повреждения в некоторых специально выбранных основных деталях каждо- го конкретного двигателя. Подсчет
повреждаемости деталей двигателя от воздействия указанных параметров целесообразно, по-видимому, вести по
деталям, испытывающим все основные
характерные нагрузки. В газотурбинном двигателе такими деталями явля- ются рабочие лопатки турбины высокого
давления (ТВД), которые являются одними из наиболее
напряженных деталей двигателя. Из действующих на рабочие лопатки турби- ны нагрузок реально можно учесть влияние
статических напряжений от центробежных и
газодинамических сил в условиях высоких температур. Воздействующие на рабочие лопатки
турбины статические напряжения и температура являются
показателями напряженности
режимов работы двигателя и могут служить основой для приведения режимов к
одному эквивалентному. Необходимая информация для подсчета
Исходя из того, что подсчет эквивалентной наработки будет производиться в условиях
эксплуатации, очевидно, что вычисление её должно базироваться на парамет- рах, характеризующих работу авиадвигателя,
по которым можно бы было оценивать накопление
повреждения в некоторых специально выбранных основных деталях каждо- го конкретного двигателя. Подсчет
повреждаемости деталей двигателя от воздействия указанных параметров целесообразно, по-видимому, вести по
деталям, испытывающим все основные
характерные нагрузки. В газотурбинном двигателе такими деталями явля- ются рабочие лопатки турбины высокого
давления (ТВД), которые являются одними из наиболее
напряженных деталей двигателя. Из действующих на рабочие лопатки турби- ны нагрузок реально можно учесть влияние
статических напряжений от центробежных и
газодинамических сил в условиях высоких температур. Воздействующие на рабочие лопатки
турбины статические напряжения и температура являются
показателями напряженности
режимов работы двигателя и могут служить основой для приведения режимов к
одному эквивалентному. Необходимая информация для подсчета
|
700°С
800°С
σ А B C D i
900°С
1000°С 1100°С
τ(1100,σi) τ(1000,σi) τ(900,σi) τ(800,σi) Наработка до разрушения τ, час |
эквивалентной наработки при этом может быть получена по двум из- вестным контролируемым пара- метрам: числу оборотов и темпера- туре газа (или температуре матери- ала лопаток). Исходя из статиче- ского характера рассматриваемых нагрузок, можно использовать кри- вые длительной прочности. Типичный вид характеристик дли- тельной прочности представлен на рис. 6.46 (слева). |
![]() τ, час
τ, час
![]() D
D
τi
C
ti
B
A
t,°С
Исходя из кривых длительной прочности (в логарифмической си- стеме координат), показанных на рис. 6.46, можно построить зависимость времени работы до разрушения τ при различной температуре материала и постоянном напряжении σi (т.е. числе оборотов), изображенную на рис. 6.47 (слева).
τрi − время работы до разрушения на i-ом режиме;
Ti − температура материала лопаток
Температура материала лопаток
на i-ом режиме.
A, B, C, D – точки, снятые с кривых длительной прочности (рис. 6.46) при постоянном напряжении σi
![]()
![]() Рисунок 6.48 (слева) Общий вид зависимости коэффициента
приведения r от температуры лопаток t
Рисунок 6.48 (слева) Общий вид зависимости коэффициента
приведения r от температуры лопаток t
и частоты вращения турбины n
t,°С
t1 t2 t3 Температура материала лопаток
В связи с отмеченным влиянием температуры материала лопаток на темп расхо- дования запаса их долговечности, для подсчёта фактической наработки целесообразно использовать не абсолютное время работы двигателя на i-ом режиме до разрушения ло-
паток τрi , а время работы до разрушения на режиме приведения τрПР. Отношение приве- дённого времени к абсолютному можно назвать коэффициентом приведения:
ri = τрПР./τрi (6.33)
Зависимость коэффициента приведения от температуры лопаток и частоты вра- щения турбины изображается семейством кривых, характерный вид которых показан на рис. 6.48.
![]() 2000 200
2000 200
1800
![]() 1600
1600
1400
1200
1000
150
![]() 100
100
800
600
50
400
200
850 900 950 1000 1050 1100
Температура лопаток t,°C
σ1 =196 МПа σ2 = 147 МПа σ3 = 98 МПа
Рисунок 6.49 –Зависимости времени до разрушения τ и коэффициента приведения r от температуры лопаток t и частоты вращения турбины n для сплава ЖС6-К
На рис. 6.49 в качестве примера приведены соответствующие зависимости для одного из жаропрочных сплавов. По найденным зависимостям коэффициента приведе- ния режима можно производить подсчет эквивалентной наработки на i–ом режиме:
τэi = ri ∙Δτi (6.34)
где ri – коэффициент приведения, определённый для данного режима;
Δτi, − время воздействия напряжения и температуры, характерных для данного режима.
Формула представляет собой, по сути дела, интерпретацию гипотезы линейного суммирования повреждений. Описанный алгоритм позволяет с помощью относительно простых аппаратурных средств осуществить в реальной эксплуатации учёт эквивалентной наработки каждого конкретного двигателя по таким параметрам, контро- лирующим его работу, как температура газа за турбиной высокого давления (она изме- ряется батареей термопар, установленных в газовом потоке за ТВД) с последующим её пересчётом на температуру рабочих лопаток турбины, или непосредственно измеряемая температура материала рабочих лопаток (для этого может использоваться специальный пирометр, установленный в корпусе турбины), а также и частота вращения ротора тур- бокомпрессорного блока высокого давления (она измеряется штатной системой кон- троля теплотехнических параметров ГТД).
Суть интегральной оценки и прогнозирования остатка ресурса энергетических установок заключается в учете выработанной части ресурса и переходе к временным значениям, соответствующим этой части на каждом рабочем режиме. При вычитании полученных временных значений из значений ресурсов на соответствующих режимах получим величины запасов ресурса на каждом из контролируемых режимов. По этим запасам можно определять, сколько времени может двигатель эксплуатироваться при заданной мощности до полной выработки ресурса. Практическая реализация этого принципа оценки остаточного ресурса может быть выполнена либо с помощью авто- номного счётчика наработки ресурса, либо путём включения соответствующего про- граммного модуля в состав программного обеспечения централизованной системы кон- троля и диагностики.
Важной предпосылкой успешного применения прогнозирующих методик являет- ся предварительный анализ конструктивных и эксплуатационных особенностей объекта
с целью определения наиболее нагруженных деталей, лимитирующих его надёжность, характерных процессов деградации их технического состояния во время эксплуатации и параметров, характеризующих интенсивность этих процессов или их влияние на работо- способность объекта. При рассмотрении достаточно локальных конструктивных узлов машин или систем такой анализ даёт достаточно очевидные и односложные результаты.
Задача существенно усложняется, если целью прогнозирования является оценка фактической наработки и остаточного ресурса сложного объекта, длительная работо- способность которого обеспечивается долговечностью нескольких конструктивных уз- лов, темпы развития эксплуатационных повреждений которых определяются различны- ми физико-химическими процессами. В качестве примера такого многопланового объ- екта может быть рассмотрен судовой дизель. Структурный анализ судового дизеля по- казывает, что это сложная машина, в состав которой входит значительное количество узлов и деталей, техническое состояние которых лимитирует возможность длительной, безотказной и безопасной эксплуатации судовой энергетической установки. Несмотря на постоянное повышение качества схемных и конструктивных решений, а также при- менение прогрессивных конструкционных материалов и технологий изготовления, пока не удаётся полностью исключить развитие эксплуатационных повреждений высокона- пряжённых узлов и деталей дизеля (см. раздел 2.1). В табл. 6.14 и 6.15 приведены ре- зультаты статистической обработки опыта эксплуатации судовых дизелей [335].
Таблица 6.14 Усреднённые ресурсы до списания основных деталей и узлов современных судовых дизелей
|
№ |
Наименование узла |
Средний ресурс тыс. ч. |
||
|
МОД |
СОД |
ВОД |
||
|
1 |
Фундаментная рама; коленчатый вал; блок цилин- дров; шток поршня; шатун; распределительный вал; крышка цилиндра |
100 – 120 и выше |
50 − 80 |
20 − 40 |
|
2 |
Втулки цилиндра, поршень |
60 |
40 |
10 − 20 |
|
3 |
Поршневые кольца |
12 |
8 − 10 |
6 − 10 |
|
4 |
Рамовый, мотылевый, головной подшипники |
60 |
40 |
10 − 20 |
|
5 |
Выпускной клапан |
30 |
20 |
10 |
|
6 |
Топливный насос |
25 |
15 |
10 |
|
7 |
Форсунка: игла и сопло распылителя |
15 |
15 |
6 − 10 |
|
8 |
Газотурбонагнетатель |
60 − 80 |
40 − 50 |
15 − 20 |
|
9 |
Ответственные крепежные элементы: мотылевые болты, анкерные связи, шпильки крепления под- шипников, крышки цилиндров и др. |
100 − 120 |
30 − 80 |
10 − 40 |
Таблица 6.15 Характерные причины отказов судовых дизелей
|
Тип дизелей |
МОД |
СОД |
ВОД |
|
Область эксплуатации |
Морской флот |
Речной и про- мысловый флот |
Военно-морской флот |
|
Износы |
40 − 45 |
35 − 45 |
30 − 45 |
|
Трещины и поломки |
10 − 12 |
25 − 30 |
20 − 25 |
|
Загрязнение, закоксовывание |
16 − 18 |
8 − 10 |
5 − 7 |
|
Эрозия, кавитация, коррозия |
19 − 22 |
18 − 20 |
22 − 24 |
|
Нарушение герметичности |
4 − 6 |
1 − 3 |
1 − 3 |
|
Старение материалов |
2 − 3 |
3 − 5 |
5 − 6 |
В целом, проведённая типизация характерных дефектов судовых дизелей позво- ляет выделить две основные группы эксплуатационных повреждений.
К первой группе можно отнести такие неисправности, как трещины и поломки де- талей. В ряде случаев они могут быть вызваны краткосрочными силовыми перегрузками на фоне изначально имевшихся дефектов конструкционных материалов и нарушения технологии изготовления деталей. Снижение вероятности возникновения таких неис- правностей требует, прежде всего, повышения технологической культуры производства, совершенствования заводских методов контроля качества продукции и исключения ре- жимов эксплуатации судовой энергетической установки, связанных с перегрузками главного двигателя. Эти неисправности носят внезапный характер, до факта поломки они себя никак не проявляют и штатной системой централизованного контроля пара- метров не обнаруживаются. Поэтому применение какой-то стратегии мониторинга этих случайных процессов во время эксплуатации с целью оценки их влияния на долговеч- ность дизеля представляется затруднительным.
Другой характерной причиной таких отказов является накопление усталости ме- талла при длительном воздействии переменных силовых и температурных напряжений, обусловленных циклическим принципом действия дизеля. Этот процесс носит посте- пенный, растянутый во времени характер, и это открывает определённые перспективы для его мониторинга. Непосредственный контроль во время эксплуатации повреждений внутренней структуры конструкционных материалов без разборки дизеля и применения специальных методов интроскопии невозможен, однако косвенная оценка интенсивно- сти этих процессов может быть обеспечена путём регистрации истории эксплуатацион- ных нагружений соответствующих деталей.
Понятно, что технически невозможно организовать индивидуальный контроль эксплуатационных нагрузок каждой детали: требуется применение обобщённого показа- теля, характеризующего условия накопления усталостных повреждений узлов дизеля. При выборе такого показателя можно исходить из того, что степень развития усталости металла при циклическом изменении температурных и силовых нагрузок определяется амплитудой и количеством этих циклов. В первом приближении можно предположить, что амплитуда циклических деформаций силовых деталей дизеля пропорциональна мо- менту на валу дизеля, и каждый цикл нагружения «съедает» пропорциональную его ам- плитуде долю запаса долговечности деталей дизеля, повреждаемых в результате устало- сти конструкционного материала. Накопленное количество таких циклов определяется произведением частоты вращения дизеля на время его работы на данном режиме. Отсю- да следует, что произведение вращающего момента на частоту вращения и время работы на данном режиме можно рассматривать в качестве обобщённого показателя накоплен- ных усталостных повреждений конструкционных материалов силовых деталей дизеля. Это же произведение определяет и работу, совершённую двигателем за рассматривае- мый временной промежуток:
Mi∙ni∙ti = Ni∙ti = Ai (6.36) где Mi − вращающий момент;
ni – частота вращения;
ti − время работы двигателя на данном режиме;
Ni – полезная мощность;
Ai – полезная работа, совершённая дизелем за время ti
Ко второй группе эксплуатационных повреждений дизеля можно отнести износы узлов трения. Для некоторых из них известны частные методики контроля интенсивно- сти износовых процессов и оценки фактической величины износа (зазоров) [3], однако использование их для комплексной оценки фактической наработки и остаточного ресур- са дизеля в целом довольно затруднительно ввиду возможной «конкурентности прогно- зов», да и трудно себе представить диагностическую систему, в состав которой входит столь значительное количество разнородных измерительных трактов.
Типичной причиной ускоренных износов является нарушение качества смазки трущихся деталей в результате неисправностей элементов циркуляционной масляной системы или ухудшения качества самого масла (загрязнения, обводнения, расслоения, изменения вязкости и т.п.). Определённое влияние на интенсивность износа деталей ци- линдро-поршневой группы оказывает сорт, качество и вязкость топлива. При поддержа-
нии нормального технического состояния масляной системы, своевременных очистках и доливах свежего масла, обеспечении нормативной сортности и химико-физических по- казателей топлива, износовые процессы имеют постепенный характер, растянутый во времени. Их интенсивность определяется уровнем силового взаимодействия и скоро- стью относительного перемещения трущихся деталей. Уровень силового взаимодей- ствия является функцией момента, развиваемого на валу дизеля, а скорость относитель- ного перемещения деталей определяется частотой вращения. Накопленная величина из- носа, таким образом, будет пропорциональна моменту на валу дизеля и накопленному пути трения, который, в свою очередь, пропорционален произведению частоты враще- ния на время работы дизеля на рассматриваемом режиме.
Для получения обобщённой оценки накопленного износа трущихся деталей дом- ножим момент на произведение частоты вращения и времени работу дизеля на данном режиме и в результате получим то же самое выражение (6.34), что означает, что работа, совершённая за время функционирования двигателя на рассматриваемом режиме, может являться показателем не только усталостных, но и износовых повреждений деталей (к такому же выражению можно прийти и анализируя зависимость износа от контактного напряжения и пути трения).
![]() N3
N3
Рисунок 6.50 (слева) –
Графическая иллюстрация
N2
праксеологической
N1 концепции долговечности
двигателя
R3 R2 R1
Проведённый анализ позволяет предположить наличие тесной корреляционной связи между запасом долговечности двигателя, заложенным в процессе его проектиро- вания и изготовления, и количеством работы, которое он может совершить за время его эксплуатации. Иными словами, в качестве показателя израсходованного ресурса мо- жетрассматриваться регистрация полезной работы, совершённой двигателем за наблю- даемый период эксплуатации [119, 396, 422] (рис. 6.50). Такая концепция согласуется с
принципами оценки полезности тех или иных объектов, которые рассматриваются та- ким научным направлением, как праксеология.
![]() Практическая реализация этой концепции требует
учёта многорежимного харак-
тера эксплуатации транспортных дизелей (рис.6.51).
Практическая реализация этой концепции требует
учёта многорежимного харак-
тера эксплуатации транспортных дизелей (рис.6.51).
|
N, % 100 1
75 2
50 4 3 25
0 25 50 75 RК ,% |
Рисунок 6.51 (слева) – Спектр мощностей транспортных дизелей: 1− главный двигатель речного судна; 2 − главный двигатель рыболовецкого сейнера; 3,4 − дизели магистрального и маневрового тепловозов. Для многорежимного двигателя сов- местное применение праксеологического подхода и теории линейного суммирова- ния эксплуатационных повреждений вы- ражается в реализации двух принципов: |
- интенсивность расходования запаса долговечности на каждом режиме пропорцио- нальна мощности;
∑ (6.35) Графическая иллюстрация указанных принципов представлена на рис. 6.52.
− накопленное уменьшение запаса долговечности ΔRст.р. определяется суммированием частичных его уменьшений
ΔRiна зарегистрированных стационарных режимах:
![]()
![]() 100%
100%
0%
Рисунок 6.52 – Расходование запаса долговечности двигателя
1, 2, 3, 4 ,5 – темпы расходования ресурса на различных мощностях (N1>N2>N3>N4>N5);
t1, t2, t3, t4, t5 – длительности работы двигателя на соответствующих режимах.
Следует иметь в виду, что применение описанного алгоритма, ориентированного только на учёт произведённой двигателем работы, обеспечивает приближённую оценку израсходованного и остаточного ресурсов. Для более точного определения этих показа- телей необходимо учитывать влияние на долговечность двигателя количества динамич- ных режимов (пусков и изменений мощности), а также времени работы двигателя на хо- лостом ходу:
ΔR = ΔRст.р. + ΔRпуск. + ΔRизм.+ ΔRХХ (6.36)
где ΔR − общая часть ресурса, израсходованная двигателем с момента начала эксплуатации;
ΔRст.р. − часть ресурса, израсходованная двигателем при работе на стационарных режимах;
ΔRпуск. − часть ресурса, израсходованная двигателем при пусках;
ΔRизм. − часть ресурса, израсходованная двигателем в результате изменений режимов;
ΔRХХ − часть ресурса, израсходованная двигателем на холостом ходу.
В соответствии с рассматриваемой концепцией степень расходования ресурса на холостом ходу можно считать пропорциональной количеству энергии топлива, израсхо- дованному на этом режиме:
Ахх = К∙Вехх∙Q∙tхх (6.37) где Вехх – часовой расход топлива на холостом ходу, кг/час;
Q – теплотворная способность топлива, ккал/кг;
tхх – суммарное время работы двигателя на холостом ходу, час;
К = 1,16∙10-3 – коэффициент.
Расчёт степени деградации деталей двигателя при пуске может быть выполнен по эквивалентной величине преобразованной энергии, соответствующей равновеликому износу на стационарном режиме:
Aп = К∙Вехх∙Q∙tп∙kтм∙Ψ (6.38) где tп – время с момента запуска до приёма нагрузки, час;
kтм – коэффициент, учитывающий изменение интенсивности износа при разных температурах масла при пуске;
Ψ – коэффициент, учитывающий изменение интенсивности износа при ненормативной частоте вращения двигателя.
Таблица 6.14 Влияние температуры масла на интенсивность износа при пуске двигателя
|
Температура масла, °С |
10÷15 |
16÷20 |
21÷25 |
26÷30 |
31÷40 |
|
kтм |
3,0 |
2,5 |
2,0 |
1,5 |
1.3 |
Таблица 6.15 Влияние пониженной частоты вращения двигателя на интенсивность износа при пуске двигателя
|
n, об/мин |
400 |
500 |
600 |
750 |
|
Ψ |
1,3 |
1,0 |
1,0 |
1,0 |
Накопленный расход запаса долговечности двигателя при пусках определяется умножением единичного расхода на количество пусков за наблюдаемый период. Оценка степени расходования ресурса при изменениях нагрузки можно выполнять аналогичным образом с помощью коэффициента, учитывающего зависимость интенсивности износа от разности нагрузок до и после переходного процесса, а также учитывая число таких процессов за наблюдаемый период.
В качестве примера можно рассмотреть оценку остаточного ресурса двигателя при наработке с начала установки 40000 часов [5]. В соответствии с техническими усло- виями расчётный ресурс двигателя до капитального ремонта составляет 48000 часов, поэтому при указанной выше наработке расчётный остаточный ресурс, определённый без учёта фактических режимов эксплуатации, будет равен 8000 часов.
Фактическое распределение наработки по режимам следующее:
− максимальная мощность (583 кВт) – 2000 ч;
− номинальная мощность (530 кВт) – 25000 ч;
− мощность среднего хода (400 кВт) – 10000 ч;
− мощность малого хода (300 кВт) – 1400 ч;
− мощность самого малого хода (200 кВт) – 1400 ч;
− работа на холостом ходу (300 кВт) – 200 ч;
− количество пусков – 2000;
− изменений режимов – 6200.
Расчётный ресурс для указанного спектра режимов в соответствие с изложенной методикой будет составлять 51600 часов, а расчётный остаточный ресурс после нара- ботки 40000 часов будет равен 11600 часов (т.е. на 3600 часов больше, чем по техниче-
ским условиям). Разумеется, такой прогноз может быть корректным при условии сохра- нения и на прогнозируемый период аналогичного распределения режимов.
Приведённый пример иллюстрирует возможность оптимизировать расходы на поддержание длительной работоспособности оборудования путём организации учёта фактического распределения режимов эксплуатации оборудования и применения про- гнозирующих алгоритмов, учитывающих влияние режимов эксплуатации на интенсив- ность деградации технического состояния двигателей.
Сравнительный анализ специфических особенностей применения экстраполяци- онного и причинно-следственного методов прогнозирования позволяет сделать вывод, что рассмотренные методы имеют свои достоинства, недостатки и, соответственно, свои области применения.
Несомненным достоинством экстраполяционного метода является то, что для его применения не требуется предварительное исследование качественных и количествен- ных характеристик физико-химических процессов деградации технического состояния объекта. Метод рассчитан на минимальное число контролируемых параметров объекта.
Недостатком является то, что для формирования прогноза требуется период пред- варительного наблюдения за объектом, в течение которого производится накопление временного ряда. Кроме того, метод эффективен только при монотонном изменении во времени контролируемого диагностического параметра. Отсутствие контроля условий эксплуатации ограничивает возможность корректного применения экстраполяционного метода только к однорежимным объектам или к объектам, у которых частота изменения режимов существенно выше частоты замеров параметра, благодаря чему влияние режи- ма удаётся ослабить применением интегрального сглаживания временного ряда.
Как показано выше, этот недостаток можно в значительной степени компенсиро- вать за счёт модернизации алгоритма однопараметрического прогнозирования и приме- нения специальных методик, предусматривающих использование линеаризованных но- мограмм и нелинейных регрессионных моделей с целью обеспечения учёта изменения режимов работы объекта.
Причинно-следственный метод пригоден для объектов с любым характером из- менения режимов, и для его применения не требуется предварительный период накоп- ления данных во время эксплуатации объекта. Однако обязательным условием приме- нимости метода является выполнение предварительных исследований разрушающего
процесса с целью получения зависимости интенсивности этого процесса от условий эксплуатации объекта.
Обобщая особенности рассмотренных методов прогнозирования, следует отме- тить, что наряду с отмеченными выше достоинствами они имеют и ряд недостатков. Главными из них являются высокая дисперсия прогнозов (особенно средне- и долго- срочных), отсутствие универсальности, т.е. возможности эффективного использования для широкой номенклатуры оборудования и всего спектра эксплуатационных условий, а также отсутствие приемлемого по стоимости и трудоёмкости способа получения исход- ных характеристик долговечности.
Эволюция методологии решения прогнозных задач в метеорологии, медицине, демографии и других областях свидетельствует о том, что кардинальным направлением повышения достоверности прогнозов является переход от частных методик к системной организации прогнозирования.
Основные принципы системного подхода:
- наблюдаемый объект рассматривается в виде системы, состоящей из типовых элемен- тов, обладающих свойством универсальности для всего многообразия оборудования;
- наблюдаемый объект рассматривается в качестве элемента системы более высокого уровня, причем поведение системы описывается многофакторной динамической мо- делью, отражающей деградацию технического состояния элементов во времени.
Реализация первого принципа требует, прежде всего, типизации элементов судо- вого энергетического оборудования и соответствующих процессов деградации их тех- нического состояния в процессе эксплуатации и последующей разработки типовых ме- тодик прогнозирования.
Реализация второго принципа предполагает комплексную организацию контроля и прогнозирования состояния наиболее нагруженных элементов энергетического обору- дования, лимитирующих его долговечность на всех этапах жизненного цикла энергети- ческих установок.
|
Контроль качества изготовления и монтажа |
|
|
|
|
||
|
|
||
|
Регистрация режимов функционирования |
|
|
|
|
||
|
|
||
|
Регистрация эксплуатационных нагружений |
|
|
|
|
||
|
|
||
|
Регистрация признаков разрушающих процессов |
|
|
|
|
||
|
|
||
|
Техническая диагностика |
|
|
|
|
||
|
|
||
|
|
|
|
![]() Рисунок
6.54 –Системная организация информационной поддержки мероприятий, наце- ленных
на обеспечение длительной надёжной эксплуатации оборудования
Рисунок
6.54 –Системная организация информационной поддержки мероприятий, наце- ленных
на обеспечение длительной надёжной эксплуатации оборудования
Таким образом, системный подход позволяет:
- унифицировать состав типовых элементов оборудования и соответствующих методик определения характеристик их долговечности;
- повысить адекватность модели на базовом временном интервале и достоверность прогнозирования за счет корректирующей информации, получаемой в результате вы- ходного контроля на производстве, регистрации эксплуатационных режимов и физи- ческих признаков деградации состояния, а также диагностирования оборудования во время его эксплуатации;
- организовать комплексное применение мероприятий, направленных на обеспечение эксплуатационной надёжности судового энергетического оборудования.
Актуальность выбора эффективных методов прогнозирования и совершенствования методик их применения обоснована тем, что обеспечение достоверных прогнозов изменений технического состояния и оценок остаточного ресурса судового энергетического оборудования в процессе эксплуатации является необходимым условием обоснованного планирования и оптимизации обслуживания оборудования и снижения вероятности внезапных отказов и аварий. Выполненный сравни- тельный анализ функциональных возможностей нескольких фактографических методов прогнозирования позволил оценить их достоинства и недостатки и опре- делить рациональные области применения.
Показано, в частности, что стохастический (вероятностный) метод прогнозирования, использующий в качестве информационной базы статистические данные, обобщающие опыт испытаний и эксплуатации партий однотипных изделий, мо- жет быть использован для вероятностной оценки ожидаемой на заданный период эксплуатации надёжности оборудования при наличии представительных выборок результатов наблюдений за отказами аналогичных видов оборудования. Предложена методика статистической обработки таких выборок и соответствующее программное обеспечение, позволяющее в режиме диалога с персональным компьютером определять вид закона распределения, эмпирические и теоретические параметры распределения, и в частности, плотность вероятности и функцию распределения, которые могут быть использованы для формирования прогнозных оценок надёжности оборудования. Работоспособность предложенного алгоритмического и программного обеспечения подтверждена выполненным анализом статистических данных о наработках на отказ партии судовых насосов.
Вместе с тем, отмечено, что в наибольшей степени этот метод прогнозирования эффективен в условиях массового производства однотипных изделий с относительно короткими сроками службы, поскольку эти условия позволяют в относительно короткие промежутки времени сформировать достаточно представительные выборки, характеризующие безотказность и долговечность этих изделий. Для судового энергетического оборудования формирование таких выборок затруднено мелкосерийным, а зачастую и единичным характером постройки судов и кораблей и относительно большой долговечностью оборудования. Кроме того, показано, что при относительно высоких значениях коэффициентов вариации ресурсов, обусловленных большим разнообразием и изменчивостью районов плавания, условий эксплуатации, режимов использования и стратегий обслуживания судового оборудования, разработка методик прогнозирования должна быть нацелена на формирование не групповых среднестатистических оценок, а индивидуальных прогнозов темпов деградации технического состояния и остаточного ресурса конкретных машин и механизмов.
Показано, что наиболее простым методом, ориентированным на формирование индивидуальных прогнозов изменения технического состояния оборудования, яв- ляется экстраполяционное прогнозирование, поскольку его применение не требует предварительного исследования физико-химических процессов, вызывающих эксплуатационную деградацию оборудования. Однако, анализ известных методик однопараметрического экстраполяционного прогнозирования выявил невозможность их корректного применения для прогнозирования состояния многорежимных объектов. Для расширения сферы применения экстраполяционного метода прогнозирования предложено использовать результаты ресурсных испытаний диагностируемого узла на номинальном режиме для построения специальной номограммы, в основу которой положено предположение о линейной функциональной зависимости контролируемого параметра от режима работы диагностируемого механизма. Работоспособность предложенного алгоритма была экспериментально апробирована с помощью специальной стендовой установки для ускоренных ресурсных испытаний подшипников качения корабельных газотурбинных двигателей.
Для постановки более точных прогнозов состояния многорежимных объектов предложено для обеспечения инвариантности результатов мониторинга диагно- стического параметра по отношению к режимам механизма в моменты проведения периодических измерений использовать нелинейную регрессионную модель объекта, полученную в результате предварительного многофакторного эксперимента. Работоспособность предложенной методики подтверждена путём реализации центрально-композиционного плана испытаний центробежного насоса при исследовании влияния на его виброактивность степени изношенности подшипника и режимных факторов (частоты вращения и давления смазки).
Для объектов, изменяющих в процессе эксплуатации режимы использования, а также объектов, оценка технического состояния которых с помощью непосредственно измеряемого диагностического параметра не представляется возможной, предложено использовать причинно-следственный метод прогнозирования, предусматривающий во время эксплуатации контроль режимов нагружения диагностируемого узла, оценку трендов деградации его технического состояния и формирование прогнозов путём интегрирования трендов в пределах заданных интервалов прогнозирования.
Рассмотрено три варианта реализации этого метода прогнозирования:
- с использованием гипотезы линейного суммирования повреждений и методики расчёта эквивалентной наработки;
- с использованием многофакторной регрессионной модели, характеризующей зависимость интенсивности развития эксплуатационных повреждений от режимных параметров объекта.
- с использованием праксеологического подхода к оценке долговечности энергетического оборудования.
В качестве примеров реализации указанных методических принципов разработаны технические предложения для обеспечения оценки степени израсходования ресурса и прогнозирования долговечности судовых сильфонных компенсаторов, трубопроводов судовой системы охлаждения, морских газовых турбин и дизелей.
Предложена методика экономической оценки эффективности прогнозирования долговечности энергомеханического оборудования.
Предложена системная организация информационной поддержки мероприятий, нацеленных на обеспечение длительной надёжной эксплуатации оборудования.
Список используемых источников
1. Вайнштейдт В.А. Судовые двигатели внутреннего сгорания. - Л.: Судостроение, 2016.
2. Гуцуляк В. Н. Российское и международное морское право (публичное и частное) Москва: Центр морского права [и др.], 2017.
3. Гуцуляк В.Н. Международное морское право (публичное и частное): учебное пособие для студентов высших учебных заведений Ростов-на-Дону: Феникс, 2016.
4. Возницкий И.В., Камкин С.В., Шмелев В.П., Осташенков В.Ф. Рабочие процессы судовых дизелей. - М.: Транспорт, 2015.
5. Гаврилов В.С., Камкин С.В., Шмелев В.П. Техническая эксплуатация судовых дизельных установок. - М.: Транспорт, 2017.
6. Васюнкин В.В. Живучесть корабля. Теория количественной оценки ; С-Пб : ООО "Галея Принт", 2016.
7. Камкин С.В. Газообмен и наддув судовых дизелей. - Л.: Судостроение,2016.
8. Камкин С.В., Лемещенко А.Л., Пунда А.С. Повышение экономичности судовых дизелей. - СПб.: Судостроение, 2015.
9. Петровский Н.В. Судовые двигатели внутреннего сгорания и их эксплуатация. - М.: Транспорт, 2017.
10. Дмитриев В. И. Обеспечение безопасности плавания судов: Учебное пособие. - М.: МОРКНИГА, 2018. - 349 с.
11. Правила классификации и постройки морских судов, ч. VI. Противопожарная защита НД №2-020101-104 / отв. за вып. А.В. Зухарь. - ; СПб., 2018. - 113 с. .
12. Голота Г.Ф.. Судостроение. Нормирование в судоремонте, 2016
13. Регистровая книга судов (редакция 2015 года) .2016
14. Российский Речной Регистр. 2013. «Российский Речной Регистр. Правила» (изд. 2015 г.)
15. Юрий Дейнего Охрана человеческой жизни на море. СОЛАС-74. 2015
16. Носенко В.М. Судовые энергетические установки: Учебное пособие / В.М. Николаев, 2016. - 367 с.
17. Позолотин Л.А., Торский В.Г. Конвенция ПДНВ-78 (с поправками). Кодекс ПДНВ-95. Основные положения и комментарии 2017.
18. Издательство Эксмо . История российского флота 2018
19. Моркнига. Правила по охране труда на судах морского и речного флота. 2015
20. Камкин С.В. Газообмен и наддув судовых дизелей. - Л.: Судостроение, 2015.
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.