Application of the first law of thermodynamics to isoprocesses Worksheet

Thermodynamics 1st Law

Part 1:  Multiple Choice Questions

1.       Which of the following is equivalent to the principle of energy conservation?

A.      Newton’s first law

B.      The first law of thermodynamics

C.      Newton’s second law

D.      The second law of thermodynamics

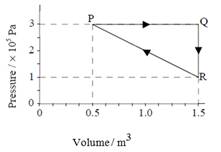2.       An ideal gas undergoes the thermodynamic changes represented in the P –V diagram below
(P → Q → R → P).

          Which of the following is the net work done by the gas in a cycle?

A.      4.5 × 105 J

B.      3.0 × 105 J

C.      1.0 × 105 J

D.      Zero

3.       The diagram shows the pressure volume relationship for a fixed mass of an ideal gas that undergoes a cycle XYZ.

          In which part(s) of the cycle is external work done on the gas?

A.      Y → Z only

B.      Y → Z and Z → X only

C.      X → Y and Z → X only

D.      X → Y only

4.       The diagram shows the pressure–volume (PV) relationship for a gas.

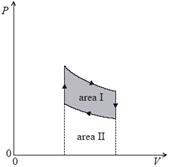
          Which of the following area(s) is/are equal to the work done by the gas as it expands?

A.      area I

B.      area II

C.      area I + area II

D.      area I – area II

5.       The diagram shows the pressure/volume (p/V) diagram for one cycle PQRS of an engine.

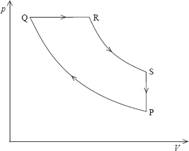
In which sections of the cycle is work done on the engine?

A.      SP only

B.      PQ only

C.      SP and PQ only

D.      RS and SP only

6.      The first law of thermodynamics states that ΔU the change in internal energy of a system is related to the heat Q supplied to it and W the work on it by the equation:

ΔU = Q + W

What are ΔU, Q and W for a constant mass of ideal gas whose temperature is decreased at constant pressure?

   ΔU                             Q                                W

A    negative                        negative                        negative

B    positive                        negative                       positive

C    negative                       negative                       positve       

D    negative                       positive                         positive      

Part II:  Structured Questions

7.      The mean speed of a helium atom at a temperature of 0 °C is 1.3 km s^–1. Estimate the mean speed of helium atoms on the surface of a star where the temperature is 10 000 K. [6]

8.      The surface temperature of the Sun is about 5400 K. On its surface, particles behave like the atoms of an ideal gas. The atmosphere of the Sun mainly consists of hydrogen nuclei.
These nuclei move in random motion.

a    Explain what is meant by random motion. [1]

b   i     Calculate the mean translational kinetic energy of a hydrogen nucleus on the surface of the Sun. [2]

ii  Estimate the mean speed of such a hydrogen nucleus. (The mass of hydrogen nucleus is 1.7 ´ 10⁻²⁷ kg.)  

9.      The P–V diagram shows the expansion of a fixed mass of an ideal gas, from state A to state B.

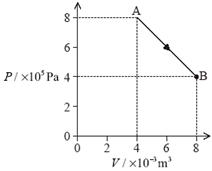
          The temperature of the gas in state A is 400 K.

(a)     Calculate the temperature of the gas in state B. [1]

(b)     (i)      Calculate the work done by the gas in expanding from state A to state B. [2]

(ii)     Determine the amount of thermal energy transferred during the expansion from state A to state B. [2]

(c)     The gas is isothermally compressed from state B back to state A.

(i)      Using the P–V diagram axes below, draw the variation of pressure with volume for this isothermal compression. [1]

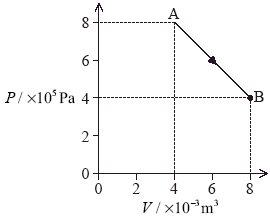
(ii)     State and explain whether the magnitude of the thermal energy transferred in this case would be less than, equal to or greater than the thermal energy transferred in (b)(ii). [2]

10.   (a) (i)State the basic assumption of the kinetic theory of gasses that leads to the conclusion that the potential energy between the atoms of an ideal gas is zero.

(ii) State what is meant by the internal energy of a substance.

(iii) Explain why an increase in internal energy of a gas is directly related to a rise in the temperature of the gas.

(b) A fixed mass of an ideal gas undergoes a cycle PQRP of changes as shown in the following figure.

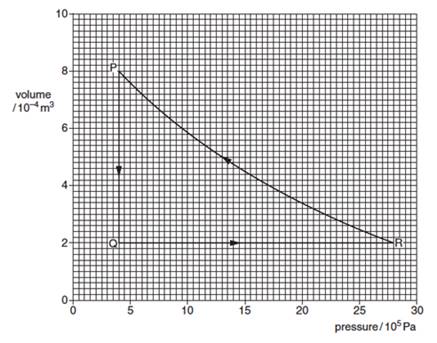
(i)                  State the change in the internal energy of the gas duering one complete cycle PQRP. [1]

(ii)                Calculate the work done on the gas during the change from P to Q. [2]

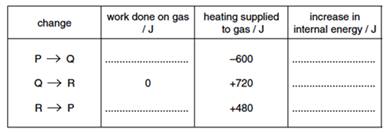
(iii)              Some energy changes during the cycle are shown in the following table. Complete the table.