Арифметические и логические основы работы компьютера.docx

Арифметические и логические основы работы компьютера

Логика, как наука развивается с IV в. до н. э. начиная с трудов Аристотеля. Именно он подверг анализу человеческое мышление, такие его формы, как понятие, суждение, умозаключение. 

Логика – (от греч. “логос”, означающего “слово” и “смысл”) – наука о законах, формах и операциях правильного мышления. Ее основная задача заключается в нахождении и систематизации правильных способов рассуждения.  

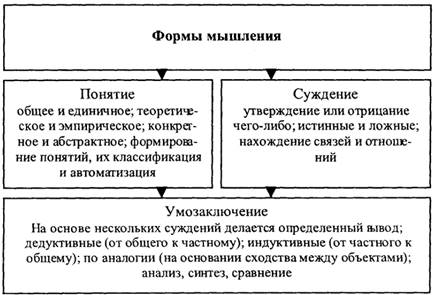
 Рис. 1. Основные формы абстрактного мышления

Понятие – это форма мышления, в которой отражаются существенные признаки отдельного предмета или класса однородных предметов. Всякое понятие имеет содержание и объем. Например, понятие “Черное море” – отражает единичный предмет, “Сиамская кошка” – отражает класс сиамских кошек.

Высказывание (суждение) – некоторое предложение, которое может быть истинно (верно) или ложно. Например, Абакан – столица Хакасии. Утверждение – суждение, которое требуется доказать или опровергнуть. Рассуждение – цепочка высказываний или утверждений, определенным образом связанных друг с другом.

Умозаключение – логическая операция, в результате которой из одного или нескольких данных суждений получается (выводится) новое суждение.  Умозаключения бывают:  Дедуктивные (от общего к частному) – Все ученики ходят в школу. Вася – ученик. Вася ходит в школу.  Индуктивные (от частного к общему) – Банан и персик – сладкие. Значит, все фрукты сладкие на вкус.  Аналогия – Наши коровы едят траву и дают молоко. В Австралии есть поля, коровы едят эту траву. Следовательно, австралийские коровы тоже дают молоко.

В алгебре логики высказывания обозначаются именами логических переменных (А, В, С). Истина, ложь – логические константы.         

 Логическое выражение – запись или устное утверждение, в которое, наряду с постоянными, обязательно входят переменные величины (объекты). В зависимости от значений этих переменных логическое выражение может принимать одно из двух возможных значений: ИСТИНА (логическая 1) или ЛОЖЬ (логический 0).

Сложное логическое выражение – логическое выражение, составленное из одного или нескольких простых (или сложных) логических выражений, связанных с помощью логических операций.

Логические операции и таблицы истинности

1) Логическое умножение или конъюнкция:

Конъюнкция - это сложное логическое выражение, которое считается истинным в том и только том случае, когда оба простых выражения являются истинными, во всех остальных случаях данное сложеное выражение ложно.
Обозначение: F = A & B.

Таблица истинности для конъюнкции

2) Логическое сложение или дизъюнкция:

Дизъюнкция - это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно тогда и только тогда, когда оба простых логических выраженныя ложны.
Обозначение: F = A + B.

Таблица истинности для дизъюнкции

3) Логическое отрицание или инверсия:

Инверсия - это сложное логическое выражение, если исходное логическое выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное логическое выражение ложно, то результат отрицания будет истинным. Другими простыми слова, данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО.

Таблица истинности для инверсии

4) Логическое следование или импликация:

Импликация - это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь. Тоесть данная логическая операция связывает два простых логических выражения, из которых первое является условием (А), а второе (В) является следствием.

Таблица истинности для импликации

5) Логическая равнозначность или эквивалентность:

Эквивалентность - это сложное логическое выражение, которое является истинным тогда и только тогда, когда оба простых логических выражения имеют одинаковую истинность.

Таблица истинности для эквивалентности

Порядок выполнения логических операций в сложном логическом выражении

1. Инверсия;

2. Конъюнкция;

3. Дизъюнкция;

4. Импликация;

5. Эквивалентность.

Для изменения указанного порядка выполнения логических операций используются скобки.