
методические рекомендации с примерами по выполнению практических заданий
для студентов и преподавателей профессиональных образовательных учреждений
специальности 08.02.01 Строительство и эксплуатация зданий и сооружений
по учебной дисциплине
«ТЕХНИЧЕСКАЯ МЕХАНИКА»
Раздел «Статика»
Оглавление
Практическое занятие №1 . Решение задач на определение равнодействующей
Практическое занятие №2 . Решение задач на определение усилий в стержнях
Практическое занятие №3 . Решение задач на определение опорных реакций в однопролетных балках
Практическое занятие №4 . Решение задач на определение опорных реакций в консольных балках
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №5 Решение задач на определение опорных реакций в рамах и фермах…………………………………………………………………………………………
Практическое занятие №6 Решение задач на определение положения центра тяжести в сложных фигурах
1.
Практическое занятие №1 . Решение задач на определение равнодействующей
Цель: знакомство с основными понятиями и аксиомами статики;
Изучение плоской системы сходящихся сил. Изучение силового многоугольника. Изучение геометрических условий равновесия системы
Ход работы:
Задание 1. верно обозначить все силы, действующие на тело;.
Задание 2. Изобразить координатные оси, выбрать их направления;.
Задание 3. Определить проекции векторов на оси; записать уравнения.
Если в некотором направлении тело двигается равномерно или покоится, то алгебраическая сумма (с учетом знаков) проекций сил равна нулю.
Если в некотором направлении тело движется равноускоренно, то алгебраическая сумма проекций сил равна произведению массы на ускорение, согласно второму закону Ньютона.
Пояснения к работе:
Равнодействующая это векторная сумма всех сил, действующих на тело.
Взаимосвязь со вторым законом Ньютона
Вспомним закон Ньютона:
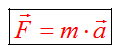
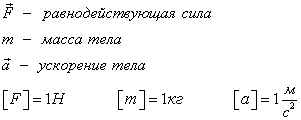
Равнодействующая сила может быть равна нулю в том случае, когда одна сила компенсируется другой, такой же силой, но противоположной по направлению. В этом случае тело находится в покое или движется равномерно.
|
|
Примеры
На движущееся равномерно по горизонтальной поверхности тело, действуют сила тяжести, сила реакции опоры, сила трения и сила, под действием которой тело движется.
Обозначим силы, выберем координатные оси
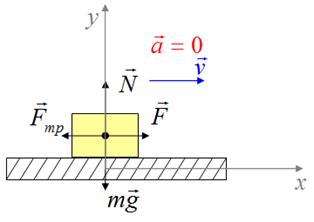
Найдем проекции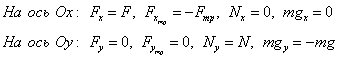
Записываем уравнения
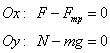
Главное запомнить
1)
Если тело покоится или движется равномерно, то равнодействующая сила равна нулю
и ускорение равно нулю;
2) Уметь записывать уравнения проекций действующих на тело сил
Типовые задачи /решать двумя способами графическим и аналитическим/
1. Определить равнодействующую двух сил 5 и 12 ньютонов, если известно, что угол между ними равен 90 градусов.
2. Прочно застрявшую в грязи машину вытягивают двумя тракторами с силой тяги каждого по 0,5 тонны. Угол между тросами, соединяющими машину и трактора - 20 градусов. Длины тросов - 5 и 10 метров. Определите суммарную силу вытаскивания машины.
3. На неподвижно зависший в воздухе вертолет действует сила тяжести, боковой ветер и сила тяги винта. Чему равна равнодействующая всех сил?
4. Фонарь в саду подвешен на двух тросах, растянутых между деревьями так, что угол между ними 120 градусов. Натяжение каждого троса 100 ньютонов. Определите равнодействующую сил натяжения.
 Краткая теория:
Краткая теория:
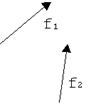
Сложение
сил производится по правилам сложения векторов. Пусть есть две силы: f1 и f2.
Надо найти их сумму.
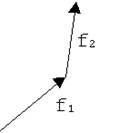
Перенесем по правилу сложения векторов начало второго вектора в конец первого.
Соединим начало первого вектора с концом второго. Полученный вектор - искомая сумма.
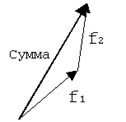
Равнодействующая сил - это сила, которая заменяет действие нескольких сил. Равнодействующая сил находится как их сумма. Равнодействующая - тоже сила и подчиняется всем их правилам.
Возможные особенности задач:
Могут встретиться задачи, в которых заданы геометрические особенности места положения взаимодействующих тел. Эти особенности не всегда совпадают с расположением сил!
Формулы для решения:
Для решения используются геометрические формулы и построения. Как правило, решается прямоугольный треугольник с использованием знаменитого соотношения:
![]()
Алгоритм решения типовой задачи:
1. Кратко записываем условие задачи.
2. Изображаем условие графически в произвольной системе отсчета, указав действующие на тело (точку) силы.
3. Проводим геометрические построения для нахождения искомой силы.
4. Проводим аналитическое решение в общем виде.
5. Подставляем величины в общее решение, вычисляем.
6. Записываем ответ.
Примеры решения:
Задача 1.
Определить равнодействующую двух сил 5 и 12 ньютонов, если известно, что угол между ними равен 90 градусов.
Решение.
1. Кратко записываем условие задачи.
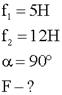
2. Изображаем условие графически в произвольной системе отсчета, указав
действующие на тело 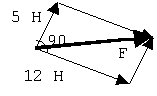
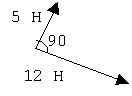 (точку) силы.
(точку) силы.
3. Проводим геометрические построения для
нахождения искомой равнодействующей силы. Это сумма двух заданных сил.
Переносим силы, совмещая начало силы 2 с концом силы 1. Проще всего это
построение выполнить в виде параллелограмма. Часто его так и называют:
"параллелограмм сил".
4. Проводим аналитическое решение в общем виде.
По условию нам дан прямоугольный треугольник, где роль гипотенузы выполняет сила F. Находим ее:
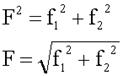
Направление равнодействующей (не
забудем, что сила - вектор!) определим через угол между ней и силой f2,
обозначив его через "альфа".
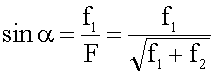
5. Подставляем величины в общее решение, вычисляем.
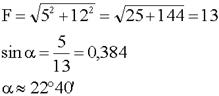
6. Ответ: Величина равнодействующей равна 13 ньютонам, угол между равнодействующей и силой в 12 ньютонов 22 градуса 40 минут.
Задача 2.
Прочно застрявшую в грязи машину вытягивают двумя тракторами с силой тяги каждого по 4900 ньютонов. Угол между тросами, соединяющими машину и трактора - 20 градусов. Длины тросов - 5 и 10 метров. Определите суммарную силу вытаскивания машины.
Решение.
1. Кратко записываем условие задачи.
2. Изображаем условие графически в произвольной системе отсчета, указав
действующие на 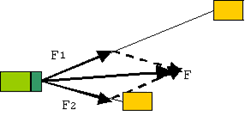 тело силы.
тело силы.
3. Проводим геометрические построения для нахождения искомой силы.
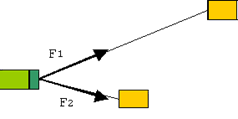 4. Проводим аналитическое решение в общем виде.
4. Проводим аналитическое решение в общем виде.
Обратим внимание на то, что длина
тросов здесь не важна. Важна величина сил.
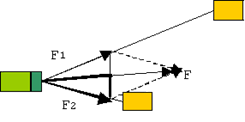 Проводим вторую диагональ построенного параллелограмма сил.
Проводим вторую диагональ построенного параллелограмма сил.
По известным из геометрии теоремам, диагонали в параллелограмме пересекаются под прямым углом и делят углы при вершинах параллелограмма пополам. Таким образом, каждая из сил представляет собой гипотенузу в прямоугольном треугольнике с известным углом 10 градусов.
Таким образом, половина общей силы
тяги 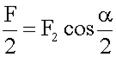
А вся сила 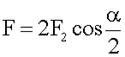
5. Подставляем величины в общее решение, вычисляем.
![]()
6. Ответ: Общая сила, с которой вытягивается застрявшая машина 0,985 тонны, или в системе СИ - 9670 ньютонов.
Задача 3.
На неподвижно зависший в воздухе вертолет действует сила тяжести, боковой ветер и сила тяги винта. Чему равна равнодействующая всех сил?
Решение.
Наличие силы вызывает изменение скорости или деформацию. Поскольку вертолет остается в рабочем состоянии, то, очевидно, что деформации нет. Нет и изменения скорости. Следовательно, мы можем сразу записать ответ: равнодействующая всех сил равна нулю.
Задача 4.
Фонарь в саду подвешен на двух тросах, растянутых между деревьями так, что угол между ними 120 градусов. Натяжение каждого троса 100 ньютонов. Определите равнодействующую сил натяжения.
Решение.
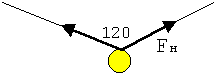 1. Кратко записываем условие задачи.
1. Кратко записываем условие задачи.
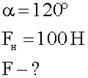
2. Изображаем условие графически.
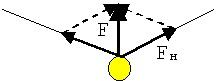 3. Проводим геометрические построения для нахождения
искомой силы.
3. Проводим геометрические построения для нахождения
искомой силы.
4. Проводим аналитическое решение в общем виде.
Поскольку
диагональ параллелограмма делит угол при вершине пополам, то треугольник,
представляющий собой половину параллелограмма - равносторонний, так как имеет
две заведомо равные стороны (стороны параллелограмма) и угол при основании,
равный 60 градусам. Отсюда ясно, что ![]()
5. Подставляем величины в общее
решение, вычисляем. ![]()
6. Ответ: Равнодействующая сил натяжения равна 100 ньютонам.
Вопросы для защиты практической работы:
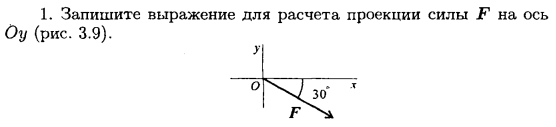
|
2. Нарисуйте в масштабе (1кН – 0,5 см) систему из 3х сходящихся сил: F1 = 6 кН, F2 = 8 кН, F3 = 3 кН, сохраняя их направление и найдите равнодействующую системы сил, построив силовой многоугольник. |
|
|
3. Какой из приведенных силовых многоугольников соответствует уравновешенной системе сил ?
|
|
4.Что такое равнодействующая сил? Чем она отличается от уравновешивающей силы?
5. Чем реальное тело отличается от абсолютно твердого тела?
6. Чем материальная точка отличается от обычной точки?
Варианты заданий
Определите равнодействующую системы сил геометрическим методом
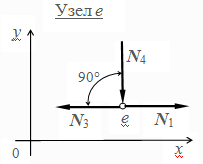
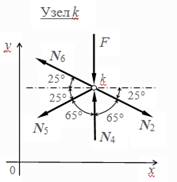
Узел S
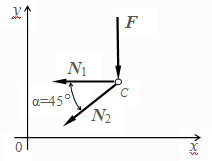
|
Вариант |
Узел e |
Узел k |
Узел S |
||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
|
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
|
|
N1,кН |
20 |
60 |
8 |
65 |
|
|
|
|
|
15 |
27 |
13 |
74 |
|
N2 кН |
|
|
|
|
22 |
19 |
18 |
9 |
69 |
39 |
17 |
55 |
19 |
|
N3 кН |
12 |
19 |
40 |
7 |
|
|
|
|
|
|
|
|
|
|
N4 кН |
5 |
36 |
13 |
28 |
35 |
39 |
54 |
67 |
70 |
|
|
|
|
|
N5 кН |
|
|
|
|
16 |
27 |
17 |
53 |
45 |
|
|
|
|
|
N6 кН |
|
|
|
|
67 |
8 |
32 |
12 |
37 |
|
|
|
|
|
F кН |
|
|
|
|
16 |
25 |
33 |
17 |
28 |
67 |
28 |
81 |
30 |
Практическое занятие №2 . Решение задач на определение усилий в стержнях
Цель: знакомство с плоской системой сходящихся сил; знакомство с понятием –связь, виды связей.
Изучение направления усилий в элементах связей. Изучение геометрических условий равновесия системы
Ход работы:
Задание 1. Обозначьте направление связей в стержнях и гибких подвесах, а так же все силы, действующие на тело;
Задание 2. Условно вырезаем узел, заменяя нить и стержень, возникающими в них усилиями. Узел остается в равновесии. Устанавливаем положение координатных осей и проецируем силы на оси, для обеспечения равновесия должны выполняться условия равновесия системы уравнений (∑X = 0; ∑Y = 0).
3. Составляем систему уравнений и решаем ее относительно неизвестных.
Получили отрицательное значение усилия, следовательно, вектор усилия нужно направить в другую сторону.
Пояснения к работе:
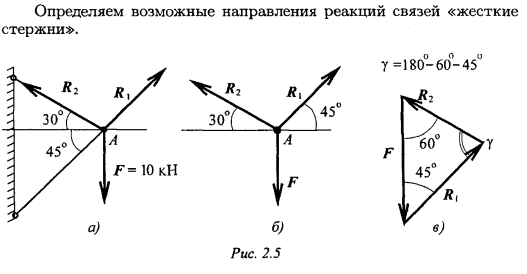
![]()
![]()

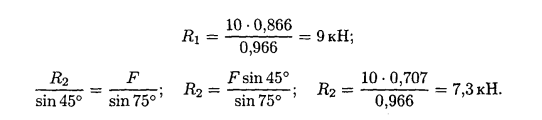
Пример выполнения:
Определить величину и направление реакций связей для схемы, приведенной на рисунке под действием груза G= 30 кН.
Проверить правильность определения реакций.
Решение. В задаче рассматривается равновесие тела, опирающегося на плоскость и подвешенного на нити.
Заменим тело точкой О, совпадающей с центром тяжести.
Приложим к точке О активную силу, которой является собственный вес тела G. Направим ее вниз (рис. 1, б).
1. Мысленно отбросим связи - плоскость и нить. Заменим их действие на точку О реакциями связей. Реакция плоскости (обозначим ее R) проходит по нормали к плоскости в точке А, а реакция или усилие в нити (обозначим ее S) - по нити от точки. Обе реакции и вес тела или линии их действия должны пересекаться в точке О.
Изобразим действующие силы в виде системы трех сходящихся сил на
отдельном чертеже (рис. 1, в). 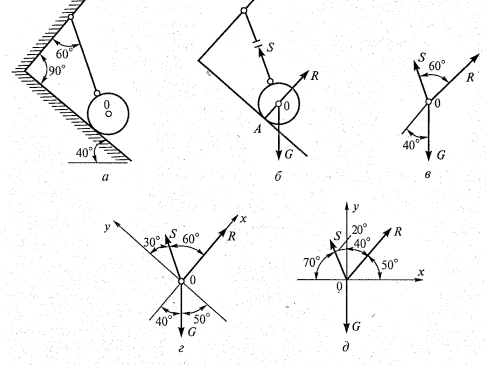
2. Выберем положение системы координат. Начало координат совмещаем с точкой О. Ось х совмещаем с направлением линии действия реакции R, а ось у направим перпендикулярно оси х с. 1, г). Определим углы между осями координат и реакциями R и S. Обычно рис. 1, б и 1, в не выполняют отдельно, а сразу от рис. 1, а переходят к рис. 1, г. Можно было ось у совместить с усилием S, и ось х направить по углом 90°, тогда решение было другим.
3. Составим сумму проекций всех сил на оси координат:
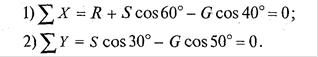
им систему уравнений. Из второго уравнения находим
![]()
первого уравнения находим
![]()
4. Проверим решение, для чего расположим оси координат,
показано на рис. 1, д. Составим уравнения равновесия для вновь принятых осей:
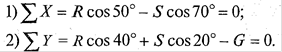
Решим систему уравнений способом подстановки.
Из первого уравнения найдем R:

Подставим это выражение во второе уравнение:
![]()
Отсюда находим
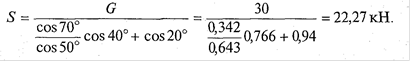
теперь найдем R:
![]()
Ответ: R = 11,84 кН; S,.= 22,27 кН.
Задания для практического занятия №2
Определить величину и направление реакций связей, графическим и аналитическим способами, провести проверку.
Варианты
1.
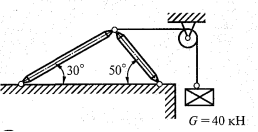 2.
2.
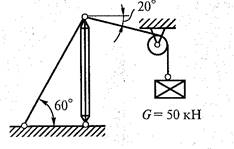
3 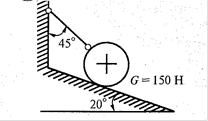 4
4 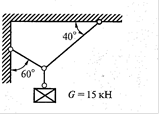
5. 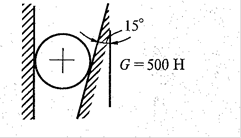 6.
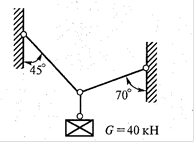
6. 
7. 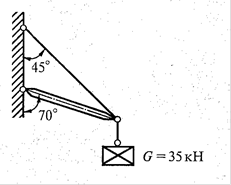 8.
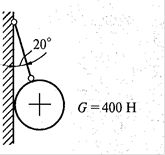
8. 
![]() 9.
9. 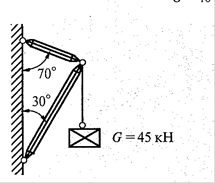 10.
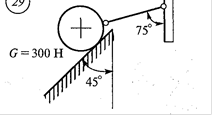
10. 
Вопросы для защиты практической работы:
1. Что такое проекция силы на ось?
2. В каком случае проекция силы на ось будет равна 0?
Практическое занятие №3 . Решение задач на определение опорных реакций в однопролетных балках
Цель: знакомство с системой произвольно расположенных сил; знакомство с понятием –реакции опоры.
Научиться применять на практике уравнения равновесия.
Изучение направления реакций. Изучение условий равновесия балки.
Ход работы:
Задание 1. обозначить направление реакций опор;.
Задание 2. Устанавливаем положение координатных осей и проектируем силы на оси, для обеспечения равновесия должна выполняться система уравнений
Задание 3. Из трех форм уравнений равновесия выбираем подходящую и составляем систему уравнений равновесия для простой балки : относительно опоры А и опоры В.
Задание 4 Решая систему уравнений находим реакции опор.
Задание 5. В качестве проверки решаем третье уравнение равновесия, которое не использовалось в нахождении опорных реакций.
Пояснения к работе:
![]()

![]()

Для определения неизвестных опорных реакций используем формулы уравнений равновесия:
Первая форма
![]() Fx = 0;( ∑ X
= 0)
Fx = 0;( ∑ X
= 0)
![]() Fy = 0. (∑
Y = 0)
Fy = 0. (∑
Y = 0)
![]()
Вторая форма
![]()
Третья форма (уравнения моментов)
![]()
Если на тело наряду с плоской системой сил Fl F2 , , . . , Fn действует система лежащих в той же плоскости пар с моментами m1,m2, . . ., mn, то при составлении условий равновесия в уравнения проекций пары не войдут, так как сумма проекций сил пары на любую ось равна нулю.
Некоторые особенности расчета при определении опорных реакций
![]()
![]()

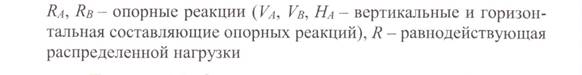
Пример
![]()
![]()
![]()

![]()
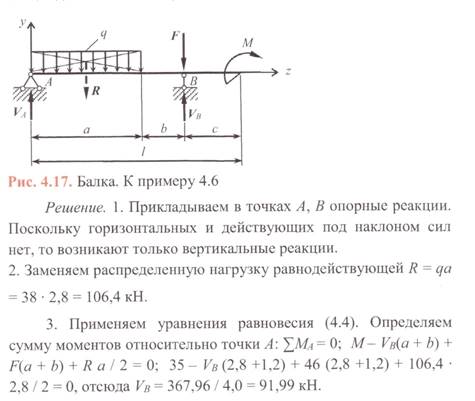

Задания для практического занятия №3
Используя уравнения равновесия плоской произвольной системы сил действующих на балку определить опорные реакции.
Вариант 1
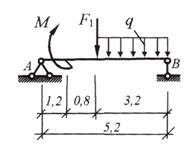
Вариант 2
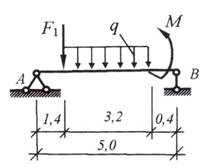
Вариант 3
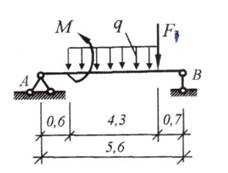
Вариант 4
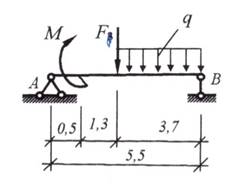
Значения нагрузок
|
№ варианта |
M, кН м |
q, кН/м |
F, кН |
|
1 |
1,1 |
1,1 |
1,1 |
|
2 |
1,2 |
1,2 |
1,2 |
|
3 |
1,3 |
1,3 |
1,3 |
|
4 |
1,4 |
1,4 |
1,4 |
Вопросы для защиты практической работы:
1.Перечислить виды опор в расчетных схемах балок.
2. Сколько реакций опор возникает в шарнирно подвижной опоре?
Практическое занятие №4 . Решение задач на определение опорных реакций в консольных балках
Цель: знакомство с системой произвольно расположенных сил; знакомство с понятием –реакции опоры.
Научиться применять на практике уравнения равновесия.
Изучение направления реакций. Изучение условий равновесия консольной балки.
Ход работы:
Задание 1. Перечертить схему балки. Обозначить направление реакций опор;.
Задание 2. Заменяем распределенную нагрузку- равнодействующей.
Задание 3. Установить положение координатных осей и спроектировать силы на оси, для обеспечения равновесия должна выполняться система уравнений
Задание 4. Из трех форм уравнений равновесия выбираем подходящую и составляем систему уравнений равновесия.
Задание 5 Решая систему уравнений находим реакции в жесткой заделке.
Задание 6. В качестве проверки решаем третье уравнение равновесия, которое не использовалось в нахождении опорных реакций.
![]()
![]()


Задания для практического занятия №4
Расчетную схему балки принять по заданию. Данные для расчета принять по таблице.
1.
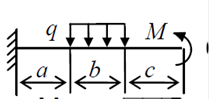
2.
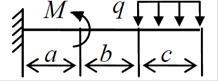
3
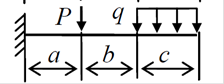
4.
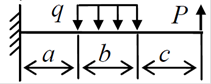
5.
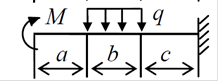
6.
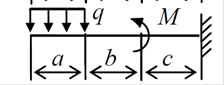
7
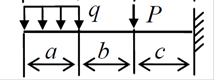
8.
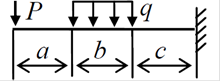
9.
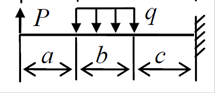
10.
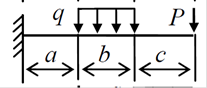
Варианты заданий:
|
№ варианта |
№ схемы |
а, м |
b, м |
c, м |
M, кН м |
g, кН/м |
P, кН |
|
|
1 |
14 |
1 |
1,1 |
1,1 |
1,1 |
1,1 |
1,1 |
|
|
2 |
15 |
2 |
1,2 |
1,2 |
1,2 |
1,2 |
1,2 |
|
|
3 |
16 |
3 |
1,3 |
1,3 |
1,3 |
|
1,3 |
1,3 |
|
4 |
17 |
4 |
1,4 |
1,4 |
1,4 |
|
1,4 |
1,4 |
|
5 |
18 |
5 |
1,5 |
1,5 |
1,5 |
1,5 |
1,5 |
|
|
6 |
19 |
6 |
1,6 |
1,6 |
1,6 |
1,6 |
1,6 |
|
|
7 |
20 |
7 |
1,7 |
1,7 |
1,7 |
|
1,7 |
1,7 |
|
8 |
21 |
8 |
1,8 |
1,8 |
1,8 |
|
1,8 |
1,8 |
|
9 |
22 |
9 |
1.9 |
1.9 |
1.9 |
|
1,9 |
1,9 |
|
10 |
23 |
10 |
0,9 |
0,9 |
0,9 |
|
0,9 |
0,9 |
|
11 |
24 |
1 |
0,8 |
0,8 |
0,8 |
0,8 |
0,8 |
|
|
12 |
25 |
2 |
0,5 |
0,5 |
0,5 |
0,5 |
0,5 |
|
|
13 |
26 |
3 |
0,6 |
0,6 |
0,6 |
|
0,6 |
0,6 |
Вопросы для защиты практической работы:
1.Какие опорные реакции возникают в шарнирных опорах?
2.Правило знаков для определения опорных реакций?
Практическое занятие №5
Решение задач на определение опорных реакций в рамах.
Ход работы:
1. Перечертить схему рамы. Обозначить направление реакций опор;
2. Заменяем распределенную нагрузку- равнодействующей.
3. Установить положение координатных осей и спроектировать силы на оси, для обеспечения равновесия должна выполняться система уравнений
4. Из трех форм уравнений равновесия выбираем подходящую и составляем систему уравнений равновесия.
5 Решая систему уравнений находим реакции опор.
6. В качестве проверки решаем уравнение равновесия, которое не использовалось в нахождении опорных реакций.
Задание 1
Пояснения к работе:
Пример выполнения задания- найти опорные реакции рамы. На раму действуют внешние нагрузки: F1 = 47 кН, F2 = 30 кН и распределенная нагрузка интенсивностью q = 24 кН/м. Расстояния приложения сил a = 2,1 м, b = 1,4 м. Пролет рамы l = 4 м, высота h = 4,5 м.
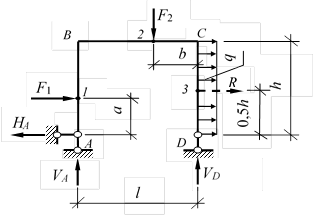
Решение:
Равнодействующая распределенной нагрузки R = qh = 24·4,5 = 108 кН. Определяем опорные реакции. На схеме рамы показываем возникающие в опорных стержнях реакции. Для определения реакций раму располагаем внутри координатных осей, направляем ось Х слева направо, ось Y снизу вверх.
Составляем уравнения равновесия:
Определяем горизонтальную реакцию: ∑Х = 0; – HА + F1 + R = 0; HА = 47 + 108 = 155 кН.
Определяем вертикальные реакции:
∑МА = 0; – VD˕l + R·0,5h + F2(l – b) + F1˕ а = 0; – VD·4 + 108·0,5·4,5+ 30(4 – 1,4) + 47·2,1 = 0; VD = 419,7/4 = 104,925 кН.
∑МD = 0; VА˕l + F1˕ а – F2 ˕b + R·0,5h = 0; VА·4 + 47·2,1 – 30·1,4 + 108·0,5·4,5 = 0; VА = – 299,7/4 = – 74,925 кН. Знак минус указывает, что направление действия реакции VА принято неправильно. Оставляем первоначально принятое направление реакций, но значение реакции VА будем подставлять во все последующие расчеты со знаком минус.
Проверка. ∑Y = 0; VА – F2 + VD = 0; (– 74,925) – 30 + 104,925 = 0; 0 = 0. Значения вертикальных реакций определены правильно.
Задание 1. Используя уравнения равновесия плоской произвольной системы сил действующих на раму определить опорные реакции.
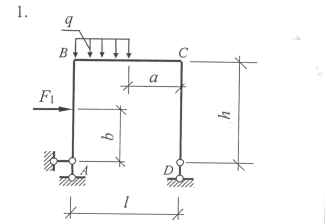
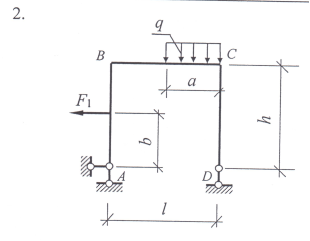
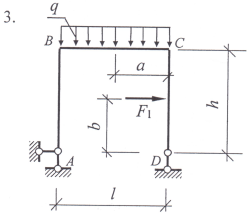
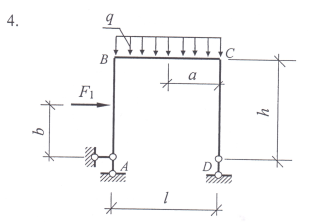
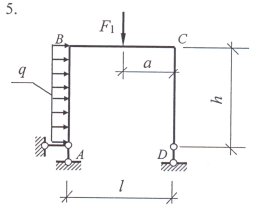
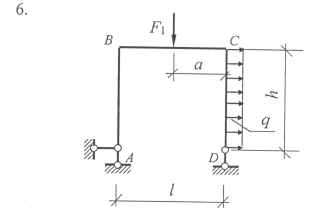
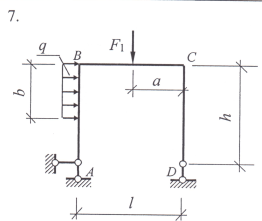
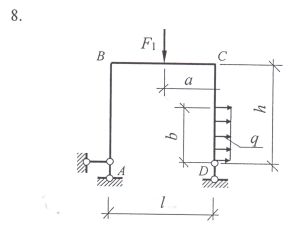
Варианты заданий:
|
№ варианта |
№ схемы |
а, м |
b, м |
l, м |
h,м |
q, кН/м |
F1, кН |
|
|
1 |
14 |
1 |
1,1 |
1,1 |
2,2 |
2,0 |
1,1 |
1,1 |
|
2 |
15 |
2 |
1,2 |
1,2 |
2,4 |
2,4 |
1,2 |
1,2 |
|
3 |
16 |
3 |
1,3 |
1,3 |
2,6 |
2,2 |
1,3 |
1,3 |
|
4 |
17 |
4 |
1,4 |
1,4 |
2,8 |
2,1 |
1,4 |
1,4 |
|
5 |
18 |
5 |
1,5 |
1,5 |
3,0 |
2,5 |
1,5 |
1,5 |
|
6 |
19 |
6 |
1,6 |
1,6 |
3,2 |
2,6 |
1,6 |
1,6 |
|
7 |
20 |
7 |
1,7 |
1,7 |
3,4 |
3,0 |
1,7 |
1,7 |
|
8 |
21 |
8 |
1,8 |
1,8 |
3,6 |
3,2 |
1,8 |
1,8 |
|
9 |
22 |
1 |
1.9 |
1.9 |
3,8 |
3,6 |
1,9 |
1,9 |
|
10 |
23 |
2 |
0,9 |
0,9 |
1,8 |
2,0 |
0,9 |
0,9 |
|
11 |
24 |
3 |
2,0 |
0,8 |
4,0 |
2,2 |
0,8 |
0,8 |
|
12 |
25 |
4 |
2,1 |
0,5 |
4,2 |
3,0 |
0,5 |
0,5 |
|
13 |
26 |
5 |
2,2 |
0,6 |
4,4 |
3,1 |
0,6 |
0,6 |
Практическое занятие №6 Решение задач на определение положения центра тяжести в сложных фигурах
Цель: Для решения инженерных задач часто необходимо находить центры тяжести плоских фигур. Вообще плоские фигуры не обладают весом т.к. не обладают объемом, но многие тела имеют одинаковое сечение по всей своей длине и для нахождения центра тяжести таких тел, достаточно найти центр тяжести этого сечения.
Научиться находить центр тяжести конструктивных элементов.
Необходимые материалы и оборудование:
Учебный класс, индивидуальные задания, справочные материалы для практического занятия.
Ход работы:
Задание 1. Устанавливаем положение координатных осей, совмещая их с нижним контуром детали.
Ось симметрии всего сечения всегда проходит через его центр тяжести, соответственно, при таком положении координатной оси, одна из координат Xc=0 либо Yc = 0;
Задание 2. Мысленно разделяем форму сечения на отдельные простейшие фигуры Задание 3. Находим координату Y для каждой фигуры, используя данные справочных таблиц сортамента- расстояние до центра тяжести профилей--X0 или Z0.
Устанавливаем расстояния от центров тяжести каждой составляющей сечение фигуры до координатной оси X
Задание 4 Устанавливаем по справочным материалам либо расчитываем площади отдельных фигур Ai ·
Задание 5. Определяем статические моменты инерции отдельных фигур
до оси (Sy,i = Ai ·xi)
Задание 6 Определяем общую площадь сечения . Если в сечении имеются отверстия , знак минус показывает, что площадь отсутствует;
Задание 7 Определяем положение ЦТ по формулам
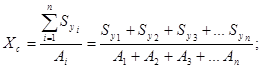
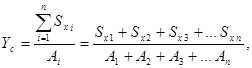
Пояснения к работе:
Определение центра тяжести плоских фигур важно для решения ряда задач по расчету строительных конструкций, сваренных из прокатных стальных элементов, или составленных из других конструктивных материалов. Сечение стального проката выполняют в виде двутавров, швеллеров, уголков, листов и др. Каталог производимых металлургическими заводами элементов называют сортаментом проката. Сортамент, кроме внешних форм и размеров производимых элементов, содержит их характеристики, позволяющие выполнять расчеты прочности.
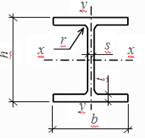
|
Балки двутавровые (двутавры) стальные горячекатаные с параллельными гранями полок, типа Б (балочные), Ш (широкополочные), К (колонные). ГОСТ 26020 – 83
Обозначения: h – высота балки, b – ширина балки, s – толщина стенки, t – средняя толщина полки, А – площадь сечения двутавра, см2.
|
|
Уголки стальные горячекатаные равнополочные. ГОСТ 8509 – 96 Обозначения: h – высота полки, b – ширина полки, t – средняя толщина полки, z0 – расстояние до центра тяжести уголка, А – площадь сечения уголка, см2.
|
|
Швеллеры с уклоном внутренних граней полок. ГОСТ 8240-97 Обозначения: h – высота швеллера; b – ширина швеллера; s – толщина стенки; t – средняя толщина полки; z0 – расстояние до центра тяжести швеллера, А – площадь сечения швеллера, см2.
|
Пример 1. Определить центр тяжести сечения колонны, сваренной из прокатных элементов (рис. 12). Швеллер № 30У (обозначен позицией 1) в соответствии с данными сортамента имеет площадь сечения А1 = 40,5 см2, расстояние до центра тяжести швеллера z01 = 2,52 см, высота швеллера h = 300 мм (см. ГОСТ 8240-97). Уголок 125×125×8 (позиция 2) имеет высоту и ширину полок 125 мм и среднюю их толщину 8 мм, площадь сечения одного уголка А2 = 19,69 см2, расстояние до центра тяжести z02 = 3,36 см (см. ГОСТ 8509-97).
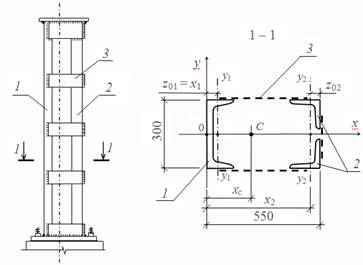 Рисунок 1 - Колонна и ее
сечение.
Рисунок 1 - Колонна и ее
сечение.
1 – швеллер № 30У; 2 – уголок 125×125×8; 3 – планка, соединяющая швеллер с уголком
Решение. 1.
1. Устанавливаем расстояния от центров тяжести каждой составляющей сечение фигуры до координатной оси у: расстояние от оси у1 (проходящей через центр тяжести швеллера) до основной оси у – соответствует расстоянию х1 = z01 = 2,52 см; расстояние от оси у2 (проходящей через центры тяжести уголков) до основной оси у – соответствует расстоянию х2 = 55 – z02 = 55 – 3,36 = 51,64 см;
2. 3. Определяем статические моменты инерции отдельных фигур до оси у (Sy,i = Ai ·xi): для первой фигуры Sy,1 = A1 x1 = 40,5·2,52 = 102,06 см3; для второй фигуры (учитывая, что имеем два симметрично расположенных уголка) Sy,2 = 2A2 x2 = 2·19,69·51,64 = 2033,58 см3; 4. Определяем площадь сечения колонны А = А1 + 2А2 = 40,5 + 2·19,69 = 79,88 см2; 5. Определяем положение центра тяжести сечения колонны
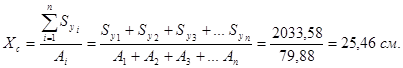
Положение центра тяжести сечения колонны определено (Xc = 25,46 см; Yc = 0).
Пример 2. Определить положение центра тяжести сечения, состоящего из простых геометрических фигур
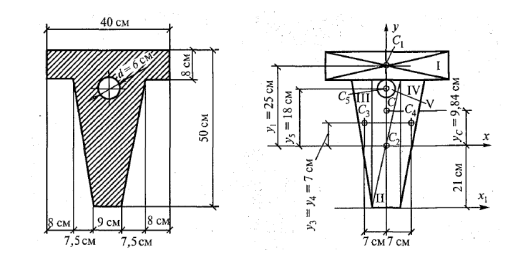
Решение. 1. Разобьем сечение на пять фигур: два прямоугольника I и II, два треугольника III и IV и круг V.
Укажем центры тяжести простых фигур С1, С2, С3, С4 , С5.
1. Выберем систему координат. Ось х проведем через центр тяжести С2 прямоугольника, а ось у совместим с осью симметрии сечения.
2. Определим координаты центра тяжести сечения:
Хс = О, так как ось у совпадает с осью симметрии;
![]()
Используя справочные данные, определим площади фигур и координаты центров тяжести:
А = 40 ·8 =
320 см 2 ; ![]()
![]()
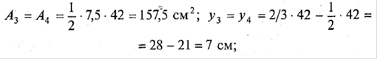
![]()
ставим числовые значения в формулу
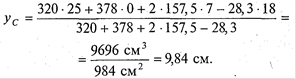
Для проверки решения ОСЬ Х1 МОЖНО провести ПО нижней грани сечения. В этом случае Ус = 30,84 см. Поскольку 30,84 - 21 = 9,84 см, то решение верно.
Ответ: Ус = 9,84 см, если ось х проходит через центр тяжести С2 .
Оси – относительны, но положение центра тяжести не зависит от положения оси.
Задания для практического занятия №6
Определить положение центра тяжести составного сечения в соответствии с заданием
Схема 1.
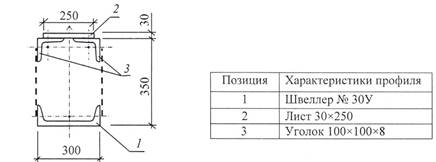
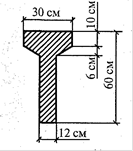
Схема 2.
![]()
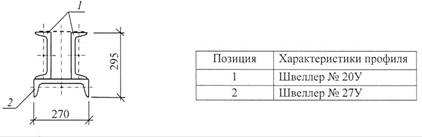
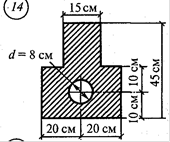
Схема 3.
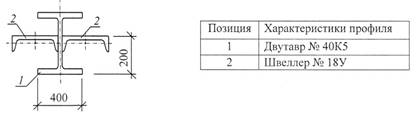
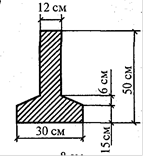
![]()
![]() Схема 4.
Схема 4.

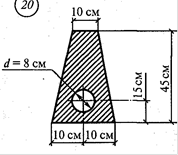
Схема 5.
![]()
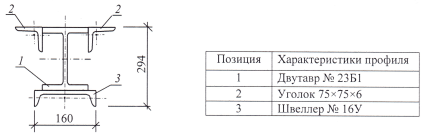
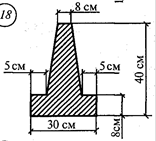
Схема 6.
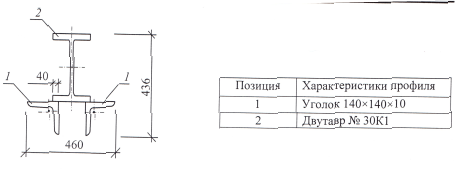
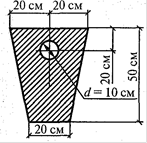
Схема 7.
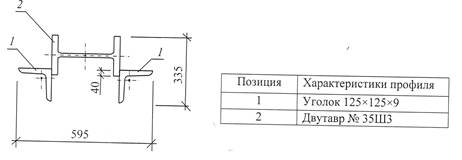
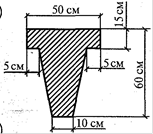
Схема 8.
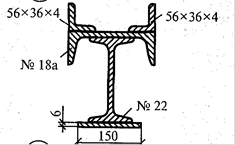
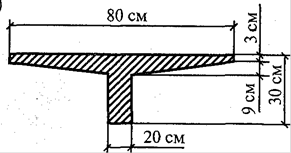
Схема 9.
![]()
![]()
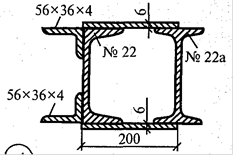
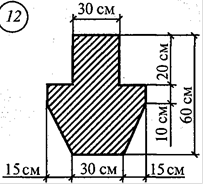
Варианты заданий:
|
№ варианта |
1 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
19 |
21 |
23 |
25 |
|
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
22 |
24 |
26 |
|
|
№ схемы |
Схема 1 |
Схема 2 |
Схема 3 |
Схема 4 |
Схема 5 |
Схема 6 |
Схема 7 |
Схема 8 |
Схема 9 |
Схема 1 |
Схема 2 |
Схема 3 |
Схема 4 |
Вопросы для защиты практической работы:
1. Что такое центр тяжести тела? Как его определить?
2. Что такое статические моменты инерции?
3. Что такое сортамент?
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.