АРИФМЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ КОМПЬЮТЕРА

АРИФМЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ КОМПЬЮТЕРА

Сложение в двоичной системе счисления

Правила сложения:

0 + 0 = 0
0+1 = 1
1+0=1

1 + 1 = 10 (результат сложения двух единиц: ноль и единица переноса в старший разряд)

Сложение двоичных чисел выполняют в столбик.

Пример:       10110₂

⁺    101₂

11011₂

Выполните сложение двоичных чисел:

101,101 + 11,01=

10101,11 + 1111,011=

1011011,1 +101010,01 =

110111,101 +10101,1 =

Умножение

Правила умножения:

0*0 = 0

0*1=0

1*0 = 0

1*1 = 1

Умножение двоичных чисел производится в стол­бик аналогично умножению десятичных чисел.

Пример:       

   1101₂

 ^х  

        11₂

₊  1101

 1101

                                                                       100111₂

Выполните умножение двоичных чисел:

1101*101 =

101,1*11,1=

1001,01*11 =

11011*110,1=

Вычитание

Правила вычитания:

0-0 = 0

1-0 = 1

1-1=0

10 - 1 = 1

(из нуля вычесть единицу нельзя, поэтому для вычитания необходимо занять единицу у старше­го разряда)

Пример:      1001

                          -

                      110

                     -----

                         11

Выполните  вычитание двоичных чисел с последующей проверкой сложением:

10101-110 =

1000011 - 101 =

Выполните деление двоичных чисел. Сде­лайте проверку в десятичной системе счисления.

1111 : 101 =

11100111 : 1011 =

1000001 : 1101 =

ПЕРЕВОД ЧИСЕЛ ИЗ ОДНОЙ СИСТЕМЫ СЧИСЛЕНИЯ В ДРУГУЮ

Триада - группа из трех разрядов (нулей и еди­ниц). Из триад можно составить восемь различных дво­ичных чисел (2³ = 8).

Тетрада - группа из четырех разрядов. Из тетрад можно составить шестнадцать различных двоичных чи­сел (2⁴ = 16).

Перевод чисел по схеме N₂ —> N₈

Алгоритм перевода:

1)  двоичное число разбивается на триады: целая часть - справа налево; дробная часть - слева направо;

2)  в дробную часть справа можно дописывать недостающее число нулей;

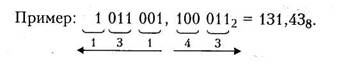3)  под каждой триадой пишется соответствующее восьмеричное число.

Перевод чисел по схеме N₂ —> N₁₆

Алгоритм перевода:

1)  двоичное число разбивается на тетрады: целая часть - справа налево; дробная часть - слева направо;

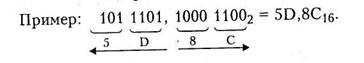2)  в дробную часть справа можно дописывать не­достающее число нулей;

3)  под каждой тетрадой пишется соответствующее шестнадцатеричное число.