Поделиться
ARITHMETIC_AND_GEOMETRIK_SEQUENCES.pdf
M O D U L
A R S Y S
Arithmetic and Geometric
SEQUENCES
Cem Giray
Zamboi(
h ttp: //book.zorn bok. com
This
book is about arithmetic and geometric sequences, and their applications. Many
people apply the princtples of number sequences in their daily lives Without
recognizing them. This book introduces these principles and shows how they
solve concrete problems. Sequences have important applications in communication
systems, global positioning systems, software testing, cryptography, computer
simulation, and stream ciphers. For manu students these tools and the
algorithms used to develop them will be as fundamental in their professional
work as the tools of mathematical analysis. For this reason, this book goes
beyond a purely analytical approach to sequences, and draws on techniques and
examples from applied math and mathematical modeling
The language of the book is student-friendly more than purely
mathematical. It tries to explain the topic as a teacher would explain it in
the classroom, so some exercises prompt the student to think for him or herself
Since the book focuses on developing algorithms and modeling applications, the
examples do not require complex calculations.
The book is divided into three sections. The first section,
real number sequences, deals With general number 
sequences With a
specific pattern, and forms the basis of the book. In the second and third
sections we study two 
of the most frequent types of sequence,
arithmetic and geometric, consecutively.
Each section is
followed by plenty of exercises. More difficult problems are denoted by a
single or double star, where the former means problems for upper-intermediate
level students, and the latter means problems aÚ advanced level. Most of
the problems reflect ski IIS or problem-solving techniques encountered in the
section. Every exercise set also contains problems whose solution method is not
cowered iw an example. In these problems students may be required to work a
little beyond the material discussed in the text, or to use the concepts in
ways not illustrated in the examples. All of these problems can be solved using
skills the student should already have ma stered
Following each section we discuss an actiTitu or project related to the material covered. The topics are the Fibonacci sequence, polygonal numbers, magic squares, the Sierpinski pyramid, and the Koch snowflake. These sections can be used as term projects to increase the students' understanding of the topic.
The book follows a linear approach, with material in the latter sections building on concepts and math covered previously in the text. For this reason, there are several self-test Check Yourself' sections that check students' understanding of the material at key points. 'Check Yourself' sections include a rapid answer kev that allows students to measure their own performance and understanding. Successful completion of each self-test section allows students to advance to the next topic.
The book ends With ret'ieu• materials, beginning With a brief summary
of the chapter highlights. Following these highlights is a concept check test
that asks the student to summarize the main ideas cowered in the book.
Following the concept check, review tests cover material from the entire book
Acknow ledg ements
Many friends and colleagues were of great help in writing this textbook. A
number of people need to be recognized and thanked for their contributions,
including Mustafa Ktnkçt at Zambak Publications, and Serdar Çam
for his typesetting and design
Cem Gira.!f
To the StudentThis book is designed so
that you can use it Section 1 effectivelU_ Each section has its own special 
color that you can see at the bottom
of the
Section 2
page
Section 3
Different Pieces of information in this book are useful in different waus_ Look at the types of information, and how they appear in the book.
Notes help you focus on important
details. When you see a note, read it twice! Make
Check Yourself sections help you check your understanding of what you have Just studied. Solve them alone and then check your answers against the answer key provided. If your answers are correct, you can move on to the next section.
A small notebook in
the left margin of a page reminds you of material that is related to the topic
you are studying. Notebook text helps you to remember the math you need to
understand the material. It might help you to see your mistakes, too! Notebooks
are the same color as the sectionb
you are studying
The general ofa geometric sequence (4)
general term of an
Exercises at the end of each section cower the material in
the whole section. You should be able to solve all the problems without any
special sumbol_ next to a question means the question is a bit harder next to a
question means the question is for students who are looking for a challenge!
The answers to the exercises are at the back of the book. com
 |
Special windows highlight important new information. Windows may
contain formulas, properties, or solution procedures, etc. They are the same
color as the section.
EXERCISES
A. Sequences
1. state whether each term is a general term
The Chapter Summary summarizes all the important material that has been covered in the chapter. The Concept Check section contains oral questions. In order to answer them you don't need paper or pen If you answer Concept Check questions correctly, it means you know that topic!
The answers to Concept Check questions are in the material
you studied. Go back over the 
material if you are not sure about an
answer to a Concept Check question
Finally, chapter review tests are in increasing order of
difficulty and contain multiple choice questions. The answer key for these
tests is at 
the back of the book.
 |
CONTENTS
REAL NUMBER SEQUENCES 2 3. GEOMETRIC SEQUENCES 42
A. SEQUENCES . 3 A. GEOMETRIC SEQUENCES 42
1. Defimnon 3 Deñmnon 42
2. Criteria the of a 2. General Term 43
Sequence 3 Advanced General Term Formula
B. TYPES OF SEQUENCE 6 4 Common RŽì1io Formula 46
Middle Term Formula
Fmlie and Ilnfimve Sequences .
(Geomei_rr: Mean) . 47
Monotone Sequences 7
3. Piecewise Seq uences 9 B. SUM OF THE TERMS OF A
4. Recursv.'elx Defined Sequences 10 GEOMETRIC SEQUENCE 51
Activity: The Fibonacci Sequence L Sum of the First Terms
and the Golden Ratio 12 2. Applied Problems . 55
EXERCISES 1 16 C. INFINITE SUM OF A GEOMETRIC
Actú'itu: Polygonal Num bers 18 SEQUENCE (OPTIONAL) . 57
Infimle Sum Formula 57
2. Repeanng Decimals
2. ARITHMETIC SEQUENCES 19 3 Equanons Infiniielv
A. ARITHMETIC SEQUENCES . 19 Manv Terms . 59
l. D e fininon 19 4 Applied Problems 61
2 General Term . 20 Activity: The Sierpinski Pyramid 62
3 Advanced General Term Formula EXERCISES 3 63
4 Middle Term Formula Activity: The Roch Snowflake 66
(Anthmenc Mean) 25
CHAPTER SUMMARY . 68
B. SUM OF THE TERMS OF AN CONCEPT CHECK . 69
ARITHMETIC SEQUENCE CHAPTER REVIEW TEST 70
l. Sum of the First Terms 27 CHAPTER REVIEW TEST 2 72
2 Applied Problems . 31 CHAPTER REVIEW TEST a .
EXERCISES 2 36 ANSWERS . 76
Activity: Magic Squares 40 GLOSSARY 78
An mterestmg unsolved problem m mathemancs concerns the 'hailstone sequence', which IS defined as follows: Start With any positive Integer. If that number IS odd, then multlplv It by three and add one. If it IS even, divide it by two. Then repeat. For example, startmg with the number 10 we get the hailstone sequence 10, 5, 16, 8, 4, 2, 1 Some mathematicians have conyectured (guessed) that no matter what number you start with, you "'111 always reach 1. This conjecture has been found true for all startmg values up to However, the conjecture, which IS known as the 'Collatz Problem', '311+1 Problem', or 'Syracuse Algorithm', still has not been proved true for all numbers.
Number sequences have been an interestmg area for all mathematicians throughout history. Geometnc sequences appear on Babvloman tablets datmg back to 2100 BC. Anthmenc sequences were first found m the Ahmes Papyrus which IS dated at 1550 BC. The reason behind the names 'arithmenc' and 'geometnc' IS that each term in a geometric (or anthmetic) sequence is the geometnc (or anthmenc) mean of Its successor and predecessor. If we think of a rectangle With Side lengths x and y, then the geometric mean is the Side length of a square that has the same area as this rectangle. Fmdmg the dimensions of a square with the same area as a Oven rectangle was considered m those days as a very geometric problem. Although the anthmenc mean (X + y)/2 can also be Interpreted geometncally (it IS the length of the sides of a square havmg the same penmeter as the rectangle) , lengths were viewed more as anthmenc, because It IS easier to handle lengths by addition and subtraction, Without havmg to thmk about two-dimensional concepts such as area. Although both problems Involve anthmenc and can be Interpreted geometncallv, m ancient times one was viewed as much more geometnc than the other, therefore the names.
Zeno (490-425 B.C.) was a mathemancran whose paradoxes about monon puzzled mathemanclans for centunes. They mvolved the sum of an mfimte number of positive terms to a finite number. Zeno wasn't the only ancient mathematician to work on sequences. Several of the ancient Greek mathematicians used sequences to measure areas and volumes of shapes and regons. By using his reasonmg techmque called the 'method', Archimedes (28 7-212 B.C.) constructed several examples and tned to explain how mfimte sums could have finite results. Among his many results was that the area under a parabolic arc is always two-thirds the base times the height.
The next major contributor to this area of mathematics was Fibonacci
(1170-1240). He discovered a sequence ofmtegers m which each number is equal to
the sum of the precedmg two numbers (1 1
), and introduced It as a model of the
breedmg population of rabbits. This sequence has many remarkable properties and
contmues to find apphcanons in many areas of modern mathemancs and science.
Durmg this same penod, Chinese astronomers developed numencal techmques to
analyze their observanon data and used the idea of finite differences to help
analyze trends in their data.
 |
years later, Stevm (1548-1620) understood
the physical and mathematical concepnons of acceleration due 
to gravity
usmg senes and sequences. During that time Galileo (1564-1642) applied
mathematics to the sciences, especially astronomy. Based on his study of
Archimedes, Galileo Improved our understandmg of hydrostatics. He developed
equations for free-fall monon under gravity and the monon of the planets. Up
until the middle of the 17th century, mathemanclans developed and analyzed
senes of numbers.
Newton (1642-1727) and Lelbnitz (1646-1716) developed several senes representations for functions. Maclaurm (1698-1746), Euler (1707-1783), and Founer (1768-1830) often used mfimte senes to develop new methods m mathematics. Sequences and senes have become standard tools for approxnnatmg functions and calculating results in numencal computing.
The self-educated Indian mathematician Srmwasa
Ramanujan (1887-1920) used sequences and power senes to develop results m
number theory. RamanuJan's work was theoretical and produced many Important results
used by mathematicians m the 20th century.
一
耳
帚,
-Ah.
,·气氵丆
Real number sequences are strmgs of numbers. They play an Important role m our everyday hves. For example, the followmg sequence:
20, 20.5, 21 22, 23.4, 23.6
Oves the temperature measured m a city at midday for five consecutive
days. It looks like the 
temperature IS nsmg, but It IS not
possible to exactly predict the future temperature.
The sequence:
64, 32, 16, 8
IS the number of teams which play m each round of a tournament so that at the end of each game one team IS ehmmated and the other qualifies for the next round. Now we can easily predict the next numbers: 4, 2, and 1. Smce there WILI be one champion, the sequence Will end at 1 that IS, the sequence has a fimte number of terms, Sequences may be fimte 111 number or mfimte.
Look at the followmg sequence:
1000, 1100, 1210
This IS the total money owned by an Investor at the end of each successive
year. The capital mcreases by 10% every year. You can predict the next number m
the sequence to be 1331 
Each successive term here is 110% of or
1.1 times, the previous term.
Real number sequences mav follow an easily recogmzable
pattern or they may not. Recently a great deal of mathematical work has
concentrated on decidmg whether certain number sequences follow a pattern (that
is we can predict consecutive terms) or whether they are random (that IS, we
cannot predict consecutive terms)
This work forms the basis of chaos theory, speech recogmnon, weather predicnon and financial management, which are just a few examples of an almost endless IISt. In this book we WILL consider real number sequences which follow a pattern.
1. Definition
If someone asked you to list the
squares of all the natural numbers, vou might beun by writing
4, 9, 16, 25, 36
But vou would soon realize that It IS actually Impossible to list all these numbers smce there are an mfimte number of them. However, we can represent this collecnon of numbers 111 several different ways.
|
|
|
|
|
|
|
A function is a relation between two sets A and B that assigns to each element of set A exactlv one e lement of set B |
||||
For example we can also express the above list of numbers by wrltmg
f(l), f(2), f(3), f(4), f(5), f(6), ...,
f(n), 
wheref(n) = n2 . Heref(l) IS
the first term, f(2) IS the second term, and so on.f(n) 11 2 Is a
funcnon of n, defined m the set of natural numbers,
|
Definition |
|
|
A function which is defined m the set
of natural numbers is called a sequence.
However,
we do not usually use functional notation to describe sequences. Instead, we denote the first term by a a, the
second term by and so on. So for the above list
9, - 16, as — 25, a 6 — 36 a
Here, al IS the first term, 
the
second term, ag IS the third term,
a IS the nth term, or the general term.
Smce this IS just a matter of notation, we can use another letter instead of the letter a. For example, we can also use b n, c , (In, etc. as the name for the general term of a sequence.
Solution
Example 2
Solution
EX am ple 3
Solution
An expresswn Like IS nonsense smce we cannot talk about the 26th term of a sequence. Remember that a sequence a function which IS defined m the set of natural numbers, and 2.6 IS not a natural number. Clearly, expressions like ao, are also meanmgless. We say that such terms are undefined.
In a sequence, n should always be a natural number, but the value of a mav be any real number dependmg on the formula for the general term of the sequence.
1
 |
Smce we are lookmg for the first five terms, we Just recalculate the general term for
n = l, 2, 3, 4, 5, which
oves 
Gwen the
sequence With general term a
find
as, a 2, a
We just have to recalculate the formula for a choosmg Instead of n the numbers 5, —2, and
3 395 79
100.
SO as and 
Clearly, a IS undefined, since —2 is
not a natural
2 200 40 number.
2 3 4
Fmd a suitable general term b n for the sequence whose first four terms are
2 3 4 5
We need to find a pattern. Nonce that the numerator of each fracnon IS equal to the term
position and the
denominator is one more than the term position, so we can write b
1 Wilte the first five
terms of the sequence whose general term IS cn
2. Find a suitable general term an for the sequence whose first four terms are 2, 4, 6, 8.
3. Gwen
the sequence With general term b 2n + 3, find bs, bo, and b 43
-1
2. 2n 3. 13, undefined, 89
If there IS at least one natural number which makes the general term of a sequence undefined, then there is no such sequence.
|
Solution Solution Exam ple 7 Solution |
Note that the expression Ux IS only meanmgful when x 0. So we need 0 to be true 1 for any natural number n. If we solve this equation for n, the
solution set (— 41 i.e. 2 between and 4, mcluswe. When we take the natural numbers m this solution set, we get 2 {1 2, 3, 4}, which means that only aj, (12, aa, a 4 are defined. So an IS not the general term of a sequence. Is a
It IS the general term of a
sequence. Choosmg n = I 2, 3 we get al = 2, a SO Gwen b a. 2n + 5 n 10th term 6th term not a term |
 |
a general term of a sequence? Why?
Solution No, because we cannot find a proper value for n = 2
Exam ple 5 Is a
a general term of a sequence? Why?
1. Is a
a
general term of a sequence? Why?
2. For which values of a IS b n 2 + a general term of a sequence?
3. Which term of the sequence With general term a
5n+7 12
|
Exam ple 8 Solution |
How many
terms of the sequence with general term a We are lookmgfor the number ofvalues of n for which a < 0. In other words we should find |
1.
yes, because an IS defined for all n e N a e I—I
-611-7
 |
we get ( l) u(—, 7). The natural numbers m this solution set are 1 2, 3, 4, 5, and 6.
Therefore, six terms of this sequence are negative.
A sequence may contain a fimte or mfimte number of terms.
For example the sequence (a.)contams n terms, which is a fimte number of terms. The sequence (bn) = (1 4, 9, n , ...) contams mfimtely many terms.
If a sequence contains a countable number of terms, then we sav it is a finite sequence.
If a sequence contains infinitely many terms, then we say it is an infinite sequence.
EX am ple 9 State whether the followmg sequences are finite or mfimte.
a. The sequence of all odd numbers.
b. (a) = (-10, -5, O, 5, 10, 15, 150)
Solution a. The sequence of all odd numbers 1 3, 5, 7,
Smce there are mfimtely many numbers here, the sequence is infimte.
b. This
sequence has a fimte number of terms smce the last term (150) IS oven.
c. The sequence is Infinite, as the notation shows that there are Infinitely many
numbers.
In this book, If we do not say a sequence fimte, then It IS an mfimte
sequence.
If each term of a sequence IS greater than the previous term, then the sequence IS called an mcreasmg sequence.
Symbolically, (an) is an mcreasmg sequence If ar >
an
If an +1 an, then (an) IS a nondecreasing sequence.
If each term of a sequence IS less than the previous term, then that
sequence IS called a decreasmg sequence.
Symbolically (a) IS a decreasmg sequence If an4] < an.
If a a , then (an) IS a nonmcreasmg sequence.
In general anv mcreasmg, nondecreasmg, decreasmg, or
nonmcreasmg sequence is called a 
monotone sequ ence
For example, the sequence 10, 8, 6, 4, a decreasmg sequence smce each consecunve term IS less than the previous one. Therefore, It IS a monotone sequence.
The sequence I I 2, 3, 5, ... IS a nondecreasmg sequence, because the first two terms are equal. It is also a monotone sequence.
Consider the sequence 4, 1, 0, 1, 4 Obviously we cannot put this sequence mto any of the categones of sequence defined above. Therefore, It IS not monotone.
We can rewnte the above critena for increasmg and decreasing sequences in a different way:
If a
|
Exam ple |
|
Solution |
If a = 2n, thena 20b + 1) = 2n + 2, and so a |
|
|
|
Smce2 > O, (an) IS an increasmg sequence. |
|
||
|
|
Prove that
the sequence with general term b |
1
|
IS a decreasmg sequence . |
|
Solution |
If
bm 1 1 -1 |
|
|
10 Prove that the sequence (an) "'Ith general term an
2n IS
an mcreasmg sequence.
-1 Smce n Is a natural number, n + 1 >
0 and n + 2 > 0. That means b
Therefore, (b) IS a decreasmg sequence.
 |
Given the sequence With general term a n2 + 8n 3,
a. find
the biggest term.
b.
state whether the sequence IS
monotone or not.
|
|
|
|
|
|
|
The peak point of a parabola vive n by f(x) = ax2 + bx + c is
|
||||
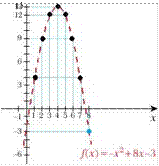Solution a. If we
thmk about the general term m funcnonal notanon, we have f(x) x 2 +
8x — 3, whose graph is the parabola shown opposite.
Here, note that we cannot talk about a mmimum value. Clearly, the parabola takes its maximum value at Its peak pomt and so does the sequence, provided that the x-coordmate at that peak pomt IS a natural number. The peak pomt of the parabola hes at
8
4. Smce 4 e N, the biggest term of the 
2
sequence IS f(4) = 13. (What would you do If the x-coordinate at the peak pomt
was not a natural number?)
b, If we look at the above parabola's values for natural values of x (the black dots), we can see that the sequence IS mcreasmg before x = 4 and then decreasmg. Therefore, the sequence cannot be defined as Increasmg or decreasmg, which means that It IS not monotone.
State If the followmg sequences are finite
or mfimte.
1
a. The
sequence with general term c
54
2. Prove that (an) (2 — 5n) is a decreasmg sequence.
3. Classify the followmg sequences as mcreasmg or decreasmg.
a. (an) = (2n + l) b. (4) c.
(n2
— 4n) 
2n-8
4. For
which term(s) does the sequence (c) — (n 2 - 5n + 7) take Its mmmum
value?
Hint:
Consider the nearest natural x-coordinates to the minimum of the uaph of f(x)
Answers
l. a. mfimte b finite c infinite mcreasmg b decreasmg not a sequence neither
4. n = 2 and = 3, I.e. the second and third terms
 |
If the general term of a sequence IS defined by more than one formula, then It IS called a plecemse sequence.
For example, the sequence With general term
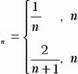n IS even
a
IS odd
is a piecewise sequence.
n IS even
Write the first four terms of the
piecewise sequence with general term a
n IS odd
1 2
Solution To find al and ag we use smce n is odd and to find a 2 and a4we use smce n is even.
2 1 2
So al l, an a, and
a4
n < 10
Given the piecewise sequence With general
term an
8 n
> 10
a. find
b. find al
C. find the term which is equal to 0.
Solution a, 
When
n = 20, an = n — 8. So ago b. 
When n = 1 an = 511. So aj
c. If a term is equal to 0, then a O. This means
O (for n
< 10) or 0 (forn 10) n - 8 ¥10
n
O 
N or n = 5
 |
Sometimes the terms m a sequence may depend on the other terms. Such a sequence is called a recursively defined sequence .
For example, the sequence oven With general term an an + 3 and first term al 4 Is a recursively defined sequence.
|
Exam ple |
15 Gwen al = 4 and a
a. find a 
b, find the general term of the sequence.
Solution a. Note that choosmg n 2 will not help us to find smce we Will get an equation Ilk-e ag — + 3, which needs aa to get (12.
But
If we choose n l, we Will get a 1 + 3. Usmgal 4, we find a
7.
b. 
Recursively
defined sequences have terms which depend on prevzous ones like the falltng
domznoes above
|
Exam ple |
16 Gwen f] = 1,f2 1 f = fn _ 2 + fn _ 1 (for n > 3), find the first SIX terms of the sequence.
Solution When we consider the general term, we nonce that It IS not possible to calculate a term's
value unless we know the two previous terms. Smce we are given the first and second terms, With the help of the general term we can find the third term.
Choosmg n = 3, the formula for general term becomesf3 = + f2
2.
Now It IS possible to find q, and then by the same procedure as and a
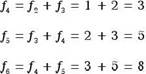
The first SIX terms are l, I, 2, 3, 5, 8.
Smce recursively defined sequences have terms which depend on
previous ones like a cham 
we calculate the terms one by one to find
the desired term. In the above example, unless we find a direct formula for the
general term (IS It possible?), It "'Ill take too much time and effort to
find f]
|
BONACCI QUENCE The sequence in the previous example is called the |
I-DEN |
TIO |
time = O Fibonacci sequence, named after the 13th century Italian mathematician Fibonacci, who used it to solve a problem about the breeding of rabbits. Fibonacci considered the followmg problem :
Suppose that rabbits live forever and that every month each pail produces a new pair that becomes productive at age two months. If we start with one newborn pall, how many pairs of rabbits Will we have m the nth month? As a solution, Fibonacci found the following sequence:
1 2, 3, 5, 8, 13, 21 34, 55, 89, 144, 233,
This sequence also occurs in numerous other aspects of the natural world.
The planets in our solar system are spaced in a Fibonacci sequence.
We can make a picture showmg the Fibonacci numbers If we start With two small squares whose sides are each one unit long next to each other. Then we draw a square with Side length two umts (1 + 1 units) next to both of these . We can now draw a new square which touches the square With Side one unit and the square with side two umts, and therefore has Side three units. Then we draw another square touching the two previous squares (side five units), and so on. We can continue adding squares around the picture, each new square havmg a Side which is as long as the sum of the sides of the two previous squares. Now we can draw a spiral by connecting the quarter circles in each square, as shown on the next page. This is a spiral (the Fibonacci Spiral). A similar curve to this occurs m nature as the shape of a nautilus.
3 3
2
13
A nautilus has the same shape as the Fibonacci spiral.
The rano of two successive Fibonacci numbers gets closer to the number 1.618 as the value of n gets 2
bigger. This number IS a special number m mathematics and IS known as the golden mt10.
The ancient Greeks also considered a line segment divided mto two parts such that the ratio of the shorter part of length one unit to the longer part is the same as the rano of the longer part to the whole segment.
x
This leads to the equanon whose positive solunon IS x Thus, the segment shown divided into
X 2
the golden rat10!
A rectangle in which the ratio of one Side to the other gives the golden ratio is called a golden rectangle. The Golden Rectangle is a unique and a very Important shape m mathematics. It appears m nature and music, and also often used in art and architecture. The Golden Rectangle is believed to be one of the most pleasing and beautiful shapes
for the human eye.
The golden ratio is frequently used in architecture.
x
1.618
The ratio of the length of your arm to the length from the elbow down to the end of your hand is approximately equal to the golden ratio.
|
Exam ple |
17 Given a F 6 and (n + 2) • an 3an (forn > 2), find aa.
Solution Th1S time we are oven the fifth term and the third term IS required. Tms means we should think backwards. That is, first we should find a4 and then aa.
18
Choosmg
n = 5, the formula for general term becomes 7a,
.3as, I.e. a4 Now
It IS
9
possible to find aa by choosmgn = 4: 6aa
= .3a„ so aa
7
Gwen 1
and a an_l + n (for n > 2), find a
Solution Smce we axe uven a recursively defined sequence, It Will take too much effort to find the
hundredth term unless we find a more practical wav. Let us write a few terms:
Clearly,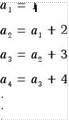 
agg a. 98 + 99
a agg 1 00
99+1
+2+3+4+ +99+100which we can snnpllfy as
Arithmetic and Geometric Sequemes
Real nrber
+ 99 + 100 (1)
01
1. (2)
Addmg equanons (1) and (2) we get
20.
|
100 terms
Smce 2a1
5050.
Recursively defined sequences are frequently used m computer programming.
Their disadvantage is that we
cannot find anv term directly, but their advantage is that we can successfully
model more complicated systems as we saw for Fibonacci's problem.
1.Gwen an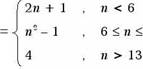 
13,
find the biggest and smallest terms of the sequence.
1
2.Gwen
al an (for n 2), find 
3.
Gwen a 1 2an + 1 (for n 2), which term of
the sequence is equal to 63?
Answers
l. al 3 biggest, al smallest 2. 3.5 3. 6th
l. State whether each term IS a general term of a sequence or not.
a. 3n - 76 b. c.
2n-1
4 13 1
d. f.
4 4
g. n 5 h. 1.
Fmd
a suitable formula for the general terms of the sequences whose first few terms
are uven,
|
a. |
1 |
b. |
|
|
c. |
o 3, 8, 15 |
1 8 d. |
27 |
|
|
|
5 7 |
9 |
e, 2, 6, 12, 20, 30
3. Find the stated terms for the sequence With the given general term.
a. a 2n + 3, find the first three terms and a 37
b. a find the first three terms and agg c. a find the first three terms and as
How many terms of the sequence With general term an = n 2 — 6n — 16 are negative?
5. How many terms of the sequence With general
3n-7 term a are less than — ?
5
60 For the sequence with general
term n2 —2n a
and as 5,
find k.
Find a suitable general term (not
piecemse) for the sequence whose first five terms are 2, 4, 6, 8
34. What IS the sLXth term?
8, For the sequence with general term
n even a
n odd find a 4 + a
9. Fmd a suitable general term for the sequence whose first six terms are 2, I, 4, 3, 6, 5.
Prove that the sequence With general term
a. a 4n — 17 is mcreasmg.
b. 25 • (—) " IS decreasmg.
311-7
111„ State whether the sequence
is
monotone or not.
12. Fmd the biggest and smallest terms (If they exist) of the sequences With the followmg general terms.
a. a 3n — 5 b. b
3n—5
c.
Arithmetic and Geometric Sequemes
130 Fmd the first four terms and, If possible, the
|
general term of the recursively defined sequences. |
Given the sequence with general term a |
|||
|
a. 1 2a b. 3, c. 3, an |
|
a find a |
||
|
Write the follow-mg sequences recursively. |
|
20. How many terms of the sequence with general -72 term a are Integers? 21. How many terms of the sequence With general |
||
|
a. a .3n b. |
|
|
||
|
Given a sequence With a find |
2 |
and au |
3, |
term a are Integers? |
|
Consider a sequence with an |
|
|
and |
Fm d the greatest Integer b for which the 1m -3 |
|
Is 1980 a term of th1S seq uence? Mixed Problems IL 70 Gwen the sequences with general terms |
|
sequence With general term an is 311-2 mcreasmg. |
||
|
2)" , find |
23, Fmd all values of p for which the sequence With |
|||
|
where dn = a. • b n cn + Gwen the sequence With general term a a find |
+ p general term c IS mcreasmg. 2004 |
|||
|
a |
24, The sequence (fn) where fl = = I = fn.l + is known as the Fibonacci sequence. |
|||
|
2) 2, 1 where we N |
Prove thatf12 + f + |
|||
Real nrber
At the begmnmgof this book we looked at the sequence 1 4, 9, 16, 25t 36, . We
36
|
call the numbers in th1S sequence square numbers. We can generate the square |
|
|
numbers by creatmg a sequence of nested squares like the one on the nght. |
23 |
|
Startmg from a common vertex, each square has sides one unit longer than the |
16 |
|
previous square. When we count the number of pomts in each successive square, we get the sequence of square numbers |
9 4 |
(first square = 1 pomt, second square = 4 pomts, third square = 9 pomts, etc.)
Polygonal numbers are numbers which form sequences like the one above for different polygons. The Pythagoreans named these numbers after the polygons that defined them.
Tnangular numbers
1 3 6 10 13 21
Square numbers
4 9 16 25
Pentagonal numbers
5 12 22 35
Polygonal numbers have many mterestmg relationships between them. For example, the sum of anv two consecutive triangular numbers is a square number, and eight times anv tnangular number plus one IS always a square number.
Can vou find any more patterns? Can vou find the general term for each set of polygonal numbers?
If a sequence (a) has the same difference d between its consecunve terms, then It IS called
In other words, (an) IS anthmenc If a a + d such than n e N, d e IR. We call d the common difference of the anthmenc sequence. In this book, from now on we WILI use a to denote general term ofan anthmenc sequence and d (the first letter of the Latm word differentia, meaning difference) for the common difference.
If d is positive, we say the arithmenc sequence is mcreasmg. If d IS negative, we say the arithmetic sequence is decreasmg. What can you say when d IS zero?
|
EXAMPLE |
19 
State whether the followmg sequences
are anthmenc or not. If a sequence IS anthmenc, find the common difference.
a.
7, 10, 13, 16, b. 3, -2, -7, -12,
C. 1, 4, 9, 16,
Solution a.
anthmenc, d = 3 b. anthmenc, d 
5 c. not anthmenc d. anthmetic, d = 0
|
EXAMPLE |
20 State whether the sequences With the followmg general terms are arithmetic or not. If a sequence is arithmetic, find the common difference.
Solution a. a4n + 1
so the difference between each consecutive term is a(4n — 3) = 4, which is
constant. Therefore, (an) is an anthmenc sequence and d = 4.
b.
a
l , so the difference between
each consecutive term IS a a 
which is not constant.
Therefore, (an) is not an arithmetic sequence.
c. a (n + l), so the difference between two consecutive terms IS
a(no — n) = 2n, which IS not constant.
Therefore, (an) is not an anthmenc sequence .
d.
By rewntmg the general term we have a
Smce n —4 (smce we
are
talkmg about a sequence), we have an = n + l. Therefore, a (n
+ I) + l, and the difference between the consecunve terms IS a
l, which IS constant.
Therefore,
(a) IS
an anthmetic sequence and d = 1
 |
With the help of the above example we can nonce that If the formula
for general term of a sequence uves us a Imear function, then It Is arithmetic.
NoteThe
general term of an arithmenc sequence is Imear.
|
recursively. The formula IS denved as follows: If (a r) IS anthmenc, then we only know that a |
Anthmett£ yrowth IS unear a + d, Let us write a few terms, |
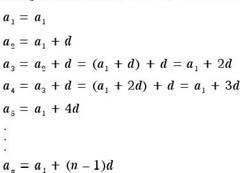Smce arithmenc sequences have many apphcanons, it is much
better to express the general term directly, Instead of
This is the general term of an anthmenc sequence.
|
|
|
The general term of an arithmetic sequence (an) with common difference d is a al+(n — l)d. |
3, 2, 7 are the first three terms of an
anthmenc sequence (an). Fmd the twentieth term.
Solution We know that al = —3 and d = aa —
5.
Usmg the general term formula, a a 1 + (n — l)d a 3 + (20- 1) • 5 = 92.
|
EXAMPLE |
(an)
is an arithmetic sequence with a
4, as 25. Find the common
difference and a]
Solution Usmg the general term formula,
a a 1 + (n — l)d as
25 4 + 7d. So we have d = 3.
a al + (100 - l)d = 4 + 100 • 3 = 304
 |
3 and common difference 4. Is 59 a term of this sequence?
Solution For 59
to be a term of the anthmenc sequence, it must satisfy the general term formula
such that n a natural number. al + (n — l)d
3 + 0- 1) . 4
15
Since 15 is a natural number, 59 is the 15th term of this sequence.
|
EXAMPLE |
24
Find the number of terms m the arithmetic sequence 1 4, 7, 91
Solution Here we have a finite sequence. Usmg the general term formula
a a 1 + (n — l)d
91 = 1 + 0 - 1) . 3
n = 31
Therefore, this sequence has 31 terms.
an — al
 |
Note
that If we rewrite the general term formula terms of n, we get n
+1, which is
the number of terms m a fimte arithmenc seq uence.
|
NUMBER OF TERMS OF A FINITE ARITHMETIC SEQUENCE |
|
first term, a IS the last term, and d IS the common difference. |
|
EXAMPLE 25 Solution |
How many two-digit numbers are divisible by 5? These numbers form a fimte anthmetic sequence since the number of two-thut numbers is finite, and the difference between consecunve numbers m this sequence IS constant, that is
Therefore, n18. Therefore, 18 two-diut numbers are divisible by 5. Check Yourself 5 1. Is the sequence With general term an 5n + 9 an anthmenc sequence? Why? 2. 6, 2, —2 are the first three terms of an arithmetic sequence (a) . Fmd the 30th term. 3. (an) IS an arithmenc sequence with aj 7, 70. Find the common difference and |
al
4. (an) is an anthmetic sequence With aj —1 and common difference 9. Which term of this sequence IS 89?
5. How many three-thut numbers are divisible by 30?
Answers
l. yes; linear formula 2. -110 3. 7; 707 4. 11 th 5. 30
EXAMPLE (an) IS an arithmetic sequence With al 34 and common difference 3. Find aa.
|
Solution |
Usmg the general term formula, |
SO ag 10.
In this example, we calculated the first term of the sequence (al) from an, then used this value to find aa. However, there is a quicker wav to solve this problem: m general, If we know the common difference and any term of an arithmenc sequence, we can find the required term Without findmg the first term. Look at the calculation: If we know a and d, to find an we can write:
Subtractmg (2) 
from (l), we get an a (n —p)d. So ar = a +
(n —p)d.
|
|
|
The general term of an
arithmetic sequence (a) with common difference d is a |
So usmg the advanced general term formula, we can solve the preuous example as follows:
ap + (n — p)d
+ (11 -3) . 3
a.3 + 24
 |
Note that when p = 1 the advanced general
term formula becomes the general term formula we studied previously.
|
EXAMPLE |
(an) IS an arithmenc sequence With as 14 and ajo 34. Fmd the common difference.
Solution Usmg the
advanced general term formula, ap + (n —p)d
+ (10 
14 + 5d
EXAMPLE (an) IS an arithmetic sequence With ag — 42. Find a
|
Solution |
Usmg the advanced general term formula, |
d 6.
Therefore, a 10
a 3
- 6 = 18.
4,
x, y, z, and 24 are five consecutive terms of an anthmetic sequence. Fmd x, y,
and z.
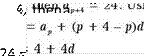Solution Let a 24.
Usmg the advanced general term formula,
a p44
Smce the difference between
consecutive terms is 5, x = 9,
14
19.
|
EXAMPLE |
We Insert five numbers m mcreasmg order between 12 and 42 such that all the numbers form an arithmetic sequence. Find the third number of this sequence.
|
|
|
|
|
|
|
The common difference of an arithmetic sequence formed by inserting k terms between two real numbers b and c is c—b d |
||||
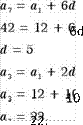Solution If we begm With two numbers
and Insert five numbers, the sequence has seven numbers 111 total. Let us call
the first number a l, the second an, and so on. We can now write the problem
differently: even an anthmenc sequence (an) With a 12, a 42, find as.
 |
Usmg the general term
formula,
EXAMPLE Given an anthmenc sequence (an) With as 10, find a2 + [114.
Solution
This time we have just a, 10 as data. Until now we have learned just one
fundamental formula a al ± (n — l)d, and the advanced general term formula we
denved from lt. We cannot find a 2 or a] 4 with the help of the general term
formula smce we need two values as data. However, remember that we are not
asked to find or al 4, but to find + au. Let's apply the advanced general term
formula, keepmg m mind that we just know a,
(1)
as + (14 -8)d. (2)
Addmg
equanons (l) and (2) we get 
as
- 6d + + 6d = 2as 20.
The solution to the previous example shows us a practical formula.
Let a and a k be terms of an anthmetlc sequence such that k < p. Then
a a
—lid (1)
a(2)
Addmg equations (l) and (2) we get
2a , or a
which means that any
term x m an anthmenc 2 sequence is half the sum of any two terms which are at
equal distance from x in the sequence.
 |
|
MIDDLE TERM FORMULA (Arith metic Mean) |
|
|
|
|
|
|
|
|
|
2 Note that m is the same distance from x as from y so x, m, y ñrm a finite arithmetic sequence |
||||
For example,
all the followmg equalities Will hold m an arithmetic sequence:
IS m the middle of aj and a
(x must be 8)
2 2 2
+ a20 a (U must be 16)
2
|
EXAMPLE |
32 5, x, 19 are three consecutive terms of an anthmenc
sequence. Fmd x
Solution
If we say al 5, 
19, then usmg the middle term formula,
3
and x — 12. Therefore, x is 12 If the sequence is
anthmenc.
2 2
Three numbers a, b, c form an
arithmenc sequence if and only If b
2
|
EXAMPLE |
33
Fmd the general term an for the arithmetic sequence With as + a,
106 and ag 37.
Solution
Usmg the middle term formula, 
So a 53.
2 2
Usmg the advanced general term formula
|
a 12
|
|
|
To write the general term we can choose a 9 or a general term formula we get |
Let us choose as, then usmg the advanced |
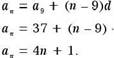4
1. (an) an anthmenc sequence mth a] 41
and common difference —4. Fmd aa
2. (an) is an arithmetic sequence with as 19, 55. Find the common difference.
3.
 |
Fill m the blanks to form an arithmetic sequence: 2, 8
|
4. Find x If x, 4, 19 form an arithmetic sequence. |
|
|
|
5. Fmd the general term an for the arithmetic sequence with aa + Answers 1. 97 2. 4 3. 2.5, —1 0.5 and then 3.5, 5, 6.5 4. -11 5. - 28 |
98 |
7. |
|
EXAMPLE |
Gwen an anthmenc sequence (an) With al = 100 and as the first negative term, how many
Integer values can d take?
Solution Let's convert the problem mto algebraic language: al = 100 a22 < 0 smce IS the first neganve term. de Z a21 20
Smce we are lookmg for the common difference (d), we need to express the above system of
Inequalities m terms of d:
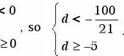
a +21d< O that IS al +20d
The only Integer that is m the solution set for the above Inequalities IS —5, so d can take only one mteger value (—5).
EXAMPLE Gwen a decreasmg arithmetic sequence (an)
With a. + a4 + as 18 and • a 4 • as -168 
find al and d.
18
Solution We are given the system
-168
Smce we are asked to find al and d, it IS more practical to express (12, a4, a6 m terms of and
d. This oves us:
(1)
=-168-168. (2)from equanon (1), al
Equanon (2) becomes:
-168
 |
Fmally, substitutmg d = —4 m equanon (l) uves us a = 18
So
the answer is al 18 and d = _4.
1. Sum of the First n Terms
Let us consider an anthmenc sequence whose first few terms are 3, 7, 11 15, 19.
The sum of the first term of th1S sequence IS obviously 3. The sum of the first two terms IS
10, the sum of the first three terms IS 21 and so on. To write this m a more formal way, let us use S to denote the of the first n terms, i.e., S al + + + a . Now we can write:
s 3
|
EXAMPLE |
36 Given the general term a .3n + 1 find the sum of first three terms.
|
Solution |
|
21 |
How could we find S o m the above example? Calculatmg terms and findmg thell sums takes tune and effort for large sums. Smce anthmenc sequences are of special Interest and Importance, we need a more efficient way of calculatmg the sums of arithmenc sequences.
The followmg theorem meets our needs;
 |
|
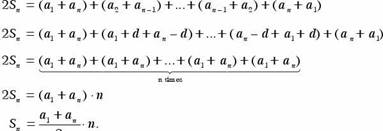
EXAMPLE 37 |
Given
an anthmenc sequence "'Ith al |
2 and as |
17, find ss. |
2
Solution|
Solution |
Usmg the sum formula, |
•27 requires al + 26d -14
+ 26 5 116.
2
—14 116
Therefore, S27 .27 1377
2
Given a
1 56 and an —14, find Sis.
Solution Usmg the sum formula,
15, so we need to find al Let us calculate
usmg an:
2 an
-14 56 + 10d? so d 7 and
aft 14d = 56 + 14 • 
Therefore, S] - 
• 15 =105. 
2
|
EXAMPLE |
40 If —5 + + 49 = 616 IS the sum of the terms of a fimte anthmenc sequence, how many terms are there m the sequence?
Solution Let us convert the problem Into algebraic language:
 |
5, a = 49, and S 616, and we need
to find p.
Usmg the sum formula,
s
•
p, that Is, 616
•
p, so p 28. So 28 numbers were added.
2 2
Smce a al + (n — l)d, we can also rewnte the sum formula as follows:
|
The sum of the first n terms of an
arithmetic sequence is S |
|
EXAMPLE |
Gwen an
anthmenc sequence With aj 
—90, find d.
Solution By usmg the alternanve formula for the sum of first n terms, we
have
2 . (-7)+ (15-1) • d 1
• 15, that Is, — 90 — •15, so d—
2 2 7
|
EXAMPLE |
42 Gwen d 4 and ss —189, find al.
|
Solution |
Usmg the alternative sum formula, |
2al —1) • d s n, and so
2
+(9-1) .4
|
2
2 Check Yourself 7 |
|
|
|
Gwen an anthmetic sequence
With a |
and a |
15, find Slo. |
|
2. |
Given
an anthmetic sequence With an |
and
d |
|
|
3. |
Given
an anthmenc sequence With a |
and ss |
find d. |
. 94. Find the sum of all the multiples of 3 between 20 and 50.
Answers
1. 95 2. 494 3. 1.75 4. 345
(an) IS a sequence of consecutive Integers With first term 3 and sum 52. How many terms are
there m this sequence?
Solution Here
a 1 
52,
n = ?
 |
|
EXAMPLE |
Usmg the alternanve sum formula,
s.
2
52
2
+511-104= 0.
Solvmg the quadranc
equanon we get n
8
or n —13 , Smce there cannot be -13 numbers, the answer IS 8.
|
EXAMPLE |
44 (an) IS an arithmenc sequence With S 11 —
S10
43 and 
87.
Fmd d.
Solution Note that the difference between Sil and SAO Is just an. Therefore, an 43 and a] 87.
a
43 4 d d 11.
|
EXAMPLE |
(an) is S 30
and s, 4. Fmda |
|
|
Solution |
Since we are looking for a term of the sequence, It is best to choose variables. |
and d as our new |
30 5 -3
that is which means 
4 1 d 1
Therefore, ag
|
EXAMPLE |
46 Find the general term ofthe arithmetic sequence (an) If the sum of the first n terms IS 3n2 411.
•n,
so 3n 2 —4n
2 2
Since
n 3n—4 
2
Choosmgn
= 1 we get a] 6 • 
—al . So a -1
Therefore, the general tenn IS a
|
EXAMPLE |
47
 |
Solution Note that the rate of population growth m the city IS decreasmg. Here, symbolically we have:
4200 (the populanon growth m the first
year that IS to be Included m the total) d 20 (the difference between the
populanon growth for consecutive years)
? (the total population growth m eleven
years from 2004 to 2014 mcluswe)
2a +10d 2. 4200+10. (-20)
45100.
2 2
So the expected total population growth IS 45,100 people.
|
EXAMPLE |
48 Every hour an annque clock chimes as many tunes as the hour. How many times does It chime between 8:00 a.m. and 7:00 p.m. inclusive?
Solution Note that the number of chimes in the oven time Interval Will not form an arithmenc
sequence smce after noon It Will restart from 1. But until noon and after noon we have two Independent finite arithmenc sequences. Therefore, let us define two sequences and deal with them Independently.
First consider the sequence up to noon.
a 1 = 8 (first chime before noon) d 1 (amount of Increase between consecunve chimes) a 12 (last chime at noon) s ? (sum until noon) a aa + (p — l)d, so 12 = 8 + (p — 1) • l . So p 5.
s •p,
so ss
.5=50.
2 2
Now consider the sequence after noon.
1 (first chime after noon)
7.
— 50 + 28 = 78. Therefore, the clock chimes 78 times.
 |
EXAMPLE 49 A farmer Picks 120 tomatoes on the first day of the harvest, and each day after, he Picks 40 more tomatoes than the previous day. How many days Will it take for the farmer to PICk a total of 3000 tomatoes?
Solution We
can describe this situation with the help of arithmetic sequence notation: 120,
d = 40, sn = 3000
2
3000 —
2 n 2 +5n —150 = 0.
Solvmg the quadratic equanon oves n —15 or n 10. Smce we cannot talk about a negativ e number of days, the answer IS ten days.
For a penod of 42 days, each dav a
mailbox received four more letters than the previous day. The total number of
letters received durmg the first 24 days of the penod IS equal to the total
number received durmg the last 18 days of the period. How many letters were
recewed durmg the entire penod?
Solution Obviously d = 4 and we are looking for S42. We can express the number of letters received
durmg the first 24 days by $4. But note that the number of letters received durmg the last
18 days of the penod is not s] s. In fact, the number of letters received durmg the last 18 days IS eq ual to the difference between the number of letters received durmg the entire penod and the number of letters received during the first 24 days, so:
s42 su or 2. S s
Usmg the alternative sum formula
2a + 23d 2a1 +41d
2 . • 24 • 42
2 2
(2¶+92) . 24 = (2(11 +164) .21
= 206.
Usmg the alternanye sum formula once more,
 |
• 42 = 12096.
2 2
So dunng the entire penod, the mailbox received 12 096 letters.
1. Startmg from 10 mcluslve, IS it possible to have a sum of 360 by addmg a sequence of consecutive even numbers?
2. (an) IS an anthmenc sequence With Sl 75 and S, 9. Find se
3. Fmd the common difference of an anthmenc sequence If the sum of the first n terms of the sequence IS even by the formula n2 — 2n.
4. A
free-falLmg object drops 9.8 meters further durmg each second than It did durmg
the 
previous second. If an oÞect falls
4.9 meters durmg the first second of its descent, how far will It fall m five
seconds?
1. yes 2. 6 3. 2 4. 122.5 meters
|
EXAMPLE |
51 a a form an anthmetic sequence. The sum of the odd-numbered terms is 15 more than sum of the eyen-numbered terms and 3ag. Fmd a
Solution Smce we are talking about two different sums, we'll divide this sequence mto two different finite sequences.
Let b n denote the odd-numbered terms With common difference 2d, so (b n)
and
let S: denote the sum of first n terms of this sequence. Note that for th1S
sequence
Let c, denote the even-numbered terms with common difference 2d, so (cn) 
and
let S ' denote the sum of first terms of this sequence. Note that for this
sequence n = 10.
Here, note that both (b) and (c) are anthmenc sequences, and both have
the same common difference which IS twice the common difference of (an)
 |
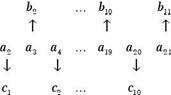
Now, let us write what we are given m a system of two variables smce we have two equations:
|
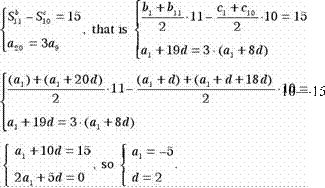
We need a |
and |
|
EXAMPLE |
52 find the sum of all the three-d10t numbers which are not divisible by 13.
Solution First of all we should reahze that all the three-thut numbers which are not thusible by 13 do not
form an arithmenc sequence, so we cannot use any sum formula. It Will also take a long tune to find and add the numbers. Therefore, let us look for a different way to express this sum.
Note that all the three-dlglt numbers form an anthmenc sequence, and all
the three-thut numbers that cue dmslble by 13 form another anthmenc sequence,
which means we can calculate these sums. Realizing that the sum we are asked to
find is the difference between the sum of all three-digit numbers and the sum
of all three-digit numbers that are divisible by 13 
we are ready to
formulize the solunon.
Let S denote the sum of all three-thut numbers, so
 |
that Is 999=100+ n—l, and so n.900 .
• 900 = 494550.
2 2
Now let sn' denote the sum of all three-thut numbers which are dmslble by 13. So,
104
(the first three-dlglt number that IS divisible by 13), b 988 (why?), S:
13 
69.
69 = 37674.
2 2
 |
We
are lookmg for S900 ssg' 494550 - 37674 three-digit numbers which are not
divisible by 13.
456 876. Th1S the sum of all the
l. State whether the following sequences are arithmetic or not.
a (a) = b. €5, 0, u, c. (a) (4n+7)
2. Find the formula for the general term an of the anthmenc sequence with the given common
difference
and first term.
a.
d 
1
3 c. d 
a] 3
2
3. Fmd the common difference and the general term a of the anthmetic sequence with the oven terms.
24
Find the general term of the arithmetic
sequence using the even data.
a.
a2
b. a,
5. Fill m the blanks to form an arithmetic sequence.
a. 3, 32.
b. 13,45
 |
Given that the followmg sequences are arithmenc, find the missmg value.
a. 
b. 
2 2
For which values of b do the following numbers form a finite arithmetic sequence?
2 1 2
a. (an)
b' b(l-b)' I-b
b. (5 + 2b, 15 + b, 31 -b)
c.
(a)
The sum of the fifth and eighth terms of an arithmetic sequence is 24, and the tenth term is 12.
Fmd the 20th term of the sequence.
Fmd the sum of the thlld and fifteenth terms of an arithmetic sequence If its nmth term is 34.
Il. The sum of the third and fifth
terms of an anthmenc sequence IS 20, and the product of the
fourth term and the sixth term IS 200. Fmd the third term of this sequence.
|
a. b. |
al
|
|
18 27, |
s,
|
|
c. |
|
7, s 16 |
332, |
|
|
d. |
|
5
|
1173, |
|
|
|
|
2, a |
|
2, |
|
f. |
|
|
—1700, p |
|
|
|
2 |
2 |
|
|
B. Sum of the Terms of an Arithmetic
Sequence
For each anthmenc sequence (an) find the nnssmg value.
g. s 00 10000, a 00
199,
a
h.
a 5n - 10, S
i.
k. al
l.
n. 4 • ss, a 54, al
91 s 10 
13. Is it possible that sum ofthe first few terms of the arithmetic sequence (—1 1 3, 5 IS 575?
14. Given an anthmetic sequence (a) mth
27, find
15.
 |
The general term of
an anthmenc sequence IS a -3. Find sso
16. The sum of the first n
terms of an anthmenc sequence can be formulized as S 4n2 — 3n.
Fmd the first three terms of the sequence.
17. The sum of the first n terms of an arithmetic sequence can be formulized as Sn = 2an 2 . Fmd d.
18. The sum of the first SIX terms of an anthmenc sequence IS 9. The sum of the first twelve terms IS 90. Fmd the sum of the thirteenth and seventeenth terms of this sequence.
19. The sum of the first twelve terms of an anthmenc sequence is 522. The sum of the first sixteen terms is 880. Find the common difference of this sequence.
20, In an anthmenc sequence the sum of the first SIX odd-numbered terms (al, ag, as, (G, as, and an) IS
60. Fmd the sum of the first eleven terms.
21. In an arithmetic sequence the difference between the sum of the first nine terms and the sum of the first seven terms is 20. Fmd the sum of the first sixteen terms.
22. The sum of the squares of the fifth and eleventh terms of an anthmenc sequence is 3, and the product of the second and fourteenth terms is 1 Fmd the product of the first and fifteenth terms of this sequence.
23. (a) is an increasmg arithmenc sequence such that the sum of the first three terms is 27 and the sum of their squares IS 275. Find the general term of the sequence.
24. Insert 43 numbers between 3 and 25 to get an anthmenc sequence. What IS the sum of all the terms?
25. A person accepts a poslnon With a company and WILI receive a salary of $27,500 for the first year. The person IS guaranteed a raise of $1500 per year for the first five years
a. Determine the person's salary durmg the sixth year of employment.
b. Determine the total amount of money earned by the person during SIX full years of employment.
26. An auditonum has 30 rows of seats with 20 seats in the first row, 24 seats m the second row, 28 seats m the third row, and so on. Fmd the total number of seats m the andltonum.
270 A bnck pano IS roughly m the shape of a trapezoid.
The pano has 20 rows of bncks. The first row has 14 bricks, and the twenneth row has 33 bncks.
How many bncks are there m the pano?
28. A grocery worker needs to stack 30 cases of
canned fruit, each contammg 24 cans. He decides to display the cans by stackmg
them in a triangle where each row above the bottom row contains one less can.
Is it possible to use all the cans and end up with a top row of only one
can?
A runner begms runnmg 5 km ma week. In each subsequent week, he increases
the distance he runs by 1.5 km.
a. How far will he run m the twenty-second week? b. What IS the total distance the man Will have covered from the begmnmg of the first week to the end of the twenty-second week?
300 A man chmbmg up a mountain climbs 800 m 111 the first hour and 25 m less than the previous hour m each subsequent hour. In how many hours can he climb 5700 m?
|
the first meter of a well, $15.25 for dnllmg the second meter, and so on. How much does It cost to drill a 100 m well? 32. Three numbers form a fimte arithmenc sequence. The sum of the numbers IS 3, and sum of their cubes is 4. Find the numbers. |
31. A well-dnLlmg company charges $15 for dnl_lmg
33. The numbers a 2, b 2, and c2 form an anthmenc
1 1 1
sequence. Show that also form
an anthmetic sequence.
34. Solve for x.
(X 28) 155.
35„ Prove that If an + ar 2 + an then (an) is an arithmetic sequence.
36. Let (an) and (b) be two anthmenc sequences With a 190. F-md the sum of the first fifty terms of these sequences combmed.
370 Two finite arithmenc sequences contain the same number of terms. The rat10 of the last term of the first sequence to the first term of the second sequence IS 4. The rano of the last term of the second sequence to the first term of the first sequence is also 4. The rano of the sum of the
first sequence to the sum of second sequence IS 2. Fmd the rat10 of the common difference of the first sequence to the common difference of the second sequence.
38. (Problem from the 18 th century BC) Divide ten slices of bread between ten people so that the second person receives 1/8 of a slice more than the first person, the third person receives 1/8 of a
slice more than the second person, and so on.
39. (Pythagoras' problem) Fmd the formula for the sum of the first n odd natural numbers.
 |
40, In an arithmetic sequence the sum of the first m terms
is equal to the sum of the first n terms. Prove that the sum of first m + n
terms equal to zero.
41. S IS the sum of the first n terms of
an anthmenc sequence (an). Show that s
o.
42. Fmd the sum of all the three-thut numbers that are not dmslble by 5 or 3.
43. (an) IS an arithmetic sequence with first terms 15,
34. (bn) IS an anthmenc sequence "'Ith first terms 7,15. Fmd the sum of the first thirty numbers that are common to both sequences.
44, Solve
x x x x x
45. For p
10
let T be the sum of the first forty terms of the arithmetic sequence with first
term p and common difference 2P — 1. find T 1 + + T10.
46. Let ABCD be a
trapezoid such that AD I l BC and AD = a, BC = c. We dlvlde non-parallel sides
into n + 1 equal segments n 1 by usmg pomts Ml 
M2, ..., Mn e IABI and
N], N2, ..., IDCI. Fmd MINI + MoN2 + + MnNn m terms of a, c, and n.
A mauc square is an arrangement of natural numbers m a square matnx so that the sum of the numbers in each column, row, and diagonal is the same number (the magic number). The number of cells on one side of the square is called the order of the magic square.
Here IS one of the earliest known mauc squares:
4 9 2
3 5 7
8 6
|
52 |
13 |
10 |
43 |
|
19 |
34 |
37 |
28 |
|
31 |
22 |
|
40 |
|
16 |
49 |
46 |
7 |
It IS a third order maOc square constructed by using the numbers 1, 2, 3, 9. Notice that the numbers in each row, column, and diagonal add up to the number 15, and 1, 2, 3, ,9 form an arithmetic sequence. This magic square was possibly constructed in 2200 B.C. China. It is known as the Lo-Shu magic square.
The famous Lo-Shü iS the oldest known magic square in the teorld_ According the b•gend, the figure above found the back a turtle which came from the fiver Lo The
"u' means 'book', 'Lo-Shu' means •The book of the rvver b'.
Below is another magic square, this time of order four. Note that its elements are from the fimte arithmenc sequence 7, 10, 13, 16 52, and the magic number is 118.
What kind of relation exists between the sequence and the mauc number? Gwen any finite arithmetic sequence of terms IS it always possible to construct a mauc square? If the numbers do not form an anthmenc sequence, IS It possible to construct a mauc square?
Try constructing your own magic square of order three using the numbers , 12, 36.
There are many unsolved puzzles concernmg magic squares. The puzzle of Yang-Hui, which was solved in the year 2000, was one of them. Accordmg to the legend the 13th century Chinese mathematician Yang-Hun gave the emperor Sung his last magc square as a Oft. This is Yang-Hui's square;
|
1668 198 1248 |
1669 199 1249 |
|
618 1038 1458 |
619 1039 1459 |
|
828 1878 408 |
829 1879 409 |
The special property of Yang-Hui's square was that the square had elements of a finite arithmetic sequence With common difference 210 such that when I was added to each cell it would become another magic square with all elements prime numbers. But the emperor wanted the magic square to also Ove prime numbers when 1 was subtracted from each cell. He promised some land along the river to the mathematician if it was completed. Unfortunately, the life of Yang-Hui wasn't long enough to solve this puzzle. Below is the solution to the problem, calculated 725 years later.
|
372839669 241608569 267854789 |
372839670 241608570 267854790 |
372839671 241608571 267854791 |
|
189116129 294101009 399085889 |
189116130 294101010 399085890 91 |
189116131 294101011 399085891 |
|
320347229 346õ9344g 215362349 |
320347230 346593450 215362350 |
320347231 346593451 2153623ö1 |
1.
DefinitionIn the previous section, we learned about
anthmenc sequences, i.e. sequences whose consecunve terms have a common
difference. In th1S chapter we Will look at another type of sequence, called a
geometric sequence. Geometnc sequences play an Important role m 
mathematics.
A sequence IS called geometnc If the ratio
between each consecutive term IS common. For example, look at the sequence 3,
6, 12, 24, 48
Obviously the rano of
each term to the previous term IS equal to 2, so we can formulize the sequence
as b n +1 b • 2. The consecunve terms of the seq uence have a common
ratio (2) 
so this sequence IS geometnc.
For the sequence 625, 125, 25, 5, 1 the formula Will be bn4-1 The
common rat10 5
1 m th1S sequence IS
5
In other words, (b) is geometnc If b
q such that n e N, q
e IR. q is called the common ratio of the sequence. In this
book, from now on we Will use b to denote the general term of a geometric
sequence, and q to denote the common ratio.
If q > 1, the geometric sequence IS mcreasmg when b] > O and decreasmg when bl < 0.
If 0 < q < 1 geometnc sequence IS mcreasmg when bl < O and decreasmg when bl > 0.
If q < O, then the sequence not monotone.
What can you say If q l? What about q = 0?
|
EXAMPLE |
53 State whether the followmg sequences are geometnc or not. If a sequence IS geometnc, find the common rano.
|
|
|
5' 25
1
Solution a.
geometnc, q 2 b. geometnc, q 1 c. not geometnc d.
geometnc, q
5
|
EXAMPLE |
54 State whether the sequences With the oven general terms are geometnc or not. If a sequence
IS geometnc, find the common ratio.
c.
Solution 
so
the ratio between each consecutive term IS 3, which IS constant. So (b n) IS a
geometnc sequence and q = 3
b.
+ 3, so the rat10 between each consecutive term IS
which Is not constant. So (b) IS not a geometric sequence.
c.
3 • 2" ¥4, so the rano between each consecunve term IS 
2,
which IS
constant. So (b n) IS a geometric sequence and q = 2
d. Smce the general term has a Imear form, this is an anthmenc sequence. It not geometnc.
With the help of the above example we can see that If the formula for
the general term of a sequence gives us an exponennal function with a Imear
exponent (a function "'Ith only one exponent variable), then It IS
geometrw
 |
The general term of a geometnc sequence exponential.
Geometric Growth is exponential
We have seen that for a geometnc sequence, bn*l bn q.
This formula IS defined recursively. If we want to make faster calculations, we
need to express the general term of a geometnc sequence more
directly. The formula IS denved as follows:
If (b r) is geometnc, then we only know that b 4-1 b u • q. Let us write a few terms.
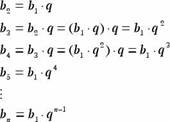
This is the general term of a geometnc sequence.
If 100, 50, 25 are the first three terms
of a geometnc sequence (b n), find the sixth term.
Solution We can calculate the common rat10 as q 
Usmg the general term formula, 
1
(b) is a geometnc sequence With 
3. Find be
3
Solution Usmg the general term formula,
1
b]
•q n Therefore, b, .34
9.
3
1
 |
-15, q
Fmd the 5 general term.
Solution Usmg the general term formula, b
How can you relate tins bžuidinç
Therefore, bn -15to a geometric sequence n
|
EXAMPLE |
58 Consider the geometnc sequence (b) with
and q
3, Is
243 a term of this
sequence?
Solution Usmg the general term formula,
1
•q" I and so bn
9
Now
243 -
and so 3 — 3 8. Therefore, n—
8.
Smce 8 IS a natural number, 243 is the eighth term of this sequence.
In a monotone
geometnc sequence b5 12 3. Fmd by
1
Solution 
3, that is
3. so q = ±
1
Since the sequence IS monotone, we take q
12,
that Is b 1 • b] • q' 12
1 1
b12 12,
that = 6dä. so6.
9
Why? Would the answer change If the sequence was not monotone? Why?
Check Yourself 9
1
1. Is the sequence mth general term b
a geometnc sequence?
Why?
3
are the first three terms of a geometric sequence (b) . Fmd the eighth term.
1
3.
 |
— 16. Find the common
rat10 4 of the sequence and b
4
4. (b) with IS a
geometnc sequence With b] 
2. Is —96 a term of this sequence?
Answers
1.
yes, because the general term formula IS exponential 24
2
4, no
1
(b)
IS a geometnc sequence With b4 56, q Fmd be.
2
1 bl • q? , that IS 56 = bl 
so bl = _448.
2
17
bu
• q 448 • (
2 4
In th1S example, we calculated the first term of the
sequence from b 4, then used this value to find bg. However, there is a quicker
way to solve this problem: m general, If we know 
the common ratio and
any term of a geometnc sequence, we can find the required term
Without findmg the first term. Look at the calculation:
Here, It is not important which term you write m the place of b n and b 
Note that when p = 1 the advanced general term formula becomes the general term formula we studied previously.
1
|
EXAMPLE |
(b) IS a geometnc sequence "'Ith b5
44 Fmd the common
rano.
32
 |
Let us formulize the procedure m the last example, which helps us to find
the common rat10 of a geometnc sequence With any two terms b and b such that p
> r.
Applvmg the advanced general term formula, b 
If p —r IS even, q = ±p-r
If p —r Is odd, q = P
(Why did we define p > r?)
|
EXAMPLE |
62
Solution Usmg the common rano formula,
4
Smce the sequence IS monotone, q Otherwise, one term would be 3
neganve and the next would be positive, and that would ove a sequence which IS neither mcreasmg nor decreasmg. Note that If we did not know that the sequence was monotone, then there would be two possible answers.
8 32
EXAMPLE (b)
IS a non-monotone geometric sequence with bo = 2, b, Which term is
9 81
Solution Smce the sequence IS not monotone, the common rano IS negative. Usmg the common rat10
 |
32 formula, q If — IS a term, then
81
|
32 be = b2 • qp - 2 that is 81 32 Smce 6 IS a natural number, 5. Middle Term Formula (Geometric Mean) |
6. |
|
EXAMPLE |
64
Given a geometric sequence (b n) with b 10, find b2 • b
Solution This tune we have just one value as data. Smce the formulas we have learned up to now
depend on more than one data value, It IS Impossible to find b2 or b]4.
However, we are not asked to find b2 or b]4, but to fmd b2 • b] 4
Let us apply the advanced general term formula, keepmg m mmd that we just know b s:
(1)
(2) Multlplvmg
(1) by (2), we get 
bs2 102 100.
The solution to the previous example uves us a practical formula.
Let b and bk be two terms of a geometnc sequence such that k < p. Then,
(1)
(2)
Multiplymg (1) and (2) we get b 
b 2 or b = ± 
b ,
which means that the square of anv term x in a geometnc sequence is equal to
the product of any two terms that are at equal distance from x in the sequence.
In the previous example note that b s was at equal distance from of b2 and b] 4
(Could we solve the
problem If we were oven b, instead of bio?)
|
MIDDLE TERM FORMULA (Geometric Mean) |
|
|
|
|
|
|
|
|
|
The geometric mean of two numbers x and y is m if m = Note that m is the same distance from x as from y, so x, m, y form a finite geome tric sequence, |
||||
For example, all the
followmg equalities WILL hold m a geometnc sequence.
b02
bf b? smce b2 Is In the middle of b] and
ba.
b/(x must be 12)
b10
|
EXAMPLE |
65 1
X, 9 are three consecutive terms of a
geometric sequence. Fmd x.
Solution If we say 9, then usmg the
middle term formula 
b22 bl • ba I.e. X I • 9.
Therefore, x IS 3 or —3 if the sequence is geometric.
Note
Three numbers a, b, c form consecutive terms of a geometnc sequence If and only if
|
EXAMPLE |
66
Fmd the common ratio q for the geometnc sequence (bn) with 32 and
b2 2
Solution Usmg the middle term formula, we get b2 • b9 b255, which IS nonsense!
Realizing that we are given b] let's write another nonsense equation: bl
• bio 
We know that there IS no but we have b2 • bg and bl • bio which are equal. That IS,
1 bl •blo = b2 •bg, so 32 •b] o = 2.
Therefore, b] o
Now usmg the general term formula,
1 1
b bl
• SO 32 q 9 . Therefore,
162
Check
Yourself 10
1 l. (b) IS a geometric sequence "'Ith b, 12 and q Fmd br 3
2, (b) IS a geometnc sequence With b? — 9 and = 72. Fl.nd the common ratio.
5
3.
 |
4
4.
Fill m the blanks If the followmg numbers form a geometnc sequenc e: —2,
-162.
Answers
4
1. 3. 40 4. 6, —18 54 or 6 -18, 54
9
|
EXAMPLE |
67
Given a monotone geometnc sequence (b) With bl + b5 30, ba + b? 120,
find b
Solution We must express these two equations m terms of two vanables, say bl and q.
(1)
so
120 120 (2)
Dlvldmg equation (2) by equation (l), we get
Since
the sequence IS monotone, q 2
30
Usmg equation (1): bl 
30, SO bl
17
|
EXAMPLE |
68 Three numbers form a geometric sequence. If we increase the second number by 2, we get an arithmetic sequence. After this, If we Increase the third number by 9, we get a geometnc sequence agam. Fmd the three mltlal numbers.
Solution Smce we are given three numbers, let us solve th1S problem With the help of the middle term formulas for arithmetic and geometnc sequences. Nammg these numbers a, b, and c respectively, we have:
geometnc sequence arithmetic sequence geometnc sequence
So we have the followmg system of three equations mth three unknowns:
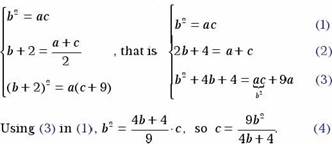
Usmg
(3) and (4) m (2), 2b + 4
- 128 o.
16
Solvmg the quadranc equanon, we get b or
b = 8. Substitutmg these numbers m (3) 25 and (4) we find a and
c respecnvely.
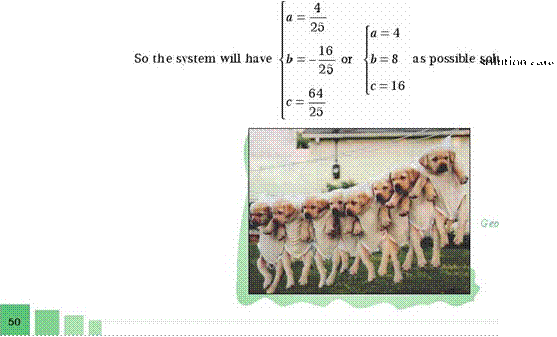Geometric 97010th ts exponential'
|
EXAMPLE |
69 Fmd four numbers formmg a geometnc sequence such that the second term is 35 less than the first term and the third term IS 560 more than the fourth term.
Solution For convemence, let us denote the terms by a, b, c, d, and the common rano as usual by q.
Our data now looks like the followmg:
b =a-35
c = (1+560.
We have to reduce the number of variables to two usmg the fact that we have a geometnc sequence.
(1)
aq a—35
so aq aq 3 + 560
• q? +560 (2)
Solvmg equation (2), we get q = ±4.
If q = —4, then a = 7, b = —28, c 112, d = —448.
35 140 560 2240
Ifq=4, then
a— 
3 3 3 3
Both of these sets of values are possible solution sets for the
problem.
Let us consider the geometric sequence With first few terms 1 2, 4, 8, 16.
The sum of the first term of this sequence IS obviously 1. The sum of the first two terms IS 3, the sum of the first three terms 7, and so on. To write this in a more formal wav, let us use S. to denote the sum of the first terms, i.e. Sn + + + bn. Now,
15
8
+ 16 31
EXAMPLE 70 Gwen the geometnc sequence with general term b 3 • (—2)" find the sum of first three
terms.
How could we find Sloo the previous example? Calculatmg terms and findmg their sums takes time and effort for large sums. As geometnc sequences gow very fast, we need a more efficient way of calculatmg these sums. The following theorem meets our needs:
Proof(1)
(2)
Subtractmg (2) from (l), we get
s 
1
Gwen
a geometnc sequence With b] and q
3, find ss.
 |
|
Solution |
Usmg the sum formula,
|
|
EXAMPLE |
72 Given a geometnc sequence with S6
3640 and q
3,
find b
Solution Usmg the sum formula,
|
|
1-3 |
I—q6 1-36 so
3640 b]and so b] 10.
|
EXAMPLE |
1
Given
a geometnc sequence With q 
b 5 and S 1820, find b]
3 p
Solution Usmg the sum formula,
1
Therefore,
b]= 1215
3
|
EXAMPLE 74 Solution |
Given a geometnc sequence with Usmg the sum formula, |
3 and S?
|
19 3 |
find q. |
19 and soTherefore,
9
5 2
|
EXAMPLE |
Solvmg the quadranc
equation, we get q
|
Check Yourself 11 |
|
|
1.
Gwen a geometnc sequence with bl |
1 and q 2, find S? |
|
2.
Gwen a geometnc sequence With Sg |
513 and q 2, find I's. |
|
3.
Gwen a geometnc sequence with q |
2, |
|
4. Gwen a
geometnc sequence mth bl Ans wers 5 1 1.
43 2. 48 3. 8 4. or 4 4 |
192 and 252, find q. |
 |
45 45
 |
32 512
Let us write the oven
equanons m terms of b] and q.
(1)
(2)
1 1
DWIdmg (2)
by (1), we getso q = ±
16 4
1
Since the
sequence IS monotone, we take q
4
Usmg this mformanon m equation (1) we get bl 6.
|
EXAMPLE |
76 Given a
geometnc sequence With S? 14 and S 14 18 find 
+ b21.
Solution Clearly, b]5 + + 
However, we are oven S? and Su, so we need to find a way of expressmg S21 m terms of the even data.
(1)
(2)
|
DWIdmg (l) by (3) we get, |
|
|
Dlvldmg (2) by (3) we get, |
(4) |
(3)
s
 |
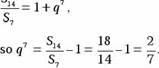(5)
Subtractmg (5) from (4) we get,
4 8
= (q7 ) 2 S
49 7
|
EXAMPLE |
(b) IS
a geometnc sequence such that the sum of the first three terms IS 91 and the
terms b] + 25, b 2 + 27, b 3 + 1 form an anthmenc sequence. Find b].
Solution Usmg the sum formula,
so
• 
= 91 (1)
Using the middle term formula for arithmetic sequences,
b] +25 + b3 +1 b] +25+bl .q 2 +1
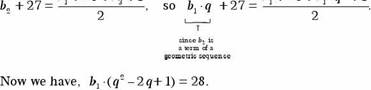(2)
DWIdmg (l) by (2) we get,
1
|
Th1S
quadratic equanon gives two solutions: q 1 then usmg equation (1) or (2) we get b] 63.
If q = 3, then usmg equation (1) or (2) we get bA Both of
these are possible values for 2. Applied Problems |
3. |
EXAMPLE
78
After the accelerator pedal of a car IS released, the driver of the car waits five seconds before applymg the brakes. Durmg each second after the first, the car covers 0.9 times the distance It covered durmg the precedmg second. If the car moved 20 m durmg the first second, how far does it move before the brakes are applied?
Solution Here we have,
 |
(total
distance covered m five seconds)
Usmg the sum formula,
1-
0.95
20. 81.902.
1-0.9
Therefore, before the brakes are applied the car moves 81.902 m.
|
EXAMPLE |
79 How many ancestors from parents through great-great-great grandparents do three unrelated people have?
Solution
Let's try to formulize the problem. Each person has two parents, a mother and a
father, and these people are disnnct because the people m the problem are
unrelated. These parents are the closest generation to the ongmal people; we
can call them the first generation. Now, each person m the first generation
also has two different parents, which we can call the second generanon. If we
contmue like this, we can see that there are five generations, and each
generation contams twice the number of people of the previous generation. This
is a geometnc sequence, and we can write, b]
6 (total number of parents of the
three unrelated people) q
2
(the
ratio between the number of people m successive generations)
(the total number of ancestors
m five generations)
Usmg the sum formula,
1-25
186.
So the three unrelated people Will have 186 ancestors from parents through great-great-great gandpar ents.
|
EXAMPLE |
80 A set of five weights has a total mass of 930 g. If the weights are arranged m order from the lightest to the heaviest, the second weight has twice the mass of the first, and so on. What IS the mass of the heaviest weight?
Solution Let us formulize the problem:
930,
2,
Usmg the sum formula,
1-25 then 930 = bl SO bl 30.
 |
|
Usmg the general term formula, b bl • q 30 . 24 Therefore, the heaviest weight has a mass of 480 g. |
480. |
|
EXAMPLE |
2
81 A ball is dropped from a height of 81 cm. Each time It bounces, It returns to of Its previous 3 height. What IS the total distance the bal-I has traveled m the aur when It hits the gound for the
fifth tune?
2
Solution Choosing bl -81 q= ss = ? won't give us the answer 3
that IS required. To understand why, let us look at the distance that the ball travels usmg the diagram opposite. We can see that except the first 81 cm, each length is covered twice. So if we define a geometnc sequence which
has 81 . — as the first term, we can formulize our answer 3
Total distance — 
341 cm.
4545
1. Gwen a monotone geometnc sequence With
b, — b
and b6
find
bl 32512 and q.
3
2. A tree loses 384 leaves durmg the first week of fall and as many leaves m each 2 successive week. At the end of seven weeks all the leaves have fallen. How many leaves
did the tree have at the start of fall?
Answers
1
1. 
2. 12 354 leaves
4
1. Infinite Sum Formula
 |
sequence gets closer to zero. We can
easily see this in the followmg examples:
when q
2 2' 4' 8 16
1 1 1
when
q
3010' 300 9000
In both examples, the
terms get closer to zero as n Increases. In the second example the approach IS more rapid than m the
first, and the sequence alternates between positive and negative numbers.
|
EXAMPLE 82 |
2 4 8 |
|
|
|
Solution |
Clearly each term of this sum IS a term of the geometnc sequence With b] |
I and q |
1
|
A simple mvestiganon
with a few more examples Will quickly reveal that for geometnc sequences with
common rano —l < q < 1, as n Increases the total sum of the terms (Sn)
eventually settles down to a constant value. In other words, we can find the mfmlte
sum of a geometric sequence With common rat10 —I < q < 1.
2
We are lookmg for the mfimte sum, I.e. S
Usmg the sum formula,
1-
0S1 2.
1
2
Here, 
0,
since 1 has no significance next to Y.
We now have an equation which helps us to calculate the mfimte sum of a
geometnc sequence.
|
Theorem |
|
|
The mfimte sum of a geometnc sequence (b n) With common
rat10 q < I is denoted by S,
and IS oven by the formula S —
 |
by the general sum formula. If we choose n
—+ -o, s b] 
Remember that the total sum of terms only settles at a constant value if—I < q < 1.
l, then the geometric sequence has no Infinite sum.
|
EXAMPLE |
83 Fmd 100 + 50 -t- 25
1 100
Solution
Here
100 and q Usmg the
mfimte sum formula, s 200.
2
2|
EXAMPLE |
84 Fmd 
10 
20
Solution Here, q 2. Therefore, there is no infimte sum. (—2 < 1).
When we use a calculator, at the end of dlvB10n we often have rational numbers With repeatmg decimals, I.e. decimals With a repeatmg sequence of one or more dlOts m the fraction part. We can use our knowledge of the mfimte sum ofa geometnc sequence to wilte repeatmg decimals as fractions.
We can wilte a repeatmg decimal such as 0.66666. as 0.6 or 0.(6). In this book, we use the
first notation.
|
EXAMPLE |
85 Wilte the number 0.72 as a fraction.
Solution Let us try to see the geometnc sequence m this question.
0.72 = 0.727272...
0.72 + 0.0072 + 0.000072 +
0.72 + 0.72 • 0.01 + 0.72 • 0.0001 +
0.72 + 0.72 . 0.01 + 0.72 . +
Now we can see that each term of this sum IS a term of the geometnc sequence "'Ith b] = 0.72, q 0.01 and we are looking for the mfimte sum, that is S.
Usmg the mfimte sum formula,
0.72 72 8 s
1-0.01 99 11
|
Solution |
We cannot express th1S number as the mfimte sum of a geometnc sequence. This number should be written so that the nonrepeatmg part IS not Included mslde the sequence. |
|
|
2.15 = 2.1555.. nonrepeatmg |
|
|
|
|
0.05 21 5 97 7 Therefore, 2.15 = 2.1+ 1-0.1 10 90 45 45 3. Equations with Infinitely Many Terms |
0.1) |
|
EXAMPLE 87 |
Solve 2 |
|
|
Solution |
In this problem our traditional methods of solvmg equations Will not help smce we cannot |
|
 |
Write the number 2.15 as a fraction
see completely which equanon we have. Let us try to see an
infimte sum of a geometnc sequence in this equation.
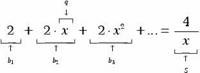
Here, we should note that this equation "'111 have a solution if
and only If Iq
that is
1. If x > l, there Is no Infinite sum.
Now, usmg the mfimte sum formula,
b] 4 2 2
s
2
< the only solution of this non-standard equation us X
3
|
EXAMPLE |
2 13
88
Solve 2x+1+X 
6
Solution Now we have:
s
 |
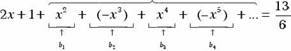(q x,
Note that smce there IS no way to express 2X + 1 m the mfimte sum, we exclude It from the geometnc sequence.
Now, usmg the mfimte sum formula,
which
means 18 x 2 
7 o.
7 1
Solvmg the quadranc equanon gives x or x both of which satisfy the condition
9 2
x < 1. So our answer is x
9 2
1 3 9 l. Can we find — + _ + _+ .
2. Fmd 2 4 8
3.
Wnte 0.06 as a fraction. 4. Solve 
8
Answers
9 1 1
l. no, because q > I 2. 3. 4. 
11 15 3
A bal-L IS dropped from a height of 50 cm.
Each time It bounces, It returns to of
Its
previous height. How far "'111 the ball travel m the air before commg to rest?
Solution This example IS very sumlax to
Example 81. The only difference IS that we are not lookmg for a fimte sum, such
as ss. Smce we are sure that the ball Will stop (q < 1), the required
distance, say S, can be expressed as follows:
1
50
3
s 
— 100 cm.
1
1- 
first fall, not part (the ball covers each 3
 |
So the ball Will travel 100 cm before commg to rest.
|
EXAMPLE |
90 Consider an equilateral tnange made from paper. We take our scissors and cut off smaller equilateral mangles from the ongmal tnangle usmg the followmg prmclple: connect the middle points of the sides of every triangle you see Cut out and throw away the middle triangle you make Repeat the process With every new triangle you see How much of the ongmal area will remain if we don't stop cuttmg?
Solution Let us look at a diagram of the problem, where x shows the area of the triangle we throw away each tune:
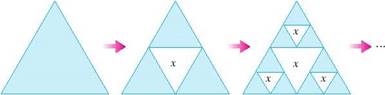
After cuttmg the first mangle, we throw away one new triangle. After cuttmg the second triangle we throw away three new triangles, and so on.
Now let a be the sldelength of our equilateral mangle, If we say S IS the area of the tnangle at the begmnmg, and S' IS the sum of the subtracted areas we have,
s
(formula for area of an equilateral
triangle with sldelength a)
4
1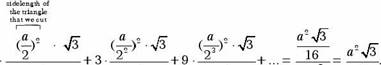 
4 4 4 3 4
we cut
out 4 one
in fi_rzt
phaze
Clearly, S - S' = O. Therefore, no area WILL remam If we don't stop cuttmg.
 |
 |
The problem
we have just looked at IS similar to the construcnon of a special structure m
mathemancs called a Slerpmski Pyramid. A Sierpmskl Pvrannd beens With a smgle
tetrahedron, I.e. a pyramid whose sides are all Identical equilateral mangles.
Each tetrahedron is placed on its triangular base, then raised and set so that
its bottom three vertices meet the top of three other tetrahedrons. Together
these four tetrahedrons create the form of a larger tetrahedron. This can be
treated as a Single umt, and become part of an even greater tetrahedron. This
process of combmmg four tetrahedrons to create a larger sone demonstrates the
beauty of math, but it also has another purpose: it shows exponential growth.
In this case the growth would be m terms of 4 to the power x. The origmal tetrahedron IS descnbed as level zero because It IS 4 to the power 0 which IS equal to 1 .
The next groupmg is described as level one because it IS 4 to the power I which is equal to four tetrahedrons.
 |
l. State whether the followmg sequences are geometnc or not.
25
a.b.
c.
The thirteenth and seventeenth terms of a
1 geometric sequence are and 48 respectively.
4
Fmd the product of the fourteenth and sixteenth
terms.
The sl,xth and eighth terms of a geometric
|
2. Fmd the general term of the geometnc sequence with the oven qualities. |
sequence
are
and 
a. b] 
b.
1 c. 1000,
d.
10
32 f.
1
32, b6
h.
2
i.
3. Fill in the blanks to form a geometric sequence.
a. 3 - 245, 3 + 243
b. 36, 4
4.
 |
Find the general term of the geometnc sequence with b 4 =
b2 + 24 and b2 + b?
5. Write the first four terms of the non-monotone geometnc sequence that IS formed by msertmg nme terms between 3 and —729.
6. Gwen a geometnc sequence With
4b 4 and ba • b6
respectively. Fmd the seventh term.
The sum of the first two terms of a monotone
geometnc sequence is 15. The first term exceeds
25
the common rano by Fmd the fourth term of
this sequence.
Given a non-monotone geometnc seq uence With
and b2 + = 216, find b 1
4
Can the numbers 10, 11 12 be terms (not necessarily conse cunve) of a geometric sequence?
12. For each geometric sequence (b) find the nnssmg value.
3
a.
b. c.
d.
13. The general term of a geometnc sequence is
140 The general term of a geometric sequence
Fmd the formula for S
20, Show that (66 
150 Fmd the common ratio of a geome tnc sequence If Sequence (Optional)
5For each geometnc sequence (b) find the nnssmg
s 4value.
a. 
16. The sum of the first four terms of a geometnc q 2 S = 12, bl 2 2
sequence
IS 20 and the sum of the next four c. S
terms is 320. Fmd the sum of the first twelve
terms.
Fmd the mfimte sums.
17. 
A
chain letter is sent to five people. Each of the a. 54 18 6 +b. 3 2
five people mails the letter to five other people 2 3 and
the process IS repeated. What is the total c. 
d. 
number of people who have received the letter 7 12 6 3 after four mmlmgs?
|
18, You want to pamt the wood around four wmdows m your house. You think that you can pamt each a, 0.21 b. 5.142 c. -3.202 d. 2.065
wmdow m 90% of the time It took to pamt the previous wmdow.
If it takes vou thirty minutes to 1 1 1 1 1 1 pamt the first wmdow, how long
WILL It take to Fm d 
pamt all four wmdows?
119. A computer solved several(b) IS a geometnc sequence With infimte sum
problems in
succession.243 and 275. Wilte the first four terms of this sequence
The time it took the computer to solve each successive problem formedA
square has sides of length 1 m. A man marks 
geometric
sequence.the mldpomts on each Side of the square and How many problems didjoms
them to create a second square, inside the the computer solve If itfirst
square, He then repeats the process to create
took 63.5 minutes to solve all the problems except a third square inside the second, and so on. If the the first, 127 minutes to solve all the problems man never stops, find:
except the last, and 31.5 mmutes to solve all the a. the sum of the penmeters of all the squares.
problems except for the first two? b. the sum of the areas of all the squares.
SequerreJ
|
3 and |
+. |
108 13 |
Fmd bl and q. |
|
30. Solve 1+ |
|
|
x |
|
|
x-1 |
x -1 |
2 |
|
311„ Solve x -2 + x-4 + |
0.1251f |
||
4 16
32. Gwen xl < I simplify I + 2x + 3x 2 + 4x 3
33. 5x — y, 2x + 3y, x + 2y form an anthmenc sequence. (U + 1) 2 , xy + 1 (x 1) 2 form a geometnc sequence. Fmd x and U
34. The first, the third, and the fifth term of a geometnc sequence are equal to the first, the fourth, and the sixteenth term of a certam anthmetic sequence respecnvely. Find the fourth term of the arithmetic sequence if its first term is 5.
|
270 The bob of a pendulum swmgs through an arc |
35. Three numbers form an anthmenc sequence. If |
|
|
30 cm long on Its first swmg. Each successwe |
we add 8 to the first number, we get a geometnc |
|
|
4 swmg is of the length of the precedmg one. |
sequence With the sum of terms equal to 26. Fmd |
|
|
5 Find the total distance that the bob travels before |
the three numbers. |
|
|
it stops. |
|
36. (an) IS an arithmenc sequence with non-zero common difference. a I • • aa, aa • al form a |
|
28. Let AP B be a nght tnangle |
|
geometnc sequence. Fmd the common rat10 of |
|
where LAP 1B = 900 . The Ime PIP2 IS drawn from PI, and |
|
the sequence. |
|
another is drawn m triangle |
|
37, x, U, z form an arithmenc sequence and U, t |
|
BPIP2, and so on. Find the sum p |
|
form a geometnc sequence such that
x + t = 21 |
|
3 of the length of all drawn lines |
|
z + U = 18. Fmdx, U, z, t. |
|
(PIP. + + + ...) = 3 and BPI |
4. |
38. Prove that the product of the first n terms of a |
|
29. (b n) is a geometric sequence With Infinite sum |
geometric
sequence (b n) IS (Ih •b |
|
 |
|
Fmd
the positive difference between the two possible answers to the teacher's
problem.
40, The arithmenc mean of 2 and a number is two less
than twice their geometnc mean. Fmd the number.
41, The numbers x, U, z form a geometnc sequence such
that x + y + z = 26. If x + 1 y + 6, z + 3 form an arithmetic sequence, find x,
y, z.
1
42. 
Ifform
an arithmetic sequence, b-a' 2b
show that a, b, c form a geometnc seq uence.
43. Fmd 11...11-22...22
16 digita g digita
OCH NOWFLAKÆ
A Koch snowflake IS another mathematical construction. We make a Koch snowflake by makmg progressive additions to an equilateral mangle. We divide the triangle's sides Into thirds, and then create a new mangle on each middle third. Then we repeat the process over and over. Thus, each snowflake shows more complexity, but every new triangle the design looks exactly like the imnal one.
Now imaone drawing a circle around the ongmal figure. Nonce that no matter how large the penmeter gets, the area of the figure remains inside the Circle. In the Koch Snowflake, an infimte penmeter encloses a fimte area. Although it sounds impossible, we can prove it as follows:
Calculating the perimeter qf the Roch Snowflake.
To snnplifv the problem, let us describe what happens to one Side of the tnangle as the procedure IS repeated. Suppose that the original length of one Side is L. Then we go through the followmg steps:
|
Step I: Step 2: Step 3: |
|
|
|
|
one segment of length L. four segments, each of length The total length of the side is now —L. 3 four times four segments, each of length The total length of the Side IS now |
|
|
4 |
4 |
L |
4 |
L. |
|
Step n: |
3 |
3 |
|
3 |
4 Total length L. 3 |
At each stage of the process, the length of one of the original sides of the triangle increases by a factor of
4
Consldermg that we measure this length three times for each snowflake (as each snowflake has three sides) 3
4 this leads to a geometnc sequence of the form 3L Smce q > 1 the sequence grows Without bound. Thus 3
the penmeter of the Koch snowflake IS mfìmte.
Calculating the area qfthe Koch Snowflake. step 3: Total axea IS
Suppose that the area of the ongmal mangle is A.
Step 1: Total area A.
3 Step 4: Total area IS
Step 2: Total area is A +3
9 9
1
9 9
3
 |
3
Note that after each term m this sum is — times the previous one. Therefore we can calculate the sum of all the 9
3
9 areas added using the formula for the sum of an mfimte geometric sequence: Area = A
4 5
This IS the area of the enure snowflake, which means that even If we repeat this procedure Without end, the total
area Will never be more than
5
If we combme our calculations of the penmeter and area of the snowflake, we have proved that an mfimte penmeter borders a finite area.
Below IS another kind of snowflake. What can you say about its area and pernneter?
Try producing your own snowflakes.
CHAPTER
SUMMARY
By the set
of natural numbers we mean all positive Integers and denote this set by H That
Is, IN = {1, 2, 3. }
A function which IS defined in the set of
natural numbers
is
called a sequence
e In a sequence, n should always be a natural number, but the value of an may be any real number dependmg on the formula for general term.
• For an anthmetlc sequence (an), al IS the first term,
az is the second term,
IS the third term,
an is the nth texm or
general
(an) (a 1, an, an,
• (an) 1?Bpsents a sequence, an lepresents Its general term
• If
theië is at least one natural number which makes the general term of a
sequence undefined, then the oven function IS not a sequence
• If a
sequence contams a countable number of terms, then we say it is finite,
otherrmse it is Infinite
• If each term of a sequence IS geater than the pi?vaous term, then the sequence is called an Increasing seq uence.
If each term of a sequence IS less than the
previous term, then the sequence IS called a decleasmg æquence
• In general any Incleasmg, nondecxpasmg, decleasmg, or nonincleasmg sequence is called a monotone E quence
• Ifthe
general term of a sequence is defined by mole than one formula, then it IS
called a plecevñse equence
Sometimes the terms in a sequence may depend on
the other terms Such a sequence IS called a recursvely defined æquence
If a sequence (an) has the same dlffelpnce d between Its consecutive tenns, then It called an arithmetic
That IS, (an) is anthmetic If an +1 am +
d and d
E d is called the common difference
If d > 0, then the arithmenc sequence IS Incleasmg. If d < 0, then the arithmetic sequence is decleasing The general term of an arithmetic sequence IS Imear
The
general term of an arithmetic sequence (an) "nth common dlffelence d is an
= a, + (n — , whelp a is any term of the sequence
n an anthmetlc sequence 
a whelp
Thxpe numbers a, b, c form consecutive terms of an
anthmetic
sequence If and only If b
b is called 2 the
arithmetic of a and c
The sum of the first n terms of an anthmetic sequence
(a) is So
If
a sequence (b n) has the same ratio q between its consecutive terms, then It is
called a geometric equence_ That IS, bas geometnc lf b ba • q , whelp q e IR
q is called the common ratio.
If q > 0, then the geometnc sequence IS monotone, If q < 0, then the geometnc sequence IS not monotone The general term of a geometnc sequence IS exponential
The general term of a geometnc sequence (b„) With
|
Arithmetic and Geometric Sequemes |
common rat10 q is b q of the sequence
In a geometric sequence bp , whelp k < p
Thxpe numbers a, b, c form consecutive terms of a geometnc sequence if and only if b2 a c We call b the geometric rœan of a and c
• The sum of the first n terms of a cometric sequence (bn) 1-qn wÂth common rat10 q IS = b
The infinite sum of a geometric sequence (bn)
common ratio q IS S
I—q
If Iq > 1 then the geometric sequence has no Infinite
Numbers such as axe called repeatmg decimals and denoted as 0.6 or O, (6),
• What is the dlffelpnce between an and (an)?
• When can a oven formula not be the general term of a sequence?
e Is It possible to find the •h th term of a sequence?
• Is It possible that a term of a sequence IS €2?
Why are lecurswely defined sequences not ven practical?
• What is an arithmetic sequence?
• When is an arithmetic sequence incxpasmg?
What the nth term of an arithmetic sequence (an) If ax = x anda = y?
How many variables do we need to know to find common dlffexpnce in an anthmenc sequence? What axe these variables?
• Which condition must be satisfied for thiee numbers to form an arithmetic sequence?
If
S IS the sum of the first n terms of an arithmenc sequence, is it possible that
s L , S2, Sy, IS also an anthmenc sequence? If so, give an example
What IS a geometric seq uence ?
When is a geomemc sequence decleasing?
Can the common rat10 of a geometnc sequence be 0? Why?
Which conchnon must be satisfied for
thxpe numbers to form a geometnc sequence ?
How can we find the sum of the first n terms of a geometric sequence with common ratio 1 ?
When can we find the Infinite sum of a eometnc sequence?
|
A turtle is 10 m away from a walks half the distance to the |
Every hour, the turtle How long vall it take |
for the turtle to walk to the nee?
What kind of problems can be solved "Ath the help of the Infinite sum of geometric sequences?
Summary 
ll. Which terms can be the general term of a
|
CHAPTER REVIEW TEST 1 |
|
|
5. How many terms of the sequence with general
term a
) are less than —?
E)
43n 2 —5n
6. Given a
) and as 3, find k.
22
3 B)
5 C) 
3
35 44 D) E) 
3 3
How many of the followmg sequences are
seq uence?
1. 11. 3
2
1 11 111 
C) 1 11 111
111.
VI. n
D) 11 111 V, VI
E) 111 1V, V, VI
 |
 |
2n - 1 B) 2n C)
D) E)
3. Given al 2 and
an4-1 
for n
find a 
27 B) 25
27 25
D) E)
2 2
4. How many terms of the sequence With general
are natural numbers?
C) 7
decreasmg?
3n—5
Il.
111. (c)
IV. (tin)
3W+2
1 
D)
4 E) 5
8. What IS the mimmum value in the sequence
2W+3
formed by a
-1 -3 2 D)
7 E) _8
9. Which one of the followmg IS the
general term of 130 (a) IS an anthmenc sequence such that 23 and as + a 4 37.
as.
49 B) 47 C) 45 D) 44
140 (a) IS a fimte anthmenc se quence With first term
last term and sum 9. How many terms
16
are there in this sequence?
B)
16 C) 32 D) 4864
15. x —2, x + 8, 3x + 2 form an arithmetic sequence.
Find x
 |
B)
11 C) 10 D)
116. (an) IS an anthmenc sequence With
3(S4
— S?) and al 1. Find the common
difference.
an anthmenc sequence?
n 2 + 2n B)C)
D)
10. Ifare consecutive terms of an
arithmenc sequence, find a + b + c.
23 23
C) D) E)
24 24 16 16
(an) IS an
arlthmenc sequence With a I8 and
35. Fmd ag.
C)
-16 D)22 E)
12. (an) is anthmenc sequence with7
and
common difference —. Find the general term.
13
B) C)B) 51 C)
51
+
2013 15
D) E)D) E)
51 51
|
CHAPTER REVIEW TEST 2 |
|
|
The sum of the first three terms of an anthmenc sequence is 33 and the sum of the first 33 terms is 3333. find the sum of the first ten terms.
320 B) 330 C) 360 D) 630 660
2. (an) IS an anthmenc sequence such that 195 and al? al = 24. Fmd al.
B) C) D) E)
3, How many of the followmg sequences are geometnc?
(b) 11.
111. (b) 2)
Iv. (b) v.
C) D) E)
a
Fmd
5. (b) is a geometric sequence with fourth term
and tenth term Find the seventh term.
32
B) C) D)
32 16
6. (b) is a geometnc sequence with first term
and common ratio —. Fmd the general term.
B) C)
14
14 D) E)
16 (b) IS a geometnc sequence such that b? — b4
|
(2n + 1) be the common rano? B) B) C) D) |
and b6 — b, Which one of the following can
c, form an anthmenc sequence.
35 b
B) D)
8. Seven numbers are Inserted between 16 and
16 to form a monotone geometnc sequence. Fmd the fourth term of this sequence.
D) E)
625 125 25 13. A ball IS dropped from a height of 10 m. Every
time It hits the ground, It bounces back to half of its
previous height. What IS the total distance that the ball has traveled when It
stops?
15 m 20 m 30 m 40 m 60 m
14. In the figure the largest square
has sides of length SIX umts. Each subsequent square
connects the mldpomts of the sides of the previous square.
The process contmues
infinitely. Fmd the difference between the total penmeter of all the squares and the total area of all the squares, as a numencal value.
24(2 + 15) B 24(2 -d5) C 24(d5- 1)
D) 2465 + 1) E) 24(2 - 45)
15.
In the figure the largest sennclrcle has radius 4 cm. A sennclrcle IS drawn
Inside this sennclrcle with the same center but half the radius. If this
process IS repeated without end what is the total area of all the semicircles?
161b 32n
A) cm B) cm C) 327t cm
 |
|
125
|
25 B) |
16 |
|
8 |
16 |
25 |
geometnc sequence. Find the
three terms of a
eighth term.
8 4
D) E)
625 125
10, A ball IS dropped from a height of 243 m. Every
1 time It hits the ground, It bounces back to of 3 its previous height. What IS the height of the ball
at the peak of its tenth bounce?
1 1 1 1 1
C)
9 27 81 243 486
square has sides of length SIX umts. Each subsequent
sq uare connects the
mldpomts of the sides of the previous square. What
is the penmeter of the mnth square m the diagram?
3 3 3
B) C) 3 D) 315 E) 615
2 2 64m
D)cm E)
641t cm2
3
|
|
|
1 |
1 |
1 |
|
112, The numbers X — 3, 3, U + 5 form both an arithmetic and a geometric sequence. Find x |
16, Fmd
|
|
|
|
|
|
1 |
1
|
|
4 E) 16 |
|
2 |
2 |
1
5. (an) is a sequence such that
116 Given U > x
> 0, snnpllfy x2 + —-+—-+
and 7. Find a,.
A) 39 B) 57 C) 75 D) 93 E) 107
3 B)
x 2
U 4 —U x
D)
2. In the figure the nght sides of the largest triangle have lengths three units and four umts respectively.
Each subsequent
60
5 — dG, x, 5 + form a monotone geometric sequence. Find the common rano
43+1
B) C)
|
CHAPTER REVIEW TEST 3 |
|
|
 |
2
D)E) 2-13
tnanue joms the midpomts of the Sides of the preuous mangle. This process contmues mfimtely.
What IS the total area of all the mangles?
16 B)
12 C) 10
 |
terms.
30 Which one of the foLLowmg IS the fraction form of
0.13
?106 B) 10 7 C)D)
101 E) 101
2 13 1
B)
15 90 75
8, Twelve numbers are inserted between 16 and 81
40 How many terms of
the sequence With general to form an arithmetic sequence. What is the
sum 211-13 term aare negative? of the twelve numbers?
3n±7
C) 7 A) 682 679 582 D) 579 E) 485
Given an arlthmenc sequence With
Sn = n(2n + 7), find the general term.
B)
- 13 E) 5n + 13
10. (c) is an arithmetic sequence With c
a. The sum of the first seven terms is 7.
Fmd ca.
3
ILIO (b) is a geometric sequence with third term a and sixth term 16a5 . Find the first term.
B)
2 3 . a
E) 2 3
a
1120 a terms axe Inserted between I + a and aa + 1 to form an anthmenc sequence. Find the common difference of the sequence.
B)
 |
(an) IS an mcreasmg anthmenc sequence With positive terms. The sum of as, and as IS 36 and the sum ofthe squares of these terms IS 450, Fmd the nineteenth term.
39 B)
42 C) D) 49 E) 54
3 9x
2 2X
The roots of the equanon 3x form an anthmenc sequence. Fmd a
|
|
D) 2 |
E) 4 |
A) 1 C) 
1
2
The mtenor anues of a quadrilateral form a geometnc sequence such that the first term is four times the thlld term. Find the greatest angle .
1960 B) 192 0 C) 1860 D) 1820
E) 176 0
RN5WERS
EXERCISES 1
l. a. yes b. yes c. yes d. no e. yes f. ves g. no h. yes 1. no
e.
n2 +n
3, a. 5, 7, 9;
77 b. 
c. 4, 615 7 
-
-4) + 2n; 132
n odd
n
even
b. 17, 21 25,
29, 33, 37, 41 
12 10. 68 11. 12 a 52
11
b. 3780 
19
h. 210 i. 20 125
320 1. 528 235
23 77
13. yes 14. 162
15. 8775 16.
17 17. 18. 49 19. 20.
110 21. 160 22. 23. 4n I 24. 630
90
25. a. $35 000
$187
500 26. 2340 27. 470 28. no 29. a. 36.5 km 456.5 km 30.
8 hours 31. $2737.50
|
16 16 16 16 |
|
|
|
|
|
|
|
|
42 . 263 700 |
43. 66 570 |
44. |
80 200 |
46. |
|
32. 33.
use the arithmetic mean formula 34. consider n = 4, 5, 6
39. 40. let m n + k and consider the sum formula
Arithmetic and Gæonzetñc
Sequence-4
number as the
sum of the terms of a geometric sequence, e.g. 666 = 6 • 10 2 + 6 •
10 + 6 21. a. b.
|
|
49 |
|
10 |
|
47 202 13
22. a. 81 doesn't
exist 23. a. 
25. 405, -270, 180 -120
26.
a. 445+ 8 b. 2 27. 150 28.
29. 30. 31. 32. 33.
0,O or 10 4 3 3
9 27 45 75
34.
5 or 20 -6, 6, 18 or 10, 
36. 37. 18 12, 6, 3 or 38.
write each factor m terms of
bl and q 39. 40.5 40. 18 or 2 41. 2, 6, 18 01 18, 62 42. solve anthmetic mean formula for b 43. 33 333 333
1.
9. 
9. 
1. 
2.
c 10. 2. 
10. 
2. 
10. 
11.
c 11. 
11. 
12.
4. 
12. 
12. 
13.
5. 
13, c 5. 
13. c
14.
c 14. c 14. 
15.
15. 
15. c
16.
16. 
16. 
Ar.sažer-s 
 |
|
existence the fact or state of existing, bemg area: any flat, curved, or mpgular expanse of a surface average. also called arithmetic mean The lesult obtained byexponent a number or variable placed as a superscript to the adding the numbers or quantities in a set and dividing thenght of another number or quantity indlcanng the number total by the number of members in the setof times the number or quantity is to be multiplied by itself Fibonacci Leonafflo Fibonacci, also called Leonardo of Pisa base - the number whose powers alp expæssedA thirteenth-century Italian mathematicnn who popularized the decimal system in Europe Fibonacci sequence; the infinite sequence of numbers, 1, 1, 2, 3, 5, 8, etc , m which each number IS the sum of the consecutzue: following one another vnthout interruption, pleuous two The sequence named after Leonardo successwe Fibonacci, who studied its properties.
criteria. a standaxd by which something can be judged or fdnžte havmg a
countable number of elements de cided džgzt: each of the symbols 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 which form a natural number e _ abblpvaatlon for id est (In Latin, 'in other words') e O abbleuatlon for exempli grana (in Latin, 'for example')inclusžue Including the limits specified element one of the objects or numbers that togethertncrease to make or become eeater In size. constitute a set.infinite havmg an unhmited or uncountable
number cf equilateral havmgall sides of equal length etc_ abbpvnanon for et cetera.integer. any number which is member of the set { —3, —2, even: a natural number which is divisible by two |
|
![Check Yourself 6 1. (an) an anthmenc sequence mth a] 41 and common difference —4](https://fs.znanio.ru/d5af0e/c7/5c/059c25ce564aad57498e0d51b77a480373.jpg)
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
a general
term of a sequence? If yes, find al + ag + aa.
is not meanmgful only
when = —e N. Since an is defined for any natural number;
=
3.8
2n
+ 5, find the term of the sequence (b) which is equal to a. 25 b. 17 c.
96
25 b. 17 C. 96
10 
6 
5. We
have al 10 (the smallest two-thut number dlvlslble by 5), and a 95 (the
greatest two-diet number divisible by 5). an — al 95-10
— p)d, where a is
any term of that sequence.
3
b.
2
. (—__)P-£, so (9 4 = e AP -2 which means p
so
SS 
2.1 0.05
+ 0.05 . 0.1 + . (0.1) 2 + 0.05 q
4 27 8
C)
-1
consider
the sum formula for each term
