Банк заданий. Геометрия 8 класс.

Примерные задачи (№3 и №4) зачета по геометрии  8 класс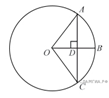

3) Ра­ди­ус OB окруж­но­сти с цен­тром в точке O пе­ре­се­ка­ет хорду AC в точке D и пер­пен­ди­ку­ля­рен ей. Най­ди­те длину хорды AC, если BD = 1 см, а ра­ди­ус окруж­но­сти равен 5 см.

4) Пе­ри­метр пря­мо­уголь­ни­ка равен 56, а диа­го­наль равна 20. Най­ди­те пло­щадь это пря­мо­уголь­ни­ка.

.

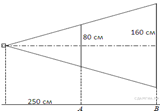
3)Про­ек­тор пол­но­стью осве­ща­ет экран A вы­со­той 80 см, рас­по­ло­жен­ный на рас­сто­я­нии 250 см от про­ек­то­ра. На каком наи­мень­шем рас­сто­я­нии (в сан­ти­мет­рах) от про­ек­то­ра нужно рас­по­ло­жить экран B вы­со­той 160 см, чтобы он был пол­но­стью освещён, если на­строй­ки про­ек­то­ра оста­ют­ся не­из­мен­ны­ми?

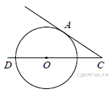
4)Най­ди­те угол АСО, если его сто­ро­на СА ка­са­ет­ся окруж­но­сти, О — центр окруж­но­сти, а дуга AD окруж­но­сти, за­ключённая внут­ри этого угла, равна 100°.

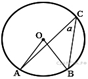
3) Най­ди­те ве­ли­чи­ну (в гра­ду­сах) впи­сан­но­го угла α, опи­ра­ю­ще­го­ся на хорду  AB, рав­ную ра­ди­у­су окруж­но­сти.

4) Пря­мая, па­рал­лель­ная ос­но­ва­ни­ям и тра­пе­ции , про­хо­дит через точку пе­ре­се­че­ния диа­го­на­лей тра­пе­ции и пе­ре­се­ка­ет её бо­ко­вые сто­ро­ны и в точ­ках и со­от­вет­ствен­но. Най­ди­те длину от­рез­ка , если см, см.

3) Два па­ро­хо­да вышли из порта, сле­дуя один на север, дру­гой на запад. Ско­ро­сти их равны со­от­вет­ствен­но 15 км/ч и 20 км/ч. Какое рас­сто­я­ние (в ки­ло­мет­рах) будет между ними через 2 часа?

4) В тре­уголь­ни­ке АВС углы А и С равны 20° и 60° со­от­вет­ствен­но. Най­ди­те угол между вы­со­той ВН и бис­сек­три­сой BD.

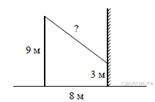
3) От стол­ба вы­со­той 9 м к дому на­тя­нут про­вод, ко­то­рый кре­пит­ся на вы­со­те 3 м от земли (см. ри­су­нок). Рас­сто­я­ние от дома до стол­ба 8 м. Вы­чис­ли­те длину про­во­да.

4) Отрезки AB и DC лежат на па­рал­лель­ных прямых, а от­рез­ки AC и BD пе­ре­се­ка­ют­ся в точке M. Най­ди­те MC, если AB = 16, DC = 24, AC = 25 .

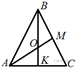
 3) В рав­но­сто­рон­нем тре­уголь­ни­ке  ABC  ме­ди­а­ны  BK  и  AM  пе­ре­се­ка­ют­ся в точке O. Най­ди­те .

4) Окруж­ность с цен­тром на сто­ро­не AC тре­уголь­ни­ка ABC про­хо­дит через вер­ши­ну C и ка­са­ет­ся пря­мой AB в точке B. Най­ди­те AC, если диа­метр окруж­но­сти равен 7,5, а AB = 2.

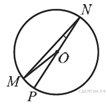
3) Най­ди­те гра­дус­ную меру ∠MON, если из­вест­но, NP — диа­метр, а гра­дус­ная мера ∠MNP равна 18°.

4) В тре­уголь­ни­ке ABC от­ме­че­ны се­ре­ди­ны M и N сто­рон BC и AC соответственно.

Пло­щадь треугольника CNM равна 57.

Най­ди­те пло­щадь четырёхугольника ABMN.

3) У тре­уголь­ни­ка со сто­ро­на­ми 16 и 2 про­ве­де­ны вы­со­ты к этим сто­ро­нам. Вы­со­та, про­ведённая к пер­вой сто­ро­не, равна 1. Чему равна вы­со­та, про­ведённая ко вто­рой сто­ро­не?

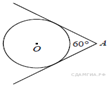
4) Из точки А про­ве­де­ны две ка­са­тель­ные к окруж­но­сти с цен­тром в точке О. Най­ди­те ра­ди­ус окруж­но­сти, если угол между ка­са­тель­ны­ми равен 60°, а рас­сто­я­ние от точки А до точки О равно 8.

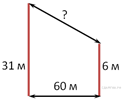
3) В 60 м одна от дру­гой рас­тут две сосны. Вы­со­та

одной 31 м, а дру­гой — 6 м. Най­ди­те рас­сто­я­ние (в мет­рах) между их вер­хуш­ка­ми.

4) Окруж­ность пе­ре­се­ка­ет сто­ро­ны AB и AC тре­уголь­ни­ка ABC в точ­ках K и P со­от­вет­ствен­но и про­хо­дит через вер­ши­ны B и C. Най­ди­те длину от­рез­ка KP, если AK = 18, а сто­ро­на AC в 1,2 раза боль­ше сто­ро­ны BC.

.

.

3) Че­ло­век ро­стом 1,7 м стоит на рас­сто­я­нии 8 шагов от стол­ба, на ко­то­ром висит фо­нарь. Тень че­ло­ве­ка равна че­ты­рем шагам. На какой вы­со­те (в мет­рах) рас­по­ло­жен фо­нарь?

4) Ос­но­ва­ния рав­но­бед­рен­ной тра­пе­ции равны 8 и 18, а пе­ри­метр равен 56.  Най­ди­те пло­щадь тра­пе­ции.

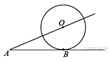
3) К окруж­но­сти с цен­тром в точке О про­ве­де­ны ка­са­тель­ная AB и се­ку­щая AO. Най­ди­те ра­ди­ус окруж­но­сти, если AB = 12 см, AO = 13 см.

4) На сто­ро­нах угла и на его бис­сек­три­се от­ло­же­ны рав­ные от­рез­ки и . Ве­ли­чи­на угла равна 160°. Опре­де­ли­те ве­ли­чи­ну угла .

3) Най­ди­те пе­ри­метр пря­мо­уголь­но­го участ­ка  земли, пло­щадь ко­то­ро­го равна 800 м² и одна сто­ро­на в 2 раза боль­ше дру­гой. Ответ дайте в мет­рах.

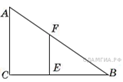
4) Окружность про­хо­дит через вер­ши­ны А и С тре­уголь­ни­ка АВС и пе­ре­се­ка­ет его сто­ро­ны АВ и ВС в точ­ках К и Е соответственно.Отрезки АЕ и СК перпендикулярны. Най­ди­те ∠КСВ, если ∠АВС = 20°.

3) В пря­мо­уголь­ном тре­уголь­ни­ке один из ка­те­тов равен 10, а угол, ле­жа­щий на­про­тив него, равен 45°. Най­ди­те пло­щадь тре­уголь­ни­ка.

4) Биссектрисы углов A и B па­рал­ле­ло­грам­ма ABCD пе­ре­се­ка­ют­ся в точке K. Най­ди­те пло­щадь параллелограмма, если BC = 19, а рас­сто­я­ние от точки K до сто­ро­ны AB равно 7.

3) В вы­пук­лом че­ты­рех­уголь­ни­ке ABCD , , , . Най­ди­те угол A. Ответ дайте в гра­ду­сах.

4)Найдите от­но­ше­ние двух сто­рон треугольника, если его медиана, вы­хо­дя­щая из их общей вершины, об­ра­зу­ет с этими сто­ро­на­ми углы в 30° и 90°.

3) Сторона ромба равна 34, а острый угол равен 60̊. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?

 4) высота треугольника разбивает его основание на два отрезка с длинами 8 и 9. Найдите длину этой высоты, если известно, что другая высота треугольника делит ее пополам.