«Банк задач для поэлементного контроля знаний по теме «Векторы»(8 клас)»

Контрольная работа

 

 

 

Подготовила:

Садовникова Надежда Евгеньевна

 

Должность:

 учитель математики

Место работы:

 ГБОУ СОШ № 443 Фрунзенского района  Санкт-Петербурга

 

 

 

 

 

 

25 августа 2022 г.

г. Санкт-Петербург

Российская Федерация

 

 

 

Содержание

 

Пояснительная записка………………………………………..…........................ 3

1 Понятие вектора. Понятие нулевого вектора. Понятие длины вектора.... .....4

1.1 Теоретические знания.............................................................................................................4

1.2 Практические задания .….......................................................................................................5

2 Понятие коллинеарных векторов. Сонаправленные и противоположно

направленные коллинеарные векторы. Свойства ненулевых векторов. Равенство векторов................................................................... …......................5

2.1 Теоретические знания. ..….....................................................................................................5

2.2 Математический диктант № 1.  …........................................................................................8

2.3 Дополнительные задачи. …...................................................................................................8

3 Правила и законы сложения (вычитания) векторов. …...................................8

3.1 Сумма двух векторов. Вычитание векторов. Сложение векторов по правилу

 треугольника. ….....................................................................................................................8

3.2 Сложение векторов по правилу параллелограмма. …......................................................  9

3.3 Математический диктант № 2.......................................................................................... . ..9

3.4 Сложение векторов по правилу многоугольника. Законы сложения векторов. .….........9

3.5 Умножение вектора на число. …..........................................................................................9

3.6 Смешанные задачи на правила и законы сложения векторов. …......................................9

4 Применение векторов к решению задач   ..................................................................9

5 Контрольная работа.  .....................................................................................10

Список литературы............……………………………………………...............11

 

 

 

 

 

Пояснительная записка

Для поэлементного контроля знаний обучающихся по теме «Векторы»      (8 класс) был сформирован банк задач, к котором в первых двух разделах:

- «Понятие вектора. Понятие нулевого вектора. Понятие длины вектора» (раздел 1);

- «Понятие коллинеарных векторов. Сонаправленные и противоположно

направленные коллинеарные векторы. Свойства ненулевых векторов. Равенство векторов» (раздел 2)

автором отдельно сформулированы задачи с целью выявления тех элементарных теоретических знаний, которыми не овладел учащийся, чтобы  в дальнейшем производить действия над векторами (задачи раздела 3) и применять векторы в решении задач (раздел 4).

Банк задач формировался к рабочей учебной программе (РУП) по геометрии 8 класса, утвержденной в образовательном учреждении, в которой работает автор. В основе РУП лежит авторская программа для общеобразовательных учреждений Т.А. Бурмистровой — издательство М., Просвещение, 2009 г., к учебнику «Геометрия 7 — 9 классы», авторов: Л. С. Атанасяна, В.Ф. Бутузова, С. Б. Кадомцева, Э. Г. Позняк, И. И. Юдиной, - М., «Просвещение», (2009 - 2014), включенного в Федеральный перечень учебников на 2016-2017 учебный год, утвержденный Минобрнауки РФ  приказом от 21 апреля 2016 года № 459.

При составлении банка задач также была использована литература учебно-методического комплекта к данному учебнику, перечисленная в разделе «Список литературы». 

В отдельном разделе данной творческой работы представлена разработанная контрольная работа по теме «Векторы» (8 класс).   

 

 

1 Понятие вектора. Понятие нулевого вектора. Понятие длины вектора.

1.1 Теоретические знания.

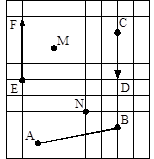
рис. 1

1. Какими буквами на рисунке 1 обозначен отрезок?

2. Какие из векторов на рисунке 1 являются нулевыми векторами? Запишите их.

3. Сколько векторов изображено на рисунке 1? Выберите вариант ответа:

а) 5      б) 4       в) 3        г) 2       д) 1

4. Выберите из представленных вариантов:

а)    б)    в)     г) АВ      д)     е)     ж)     з) RP

а) варианты, соответствующие обозначению отрезка;

б) варианты, соответствующие обозначению нулевого вектора;

в) варианты, соответствующие обозначению ненулевого вектора.

5. Выберите из представленных вариантов:

а)      б)      в) AB=6      г)      д)

варианты, соответствующие обозначению длины вектора.

6. Выберите из представленных вариантов:

а)      б)      в) MN=0      г)      д)

варианты, соответствующие обозначению длины нулевого вектора.

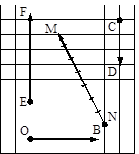
рис. 2

7. Чему равны длины векторов, изображенных на рисунке 2 (каждая клетка на рисунке 2 имеет сторону, равную единице измерения отрезков)? 

8. Выберите варианты ответа, обозначающие модуль нулевого вектора:

            а)   б)    в)    г)   д)

1.2. Практические задания.

A). Выполните практическое задание. Отметьте точки A, F, D, не лежащие на одной прямой. Начертите все ненулевые векторы, начало и конец которых совпадают с какими-то двумя из этих точек (A, F, D). Напишите все полученные векторы и укажите начало и конец каждого вектора.

Б). Выполните практическое задание. Выбрав подходящий масштаб, начертите векторы, изображающие движение автомобиля сначала на 150 км на север от поселка А до поселка B, а потом на запад на 250 км от поселка B до города C. Начертите вектор , который изображает перемещений и начальной точки в конечную.

2 Понятие коллинеарных векторов. Сонаправленные и противоположно направленные коллинеарные векторы. Свойства ненулевых векторов. Равенство векторов.

2.1 Теоретические знания.

1. Выберите варианты ответов, определяющие, какие векторы называются коллинеарными векторами:

а) если векторы лежат на одной прямой;

б) если векторы лежат на параллельных прямых;

в) если векторы лежат на пересекающихся прямых;

г) если векторы лежат на перпендикулярных прямых.

2. Применительно к векторам, представленным на рисунке 2 выберите вариант ответа, содержащий коллинеарные векторы:

а),,       б) , ,         в) ,

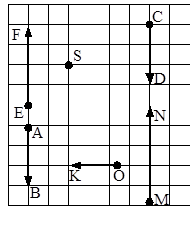
рис. 3

3. Применительно к векторам, представленным на рисунке 3, выберите варианты ответов на вопрос: каким векторам коллинеарен нулевой вектор  ?

                                    а)          б)  , ,  ,           в) всем векторам

4. Применительно к векторам, представленным на рисунке 3, выберите варианты ответов, содержащие коллинеарные векторы:

       а) ,     б) , , , ,     в), , , , ,  

5. Применительно к векторам, представленным на рисунке 3, из вариантов ответов:

                       а),      б),      в),      г),

 а) выберите варианты, содержащие сонаправленные коллинеарные векторы;

 б) выберите варианты, содержащие противоположно направленные коллинеарные векторы.

   6. Применительно к векторам, представленным на рисунке 3, какие из вариантов   записей является верными?

     а) ↑↓   б) ↑↑   в)↑↑   г)↑↑   д) ↑↓                е)↑↓   ж)↑↓    з)↑↓      и)↑↓     к)↑↑           л)↑↑     м) ↑↑

7. Применительно к векторам, представленным на рисунке 3, верны ли следующие утверждения?

1) если ↑↓ и ↑↓, то  ↑↑

2) если ↑↑, а  ↑↓, то ↑↓

Выберите правильный вариант ответа:

а) верно только утверждение 1;

б) верно только утверждение 2;

в) оба утверждения 1 и 2 верны;

г) оба утверждения 1 и 2 неверны.

8. Поверните на рисунке 3 вектор  так, чтобы выполнялось для ненулевых коллинеарных векторов утверждение утверждение 3), следующего содержания:

если ↑↑ и ↑↑, то ↑↑.

Ответ: см. рисунок 4.

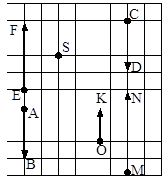
рис. 4

9. Выберите правильный вариант ответа, определяющий равенство векторов, т.е.  =  , если:

а) ↑↓ и =

б) ↑↑ и =

б) =

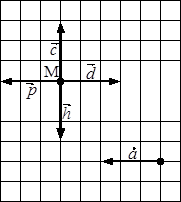
рис. 5

10. От точки М отложены вектора: , , ,  (см. рис. 5) и = ==.

Какой из векторов равен вектору  ? Выбери вариант ответа:

а)           б)         в)       г)

2.1 Математический диктант № 1.

·        Начертите вектор , укажите его начало и конец.

·        Начертите вектор , сонаправленный вектору .

·        Начертите вектор , равный вектору .

·        Начертите вектор , коллинеарный вектору .

·        Чему равна длина нулевого вектора?

·        Известно, что =. Что можно сказать о направлениях лучей AB и CD? О длинах отрезков AB и CD?

·        Известно, что = -. Что можно сказать о направлениях лучей AB и CD? О длинах отрезков AB и CD?

2.3 Дополнительные задачи.

740[1]; 741[1]; 742[1]; 747[1]; 749[1]; 751[1]; 800[1];112[2]; Вариант 2, стр. 46[3]; Вариант 3, стр. 47[3]; Вариант 4, стр. 47[3]; 50.1[5]; 50.2[5]; 50.3[5]; 50.4[5];

3 Правила и законы сложения (вычитания) векторов.

3.1 Сумма двух векторов. Вычитание векторов. Сложение векторов по правилу треугольника.

753[1]; 754[1]; 51.1[5]; 51.2[5]; 52.1[5]; 52.2[5]; 52.3[5]; 52.5[5]; 3 стр. 59[3]; 6,5,6,7 стр. 59[3]; 759[1]; 115[2]; 116[2]; С-16 В1(1)[4]; 768[1]; 772[1]; 783[1]

3.2 Сложение векторов по правилу параллелограмма.  

 4 стр. 59[3];  117[2]; 51.3[5]; 51.5[5]; 51.6[5]; С-17 В-1(2)[4]; 770[1]     

3.3 Математический диктант № 2.

·        Начертите два неколлинеарных вектора. Постройте угол между этими векторами.

·        Может ли угол между векторами быть равным: 90°, 32°, 0°, 110°, 200°, 180° ?

·        Что принимается за сумму векторов: вектор или число?

·        Начертите два неколлинеарных вектора  и . Найдите сумму этих векторов по правилу параллелограмма.

·        Начертите два коллинеарных вектора  и . Найдите сумму этих векторов по правилу треугольника.

·        Какой вектор получается в результате сложения данноговектора с нулевым вектором?

·        Чему равна сумма противоположных векторов?

3.4 Сложение векторов по правилу многоугольника. Законы сложения векторов.

 755[1]; 120[2]; 121[2]; 124[2]; 764[1]; 766[1]; С-17 В-1(1)[4]; 53.5[5]

3.5 Умножение вектора на число.

54.2(1)[5]; 775[1]; 776[1]; 777[1]; 778[1]; 779[1]; 129[2]; 130[2]; 133[2]; Вариант 1стр. 49[3]; Вариант 2 стр. 49[3];

3.5 Смешанные задачи на правила и законы сложения векторов.

756[1]; 757[1]; 758[1]; 118[2]; 119[2]; 120[2]; 122[2]; 126[2]; 768[1]; 769[1]; 770[1]; 771[1]; 772[1]; 778 [1]

4 Применение векторов к решению задач.

53.5[5]; 53.6[5]; 54.1(2)[5]; 54.2(2)[5]; 55.1[5]; 55.2[5]; 55.3[5]; 55.4[5]; 135[2]; С-18 В-2(2)[4]; С-19 В-1(1)[4]; 789[1]; 55.5[5]; 792[1]; 803[1]; 804 [1]; 807[1]; 904[1]; 905[1]; 

 

Контрольная работа

 

1. Начертите равнобедренную трапецию ABCD с основаниями BC и AD; O - точка пересечения диагоналей. Отметьте векторы , , , , , , , . Запишите: а) сонаправленные векторы; б) противоположно направленные векторы. Имеются ли среди этих векторов: равные векторы; векторы, имеющие равные длины?

 

2. Начертите неколлинеарные вектора  и , так, чтобы =3 см, =2 см. Постройте вектор  =  - .

 

3. В параллелограмме ABCD точка M середина стороны CD, N — точка на стороне AD такая, что AN : ND как 1 : 2. Выразите векторы   и  через векторы  =  и  = .

 

 

 

 

 

 

 

 

Список литературы:

1. Л.С. Атанасян и др. Геометрия. 7 — 9 классы: учеб. для общеобразоват. Учреждений / [Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.].- 20-е изд.- М.: Просвещение, 2010. - 384с.

2. Л.С. Атанасян и др. - Рабочая тетрадь по геометрии 8 класс / [Л.С. Атанасян, В.Ф. Бутузов, Ю.А. Глазков, И.И. Юдина].- М.: Просвещение, 2016. - 66с.

3. Мельникова, Н.Б. Дидактические материалы по геометрии: 8 класс: к учебнику Л.С. Атанасяна и др. «Геометрия. 7 — 9 классы» / Н.Б. Мельникова, Г.А. Захарова. М.: Издательство «Экзамен», 2014.- 175, [1]с (серия «Учебно-методический комплект»).

4. Иченская М.А. Геометрия. Самостоятельные и контрольные работы. 7 - 9 классы: пособие для учителей общеобразоват. Учреждений / М.А. Иченская. - М.: Просвещение, 2012. - 144с.

5. Зив Б.Г. Задачи по геометрии: Пособие для учащихся 7- 11 кл. общеобразоват. Учреждений / Б.Г. Зив, В.М. Мейлер, А.Г. Баханский. - 5-е изд.- М.: Просвещение, 2003. - 271с.