Блок уроков: Табличный процессор Excel

Блок уроков: Табличный процессор Excel.
Урок . Решение биквадратного уравнения в EXCEL. 

1. Постановка задачи.

    Уравнение вида: ax⁴ + bx² + c = 0, где a, b, c - любые действительные числа, называется биквадратным.

    Требуется найти такие значения переменной величины x, которые обращают уравнение в верное равенство.

2. Алгоритм решения биквадратного уравнения.

    Изложим основные пункты алгоритма решения биквадратного уравнения:

1.     Прежде всего сделаем замену y = x². Получим квадратное уравнение ay² + by + c = 0. 
       Решим полученную систему квадратных уравнений.
   
          y = x²
          ay² + by + c = 0.
   
       Начнем с решения квадратного уравнения.
       Далее в зависимости от значения переменной y будем решать второе уравнение y=x² и находить значения переменной x.
2.     С этой целью первым делом вычислим дискриминант квадратного уравнения: d = b² - 4ac.
       Далее в зависимости от значения дискриминанта d и от значений переменной y могут встретиться следующие случаи:
• Случай 1: Если d<0, то действительных решений нет.
•                Если d>=0, то вычислим 
  
  

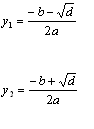
• Случай 2: Если d>=0 и y₁<0 и y₂<0, то действительных решений нет
• Случай 3: Если d>=0 и y₁>=0 и y₂>=0, то получим 4 решения биквадратного уравнения:
  
   
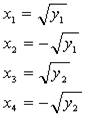
• Случай 4: Если d>=0 и y₁>=0 и y₂<0, то получим 2 решения биквадратного уравнения:
  
   
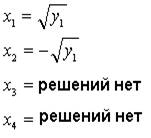
• Случай 5: Если d>=0 и y₂>=0 и y₁<0, то получим 2 решения биквадратного уравнения:
  
   

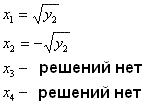
2. Блок-схема алгоритма решения биквадратного уравнения.

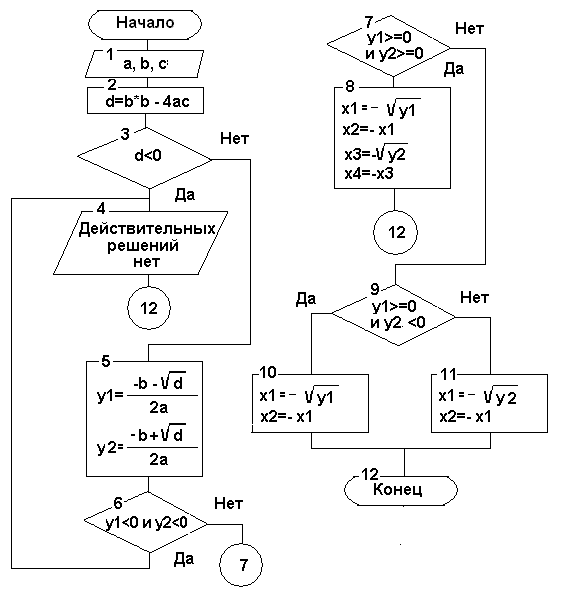
    Ниже на рисунке показана блок-схема решения биквадратного уравнения: 

 

3. Проект решения биквадратного уравнения в Excel.

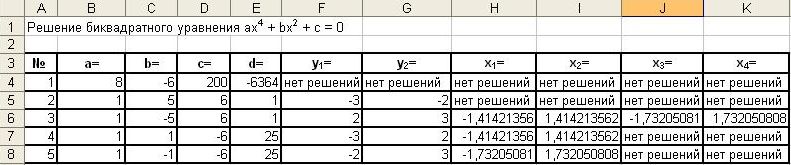
    Ниже на рисунке показан проект решения задачи отыскания корней биквадратного уравнения. 

 

    Опишем действия, необходимые для того, чтобы составить проект решения задачи в Excel.

1.     В ячейку A1 записать наименование задачи: Решение биквадратного уравнения ax⁴ + bx² + c = 0.
2.     Вторую строку пропустить.
3.     В третьей строке указать заголовки столбцов: № п/п; a= ; b= ; c= ; d= ; y₁ ; y₂ ; x₁= ; x₂= ; x₃= ; x₄= ;
4.     Начиная с 4-ой строки, будем располагать матрицу с числовыми значениями коэффициентов a, b, c исходной задачи и необходимые формулы для вычисления значений расчетных величин: d, y₁, y₂, x₁, x₂, x₃, x₄:
• В ячейку E4 поместить формулу для вычисления d
  =C4*C4 - 4B4*D4 и нажать клавишу Enter.
• В ячейку F4 поместить формулу для вычисления y₁
  =ЕСЛИ(E4<0;"решений нет";(-C4-КОРЕНЬ(E4))/(2*B4)) и нажать клавишу Enter.
• В ячейку G4 поместить формулу для вычисления y₂
  =ЕСЛИ(E4<0;"решений нет";(-C4+КОРЕНЬ(E4))/(2*B4)) и нажать клавишу Enter.
• В ячейку H4 поместить формулу для вычисления x₁
  =ЕСЛИ(E4<0;"решений нет";ЕСЛИ(И(F4<0;G4<0);"решений нет";ЕСЛИ(И(F4>=0;G4>=0);-КОРЕНЬ(F4);
  ЕСЛИ(И(F4>=0;G4<0);-КОРЕНЬ(F4);-КОРЕНЬ(G4))))) и нажать клавишу Enter.
• В ячейку I4 поместить формулу для вычисления x₂
  =ЕСЛИ(E4<0;"решений нет";ЕСЛИ(И(F4<0;G4<0);"решений нет";ЕСЛИ(И(F4>=0;G4>=0);+КОРЕНЬ(F4);
  ЕСЛИ(И(F4>=0;G4<0);+КОРЕНЬ(F4);+КОРЕНЬ(G4))))) и нажать клавишу Enter.
• В ячейку J4 поместить формулу для вычисления x₃
  =ЕСЛИ(E4<0;"решений нет";ЕСЛИ(И(F4<0;G4<0);"решений нет";ЕСЛИ(И(F4>=0;G4>=0);-КОРЕНЬ(G4);
  ЕСЛИ(И(F4>=0;G4<0);"решений нет";"решений нет")))) и нажать клавишу Enter.
• В ячейку K4 поместить формулу для вычисления x₄
  =ЕСЛИ(E4<0;"решений нет";ЕСЛИ(И(F4<0;G4<0);"решений нет";ЕСЛИ(И(F4>=0;G4>=0);+КОРЕНЬ(G4);
  ЕСЛИ(И(F4>=0;G4<0);"решений нет";"решений нет")))) и нажать клавишу Enter.
5.    Проект решения задачи вычисления корней биквадратного уравнения ax⁴ + bx² + c = 0 получен.
   Остается опробовать его или, как говорят программисты, отладить полученный проект. 
   Поместим в таблицу Excel матрицу с коэффициентами a, b, c следующих пяти исходных биквадратных уравнений: 
   
      8x⁴ - 6x² + 200 = 0 
        x⁴ + 5x² + 6 = 0 
        x⁴ - 5x² + 6 = 0 
        x⁴ + x² - 6 = 0 
        x⁴ - x² - 6 = 0 
   
   
       Здесь предусмотрены все пять случаев, которые могут встретиться при решении биквадратного уравнения, изложенных подробно в разделе: "Алгоритм решения биквадратного уравнения". На рисунке выше коэффициенты указанных уравнений введены в таблицу Excel. Их Вы видите в соответствующих столбцах "a=", "b=", "c=" названной таблицы.
       Остается выравнять по длине документа название проекта, данное в ячейке A1 первой строки: "Решение биквадратного уравнения ax⁴ + bx² + c = 0". Это можно сделать, если вначале выделить данное название по длине документа и затем нажать кнопку с буквой "а" посередине и стрелками справа, слева, сверху и снизу:  
       Помимо того, нужно четко показать столбцы и строки таблицы. Воспользуйтесь для этого командами выделения границ, представленными ниже нарисунке: 
   
   .

Скачано с www.znanio.ru
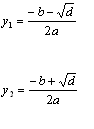
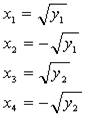
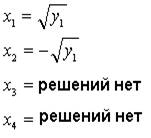
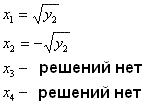