Что такое функция 7кл

Что такое функция?

Цели: ввести понятие функциональной зависимости; дать определения независимой переменной (аргумента), зависимой переменной, области определения функции, области значений функции.

Ход урока

Организационный момент

I. Устная работа.

1. Найдите значение выражения.

а) 3x – (2 + 3x)  при х = 7,862; б) 2a – (a – 0,3)  при а = 0,7;

2. Решите уравнение.

а) 3х = –9;            б) 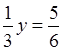;                                      в) 5а – 15 = 0;

г) 3х = 3х + 11;                д) 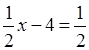(x – 8);                     е) 3y +  = 0.

II. Объяснение нового материала.

1. Основная задача первого занятия: показать, что функция – это математическая модель, позволяющая описывать и изучать разнообразные зависимости между реальными величинами.

Функция имеет общекультурное, мировоззренческое значение. При её изучении учащиеся знакомятся с идеей всеобщей связи, идеей непрерывности, бесконечности, интерполяции.

2. Объяснение проводить согласно пункту 12 учебника. Необходимо привести достаточно примеров функциональной зависимости (учебник, с. 51–53). Также нужно не только показывать зависимости, но и сразу обсуждать, в какой области человеческой деятельности применяются такие функциональные зависимости.

3. Вводим понятия независимой и зависимой переменных и определение функции как зависимости одной переменной от другой. На примерах показываем, что область определения функции может быть бесконечным и конечным множеством чисел.

III. Формирование умений и навыков.

Все задания, решаемые на этом уроке, направлены на усвоение как самого понятия функции, так и различных способов её задания (словесный, с помощью формулы, табличный, графический). Ученики должны уметь переходить от одного вида задания к другому и находить значения функции при каждом способе задания.

1. № 258, № 260.

2. Функция задана формулой у = 2 – 5х, верны ли равенства:

а) у = 12 при х = –2;                               б) у = 3 при х = ;

в) у = 20 при х = 4;                                 г) у = –0,5 при х = ?

3. № 261.

4. Функция задана графиком:

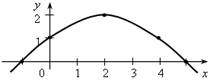
а) Найти значения функции при х = 0; 2; 3,5; –1.

б) При каком значении х значение функции равно 1; 2; 0?

в) Назвать несколько значений х, при которых значение функции положительно.

г) Назвать несколько значений х, при которых значение функции отрицательно.

5. Устно.

Результаты измерений температуры воздуха за сутки даны в следующей таблице:

а) Назовите температуру в 6 ч, 8 ч, 24 ч.

б) В какое время температура была равна +1°,  –4°,  11°?

в) Почему эту зависимость можно назвать функцией?

6. № 263.

Решение:

Если r – остаток от деления натурального числа п на 4, то можно записать n = 4 · x + r, где 0 ≤ r < 4.

Найдем соответствующие значения r:

а) Если п = 13,                 то 13 = 3 · 4 + 1,                    то есть r = 1;

б) если п = 34,                 то 34 = 8 · 4 + 2,                    то есть r = 2;

в) если п = 43,                 то 43 = 10 · 4 + 3,                  то есть r = 3;

г) если п = 100,    то 100 = 25 · 4 + 0,    то есть r = 0.

В рассматриваемой функциональной зависимости аргументом является переменная п.

Областью определения является множество чисел {13; 34; 43; 100}.

Значениями функции служат числа 0; 1; 2; 3.

IV. Итоги урока.

– Что называется функцией?

– Что называется аргументом?

– Какими способами можно задать функцию? Назовите преимущества каждого из них.

Домашнее задание: 1. № 259; № 262; № 264.

2. Функция задана графиком:

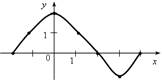
а) Найти значения функции при значениях аргумента 0; –2; 1; 3.

б) При каком значении х значение функции равно 2; 0; 1; –1?

в) Назвать несколько значений х, при которых значение функции положительно.

г) Назвать несколько значений х, при которых значение функции отрицательно.