
Действия с формулами из геометрии.
Базовый уровень из материалов ЕГЭ.
1. Среднее
геометрическое трёх чисел ![]() и c вычисляется по
формуле
и c вычисляется по
формуле ![]() Вычислите
среднее геометрическое чисел 12, 18, 27.
Вычислите
среднее геометрическое чисел 12, 18, 27.
Решение. Подставим значения в формулу и вычислим:
![]()
Ответ: 18.
2
.Длину окружности l можно вычислить по формуле
![]() где R —
радиус окружности (в метрах). Пользуясь этой формулой, найдите радиус
окружности, если её длина равна 78 м. (Считать
где R —
радиус окружности (в метрах). Пользуясь этой формулой, найдите радиус
окружности, если её длина равна 78 м. (Считать ![]() ).
).
Решение. Выразим радиус из формулы длины окружности:
![]()
Подставляя, получаем:
![]()
Ответ: 13.
3.Площадь ромба ![]() можно вычислить по формуле
можно вычислить по формуле ![]() где
где ![]() — диагонали ромба (в метрах). Пользуясь этой
формулой, найдите диагональ
— диагонали ромба (в метрах). Пользуясь этой
формулой, найдите диагональ ![]() если
диагональ
если
диагональ ![]() равна 30 м, а
площадь ромба 120 м2.
равна 30 м, а
площадь ромба 120 м2.
Решение. Подставим в формулу известные величины:
![]()
Ответ: 8.
4.Площадь трапеции ![]() можно вычислить по формуле
можно вычислить по формуле ![]() где
где ![]() — основания
трапеции, h — высота (в метрах). Пользуясь этой
формулой, найдите высоту h, если основания трапеции равны
— основания
трапеции, h — высота (в метрах). Пользуясь этой
формулой, найдите высоту h, если основания трапеции равны ![]() и
и ![]() а её площадь
а её площадь ![]()
Решение. Выразим высоту трапеции из формулы площади:
![]()
Подставляя, получаем:
![]()
Ответ: 4.
Приведём другое решение.
Подставим в формулу известные значения величин:
![]()
5.
Радиус
описанной около треугольника окружности можно найти по формуле ![]() где a — сторона треугольника,
где a — сторона треугольника, ![]() — противолежащий этой стороне угол, а R —
радиус описанной около этого треугольника окружности. Пользуясь этой формулой,
найдите
— противолежащий этой стороне угол, а R —
радиус описанной около этого треугольника окружности. Пользуясь этой формулой,
найдите ![]() если
если ![]() а
а ![]()
Решение. Выразим из формулы ![]() :
:
![]()
Подставляя, получаем:
![]()
Ответ: 0,4.
6.Радиус вписанной в
прямоугольный треугольник окружности можно найти по формуле ![]() где a и b — катеты, а c —
гипотенуза треугольника. Пользуясь этой формулой, найдите b,
если
где a и b — катеты, а c —
гипотенуза треугольника. Пользуясь этой формулой, найдите b,
если ![]() и
и ![]()
Решение. Подставим в формулу известные значения величин:
![]()
Ответ: 3,2.
7.Длину биссектрисы
треугольника, проведённой к стороне a, можно вычислить по
формуле ![]() Вычислите
Вычислите ![]() если
если ![]()
Решение. Выразим из данной
формулы ![]() :
:
![]()
Подставляя, получаем:
![]()
Ответ: 0,8.
8.Площадь треугольника
можно вычислить по формуле ![]() где b и c — стороны треугольника,
а
где b и c — стороны треугольника,
а ![]() — угол между
этими сторонами. Пользуясь этой формулой, найдите площадь треугольника,
если
— угол между
этими сторонами. Пользуясь этой формулой, найдите площадь треугольника,
если ![]() = 30°, c =
5, b = 6.
= 30°, c =
5, b = 6.
Решение. Подставим известные значения величин в формулу для нахождения площади:
![]()
Ответ: 7,5.
9.Площадь треугольника
можно вычислить по формуле ![]() где
где ![]() — длины сторон
треугольника, r — радиус вписанной окружности. Вычислите
длину стороны c, если
— длины сторон
треугольника, r — радиус вписанной окружности. Вычислите
длину стороны c, если ![]()
Решение. Подставим в формулу известные значения величин:
![]()
Ответ: 10.
10. Площадь любого выпуклого четырехугольника
можно вычислять по формуле ![]() где
где ![]() — длины его
диагоналей, а
— длины его
диагоналей, а ![]() угол между ними.
Вычислите
угол между ними.
Вычислите ![]() если
если ![]()
Решение. Выразим ![]() :
:
![]()
Подставляя, получаем:
![]()
Ответ: 0,4.
11. Площадь треугольника со сторонами a,
b, c можно найти по формуле Герона ![]() где
где
![]() Найдите
площадь треугольника со сторонами
Найдите
площадь треугольника со сторонами ![]()
![]()
![]()
Решение. Найдем полупериметр:
![]()
затем площадь:
![]()
![]()
Ответ: 66.
12.Длина биссектрисы ![]() проведенной к стороне c треугольника со сторонами a, b
и c, вычисляется по формуле
проведенной к стороне c треугольника со сторонами a, b
и c, вычисляется по формуле 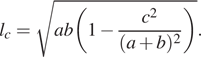 Треугольник
имеет стороны 9, 18 и 21. Найдите длину биссектрисы, проведённой к стороне
длины
Треугольник
имеет стороны 9, 18 и 21. Найдите длину биссектрисы, проведённой к стороне
длины ![]()
Решение. Найдём длину биссектрисы, проведённой к стороне длины 21:
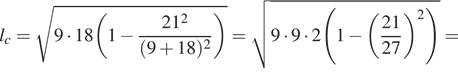
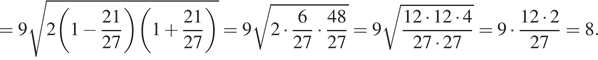
Ответ: 8.
13.Площадь поверхности
прямоугольного параллелепипеда с рёбрами ![]() и c
можно найти по формуле
и c
можно найти по формуле ![]() Найдите
площадь поверхности прямоугольного параллелепипеда с рёбрами
Найдите
площадь поверхности прямоугольного параллелепипеда с рёбрами ![]() и
и ![]()
Решение. Найдём площадь поверхности прямоугольного параллелепипида:
![]()
Ответ: 500.
14. Площадь прямоугольника вычисляется по
формуле ![]() где
d — диагональ, α — угол между
диагоналями. Пользуясь этой формулой, найдите S , если d = 10 и
где
d — диагональ, α — угол между
диагоналями. Пользуясь этой формулой, найдите S , если d = 10 и ![]()
Решение. Подставим в формулу
известные значения величин: 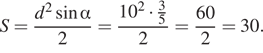
Ответ: 30.
15. Длина биссектрисы lc,
проведённой к стороне c треугольника со сторонами a, b и c,
вычисляется по формуле ![]() Найдите длину биссектрисы lc, если a = 3, b =
9,
Найдите длину биссектрисы lc, если a = 3, b =
9, ![]()
Решение. Найдём длину биссиктрисы:
![]()
![]()
![]()
![]()
![]()
![]()
Ответ: 3.
16.Теорему косинусов можно
записать в виде ![]() где
a, b и c — стороны треугольника, а
γ — угол между сторонами a и b. Пользуясь этой
формулой, найдите величину cos γ , если a = 7, b =10 и c
= 11.
где
a, b и c — стороны треугольника, а
γ — угол между сторонами a и b. Пользуясь этой
формулой, найдите величину cos γ , если a = 7, b =10 и c
= 11.
Решение. Подставим переменные в формулу:
![]()
Ответ: 0,2.
17.Радиус окружности, описанной около
треугольника, можно вычислить по формуле ![]() где a —
сторона, а α — противолежащий ей угол треугольника. Пользуясь
этой формулой, найдите R, если a = 8 и
где a —
сторона, а α — противолежащий ей угол треугольника. Пользуясь
этой формулой, найдите R, если a = 8 и ![]()
Решение. Согласно формуле, подставим данные:
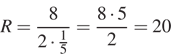
Ответ: 20
18. Площадь треугольника можно вычислить по
формуле ![]() где a, b
и c — стороны треугольника, а R —
радиус окружности, описанной около этого треугольника. Пользуясь этой формулой,
найдите b, если a = 12, с = 13,
S = 30 и R =
где a, b
и c — стороны треугольника, а R —
радиус окружности, описанной около этого треугольника. Пользуясь этой формулой,
найдите b, если a = 12, с = 13,
S = 30 и R = ![]()
Решение. Выразим и найдем b:
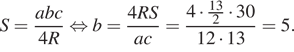
Ответ: 5.
19. Сумма углов правильного выпуклого
многоугольника вычисляется по формуле ![]() где n —
количество его углов. Пользуясь этой формулой, найдите n, если
где n —
количество его углов. Пользуясь этой формулой, найдите n, если ![]() = 6π.
= 6π.
Решение. Выразим n и подставим значения в формулу:
![]()
Ответ: 8.
20 Радиус вписанной в прямоугольный
треугольник окружности вычисляется по формуле ![]() где a
и b — катеты, а c — гипотенуза.
Пользуясь этой формулой, найдите r, если a = 8,
b = 15 и c = 17.
где a
и b — катеты, а c — гипотенуза.
Пользуясь этой формулой, найдите r, если a = 8,
b = 15 и c = 17.
Решение. Подставим в формулу известные значения величин:
![]()
Ответ: 3.
Решить самостоятельно.
1. Площадь
четырёхугольника можно вычислить по формуле ![]() где
где
![]() и
и ![]() —
длины диагоналей четырёхугольника,
—
длины диагоналей четырёхугольника, ![]() —
угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали
—
угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали ![]() если
если ![]()
![]() а
а ![]()
2. Длина
медианы ![]() проведённой к стороне
треугольника со сторонами a, b и c, вычисляется по формуле
проведённой к стороне
треугольника со сторонами a, b и c, вычисляется по формуле
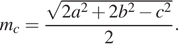 Треугольник
имеет стороны
Треугольник
имеет стороны ![]()
![]() и
и
![]() Найдите длину медианы, проведённой
к стороне длины
Найдите длину медианы, проведённой
к стороне длины ![]()
3. Площадь
трапеции S в м2 можно вычислить по формуле ![]() где
где ![]() — основания
трапеции, h — высота (в метрах). Пользуясь этой
формулой, найдите S, если a = 5, b = 3 и h = 6.
— основания
трапеции, h — высота (в метрах). Пользуясь этой
формулой, найдите S, если a = 5, b = 3 и h = 6.
4. Площадь
треугольника вычисляется по формуле ![]() где
b и с — две стороны треугольника, а
где
b и с — две стороны треугольника, а ![]() —
угол между ними. Пользуясь этой формулой, найдите площадь S, если b
= 16, с = 9 и
—
угол между ними. Пользуясь этой формулой, найдите площадь S, если b
= 16, с = 9 и ![]()
5. Площадь
треугольника можно вычислить по формуле ![]() где a, b
и c — стороны треугольника, а R —
радиус окружности, описанной около этого треугольника. Пользуясь этой формулой,
найдите площадь S, если a = 10, b = 9,
c = 17 и
где a, b
и c — стороны треугольника, а R —
радиус окружности, описанной около этого треугольника. Пользуясь этой формулой,
найдите площадь S, если a = 10, b = 9,
c = 17 и ![]()
6. Площадь треугольника
со сторонами a, b, c можно найти по формуле Герона ![]() где
где
![]() Найдите
площадь треугольника, если длины его сторон равны 7, 15, 20.
Найдите
площадь треугольника, если длины его сторон равны 7, 15, 20.
7.Радиус
вписанной в прямоугольный треугольник окружности вычисляется по формуле ![]() где a
и b — катеты, а c — гипотенуза.
Пользуясь этой формулой, найдите r, если a = 8,
b = 15 и c = 17.
где a
и b — катеты, а c — гипотенуза.
Пользуясь этой формулой, найдите r, если a = 8,
b = 15 и c = 17.
8. Площадь
параллелограмма ![]() можно
вычислить по формуле
можно
вычислить по формуле ![]() где
где ![]() —
стороны параллелограмма (в метрах). Пользуясь этой формулой, найдите площадь
параллелограмма, если его стороны 10 м и 12 м и
—
стороны параллелограмма (в метрах). Пользуясь этой формулой, найдите площадь
параллелограмма, если его стороны 10 м и 12 м и ![]()
9. .Площадь треугольника ![]() можно вычислить по формуле
можно вычислить по формуле ![]() где a —
сторона треугольника, h — высота, проведенная к этой
стороне (в метрах). Пользуясь этой формулой, найдите сторону
где a —
сторона треугольника, h — высота, проведенная к этой
стороне (в метрах). Пользуясь этой формулой, найдите сторону ![]() если площадь треугольника
равна
если площадь треугольника
равна ![]() а высота h
равна 14 м.
а высота h
равна 14 м.
10. Длина
биссектрисы lc, проведённой к стороне c треугольника
со сторонами a, b и c, вычисляется по формуле ![]() Найдите длину биссектрисы lc, если a = 3, b =
9,
Найдите длину биссектрисы lc, если a = 3, b =
9, ![]()
Ответы и решения.
1. Площадь
четырёхугольника можно вычислить по формуле ![]() где
где
![]() и
и ![]() —
длины диагоналей четырёхугольника,
—
длины диагоналей четырёхугольника, ![]() —
угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали
—
угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали ![]() если
если ![]()
![]() а
а ![]()
Решение. Выразим из исходной
формулы длину диагонали ![]() и найдем её:
и найдем её:
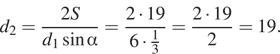
Ответ: 19.
2. Длина
медианы ![]() проведённой к стороне
треугольника со сторонами a, b и c, вычисляется по формуле
проведённой к стороне
треугольника со сторонами a, b и c, вычисляется по формуле
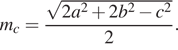 Треугольник
имеет стороны
Треугольник
имеет стороны ![]()
![]() и
и
![]() Найдите длину медианы, проведённой
к стороне длины
Найдите длину медианы, проведённой
к стороне длины ![]()
Решение. Найдём длину медианы, проведённой к стороне длины 6:
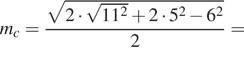
![]()
Ответ: 3.
3. Площадь
трапеции S в м2 можно вычислить по формуле ![]() где
где ![]() — основания
трапеции, h — высота (в метрах). Пользуясь этой
формулой, найдите S, если a = 5, b = 3 и h = 6.
— основания
трапеции, h — высота (в метрах). Пользуясь этой
формулой, найдите S, если a = 5, b = 3 и h = 6.
Решение. Вычислим площадь трапеции:
![]()
Ответ: 24.
4. Площадь
треугольника вычисляется по формуле ![]() где
b и с — две стороны треугольника, а
где
b и с — две стороны треугольника, а ![]() —
угол между ними. Пользуясь этой формулой, найдите площадь S, если b
= 16, с = 9 и
—
угол между ними. Пользуясь этой формулой, найдите площадь S, если b
= 16, с = 9 и ![]()
Решение. Подставим известные значения величин в формулу для нахождения площади:
![]()
Ответ: 24.
5. Площадь
треугольника можно вычислить по формуле ![]() где a, b
и c — стороны треугольника, а R —
радиус окружности, описанной около этого треугольника. Пользуясь этой формулой,
найдите площадь S, если a = 10, b = 9,
c = 17 и
где a, b
и c — стороны треугольника, а R —
радиус окружности, описанной около этого треугольника. Пользуясь этой формулой,
найдите площадь S, если a = 10, b = 9,
c = 17 и ![]()
Решение. Найдем S по формуле:
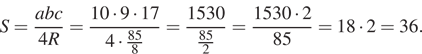
Ответ: 36.
6. Площадь треугольника
со сторонами a, b, c можно найти по формуле Герона ![]() где
где
![]() Найдите
площадь треугольника, если длины его сторон равны 7, 15, 20.
Найдите
площадь треугольника, если длины его сторон равны 7, 15, 20.
Решение. Найдем полупериметр:
![]()
затем площадь:
![]()
![]()
Ответ: 42.
7. Радиус
вписанной в прямоугольный треугольник окружности вычисляется по формуле ![]() где a
и b — катеты, а c — гипотенуза.
Пользуясь этой формулой, найдите r, если a = 8,
b = 15 и c = 17.
где a
и b — катеты, а c — гипотенуза.
Пользуясь этой формулой, найдите r, если a = 8,
b = 15 и c = 17.
Решение. Подставим в формулу известные значения величин:
![]()
Ответ: 3.
8. Площадь
параллелограмма ![]() можно
вычислить по формуле
можно
вычислить по формуле ![]() где
где ![]() —
стороны параллелограмма (в метрах). Пользуясь этой формулой, найдите площадь
параллелограмма, если его стороны 10 м и 12 м и
—
стороны параллелограмма (в метрах). Пользуясь этой формулой, найдите площадь
параллелограмма, если его стороны 10 м и 12 м и ![]()
Решение. Подставим в формулу
известные значения величин: ![]()
Ответ: 60.
9. .Площадь треугольника ![]() можно вычислить по формуле
можно вычислить по формуле ![]() где a —
сторона треугольника, h — высота, проведенная к этой
стороне (в метрах). Пользуясь этой формулой, найдите сторону
где a —
сторона треугольника, h — высота, проведенная к этой
стороне (в метрах). Пользуясь этой формулой, найдите сторону ![]() если площадь треугольника
равна
если площадь треугольника
равна ![]() а высота h
равна 14 м.
а высота h
равна 14 м.
Решение. Выразим сторону a из формулы площади треугольника:
![]()
![]()
Ответ: 4.
10. Длина
биссектрисы lc, проведённой к стороне c треугольника
со сторонами a, b и c, вычисляется по формуле ![]() Найдите длину биссектрисы lc, если a = 3, b =
9,
Найдите длину биссектрисы lc, если a = 3, b =
9, ![]()
Решение. Найдём длину биссиктрисы:
![]()
![]()
![]()
![]()
![]()
![]()
Ответ: 3.
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.