
1. На рисунке
показано дерево некоторого случайного эксперимента. Событию A
благоприятствуют элементарные события a, b и c, а событию B
благоприятствуют элементарные события b, c и d. Найдите ![]() — условную
вероятность события A при условии B.
— условную
вероятность события A при условии B. 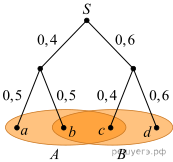
Решение. По рисунку находим вероятности элементарных событий a, b и c:
![]()
![]()
![]()
Вероятность события A равна сумме вероятностей событий a, b и c
![]()
Вероятность события B равна сумме вероятностей событий b, c и d
![]()
Вероятность произведения событий A и B равна сумме вероятностей событий b и c
![]() По формуле условной вероятности
По формуле условной вероятности ![]()
1.
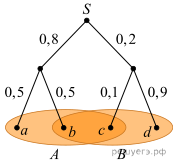 На рисунке
показано дерево некоторого случайного эксперимента. Событию A
благоприятствуют элементарные события a, b и c, а событию B
благоприятствуют элементарные события b, c и d. Найдите
На рисунке
показано дерево некоторого случайного эксперимента. Событию A
благоприятствуют элементарные события a, b и c, а событию B
благоприятствуют элементарные события b, c и d. Найдите ![]() — условную
вероятность события A при условии B.
— условную
вероятность события A при условии B.
Решение. По рисунку находим вероятности элементарных событий a, b и c:
![]()
![]()
![]()
Вероятность события A равна сумме вероятностей событий a, b и c
![]() Вероятность
события B равна сумме вероятностей событий b, c и d
Вероятность
события B равна сумме вероятностей событий b, c и d ![]()
Вероятность произведения событий A и B равна сумме вероятностей событий b и c
![]() По формуле
условной вероятности
По формуле
условной вероятности ![]()
3. 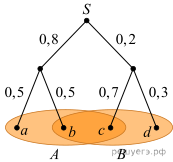 На рис.показано
дерево некот.случ.эксперимента.Событию A благоприятствуют элементарные
события a, b и c, а событию B благоприятствуют
элементарные события b, c и d. Найди— условную вероятность
события A при условии B.
На рис.показано
дерево некот.случ.эксперимента.Событию A благоприятствуют элементарные
события a, b и c, а событию B благоприятствуют
элементарные события b, c и d. Найди— условную вероятность
события A при условии B.
Решение. По
рисунку находим вероятности элементарных событий a, b и c:![]()
![]()
![]() Вероятность
события A равна сумме вероятностей событий a, b и c
Вероятность
события A равна сумме вероятностей событий a, b и c
![]() Вероятность
события B равна сумме вероятностей событий b, c и d
Вероятность
события B равна сумме вероятностей событий b, c и d ![]()
Вероятность произведения событий A и B равна сумме вероятностей событий b и c
![]() По формуле условной вероятности
По формуле условной вероятности ![]()
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.