Десятичные дроби 1

Тема.  Понятие положительной десятичной дроби.

Цель.   Введение понятия десятичной дроби, разъяснение объективной необходимости изучения десятичных дробей. Формировать у учащихся умения записывать и читать десятичные дроби.

Ход урока.

I.    Организационный момент.

II.  Проверка домашнего задания.

III.      Объяснение нового материала.

Понятие положительной десятичной дроби.

На практике в повседневной жизни часто используются дроби и дробные числа, знаменатели которых выражаются единицей с одним или несколькими нулями:

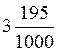 ; ; ;  и др.

Такие дроби условились записывать в строку без знаменателей, с помощью запятой.

Пример 1. Запишите в виде десятичной дроби:

1) 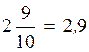 (Читают: две целых девять десятых);

2) 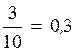 (Читают: нуль целых три десятых);

3) 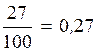 (Читают: нуль целых двадцать семь сотых);

4) 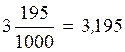 (Читают: три целых сто девяносто пять тысячных).

Числа 2,9; 0,3; 0,27; 3,195 и т.д., записанные таким способом, называют десятичными дробями. Обратите внимание, что коли-чество  цифр в числителе равно количеству нулей в знаменателе.

В записи десятичной дроби всегда есть целая и дробная часть. Их разделяет запятая. Налево от запятой записывают целую часть чис-ла, а справа от запятой записывают числитель дроби (знаменатель проговаривается, но не записывается).

У десятичных дробей, так же как и у натуральных чисел есть разряды.

Вспомним разряды у натуральных чисел. Число: 5 431. Его разряды:

Цифры, стоящие справа от запятой, называют десятичными знаками.

Первый десятичный знак (после запятой) означает число десятых, второй – число сотых, третий – число тысячных и т.д. Число: 3,195. Его разряды:

В рассмотренных примерах количество  цифр в числителе равно количеству нулей в знаменателе. Это правило всегда нужно соблюдать.

Если в числителе меньше цифр, чем нулей в знаменателе, то перед числителем пишут нули (этих разрядов в дроби нет).

IV. Закрепление изученного материала – 12 минут.

Прочитайте данные числа и запишите их в таблицу разрядов – устно:

Пример 2. Запишите в виде десятичной дроби:

1)  (Читают: одна целая три сотых);

2)  (Читают: две целых девять тысячных);

3)  (Читают: нуль целых четырнадцать тысячных);

4)  (Читают: нуль целых одна тысячная).

По числу десятичных знаков дроби можно назвать ее знаменатель.

Пример 3. Назвать знаменатель десятичной дроби:

1) 2,3         имеет 1 десятичный знак, то ее знаменатель 10;

2) 4,75       имеет 2 десятичных знака, то ее знаменатель 100;

3) 7,0025   имеет 42 десятичных знака, то ее знаменатель 10 000.

Решение упражнений. №724. Для (6а,6в,6г) №726  б (для 6б) Запишите обыкновенные и смешанные дроби в виде десятичных и прочитайте полученные записи – комментированный ответ у доски:

в)  – пять целых сто тридцать пять тысячных;

 – семнадцать целых триста девяносто девять тысячных;

 – восемь целых девятьсот девяносто девять тысячных;

 – нуль целых семьсот семьдесят семь тысячных;

 – нуль целых сто двадцать три тысячных;

 – нуль целых восемьдесят семь тысячных;

 – две целых одиннадцать тысячных.

Дополнительные при меры 734

IV.       Подведение итогов урока.

1. Какая дробь называется десятичной?

2. Как называются разряды десятичной дроби, стоящие от запятой слева? А справа?

3. Какова зависимость между количеством цифр после запятой в десятичной дроби и количеством нулей в знаменателей соответствующей обыкновенной дроби?

V.  Домашнее задание. п. 4.1 (выучить теорию). № 727(а,в), 726(а,в),    737 (первый и второй столбик).

VI.