Диагностическая работа по математике в форме ЕГЭ

1. Найдите зна­че­ние вы­ра­же­ния .

2. Найдите зна­че­ние про­из­ве­де­ния чисел  и .

3. Магазин детских товаров закупает погремушки по оптовой цене 80 рублей за одну штуку и продаёт с наценкой 60%. Сколько рублей будут стоить 2 такие погремушки, купленные в этом магазине?

4. Площадь прямоугольника равняется произведению половины квадрата диагонали и синуса угла между диагоналями. Найдите площадь прямоугольника, если длина диагонали равняется 4, а синус угла между диагоналями равен 0,5.

5. Найдите значение выражения .

6. На день рож­де­ния по­ла­га­ет­ся да­рить букет из нечётного числа цветов. Пионы стоят 40 руб­лей за штуку. У Вани есть 410 рублей. Из ка­ко­го наи­боль­ше­го числа пи­о­нов он может ку­пить букет Маше на день рождения?

7. Найдите корень уравнения .

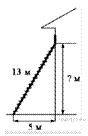
8. Пожарную лест­ни­цу дли­ной 13 м при­ста­ви­ли к окну дома (см. рисунок). Ниж­ний конец лест­ни­цы от­сто­ит от стены дома на 5 м. На какой вы­со­те рас­по­ло­же­но окно? Ответ дайте в метрах.

9. Установите со­от­вет­ствие между ве­ли­чи­на­ми и их воз­мож­ны­ми значениями: к каж­до­му эле­мен­ту пер­во­го столб­ца под­бе­ри­те со­от­вет­ству­ю­щий эле­мент из вто­ро­го столбца.

 В таб­ли­це под каж­дой буквой, со­от­вет­ству­ю­щей величине, ука­жи­те номер её воз­мож­но­го значения.

10. В чемпионате мира участвуют 12 команд, среди которых есть команда Канады. С помощью жребия их нужно разделить на четыре группы по три команды в каждой. В ящике вперемешку лежат карточки с номерами групп: 1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4. Капитаны команд тянут по одной карточке. Какова вероятность того, что команда Канады окажется в четвёртой группе?

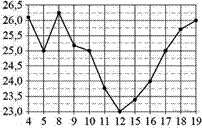
11. На ри­сун­ке жир­ны­ми точ­ка­ми по­ка­за­на цена нефти на мо­мент за­кры­тия бир­же­вых тор­гов во все ра­бо­чие дни с 4 по 19 ап­ре­ля 2002 года. По го­ри­зон­та­ли ука­зы­ва­ют­ся числа месяца, по вер­ти­ка­ли — цена бар­ре­ля нефти в дол­ла­рах США. Для на­гляд­но­сти жир­ные точки на ри­сун­ке со­еди­не­ны линиями. Опре­де­ли­те по ри­сун­ку наи­мень­шую цену нефти на мо­мент за­кры­тия тор­гов в пе­ри­од с 4 по 9 ап­ре­ля (в дол­ла­рах США за баррель).

 12. Семья из трёх человек планирует поехать из Москвы в Чебоксары. Можно ехать поездом, а можно — на своей машине. Билет на поезд на одного человека стоит 770 рублей. Автомобиль расходует 9 литров бензина на 100 километров пути, расстояние по шоссе равно 700 км, а цена бензина равна 19 рублей за литр. Сколько рублей придётся заплатить за наиболее дешёвую поездку на троих?

13. Найдите пло­щадь поверхности многогранника, изоб­ра­жен­но­го на ри­сун­ке (все дву­гран­ные углы прямые).

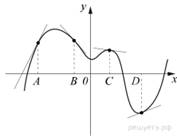14. На рисунке изображены график функции и касательные, проведённые к нему в точках с абсциссами A, B, C и D. В правом столбце указаны значения производной функции в точках A, B, C и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.

 В таблице под каждой буквой укажите соответствующий номер.

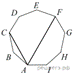15. ABCDEFGHI — правильный девятиугольник. Найдите угол CAF. Ответ дайте в градусах.

16. Сто­ро­ны ос­но­ва­ния пра­виль­ной ше­сти­уголь­ной пи­ра­ми­ды равны 14, бо­ко­вые рёбра равны 25. Най­ди­те пло­щадь бо­ко­вой по­верх­но­сти этой пирамиды.

17. На координатной прямой отмечено число т и точки А,В,С и D. Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами. Впишите в приведённую в ответе таблицу под каждой буквой соответствующий числу номер.

18. Если спортсмен, участ­ву­ю­щий в Олим­пий­ских играх, уста­но­вил ми­ро­вой рекорд, то его ре­зуль­тат яв­ля­ет­ся и олим­пий­ским рекордом. Вы­бе­ри­те утверждения, ко­то­рые сле­ду­ют из этого факта.

 1) Если ре­зуль­тат спортсмена, участ­ву­ю­ще­го в Олим­пий­ских играх, не яв­ля­ет­ся олим­пий­ским рекордом, то он не яв­ля­ет­ся и ми­ро­вым рекордом.

2) Если ре­зуль­тат спортсмена, участ­ву­ю­ще­го в Олим­пий­ских играх, является олим­пий­ским рекордом, то он яв­ля­ет­ся и ми­ро­вым рекордом.

3) Если ре­зуль­тат спортсмена, участ­ву­ю­ще­го в Олим­пий­ских играх, не яв­ля­ет­ся ми­ро­вым рекордом, то он не яв­ля­ет­ся и олим­пий­ским рекордом.

4) Если спортсмен, участ­ву­ю­щий в Олим­пий­ских играх, уста­но­вил ми­ро­вой ре­корд в беге на 100 м, то его ре­зуль­тат яв­ля­ет­ся и олим­пий­ским рекордом.

 В от­ве­те ука­жи­те но­ме­ра вы­бран­ных утвер­жде­ний без пробелов, за­пя­тых и дру­гих до­пол­ни­тель­ных символов.

19. Цифры четырёхзначного числа, крат­но­го 5, за­пи­са­ли в об­рат­ном по­ряд­ке и по­лу­чи­ли вто­рое четырёхзначное число. Затем из пер­во­го числа вычли вто­рое и по­лу­чи­ли 4536. При­ве­ди­те ровно один при­мер та­ко­го числа.

20. В кор­зи­не лежат 25 грибов: ры­жи­ки и грузди. Известно, что среди любых 11 гри­бов име­ет­ся хотя бы один рыжик, а среди любых 16 гри­бов хотя бы один груздь. Сколь­ко ры­жи­ков в корзине?