МГУ - ШКОЛЕ
М. К. Потапов А. В, Шевкин
Математика
 |
Дидактические материалы
класс
Учебное пособие для общеобразовательных организаций
13-е издание
Москва
«Просвещение»
2017
удк 373.167.1:516+ БЫС 22.1я72
Пб4
Серия «МГУ—школе» основана в 1999 году
Потапов М. К.
Пб4 Математика. Дидактические
материалы. 6 класс 
учеб. пособие для общеобразоват. организаций / М. К. Потапов, А. В.
Шевкин. 13-е изд. — М.
Просвещение, 2017. 128 с. : ил. — (МГУ — школе). 
ISBN 9786-09-045945-7.
Пособие содержит задания для подготовки к самостоятельным работам по основным темам учебника «Математика, 6» С. М. Никольского и др., а также самостоятельные и контрольные работы в четырёх вариантах.
удк 373.167.1:51 ББК 22.1я72
Учебное издание
Серия «МГУ—школе»
Потапов Михаил Константинович
Шевкин Александр Владимирович
Математика
Дидактические материалы
6 класс
Учебное пособие для общеобразовательных организаций
Центр естественно-математического образования Редакция математики и информатики
Зав. редакцией Т. А. Бурмистрова, редакторы Т. Г. Войлокова, О. В. Платонова, младший редактор Е. В. Трошко, художник О. П. Богомолова, художественный редактор О. П. Богомолова, компьютерная графика К. В. Кергелен, техническое редактирование и компьютерная вёрстка С. В. Китаевой, корректор М. Г. Волкова. Налоговая льгота Общероссийский классификатор продукции ОК 005-93— 953000. Изд. лиц. Серия ИД № 05824 от 12.09.01. Подписано в печать
25.07.16. Формат 60 х 90 1 /16 Бумага типографская. Гарнитура SchoolBook. Печать офсетная. Уч.-изд. л. 5,36. Доп. тираж 7000 экз. Заказ № 9503.
Акционерное общество «Издательство «Просвещение». 127521, Москва, 3-й проезд Марьиной рощи, 41.
Отпечатано в АО «Первая Образцовая типография», филиал «УЛЬЯНОВСКИИ
ДОМ ПЕЧАТИ». 432980, г. Ульяновск, ул. Гончарова, 14.
|
ISBN 9786-09-045945-7 |
С) Издательство «Просвещение», 2004 С) Издательство «Просвещение», 2014, с изменениями С) Художественное оформление. Издательство «Просвещение», 2 О 14 Все права защищены |
Предисловие
Дидактические материалы по курсу математики содержат 39 самостоятельных, 9 контрольных работ в четырёх вариантах и задания для самопроверки в восьми вариантах. Ко всем вариантам контрольных работ и заданий для самопроверки имеются ответы.
Содержание дидактических материалов полностью соответствует учебнику математики для 6 класса серии «МГУ — школе» и дополняет его более сложными заданиями, необходимыми для работы в классах, нацеленных на подготовку к обучению на повышенном уровне. Дидактические материалы можно использовать в классе и дома при работе по любым учебникам, а также для восполнения пробелов и самообразования.
К каждой самостоятельной работе в первой части книги даны примеры выполнения заданий, аналогичных заданиям, включённым в самостоятельную работу, но не повторяющих их. Работа с ними существенно повысит результативность выполнения самостоятельных и контрольных работ и усвоение темы в целом.
Темы, отмеченные в дидактических материалах звёздочкой, не являются обязательными для изучения в общеобразовательном классе. Темы «Вероятность события» , «Задачи на вычисление вероятности события», «Уравнения с модулями», «Решение задач с помощью уравнений», «Упрощение выражений», «Сложные задачи на проценты», «Использование вспомогательных букв при решении задач на проценты», «Практические задачи на проценты» предназначены для шестиклассников, которые любят решать сложные задачи.
Любые из самостоятельных работ учитель может использовать для контроля на отметку. Но при этом следует учесть, что самостоятельные и контрольные работы избыточны по объёму. Предполагается, что учитель самостоятельно отберёт из них часть заданий с учётом уровня подготовки учащихся по предмету и времени, отводимого на выполнение работы. Успехи в решении дополнительных задач можно оценивать дополнительной отметкой.
Задания вариантов III и IV несколько сложнее соответствующих заданий вариантов I и П. В сильных классах некоторые самостоятельные работы, отмеченные звёздочкой, можно провести как контрольные работы.
Материалы для подготовки к самостоятельным роботом
1. Масштаб
Пример 1. Масштаб карты 1 : 500 ООО. Расстояние между двумя сёлами на карте 5 см. Каково расстояние между этими сёлами на местности?
Решение. Масштаб карты 1 : 500 ООО означает, что реальное расстояние изображено на карте с уменьшением в 500 ООО раз. Поэтому расстояние между двумя сёлами на местности равно
5 см • 500 000 = 2 500 000 см = 25 000 м = 25 км.
Ответ. 25 км.
Пример 2. Расстояние между двумя городами 28 км. Каково расстояние между этими городами на карте, масштаб которой 1 : 200 ООО?
Решение. Масштаб карты 1 : 200 ООО означает, что реальное расстояние изображено на карте с уменьшением в 200 ООО раз. Поэтому расстояние между городами на карте
равно
28 км : 200 000 = 2 800 000 см : 200 000 = 14 см.
Ответ. 14 см.
Пример З. Расстояние между городами А и В равно 120 км. Расстояние между городами А и В на карте равно 6 см. Определим масштаб карты.
Решение. Масштаб карты это отношение расстояния на карте к соответствующему расстоянию на местности. Найдём это отношение, выразив расстояния в одних единицах длины:
6 см
: 120 км = 6 см : 120 ООО м = 6 см : 12 ООО ООО см 
1 : 2 000 000. Ответ.
1 : 2 ООО ООО.
Пример 4. а) Земельный участок на плане имеет вид прямоугольника со сторонами 4 см и З см. Определим площадь участка на местности, если масштаб карты равен 1 : 1000.
б) Земельный участок на плане имеет вид прямоугольника, площадь которого равна 12 см 2 . Определим площадь участка на местности, если масштаб карты равен 1 : 2000.
Решение. а) Сначала вычислим стороны участка на
местности:
4 см • 1000 = 4000 см = 40 м; З см 1000 = 3000 см = ЗО м.
Теперь вычислим площадь участка на
местности: 
1200 м— 12 а.
б) Стороны прямоугольника на плане не заданы, обозначим их а см и Ь см, тогда площадь участка на плане равна а см • Ь см = ab см 2 . Так как эта площадь равна 12 см 2 , то ab = 12.
Теперь вычислим длины сторон участка на местности:
а см • 2000 = 2000а см = 20а м; Ь см • 2000 = 2000b см = 20b м.
Теперь вычислим площадь участка
на местности: 20а м • 20b м = 400ab м 2
Так как ab = 12, то площадь участка на местности
равна
400ab 400 12 4800 48 а. Ответ. а) 12 а; б) 48 а.
2. Деление числа в данном отношении Пример 1. Разделим число 280 в отношении З : 4.
Решение. Представим число 280 в виде
суммы двух чисел, первое из которых составляет З части, а вто
4 такие же
части числа 280.
1) З 7 (частей) приходится на 280 единиц;
2) 280 : 7 40 (единиц) приходится на 1 часть;
З) 40 • З = 120 (единиц) приходится на первое число; 4) 40 • 4 = 160 (единиц) приходится на второе число. Ответ. 120 и 160.
Пример 2. Начертим отрезок АВ, длина которого 12 см. Разделим этот отрезок в отношении 1 : З.
Решение. На отрезке АВ 12 см отметим точку М (рис. 1) так, чтобы АМ : МВ 1 : З. Тогда на отрезки АМ и МВ приходятся 1 и З части соответственно.
Рис. 1
—4
(части) приходится на 12 см;
З (см) приходится на 1
часть (длина отрезка ТТ);
приходится на З части
(длина отрезка МВ).
Ответ. З см и 9 см.
Пример З. Разделим число 340 на З части
так, чтобы первая относилась ко второй как 1 : З, а вторая 
третьей как 2
: З.
Решение. Перепишем данные отношения так, чтобы второй член первого отношения был равен первому члену второго отношения: 1 : 2 : 6, 2 : 3 = 6 : 9. Представим число 340 в виде суммы трёх чисел, первое из которых составляет 2 части, второе 6 частей, а третье 9 частей числа 340.
1) 2 +6 +9 = 17 (частей) приходится на 340 единиц; 2) 340 : 17 = 20 (единиц) приходится на 1 часть;
З) 20 • 2 = 40 (единиц) 
приходится на первое
число; 4) 20 • 6 120 (единиц) 
приходится на второе число; 5) 20 • 9 =
180 (единиц) 
приходится на третье число. Ответ. 40,
120 и 180.
Пример 4. Мама хочет разделить 14 конфет между двумя детьми в отношении, обратном отношению их возрастов. Сколько конфет достанется брату, если ему З года, а его сестре 4 года?
Решение. Мама хочет
разделить 14 конфет в отношении, обратном отношению чисел З и 4, т. е. в
отношении 4 : З. Тот же результат получится, если конфеты разделить в
отношении, равном отношению чисел, обратных 4, т. е. в отношении 1 . 1 12 . 12
числам З и
1) 4 7 (частей) приходится на 14 конфет; 2) 14 : 7 = 2 (конфеты) приходится на 1 часть; З) 2 4 = 8 (конфет) досталось брату.
Ответ. 8 конфет.
З. Пропорции
Пример 1. Из чисел 24, 25, 72, 75 составим пропорцию.
Решение. Так как 75 : 25 = З и 72 : 24 = З, то составим пропорцию: 75 : 25 = 72 : 24.
Пример 2. Можно ли составить пропорцию из отно-
шений:
а) 15 : 11 и 45 : 33; б) 18 : 25 и 36 : 45?
Решение. а) Так как после умножения членов отношения 15 : 11 на З получится равное ему отношение 45 : 33, то пропорцию составить можно: 15 : 11 = 45 : 33.
б) Так как после умножения членов отношения 18 : 25 на 2 получится равное ему отношение 36 : 50, но не равное отношению 36 : 45, то из отношений 18 : 25 и 36 : 45 пропорцию составить нельзя.
Пример З. Решим пропорцию: а) 6) х : 17 - 12 : 51.
5 12'
Решение. Для решения каждой пропорции воспользуемся основным свойством пропорции: в пропорции произведение крайних членов равно произведению средних членов.
а)
5 12 '
|
12х = 25, |
х |
17,12 51 |
|
25 х |
х |
17,4 |
|
12 |
|
17 |
|
|
х |
4. |
12х - 5 • 5, 51х = 17 • 12,
12
Ответ. а) 2 2 ;
12
Пример
4. Решим пропорцию 2! х : 5 1 з . 14
2 11 • 17
Решение. По основному
свойству пропорции имеем
2
2 з
4
 |
Ответ. з
4
4. Понятие о проценте
Пример 1. На предприятии работает 120 человек, 15 0/0 из них получили премию. Сколько человек получили премию?
Решение. Найдём 15 % числа 120:
120•15 6•15
— 18
(человек) получили премию.
100 5
Ответ. 18 человек.
Пример 2. Найдём число, 45 % которого равны 27.
Решение. Так как 45 % числа равны 27, то 1 % этого
27
числа равен , а само число в 100 раз больше:
27 • 100 з • 100
60. 5
Ответ. 60.
Пример З. Сколько процентов числа 35 составляет число 14?
Решение. Число 14 составляет 14 числа 35. Выразим
35 эту долю в процентах:
14 100 2 • 100 - 40 ( 0/0).
35 5
Ответ. 40 0/0 .
Пример 4. Найдём число, 30 % которого равны 12 % числа 25.
Решение. Сначала найдём 12 % числа 25.
25•12 1,12 0
1) это число составляет 30 /0 неиз100 4 вестного числа;
з • 100
2) -10 неизвестное число.
зо
Ответ. 10.
5. Задачи но проценты
Пример 1. Вчера туристы проехали на автобусе 420 км, а сегодня на 10 % меньше. Сколько километров они проехали за два дня?
420 • 10
Решение. I способ. 1) = 42 (км) на столько
100 километров сегодня туристы проехали меньше;
2) 420 - 42 = 378 (км) проехали туристы сегодня;
3) 420+ 378 = 798 (км) — проехали туристы за два дня.
П способ. 1) 100- 10=90 ( 0/0 ) составляет сегодняшний путь от вчерашнего;
420 90
2) -378 (км) проехали туристы сегодня;
100
3) 420 + 378 = 798 (км) проехали туристы за два дня.
Ответ. 798 км.
Пример 2, Задумали число, уменьшили его на 35 % и получили 130. Какое число задумали?
Решение. 1) 100 — 35 = 65 ( 0/0 ) составляет число 130 от задуманного;
130,100
2) - 200 задуманное число.
65
Ответ. 200.
Пример З. На сколько процентов число 50 больше, чем число 40?
Решение. Число 50 сравнивают с числом 40. Число 40 составляет 100 % самого себя. Найдём, сколько процентов число 50 составляет от числа 40.
50 • 100 0
1) -125 ( /0) — составляет число 50 от числа 40;
2) 125- 100=25 ( 0/0 ) на столько процентов число 50 больше, чем число 40.
Ответ. На 25 % .
• Замечание. Если наше решение записать с помощью числового выражения
125 - = 50 • 100 - 100 - 50•100 40,100 _ (50-40) • 100
40
то его можно обобщить: чтобы найти, на сколько процентов
число а больше числа Ь, надо их разность (а — Ь) разДелить на Ь (число, с
которым сравнивают) и результат умножить на 100: 
а о.
Пример 4. На сколько процентов число 40 меньше, чем число 50?
Решение. Число 40 сравнивают с числом 50. Число 50 составляет 100 0/0 самого себя. Найдём, сколько процентов число 40 составляет от числа 50.
|
|
100 |
1)
80 ( 0/0 ) 
составляет число 40 от числа 50;
50
2)
100 - 80 = 20 (0/0) 
на столько процентов число 40 меньше, чем
число 50. Ответ. На 20 % .
• Замечание. Если наше решение записать с помощью числового выражения
100 - 80 - 40 100 50-100 _ 40,100 _ (50-40), 100
50 50 50 50 то его можно обобщить: чтобы найти, на сколько процентов число Ь меньше числа а, наДо их разность (а — Ь) разДелить на а (число, с которым сравнивают) и резуль-
тат умножить на 100: (а — Ь) • 1000 
а
Вероятность события
Пример 1. Сколько имеется четырёхзначных чисел, в записи которых есть цифры О, 1, 2, З:
а) без повторения цифр; б) с повторением цифр?
Решение. а) В старшем разряде четырёхзначного числа (в разряде тысяч) не может стоять О, следовательно, имеется три возможности поставить одну из цифр 1, 2, З в старший разряд. В следующем разряде (сотен) можно написать любую из трёх оставшихся цифр. Следовательно, две первые цифры в записи числа можно поставить З • З = 9 способами.
Две оставшиеся цифры можно поставить в оставшиеся разряды 2 • 1 2 способами.
Итак, можно написать З • З • 2 • 1 — 18 чисел.
б) В старшем разряде четырёхзначного
числа (в разряде тысяч) не может стоять О, следовательно, имеется три
возможности поставить одну из цифр 1, 2, З в старший разряд. В каждом следующем
можно написать любую из четырёх цифр. Следовательно, можно написать 
192
числа.
Ответ. а) 18 чисел; б) 192 числа.
Пример 2. Подбросили игральный кубик. Какова вероятность того, что выпадет:
а) 5 или 6 очков; б) 11 очков?
Решение. а) Всех равновозможных исходов 6: может выпасть 1, 2, З, 4, 5 или 6 очков. Только два из них
благоприятствуют событию «выпадет 5 или 6 очков». По-
2 1
этому вероятность события равна 
б) Событие «выпало 11 очков» невозможное. Его вероятность равна О.
1 Ответ. а) 
з
Пример З. Какова вероятность того, что при подбрасывании игрального кубика два раза сначала выпадет чётная сумма, а потом нечётная?
Решение. Всех возможных исходов опыта 4. Выпадет:
1) сначала чётная сумма, потом чётная;
2) сначала чётная сумма, потом нечётная; З) сначала нечётная сумма, потом чётная;
4) сначала нечётная сумма, потом нечётная.
Из них только один благоприятствует событию «сначала выпадет чётная сумма, потом нечётная», поэтому ве-
1
роятность этого события равна
4 1 Ответ. 
4
Пример 4. Случайным образом из натуральных чисел от 33 до 57 выбрали одно число. Какова вероятность того, что оно делится на 7?
Решение. Выпишем все натуральные числа от 33 до 57:
33, 34, 56, 57.
Их 57 — 32 = 25. Среди них есть числа, делящиеся на 7. Это числа 35, 42, 49, 56 их 4. Поэтому вероят-
4
ность события равна
25
4
Ответ. 
25
Задачи на вычисление вероятности события
Пример 1. В игре «Морской бой» на поле 10 располагают 1 четырёхпалубный корабль (4 клетки), 2 трёхпалубных корабля (по З клетки), З двухпалубных корабля (по 2 клетки) и 4 однопалубных корабля (по 1 клетке). Один из способов размещения кораблей показан на рисунке 2. Какова вероятность того, что игрок, не видя размещения кораблей на игровом поле и сделав один выстрел (назвав координаты одной клетки), попадёт хотя бы в один корабль?
Решение. Всего на
игровом 10 поле 10 • 10 = 100 клеток. Кораб- 9
ли занимают 8
= 20 клеток. 7 6 Следовательно,
вероятность 5 одним выстрелом попасть хотя 4
бы в один
корабль равна 20 
1 • з
100 5
2
1
Ответ.
1
5
|
Пример 2, В шкафу есть 4 вертикальных ряда по 5 ящиков в каждом. В один из ящиков в |
Рис. 2 |
каждом ряду спрятали по одной монете. Какова вероятность того, что, выдвинув случайным образом по одному ящику в каждом ряду, можно найти монеты в двух первых рядах и не найти в остальных?
Решение. В каждом из четырёх рядов можно выдвинуть один ящик пятью способами, поэтому всего имеется 5 • 5 5 5 625 способов выдвинуть по одному ящику в каждом из четырёх рядов. Из них имеется по одному способу найти монету в первом и во втором рядах и по четыре способа не найти монету в третьем и в четвёртом рядах. Всего 1 • 1 • 4 • 4 = 16 способов. Следовательно, вероятность найти монеты в двух первых рядах и не найти в
16
остальных
равна 
625
Ответ. 16
625'
Пример З. Учитель запланировал проверить две домашние работы из пяти на текущей неделе. Эти две работы он выбирает случайным образом и за невыполнение домашней работы ставит в журнал отметку «1». Определите вероятность события:
а) А — «Аня получит «1», если она не выполнит одну домашнюю работу из этих пяти;
б) В — «Боря получит ровно одну «1», если он не выполнит две домашние работы из этих пяти; в) С — «Вася получит хотя бы одну «1», если он не выполнит две домашние работы из этих пяти.
Решение. Если пронумеровать домашние задания от 1 до 5, то все возможности выбора учителем двух домашних работ можно изобразить на схеме 1.
Схема 1
12 13 14 15
23 24 25
35
45
Учитель может выбрать две домашние работы десятью способами.
а) Если Аня не выполнит одну домашнюю работу из этих пяти, например первую (для других номеров работ решение аналогично), то имеется 4 случая из 10 (на схеме 2 эти случаи выделены жирным шрифтом), что её невыполненная работа попадёт на проверку к учителю. Сле-
4 2
довательно, вероятность события А равна •
10 5 Схема 2
12 13 14 15
23 24 25
35
б) Если Боря не выполнит две домашние работы из этих пяти, например первую и вторую (для других номеров работ решение аналогично), то имеется 6 случаев из 10 (на схеме З эти случаи выделены жирным шрифтом), что ровно одна его невыполненная работа попадёт на проверку к учителю. Следовательно, вероятность события В
6 з
равна •
10 5
Схема З
12 13 14 15
23 24 25
35
45
в) Если Вася не выполнит две домашние работы из этих пяти, например первую и вторую, то имеется 7 случаев из 10 (к выделенным на схеме З случаям добавится случай 12), что одна или две его невыполненные работы попадут на проверку к учителю. Следовательно, вероят-
7
ность события С равна
10
2 з 7
Ответ.
а) в) 
5 ' 5 10
13
8, Модуль целого число. Сравнение целых чисел
Пример 1. Запишем числа,
противоположные числам: 
13; о.
Решение. Выпишем пары противоположных чисел: +12 И —12; 13 и +13; о и о.
Пример 2. Определим модули чисел: +14; —25; О.
Решение. Модуль положительного числа равен самому числу: = +14; модуль отрицательного числа равен числу, ему противоположному: l—251 = +25; модуль нуля равен нулю: = О.
Пример З. Упростим записи чисел: —(+16);
Решение. Число, противоположное числу +16, есть —16, поэтому —(+16) —16; число, противоположное числу —23, есть +23, поэтому —(—23) = + 23; число +(—17) есть — 17, поэтому +(—17) =-17.
Пример 4. Сравним числа:
а) +12 и О; б) —13 и О;
г) —15 и —16.
Решение. а) Положительное число больше нуля, поэтому +12 > О;
б) отрицательное число меньше нуля, поэтому —13 < О;
в) отрицательное число меньше положительного числа, поэтому —14 < + 13;
г) из двух отрицательных чисел больше то, у которого модуль меньше, поэтому из неравенства 1—151 < 1—161 следует, что —15 > —16.
Пример 5. Сколько целых чисел расположено между числами —12 и +15?
Решение. Между числами —12 и +15 расположены числа:
-11, 10, +13, +14.
Из них 14 положительных, один нуль и 11 отрицательных. Всего 14 + 1 + 11 = 26 чисел.
9. Сложение и вычитание целых чисел
Пример 1. Вычислим:
а) 15 (—12); б) —14 + (—16);
в) 25 + (-33); г) -13 + (-25).
Решение. а) 15 + (—12) = +(15 — 12) = +3 - 3; 
—
— (14 -4- 16) -30; в) 25 + (-33) - -(33 - 25) -8;
г) -13 + (-25) -(13 + 25) - -38.
Пример 2. Вычислим:
а) 23 - (-41); 6) -23 - (-18);
в) 25 - (-29); г) -26 - (-35).
Решение. а) 23 — (—41) = 23 + 41 = 64; 6) -23 - (-18) - 23 + 18 - -(23 - 18) - 5;
в) 25 - (-29) = 25 + 29 = 54;
г) -26 - (-35) - -26 + 35 = +(35 - 26) -
Пример З. Вычислим:
а) 33 + (-22); 6) -42 - (-23);
в) -15 + (-49); г) -31 - 35.
Решение. а) 33 + (-22) = +(33 - 22) - 11;
6) -42 - (-23) 42 + 23 -(42 - 23) = -19;
— (15 + 49) —
г) -31 - 35 
-(31 + 35) -66.
Пример 4. Вычислим:
а) 33 + (-24) - (-12); 6) -36 - (-28) + (-32).
Решение. Выполним вычисления по действиям:
а) 33 + (-24) - (-12) = 21.
1) 33 + (-24) = +(33 - 24) 9;
6) -36 - (-28) + (-32)
1) -36 - (-28) -36 + 28 -(36 28) = -8; 2) -8 + (-32) 
-40.
Пример 5. Вычислим:
-33 + (-32) + (-31) + . . + 32 + 33 + 34.
Решение. Заметим, что в этой сумме есть пары противоположных слагаемых, дающие в сумме нуль, и ещё число нуль:
-33 + (-32) + (-31)+ + 32 + 33 + 34
(—33 + 33) + (—32 + 32) + + (—1 + 1) + О +
34 = О 34 = 34.
10. Умножение и деление целых чисел
Пример 1. Вычислим:
а) -15 , 6; 6)
-11 • (-3 2 );
г) -43 •
д) -99
15
Решение. а) —15 • 6 = —(15 • 6) = —90; 6) -11 • (-32) +(11 32) = 352;
в) зо = -(30 9) 270;
г) —43 • — +43 = 43;
-11.
Пример 2. Вычислим:
а) 72 : (-24); 6)
-96
в) -51 : 17;
г)
—98 : 1; д) О : (—37); е) 49 :
Решение. а) 72 : (—24) — -(72 : 24) з; 6) -96 : = +(96 : 8) - 12;
в) -51 : 17 - : 17) - —3;
г) —98 : 1 -98;
д) о : (-37) = о;
е) 49 : = — (49 : 1) — 49.
Пример З. Вычислим:
а) 
6) -61 : (-61); в) —40 • г)
-37 : 37.
Решение. а) 42 • (—10) -420; 6) -61 : (-61) = 1;
в) -40 = +(40 • 9) = 360;
г) -37 : 37 -(37 : 37) - -1.
Пример 4. Найдём значение выражения:
а) 180 : (-624 : 312 , 45); 6) -999 : : (-111).
Решение.
а) 180 : (-624 : 312 • 45) - -2.
1) -624 : 312 -2;
2) -2 • 45 -90;
3) 180 : (-90) 2.
6) -999 : :
(-111)
1) -999 : = +(999 : 3) = 333; 2) 333 : (-111) - -3.
Пример 5. Найдём значение выражения
41 • (—42) • (—43) • 44 • (—45) : 45 : (—44) : 43 : 42.
Решение. Значение данного числового
выражения 
число положительное, так как оно содержит
множителями или делителями четыре отрицательных числа. Вычисляя модуль
результата, мы 41 умножим на 42, на 43, на 44, на 45, а потом разделим
полученное произведение на те же числа, поэтому значение данного числового
выражения есть число 41. Ответ. 41.
11. Действия с целыми числами
Пример 1.
Найдём значение выражениях49 з
(98 - 49 • (-3) - 42) : (-7).147
Решение. 1) 49 • (—3) — -147;
2) 98 - (-147) 98 + 147 = 245;
3) 245 - 42 203;14 129
4) 203 : = -29.63 63
Ответ. —29.
Пример 2. Найдём значение выражения -630 : (-28 + 7) • 2- 70.
Решение.
1) -28 + 7 = -21; 2) -630 : (-21) = 30;
3) 30 • 2=60; 4) 60 - 70 = - 60) = -10.
Ответ. —10.
Пример З. Найдём значение выражения 340 - 66 : (-8 + 2) • (-12).
Решение.12
х
11
—6; 2) 66 : =
11; 12
3) -11 • (-12) - 132; 4) 340 - 132 - 208.12
Ответ. 208.132
Пример 4. Найдём значение выражения
-840 : (36
54 : • 4.
Решение.
1) 54 : —6; 2) 36 
+6 — 42 ; 3) -840 : 42
-20; 4) -20 , 4 = -80.
Ответ. —80.
Пример 5. При каком значении а не имеет смысла выражение
100 : ((-48 . • 13 + а)?
Решение.
1) -48 : 6 -8; 2)
3) -3 • 13 - -39.
Чтобы данное выражение не имело смысла, делитель —39 + а должен равняться нулю. Это возможно лишь при а = 39.
Ответ. При а 39.
12. Представление целых чисел но координатной прямой
Пример 1. Запишем координаты точек А, В, С и D, изображённых на рисунке З. Определим расстояния ОВ, ОД ВО.
—4 —1 о 1 З
Рис. З
Решение. Точки А, В, С и D имеют координаты —6, З, 4 и —4 соответственно: А (—6), В(З), С(4) и D(—4).
• Обобщения. 1. Расстояние от точки В(Ь) до начала координат О (О) равно lbl.
2. Расстояние между точками В(Ь) и С(с) равно ф — с!.
Пример 2. Изобразим координатную ось и отметим на ней точки О (О), М (5), (—8), К (—10) и L (—6). Определим расстояния 0L и МАТ .
Решение. Изобразим на координатной оси
(рис. 4) точки О (О), М (5), (—8), К (—10)
-10 -8 —6 -1 о 1 5
Рис. 4
Определим расстояния:
OL = l-61 = 6; млт = - = l5 + = 13.
Пример З. Различные точки заданы своими координатами: О (О), М (т), (п). Определим знак числа т, если ОМ и т < п.
Решение. Если число т положительное, то из неравенства т < п следует, что число п положительное и ОМ < ОЛТ , что противоречит условию задачи. Следовательно, т число неположительное.
Число т не может быть нулём, так как точки О и М различны, следовательно, т число отрицательное.
Пример 4. Определим координату точки М отрезка о, если А (-5) и В(11) и дм: мв = 1 : з.
Решение. Разделим длину отрезка АВ в отношении
1) д 1 - (-5)l— Д 1 + 5' = 16 (ед.) длина отрезка АВ; 2) 1 + 3 = 4 (части) — приходится на 16 единиц; З) 16 : 4 =4 (ед.) приходится на 1 часть. Итак, длина отрезка АМ равна 4.
Так как координата точки М больше —5, то
она равна 
5 +4 =-1.
Ответ. —1.
13. Рациональные числа
Пример 1. Запишем числа, противоположные числам:
1 з
4 8
Решение. и 1 з
з противопо-
4 4 8 8 ложные числа.
Пример 2. Упростим записи чисел: 32), 4).
7
Решение.
+ — 2 4) 4
3' 7
Пример З. Определим
модули чисел
9
Решение. + Д _ _5
11 11'
Пример 4. Запишем число 23 в виде дроби с отри-
24
цательным числителем.
23 -23 Решение.
24 24
Пример 5. Сократим дробь: а) -36 6) -35
42
Решение. а)
-35 б)
-49
Пример 6. Приведём к знаменателю 100 дроби:
6. з
5
6•
20 120
Решение.
5 5 5-20 100'
—3 3\25 3,25 75
—4 4 4 •25 100 •
Пример 7.
Запишем числа: 13 -22
— 14 27' виде дробей с положительными знаменателями.
13 13
-22 22
Решение.
14 -27
27'
14. Сравнение рациональных чисел
Пример 1. Сравним числа:
а) 6) -11 11
17 -17 15 -15
Решение. а) 
6) -11 -11
• (-1) 11 • 17 -1,17 -17' 15 -15
Пример 2. Сравним числа:
6)
11 11
Решение. а) — 
Так как из двух дробей
с общим положительным знаменателем больше та, у которой
числитель больше и —5 < —3, то 
поэтому
Дроби можно сравнить и по другому правилу: из двух отрицательных чисел больше то, у которого модуль мень-
3 5 з
ше: поэтому
б) Так как 2 > —3, то
11 11
Дроби можно сравнить и по другому правилу: любая положительная дробь больше любой отрицательной. Так
как —>О, — <О, то 
11 11 11 11
Пример З. Сравним числа:
|
а) |
29 |
6) |
37 |
31 |
51 |
|
|
50 |
|
73 |
35 |
|
Решение. Сравним дроби по правилам: любая положительная дробь больше нуля, любая отрицательная дробь меньше нуля, любая положительная дробь больше любой отрицательной:
|
а) |
6) |
в)• |
|
50 |
73 |
35 64 |
Пример 4. Сравним числа:
15
-16
Решение. а)12 ' так
как —9 >
—16, то 
12 12
Дроби можно сравнить и по другому
правилу: если 
и Ь > с, то а > с.
Так как — >—1 и
13 -13
6) ' так
как
—16, то
зо зо 15 15,2 зо
-13 —16 поэтому зо зозо 15
Дроби можно сравнить и по другому правилу: если a > b и b > c, то а > с.
поэтому •
зо 15
16-21
Так как
56 '56
-16 >
-21, то поэтому
56 56
Пример 5. Найдём все несократимые дроби со
знаменателем 5, заключённые между числами
Решение. Решим задачу полным перебором
дробей со знаменателем 5, заключённых между дробями
Так как
то имеется только три несократимые дроби со знаменателем 5, заключённые между дробями Это
15. Сложение рациональных чисел
Пример 1. Выполним сложение:
11
15 15'
-12 12
13 13'
Пример 2. Выполним сложение:
а) 11
6) 19
56
в) -21 22 
21 + 22 
120 120 120 120
Пример З. Выполним сложение и упростим ответ:
Решение.
38 -33 38 -33
90 90 90 90 18
Пример 4. Найдём значение числового выражения
|
10 |
-12
16 16 16
16 16 16 •
16. Вычитание рациональных чисел
Пример 1. Выполним вычитание:
13 17 17 18 а) б) в)
27 27 ' 19 19
-2-5
6)
27 27 27 27
18
-17+18 
в)
19 19
Пример 2. Выполним вычитание: а) 
в) 
10 8-10
Решение.
15 з 15 15 15 15 15 '
-14+5
35 35 35 35 '
-49 
-49+2
|
Пример З. Выполним вычитание 96 |
и упростим |
ответ: |
|
11 43 22 43 22-43 Решение. |
-21 7-3 |
|
|
48 96 96 96 96 |
96 3,32 |
32 |
84 84 84 84
Пример 4. Найдём значение числового выражения
25+15-9 31
Решение.
50 50
17. Умножение рациональных чисел
Пример 1. Выполним умножение:
а) 
13
Решение. 
6) 
в) 
2 4-2 
13 13 1 13,1 13
Пример 2. Выполним умножение и упростим ответ:
Пример З. Выполним умножение и упростим ответ:
Решение.
Пример 4. Подберём такую несократимую дробь для которой верно равенство
—1 • (—1) 
1, поэтому
Теперь очевидно, что
18. Деление рациональных чисел
Пример 1. Выполним деление:
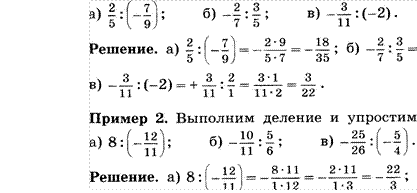
б)
11 11,1
25,4 5-
2 10
в)
26,5 13,1 13
Пример З. Выполним деление и упростим ответ:
Решение.
Пример 4. Выполним деление и упростим ответ:
25
а)
26
Решение. а) —
26
• 1 26
19. Смешанные дроби
Пример 1. Запишем в виде смешанной дроби обыкновенную дробь:
15-3347
б)
в)
-33
Решение. а)
6)
в)
Пример 2. Запишем в виде обыкновенной дроби смешанную дробь:
Решение.
а) 3? — б) —32 
13 13 13
8•1+7 15
Пример З. Вычислим:
' 6) 4 - 1! ; в) -4 , 5 7
6 зо 10
Решение.
Пример 4. Вычислим, применяя распределительный закон:
Решение.
6?-32-62.42-6?
10 10
5. Вычислим, применяя распределительный
Пример
закон:
3! , 5! + —3!
• 32—22.31
.з2-2!.з!
Решение. 
. 52-35
20. Действия с рациональными числами
Пример 1. Найдём значение выражения 3 + —
Решение. З + —
-3-1=2.
Пример 2. Найдём значение выражения
13,4
Пример З. Найдём значение выражения
Пример 4. Найдём значение выражения
Пример 5. Найдём значение выражения
21. Представление рациональных чисел на координатной прямой
Пример 1. Запишем координаты точек А, В, С и D, изображённых на рисунке 5.
Рис. 5
Решение. Единичный отрезок разделён на 4 равные части, поэтому координаты точек А, В, С и D равны соответственно 1 —,
Ответ. А 1! , В
Пример 2. Изобразим координатную ось,
выбрав удобный единичный отрезок, и отметим на ней точки О (О), м 1! , лт -12
, к
Определим:
а) расстояние МК;
б) координату середины отрезка МК.
Решение. Возьмём единичный отрезок в 6
клеток и отметим на координатной оси точки О, М, N, К и L, учитывая, что —1— 
(рис.
6).
Рис. 6
Для проверки определим по рисунку 6, что расстояние МК содержит 10 отрезков по единицы, это
10 5 1? единичного отрезка.
б) Координата середины отрезка МК есть среднее арифметическое координат его концов, т. е. чисел 1— и
Для проверки определим по рисунку 6, что половина расстояния МК содержит 5 отрезков по единицы. От1
ступив от точки М влево 5 отрезков по единицы, полу6
2 1
чим точку с координатой
Пример З. Вычислим среднее арифметическое чисел:
а) 13 и 19; 6) 13, 15 и 20.
Решение. а) Среднее арифметическое чисел 13 и 19
13+19
равно -16.
2
б) Среднее арифметическое чисел 13, 15 и 20 равно
13+15+20
—16. з
Пример 4. Среднее арифметическое двух рациональных чисел т и п больше нуля. Сравним модули чисел т и п, если известно, что т п > О.
Решение. Среднее арифметическое двух рациональ-
ных чисел т и п есть По условию задачи эта дробь
2 больше нуля и 2 > О, поэтому т + п > О. Так как сумма двух чисел с разными знаками положительна, то модуль положительного числа больше модуля отрицательного числа, т. е. т < п].
Пример 5. Определим координату точки М отрезка
АВ, если А —1!
4
Решение.
1) 4! — (ед.) — дли-
на отрезка АВ;
2) З + 4 = 7 (частей) приходится на — 49 ед.;
8
7
—
(ед.) приходится на 1 часть;
8 8
21
4) 29
(ед.) приходится на АЛЛ.
8
Так как координата точки М больше, чем -1-1 то 4 '
она равна 1—+22
4 8 8
Ответ.
8
22. Уравнения
Пример 1. Определим, какое из чисел 1, 6, —2 является корнем уравнения
2х+6- 15.
Решение. Если х = 1, то 2х + (5 — 7 х) = 2 • 1 + (5 — 7 • 1) = = 0 $ 15.
Если х = б, то 2х+6- 
12+ 5 - 42 —
—25 15.
Если х- -2, то 2х+6-
15.
Из чисел 1, 6, —2 только число —2 является корнем уравнения.
Ответ. —2.
Пример 2. Решим уравнение:
6) 3х + - зх)
Решение.
-3х + 19,
5х + 3х + 3 — 19
З =
19, 20 - 9х = -7,
8х = 19 - з, -9х = -7 - 20, 8х = 16, -9х = -27, х- 16
: 8, х = —27 : 
Ответ. а) 2; б) З.
Пример З. Решим уравнение —х + 1 
Решение. Раскроем скобки в правой части уравнения:
1
12 •
Умножим обе части уравнения на наименьшее общее кратное знаменателей дробей, т. е. на число 12:
12 1212
— Х + 12 =
з 2 12 '
4х + 12 = 6х— 1,
4х- 6х+ 12--1,
-2х=-1 - 12, -2х = -13, х -13 : (-2),
2
Ответ.
2
зо
5х-7 2х-1
Пример 4. Решим уравнение 1 . з 2
Решение. Умножим обе части уравнения на наименьшее общее кратное знаменателей дробей, т. е. на число 6:
з 2
2(5х - 7) - 3(2х- 1) = 6,
10х- 14- 6х+3= 6,
11 = 6,
6 + 11, 4х = 17, х 17 : 4,
4
1
Ответ. 4— 
4
23*. Уравнения с модулями
Пример 1. Решим уравнение:
а) рх- 11 = 3; 6) 17х-81- з; в) 15х + 2' = О.
Решение. а) Модуль числа равен З лишь в двух случаях: если это число равно либо —3, либо З:
1) 2х- 1 - —3 или 2) 2х — 1 = З.
Решив каждое из этих уравнений, получим, что корень уравнения 1) равен —1, а корень уравнения 2) равен 2. Следовательно, уравнение 12х — 11 = З имеет два корня: —1 и 2.
б) Так как ни при каком значении х модуль числа не равен отрицательному числу, то уравнение 7х — 8' = -3 не имеет корней.
в) Модуль числа равен О лишь в одном случае: если это число равно О.
+ 21 = О,
5х + 2 = 0,
2 х
2
Ответ. а) —1; 2; б) нет корней; в)
Пример 2. Решим уравнение 8 — 15х — 71 = 1.
Решение. Прибавим к обеим частям уравнения чис-
-5х- 7 = 1 -8,
-5х- 7
Умножим обе части уравнения на число —1:
Модуль числа равен 7 лишь в двух случаях: если это число равно либо —7, либо 7:
1) 5х- 7 —7 или 2) 5х — 7.
Решив каждое из этих уравнений, получим, что корень уравнения 1) равен О, а корень уравнения 2) равен
Следовательно, уравнение 8 — l5x — 7' = 1
имеет два
5 корня: О и 2! .
5
Ответ. О; 2 4
5
Пример З. Решим уравнение — 121 — 2' = 5.
Решение. Модуль числа равен 5 лишь в двух случаях: если это число равно либо —5, либо 5:
—5 или 2) 1х — 121 — 2 — 5, х- 121 =
5 + 2, 
х- 121 = 7.
Уравнение 1) не имеет корней, так как ни при каком значении х модуль числа не равен отрицательному числу.
Чтобы решить уравнение 2), надо найти корни каждого из уравнений:
3) х- 12= 7 и 4) х - 12
Решив каждое из этих уравнений, получим, что корень уравнения З) равен 19, а корень уравнения 4) равен 5.
Ответ. 5; 19.
Пример 4. Решим уравнение ll12x + 51 + 21 — 5' 6.
Решение. Заметим, что для любого значения х число l2x + + 2 положительно, поэтому данное уравнение можно переписать в виде
112x + - з! = 6.
Модуль числа равен 6 лишь в двух случаях: если это число равно либо —6, либо 6:
1) рх+ 51 - 3 —6 или 2) + 51 6,
32
Уравнение 1) не имеет корня, так как ни при каком значении х модуль числа не равен отрицательному числу. Чтобы решить уравнение 2), надо найти корни каждого из уравнений:
З) 2х+5
Решив каждое из этих уравнений, получим, что корень уравнения З) равен —7, а корень уравнения 4) ра-
корня: —7 и 2. Значит, и уравнение |l12x + + 2' — 51 = 6 имеет два корня: —7 и 2. Ответ. —7; 2.
24*. Решение задач с помощью уравнений
Пример 1. Обозначим одну неизвестную величину буквой х, выразим через х другую неизвестную величину, составим уравнение по условию задачи:
а) Одно число в 9 раз больше другого, а их сумма равна 180. Найдём меньшее число.
б) Одно число в 10 раз больше другого, а их разность равна 180. Найдём большее число.
в) Брат на З года старше сестры, а сумма их возрастов 21 год. Сколько лет сестре?
Решение. а) Пусть х меньшее число, тогда 9х 
большее число.
Их сумма равна 180. Составим уравнение: х + 180.
б) Пусть х меньшее число, тогда 10х большее число. Их разность равна 180. Составим уравнение: 10х-х= 180.
в) Пусть х лет — возраст сестры, тогда (х + З) лет — возраст брата. Сумма их возрастов равна 21. Составим
уравнение:
Х + (Х З) = 21.
Пример 2. Решим задачу с помощью уравнения.
Гайка тяжелее шайбы на 2 г, а 8 гаек и 10 шайб весят 52 г. Сколько весит одна гайка?
Решение. Пусть х г весит шайба, тогда (х + 2) г весит гайка. 8 гаек и 10 шайб весят 52 г. Составим уравнение: 10х + + 2) = 52.
Это уравнение имеет единственный корень 2, следовательно, гайка весит 2 + 2 = 4 (г). Ответ. 4 г.
Пример З. Решим задачу с помощью уравнения.
На первой полке стояло 10 книг, а на второй половина числа книг, стоявших на первой и третьей полках вместе. Всего на трёх полках стояло 39 книг. Сколько книг стояло на второй полке?
Решение. Пусть х книг стояло на третьей полке, тог-
да на второй полке стояло книг. Составим уравне-
2 ние: 10 + х +
39. Это уравнение имеет
единственный
2 корень 16, следовательно, на второй полке стояло
16+10
—13 (книг).
2
Ответ. 13 книг.
25*. Упрощение выражений
Пример 1. Приведём подобные слагаемые:
а) 7 а + Па; 6) 12а - 15а; в) —8а + 7 а;
г) —11 а — 16а; д) 4а — а; е) а + Па.
Решение. а) 7а + 11 а = (7 + 11)а = 18а;
6) 120 - 15а = (12 - 15)а — -за;
—с,
г) -11а - 16а = (-11 - 16)а -27а•,
д) 4а — а = (4 — 1)а = За;
е) а + 11а = (1 + 12а.
Пример 2. Упростим выражение:
а) 7 Ь + 8
+ 11 Ь— 1; 6) Ь- 5+ 36-6; в) -8b-9 +(b+ 3); 
Решение.
а) 7b + 8 + 116 1 (7 + 11)b + 7 = 186 + 7; 6) Ь - 5 + ЗЬ - 6-(1 + ЗУ- 11 = 46- 11;
д) 86 + 5(b- 2) - 86 + 5b -
е) 6b - 2(ЗЬ - - 6b+ 10 = 10.
Пример З. Задумали число, прибавили к нему 50, ре-
зультат умножили на З и из полученного числа вычли утроенное задуманное число. Какое число получили в результате всех вычислений?
Решение. Пусть задумали число х,
прибавили к нему 50, получили (х + 50), результат умножили на З, получили З(х +
50) и из полученного числа вычли утроенное задуманное число, т. е. 3х. В
результате получили 
+ 50) - 3х = + 150 - = 150.
Ответ. 150.
• Замечание. Про такие выражения, как 66 — 2(3b — 5) и З(х + 50) — 3х, говорят, что они не зависят от входящих в них неизвестных, так как при любом значении неизвестного значения этих выражений равны одному и тому же числу. В данном случае
6b- 2(3b- 5) = 10 и + 50) - 150.
Пример 4. Докажем, что значение выражения 3(5х- 9) - 10(х- 1) - 5х+ 7
не зависит от х.
Решение. З(5х — 9) — 10(х — 1) — 5х+ 7
= 15х — 27 — 10х + 
5)х- 10 -10 не зависит от х.
26, Десятичные дроби. Сравнение десятичных дробей
Пример 1. Запишем десятичную дробь в виде обыкновенной:
а) 0,8; 6) 0,55; в) 2,125; г) 4,050.
|
Решение. а) |
8 = |
4
|
|
|
|
10 |
5 |
100 20 |
|
125 в) 2,125=2 |
|
|
|
|
1000 |
8 |
|
1000 20 |
Пример 2. Запишем обыкновенную дробь в виде десятичной:
1 7
а) в)
2 5 ' 125
Решение. а)
7
в)
125 125,8 1000
Пример З. Запишем величину, используя десятичную дробь:
а) 12 р. 4 к.; б) 6 м 8 дм; в) 5 т 60 кг. Решение. а) 12 р. 4 к. 12,04 р.;
б) 6 м 8 дм = 6,8 дм; в) 5 т 60 кг = 5,06 т.
Пример 4. Сравним десятичные дроби:
Пример 5. Сравним дроби:
а) 5! и 5,2; 6) 72 и 7,16; в) 5! и 5,23.
20
Решение. а) 5!5,5 > 5,2, значит,
5! > 5,2;
22
Ь — 7,15, 7,15 < 7,16, значит, 
100 20
|
а) 5,90 и 5,9; Решение. |
6) 24,53 и 24,5; |
в) 9,001 и 9,01. |
|
а) 5,90 = 5,9; |
6) 24,53 > 24,5; |
в) 9,001 |
|
|
4 100 4 27. Сложение и вычитание десятичных |
дробей
|
Пример 1. Вычислим: |
|
|||
|
а) 4,24 + 3,25; |
6) 7,18+ 1,39; |
в) 18,3 + 1,83; |
||
|
г) 3,67- 2,9; Решение. |
|
з - 3,37; |
|
е) 8- 2,55. |
|
|
6) |
7,18 |
в) |
18,30 |
|
3,25 |
|
1,39 |
|
1,83 |
|
7,49; |
|
8,57 |
|
20,13; |
|
г) 3,67 |
д) |
6,30 |
|
|
|
2,90 |
|
3,37 |
|
2,55 |
|
0,77; |
|
2,93; |
|
5,45. |
Пример 2. Найдём значение выражения 0,15 + 0,015 - 0,0015 + 0,00015.
Решение. 0,15 + 0,015 - 0,0015 + 0,00015 0,16365.
1) 0,150 2) 0,1650 3) 0,16350
0,015 0,0015 0,00015
0,165; 0,1635; 0,16365.
Пример З. Найдём значение выражения
14 - (35,129 - 33,19 + 2,0032) - (27,41 - 24,148).
Решение.
14 - (35,129 - 33,19 + 2,0032) - (27,41 - 24,148) = 6,7958.
1) 35,129 2) 1,9390 3) 27,410
33,190 2,0032
1,939; 3,9422; 3,262;
14,0000 5) 10,0578
3,9422 3,2620
10,0578; 6,7958.
28. Умножение десятичных дробей
|
Пример 1. Вычислим: |
|
||
|
а) 23,53 • 10; 6) 42,42 . 100; |
в) 60,01 • 1000; |
||
|
г) 46,59 • 0,1; д) 38,44 • 0,01; |
е) 99,11 • 0,001. |
||
|
Решение. |
|
|
||
|
а) 23,53 • 235,3; |
6) 42,42 100 = 4242; |
|
||
|
в) 60,01 1000 60 010; |
г) 46,59 • = 4,659; |
|
||
|
д) 38,44 • 0,01 = 0,3844; |
е) 99,11 • 0,001 -0,09911. |
|
||
Пример 2. Известно, что 192 • 837 = 160 704. Вычислим:
|
а) 19,2 • 837; |
6) 19,2 • 83,7; |
в) 1,92 • 83,7; |
|
г) 1,92 • 8,37; |
192 • 8,37; |
е) 0,0192 • 0,837. |
Решение.
а) 19,2 837 = 16070,4; 6) 19,2 • 83,7 = 1607,04;
в) 1,92 160,704; г) 1,92 8,37 = 16,0704;
д) 0,192 •
1,60704; е) 0,0192 0,837 = 0,0160704.
Пример З. Вычислим:
а) 53,2 • 45; 6)
0,385 • 4 7
в) 0,735 0,72.
|
Решение. |
|
|
|
|
|
а) Х 53,2 45 |
6) |
0,385 |
в) |
0,735 0,72 |
2660 2695 1470
2128 1540 5145
2394,0; 1,8095; 0,52920.
Пример 4. Найдём значение числового выражения 3,2758 • 0,25 • 0,08 • 12,5 • 0,4.
Решение. Используя переместительный и сочетательный законы умножения, перепишем данное произведение в виде
(0,25 • 0,4) • (0,08 • 12,5) 3,2758.
1) 0,25 • = 0,100; 2) 0,08 • 1,000;
4) • 3,2758 0,32758.
Ответ. 0,32758.
29. Деление десятичных дробей Пример 1. Вычислим:
|
а) 52,45 : 10; |
6) 41,28 : 100; |
в) 82,21 : 1000; |
|
|
|
г) 52,45 : 0,1; |
д) 41,28 : 0,01; |
е) 82,21 : 0,001. |
|
|
|
Решение. |
|
|||
|
а) 52,45 : 10 = 5,245; |
6) 41,28 : 0,4128; |
|||
|
в) 82,21 : 1000 0,08221; |
г) 52,45 : 0,1 = 524,5; |
|||
|
д) 41,28 : 0,01 = 4128; |
е) 82,21 : 0,001 = 82 210. |
|||
Пример 2. Заменим деление на десятичную дробь делением на натуральное число:
|
а) 33,21 : 2,7; 6) 537,51 : 4,37; г) 17,2 : 0,43; д) 716,1 : 0,651; Решение. а) 33,21 : = 332,1 : 27; 6) 537,51 : 4,37 - 53 751 : 437; в) 0,3556 : 0,254 = 355,6 : 254; |
в) 0,3556 : 0,254; е) 82 111 : 0,523. |
|
51 |
|
3,7 |
|
58 |
|
421 |
|
34 |
|
750 |
|
23 |
|
0,23 |
г) 17,2 : 1720
: 43; 188,7
д) 716,1 : 0,651 = 716 100 : 651; 153 е) 82 111 : 0,523 = 82 111 000 : 523.357 357
Пример З. Вычислим:
24418
а) 18,87 : 5,1; 232 6) 244,18 : 0,58;121 в) 25,5 : 0,034.116 Решение.58 а) 18,87 : 5,1 188,7 : 51 = 3,7;58 6) 244,18 : 418 : 421;
в) 25,5 : 0,034 = 25 500 : 34 = 750. 25500
238
Пример 4. Найдём значение выражения170
0,63 : + 0,5418 : 0,18 + 0,00529 : 0,023.170 Решение. 1) 0,63 : 0,9 = 6,3 : 0,7;
5,29
2) 0,5418 : 54,18 : 18 = 3,01;46
3)
0,00529 : 0,023 =
5,29 : 23 = 0,23.69 4-5) 
+ 0,23 = 3,71 + 0,23 = 3,94. 69 Ответ. 3,94.
30. Десятичные дроби и проценты
Пример 1. На какую десятичную дробь надо умножить число, чтобы найти:
а) 16 % этого числа;
б) З % этого числа;
в) 110 % этого числа?
16
Решение. а) Чтобы найти 16 % числа, т. е. 0,16
100
числа, надо умножить это число на 0,16.
з
б) Чтобы найти 3 0/0 числа, т. е. — 0,03 числа, надо 100 умножить это число на 0,03.
110 в) Чтобы найти 11094 числа, т. е. 1,1 числа,
100 надо умножить это число на 1,1.
• Замечание. Чтобы найти р (Уо числа, надо умножить это
Р число на 
100
Пример 2. Найдём: а) 16 0/0 числа 600; б) З % числа 150;
в) 11096 числа 200.
Решение. а) 16 % числа 600 равны 0,16 • 600 96;
б) З % числа 150 равны 0,03 • 150 = 4,5;
в) 110 0/0 числа 200 равны 1,1 • 200 220.
Пример З. Найдём число, если: а) 34 % этого числа равны 170;
б) 28 % этого числа равны 56.
Решение. а) 34 % искомого числа равны 170, следова-
170 • 100
тельно, искомое число равно 500 . Тот же резуль34 тат получится, если 170 разделить на 0,34.
б) 28 % искомого числа равны 56, следовательно, искомое число равно 56 : 0,28 = 5600 : 28 = 200.
Пример 4. Найдём число, 13 % которого равны 20 % числа 260.
Решение. 1) • 260 = 52 это 20 0/0 числа 260; 2) 52 : 5200 : 13 = 400 это искомое число. Ответ. 400.
31*. Сложные задачи на проценты
Пример 1. а) Увеличим число а на 19 % этого числа. б) Уменьшим число а на 19 0/0 этого числа.
Решение. а) К числу а прибавим 19 % числа а, полу-
чим
19
а— 1,19а.
100
б) Из числа а вычтем 19 % числа а, получим
19
11090)а = 0,810.
100
• Замечание. 1. Чтобы увеличить число на р % этого числа,
надо умножить это число на 1 + Р 
2. Чтобы уменьшить число на р % этого
числа, надо умножить это число на 1— Р 
Пример 2. На какую десятичную дробь надо умножить число а, чтобы увеличить число а:
а) на 1394; б) на 2496; в) на 3594?
Решение. а) Чтобы увеличить число на 13 % , надо
13
умножить это число на 1 + 1,13.
100
б) Чтобы увеличить число на 24 0/0, надо умножить это число на 1,24. в) Чтобы увеличить число на 35 % , надо умножить это число на 1,35.
Пример З. Вкладчик положил в банк 400 ООО р. Банк начисляет ежегодно 5 % дохода на сумму вклада, находящуюся на счёте вкладчика в начале года. Какая сумма будет на счёте через два года?
Решение. За первый год сумма увеличится в
5
— = 1,05 раза. Полученная сумма увеличится
за вто-
100 рой год ещё в 1,05 раза и за два года обратится в 400 000 • 1,05 • 1,05 = 441000 (р.).
Ответ. 441 ООО р.
Пример 4. Одна акция компании стоила 150 р. В понедельник цена акции повысилась на 10 0/0, а во вторник понизилась на 1096. Сколько стала стоить одна акция этой компании после двух изменений цены?
Решение. После повышения цены акция стала стоить 15 •
1
— 165 (р.). После понижения цены
она стала стоить 165 • 1
148,5 р.
32*. Использование вспомогательных букв при решении задач но проценты
Задача 1. В понедельник цена акции повысилась на 20 0/0, во вторник она понизилась на 30 0/0. Повысилась или понизилась цена акции за эти два дня и на сколько процентов?
Решение. Пусть акция первоначально стоила а р.
После повышения цены на 20 0/0 она стала стоить
12000) = 1,2а (р.). После понижения этой цены на 30 0/0
акция стала стоить 1,2а• 1 — 13000) = 1,20 • = 0,840 (р.).
Это на а — 0,84а = 0,1 ба (р.) меньше, чем а р. Значит, за два дня цена акции уменьшилась на 16 % .
Ответ. Уменьшилась на 16 % .
Задача 2. У Вовы пятёрок на 60 0/0 меньше, чем троек. На сколько процентов у Вовы троек больше, чем пятёрок?
Решение. Пусть у Вовы было t троек, так как пятёрок у него на 60 0/0 меньше, чем троек, то пятёрок у него
60 было t — 
100
У Вовы троек больше, чем пятёрок, на
(t - 0,40 100 0/0 0,6t 100 0/0 1500/0. 0,4t 0,4t
Ответ. На 150 0/0.
Задача З. Второе число на 5094 больше, чем первое, и на 50 0/0 меньше, чем третье.
а) На сколько процентов третье число больше, чем первое?
б) На сколько процентов первое число меньше, чем третье?
Решение. Здесь второе число сравнивают с двумя неизвестными числами первым и третьим. Пусть Р первое число, t третье число. По условию задачи второе число равно 1 + К)•р=1,5р, или 1 15000) •t=O,5t.
Так как это одно и то же число, то 1,5р = 0,5t, откуда следует, что t = Зр.
а) Третье число больше, чем первое, на 
Р (Зр— р) • 10094 - 200 .
41
б) Первое число меньше, чем третье, на 
(Зр — р) •
100 (Уо 
зр з
Ответ. а) На 200 0/0 ; б) на 66?
33*. Практические задачи но проценты
Задача 1. Трава при сушке теряет 80 % своей массы.
а) Сколько килограммов сушёной травы получится из 500 кг свежей?
б) Сколько тонн свежей травы надо накосить, чтобы получить из неё З т сушёной?
Решение. 100 — 80 = 20 ( % ) — массы свежей травы составляет масса сушёной травы.
а) 500 = 100 (кг) столько сушёной травы получится.
6) з : 15 (т) столько свежей травы надо накосить.
Ответ. а) 100 кг; б) 15 т.
Задача 2. Трава содержит 82 % воды. При сушке она теряет 80 % своей массы. Сколько процентов воды содержит сушёная трава?
Решение. Пусть х кг масса свежей травы,
тогда в ней содержится 0,82х кг воды и х — 0,82х = 0,18х (кг) вещества, не
содержащего воды, назовём его сухим веществом. Масса сушёной травы составляет
100 — 80 
— 20 ( % ) массы свежей травы. Масса
сушёной травы равна 0,2х кг, в ней содержится 0,18х кг сухого вещества и 0,2х —
0,18х = 0,02х (кг) воды.
Сушёная трава содержит 0,02х • 100 (К) — 10 0/0 воды. 0,2х
Ответ. 10 0/0
Задача З. Трава содержит 82 % воды. Её немного подсушили, и теперь она содержит 55 % воды. Сколько процентов своей массы трава потеряла при сушке?
Решение. Пусть х кг масса свежей травы, тогда в ней содержится 0,82х кг воды и х — 0,82х = 0,18х (кг) сухого вещества. После подсушки сухое вещество составляет 100 — 55 = 45 ( % ) массы сушёной травы, поэтому масса сушёной травы равна 0,18х : 0,45 = 0,4х (кг).
Итак, трава при сушке потеряла х — 0,4х = 0,6х, т. е. 60 0/0 от х.
60 %
34. Десятичные дроби произвольного знака
Пример 1. Найдём значение выражения (0,48 - 0,05 (-3,2)) : (-0,8).
|
Решение. 1) 0,05 • (-3,2) -0,16; 3,2 |
0,48 |
|
2) 0,48 - (-0,16) = 0,48 + 0,16 = 0,64; 0,05 |
0,16 |
|
3) 0,64 : (-0, 8 ) = -(6,4 : 8) -0,8. 0,160 Ответ. —0,8 Пример 2. Найдём значение выражения 2,6 + 0,924 : (-0,54 + 0,26). Решение. |
0,64 |
|
28 |
|
3,3 |
1)
-0,54 +
0,26 = -(0,54 - 0,26)54 92,4
-0,28; 0,26 84
0,28 84
2)
0,924 : (-0,28) -
-(0,924 : 0,28) 
84
- -(92,4 : 28) - -3,3;
3) + (-3,3) -(3,з - 2,6) - -0,7. Ответ. —0,7.
Пример З. Найдём значение выражения
(-6,12 + 3,7) (-0,7)
Решение.
1) 
-6,12 + = -(6,12 - 3,7) - -2,42; 6,12 2,42
2) -2,42 (-0,7) = 1,694,3,70 0,7
3) 1,694 - 9,5 - -(9,5 - 1,694) -2 , 42 1,694
- -7,806;
4) -7,806 + 0,09 - -(7,806 - 0,09)9,500 7,806
-7,716. 1,694 0,090 7,806 7,716
Ответ. —7,716.
Пример 4. Найдём значение выражения
(—0,45) : — • (—0,3)) : (-0,05).
|
225 |
|
|
Решение.5,7
0,3
2) 0,54 - (-1,71) = 0,54 + 1,71 = 2,25;1,71
3) -0,45 : 2,25 - — 4 5 : 22 5 -0,2;45,0
4) -0,2 : (-0,05) = : 0,05 = 20 : 5 = 4.450
о
Ответ. 4.
Пример 5. Найдём значение выражения
3,48 • (-0,2 + 2,09) - 2,09 • (3,48 - 0,2).
Решение. Раскрыв скобки, получим, что в сумме есть два противоположных слагаемых:
3,48 • (-0,2 + 2,09) - 2,09 • (3,48 -
0,2) 
-3,48 • + 3,48 2,09 - 2,09 3,48 + 2,09 -
дз
-
-3,48 +
2,09 (-3,48 + 2,09)
-(3,48 - 2,09) - -1,39 -0,278. Ответ.
—0,278.
35. Совместные действия с обыкновенными и десятичными дробями произвольного знака
Пример 1. Вычислим: а) - 0,73; 6) 
в) 
К).
з 5 2
4 11 5
Решение.
Пример 2. Вычислим:
1
2,3; в) 1
5); г) -3,15 .
72
Решение. а) —3! + 1,8 —3,6 + 1 8 -1,8;
10-27 17
9 9 10 10 90 90
'
—4;
7 2
1 г) -3,15 : 4- - -3,15 : 
-0,7.
2
Пример З. Найдём значение выражения
-1,61: 2-5 
2. (-2,5)
6 5 5
-
2 22
Решение. 1) • (-2,5)-0,4 - -1; 2)
5 66
161 23 161•6 
• 6 100 • 23 100 • 1 -0,42; 6 100
4)
-0,42-3!
-3,62.
5
— 3,62.
Пример 4. Найдём значение выражения
Решение. 1) 3,52 6
з
3) 32:3--5 19 . 23 19,6 19 .
6-23 23
з
= + 0,75 0,95;
4
з
5) 0,2 - -0,75 -0,55;
4
95 19
6)
0,95 : (-0,55) -
-95 : 55 
'
55 11
7)
129319,11 11
23•19 23
11 Ответ. 
23
36. Приближения десятичных дробей
Пример 1. Укажем приближение десятичной дроби
35,472 с недостатком с точностью:
а) до одной единицы; б) до одной десятой;
в) до одной сотой.
Решение.
а) 35,472 35; 6) 35,472 35,4; в) 35,472 35,47.
Пример 2. Укажем приближение десятичной дроби 82,608 с избытком с точностью: а) до одной единицы;
б) до одной десятой; в) до одной сотой.
Решение.
а) 82,608 83; 6) 82,608 82,7; в) 82,608 82,61.
Пример З. Округлим десятичную дробь 27,417:
а) до единиц; б) до десятых; в) до сотых.
Решение.
а) 27,417- 27; 6) 27,417 = 27,4; в) 27,417 = 27,42.
Пример 4. Округлим десятичную дробь:
а) 437,15 до единиц; б) 11,985 до десятых;
в) 21,288 до сотых.
45
Решение.
а) 437,15 - 437; 6)
11,985- 12,0; в) 
Пример 5. Округлим десятичную дробь а = 1928,3745:
|
а) до единиц; |
б) до десятых; |
в) до сотых; |
|
г) до тысячных; ж) до тысяч. Решение. |
д) до десятков; |
е) до сотен; |
|
а) 1928; |
6) 1928,4; |
в) 1928,37; |
|
г) 1928,375; ж) а = 2000. |
д) а 1930; |
е) 1900; |
37. Приближённые вычисления
Пример 1. Округлив числа а и Ь с точностью до 0,01, вычислим приближённо сумму а + Ь и разность а — Ь:
а) а = 5,437; 2,294; 6) а = 39,249; Ь = 1,739.
Решение. а) а 5,44; Ь 2,29; а + Ь = 5,44 + 2,29 = 7,73; а - Ь = 5,44 - 2,29 = 3,15. 6) а х 39,25; 1,74; а + Ь - 39,25 + 1,74 = 40,99; а - Ь = 39,25 - 1,74 = 37,51.
Пример 2. Округлим числа а и Ь с точностью до трёх значащих цифр, вычислим приближённо произведение а • Ь и частное а : Ь. Результат округлим с точностью до трёх значащих цифр:
а) а = 36,28; Ь = 5,184; 6) а = 71,25; Ь - 5,612.
Решение. а) а 36,3; Ь 5,18;
36,3 • 5,18 = 188,034 188; а : 36,3 : 5,18 7,007... 7,01. 6) 71,3;
5,61; а • Ь = 71,3 5,61 = 399,993 400; а : Ь - 71,3 : 5,61 12,70... 12,7.
Пример З. Стороны прямоугольника измерили приближённо: а 11,9 м, Ь 5,29 м. Вычислим приближённо:
а) периметр прямоугольника с точностью до десятых долей метра;
б) площадь прямоугольника с точностью до трёх значащих цифр.
Решение. а) Периметр прямоугольника со
сторонами а и Ь равен Р = 2(а + Ь). Округлим длину Ь до десятых: 
5,3 м и
вычислим приближённо периметр: Р- + 5,3) = 34,4 (м).
Дб
б) Площадь прямоугольника со сторонами а и Ь равна S ab. Вычислим приближённо площадь:
11,9 • 5,29 = 62,951 -63,0 (м 2 ).
Ответ. а) Р = 34,4 м; б) S = 63,0 м 2 .
38*. Периодические десятичные дроби
Пример 1. Запишем обыкновенную дробь:
33 50 а)
50 33 в виде конечной десятичной дроби или бесконечной периодической десятичной дроби.
33 33•2 66
|
33 |
|
1,5151... |
Решение. а) 0,66.50,0
50 50,2 100
33
50170
6) дробь несократимая, разло-165
33 жение её знаменателя содержит множи-50 тель З, отличный от 2 и 5, следователь-33 но, эта дробь разлагается в170 периодическую десятичную дробь. Разде-165
50 лим числитель этой дроби на
знаменатель уголком: 50 : 33 = 1,5151... 
Пример 2. Покажем, как можно записать в виде обыкновенной дроби периодическую десятичную дробь:
Решение. а) Пусть х 0,(8) — 0,888 тогда
10х = 8,888
10х - х = 8,888... - 0,888
8 х 
9
6)
Пусть х = 
0,3636 тогда
100х = 36,3636
100х - х 36,3636... - 0,3636
99х = 36,
36
х
99
4 х
11 •
в)
Пусть х = 
0,17272 тогда
1,7272
= 172,7272
1000х - 10х = 172,7272... - 1,7272
990х = 171,
171 х
990 '
19 х
1 10 •
Пример З. Покажем, что периодическая дробь 5,7(9) равна конечной десятичной дроби.
Решение. Пусть х 5, 7 (9) = 5,7999 тогда
10х = 57,999
100х = 579,999
100х - 10х 579,999... - 57,999 90х =
522, х = 5,8.
Итак, 
5,8.
Пример 4. Найдём значение выражения
Решение. Так как 0,(27) 27
99
_4Ц, то
99 11 з — 1 +42 3-3 + 42- 
9 5.
11 з 11 11 • 1 11 11 11
39. Длина окружности и площадь круга
Пример 1. Вычислим приближённо длину окружности, если:
а) её радиус равен 15 см; б) её диаметр равен 16 м.
Решение. Используя приближение числа п до трёх значащих цифр, вычислим длину окружности по форму-
ле:
а) С = 94,2 (см); 6) С = па 3,14 • 16 = 50,24 (м).
Ответ. а) 94,2 см; б) 50,24 м.
Пример 2. Вычислим приближённо площадь круга, если его радиус равен 13 см.
Решение. Используя приближение числа п до трёх значащих цифр, вычислим площадь круга по формуле
S = 3,14 • 13 2 = 530,66 531 (см 2 ).
Ответ. 531 см2
Пример З. Из справочника выписали приближение числа л 3,14159265. Сколько первых цифр числа л надо взять для приближённого вычисления:
а) длины окружности, если её радиус приближённо равен 12,6 см;
б) площади круга, если его радиус приближённо равен 2,1 м?
Вычислим приближённо длину окружности и площадь круга.
Решение. а) Радиус окружности измерен с точностью до третьей значащей цифры, следовательно, множитель л и произведение должны содержать не больше трёх значащих цифр.
С = 
79,128 = 79,1 (см).
б) Радиус круга измерен с точностью до второй значащей цифры, следовательно, множители п, R2 и произведение должны содержать не больше двух значащих цифр.
R2
41 4,4;
= 13,64 14 (м2 ).
Ответ. 14 м 2
РАЗДЕЛ l l
Самостоятельные работы
Масштаб
Вариант I
1. Масштаб карты 1 : 200 ООО. Расстояние между двумя сёлами на карте 10 см. Чему равно расстояние между этими сёлами на местности?
2. Расстояние между двумя городами 40 км. Чему равно расстояние между этими городами на карте, масштаб которой 1 : 1 ООО ООО?
З. Расстояние между городами А и В равно 150 км. Расстояние между городами А и В на карте равно З см. Определите масштаб карты.
4*. Земельный участок на плане имеет вид прямоугольника со сторонами 5 см и 4 см. Определите площадь участка на местности, если масштаб карты равен 1 : 500.
Вариант II
1. Масштаб карты 1 : 1 ООО ООО. Расстояние между двумя сёлами на карте 8 см. Чему равно расстояние между этими сёлами на местности?
2. Расстояние между двумя городами 100 км. Чему равно расстояние между этими городами на карте, масштаб которой 1 : 2 ООО ООО?
З. Расстояние между городами А и В равно 140 км. Расстояние между городами А и В на карте равно 7 см. Определите масштаб карты.
4*. Земельный участок на плане имеет вид прямоугольника со сторонами 6 см и 5 см. Определите площадь участка на местности, если масштаб карты равен 1 : 500.
Вариант III
1. Масштаб карты 1 : 250 ООО. Расстояние между двумя сёлами на карте 16 см. Чему равно расстояние между этими сёлами на местности?
2. Расстояние между двумя городами 24 км. Чему равно расстояние между этими городами на карте, масштаб которой 1 : 400 ООО?
З. Расстояние между городами А и В равно 200 км. Расстояние между городами А и В на карте равно 8 см. Определите масштаб карты.
4*. Земельный участок на плане имеет вид прямоугольника, площадь которого равна 10 см 2 . Определите площадь участка на местности, если масштаб карты равен 1 : 1000.
Вариант IV
1. Масштаб карты 1 : 125 ООО. Расстояние между двумя сёлами на карте 12 см. Чему равно расстояние между этими сёлами на местности?
2. Расстояние между двумя городами 25 км. Чему равно расстояние между этими городами на карте, масштаб которой 1 : 500 ООО?
З. Расстояние между городами А и В равно 360 км. Расстояние между городами А и В на карте равно 9 см. Определите масштаб карты.
4*. Земельный участок на плане имеет вид прямоугольника, площадь которого равна 15 см 2 . Определите площадь участка на местности, если масштаб карты равен 1 : 1000.
Деление числа в данном отношении
Вариант I
1.
Разделите число 125 в отношении: 
6) 3 : 2.
2. Начертите отрезок АВ, длина которого 14 см. Разделите этот отрезок в отношении З : 4.
З. Разделите число 120 на три части так, чтобы первая относилась ко второй как 1 : 2, а вторая к третьей как 2 : З.
4*. Мама хочет разделить 22 конфеты между двумя детьми в отношении, обратном отношению их возрастов. Определите, сколько конфет достанется брату, если ему 6 лет, а его сестре 5 лет.
II
1. Разделите число 140 в отношении:
а) 1 : 6; 6) 2 : 5.
2. Начертите отрезок АВ, длина которого 10 см. Разделите этот отрезок в отношении 2 : З.
З. Разделите число 160 на три части так, чтобы первая относилась ко второй как 1 : З, а вторая к третьей как З : 4.
4*. Мама хочет разделить 18 конфет между двумя детьми в отношении, обратном отношению их возрастов. Определите, сколько конфет достанется сестре, если ей 5 лет, а её брату 4 года.
Вариант III
1. Разделите число 150 в отношении:
а) 3 : 2; 6) з : 12.
2. Начертите отрезок MN, длина которого 15 см. Разделите этот отрезок в отношении З : 2.
З. Разделите число 170 на три части так, чтобы первая относилась ко второй как 1 : 2, а вторая к третьей как З : 4.
4*. Мама хочет разделить 6 конфет между двумя детьми в отношении, обратном отношению их возрастов. Определите, сколько конфет достанется брату, если ему 6 лет, а его сестре З года.
Вариант IV
1.
Разделите число 140 в отношении: 
6) 2 : 12.
2. Начертите отрезок MN, длина которого 16 см. Разделите этот отрезок в отношении З : 5.
З. Разделите число 260 на три части так, чтобы первая относилась ко второй как 2 : 1, а вторая к третьей как З : 4.
4*. Мама хочет разделить 12 конфет между двумя детьми в отношении, обратном отношению их возрастов. Определите, сколько конфет достанется сестре, если ей 6 лет, а её брату 2 года.
с-з Пропорции
Вариант I
1. Из чисел 25, 6, 5, 30 составьте пропорцию.
2. Можно ли составить пропорцию из отношений:
а) и 3 : 12; 6) и 21 : 15?
З. Решите пропорцию:
а) 27 з. 6) 12 : 5 - 20 : х.
4* Решите пропорцию 
Вариант II
1. Из чисел 24, 9, 8, 27 составьте пропорцию.
2. Можно ли составить пропорцию из отношений:
а) 15 : 3 и 25 : 5; 6) и 12 : 32?
З. Решите пропорцию: а) 
х з 6)
х : 13 24 : 39.
24 28'
4* Решите пропорцию 2—х : 28 _ 4Ц : 1 9 •
9 13 19
Вариант III
1. Из чисел 28, 42, 36, 54 составьте пропорцию.
2. Можно ли составить пропорцию из отношений:
а) 24 : 17 и 34:48; 6) 13 : 12 и 39 : 36?
З. Решите пропорцию:
а) 21 з.
4* Решите пропорцию 42х : 2— 1 =2! : 32.
13 9 11
Вариант IV
1. Из чисел 26, 39, 36, 24 составьте пропорцию.
2. Можно ли составить пропорцию из отношений:
а) 18 : 17 и 54: 51; 6) 15 : 28 и 56 : 30?
З. Решите пропорцию:
Х 5
а) • 12 = 25 : 20.
21 28'
4*. Решите пропорцию зцх:5-з 2Ц : 5 2 .
4 23 11
Понятие о проценте
I
1. Мужчины составляют 60 % всех работающих на заводе. Сколько мужчин работает на заводе, если всех работающих 2500 человек?
2. Найдите число, 12 % которого равны 48.
З. Сколько процентов числа 50 составляет число 20?
4*. Найдите число, 6 % которого равны 16 % числа 75.
Вариант II
1. На швейной фабрике работает 2400 человек, 90 % их числа составляют женщины. Сколько женщин работает на швейной фабрике?
2. Найдите число, 15 % которого равны 45.
З. Сколько процентов числа 25 составляет число 10?
4*. Найдите число, 4 % которого равны 75 % числа 16.
Вариант III
1. Мужчины составляют 45 % всех работников цеха. Сколько женщин работает в цехе, если всех работников 360 человек?
2. Найдите число, 48 % которого равны 12.
З. Сколько процентов числа 60 составляет число 84?
4*. Найдите число, 15 % которого равны 17 % числа 60.
Вариант IV
1. На предприятии работает 450 человек, 54 % их числа составляют женщины. Сколько мужчин работает на предприятии?
2. Найдите число, 60 % которого равны 15.
З. Сколько процентов числа 25 составляет число 40?
4* Найдите число, 16 % которого равны 15 % числа 80.
с-5 Задачи на проценты
Вариант I
1. Вчера продали 180 кг овощей, а сегодня на 20 0/0 меньше, чем вчера. Сколько килограммов овощей продали за эти два дня?
2. Задумали число, увеличили его на 25 % и получили 750. Какое число задумали?
З. На сколько процентов число 120 меньше, чем число
4*. На сколько процентов число 20
больше, чем число 16
Вариант II
1. Вчера продали 150 кг фруктов, а сегодня на 30 0/0 больше, чем вчера. Сколько килограммов фруктов продано за эти два дня?
2. Задумали число, уменьшили его на 20 % и получили 320. Какое число задумали?
З. На сколько процентов число 220 больше, чем число
4*. На сколько процентов число 16 меньше, чем число
Вариант III
1. Туристы проехали на автобусе 220 км, а оставшиеся 45 % намеченного маршрута они проехали на электричке. Какова длина намеченного маршрута?
2. Задумали число, увеличили его на 65 % и получили 33. Какое число задумали?
З. На сколько процентов число 8 меньше, чем число 10? 4* На сколько процентов число 15 больше, чем число
Вариант IV
1. Туристы проехали на автобусе 55 % намеченного маршрута, а оставшиеся 180 км они проехали на электричке. Какова длина намеченного маршрута?
2. Задумали число, уменьшили его на 75 % и получили 80. Какое число задумали?
З. На сколько процентов число 10 больше, чем число 8? 4* На сколько процентов число 12 меньше, чем число
Вероятность события
I
1. Запишите все трёхзначные числа, в записи которых есть только цифры О, 5, 7:
а) без повторения цифр;
б) с повторением цифр.
2. Подбросили игральный кубик. Какова вероятность того, что выпадет:
а) 4 очка;
б) нечётное число очков?
З. Какова вероятность того, что при подбрасывании монеты два раза оба раза выпадет орёл?
4*. Случайным образом из натуральных чисел от 22 до 44 выбрали одно число. Какова вероятность того, что оно делится на 9?
Вариант II
1. Запишите все трёхзначные числа, в записи которых есть только цифры О, 9, З:
а) без повторения цифр;
б) с повторением цифр.
2. Подбросили игральный кубик. Какова вероятность того, что выпадет:
а) 5 очков;
б) чётное число очков?
З. Какова вероятность того, что при подбрасывании монеты два раза оба раза выпадет решка?
4*. Случайным образом из натуральных чисел от 13 до 35 выбрали одно число. Какова вероятность того, что оно делится на 9?
Вариант III
1. Сколько имеется четырёхзначных чисел, в записи которых есть только цифры О, 6, 7, 9:
а) без повторения цифр;
б) с повторением цифр?
2. Подбросили игральный кубик. Какова вероятность того, что выпадет:
а) 4 очка или 5 очков;
б) О очков?
З. Какова вероятность того, что при подбрасывании монеты два раза сначала выпадет орёл, потом решка?
4*. Случайным образом из натуральных чисел от 14 до 39 выбрали одно число. Какова вероятность того, что оно делится на 2?
Вариант IV
1. Сколько имеется четырёхзначных чисел, в записи которых есть только цифры О, 4, 6, 8:
а) без повторения цифр;
б) с повторением цифр?
2. Подбросили игральный кубик. Какова вероятность того, что выпадет:
а) З очка или 4 очка;
б) 7 очков?
З. Какова вероятность того, что при подбрасывании монеты два раза сначала выпадет решка, потом орёл?
4*. Случайным образом из натуральных чисел от 25 до 55 выбрали одно число. Какова вероятность того, что оно делится на З?
С—7* Задачи на вычисление вероятности события
Вариант I
1. В игре «Морской бой» на поле 10 Х 10 располагают 1 четырёхпалубный корабль (4 клетки), 2 трёхпалубных корабля (по З клетки), З двухпалубных корабля (по 2 клетки) и 4 однопалубных корабля (по 1 клетке). Какова вероятность того, что игрок, не видя размещения кораблей на игровом поле и сделав один выстрел (назвав координаты одной клетки), попадёт в четырёхпалубный корабль?
2. В шкафу есть З вертикальных ряда по 4 ящика в каждом. В один из ящиков в каждом ряду спрятали по одной монете. Какова вероятность того, что, выдвинув случайным образом по одному ящику в каждом ряду, можно найти монеты в двух первых рядах и не найти в третьем?
3*. Учитель запланировал проверить две домашние работы из пяти на текущей неделе. Эти две работы он выбирает случайным образом и за невыполнение домашней работы ставит в журнал отметку «1». Определите вероятность события «Вася получит ровно одну «1», если он не выполнит три домашние работы из этих пяти.
II
1. В игре «Морской бой» на поле 10 х 10 располагают 1 четырёхпалубный корабль (4 клетки), 2 трёхпалубных корабля (по З клетки), З двухпалубных корабля (по 2 клетки) и 4 однопалубных корабля (по 1 клетке). Какова вероятность того, что игрок, не видя размещения кораблей на игровом поле и сделав один выстрел (назвав координаты одной клетки), попадёт хотя бы в один однопалубный корабль?
2. В шкафу есть З вертикальных ряда по 4 ящика в каждом. В один ящик в каждом ряду спрятали одну монету. Какова вероятность того, что, выдвинув случайным образом по одному ящику в каждом ряду, можно найти монеты в первом ряду и не найти в остальных?
3* Учитель запланировал проверить две домашние работы из пяти на текущей неделе. Эти две работы он выбирает случайным образом и за невыполнение домашней работы ставит в журнал отметку «1». Определите вероятность события «Боря получит две «1», если он не выполнит три домашние работы из этих пяти.
Вариант III
1. В игре «Морской бой» на поле 10 х 10 располагают 1 четырёхпалубный корабль (4 клетки), 2 трёхпалубных корабля (по З клетки), З двухпалубных корабля (по 2 клетки) и 4 однопалубных корабля (по 1 клетке). Какова вероятность того, что игрок, не видя размещения кораблей на игровом поле и сделав один выстрел (назвав координаты одной клетки), попадёт хотя бы в один двухпалубный корабль?
2. В шкафу есть 4 вертикальных ряда по 4 ящика в каждом. В один из ящиков в каждом ряду спрятали по одной монете. Какова вероятность того, что, выдвинув случайным образом по одному ящику в каждом ряду, можно найти монеты в трёх первых рядах и не найти в четвёртом?
3*. Учитель запланировал проверить две домашние работы из шести на текущей неделе. Эти две работы он выбирает случайным образом и за невыполнение домашней работы ставит в журнал отметку «1». Определите вероятность события «Катя получит одну «1», если она не выполнит одну домашнюю работу из этих шести.
Вариант IV
1. В игре «Морской бой» на поле 10 х 10 располагают 1 четырёхпалубный корабль (4 клетки), 2 трёхпалубных корабля (по З клетки), З двухпалубных корабля (по 2 клетки) и 4 однопалубных корабля (по 1 клетке). Какова вероятность того, что игрок, не видя размещения кораблей на игровом поле и сделав один выстрел (назвав координаты одной клетки), попадёт хотя бы в один трёхпалубный корабль?
2. В шкафу есть 4 вертикальных ряда по 4 ящика в каждом. В один из ящиков в каждом ряду спрятали по одной монете. Какова вероятность того, что, выдвинув случайным образом по одному ящику в каждом ряду, можно найти монеты в третьем и четвёртом рядах и не найти в остальных?
3*. Учитель запланировал проверить две домашние работы из шести на текущей неделе. Эти две работы он выбирает случайным образом и за невыполнение домашней работы ставит в журнал отметку «1». Определите вероятность события «Оля получит хотя бы одну «1», если она не выполнит две домашние работы из этих шести.
Модуль целого числа. Сравнение целых чисел
Вариант I
1. Запишите числа, противоположные числам: +5; —2; О.
2. Определите модули чисел: +8; —6; О.
З. Упростите записи чисел: —(+5)
4. Сравните числа:
г) —11 и —7; д) +20 И +30; е) -20 и -30.
Сколько целых чисел расположено между
числами
Вариант II
1.
Запишите числа, противоположные числам: +7;
2. Определите модули чисел: +5; —8; О.
З. Упростите записи чисел: +(—7); —(+9);
4. Сравните числа:
в)
—11 и +8;
г)
—12 и —9; д) +30 и +40; е) —30 и
5*. Сколько целых чисел расположено между числами -16 и +17?
Вариант III
1.
Запишите числа,
противоположные числам: 
-12.
2. Определите модули чисел: +13; —60; О.
З. Упростите записи чисел + 22 ) ;
4. Сравните числа:
а) +12 и О; б) —21 и О; в) —10 и +4;
г) —10 и —11; д) +300 И +200; е) -300 и -200.
5*. Сколько целых чисел расположено между числами -21 и +22?
Вариант IV
1.
Запишите числа, противоположные числам: +12; о; -16.
2. Определите модули чисел: +11; О; —34.
З. Упростите записи чисел: +(+10);
+(—11) 
13).
4. Сравните числа:
а) +22 и О; 6) -11 и о; в) —16 и +5;
г) -18 и -17; д) +300 и +400; е) -300 и -400.
5*. Сколько целых чисел расположено между числами -22 и +23?
с-9 Сложение и вычитание целых чисел
Вариант I
Вычислите (1—5):
1.
а) 13 +
в)
2. а) 13 - (-2);
З. а) 43 + (-12);
в)
г) -12 - (-5). 6) -52 - (-13);
г) -11 - 51.
6)
-26 - + (-12);
г) -10 - (-10) + 4. 26.
Вариант II
Вычислите (1—5)
1.
а) 15 +
в) —6 + 10; г) -11 + (-3).
2.
а) 15 -
в) —6 — 10;
а) 34 + (—11); 6) -32 - (-23);
в) -7 + (-54); г) -24 - 34.
4. а) 42 + (-26) - (-16); 6) -36 - + (-22);
в) —48 + 48 -4-
г) -11 5. 
+ 34 + 35 + 36.
Вариант III
Вычислите (1—5)
1. а) 23 + (-12); 
|
|
В) 15 (—19); |
г) 32 + (-12). |
|
2. |
а) 23 - (-12); |
|
|
|
в) 15 — (—19); |
г) -32 - (-12). |
|
|
а) 43 + (—15); |
6) -36-( 63) |
|
|
в) —16 + (—51); |
г) -41 - 37. |
|
4. |
а) 442 + (-39) - |
|
|
|
в) -333 + 333 - |
|
|
|
—45 + (—44) + (— |
|
Вариант IV
Вычислите (1—5)
|
1. |
а) 35 + (-11); |
б) —22 + (—15); |
|
|
в) 25 + (-39); |
Г) |
|
2. |
а) 35 - (-11); |
6) -22 - (-15); |
|
|
в) 25 - (-39); |
г) -33 - (-42). |
|
|
а) 42 + (—16); |
6) -37 - (-62); |
|
|
в) -17 + (-52); |
г) -39 - 35. |
4. а) 422 + (-26) - (—36); 6) -465 - (-47) + (-27);
в) -125+ 125 - (-5); г) -38 - (-38) -4. 
51) + . . + 53 + 54 + 55.
с- 1 0 Умножение и деление целых чисел
I
Вычислите (1—3):
1.
а) -12 , 5;
в) 26 • (-12);
г) -48 •
д) -57 • о; 
2. а) 72 : (-24); 6) -96 : (-8); в) -49 : 7;
д) о : (-42); е)
-54 :
з. а) 41 • 6) -37 : (-37); в) -25 • г) —39 : 39.
4. Найдите значение выражения:
а) 172 : (-422 : 211 43); 6) -432 : (-9) : (-24).
5*. Найдите значение выражения
52 • (-53) • (-54) • 55 • (-56) : 56 : (-55) : 54 : (-53).
Вариант II
Вычислите (1—3)
1.
в) 24 • (—14);
д) -86 • о; е) -38 • 1.
|
2. |
а) 86 : (-43); г) -79 : |
6) -63 : д) О : (—44); |
|
в) -42 : з;
|
|
з. |
а) -38 • з; |
6) 39 : (-39); |
|
|
4. Найдите значение выражения:
а) 272 : (448 : (-112) • 34); 6) -368 : (-8) : (-23).
5*. Найдите значение выражения
63 (-64) • (-65) • 66 • (-67) : 67 : (-66) : 65 : (-64).
Вариант III
Вычислите (1—3)
1. а) -15 • 7;в) 27 • (-13);
г) —45 • (—1); д) -787 е) 79 • 1.
|
2. |
а) 78 : (-26); |
6) -91 : |
в) -64 : 8; |
|
|
г) -98 : 1; |
д) о : (-394); |
е) |
з. а) 45 6)
-390 : (-39); в) -125
г) —59 : 59.
4. Найдите значение выражения:
а) -282 : (-639 : (-213) 47); 6) -266 : (-19) : (-14).
5*. Найдите значение выражения
57 • (-58) • (-59) • 60 • (-61) : 60 : (-59) : 58 : 57.
IV
Вычислите (1—3)
|
1. |
а) -23 • 5; |
|
в) 26 • (-11); |
|
|
г) -87 • |
д) -99 • о; |
е) -101 • 1. |
|
2. |
а) 94 : (-47); |
6) -63 : (-7); |
в) —54 : 9; |
|
|
г) -88 : (-1); |
д) о : (-95); |
е) |
з. а) -82 • з; 6) 650 : (-65);
г) -93 : 93.
4. Найдите значение выражения:
а) 264 : (452 : (-113) • 33); 6) -252 : (-9) : (-28).
5*. Найдите значение выражения
75 (-76) (-77) 78 (-79) : 78 : (-77) : 76 : 75.
с-1 1 Действия с целыми числами
Вариант I
Найдите значение выражения (1—4):
1. (72 - 36 • - 24) : (-8).
2. -420 : (-14 - 7) • з - 7.
з. 340 - 72 : (-7 + 3) • (-6).
4. -405 : (36 - 45 : з.
5*. При каком значении а не имеет смысла выражение 200 : ((-55 : 5 + 9) 24 + а)?
Вариант II
Найдите значение выражения (1—4):
1. (180 - 11 • - 18) : (-3).
2. -250 : (-17+ 7) • 4 - 8.
з. 130 - 84 : (-11 + 5) • (-7).
4. -540 : (45 - 36 :
5* При каком значении а не имеет смысла выражение
ЗОО : ((-66 : 11 + 4) • 25 - а)?
III
Найдите значение выражения (1—4)
1. (-620 - 14 + 36) : (-250).
2. 720 : (-12 - 36) • (-12) - 4.
з. 240 - 240 : (-55 + 15) •
4. -490 : (84 - 84 : • 5.
5*. При каком значении а не имеет смысла выражение
400 : ((-88 : 11 + 2) • 36 - а)?
Вариант IV
Найдите значение выражения (1—4):
1. (-347 - 18 • (-5) + 27) : (-115).
2. -220 : (-36 + 14) • 11 - 8.
з. 280 - 280 : (-16 + 2) • 2.
4. -840 : (70 - 70 :
При каком значении а
не имеет смысла выражение 500 : «-77 : 7 + 7) 23 + а)?
с-12 Представление целых чисел на координатной прямой
Вариант I
1. Запишите координаты точек А, В, С и 1), изображённых на рисунке.
Определите расстояния ОД ОВ, ВО.
2. Изобразите координатную ось, выбрав удобный единичный отрезок, и отметьте на ней точки 0(0), М(2), N(—3), К(5) и Ц —6). Определите расстояния OL и MN.
З. Различные точки заданы своими координатами: 0(0), М(т), N(n). Сравните модули целых чисел т и п, если ОМ > 0N.
4*. Определите координату точки М отрезка АВ, если
Вариант П
1. Запишите координаты точек А, В, С и D, изображённых на рисунке.
Определите расстояния ОС, ОА, АС.
2. Изобразите координатную ось, выбрав удобный единичный отрезок, и отметьте на ней точки 0(0), М(З), N(—2), К(б) и Ц— 7). Определите расстояния ОК и ML.
З. Различные точки заданы своими координатами: 0(0), М(т), N(n). Сравните модули целых чисел т и п, если ОМ < 0N.
4*. Определите координату точки М отрезка АВ, если
Вариант III
1. Запишите координаты точек А, В, С и D, изображённых на рисунке.
Определите расстояния ОА, ОД АО.
2. Изобразите координатную ось, выбрав удобный единичный отрезок, и отметьте на ней точки 0(0), М(4), N(—5), Щ 7) и Ц —8). Определите расстояния 0L и МК.
З. Различные точки заданы своими координатами: 0(0), М(т), N(n). Определите знак числа т, если ОМ > ОЛТ
4*. Определите координату точки М отрезка АВ, если А(-8) и В(7) и АМ•. МВ - 2 : З.
Вариант IV
1. Запишите координаты точек А, В, С и D, изображённых на рисунке.
Определите расстояния ОС, АО, АС.
2. Изобразите координатную ось, выбрав удобный единичный отрезок, и отметьте на ней точки 0(0), М(4), N(—3), Щ 7) и Ц —6). Определите расстояния ОК и ML.
З. Различные точки заданы своими координатами: 0(0), М(т), N(n). Определите знак числа п, если ОМ < ОЛТ
4*. Определите координату точки М отрезка АВ, если
с-13 Рациональные числа
Вариант I
1.
Запишите числа, противоположные числам
4
2.
Упростите записи чисел: + 81), 
З.
Определите модули чисел: + ;
7 з
4. Запишите число в виде дроби:
4
а) с отрицательным числителем;
б) с отрицательным знаменателем.
36
-35
5.
Сократите дроби 
42 ' -49'
-11 -21
6. Приведите к знаменателю 100 дроби: • 25 -28
11 -21 32 — 41
7*. Запишите числа: — в виде дробей 
12' -22' -33' — 42
с положительными знаменателями.
Вариант П
1 2
1.
Запишите числа,
противоположные числам: 
О. 7 9
2.
Упростите записи чисел:4).
7 4 з
З. Определите модули чисел: +—; ——; О.
5 4 5
4. Запишите число в виде дроби:
6
а) с отрицательным знаменателем;
б) с отрицательным числителем.
5. Сократите дроби: 35. -32 •
56 ' -48
6.
Приведите к знаменателю 100 дроби • -9. -12
• 20' -30
7*. Запишите числа: 10 -20 31 — в виде дробей -11' -21 ' -32' —44
с положительными знаменателями.
Вариант III
1.
Запишите числа, противоположные числам • 
5 6
2.
Упростите записи чисел: + -е—
7
З. Определите модули чисел
з
4. Запишите число в виде дроби с отрицательным 4 числителем.
5. Сократите дроби • 19 -36 •
— 45
13 -35 6. Приведите к знаменателю 120 дроби:
24 —56
23
-12 33
7*. Запишите числа:виде дро-
-24' -25' -35' —49
бей с положительными знаменателями.
Вариант
1.
Запишите числа, противоположные числам
5 з
2.
Упростите записи чисел: 1134). 4)
7
З.
Определите модули чисел: 7. 13
8' 14'
5
4. Запишите число в виде дроби с отрицательным 6 знаменателем.
5. Сократите дроби • 48 -26•
• -54' -39
6. Приведите к знаменателю 150 дроби: -13. -18 •
25 ' -27
7*.
Запишите числа• 17 -12 35 
виде дро-
• -19' -29' -37' -49
бей с положительными знаменателями.
с-14 Сравнение рациональных чисел
I
Сравните числа (1—4):
1.
17 17
6)
16 Найдите все несократимые дроби со
знаменателем 5, заключённые между числами
Вариант II
Сравните числа (1—4):
1.
а) и 6) 
2.
б)
14 14
З.в)
4.б) 17 -11 в)
36
5*. Найдите все несократимые дроби со знаменателем 5, заключённые между числами
Вариант III
Сравните числа (1—4)
-1313
1.
а) 6) 
-13 13 —15 15
2.
а)
14 14
12 32 39 52
З. а)
в)
51 71 52 61
19
4.
в)
32
5*. Найдите все несократимые дроби со знаменателем 8, заключённые между числами —1 и .
IV
Сравните числа 
-12 12
6)
11 -11 -13 13
-12
2. а)
13 13
31 41
З. и О; в)
27 52 53 51
37 
4. 6)
48 
5*. Найдите все несократимые дроби со
знаменателем 8, заключённые между числами —1 и
с-15 Сложение рациональных чисел
Вариант I
Выполните сложение (1—2):
1.
в)
11 11
2.
а)
11 •
1224 36
З. Выполните сложение и упростите ответ: 
13
42 14
4*. Найдите значение числового выражения
Вариант II
Выполните сложение (1—2):
1, б)
2. б) в)
•
1824
З. Выполните сложение и упростите ответ: 
11 
48 16
4*. Найдите значение числового выражения
III
Выполните сложение (1—2):
а)
13 •
13 1317 17
2. в)
11
• 2718
З. Выполните сложение и упростите ответ:
3926
4*. Найдите значение числового выражения
Вариант IV
Выполните сложение (1—2)
1.
а)
11 1117
|
2. |
|
36 27 •
З. Выполните сложение и упростите ответ: 
25
4*. Найдите значение числового выражения
с-16 Вычитание рациональных чисел
Вариант I
Выполните вычитание (1—2):
1, а)
в)
2.
а) в)
16 4'18 24
|
З. |
Выполните вычитание и
упростите ответ: |
48 16
4*. Найдите значение числового выражения 
•
II
Выполните вычитание (1—2):
6) в)
11 11
2. 
6)
5 15'
З.
Выполните вычитание и упростите ответ: •
42 14
4* Найдите значение числового выражения 
Вариант III
Выполните вычитание
(1—2)
1.
а) 
6)
11 11' 13 13'
2.
б) в)
36 27
З. Выполните вычитание и упростите ответ:
4*. Найдите значение числового выражения•
Вариант IV
Выполните вычитание
(1—2)
1. а)
13 13' 11 11'
2.
11 13 З. Выполните
вычитание и упростите ответ:
4* Найдите значение числового выражения•
с-17 Умножение рациональных чисел
Вариант I
1. Выполните умножение:
б)
10
Выполните умножение и упростите ответ (2—3)
2.
а)
4*. Подберите такую несократимую дробь 2 , для которой
верно равенство
Вариант II
1.
Выполните умножение: 
в)
7 5 '
Выполните умножение и упростите ответ (2—3)
2.
 |
з.
4*. Подберите такую несократимую дробь 2 , для которой
верно равенство
Вариант III
1. Выполните умножение:
Выполните умножение и упростите ответ (2—3)
2. 
з. 17. 12 13
13 • 14
4*. Подберите такую несократимую дробь 2 , для которой
верно равенство
Вариант IV
1. Выполните умножение:
а) 
Выполните умножение и упростите ответ (2—3)
2.
з. 18.
4*. Подберите такую несократимую дробь 2 , для которой верно равенство
с-18 Деление
рациональных чисел
Вариант I
1. Выполните деление:
Выполните деление и упростите ответ (2—4)
2. 
б)
15 —8:2 в) -27 : (-18).
17
Вариант II
1. Выполните деление:
5 . 7
а)
Выполните деление и упростите ответ (2—4)
2.
3 . 5 в)
22 
21
б)
в)
-28 : (-21).
Вариант III
1. Выполните деление:
13
2. 
Вариант IV
1. Выполните деление:
14
13
Выполните деление и упростите ответ (2—4):
2. 
в) -45 : (-18).
|
с-19 Вариант I |
|
Смешанные дроби |
|
1. Запишите дробь: |
в |
виде смешанной дроби обыкновенную |
|
11 а) |
|
|
|
2. Запишите дробь: |
в |
виде обыкновенной дроби смешанную |
6) -13. в)
37
11' 
З. Вычислите:
в) -5,32;
10
е) -12-2!
з)
Вычислите, применяя распределительный закон (4—5)
4. 
|
1. |
Запишите дробь: |
в |
виде смешанной дроби обыкновенную |
|
|
|
15 а) |
|
-12 6) |
35 |
|
2. |
Запишите дробь: |
в |
виде обыкновенной |
дроби смешанную |
|
|
а) 12; |
|
6) |
в) —3 2 . |
Вариант II
 |
11
З. Вычислите:
и) —1?.0.
Вычислите, применяя распределительный закон (4—5)
4.
Вариант III
1. Запишите в виде смешанной дроби обыкновенную дробь:
24 -33. 57
6) •
16
2. Запишите в виде обыкновенной дроби смешанную дробь:
6) -54; в) -зц.
12
З. Вычислите:
в)
15'
д)
—62 + 22; 
11 11'
и)
Вычислите, применяя распределительный закон (4—5)
-13! .1—
16 •
23 23
|
5*. 11 Вариант IV |
-112 . |
||
|
|
11 |
||
|
1. |
Запишите дробь: |
в |
виде смешаннои дроби обыкновенную |
|
|
25. |
|
17 |
|
2. |
Запишите дробь: |
в |
виде обыкновенной дроби смешанную |
|
|
а) 5 4 ; |
|
13 |
|
З. |
Вычислите:
|
|
|
6) 
в) •
г)
3! : (—15); д) —52 е) -32-
ж)
4 2 .
з) и)
13
Вычислите, применяя распределительный закон (4—5)
4. -11!.1 11 -11!.2!!.
27 27
5*. 12112 .72+ -122 . - 12— 12 12
с-20 Действия с рациональными числами Вариант I
Найдите значение выражения (1—5)
1. 
з 10 • 15 •
з. 
5*. 22. 5- 11
2 +112. 2
13 13 13 13
Вариант II
Найдите значение выражения (1—5)
2-
2 
11 11
Вариант III
Найдите значение выражения (1—5)
1. з.
52.
122- + 122- . 5
15 15 15 15
Вариант IV
Найдите значение выражения (1—5):
1. 7+12. 
с-21 Представление рациональных чисел на координатной прямой Вариант I
1. Запишите координаты точек А, В, С и D, изображённых на рисунке.
2. Изобразите координатную ось, выбрав удобный единичный отрезок, и отметьте на ней точки 0(0), М Д , лт —1! , К —2! и 1., 1! . Определите:
а) расстояние МК;
б) координату середины отрезка МК.
З. Вычислите среднее арифметическое чисел:
б) З, 8 и 10.
4. Среднее арифметическое двух рациональных чисел т и п больше нуля. Сравните модули чисел т и п, если известно, что т > О, п < О.
5*. Определите координату точки М
отрезка АВ, если А -2 2 , В 5!
2
Вариант II
1. Запишите координаты точек А, В, С и D, изображённых на рисунке.
2. Изобразите координатную ось, выбрав удобный единичный отрезок, и отметьте на ней точки 0(0), М Ц , лт —1 2 , К —2! и 1., 3! . Определите:
а) расстояние NL;
б) координату середины отрезка kL.
З. Вычислите среднее арифметическое чисел:
4. Среднее арифметическое двух рациональных чисел т и п меньше нуля. Сравните модули чисел т и п, если известно, что т > О, п < О.
5*. Определите координату точки М
отрезка АВ, если А -3 2 , В 4?
з
Вариант III
1. Запишите координаты точек А, В, С и D, изображённых на рисунке.
2. Изобразите координатную ось, выбрав удобный единичный отрезок, и отметьте на ней точки 0(0),
Определите:
а) расстояние kL;
б) координату середины отрезка NL.
З. Вычислите среднее арифметическое чисел:
в) 5, 6, 7 и 10.
4. Среднее арифметическое двух рациональных чисел т и п больше нуля. Сравните модули чисел т и п, если известно, что т > п.
5*. Определите координату точки М отрезка АВ, если
з
Вариант IV
1. Запишите координаты точек А, В, С и 1), изображённых на рисунке.
2.
Изобразите координатную ось, выбрав удобный единичный отрезок, и
отметьте на ней точки 0(0), М Д , -1! , К 2! 
-15 . Определите:
а) расстояние ML;
б) координату середины отрезка Nk.
З. Вычислите среднее арифметическое чисел:
4. Среднее арифметическое двух рациональных чисел т и п меньше нуля. Сравните модули чисел т и п, если известно, что т > п.
5*. Определите координату точки М отрезка АВ, если
А -4! , В 42 и АЛЛ : МВ - 6 : 5.
з
с-22 Уравнения Вариант I
1. Определите, какое из чисел З, 5, —2 является корнем уравнения
х + (8 - зх) = 12.
Решите уравнение (2—4):
эх) = 13.
1 1
з. —х—1=— 43)
2
4* 3х-1 _ 2х+3
- 1.
4 з
Вариант II
1. Определите, какое
из чисел 4, 6, —3 является корнем уравнения
х + (7 - 2х) = 10.
Решите уравнение
(2—4): 2. а) 3х+ 5- 23.
з. —х—11 з
3х+2 2х-1
-2.
4 з
Вариант III
1. Определите, какое из чисел —3, —5, 2 является корнем уравнения
2х + (11 - 4х) = 21.
Решите уравнение (2—4):
2.
а) 7х + 13 - -5х+
25; 
29.
з. 
4х+1 3х-2
-3.
2 5
Вариант IV
1. Определите, какое из чисел —3, —4, 4 является корнем уравнения
3х + (13 - 8х) = 33.
Решите уравнение (2—4)
2. а) бх + 12 -7х + 25; 6) х + - зх) - 35.
з.54).
4.
2 5
с-23* Уравнения с модулями
Вариант I
Решите уравнение (1—4):
1.
а) 13х - 11 = 2; б)
Вх
2. 13-12х-91= 12.
Вариант II
Решите уравнение
б) 9х 6l -2;
71 — О.
2. 14- 12х- 71 = 11.
Вариант III
Решите уравнение
6) дох- 5' -3;
о.
10.
з] + 61 = 6.
Вариант IV
Решите уравнение (1—4):
О.
2. 16
З. Их — 2] — 5' = 6. 
орх + - + 3' = 6.
с-24* Решение задач с помощью уравнений Вариант I
1. Обозначьте одну неизвестную величину буквой х, выразите через х другую неизвестную величину, составьте уравнение по условию задачи:
а) Одно число в 6 раз больше другого, а их сумма равна 140. Найдите меньшее число. б) Одно число в 5 раз больше другого, а их разность равна 160. Найдите меньшее число.
в) Брат на 5 лет старше сестры, а сумма их возрастов 23 года. Сколько лет сестре?
Решите задачу с помощью уравнения (2—3):
2. За 4 одинаковых блокнота и 2 одинаковых альбома заплатили 112 р. Один альбом дороже одного блокнота на 8 р. Сколько стоит один блокнот?
3*. В первом классе было 28 учащихся, а во втором половина числа учащихся первого и третьего классов вместе. Всего в трёх классах было 90 учащихся. Сколько учащихся было во втором классе?
Вариант II
1. Обозначьте одну неизвестную величину буквой х, выразите через х другую неизвестную величину, составьте уравнение по условию задачи:
а) Одно число в 5 раз больше другого, а их сумма равна 180. Найдите меньшее число. б) Одно число в 6 раз больше другого, а их разность равна 120. Найдите меньшее число.
в) У сестры на 20 р. больше, чем у брата, а вместе у них 100 р. Сколько рублей у брата?
Решите задачу с помощью уравнения (2—3):
2. За 4 булочки и 2 ватрушки заплатили 68 р. Одна ватрушка на 4 р. дороже одной булочки. Сколько стоит одна булочка?
3*. В первом классе было 29 учащихся, а во втором половина числа учащихся первого и третьего классов вместе. Всего в трёх классах было 84 учащихся. Сколько учащихся было во втором классе?
Вариант III
1. Обозначьте одну неизвестную величину буквой х, выразите через х другую неизвестную величину, составьте уравнение по условию задачи:
а) Одно число в 7 раз больше другого, а их сумма равна 440. Найдите большее число. б) Одно число в 8 раз больше другого, а их разность равна 420. Найдите большее число.
в) Сегодня Катя выполнила домашнее задание по математике на 10 мин быстрее, чем вчера, а за эти два дня она потратила на домашние задания по математике 60 мин. Сколько минут Катя выполняла домашнее задание по математике вчера?
Решите задачу с помощью уравнения (2—3):
2. Первую часть пути поезд прошёл за 5 ч, а втоРУК) за З ч. Первую часть пути он шёл с некоторой постоянной скоростью, а вторую часть пути со скоростью, на 10 км/ч большей. Всего он прошёл 510 км. Чему равна скорость поезда на первом участке пути?
3*. Ученик задумал число, увеличил его
в 2 раза, к полученному числу прибавил задуманное, затем полученную сумму
уменьшил в 4 раза и получил 27. Какое 
число он задумал?
Вариант IV
1. Обозначьте одну неизвестную величину буквой х, выразите через х другую неизвестную величину, составьте уравнение по условию задачи:
а) Одно число в 8 раз больше другого, а их сумма равна 360. Найдите большее число. б) Одно число в 7 раз больше другого, а их разность равна 360. Найдите большее число.
в) Сегодня Вася прочитал на 6 страниц больше, чем вчера, а за эти два дня он прочитал 56 страниц. Сколько страниц он прочитал вчера?
Решите задачу с помощью уравнения (2—3):
2. Первую часть пути автомобиль проехал за 4 ч, а втоРУК) за З ч. Первую часть пути он ехал с некоторой постоянной скоростью, а вторую часть пути со скоростью, на 10 км/ч большей. Всего он проехал 520 км. Чему равна скорость автомобиля на первом участке пути?
Ученик задумал число,
увеличил его в З раза, к полученному числу прибавил задуманное, затем
полученную сумму уменьшил в З раза и получил 28. Какое число он задумал?
с-25 Упрощение выражений
Вариант I
1. Приведите подобные слагаемые:
а) 4а + 5а; 6)
130- 2а•,
г) -70 - ба; д) За — а; е) а + 8а.
2. Упростите выражение:
а) 46+ 5+ ЗЬ- З•, 6) Ь- 4 + 56- 7;
- 9);
д) 76 + 3(b- 1);
З. Задумали число, прибавили к нему 20, результат умножили на 2 и из полученного числа вычли удвоенное задуманное число. Какое число получили в результате всех вычислений?
4*. Докажите, что значение выражения
7(8х- 1)- 11(х + 13) - 45х- 1 не зависит от х.
Вариант II
1. Приведите подобные слагаемые:
6) 110 - за;
г) —4а — ба; д) 7а — а;
2. Упростите выражение:
а) ЗЬ+6+ 46-4; 6) Ь- 5 +46-8;
г) (36- 5) - (26- 9);
д) 5b + 4(b — 2); е) 56- + 2).
З. Задумали число, прибавили к нему 10, результат умножили на З и из полученного числа вычли утроенное задуманное число. Какое число получили в результате всех вычислений?
4*. Докажите, что значение выражения
8(7х + 3) - 22(х - 1) - 34х + 9
не зависит от х.
Вариант III
1. Приведите подобные слагаемые:
а) 12а + 15а; 6) 12а - 12а•,
г) -270 - 16а; д) 31а — а;
в) —1 За + 14а;
е) а + 18а.
|
2. |
Упростите выражение: а) 7b+ 7+ 11b- 13; 6) Ь- 24 + 156-17;
д) 86 + 9(b- 7); е) 56- 22(b + 4). |
|
З. |
Задумали число, прибавили к нему 20, результат ум- |
г)
(126- 9) - (9b - 8);ножили на 2 и к тому, что получилось, прибавили 7. Из полученного числа вычли удвоенное задуманное число. Какое число получили в результате всех вычислений?
4*. Докажите, что значение выражения
6(7х+ 1) - 33(х+ 13) - - 13
не зависит от х.
Вариант IV
1.
Приведите подобные слагаемые: 
а) 14а + 1 За; 6) 15а- 11а•, в) —3а + За;
г) —6а — ба; д) 32а — а; е) а + 19а.
2. Упростите выражение:
а) 6b+ 6+ 136- 11; б) ь- 23 + 136-8;
в) -1ЗЬ-8+(Ь + 8); г) (126 - 8) - (9b - 9);
д)
96 + чь- 6); 
З. Задумали число, прибавили к нему 10, результат умножили на З и к тому, что получилось, прибавили 6. Из полученного числа вычли утроенное задуманное число. Какое число получили в результате всех вычислений?
4*. Докажите, что значение выражения
7(6х - 3) - 44(х+ 13) + 2х+ 15
не зависит от х.
с-26 Десятичные дроби. Сравнение десятичных дробей
Вариант I
1. Запишите десятичную дробь в виде обыкновенной дроби:
а) 0,3; 6) 0,24; в) 3,025; г) 4,50.
2. Запишите обыкновенную дробь в виде десятичной дроби:
12 з
в)
• 4'5' 25
З. Запишите величину, используя десятичную дробь:
а) 13 р. 45 к.; б) 5 м 2 дм; в) 4 т 50 кг.
4. Сравните десятичные дроби:
а) 3,80 и 3,8; 6) 52,47 и 52,7;
в) 4,003 и 4,03; г) 3,51 и 4.
|
5*. Сравните дроби: |
|
|
|
а) 3! и 3,1; Вариант II |
6) 32 и 3,27; 25 |
|
|
1. Запишите дроби: |
десятичную дробь в |
виде обыкновенной |
|
а) 0,7; |
6) 0,25; в) 3,012; |
г) 3,40. |
|
2. Запишите |
обыкновенную дробь |
в виде десятичной |
дроби:
з 4 1
6) в) •
4' 5' 20
З. Запишите величину, используя десятичную дробь:
а) 28 р. 12 к.; б) 2 м 5 дм; в) 5 т 40 кг.
4. Сравните десятичные дроби:
а) 8,3 и 8,30; 6) 43,58 и 43,8;
в) 3,04 и 3,004; г) 5,41 и 6.
5*. Сравните дроби:
|
а) 4? и 4,5, 6) 52 и 5,23; 25 Вариант III |
и 1,24. |
|
1. Запишите десятичную дробь в дроби: |
виде обыкновенной |
|
а) 0,15; 6) 2,08; в) 5,036; |
г) 6,050. |
|
2. Запишите обыкновенную дробь дроби: з з 4 а) в) |
в виде десятичной |
• 20' 8' 125
З. Запишите величину, используя десятичную дробь:
а) 32 р. 5 к.; б) 6 м З дм; в) 7 т 5 кг.
4. Сравните десятичные дроби:
а) 5,070 и 5,07; 6) 42,43 и 42,34;
в) 7,006 и 7,06; г) 7,56 и 8.
5*. Сравните дроби: 
а) 5! и 5,5, и 7,14; в) 32 и 3,36.
25 20
Вариант IV
|
1. |
Запишите дроби: |
десятичную дробь в виде обыкновенной |
|
|
а) 0,45; |
6) 3,04; в) 4,075; г) 5,050. |
|
2. |
Запишите |
обыкновенную дробь в виде десятичной |
дроби:
7 1 з
а) 6) в) • 20' 8' 125
З. Запишите величину, используя десятичную дробь:
а) 19р. 7 к.; б) Зм 6 дм; в) 5 т 7 кг.
4. Сравните десятичные дроби:
а) 7,050 и 7,05; б) 4 42 и ;
в) 6,07 и 6,007; г) 6,51 и 7.
5*. Сравните дроби:
а) 6! и 6,9; б) 42 и 4,11; в) 5 2 и 5,14.
25 20
с-27 Сложение и вычитание десятичных дробей
|
Вариант I 1. Вычислите: |
|
|
|
а) 3,54 + 2,31; |
6) 6,09 + 7,38; |
в) 15,7+ 1,57; |
|
г) 3,29 - 1,8; |
д) - 1,28; |
е) 7- 3,54. |
Найдите значение выражения (2—3)
2. + 0,03 -0,003 + 0,0003.
13 - (24,903 - 21,22 + 3,0434) - (38,52 34
Вариант II
1. Вычислите:
|
а) 2,73 + 3,24; |
6) 7,25 + 2,08; |
в) 35,4 + 3,54; |
|
г) 5,37-2,9; |
д) - 1,36; |
е) — 2,45. |
Найдите значение выражения (2—3)
2.
-0,002 + 0,0002.
15 - (44,132 - 39,28 + 3,0502) - (43,34 42,813).
Вариант III
1. Вычислите:
а) 5,42 +
2,39;
+ 7,921; 23,95 + 3,395;
г) 4,729- 1,99; д)
- 5,98; е) 8-2,37.
Найдите значение выражения (2—3):
2.
-0,0023.
18 - (45,291 -40,17 + 4,0603) - (57,49 - 54,139).
Вариант IV
1. Вычислите:
а) 7,56 + 3,28; 6) 4,529 +0,8; в) 3,259 + 32,59;
г) 5,789- 2,99; д) - 2,89; е) 7- 3,28.
Найдите значение выражения (2—3):
2.
-0,0032.
+ 5,0424) - (64,23 - 60,391).
|
с-28 Вариант I 1. Вычислите: |
Умножение десятичных дробей |
|
|
а) 54,56 • 10; |
6) 37,57 • 100; |
в) 89,19 • 1000; |
|
г) 54,56 • 0,1; |
д) 37,57 • 0,01; |
е) 89,19 • 0,001. |
|
2. Известно, что |
123 • 654 = 80 442. |
Вычислите: |
|
а) 12,3 • 654; |
6) 12,3, 65,4; |
в) 1,23 • 65,4; |
|
г) 1,23 • 6,54; З. Вычислите: |
д) 0,123 6,54; |
е) 0,0123 . 6,54. |
|
а) 39,1 • 83; |
6) 0,375 • 4,2; |
в) 0,765 • 0,23. |
4*. Найдите значение числового выражения
4,5678 • 0,25 • • 1,25 • 0,04.
Вариант II
1. Вычислите:
а) 45,65 • 10; 6) 73,85 . 100; в) 98,91 • 1000;
г) 45,65 0,1; д) 73,85 • 0,01; е) 98,91 • 0,001.
2. Известно, что 321 • 234 = 75 114. Вычислите:
а) 32,1 • 234; 6) 32,1 23,4; в) 32,1 2,34;
г) 3,21 • 2,34; д) 0,321 2,34; е) 0,0321 • 2,34.
З. Вычислите:
а) 53,2 34; 0,237 • 5,3; 0,657 • 0,32.
4*. Найдите значение числового выражения
5,6789 • 2,5 0,08 • 12,5 • 0,04.
Вариант III
1. Вычислите:
|
|
а) 14,76 10; 6) 87,98 . 100; |
в) 78,46 1000; |
|
|
|
е) 78,46 • 0,001. |
|
2. |
Известно, что 234 765 = 179 010. |
Вычислите: |
|
|
а) 234 • 76,5; 6) 23,4 76,5; |
в) 2,34 • 76,5; |
|
|
г) 23,4 • 0,765; д) 2,34 0,765; |
е) 0,234 • 0,765. |
|
З. |
Вычислите: |
|
|
|
а) 92,3 • 35; 6) 0,754 • 14,2; |
в) 0,654 • 0,304. |
4*. Найдите значение числового выражения
13,456 0,25 • • 0,125 • 0,4.
Вариант
1. Вычислите:
|
|
а) 41,67 • 10; 6) 78,89 100; |
в) 87,64 • 1000; |
|
|
г) 41,67 , 0,1; д) 78,89 • 0,01; |
е) 87,64 • 0,001. |
|
2. |
Известно, что 432 • 345 = 149 040. |
Вычислите: |
|
|
а) 43,2 • 345; 6) 43,2 34,5; |
в) 4,32 34,5; |
|
|
г) 0,432 34,5; д) 0,432 3,45; |
е) 0,0432 • 3,45. |
|
З. |
Вычислите: |
|
|
|
а) 93,2 • 53; 6) 0,745 12,4; |
в) 0,543 • 0,203. |
4*. Найдите значение числового выражения
14,567 • 2,5 • 0,08 • 1,25 • 0,04.
с-29 Деление десятичных дробей
Вариант I
1. Вычислите:
а) 47,25 : 10; 6) 23,67 : 100; в) 91,58 : 1000;
г) 47,25 : 0,1; д) 23,67 : 0,01; е) 91,58 : 0,001.
2. Перенесите запятую в делимом и делителе так, чтобы делитель стал натуральным числом:
а) 9,18 : 3,4;
в) 0,2916 : 0,324;
д) 675,6 : 0,563; 6) 89,708 : 5,47;
г) 15,3 : 0,45;
е) 14 136 : 0,456.
З. Вычислите:
а) 15,12 : 4,2; 217,6 : 0,34; 22,1 : 0,065.
4*. Найдите значение выражения
0,75 : 
+ 0,7182 : 0,14 + 0,00532 : 0,028.
Вариант II
1. Вычислите:
а) 74,52 : 10; 6) 32,76 : 100; в) 19,85 : 1000;
г) 74,52 : 0,1; д) 32,76 : 0,01; е) 19,85 : 0,001.
2.
Перенесите 
в делимом и
делителе так, чтобы делитель стал натуральным числом:
|
а) 6,88 : 4,3; |
6) 23,318 : 6,27; |
|
в) 0,7254 : 0,234; |
г) 32,4 : 0,54; |
|
д) 783,6 : 0,653; |
е) 53 298 : 0,567. |
З. Вычислите:
а) 24,48 : 3,6; 6) 301,5 : 0,45; в) 518,7 : 0,057.
4*. Найдите значение выражения
|
а) 67,54 : 10; |
|
в) 79,86 : 1000; |
|
г) 67,54 : 0,1; |
|
е) 79,86 : 0,001. |
0,96 : 
+ 0,7695 : 0,15 + 0,00486 : 0,027.
Вариант III
1. Вычислите:
|
а) 76,45 : 10; |
6) 43,65 : 100; |
в) 97,68 : 1000; |
|
г) 76,45 : 0,1; |
д) 43,65 : 0,01; |
е) 97,68 : 0,001. |
2. Перенесите запятую в делимом и делителе так, чтобы делитель стал натуральным числом:
|
а) 54,88 : 5,6; |
6) 42,462 : 6,74; |
|
в) 1,0602 : 0,342; |
г) 60,45 : 0,65; |
|
д) 733,2 : 0,564; |
е) 12 255 : 0,645. |
З. Вычислите:
а) 87,22 : 8,9; 6) 172,8 : 0,64; в) 30,6 : 0,075.
4*. Найдите значение выражения
0,91 : + 0,9824 : 0,16 + 0,00936 : 0,039.
Вариант IV
1. Вычислите:
2. Перенесите запятую в делимом и делителе так, чтобы делитель стал натуральным числом:
а) 4,68 : 6,5; 6) 24,684 : 7,26; в) 0,2538 : 0,423;
г) 72,8 : 0,56; д) 502,2 : 0,465; е) 21 696 : 0,678.
З. Вычислите:
а) 59,78 : 9,8; 6) 345,6 : 0,54; в) 516,8 : 0,085.
4*. Найдите значение выражения
0,96 : + 0,5418 : 0,17 + 0,00133 : 0,038.
с-зо Десятичные дроби и проценты
Вариант I
1. На какую десятичную дробь надо умножить число, чтобы найти:
а) 13 % этого числа;
б) 9 % этого числа;
в) 12094 этого числа?
2. Найдите:
а) 12 % числа 450;
б) 8 % числа ЗОО;
в) 110 0/0 числа 550.
З. Найдите число, если:
а) 24 % этого числа равны 480;
б) 18 % этого числа равны 540.
4*. Найдите число, 14 % которого равны 17 % числа 280.
Вариант II
1. На какую десятичную дробь надо умножить число, чтобы найти:
а) 15 % этого числа;
б) 7 % этого числа;
в) 130 % этого числа?
2. Найдите:
а) 14 % числа 350;
б) 6 % числа 700;
в) 120 % числа 450.
З. Найдите число, если:
а) 32 % этого числа равны 640;
б) 27 % этого числа равны 810.
4*. Найдите число, 15 % которого равны 16 % числа ЗОО.
Вариант III
1. На какую десятичную дробь надо умножить число, чтобы найти:
|
|
а) 27 % этого числа; в) 140 % этого числа? |
б) 4 % этого числа; |
|
2. |
Найдите: |
|
|
|
а) 28 % числа 650; в) 125 % числа 580. |
б) 3 0/0 числа 900; |
З. Найдите число, если:
а) 34 % этого числа равны 17;
б) 36 % этого числа равны 90.
4*. Найдите число, 16 % которого равны 15 % числа 320.
Вариант IV
1. На какую десятичную дробь надо умножить число, чтобы найти:
|
|
а) 29 % этого числа; в) 150 0/0 этого числа? |
б) 5 % этого числа; |
|
2. |
Найдите: |
|
|
|
а) 24 % числа 550; |
б) 8 % числа 700; |
в) 135 % числа 480.
З. Найдите число, если:
а) 32 % этого числа равны 16;
б) 38 % этого числа равны 133.
4*. Найдите число, 17 % которого равны 14 % числа 340.
с-31* Сложные задачи на проценты Вариант 
1. Увеличьте число а на 14 % этого числа.
2. На какую десятичную дробь надо умножить число а, чтобы увеличить его:
а) на 1596; б) на 2096; в) на 27 0/0?
З. Вкладчик положил в банк 20 ООО р. Банк начисляет ежегодно 9 % дохода на сумму вклада, находящуюся на счёте вкладчика в начале года. Какая сумма будет на счёте через два года?
4*. Одна акция компании стоила 50 р. Во вторник цена акции повысилась на 10 % , а в среду понизилась на 10 0/0. Сколько стала стоить одна акция этой компании после двух изменений цены?
Вариант II
1. Увеличьте число а на 15 % этого числа.
2. На какую десятичную дробь надо умножить число а, чтобы увеличить его:
а) на 14 0/0 ; б) на 25 % ; в) на 2996?
З. Вкладчик положил в банк 30 ООО р. Банк начисляет ежегодно 8 % дохода на сумму вклада, находящуюся на счёте вкладчика в начале года. Какая сумма будет на счёте через два года?
4*. Одна акция компании стоила 100 р. В среду цена акции понизилась на 10 0/0, а в четверг повысилась на 10 0/0. Сколько стала стоить одна акция этой компании после двух изменений цены?
Вариант III
1. Увеличьте число а на 24 % этого числа.
2. На какую десятичную дробь надо умножить число а, чтобы увеличить его:
а) на 2194; 6) на 37%•, в) на 7,5 0/0?
З. Вкладчик положил в банк 40 ООО р. Банк начисляет ежегодно 11 % дохода на сумму вклада, находящуюся на счёте вкладчика в начале года. Какая сумма будет на счёте через два года?
4*. Одна акция компании стоила 150 р. За первую неделю цена акции повысилась на 20 % , а за следующую понизилась на 20 % . Сколько стала стоить одна акция этой компании после двух изменений цены?
Вариант IV
1. Увеличьте число а на 23 % этого числа.
2. На какую десятичную дробь надо умножить число а, чтобы увеличить его:
а) на 22 0/0 ; б) на 36 % ; в) на 6,5 0/0?
З. Вкладчик положил в банк 50 ООО р. Банк начисляет ежегодно 12 % дохода на сумму вклада, находящуюся на счёте вкладчика в начале года. Какая сумма будет на счёте через два года?
4*. Одна акция компании стоила 200 р. За первую неделю цена акции понизилась на 30 % , а за следующую повысилась на 30 % . Сколько стала стоить одна акция этой компании после двух изменений цены?
с-32* Использование вспомогательных букв при решении задач на проценты Вариант I
1. Во вторник цена акции повысилась на 30 % , в среду она понизилась на 10 % . Повысилась или понизилась цена акции за эти два дня и на сколько процентов?
2. У Васи пятёрок на 75 % меньше, чем у Коли. На сколько процентов у Коли пятёрок больше, чем у Васи?
3*. Первое число на 40 0/0 больше, чем второе, и на 60 % меньше, чем третье. На сколько процентов третье число больше, чем второе?
Вариант II
1. Во вторник цена акции повысилась на 10 % , в среду она понизилась на 30 % . Повысилась или понизилась цена акции за эти два дня и на сколько процентов?
2. У Маши пятёрок на 150 % больше, чем у Вали. На сколько процентов у Вали пятёрок меньше, чем у Маши?
3*. Первое число на 40 0/0 меньше, чем второе, и на 25 % больше, чем третье. На сколько процентов третье число меньше, чем второе?
Вариант III
1. Во вторник цена акции повысилась на 20 0/0, в среду она понизилась на 40 0/0. Повысилась или понизилась цена акции за эти два дня и на сколько процентов?
2. Первое число на 20 % меньше, чем второе. На сколько процентов второе число больше, чем первое?
3*. На помидоры мама потратила денег на 25 % меньше, чем на огурцы, и на 200 0/0 больше, чем на картофель. На сколько процентов меньше она потратила денег на картофель, чем на огурцы?
Вариант IV
1. Во вторник цена акции повысилась на 40 % , в среду она понизилась на 20 % . Повысилась или понизилась цена акции за эти два дня и на сколько процентов?
2. Первое число на 25 % больше, чем второе. На сколько процентов второе число меньше, чем первое?
3*. На груши папа потратил денег на 50 % меньше, чем на сливы, и на 50 % больше, чем на яблоки. На сколько процентов больше он потратил денег на сливы, чем на яблоки?
Практические задачи но проценты
I
1. Яблоки при сушке теряют 75 % своей массы.
а) Сколько килограммов сушёных яблок получится из 50 кг свежих?
б) Сколько килограммов свежих яблок надо взять, чтобы получить 2,5 кг сушёных?
2. Яблоки содержат 78 % воды. При сушке они теряют 75 % своей массы. Сколько процентов воды содержат сушёные яблоки?
3*. Яблоки содержат 78 % воды. Их немного подсушили, и теперь они содержат 45 % воды. Сколько процентов своей массы яблоки потеряли при сушке?
Вариант II
1. Груши при сушке теряют 80 0/0 своей массы.
а) Сколько килограммов сушёных груш получится из 45 кг свежих?
б) Сколько килограммов свежих груш надо взять, чтобы получить 3,2 кг сушёных?
2. Груши содержат 83 % воды. При сушке они теряют 80 0/0 своей массы. Сколько процентов воды содержат сушёные груши?
3*. Груши содержат 83 % воды. Их немного подсушили, и теперь они содержат 75 % воды. Сколько процентов своей массы груши потеряли при сушке?
Вариант III
1. Сливы при сушке теряют 76 % своей массы.
а) Сколько килограммов сушёных слив получится из 60 кг свежих?
б) Сколько килограммов свежих слив надо взять, чтобы получить 28,8 кг сушёных?
2. Сливы содержат 79 % воды. При сушке они теряют 76 % своей массы. Сколько процентов воды содержат сушёные сливы?
3*. Сливы содержат 79 % воды. Их немного подсушили, и теперь они содержат 70 % воды. Сколько процентов своей массы сливы потеряли при сушке?
Вариант IV
1. Абрикосы при сушке теряют 65 % своей массы.
а) Сколько килограммов сушёных абрикосов получится из 44 кг свежих?
б) Сколько килограммов свежих абрикосов надо взять, чтобы получить 17,5 кг сушёных?
2. Абрикосы содержат 72 % воды. При сушке они теряют 65 % своей массы. Сколько процентов воды содержат сушёные абрикосы?
3*. Абрикосы содержат 72 % воды. Их немного подсушили, и теперь они содержат 60 % воды. Сколько процентов своей массы абрикосы потеряли при сушке?
С—34 Десятичные дроби произвольного знака Вариант I
Найдите значение выражения (1—5):
1. (0,24 - 0,08 • (-2,3)) : (-0,4).
2. 9,8 - 4,8 : (-0,65 - 0,15).
з. (-7,2 + 4,4) • (-0,5) - 3,9 + 0,4.
4. (-0,42) : (1,75 - 3,5 • (-0,1)) : (-0,05).
5,25 • (-0,1 + 3,05) - 3,05 • (5,25 -0,1).
Вариант П
Найдите значение выражения (1—5):
1. (8,56 + 7,2 • (-0,85)) : (-0,8).
2. 8,62 - 12,8 : (-2,4 - 0,8).
з. (-5,7 + 3,3) • (-3,5) - 8,9 + 0,4.
4. (-14,4) : (2,4 - 0,8 • (-4,5)) :
(-0,15). 
4,64 • (—0,1 + — • (4,64 — 
Вариант III
Найдите значение выражения (1—5):
1. (1,356 + 0,15 (-0,64)) : (-0,12).
2. - 2,4 : (-1,15 - 0,35).
з. (-7,4 + 2,6) • (-2,5) - 3,8 + 1,2.
4. 24,3) : (4,5 - 4,5 • (-0,8)) : (-0,25).
9,57 • (-0,4 + 6,07) - 6,07 • (9,57 - 0,4).
IV
Найдите значение выражения (1—5)
1. (0,462 - 0,28 • (-3,5)) : (-0,35). 2. 4,08 - 3,84 : (-3,3 - 1,5).
з. (-9,6 + 5,2) • (-1,5) - + 1,3.
4. (-9,24) : (2,8 - 2,8 • (-0,5)) : (-0,4).
3,14 • (-0,3 + 9,04) - 9,04 • (3,14 - 0,3).
с-35 Совместные действия с обыкновенными и десятичными дробями произвольного знака
Вариант I
Вычислите (1—2)
1.
-0,3; 
в) г)
о 48 12 
13
2.
-3,3;
г) -3,25 : 2!.
Найдите значение выражения (3—4)
-2 18 •
25
Вариант II
Вычислите (1—2)
|
|
|
Найдите значение выражения (3—4)
З. —5,25 : 5!+2. (—1,4) З19 •
20
Вариант III
Вычислите (1—2):
|
1. |
а) |
|
б) + 0,3; |
|
|
|
- . 1,2; |
г) о 72 48 49 |
|
2. |
|
|
6) 3 1 -5,7; |
Найдите значение
выражения (3—4) 
-22.
95
Вариант IV
Вычислите (1—2)
1. — 0,4; б) + 0,5;
11
15 в) г)
о 75
46
2.
4,8;
в) 1! . (—3,5); г) -4,32 : 2!.
Найдите значение выражения (3—4)
-2Ц •
85
с-36 Приближения десятичных дробей
I
1. Укажите приближение десятичной дроби 13,529 с недостатком с точностью: а) до одной единицы; б) до одной десятой; в) до одной сотой.
2. Укажите приближение десятичной дроби 13,529 с избытком с точностью: а) до одной единицы; б) до одной десятой; в) до одной сотой.
З. Округлите десятичную дробь 13,529: а) до единиц;
б) до десятых; в) до сотых.
4. Округлите десятичную дробь: а) 143,95 до единиц;
б) 19,328 до десятых; в) 1,928 до сотых.
5*. Округлите десятичную дробь а 9382, 7461:
а) до единиц; б) до десятых; в) до сотых;
г) до тысячных; д) до десятков; е) до сотен;
ж) до тысяч.
Вариант II
1. Укажите приближение десятичной дроби 26,294 с недостатком с точностью: а) до одной единицы; б) до одной десятой; в) до одной сотой.
2. Укажите приближение десятичной дроби 26,294 с избытком с точностью: а) до одной единицы; б) до одной десятой; в) до одной сотой.
З. Округлите десятичную дробь 26,294: а) до единиц;
б) до десятых; в) до сотых.
4. Округлите десятичную дробь: а) 254,82 до единиц;
б) 18,237 до десятых; в) 3,546 до сотых.
5* Округлите десятичную дробь а = 3829,4617:
а) до единиц; б) до десятых; в) до сотых;
г) до тысячных; д) до десятков; е) до сотен;
ж) до тысяч.
Вариант III
1. Укажите приближение десятичной дроби 51,738 с недостатком с точностью: а) до одной единицы; б) до одной десятой; в) до одной сотой.
2. Укажите приближение десятичной дроби 51,738 с избытком с точностью: а) до одной единицы; б) до одной десятой; в) до одной сотой.
З. Округлите десятичную дробь 51,738: а) до десятков;
б) до единиц; в) до десятых; г) до сотых.
4. Округлите десятичную дробь: а) 149,81 до единиц;
б) 24,137 до десятых; в) 11,835 до сотых.
5*. Округлите десятичную дробь а 8293,6174:
а) до единиц; б) до десятых; в) до сотых;
г) до тысячных; д) до десятков; е) до сотен;
ж) до тысяч.
Вариант IV
1. Укажите приближение десятичной дроби 25,384 с недостатком с точностью: а) до одной единицы; б) до одной десятой; в) до одной сотой.
2. Укажите приближение десятичной дроби 25,384 с избытком с точностью: а) до одной единицы; б) до одной десятой; в) до одной сотой.
З. Округлите десятичную дробь 25,384: а) до десятков;
б) до единиц; в) до десятых; г) до сотых.
4. Округлите десятичную дробь: а) 239,52 до единиц;
б) 34,346 до десятых; в) 22,829 до сотых.
5*. Округлите десятичную дробь а 2938,1746:
а) до единиц; б) до десятых; в) до сотых;
г) до тысячных; д) до десятков; е) до сотен;
ж) до тысяч.
С-37 Приближённые вычисления
Вариант I
1. Округлив числа а и Ь с точностью до 0,01, вычислите приближённо сумму а + Ь и разность а — Ь:
а) а = 4,8394, Ь = 1,783; 6) а = 45,394, 23,728.
2. Округлите числа а и Ь с точностью до двух значащих цифр, вычислите приближённо произведение а • Ь и частное а : Ь. Результат округлите с точностью до двух значащих цифр:
а) а = 25,19, Ь-
4,354; 6) а = 53,74,
3*. Стороны прямоугольника измерили приближённо: а 12,7 м, Ь 4,88 м. Вычислите приближённо:
а) периметр прямоугольника с точностью до десятых долей метра;
б) площадь прямоугольника с точностью до трёх значащих цифр.
II
1. Округлив числа а и Ь с точностью до 0,01, вычислите приближённо сумму а + Ь и разность а — Ь:
а) а = 5,9283, 2,694; 6) а = 36,483, Ь- 44,937.
2. Округлите числа а и Ь с точностью до двух значащих цифр, вычислите приближённо произведение а • Ь и частное а : Ь. Результат округлите с точностью до двух значащих цифр:
а) а - 32,27, Ь- 4,263; 6) а = 46,62, 5,729.
3*. Стороны прямоугольника измерили приближённо: а 13,2 м, b z 4,09 м. Вычислите приближённо:
а) периметр прямоугольника с точностью до десятых долей метра;
б) площадь прямоугольника с точностью до трёх значащих цифр.
Вариант III
1. Округлив числа а и Ь с точностью до 0,01, вычислите приближённо сумму а + Ь и разность а — Ь:
а) а = 5,9082, 3,691; 6) а = 38,083, 21,906.
2. Округлите числа а и Ь с точностью до трёх значащих цифр, вычислите приближённо произведение а • Ь и частное а : Ь. Результат округлите с точностью до трёх значащих цифр:
6) а = 73,519,
3*. Стороны прямоугольника измерили приближённо: а 14,7 м, Ь 3,74 м. Вычислите приближённо:
а) периметр прямоугольника с точностью до десятых долей метра;
б) площадь прямоугольника с точностью до трёх значащих цифр.
Вариант
1. Округлив числа а и Ь с точностью до 0,01, вычислите приближённо сумму а + Ь и разность а — Ь:
а) а = 2,9362, Ь-
2,791; 6) 
Ь- 14,809.
2. Округлите числа а и Ь с точностью до трёх значащих цифр, вычислите приближённо произведение а • Ь и частное а : Ь. Результат округлите с точностью до трёх значащих цифр:
а) а = 75,38, 
6) а = 93,428, Ь-
9,8091.
3*. Стороны прямоугольника измерили приближённо: а 14,8 м, Ь 4,12 м. Вычислите приближённо:
а) периметр прямоугольника с точностью до десятых долей метра;
б) площадь прямоугольника с точностью до трёх значащих цифр.
с-38* Периодические десятичные дроби Вариант I
1. Запишите обыкновенную дробь:
11 25 а) б)
25' 11 в виде конечной десятичной дроби или бесконечной периодической десятичной дроби.
2. Покажите, как можно записать в виде обыкновенной дроби периодическую десятичную дробь:
З. Покажите, что периодическая дробь 2,1(9) равна конечной десятичной дроби.
4*. Найдите значение выражения + 1,(81).
Вариант П
1. Запишите обыкновенную дробь:
1120
6)
20' 11 в виде конечной десятичной дроби или бесконечной периодической десятичной дроби.
2. Покажите, как можно записать в виде обыкновенной дроби периодическую десятичную дробь:
З. Покажите, что периодическая дробь 1,2(9) равна конечной десятичной дроби.
4*. Найдите значение выражения + 2,(45).
Вариант III
1. Запишите обыкновенную дробь:
18. 6) 25
25' 18 в виде конечной десятичной дроби или бесконечной периодической десятичной дроби.
2, Покажите, как можно записать в виде обыкновенной дроби периодическую десятичную дробь:
З. Покажите, что периодическая дробь 5,4(9) равна конечной десятичной дроби.
4*. Найдите значение выражения + 3,(72).
Вариант IV
1. Запишите обыкновенную дробь:
а) 54. 6) 45
45 54
в виде конечной десятичной дроби или бесконечной периодической десятичной дроби.
2. Покажите, как можно записать в виде обыкновенной дроби периодическую десятичную дробь:
З. Покажите, что периодическая дробь 4,5(9) равна конечной десятичной дроби.
4*. Найдите значение выражения
с-39 Длина окружности и площадь круга
Вариант I
1. Вычислите приближённо длину окружности, если:
а) её радиус равен 5 см; б) её диаметр равен 6 м.
2. Вычислите приближённо площадь круга, если его радиус равен 7 см.
3*. Из справочника выписали приближение числа п
3,14159265. Сколько первых цифр числа п
надо взять для приближённого вычисления:
а) длины окружности, если её радиус приближённо равен 2,56 см;
б) площади круга, если его радиус приближённо равен 1,6 м?
Вычислите приближённо длину окружности и площадь круга.
Вариант II
1. Вычислите приближённо длину окружности, если:
а) её радиус равен 7 см; б) её диаметр равен 8 м.
2. Вычислите приближённо площадь круга, если его радиус равен 8 см.
3*. Из справочника выписали приближение числа п
3,14159265. Сколько первых цифр числа п надо взять для приближённого
вычисления:
а) длины окружности, если её радиус приближённо равен 3,24 см;
б) площади круга, если его радиус приближённо равен 1,5 м?
Вычислите приближённо длину окружности и площадь круга.
Вариант III
1. Вычислите приближённо длину окружности, если:
а) её радиус равен 9 см; б) её диаметр равен 10 м.
2. Вычислите приближённо площадь круга, если его радиус равен 11 см.
3*. Из справочника выписали приближение числа п
3,14159265. Сколько первых цифр числа п
надо взять для приближённого вычисления:
а) длины окружности, если её радиус приближённо равен 4,56 см;
б) площади круга, если его радиус приближённо равен 1,8 м?
Вычислите приближённо длину окружности и площадь круга.
Вариант IV
1. Вычислите приближённо длину окружности, если:
а) её радиус равен 11 см; б) её диаметр равен 12 м.
2. Вычислите приближённо площадь круга, если его радиус равен 9 см.
3*. Из справочника выписали приближение числа п
3,14159265. Сколько первых цифр числа п надо взять для приближённого
вычисления:
а) длины окружности, если её радиус приближённо равен 4,65 см;
б) площади круга, если его радиус приближённо равен 1,9 м?
Вычислите приближённо длину окружности и площадь круга.
РАЗДЕЛ l l l
Контрольные работы
I
1. Упростите отношение:
48 45 м 12 м
а) 6) в)
42' 54 м 2400 см
2.
Разделите число 120 в отношении 2
З. Решите пропорцию:
а) х 17. 6) 13 х • 8 4 24 — 36
4. Решите задачу с помощью пропорции:
а) 12 м сукна стоят 87 р. Сколько стоят 8 м этого сук-
б) Девять рабочих выполнили задание за 4 дня. Сколько рабочих могут выполнить задание за 6 дней?
5*. Определите масштаб плана, если участок площадью 7200 м2 изображён на этом плане в виде прямоугольника со сторонами 12 см и 6 см.
Вариант II
1. Упростите отношение:
35. 42 кг 18 дм а) 6) в)
56 49 кг 270 см
2.
Разделите число 150 в отношении З
З. Решите пропорцию: х 10 11 х
9 з 42 63 •
4. Решите задачу с помощью пропорции:
а) 8 м сукна стоят 54 р. Сколько стоят 12 м этого сук-
б) Восемь рабочих выполнили задание за З дня. За сколько дней могут выполнить задание 6 рабочих?
5*. Определите масштаб плана, если участок площадью 4800 м2 изображён на этом плане в виде прямоугольника со сторонами 8 см и 6 см.
Вариант III
1. Упростите отношение:
95 54
км 18 кг а) 6) в) 
4500 м 3200 г
2. Младшему брату 8 лет, старшему 12 лет. Они разделили 10 яблок между собой пропорционально числу лет каждого, т. е. в отношении 8 : 12. Сколько яблок досталось каждому?
З. Решите пропорцию:
7 35 11 х а) 6) 
21 49
4. Решите задачу с помощью пропорции:
а) На 24 м забора израсходовали 7 кг краски. Сколько краски израсходуют на 36 м этого забора?
б) Восемь рабочих могут выполнить задание за 6 дней. Сколько рабочих надо пригласить ещё, чтобы все вместе они выполнили это задание за 4 дня?
5*. Участок площадью 600 м 2 изображён на плане в виде прямоугольника. Определите площадь прямоугольника, если масштаб плана 1 : 1000.
Вариант IV
1. Упростите отношение:
85 48 км 26 кг а) 6) ' в) 
102' 3200 м 3900 г
2. Младшей сестре 7 лет, старшей 14 лет. Они разделили 12 конфет между собой пропорционально числу лет каждой, т. е. в отношении 7 : 14. Сколько конфет досталось каждой?
З. Решите пропорцию:
6 36 13 х а)• 35 42
4. Решите задачу с помощью пропорции:
а) На 24 м забора израсходовали 9 кг краски. Сколько краски израсходуют на 28 м этого забора?
б) Девять рабочих могут выполнить задание за 8 дней. Сколько рабочих надо пригласить ещё, чтобы все вместе они выполнили это задание за 6 дней?
5*. Участок изображён на плане в виде прямоугольника площадью 8 см 2 . Определите площадь земельного участка, если масштаб плана 1 : 1000.
I
1. Начертите отрезок АД длина которого равна 8 см. Постройте:
а) отрезок MN, длина которого составляет 25 % длины отрезка АВ; б) отрезок ХУ, длина которого составляет 150 % длины отрезка АВ.
2. Вычислите 20 % числа 35.
З. Было 500 р. Потратили 40 0/0 всей суммы и 50 % остатка. Сколько денег осталось?
4. За контрольную работу учащиеся 8 класса получили 4 отметки «5», 10 отметок «4», 10 отметок «З». Других отметок не было. Постройте круговую диаграмму по этим данным.
5*. Товар стоил 400 р. Определите его цену после двух повышений цены сначала на 20 % , потом на 10 0/0 .
Вариант II
1. Начертите отрезок АВ, длина которого равна 8 см. Постройте:
а) отрезок MN, длина которого составляет 50 0/0 длины отрезка АВ; б) отрезок ХУ, длина которого составляет 125 % длины отрезка АВ.
2. Вычислите 35 % числа 20.
З. Было 500 р. Потратили 50 % всей суммы и 40 0/0 остатка. Сколько денег осталось?
4. За контрольную работу учащиеся 9 класса получили 6 отметок «5», 10 отметок «4», 8 отметок «З». Других отметок не было. Постройте круговую диаграмму по этим данным.
5*. Товар стоил 600 р. Определите его цену после двух повышений цены сначала на 10 0/0, потом на 20 0/0.
Вариант III
1. Начертите квадрат, сторона которого равна 4 см. Постройте:
а) прямоугольник, площадь которого составляет 75 % площади квадрата;
б) прямоугольник, 40 0/0 площади которого равны площади квадрата.
2. Докажите, что 17 % числа 23 равны 23 % числа 17.
З. Было 600 р. Потратили 55 % всей суммы и 30 % остатка. Сколько денег осталось?
4. За контрольную работу учащиеся 10 класса получили 8 отметок «5», 12 отметок «4», 16 отметок «З». Других отметок не было. Постройте круговую диаграмму по этим данным.
5*. Товар стоил 500 р. Определите его цену после двух изменений цены — сначала повышения на 1096, потом понижения на 20 % .
Вариант IV
1. Начертите квадрат, сторона которого равна 8 см. Постройте:
а) прямоугольник, площадь которого составляет 25 % площади квадрата;
б) прямоугольник, 80 % площади которого равны площади квадрата.
2. Докажите, что 27 % числа 13 равны 13 % числа 27.
З. Было 600 р. Потратили 30 0/0 всей суммы и 55 % остатка. Сколько денег осталось?
4. За контрольную работу учащиеся 11 класса получили 4 отметки «5», 16 отметок «4», 16 отметок «З». Других отметок не было. Постройте круговую диаграмму по этим данным.
5*. Товар стоил 500 р. Определите его цену после двух изменений цены — сначала понижения на 20 0/0, потом повышения на 10 % .
К—3 Вариант I
1. Сравните числа —295 и —925.
2. Вычислите:
а) -49 + (-57); 6) -32 - (-13);
в) 124 • (-25); г) -549 : (-9).
З. Вычислите наиболее простым способом:
а) -48 25 + 28 • 25; 6) -138 + 24 - (29 138).
4. Найдите значение выражения
(54 : - 24 • : (-3).
5. Изобразите на координатной оси точки 0(0), А(5), щ-4).
За 4 дня З курицы снесли 8 яиц.
Сколько яиц снесли бы 2 курицы за З дня?
К—3 II
1. Сравните числа -367 и -637.
2. Вычислите:
а) -46 + (-53); 6) -45 - (-23);
в) -24 • (-125); г) 477 : (-9).
З. Вычислите наиболее простым способом:
а) -36 • 29 + 16 • 29; 6) -234 + 27 - (35 - 234).
4. Найдите значение выражения
(-49 : 7 - (-42 • з» : (-7).
5. Изобразите на координатной оси точки 0(0), А(—5),
6*. За З дня 4 курицы снесли 6 яиц. Сколько яиц снесли бы З курицы за 2 дня?
К—3 Вариант III
1. Сравните числа -1991 и -9191.
2. Вычислите:
а) -84 + 48; 6) -52 - (-25);
в) -48 (-105); г) 1339 : (-13).
З. Вычислите наиболее простым способом:
а) -39 , 91 + 6) -679 + 28 - (45 - 679).
4. Найдите значение выражения
(-204 : 4 - (-34 • з» : (-17).
5. Изобразите на координатной оси точки 0(0), А(—б), Щ 7). Определите длину отрезка АВ.
6*. За З ч 4 солдата начистили 2 ведра картошки. Сколько вёдер картошки начистили бы З солдата за 2 ч?
К—3 Вариант IV
1. Сравните числа —9292 и —2992.
2. Вычислите:
а) -93 + 39; б) —64 — (—46);
в) -85 (-104); г) 1272 : (-12).
З. Вычислите наиболее простым способом:
а) -46 • 82 + 36 82; 6) -846 + 39 - (48 - 846).
4. Найдите значение выражения
(-240 : 5 - (-32 • 4)) : (-16).
5.
Изобразите на координатной оси точки 0(0), 
Вб).
Определите длину отрезка АВ.
6*. За 4 ч 6 солдат начистили 4 ведра картошки. Сколько вёдер картошки начистили бы 4 солдата за З ч?
Вариант I
Вычислите (1—2):
1. 
г) 
1 3 2 10 2.
12 • 5 з 9
З. Вычислите, применяя законы умножения:
3 7 3 7 5
7 • 13 7 • 13' 6) 5 • 9 5 9 6
4. Первая бригада может выполнить задание за 24 ч, а вторая — за 48 ч. За сколько часов совместной работы они могут выполнить это задание?
5*. Через два крана бак наполнился за 8 мин. Если бы был открыт только первый кран, то бак наполнился бы за 12 мин. За сколько минут наполнился бы бак через один второй кран?
Вариант II
Вычислите (1—2):
1.в) з 5 5
2. 
З. Вычислите, применяя законы умножения:
з 7 3 7 '2
5 ' 11 5 • 11' б) 4 • 8 4 8 3
4. Первая бригада может выполнить задание за 16 ч, а вторая — за 48 ч. За сколько часов совместной работы они могут выполнить это задание?
5*. Через два крана бак наполнился за 9 мин. Если бы был открыт только первый кран, то бак наполнился бы за 36 мин. За сколько минут наполнился бы бак через один второй кран?
III
|
|
Вычислите (1—2): |
|
|
1. |
6) |
7 |
|
|
|
12' |
|
|
12 15 13 в) |
11 |
|
|
35 16' 28 |
14 |
г)
9 2.
16 • 7 4
З. Вычислите, применяя законы умножения:
4 15 7 15 13 8 13 8 10
а) 11 • 17 11 • 17' б) 15 19 15 19 13
4. Первая бригада может выполнить задание за 36 ч, а вторая — за 45 ч. За сколько часов совместной работы они могут выполнить это задание?
5*. Через два крана бак наполнился за 15 мин. Если бы был открыт только первый кран, то бак наполнился бы за 24 мин. За сколько минут наполнился бы бак через один второй кран?
Вариант IV
Вычислите (1—2):
1. 6)
4 
5
9 12'
14 20
в) 25 • 21'
2. 
З. Вычислите, применяя законы умножения:
8 13 24 37 24
37 15 а)
б)
19 • 15 19 • 15' 25 43 25 43 16
4. Первая бригада может выполнить задание за 21 ч, а вторая — за 28 ч. За сколько часов совместной работы они могут выполнить это задание?
5*. Через два крана бак наполнился за 18 мин. Если бы был открыт только первый кран, то бак наполнился бы за 30 мин. За сколько минут наполнился бы бак через один второй кран?
Вариант I
1. Решите уравнение:
з а) 3х - 2 = 5; 6) 5х - 2х + 3 = 6; — Х 14. 5
Решите с помощью уравнения задачу (2—3):
2. Задумали число, умножили его на 5, из результата вычли 12 и получили 38. Какое число задумали?
З. В одном куске полотна на 7 м больше, чем в другом, а всего в двух кусках 23 м. Сколько метров полотна в каждом куске?
Найдите значение выражения 3х— 2 при х =
1? .
з 5*. Упростите выражение 2х — З — (5х — 4).
6*. Зависит ли от значения х значение выражения
3(2х - 1) - 2(5х - 4) - (2 - 4х)?
Вариант П
1. Решите уравнение:
б) 6х— 2х+ 5; 2х-
11.
5
Решите с помощью уравнения задачу (2—3):
2. Задумали число, умножили его на 4, к результату прибавили 13 и получили 57. Какое число задумали?
З. Маша на З года старше Даши, а сумма их возрастов 27 лет. Сколько лет каждой?
1
4*. Найдите значение выражения 5х —
1 при х 1— 
5 5*. Упростите выражение 3х — 5 — (7х —
З).
6*. Зависит ли от значения х значение выражения 4(3х - 2) - 2(4х - 1) - (4х - 9)?
К—5 Вариант III
1. Решите уравнение:
а) 4х — 8; 6)
5х- 2х+4=8; 
16.
4
Решите с помощью уравнения задачу (2—3):
2. Задумали число, прибавили к нему 12 и результат умножили на 5. Получилось 90. Какое число задумаЛИ ?
З. В одном мотке лески на 4 м больше, чем в другом, а всего в двух мотках 28 м лески. Сколько лески в каждом мотке?
1
4*. Найдите значение выражения 7х — 11 при х = 2—. 2
5*. Упростите выражение 5х — 6 — (8х — 7).
6*. Зависит ли от значения х значение выражения
5(3х - 3) - 2(6х + 1) - (3х + 1)?
К—5 Вариант IV
1. Решите уравнение: з а) 5х-4= 7; б) 6х — 3х+ 1 = 8; - х = 17. 5
Решите с помощью уравнения задачу (2—3):
2. Задумали число, из него вычли 11 и результат умножили на 4. Получилось 84. Какое число задумали?
З. В одном мотке проволоки на 5 м больше, чем в другом, а всего в двух мотках 29 м проволоки. Сколько проволоки в каждом мотке?
1 4*. Найдите значение выражения 5х — 9 при х = 2— . з 5*. Упростите выражение 4х — 7 — (6х — 8).
6*. Зависит ли от значения х значение выражения
6(2х - 4) - 3(3х + 5) - (3х + 6)?
Вариант I
1. Вычислите:
а) 4,23 + 1,7; 6) 3,29 - 1,9;
в) 3,25 • 0,8; г) 13,104 : 4,2.
2.
Найдите 
выражения
(5,27 - 24,9 • (0,48 - 0,38)) : 0,2.
З. В магазин привезли 320 кг картофеля. Продали 0,6 этого картофеля. Сколько килограммов картофеля осталось продать?
4. Сколько деталей должен обточить токарь за смену, если он уже выполнил 0,8 сменного задания и ему осталось обточить 10 деталей?
5*. Упростите выражение 13х + 2 — (5х — 11) и найдите его значение при х = 0,8.
6*. Вычислите, не умножая столбиком:
123,45 • 6,789 - 678,9 • 1,2345.
Вариант II
1. Вычислите:
а) 5,37 + 2,3; 6) 4,18 - 2,8;
в) • 0,25; г) 7,488 : 2,4.
2. Найдите значение выражения
(4,57 - 27,1 (1,56 - 1,46)) : 0,2.
З. В магазин привезли 280 кг картофеля. Продали 0,8 этого картофеля. Сколько килограммов картофеля осталось продать?
4. Турист прошёл 0,6 длины маршрута, и ему осталось пройти ещё 12 км. Какова длина маршрута?
5*. Упростите выражение 15х + 4 — (8х — 12) и найдите его значение при х = 0,7.
6*. Вычислите, не умножая столбиком:
12,34 • 567,89 - 56,789 • 123,4.
Вариант III
1. Вычислите:
а) 5,83 +4,7; 6) 5,29 - 3,9;
в) 6,4 • 0,25; г) 14,688 : 3,6.
2. Найдите значение выражения
(4,67 - 23,5 • (3,57 - 3,47)) : 0,4.
З. Бригада токарей должна обточить 480 деталей. Уже обточили 0,6 этого количества деталей. Сколько деталей осталось обточить?
4. Велосипедист проехал 0,7 длины маршрута, и ему осталось проехать ещё 9 км. Какова длина маршрута?
5*. Упростите выражение 16х + 7 — (9х — 15) и найдите его значение при х = 0,7.
6*. Вычислите, не умножая столбиком:
2,345 • 67,891 - 6,7891 • 23,45.
Вариант IV
1. Вычислите:
а) 6,34 + 3,6; 6) 6,19 - 2,9;
в) 3,2. 0,75; г) 20,536 : 3,4.
2. Найдите значение выражения
(5,28 - 24,8 (4,48 - 4,38)) : 0,5.
З. Шофёр должен проехать 350 км. Он уже проехал 0,7 намеченного пути. Сколько километров ему осталось проехать?
4. Какова площадь поля, если комбайнер убрал урожай с 0,4 площади этого поля и ему осталось убрать урожай с 12 га?
5*. Упростите выражение 15х + 6 — (10х — 14) и найдите его значение при х = 0,7.
6* Вычислите, не умножая столбиком:
34,567 • 89,12 - 891,2 • 3,4567.
Вариант I
1. Вычислите:
а) • (-5,02); 6) 18,605 : 6,1; в) -5,2 : 0,04.
2. Вычислите рациональным способом:
-0,48 0,25
(-0,12 - 0,13) • 0,24 '
З. В коробке оказалось 12 бракованных лампочек, что составило 4 % числа всех лампочек. Сколько целых лампочек было в коробке?
4. Потратили 80 0/0 имевшихся денег, и осталось 60 р. Сколько денег было первоначально?
5*. Упростите выражение 3,2 • (х — 5) — 6 • (1,5х — 1).
6*. С помощью калькулятора выполнили деление: 0,00125 : 356 0,0000035.
С помощью того же калькулятора найдите ещё две значащие цифры частного.
Вариант II
1. Вычислите:
а) -2,7 • 3,04; 6) 25,578 : 6,3; в) 4,8 : (-0,03).
2. Вычислите рациональным способом:
-0,36 • 0,28
(-0,15-0,13) • 0,18
З. Потратили 48 р., что составило 40 0/0 имевшихся денег. Сколько денег осталось?
4. Прочитали 15 % всех страниц книги, и осталось прочитать 170 страниц. Сколько страниц в книге? 5*. Упростите выражение 5,1 • (х — 2) — З • (1,2х — 2).
6*. С помощью калькулятора выполнили деление:
0,00243 : 453 0,0000053.
С помощью того же калькулятора найдите ещё две значащие цифры частного.
Вариант III
1. Вычислите:
а) (-6,03); 6) 26,455 : 6,5; в) -3,6 : 0,08.
2. Вычислите рациональным способом:
-0,39 0,48
(-0,25 - 0,23) • 0,13 •
З. В выборах приняли участие 39 тыс. избирателей города Н., что составило 65 % всех избирателей этого города. Сколько избирателей города Н. не участвовало в выборах?
4. Прошли 45 % длины маршрута, и осталось пройти 11 км. Какова длина маршрута?
5*. Упростите выражение 5,6 • (х — 4) — 4 • (1,2х — 5).
6*. С помощью калькулятора выполнили деление:
0,00124 : 432 0,0000028.
С помощью того же калькулятора найдите ещё три значащие цифры частного.
Вариант IV
1. Вычислите:
а) -3,8 • 4,06; 6) 26,112 : 6,4; в) 4,9 : (-0,07).
2. Вычислите рациональным способом:
-0,42 • 0,49
(-0,24 - 0,25) 0,14
З. В выборах приняли участие 48 тыс. избирателей города М., что составило 64 % всех избирателей этого города. Сколько избирателей города М. не участвовало в выборах?
4. Проехали 55 % длины маршрута, и осталось проехать 18 км. Какова длина маршрута?
5*. Упростите выражение 6,5 • (х — 5) — 5 • (1,2х — 4).
6*. С помощью калькулятора выполнили деление:
0,00234 : 543 0,0000043.
С помощью того же калькулятора найдите ещё три значащие цифры частного.
Вариант I
1. Запишите в виде периодической дроби обыкновенную дробь:
5 13
а) 6) •
99
2.
Найдите обыкновенную дробь, равную периодической дроби
З. Радиус окружности равен 12 см. Вычислите приближённо длину окружности и площадь ограниченного ею круга, считая л 3,14.
4. Решите уравнение 3,5х — 2,8 1,4х + 1,4.
5. Трава при сушке теряет 80 0/0 своей массы. Сколько тонн травы надо накосить, чтобы насушить 12 т сена?
6*. В коробке лежит 5 чёрных и 7 белых шаров. Какое наименьшее число шаров надо взять из коробки не глядя, чтобы среди них оказалось 2 шара одного цве-
Вариант II
1. Запишите в виде периодической дроби обыкновенную дробь:
4. 17
99 •
2. Найдите обыкновенную дробь, равную периодической дроби 0,(5).
З. Радиус окружности равен 11 см. Вычислите приближённо длину окружности и площадь ограниченного ею круга, считая п 3,14.
4. Решите уравнение 3,6х — 2,5 = 1,2х + 2,3.
5. Груши при сушке теряют 70 0/0 своей массы. Сколько килограммов свежих груш надо взять, чтобы получить 27 кг сушёных?
6*. В коробке лежит 6 чёрных шаров и 4 белых шара. Какое наименьшее число шаров надо взять из коробки не глядя, чтобы среди них оказалось 2 шара одного цвета?
к--8 Вариант III
1. Запишите в виде периодической дроби обыкновенную дробь:
7 17
6)
33
2. Найдите обыкновенную дробь, равную периодической дроби 0,(8).
З. Радиус окружности равен 14 см. Вычислите приближённо длину окружности и площадь ограниченного ею круга, считая п 3,14.
4. Решите уравнение 4,3х — 3,5 = 2,5х + 1,9.
5. Яблоки при сушке теряют 75 % своей массы. Сколько килограммов свежих яблок надо взять, чтобы получить 48 кг сушёных?
6*. В коробке лежит 5 чёрных и 7 белых шаров. Какое наименьшее число шаров надо взять из коробки не глядя, чтобы среди них оказалось 2 шара разного цвета?
Вариант IV
1. Запишите в виде периодической дроби обыкновенную дробь:
8 13
33
2. Найдите обыкновенную дробь, равную периодической дроби 0,(7).
З. Радиус окружности равен 15 см. Вычислите приближённо длину окружности и площадь ограниченного ею круга, считая л 3,14.
4. Решите уравнение 4,5х — 3,9 = 2,6х + 1,8.
5. Сливы при сушке теряют 65 % своей массы. Сколько килограммов свежих слив надо взять, чтобы получить 70 кг сушёных?
6*. В коробке лежит 6 чёрных шаров и 4 белых шара. Какое наименьшее число шаров надо взять из коробки не глядя, чтобы среди них оказалось 2 шара разного цвета?
Вариант I
1. Вычислите: з 2
а) 
6) 3,25 • 50,6.
10 15'
2. Шесть рабочих могут выполнить работу за 15 дней. За сколько дней выполнят эту работу 10 рабочих, если будут работать с такой же производительностью?
З. Вычислите•
7 • 11
4. Найдите значение выражения 0,3а — 7 при а —5.
5. В магазин привезли печенье. В первый день продали 52 кг печенья, а во второй день — в 1,3 раза меньше, чем в первый. Сколько килограммов печенья привез-
1
ли в магазин, если за два дня продали привезён-
з ного печенья?
6*. Вычислите наиболее простым способом: (6,8 - 2,76) + (2,76 - 4,8).
Вариант II
1.
Вычислите:
а) — 15 12'
2. Поле площадью 24 га занято под картофель и капусту. Под капусту занято на 3,6 га меньше, чем под картофель. Какая площадь занята под капусту? З. Вычислите: 94,3 : 4,6 — 1,75 • 0,6.
4. Упростите выражение —6а — 7 + 4а — 1.
5. Определите, сколько человек на уроке физкультуры,
2 если присутствующих на уроке прыгают в длину,
5
25 % прыгают в высоту, а остальные 7 человек играют в мяч.
Вычислите наиболее простым способом:
Вариант III
1 2
1. Вычислите: а) 5— —1 6) : 0,48.
2 3'
2. Из 240 фруктовых деревьев 35 % составляют яблони,
а остальные деревья — грушевые. Сколько грушевых деревьев?
4 З. Вычислите: 2,4 • — + :
21 4
4.
Решите пропорцию
х
5. Расстояние между двумя городами равно 360 км. Легковая машина проходит это расстояние за 4 ч, а грузовая — за 6 ч. Через сколько часов встретятся машины, если одновременно выедут из этих городов навстречу друг другу?
Вычислите наиболее простым способом:
2,25 + 2,25 6,5 - 17,5.
Вариант IV
1. Вычислите:
6) 39:3.
2
2. Туристы прошли намеченного пути, и им осталось 5 пройти 12 км. Определите длину пути.
З. Вычислите: 18,9 + 5,58
48-0,15
4. Решите уравнение 7 — 5х = х — 5.
5. В магазин привезли 2,2 т огурцов и помидоров. Когда продали 490 кг огурцов и 350 кг помидоров, то тех и других овощей осталось поровну. Сколько килограммов помидоров привезли в магазин?
6*. Вычислите наиболее простым способом:
(46
РАЗДЕЛ lV
Задания для самопроверки
Вариант 1
1.1. Вычислите:
5 1
а) 6) 2,25 • 30,4.
12 8'
1.2. Трое рабочих могут выполнить задание за 8 дней. За сколько дней это задание выполнят двое рабочих, если будут работать с такой же производительностью?
1.3. 
Вычислите:
2 . 7 + 25 • 10
1.4. В первый день ученик прочитал 28 страниц, во второй день — в 1,5 раза больше, чем в первый. Сколько страниц в книге, если за эти два дня ученик прочи-
5
тал числа страниц книги?
7
1.5. Вычислите наиболее простым способом:
(7,51 - 1,98) + (1,98 - 2,51).
1.6. Найдите значение выражения 7 — 2а при а -0,5.
Вариант 2
2.1. Вычислите:
: 1,1.
12 14з
2.2. За конфеты заплатили на 5,4 р. больше, чем за печенье, а за всё вместе заплатили 42 р. Сколько заплатили за конфеты?
2.3. Вычислите: 27,54 : 5,1 — 8,4.
2.4. До обеда магазин продал 60 0/0, а после обеда — ещё
з
привезённых яблок. К концу дня осталось
продать
8
6 кг яблок. Сколько килограммов яблок привезли в магазин?
2.5. Вычислите наиболее простым способом:
—2!.2Ц+4
17 5 17 
2.6. Упростите выражение 7х — 3,2 — 2х + 1.
Вариант З
3.1. Вычислите:
6) : 0,3. з 2
3.2. За месяц работы бригада установила 45 % всех окон. Сколько окон ей осталось установить, если всего она должна установить 320 окон?
3.3. Вычислите:
3.4.
Решите пропорцию
35 2
3.5. Некоторое задание первый рабочий может выполнить за 4 ч, а второй за 6 ч. За сколько часов это задание выполнят оба этих рабочих при совместной рабо-
3.6. Вычислите наиболее простым способом: 12,75 • + 2,25 • - 15 • 3,5.
Вариант 4
4.1. Вычислите:
5
5
4.2. Ученик потратил имевшихся у него денег на по-
7 купку учебника и оставшиеся 12 р. на покупку тетрадей. Сколько денег он потратил?
4.3. Вычислите: 3,2 + 0,64 5,5
4,8 : з
4.4, Решите уравнение 5(х — З) = х + 1.
4.5. В магазине было 320 кг яблок и винограда. Когда продали 115 кг яблок и 97 кг винограда, то яблок и винограда осталось поровну. Сколько килограммов яблок было в магазине первоначально?
4.6. Вычислите
наиболее простым способом: 132+7?
Вариант 5
5.1. Вычислите:
729-428-729•311 +117-71
122
5.2. Укажите хотя бы одну обыкновенную дробь, большую 0,7, но меньшую 0,8.
2
5.3. Ученик имел 54 р. Он потратил имевшейся у него
9
2
суммы на покупку книги и остатка на покупку
7 тетрадей. Сколько денег у него осталось после этих покупок?
5.4. Первая труба наполнит бассейн за 24 мин, а вторая — за 40 мин. За сколько минут наполнится бассейн, если открыть обе эти трубы?
5.5. Запишите все трёхзначные числа, используя только цифры 4, 5 и 6 без повторения.
Вариант 6
6.1. Вычислите:
19,98 : 22,2) : + 0,35;
2 0
6.2. Что больше: от 120 или 40 /0 от 150? з
2
6.3. Когда коллекция марок увеличится на имеющегося
5 числа марок, то в ней будет 350 марок. Сколько марок в коллекции сейчас?
6.4. Две бригады рабочих при совместной работе выполнили задание за 6 дней. Это задание могла бы выполнить одна первая бригада за 18 дней. За сколько дней это задание могла бы выполнить одна вторая бригада?
6.5. Сколько трёхзначных чисел можно составить, используя только цифры 1, 7 и 9 без повторения?
Вариант 7
7.1. Вычислите:
а) 13? . 2!
12 2!) : 12 .3 1 + 1
7 14 
6) 9,36 : (-9) - (-1,8).
7.2. Укажите хотя бы одну десятичную дробь, большую
з 4 
но меньшую 
11' 11'
7.3. Товар стоил 400 р. Его цена увеличилась на 15 0/0, а через некоторое время ещё на 10 0/0. Сколько теперь стоит этот товар?
7.4. Имеющегося запаса кормов хватило бы для 120 коров на 4 месяца. На сколько месяцев хватит этого запаса кормов, если хозяйство продаст 24 коровы?
7.5. Сколько четырёхзначных чисел можно составить, используя только цифры 1, 2, О и 6 без повторения?
Вариант 8
8.1. Вычислите:
6) (-34 28 - 34 (-98)) : 35.
з
8.2. Что больше: 25 % от 180 или от 140?
7
8.3. После снижения цены на 20 % товар стоит 480 р. Сколько стоил этот товар до снижения цены?
8.4. Бригада из 18 рабочих может заасфальтировать участок дороги за 10 дней. Сколько рабочих надо добавить в эту бригаду, чтобы заасфальтировать участок дороги на один день раньше?
8.5. Сколько трёхзначных чисел можно составить, используя только цифры 2, О и 8 с повторением?
Ответы
Ответы к контрольным работам
8 1 2. 48 и 72. З. а) 34; 6) 19!. 4. а) 58 р.;
б) 6 рабочих. 5. 1 : 1000. Указание: Сначала определите, во сколько раз надо увеличить стороны прямоугольника, чтобы получить данную площадь.
|
8' |
|
|
б) за 4 дня. 5. 1 : 1000. |
|
|
5 45 В—Ш. 1. а) • б) 12; в) — |
6) 25 2 . |
|
6' 8 4. а) 10! кг; б) 12 рабочих. 5. 6 см 2 |
з |
|
5 20
6' з 4. а) 10! кг; б) 12 рабочих. 5. 800 м2 |
б) 15 3 |
5 6 2
К—2
В--1. 1. а) 
6) ХУ- 12 см. 2. 7. З. 150 р. 5. 528 р.
В—П. 1. а) МАТ = 4 см; 6) ХУ = 10 см. 2. 7. З. 15О р. 5. 792 р.
B—III. 1. а) Площадь прямоугольника 12 см 2 ; стороны прямоугольника, например, З и 4 см; б) площадь прямоугольника 40 см2 ; стороны прямоугольника, например, 10 и 4 см. З. 189 р. 5. 440 .
B—IV. 1. Площадь прямоугольника 16 см2 ; стороны прямоугольника, например, 2 и 8 см; б) площадь прямоугольника 80 см 2 ; стороны прямоугольника, например, 10 и 8 см. З. 189 р.
5. 440 р.
|
B—I. 1. -295 > -925. 2. а) -106; 6) —19; З. а) —500; б) —5. 4. —37. 6. 4 яйца. |
в) -3100; |
г) 61. |
|
в—п. 1. -367 > -637. 2. а) -99; 6) -22; З. а) -580; б) —8. 4. —17. 6. З яйца. |
в) 3000; |
г) -53. |
|
В—Ш. 1. -1991 > -9191. 2. а) -36; 6) —27; З. а) -910; б) —17. 4. —3. 6. 1 ведро. |
в) 5040; |
г) -103. |
|
B—IV. 1. -9292 < -2992. 2. а) -54; 6) |
в) 8840; |
г) —106. |
З. а) -820; 
. —5. 6. 2 ведра.
з 5 з 115 1
в) г) • •
12' 20
20 13' 
4. За 16 ч. 5. За 24 мин
1 11
В—П. 1. а) - в)
4 30'
4. За 12 ч. 5. За 12 мин.
4 29
В—Ш. 1. а) 6) в) 15' 24'
4. За 20 ч. 5. За 40 мин.
B—IV. 1. а) з б) 31
36'
1 2 1 7 1
г) 2.
3' з 60
9 13 19 15
г) 2.
28' 168 17' з
8 35 17 8
в) г)
• 2. 
 |
15' 24 210 19'
9
 |
6) 4. За 12 ч. 5. За 45 мин
10
|
в—6) 1; в) -10. 2. 10. З. 15 и 8 м. 4.
|
|
|
6. нет 1; в) -15. 2. 11. з. 15 и 12 лет. 4.
6. Нет |
|
|
в— |
|
|
4 3' 5. -3х + 1. 6. нет. |
2 |
|
11 7 |
2 |
|
B—IV. 1. а) б) |
|
2'
1
 |
7
53'
5.
-2х + 1. 6. Нет.
К—6
B—I. 1. а) 5,93; 6) 1,39; в) 2,6; г) 3,12. 2. 13,9. з. 128 кг. 4. 50 деталей. 5. 19,4. 6. О.
В—П. 1. а) 7,67; 6) 1,38; в) 1,55; г) 3,12. 2. 9,3. З. 56 кг. 4. зо км. 5. 20,9. 6. о.
В—Ш. 1. а) 10,53; 6) 1,39; в) 1,6; г) 4,08. 2. 5,8. З. 192 детали. 4. 30 км. 5. 26,9. 6. О.
B—IV. 1. а) 9,94; 6) 3,29; в) 2,4; г) 6,04. 2. 5,6. З. 105 км. 4. 20 га. 5. 23,5. 6. О.
B—I. 1. а) -18,574; 6) 3,05; в) -130. 2. 2. З. 288 лампочек. 4. ЗОО р. 5. —5,8х — 10. 6. Можно, например, разделить 1,25 на 356.
В—П. 1. а) -8,208; 6) 4,06; в) -160. 2. 2. З. 72 р. 4. 200 страниц. 5. —1,5х — 4,2. 6. Можно, например, разделить 2,43 на 453. В—Ш. 1. а) -22,914; 6) 4,07; в) -45. 2. З. З. 21 тыс. избирателей. 4. 20 км. 5. 0,8х — 2,4. 6. Можно, например, разделить 12,4 на 432.
B—IV. 1. а) -15,428; 6) 4,08; в) -70. 2. З. З. 27 тыс. избирателей. 4. 40 км. 5. 0,5х — 12,5. 6. Можно, например, разделить 23,4 на 543.
1 26
|
в—1. 5. 60 т. 6. З шара. |
2
|
З. 75,36 см и 452,16 см 2 |
|
в—п. 5. 90 кг. 6. З шара. |
5
9 |
З. 69,08 см и 379,94 см 2 . |
|
в—ш. 1. 5. 192 кг. 6. 8 шаров. |
9 |
з. 87,92 см и 615,44 см2 |
|
B—IV. 1. а) 6) |
7 2 |
з. 94,2 см и 706,5 см 2 . |
5. 200 кг. 6. 7 шаров.
К—9
1
• б) 164,45. 2. За 9 дней. З. 1,5. 4. -8,5. 5. 276 кг.
6'
В—П. 1. а) 11 • 6) 1?. 2. 10,2 га. З. 19,45. 4. —2а — 8. 5. 20 уча20' щихся. 6. 5.
В—Ш. 1. а) 3 2 ; б) 0,625. 2. 156 деревьев. З. 1,225. 4. 47,25.
6
5. Через 2,4 ч. 6. 5.
B—IV. 1. а) 6 2 ; 2. 20 км. З. 3,4. 4. 2. 5. 1030 кг. 6. 5.
6 7
Ответы к заданиям для самопроверки
7 5
1.1. а) 6) 68,4. 1.2. За 12 дней. 1.3. 1— • 1.4. 98 стра24 21
79
ниц. 1.5. 5. 1.6. 8. 2.1.
а) 
2.2. 23,7 р. 2.3. -7,2.
84' з
2.4. 240 кг. 2.5. з. 2.6. 5х-2,2. 3.1. а) 1 5 ; 6) 21-1 3.2. 176 6
окон. 3.3.
3,1. 3.4. 52,5. 3.5. за ч. 3.6. О. 4.1. а) 8 2 ; 
15 5
4.2. 42 р. 4.3. 4,2. 4.4. 4. 4.5. 169 кг. 4.6. 15. 5.1. а) 2; 6) 5. з
5.2. Например, 5.3. 30 р. 5.4. 15 мин. 5.5. 456, 465, 546,
564, 645, 654. 6.1. а) 12; 6) -2 2 . 6.2. от 120 больше, чем
21 з
4094 от 150. 6.3. 250 марок. 6.4. За 9 дней. 6.5. 6 чисел.
7.1. а) 7; 6) 4. 7.2. Например, 0,3. 7.3. 506 р. 7.4. На 5 месяцев.
з 7.5. 18 чисел. 8.1. а) 1; б) 68. 8.2.
25 % от 180 меньше, чем 
7 от 140. 8.3. 600 р. 8.4. 2 рабочих. 8.5. 18 чисел.
Содержание
Предисловие
Раздел 1. Материалы для подготовки к
самостоятельным работам
2. З. 4.
5.
10
|
7*. Задачи на вычисление вероятности события |
11 |
|
8. Модуль целого числа. Сравнение целых чисел . |
14 |
|
9. Сложение и вычитание целых чисел |
14 |
|
10. Умножение и деление целых чисел |
15 |
|
11. Действия с целыми числами... |
17 |
|
12. Представление целых чисел на координатной прямой |
18 |
|
13. Рациональные числа |
19 |
|
14. Сравнение рациональных чисел |
20 |
|
15. Сложение рациональных чисел .. . |
22 |
|
16. Вычитание рациональных чисел |
22 |
|
17. Умножение рациональных чисел . |
23 |
|
18. Деление рациональных чисел |
24 |
|
19. Смешанные дроби |
25 |
|
20.
Действия с
рациональными числами 21. Представление рациональных чисел на координатной |
27 |
|
прямой |
27 |
22. Уравнения
зо
23 Уравнения с модулями
31
24 Решение задач с помощью уравнений .
. 33
25 Упрощение выражений
34
26. Десятичные дроби. Сравнение
десятичных дробей. .
35
27. Сложение и вычитание десятичных
дробей . .
36
28. Умножение десятичных дробей
37
29. Деление десятичных дробей
38
30. Десятичные дроби и проценты.
38
31 * , Сложные задачи на проценты
39
32 Использование вспомогательных букв
при решении задач на проценты
. 41
|
33 Практические задачи на проценты . |
42 |
|
34.
Десятичные
дроби произвольного знака. 35. Совместные действия с обыкновенными и десятичными |
43 |
|
дробями произвольного знака |
44 |
36. 
Приближения десятичных дробей
37. Приближённые вычисления
|
38 Периодические десятичные дроби |
|
|
39. Длина окружности и площадь круга. . |
|
|
Раздел П. Самостоятельные работы |
|
Раздел III. Контрольные работы
105
Раздел IV. Задания для самопроверки .
..121
Ответы
.........125
128
Дидактические материалы 6 класс Потапов М.К.
МГУ - ШКОЛЕ М. К. Потапов А.
Москва «Просвещение» 2017 удк 373
Учебное пособие для общеобразовательных организаций
Дидактические материалы можно использовать в классе и дома при работе по любым учебникам, а также для восполнения пробелов и самообразования
Задания вариантов III и IV несколько сложнее соответствующих заданий вариантов
Пример З. Расстояние между городами
Решение. а) Сначала вычислим стороны участка на местности: 4 см • 1000 = 4000 см = 40 м;
Решение. а) Сначала вычислим стороны участка на местности: 4 см • 1000 = 4000 см = 40 м;
Пример 2. Начертим отрезок АВ, длина которого 12 см
Сколько конфет достанется брату, если ему
Решение. Для решения каждой пропорции воспользуемся основным свойством пропорции: в пропорции произведение крайних членов равно произведению средних членов
Понятие о проценте Пример 1.
Ответ. 10. 5. Задачи но проценты
Решение. 1) 100 — 35 = 65 ( 0 /0 ) составляет число 130 от задуманного; 130,100 2) - 200 задуманное число
Решение. Число 40 сравнивают с числом 50
Следовательно, две первые цифры в записи числа можно поставить
По- 2 1 этому вероятность события равна б)
Ответ. 25 Задачи на вычисление вероятности события
Пример 2, В шкафу есть 4 вертикальных ряда по 5 ящиков в каждом
В — «Боря получит ровно одну «1», если он не выполнит две домашние работы из этих пяти; в)
Если Боря не выполнит две домашние работы из этих пяти, например первую и вторую (для других номеров работ решение аналогично), то имеется 6 случаев из…
Модуль целого число. Сравнение целых чисел
Пример 5. Сколько целых чисел расположено между числами —12 и +15?
Решение. а) 33 + (-22) = +(33 - 22) - 11; 6) -42 - (-23) 42 + 23 -(42 - 23) = -19; — (15…
Решение. а) —15 • 6 = —(15 • 6) = —90; 6) -11 • (-32) +(11 32) = 352; в) зо = -(30 9) 270;…
Пример 5. Найдём значение выражения 41 • (—42) • (—43) • 44 • (—45) : 45 : (—44) : 43 : 42
Ответ. —10. Пример З. Найдём значение выражения 340 - 66 : (-8 + 2) • (-12)
Представление целых чисел но координатной прямой
Пример З. Различные точки заданы своими координатами:
Решение. + — 2 4) 4 3' 7
Решение. 4 5 5-20 100' —3 3\25 3,25 75 —4 4 4 •25 100 •
Дроби можно сравнить и по другому правилу: из двух отрицательных чисел больше то, у которого модуль мень- 3 5 з ше: поэтому б)
Пример 4. Сравним числа: 15 -16
Решение. Решим задачу полным перебором дробей со знаменателем 5, заключённых между дробями
Пример З. Выполним сложение и упростим ответ:
Пример 2. Выполним вычитание: а) в) 10 8-10
Умножение рациональных чисел
Теперь очевидно, что 18. Деление рациональных чисел
Решение. Пример 4. Выполним деление и упростим ответ: 25 а) 26
Решение. а) 3? — б) —32 13 13 13 8•1+7 15
Пример 4. Вычислим, применяя распределительный закон:
Действия с рациональными числами
Представление рациональных чисел на координатной прямой
Рис. 6 Для проверки определим по рисунку 6, что расстояние
Пример 4. Среднее арифметическое двух рациональных чисел т и п больше нуля
Ответ. 8
Уравнения Пример 1. Определим, какое из чисел 1, 6, —2 является корнем уравнения 2х+6- 15
Умножим обе части уравнения на наименьшее общее кратное знаменателей дробей, т
Ответ. 4— 4 23*. Уравнения с модулями
© ООО «Знанио»
С вами с 2009 года.
