Дидактические материалы на Тему: «Построение сечения многогранников метод «следов» »

ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ «НОВОАЗОВСКАЯ ШКОЛА №2 НОВОАЗОВСКОГО МУНИЦИПАЛЬНОГО ОКРУГА»

Дидактические материалы

на Тему:

«Построение сечения многогранников метод «следов» »

Выполнил:

Учитель математики

Щедловский К.А.

2025 год

Новоазовск

Пояснительная записка

Цели и задачи материала

Цель: Развитие пространственного воображения учащихся и формирование базовых геометрических представлений посредством освоения методов построения сечений многогранников.

Задачи:

Обучение технике построения сечений правильных и неправильных многогранников различными плоскостями.

Формирование навыка анализа взаимного расположения граней и вершин многогранника относительно секущей плоскости.

Совершенствование умения решать практические задачи геометрии, связанных с изучением объемов и площадей фигур.

Подготовка обучающихся к успешному выполнению заданий ЕГЭ по математике, включающих задания на построение сечений.

Актуальность

Актуальность данного дидактического материала обусловлена несколькими факторами:

Обучающая роль: Материал способствует развитию абстрактного мышления и позволяет школьникам углубленно изучить тему стереометрии.

Практическое применение: Освоенные навыки пригодятся учащимся при выполнении контрольных работ, экзаменов и олимпиад по математике.

Подготовка к ЕГЭ: Многие экзаменационные задания требуют понимания свойств сечений и способности грамотно построить сечения различных многогранников.

Развитие познавательного интереса: Тематика интересна сама по себе, поскольку развивает интерес к изучению трехмерных объектов и улучшает визуальное восприятие пространства.

Ожидаемые результаты

Использование данного дидактического материала позволит ученикам:

Уметь строить сечения куба, параллелепипеда, призмы и пирамиды различными способами.

Понимать свойства полученных сечений, включая форму, размеры и положение относительно исходного многогранника.

Применять полученные знания для решения практических задач, связанных с расчетом площади поверхности и объема тела.

Повышать уровень своей подготовки к успешной сдаче итоговых экзаменов по математике.

Рекомендации по использованию

Материал рекомендуется применять следующим образом:

Для учителя:

Перед началом занятия убедитесь, что ученики обладают базовыми представлениями о понятиях грани, вершины, ребра и диагонали многогранников.

Проведите демонстрационный урок, показывая поэтапно процесс построения сечений разных типов.

Используйте интерактивные методы обучения: виртуальные модели многогранников, компьютерные программы моделирования.

Предложите самостоятельную работу с использованием готовых шаблонов многогранников для практической отработки навыка.

Для учеников:

Выполняйте упражнения последовательно, начиная с простых примеров и постепенно переходя к более сложным.

Попробуйте самостоятельно создать чертежи сечений разными методами, сверяя результаты с предложенными образцами.

Решайте дополнительные задачи повышенной сложности для закрепления теоретических знаний.

Участвуйте активно в классных дискуссиях и проверяйте свои навыки друг друга в ходе групповой работы.

Таким образом, использование данного дидактического материала существенно повысит качество усвоения предмета и подготовит школьников к успешным результатам на итоговом контроле знаний.

Метод «Следов»

Метод включает три важных пункта: сначала нужно построить линию пересечения (след) секущей плоскости с плоскостью основания многогранника; затем найти точки пересечения секущей плоскости с рёбрами многогранника, а после этого построить и заштриховать сечение. В основе построения сечения методом следов лежат две теоремы:

1. если две точки прямой принадлежат плоскости, то и вся прямая принадлежит плоскости;

2. если плоскость проходит через прямую, параллельную другой плоскости, и эти плоскости пересекаются, то линия их пересечения параллельна первой прямой

Метод вспомогательных сечений

Метод применяется при построении сечений в тех случаях, когда неудобно находить след секущей плоскости. Например, след получается очень далеко от заданной фигуры.

Комбинированный метод

Суть метода состоит в применении теорем о параллельности прямых и плоскостей в пространстве в сочетании с методом следов или методом вспомогательных сечений.

Порядок построения сечений многогранников

Чтобы построить сечение, необходимо выделить минимум три точки, в которых секущая плоскость пересекает объёмное тело, а затем соединить их.

Чтобы построить сечение объёмной фигуры, необходимо решить две задачи:

1. Найти линии, по которым пересекаются две плоскости.

Для этого необходимо рассмотреть секущую плоскость и плоскость грани объёмной фигуры. Найти хотя бы две точки, в которых эти плоскости пересекаются. После этого точки необходимо соединить прямой. Аналогичные построения выполнить со всеми гранями, которые пересекаются с секущей плоскостью.

2. Найти точку, в которой некоторая прямая пересекает плоскость.

Данная задача сводится к обратному. Рассматриваем грани объёмной фигуры, находим точки, в которых данные грани пересекают секущую плоскость, и ставим на этом месте точки. После нахождения всех точек пересечения, соединяем их последовательно.

Задача

Построить сечение параллелепипеда ABCDA₁B₁C₁D₁ плоскостью, проходящей через точки P, Q, R (рис. 8).

Решение.

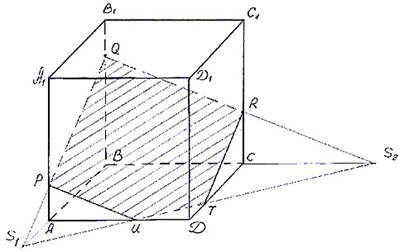
Рисунок 1 –чертеж к задаче №1

1.            Построим след секущей плоскости на плоскость нижнего основания параллелепипеда. Рассмотрим грань АА₁В₁В. В этой грани лежат точки сечения P и Q. Проведем прямую PQ.

2.            Продолжим прямую PQ, которая принадлежит сечению, до пересечения с прямой АВ. Получим точку S₁, принадлежащую следу.

3.            Аналогично получаем точку S₂ пересечением прямых QR и BC.

4.            Прямая S₁S₂ - след секущей плоскости на плоскость нижнего основания параллелепипеда.

5.            Прямая S₁S₂ пересекает сторону AD в точке U, сторону CD в точке Т. Соединим точки P и U, так как они лежат в одной плоскости грани АА₁D₁D. Аналогично получаем TU и RT.

6.            PQRTU – искомое сечение.

Задания для закрепления

Список источников

1.     https://ru.ruwiki.ru/wiki/%D0%A1%D0%B5%D1%87%D0%B5%D0%BD%D0%B8%D0%B5_%D0%BA%D1%83%D0%B1%D0%B0,_%D0%BF%D1%80%D0%B8%D0%B7%D0%BC%D1%8B,_%D0%BF%D0%B8%D1%80%D0%B0%D0%BC%D0%B8%D0%B4%D1%8B

2.     Скачано с www.znanio.ru