Дидактический материал на напряженность гравитационного поля

1.8.1. Закон всемирного тяготения

Все тела обладающие массой притягиваются друг к другу. Исаак Ньютон на основе многолетних данных астрономических наблюдений и законов динамики сформулировал закон всемирного тяготения: две любые материальные точки массами m₁ и m₂ притягиваются друг к другу вдоль линии соединяющей точки с силой прямо пропорциональной произведению масс точек и обратно пропорциональной квадрату расстояния (r) между ними:

где 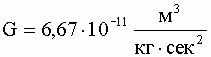- гравитационная постоянная. Из формулы видно, что величина гравитационного взаимодействия не зависит от среды, в которой находятся взаимодействующие тела, гравитационное взаимодействие существует и в вакууме. На рисунке1.8.1 изображено направление сил гравитационного взаимодействия двух материальных точек.

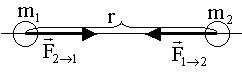
Рис. 1.8.1.

1.8.2. Сила тяжести, вес тела

Земля не является "материальной точкой" для тел, расположенных на ее поверхности. Теоретически доказано, что сила, с которой Земля притягивает тела, расположенные вне ее, равна силе, которую создавала бы материальная точка массой (М), равной массе Земли, и расположенная в центре Земли. Назовем силой тяжести силу, с которой тело взаимодействует с планетой, вблизи которой оно находится.

В соответствии с законом всемирного тяготения на материальную точку массой (m) со стороны Земли будет действовать сила тяжести, равная

где R - радиус Земли, в месте расположения точки. Выражение (1.8.2.) можно переписать в виде:

где g - имеет смысл ускорения, с которым движутся под действием силы тяжести все материальные тела у поверхности Земли.

Согласно фундаментальному физическому закону - обобщенному закону Галилея, все тела в одном и том же поле тяготения падают с одинаковым ускорением. Оно изменяется вблизи поверхности Земли с широтой в пределах от 9,780 м/с² на экваторе до 9,832 м/с² на полюсах. Это обусловлено суточным вращением Земли, с одной стороны, и сплюснутостью Земли - с другой (экваториальный и полярный радиусы Земли равны соответственно 6378 и 6357 км). Так как различие значений g невелико, ускорение свободного падания, которое используется при решении практических задач, принимается равным 9,81 м/с².

Пусть тело расположено на расстоянии (±h) от поверхности Земли (знак плюс - над поверхностью, знак минус - под поверхностью), тогда сила тяжести с удалением от поверхности Земли уменьшается, а при приближении к центру Земли - увеличивается:

Вес тела - сила, с которой тело вследствие тяготения к Земле действует на опору или подвес, удерживающую тело от свободного падения.

Вес тела проявляется, когда тело движется с ускорением отличным от ускорения свободного падения (g), т.е. когда на тело кроме силы тяжести действуют другие силы. Если тело движется в поле тяготения Земли с ускорением , то к этому телу приложена дополнительная сила , удовлетворяющая условию:

.

Тогда вес тела

Вес тела, движущегося с ускорением равен произведению массы тела на геометрическую разность ускорения свободного падения и ускорения тела.

Если тело движется с ускорением равным ускорению силы тяжести, то вес тела будет равен нулю:

Например,

1) вес тела равен нулю когда тело движется с ускорением равным ускорению силы тяжести () в лифте вертикально вниз;

2) космический корабль движется по орбите, при этом его центростремительное ускорение 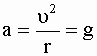, направлено так же как ускорение силы тяжести вдоль радиуса к центру Земли, и вес всех тел находящихся в корабле равен нулю.

1.8.3. Гравитационное поле - напряженность и потенциал

Закон всемирного тяготения определяет величину и направление силы всемирного тяготения, но не отвечает на вопрос как осуществляется это взаимодействие. Гравитационное взаимодействие между телами осуществляется с помощью поля тяготения, или гравитационного поля.

Гравитационное поле - это особый вид материи, который создается вокруг любого тела обладающего массой, главное свойство гравитационного поля - действовать на тела, обладающие массой. Как и любое поле - гравитационное поле характеризуется с помощью двух физических величин:

1.Напряженность гравитационного поля (), силовая характеристика поля, равна силе, действующей со стороны поля на материальную точку единичной массы, и совпадает по направлению с действующей силой (это ничто иное как ускорение, с которым тело движется в поле тяготения):

Единица измерения напряженности гравитационного поля [g]=м/с².

Линия напряженности гравитационного поля - линия, касательные, к каждой точке которой совпадает с вектором напряженности.

На всякое тело массой m, внесенное в поле, действует сила тяготения или сила тяжести, равная произведению массы тела на напряженность гравитационного поля в месте расположения тела:

Независимо от своей массы все тела под действием силы тяжести движутся с одинаковым ускорением ()

2. Потенциал гравитационного поля (φ) - энергетическая характеристика поля, скалярная величина, определяемая потенциальной энергией тела единичной массы в данной точке поля:

Единица измерения [φ]=Дж/кг.

Потенциальная энергия тела в гравитационном поле равна:

Тогда работа гравитационного поля по перемещению тела из точки с потенциалом φ₁ в точку с потенциалом φ₂ равна:

,

Работа гравитационного поля по перемещению тела между двумя точками не зависит от траектории движения тела, а определяется только разностью потенциалов начальной и конечной точек, на замкнутом пути работа гравитационного поля равна нулю. То есть, сила всемирного тяготения и сила тяжести являются консервативными.

Эквипотенциальные поверхности - поверхности, образованные точками поля, потенциал которых одинаков. Работа гравитационного поля при движении тела вдоль эквипотенциальной поверхности равна нулю.

Можно дать второе определение потенциала поля тяготения - это работа по перемещению единичной массы из данной точки поля в бесконечность.

1.8.4. Гравитационное поле материальной точки

В качестве примера рассмотрим гравитационное поле материальной точки.

1. Напряженность гравитационного поля материальной точки массой (M) прямо пропорциональна массе точки, и убывает по величине обратно пропорционально расстоянию от этой точки (r), направлена вдоль лучей, сходящихся в точке - источнике поля:

2. Потенциал гравитационного поля материальной точки массой (M) - прямо пропорционален массе материальной точки, создающей поле и убывает обратно пропорционально расстоянию от источника поля:

Из формулы (1.8.11) вытекает, что геометрическое место точек с одинаковым потенциалом, т.е. эквипотенциальные поверхности данного поля - это сферические поверхности.

Наглядную картину поля представляет набор линий напряженности и эквипотенциальных поверхностей, например, гравитационное поле материальной точки представлено на рисунке (1.8.2).

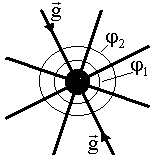
Рис. 1.8.2.

Потенциальная энергия тела массой (m), находящегося на расстоянии r от источника гравитационного поля - тела массой (M):

.

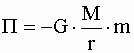Мы уже упоминали, что гравитационное поле Земли можно рассматривать, как поле материальной точки расположенной в центре Земли. Тогда потенциальная энергия тела, находящегося на высоте h относительно Земли:

,

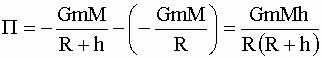где R - радиус Земли. Так как

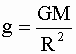, и, учитывая, что h<<R, получаем

.

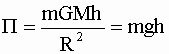Потенциальная энергия тела на высоте h над поверхностью Земли, равна:

1.8.5. Взаимосвязь между потенциалом и напряженностью гравитационного поля

Рассмотрим взаимосвязь между потенциалом и напряженностью поля тяготения.

Элементарная работа, совершаемая полем при малом перемещении тела массой (m), равна

.

С другой стороны ,

где dl - элементарное перемещение.

Следовательно, , или .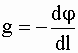

Величина dφ/dl характеризует изменение потенциала на единицу длины в направлении перемещения в поле тяготения, это ничто иное, как градиент потенциала.

Таким образом, напряженность гравитационного поля численно равна градиенту потенциала гравитационного поля и направлена в сторону его уменьшения:

Скачано с www.znanio.ru