

Цели работы:
ü систематизация математических знаний и практических умений по разделу «Стереометрия»;
ü развитие познавательной способности и активности, самостоятельности, ответственности и организованности;
ü знакомство с историей развития математики.
Содержание работы:
Часть 1 (изложение теории):
1.1. Понятие перпендикулярности для прямых и плоскостей. Определения и признаки.
1.2. Почему мы изучаем эти понятия. Примеры из жизни.
Часть 2 (решение задач):
2.1. В прямоугольном параллелепипеде ABCDA1B1C1D1 найти диагонали BD и AC1, если он имеет размеры 7 м, 5 м и 3 м.
2.2. Через вершину угла C треугольника ABC проведена плоскость, параллельная гипотенузе, на расстоянии 1 м от нее. Проекции катетов на эту плоскость равны 3 м и 5 м. Найти гипотенузу.
Часть 3 (изготовление модели):
3.1. Изготовление модели правильной пятиугольной призмы (указать длину ребер, количество вершин, ребер, граней, площадь поверхности, объем).
3.2. Изобразить диагональное сечение модели.
Часть 4 (решение задач по теме: «Декартовы координаты»):
4.1. Заданы координаты точек A(1;1;-3), B(1;-6;-3). Построить эти точки в заданной системе координат. Определить расстояние между A и B.
4.2. Заданы координаты точек A(-1;4;-3), B(7;0;-1), C(1;3;-6), D(0;4;-3). Определить:
а) координаты векторов AB и CD;
б) длину векторов AB и CD;
в) сумму векторов AB+CD;
г) скалярное произведение векторов AB и CD;
д) угол между векторами AB и CD.
Часть 1 (изложение теории):
1.1. Понятие перпендикулярности для прямых и плоскостей. Определения и признаки.
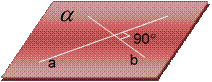
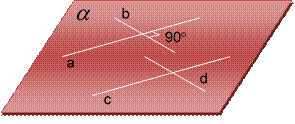
Перпендикулярность двух прямых
Определение 1:
Две прямые называются перпендикулярными, если они пересекаются под прямым углом.
Теорема 1:
Если две пересекающиеся прямые параллельны соответственно двум перпендикулярным прямым, то они тоже перпендикулярны.
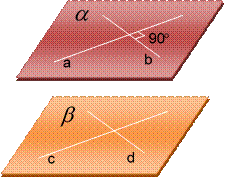
______________________________________________________________
Перпендикулярность прямой и плоскости
Определение 2:
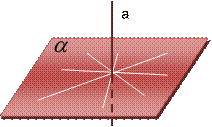 Прямая,
пересекающая плоскость, называется перпендикулярной этой
плоскости, если она перпендикулярна любой прямой, которая лежит в данной
плоскости и проходит через точку пересечения данной прямой и плоскости.
Прямая,
пересекающая плоскость, называется перпендикулярной этой
плоскости, если она перпендикулярна любой прямой, которая лежит в данной
плоскости и проходит через точку пересечения данной прямой и плоскости.
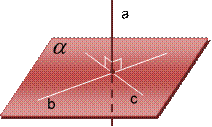
Теорема 2 (признак перпендикулярности прямой и плоскости):
Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна данной плоскости.
 |
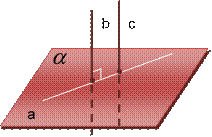
Теорема 3 (свойство перпендикулярных прямой и плоскости):
Если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой.
 |
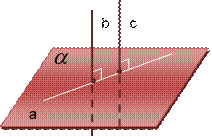
Теорема 4 (свойство перпендикулярных прямой и плоскости):
Две прямые, перпендикулярные одной и той же плоскости, параллельны.
 |
______________________________________________________________
Перпендикулярность трех прямых
Определение 3:
Перпендикуляром, опущенным из данной точки на данную плоскость, называется отрезок, соединяющий данный отрезок с точкой плоскости и лежащий на прямой, перпендикулярной плоскости.
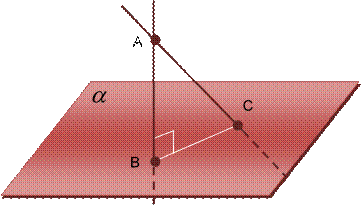
Определение 4:
Наклонной, проведенной из данной точки к данной плоскости, называется любой отрезок, соединяющий данную точку с точкой плоскости, не являющийся перпендикуляром к плоскости.
Определение 5:
Отрезок, соединяющий основания перпендикуляра и наклонной, проведенных из одной и той же точки, называется проекцией наклонной.
 |
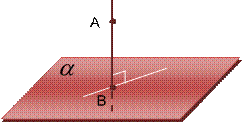
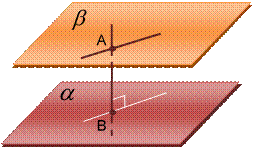
Определение 6:
Расстоянием от точки до плоскости называется длина перпендикуляра, опущенного из этой точки на плоскость.
 |
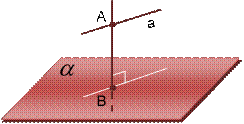
Определение 7:
Расстоянием от прямой до параллельной ей плоскости называется расстояние от любой точки этой прямой до плоскости.
 |
Определение 8:
Расстоянием между параллельными плоскостями называется расстояние от любой точки одной плоскости до другой плоскости.
 |
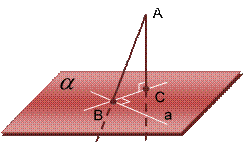
Теорема 5 (теорема о трех перпендикулярах):
Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна наклонной. И обратно: если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.
 |
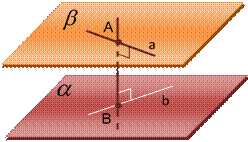
Определение 9:
Общим перпендикуляром двух скрещивающихся прямых называется отрезок с концами на этих прямых, являющийся перпендикуляром к каждой из них.
Теорема 6:
Две скрещивающиеся прямые имеют общий перпендикуляр, и притом только один. Он является общим перпендикуляром параллельных плоскостей, проходящих через эти прямые.
 |
Определение 10:
Расстоянием между скрещивающимися прямыми называется длина их общего перпендикуляра.
______________________________________________________________
Перпендикулярность двух плоскостей
Определение 11:
Две пересекающиеся плоскости называются перпендикулярными, если третья плоскость, перпендикулярная прямой пересечения этих плоскостей, пересекает их по перпендикулярным прямым.
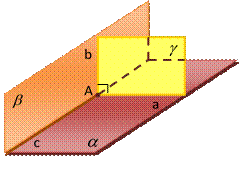 |
Теорема 7 (признак перпендикулярности плоскостей):
Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
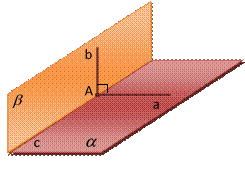 |
______________________________________________________________
1.2. Почему мы изучаем эти понятия. Примеры из жизни.
Данный раздел изучается для:
ü изучения закономерностей между геометрическими объектами в пространстве;
ü дальнейшего использования при решении задач, связанными с геометрическими телами;
ü применения полученных знаний по изученной теме в жизненных ситуациях.
Приведем примеры применения данной темы в жизненных ситуациях:
ü окружающая нас обстановка дает много примеров, иллюстрирующих перпендикулярность прямой и плоскости: непокосившийся телеграфный столб стоит прямо, т.е. перпендикулярно к плоскости земли; так же расположены колонны здания по отношению к плоскости фундамента, линии пересечения стен по отношению к плоскости пола и т.д.;
ü когда мы говорим, что некоторый предмет, например, лампочка уличного фонаря, находится на высоте 6 м от земли, то имеем ввиду, что расстояние от лампочки до поверхности земли измеряется по перпендикуляру, проведенному от лампочки к плоскости земли;
ü в обыденной жизни мы часто встречаемся с предметами, состоящими из перпендикулярных плоскостей: двускатные крыши зданий, полураскрытая папка, стена комнаты совместно с полом и т.д.
ü в черчении применяется ортогональное проектирование, т.е. параллельное проектирование прямыми, перпендикулярными плоскости проекции; чертежи деталей машин получаются путем ортогонального проектирования на одну, два или три перпендикулярные плоскости, эти плоскости называются плоскостями проекций.
Часть 2 (решение задач):
2.1. В прямоугольном параллелепипеде ABCDA1B1C1D1 найти диагонали BD и AC1, если он имеет размеры 7 м, 5 м и 3 м.
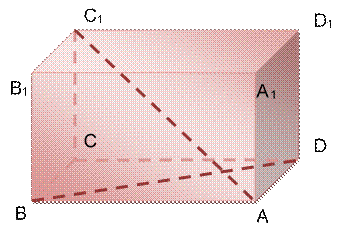
Дано: ABCDA1B1C1D1 – прямоуг. параллелепипед;
его размеры – 7 м, 5 м и 3 м
Найти: BD и AC1
Решение:
1) Рассмотрим случай, когда AB = 7 м, AD = 5 м, AA1 = 3 м.
Рассмотрим ΔABD – прямоугольный (т.к. ABCD – прямоугольник):
По теореме Пифагора: BD2 = AB2 + AD2 = 72 + 52 = 49 + 25 = 74
BD
= ![]() м;
м;
2) Рассмотрим случай, когда AB = 5 м, AD = 3 м, AA1 = 7 м.
Рассмотрим ΔABD – прямоугольный (т.к. ABCD – прямоугольник):
По теореме Пифагора: BD2 = AB2 + AD2 = 52 + 32 = 25 + 9 = 34
BD
= ![]() м;
м;
3) Рассмотрим случай, когда AB = 7 м, AD = 3 м, AA1 = 5 м.
Рассмотрим ΔABD – прямоугольный (т.к. ABCD – прямоугольник):
По теореме Пифагора: BD2 = AB2 + AD2 = 72 + 32 = 49 + 9 = 58
BD
= ![]() м;
м;
4) По теореме о длине диагонали прямоугольного параллелепипеда:
AC12
= AB2 + AD2 + AA12 = 72
+ 52 + 32 = 49 + 25 + 9 = 83; AC1 = ![]() м
м
Длина диагонали прямоугольного параллелепипеда не зависит от того, какие именно его ребра являются длиной, шириной или высотой.
Ответ: BD = ![]() м, либо BD =
м, либо BD = ![]() м, либо BD =
м, либо BD = ![]() м, AC1 =
м, AC1 = ![]() м.
м.
2.2. Через вершину угла C треугольника ABC проведена плоскость, параллельная гипотенузе, на расстоянии 1 м от нее. Проекции катетов на эту плоскость равны 3 м и 5 м. Найти гипотенузу.
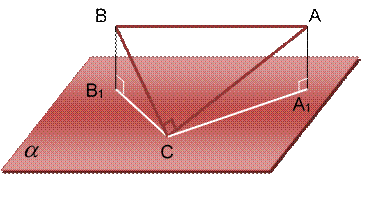
Дано: ΔABC – прямоугольный; ![]() ;
; ![]() ;
; ![]() 1 м;
1 м;
проекция BC на ![]() равно 3 м;
равно 3 м;
проекция AC на ![]() равно 5 м
равно 5 м
Найти: AB
Решение:
1) Построим ![]() и
и ![]() , тогда получим:
, тогда получим:
CA1 – проекция AC на ![]() Þ CA1 = 5 м
Þ CA1 = 5 м
CB1 – проекция BC на ![]() Þ CB1 = 3 м
Þ CB1 = 3 м
![]() AA1 = BB1 = 1 м;
AA1 = BB1 = 1 м;
2) Рассмотрим ΔCAA1 – прямоугольный:
По теореме Пифагора: AC2 = AA12 + CA12 = 12 + 52 = 1 + 25 = 26
AC
= ![]() м;
м;
3) Рассмотрим ΔCBB1 – прямоугольный:
По теореме Пифагора: BC2 = BB12 + CB12 = 12 + 32 = 1 + 9 = 10
BC
= ![]() м;
м;
4) Рассмотрим ΔABC – прямоугольный:
По теореме Пифагора: AB2 = AC2 + BC2 = 26 + 10 = 36
AB = ![]() м.
м.
Ответ: AB = 6 м.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.