Дидактический материал с презентацией по теме "Треугольники". 7 класс.

Дидактический материал

к темам  главы «Треугольники»

(геометрия, 7 класс)

Блок “Решаем устно» (Анализируем, логически рассуждаем и даём ответ) (Слайд 2)

Цель: организации  устного опроса, проблемных или эвристических бесед,  активизация опорных знаний обучающихся по теме, развитие логического мышления (формирование и развитие мыслительных общеучебных умений и навыков).  

Ø Первый признак равенства треугольников (слайд 3)

Будьте внимательны. Сначала думаем, при необходимости делаем чертёж,  а потом отвечаем.

А1. В треугольниках АВС и А₁В₁С₁

        АВ = А₁В₁, ВС = В₁С₁, ÐВ = ÐВ₁.

Можно ли утверждать, что данные треугольники равны? [Да]

А2. В треугольниках АВС и А₁В₁С₁

        АВ = А₁В₁,  ÐА = ÐА₁.

Какое условие необходимо добавить, чтобы данные треугольники были равны по первому признаку? [АС = А₁С ₁]

А3. В треугольниках АВС и А₁В₁С₁

        АВ = А₁В₁, ВС = В₁С₁, АС = А₁С ₁,   ÐА = ÐА₁.

Какое из данных условий можно удалить, чтобы оставшиеся условия гарантировали равенство треугольников по первому признаку? [ВС = В₁С₁]

Б1. В треугольниках АВС и MNK

        АВ = NK, ВС = MK, ÐВ = ÐK.

Можно ли утверждать, что данные треугольники равны? [Да]

Б2. В треугольниках АВС и АВС₁

         ÐВАС = ÐВАС₁.

Какое условие необходимо добавить, чтобы данные треугольники были равны по первому признаку? [АС = АС ₁]

Б3 В треугольниках АВС и АВ₁С

        АВ = АВ₁, ВС = В₁С,  ÐВАС = ÐВ₁АС.

Какое из данных условий можно удалить, чтобы оставшиеся условия гарантировали равенство треугольников по первому признаку? [ВС = В₁С]

Ø Медианы, биссектрисы и высоты треугольника (слайд 4)

Анализируем поставленный вопрос, вспоминая определения.

А1. Верно ли, что медиана любого треугольника перпендикулярна к стороне, к которой она проведена? [Нет]

А2. Верно ли, что высота любого треугольника делит пополам одну из его сторон? [Нет]

Б1. Верно ли, что биссектриса  треугольника может лежать вне треугольника? [Нет]

Б2. Могут ли  два каких-либо угла треугольника иметь различные величины, если две его стороны равны? [Да]

В1. Верно ли, что медиана треугольника делит его на два треугольника с равными периметрами? [Нет]

Ø Равнобедренный треугольник (слайд 5 )

А1. Могут ли все углы треугольника иметь разные величины, если  все его стороны равны? [Нет]

А2. Могут ли все углы треугольника иметь разные величины, если  две его стороны равны? [Нет]

А3. В равнобедренном треугольнике АВС с основанием АС проведена биссектриса ВМ. Точка К лежит на отрезке АВ. Определите, является ли отрезок КМ медианой, биссектрисой или высотой треугольника АВС. [медиана]

А4. В равнобедренном треугольнике АВС с основанием АС проведена биссектриса ВМ. Точка D лежит на отрезке MC. Определите, является ли отрезок BМ медианой, биссектрисой или высотой треугольника АВD. [высота]

Б1. Могут ли два каких-либо  угла  треугольника иметь разные величины, если  две его стороны равны? [Да]

Б2. Могут ли два каких-либо  угла  треугольника иметь разные величины, если  все его стороны равны? [Нет]

Б3. В данном треугольнике построили все медианы и все высоты. Определите наибольшее и наименьшее возможное количество отрезков, построенных внутри треугольника. [6; 3]

Б4. В равнобедренном треугольнике АВС с основанием АС проведена медиана ВH и на ней отмечена точка D.  Определите, является ли отрезок CH медианой, биссектрисой или высотой треугольника CВD. [высота]

Ø Второй и третий признаки равенства треугольников (слайд 6)

А1. В треугольниках АВС и А₁В₁С₁   АС = А₁С₁, ÐА = ÐА₁, ÐС = ÐС₁. Можно ли утверждать, что данные треугольники равны? [Да]

А2. Верно ли, что если у двух равнобедренных треугольников равны углы при основании, то такие треугольники равны? [Нет]

А3. В треугольниках АВС и А₁В₁С₁   АС = А₁С₁, ÐА = ÐА₁. Какое условие необходимо добавить, чтобы данные треугольники были равны по второму признаку? [ÐС = ÐС₁]

А4. В треугольниках АВС и А₁В₁С₁

        АВ = АВ₁, ВС = В₁С,  АС = А₁С₁, ÐА = ÐА₁.

Какое из данных условий можно удалить, чтобы оставшиеся условия гарантировали равенство треугольников по третьему признаку? [ÐА = ÐА₁]

Б1. В треугольниках АВС и MNK   ВС = NK, ÐВ = ÐN, ÐС = ÐM. Можно ли утверждать, что данные треугольники равны? [Нет]

Б2. В треугольниках АВС и АВС₁

         ÐВАС = ÐВАС₁.

Какое условие необходимо добавить, чтобы данные  треугольники были равны  по второму признаку? [ÐАВС = ÐАВС₁]

В1. В треугольниках АВС и MNK   ВС = NK, ÐВ = ÐN, ÐА = ÐM. Можно ли утверждать, что данные треугольники равны? [Нет]

В2. Даны треугольники АВС и А₁В₁С₁ и три равенства соответствующих элементов, позволяющие доказать равенство треугольников по второму признаку. В условии задачи равенство ÐА = ÐА₁ заменили равенством

ВС = В₁С₁ . На основании какого признака теперь можно доказать равенство треугольников? [По первому] 

Блок «Читаем  рисунки» (слайд 7)

Цель: развитие устной математической речи, отработка умения читать чертёж, т.е. видеть на чертеже соответственно равные элементы и делать содержательные ссылки на признаки (треугольники равны по двум сторонам и углу между ними), а не формальные (треугольники равны по первому признаку), видеть на рисунке  высоту, медиану, биссектрису треугольника.

Ø Первый признак равенства  треугольников (слайд 8)

 

Один  рисунок, который можно прочитать следующим образом:

 D MNP = D FEK по двум сторонам и углу между, т.к. MN = FE, NP = EK, Ð N = Ð E.  

Ø Медианы, биссектрисы и высоты треугольника (слайд 9)

Два рисунка:

- В D АВС проведена BN – медиана, т.к. AN = CN;  АМ – высота, т.к. AМ ^ВC.

- В DАВС проведена ВЕ – биссектриса, т.к. ÐАВЕ = ÐСВЕ; СD – высота, т.к. CD^AB.

Ø Равнобедренный треугольник (слайд 10)

Один рисунок:

D АВС – равнобедренный, т.к. АВ = АС, ВС – основание, АМ – медиана, биссектриса и высота данного треугольника.

Ø Второй и третий признак равенства треугольников (слайд 11)

Два рисунка:

- Треугольники ABC и KMN равны по стороне и двум прилежащим к ней углам, т.к. BC =  MN,  ÐB = ÐM, ÐC = ÐN.

- Треугольники АВС и КАС равны по трём сторонам, т.к. АВ = КС, АК = ВС, АС – общая.

Ø Задачи на смекалку (слайд 18) (переход на данный слайд размещён на слайде 7)

ü    Первый признак равенства треугольников (слайд 19)

1) Среди данных пяти треугольников есть равные. Назовите их.

                                                                                             

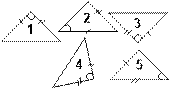
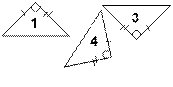
2)          

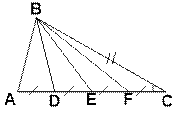
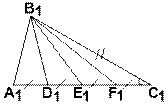
Даны D АВС и D А₁В₁С₁. Известно, что AD = DE = EF = FC = A₁D₁ = D₁E₁ = E₁F₁ = F₁C₁, ÐС = ÐС₁.  Докажите, что D ABD = D A₁B₁D₁.

ü    Равнобедренный треугольник (слайд 20)

1.        

Представьте себе, что равные треугольники АВС и А₁В₁С₁   переместились так, что точки А и А₁ и точки С и С₁ совпали. Проведите мысленно отрезок ВВ₁. Докажите, не выполняя нового чертежа, что АС ^ ВВ₁. [показать рисунок  или продемонстрировать на модели]

2. Дан равнобедренный треугольник АВС с основанием АС. Где надо отметить точку К, чтобы DАКВ = DСКВ? [Точку надо взять на высоте, проведённой к основанию треугольника]

3. В треугольнике АВС АВ = 3,2 см, ВС = 3,2 см. Каков периметр треугольника, если у него все углы равны? [9,6 см, т.к. треугольник равносторонний]

ü Построения с помощью циркуля и линейки (слайд 21)

1.

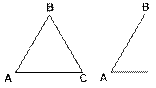
Дан равносторонний треугольник АВС. Часть этого треугольника стёрли и получили новую фигуру. Восстановите данный треугольник.

[В презентации с помощью анимации выполнено построение: продолжить основание и на нём от точки А отложить длину отрезка АВ, полученную точку С соединить с точкой В. DАВС - искомый]

2. Как разделить отрезок пополам, пользуясь только шаблоном острого угла?

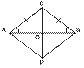[Углы ОАС, ОВС, ОВD и OAD построены с помощью шаблона.

D АСВ равнобедренный, значит, АС = ВС, ОС – медиана (Аналогично DАDB - равнобедренный). Следовательно, АО = ОВ.]

Блок «Доказываем» (слайд 12)

Цель: отработка теоретических знаний по текущему материалу, отработка умения читать чертёж, т.е. видеть на чертеже соответственно равные элементы и делать содержательные ссылки на признаки (треугольники равны по двум сторонам и углу между ними), а не формальные (треугольники равны по первому признаку),  развитие устной математической речи.

Ø Первый признак равенства треугольников (слайд 13)

Задание. Найдите пары равных треугольников и докажите их равенство.

 

На слайде девять готовых  чертежей.

 

Ø Второй и третий признаки равенства треугольников (слайд 14)

 

На слайде девять готовых чертежей.

 

Блок «Чтение заданий» (слайд 15)

Цель: отработка теоретических знаний по текущему материалу; развитие устной (или письменной) речи; организация устных (или письменных) вычислений по готовому чертежу для выработки навыков применения соответствующих теорем.

По данному блоку  обучающимся можно предложить задания: 1) прочесть задание по краткой записи или 2) устно (письменно) вычислить  или  3) сначала: по словесной формулировке (учитель зачитывает задачу в соответствии с краткой записью, расположенной на слайде) выполнить чертёж и составить краткую запись, а потом: для проверки – показать краткую запись на слайде.

Ø Периметр равнобедренного треугольника (слайд 16)

Задания. 1) Составить задачу, используя данные. 2) Найдите стороны треугольника.

 

На слайде шесть задач: рисунок и краткое условие задачи.

 

Например, задача 1: В равнобедренном треугольнике сторона АС длиннее стороны АВ на 3 см. Периметр треугольника равен 15,6 см. Найдите стороны треугольника.

Задачи снабжены ответами.

Ø Свойства равнобедренного треугольника (слайд 17)

Задания. 1) Прочитать рисунок. 2) Найдите угол ВСА. 

 

На слайде семь готовых рисунков.

 

Например, рисунок 1: 1) В равнобедренном треугольнике АВС угол А равен 70⁰.

 

Блок «Самостоятельно решаем» (слайд 23) 

Цель: организация обучающей самостоятельной работы обучающихся в процессе решения задач или организация самостоятельной работы, контролирующей состояние знаний обучающихся, развитие письменной математической речи.

Ø Первый признак равенства треугольников (слайд 24).

1) Докажите равенство треугольников ADC и ABC, изображённых на рисунке, если AD = AB  и Ð1 = Ð2. 2) Найдите углы ADC и ACD, если ÐACB = 380, ÐABC = 1020.

1.   

 

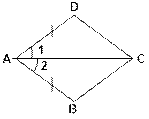
1) Докажите равенство треугольников ABC и ADC, изображённых на рисунке, если BC = AD  и Ð1 = Ð2. 2) Найдите углы ACD и ADC, если ÐABC = 1080, ÐBAC = 320.

2.

 

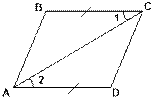
Ø Медианы, биссектрисы и высоты треугольника (слайд 25).

1. В треугольнике АВС сторона АВ равна стороне ВС, ВК – биссектриса угла В. Докажите,  что D АВК = D СВК.

2. В треугольнике MNK проведены медианы MC, KA и NB. Найдите периметр треугольника MNK, если известно, что NA = 3 м, MB = 5 м и KC = 7 м.

3. AN – высота D ABC,  BN = NC. Докажите  равенство треугольников  BAN и  CAN.

Ø Равнобедренный треугольник (слайд 26).

1. В равнобедренном треугольнике сумма всех углов равна 180⁰. Найдите углы этого треугольника, если известно, что один из них равен 110⁰.

2. В равнобедренном треугольнике сумма всех углов равна 180⁰. Найдите углы этого треугольника, если известно, что один из них равен 46⁰ (Рассмотреть все возможные случаи).

Ø Второй и третий признаки равенства треугольников (слайд 27).

1) Докажите равенство треугольников АВО и DСО, изображённых на рисунке, если АО = ОD и Ð А = Ð D. 2) Найдите стороны треугольника COD, если  АО = 5 дм, ВО = 7 дм и АВ = 6 дм.

1.  

 

 

 

 

 

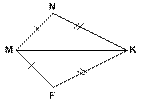
На рисунке MN = MF, NK = KF. Докажите, что луч MK  является биссектрисой угла NMF.

2.

 

Используемая литература:

 

1. Геометрия: учебник для 7 – 9 кл. общеобразовательных учреждений /Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др. – М: Просвещение, 2011

2. Изучение геометрии в  7 – 9 классах: Методические рекомендации к учебнику: Книга для учителя / Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др. – М: Просвещение, 2000

3. А.П.Ершова, В.В.Голобородько Устные проверочные и зачетные работы по всем темам курса геометрии 7 – 9 классов. – М: Илекса, 2007.

4. С.М.Саврасова, Г.А.Ястребинецкий Упражнения по планиметрии на готовых чертежах: Пособие для учителя.  – М: Просвещение, 1987.

4. М.Ю.Шуба Занимательные задания в обучении математике: Книга для учителя – М: Просвещение, 1994.

Скачано с www.znanio.ru