Разработка урока по теме: "Параллельные и перпендикулярные прямые"

Урок: математика

Тема: Параллельные и перпендикулярные прямые. Ломаная, многоугольник. Длина ломаной, периметр многоугольника

Класс: 5

Цели урока:

Дидактическая: формировать наглядно-образное представление о геометрических фигурах: перпендикулярные и параллельные прямые;

ломаная, замкнутые и незамкнутые ломаные;

 многоугольник;

изучить свойства длины;

учить:

распознавать, читать и изображать элементы многоугольника;

строить параллельные и перпендикулярные прямые с помощью угольника;

вычислять периметр многоугольника;

решать практико-ориентированные задачи, задачи с межпредметным содержанием, анализировать и исследовать полученные результаты.

Развивающая: развитие логического мышления, памяти, связной речи, вычислительных навыков.

Воспитательная: воспитание аккуратности, дисциплины, ответственного отношения к учебе, самоконтроля, культуры учебного труда.

Ход урока

1.     Организационный момент.

2.     Актуализация знаний.

1.      Индивидуальный опрос учащихся у доски.

Карточка 1. На прямой АВ отметьте:

а) точку М, принадлежащую отрезку АВ;

б) точку К, принадлежащую лучу АВ, но не принадлежащую отрезку АВ;

в) точку С, не принадлежащую лучу АВ.

Карточка 2. Даны четыре точки А, В, С, D. Постройте все возможные отрезки с концами в точках А, В, С, D. Запишите все отрезки.

2. Фронтальная работа с классом.

·         Сколько прямых можно провести через одну точку?

·         Сколько прямых можно провести через две точки?

·         Как называют прямую, проходящую через точки А и В?

·         Прямые АВ и ВА совпадают или нет?

·         Сколько общих точек могут иметь две прямые?

·         Чем отличается изображение луча от изображения отрезка?

·         Назовите точку, являющуюся началом луча CD.

·         Совпадают ли лучи КМ и МК?

3.     Целеполагание

На этом уроке вы познакомитесь с перпендикулярными прямыми. Научитесь строить такие прямые с помощью чертежного треугольника. Узнаете, как определить, являются ли данные прямые перпендикулярными. Выполните упражнение на данную тему.

4.     Изучение нового материала

Определение

Две прямые на плоскости, которые не пересекаются, называются параллельными

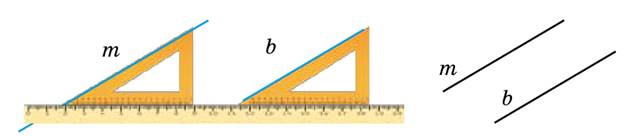
I. Пусть дана некоторая прямая m. Построить прямую b, ей параллельную, можно с помощью угольника и линейки (рис. 20). Для этого:

1) одну сторону угольника расположить вдоль прямой m;

2) положение угольника зафиксировать линейкой;

3) передвинуть угольник вдоль линейки и провести новую прямую b.

Опре­де­ле­ние.

Две пря­мые, об­ра­зу­ю­щие при пе­ре­се­че­нии пря­мые углы, на­зы­ва­ют пер­пен­ди­ку­ляр­ны­ми (рис. 1).

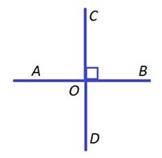
Рис. 1. Пер­пен­ди­ку­ляр­ные пря­мые

Пишут: . Чи­та­ют: «Пря­мая AB пер­пен­ди­ку­ляр­на пря­мой CD».

Сфор­му­ли­ро­ван­ное опре­де­ле­ние пред­по­ла­га­ет два факта:

·      если пря­мая  пе­ре­се­ка­ет пря­мую  в точке , и при этом , то такие пря­мые вза­им­но пер­пен­ди­ку­ляр­ны;

·      если пря­мая  пер­пен­ди­ку­ляр­на пря­мой , то мы имеем право ска­зать, что .

Для опре­де­ле­ния пря­мых углов ис­поль­зу­ют чер­теж­ный тре­уголь­ник. Сна­ча­ла можно опре­де­лить на глаз, яв­ля­ют­ся ли дан­ные углы пря­мы­ми. Затем про­ве­рить с по­мо­щью чер­теж­но­го тре­уголь­ни­ка (рис. 2).

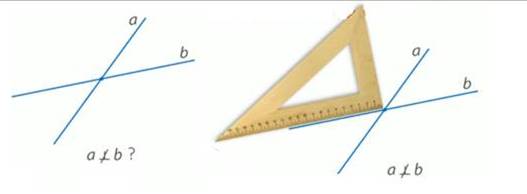
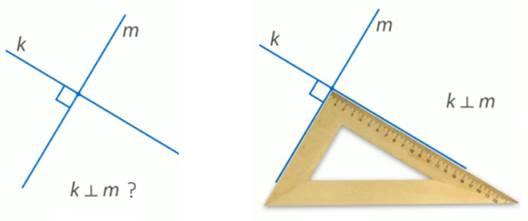
Рис. 2. Про­вер­ка с по­мо­щью чер­теж­но­го тре­уголь­ни­ка

Для вы­чер­чи­ва­ния пря­мых углов можно ис­поль­зо­вать транс­пор­тир или чер­теж­ный тре­уголь­ник. Рас­смот­рим слу­чай по­стро­е­ния пря­мой, пер­пен­ди­ку­ляр­ной к дан­ной, через точку, ле­жа­щую на дан­ной пря­мой.

По­стро­им пря­мую АВ и от­ме­тим на ней точку С (рис. 3).

Рис. 3. Ил­лю­стра­ция к за­да­че

При­кла­ды­ва­ем чер­теж­ный тре­уголь­ник так, чтобы его вер­ши­на сов­па­ла с точ­кой С. Про­во­дим пря­мую КО, пер­пен­ди­ку­ляр­ную пря­мой АВ (рис. 4).

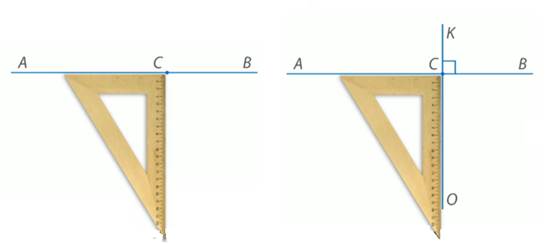
Рис. 4. Ил­лю­стра­ция к за­да­че

Ока­зы­ва­ет­ся, через каж­дую точку пря­мой можно про­ве­сти толь­ко одну пря­мую, пер­пен­ди­ку­ляр­ную дан­ной.

На­учим­ся стро­ить пря­мую, пер­пен­ди­ку­ляр­ную дан­ной, через точку, не ле­жа­щую на дан­ной пря­мой. По­стро­им про­из­воль­ную пря­мую АВ и вне пря­мой от­ме­тим точку С (рис. 5).

Рис. 5. Ил­лю­стра­ция к за­да­че

При­кла­ды­ва­ем чер­теж­ный тре­уголь­ник. Про­во­дим пря­мую, пер­пен­ди­ку­ляр­ную дан­ной (рис. 6).

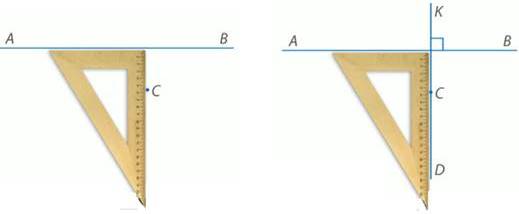
Рис. 6. Ил­лю­стра­ция к за­да­че По­строй­те пря­мой угол А, на его сто­ро­нах от­меть­те по одной точке и через эти точки про­ве­ди­те пря­мые, пер­пен­ди­ку­ляр­ные сто­ро­нам этого угла. От­меть­те точку пе­ре­се­че­ния и опре­де­ли­те, что за че­ты­рех­уголь­ник по­лу­чил­ся (рис. 7).

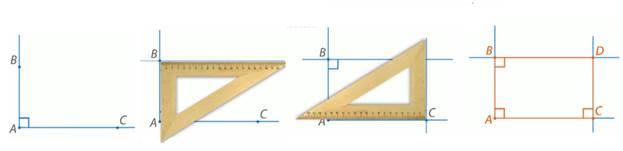
Рис. 7. Ил­лю­стра­ция к за­да­че

Ре­ше­ние.

;

, значит ;

, значит

Вывод:  – пря­мо­уголь­ник.

Физкультминутка

5.     Закрепление изученного

№ 260, 261, 262

№ 262

Ответ:

6.     Подведение итогов урока

1.      Какие прямые называются параллельными, а какие перпендикулярными?

2.      Как проверить, что прямые параллельны?

3.      Как проверить, что прямые перпендикулярны?

4.      Как построить прямую, параллельную данной?

5.      Как построить прямую, перпендикулярную данной?

7.     Домашнее задание.

Глава 3, § 11, № 271

8.     Рефлексия

Метод незаконченных предложений

Сегодня на уроке я научился…

Мне было интересно…

Мне было трудно…

У меня получилось…

Теперь я могу…

Литература

Герасимов, В. Д. Математика : учеб. пособие для 5 кл. учреждений общ. сред, образования с рус. яз. обучения / В. Д. Герасимов, О. Н. Пирютко. — Минск : Адукацыя i выхаванне, 2017.