Дидактикалық материал № 1

Геометрическая вероятность

Цели и задачи: 1) Познакомить учащихся с одним из возможных способов задания 

                            вероятности;

                           2) Повторение пройденного и закрепление навыков формализации

                           текстовых вероятностных задач с помощью геометрических фигур.

Результаты обучения:

                                     1) Знать определение геометрической вероятности выбора точки

                                      внутри фигуры на плоскости и прямой;

                                      2) Уметь решать простейшие задачи на геометрическую вероятность,

                                      зная площади фигур или умея их вычислять.

I. Выбор точки из фигуры на плоскости.

Пример 1.  Рассмотрим мысленный эксперимент: точку наудачу бросают на квадрат, сторона которого равна 1. Спрашивается, какова вероятность события, которое состоит в том, что расстояние от этой точки до ближайшей стороны квадрата не больше чем ?

В этой задаче речь идет о так называемой геометрической вероятности.

Рассмотрим более общие условия опыта.

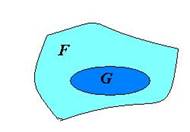
Точку наудачу бросают в фигуру F на плоскости. Какова вероятность того, что точка попадает в некоторую фигуру G, которая содержится в фигуре F.

Ответ зависит от того, какой смысл мы вкладываем в выражение «бросить точку наудачу».

Обычно это выражение трактуют так:

1.      Брошенная точка может попасть в любую часть фигуры F.

2.      Вероятность того, что точка попадает в некоторую фигуру G внутри фигуры F, прямо пропорциональна площади фигуры G.

Подведем итог: пусть  и   - площади фигур F и G . Вероятность события А «точка Х принадлежит фигуре G, которая содержится в фигуре F», равна 

.

Заметим, что площадь фигуры G не больше, чем площадь фигуры F, поэтому

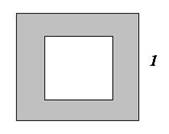Вернемся к нашей задаче. Фигура F в этом примере квадрат со стороной 1. Поэтому  =1. 

Точка удалена от границы квадрата не более чем на , если она попала в заштрихованную на рисунке фигуру  G.  Чтобы найти площадь , нужно из площади фигуры F вычесть площадь внутреннего квадрата со стороной .

Тогда вероятность того, что точка попала в фигуру G, равна 

Пример 2.  Из треугольника АВС случайным образом выбирается точка Х. Найти вероятность того, что она принадлежит треугольнику, вершинами которого являются середины сторон треугольника.

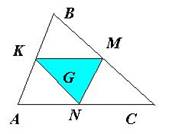Решение:  Средние линии треугольника разбивают его на 4 равных треугольников. Значит,

Вероятность того, что точка Х принадлежит треугольнику KMN, равна:

Вывод. Вероятность попадания точки в некоторую фигуру прямо пропорциональна площади этой фигуры.

Задача.  Нетерпеливые дуэлянты.

Дуэли в городе Осторожности редко кончаются печальным исходом. Дело в том, что каждый дуэлянт прибывает на место встречи в случайный момент времени между 5 и 6 часами утра и, прождав соперника 5 минут, удаляется. В случае же прибытия последнего в эти 5 минут дуэль состоится. Какая часть дуэлей действительно заканчивается поединком?

Решение:  Пусть х и  у обозначают время прибытия 1-го т 2-го дуэлянтов соответственно, измеренное в долях часа начиная с 5 часов.

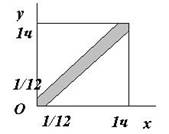Дуэлянты встречаются, если  , т.е. x - < y < x + .

Изобразим это на чертеже.

Заштрихованная часть квадрата отвечает случаю, когда дуэлянты встречаются.

Площадь всего квадрата 1, площадь заштрихованной части:

.

Значит, шансы на поединок равны .

II. Выбор точки из отрезка и дуги окружности.

Рассмотрим мысленный эксперимент, который состоит в случайном выборе одной точки Х из некоторого отрезка MN.

Это можно понимать так, будто точку Х случайным образом «бросают» на отрезок. Элементарным событием в этом опыте может стать выбор любой точки отрезка.

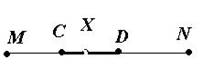Пусть отрезок CD содержится в отрезке MN. Нас интересует событие А, состоящее в том, что выбранная точка Х принадлежит отрезку CD.

Метод вычисления этой вероятности тот же, что для фигур на плоскости: вероятность пропорциональна длине отрезка CD.

Следовательно, вероятность события А «точка Х принадлежит отрезку CD, содержащемуся в отрезке MN»  равна,  .

Пример 1.  Внутри отрезка MN случайным образом выбирается точка Х. Найдите вероятность того, что точка Х ближе к точке N, чем к M.

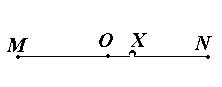Решение:  Пусть точка О – середина отрезка MN. Наше событие наступит тогда, когда точка Х лежит внутри отрезка ON.

 Тогда   .

Ничего не меняется, если точка Х выбирается не из отрезка, а из дуги некоторой кривой линии.

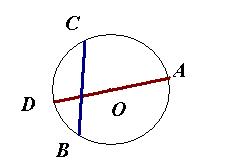Пример 2.  На окружности даны точки А и В, причем эти точки не являются диаметрально противоположными. На этой же окружности выбирается точка С. Найти вероятность того, что отрезок ВС пересечет диаметр окружности, проходящий через точку А.

Решение:  Пусть длина окружности равна L. Интересующее нас событие К «отрезок ВС пересекает диаметр DA» наступает, только если т.С лежит на полуокружности DA, не содержащей точку В. Длина этой полуокружности равна L. 

.

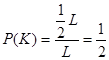Пример 3.  На окружности взята точка А. На окружность «бросают» точку В. Какова вероятность того, что длина хорда АВ будет меньше радиуса окружности.

Решение:  Пусть r – радиус окружности.

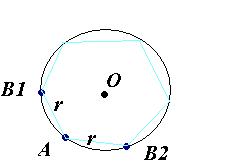
 Для того чтобы хорда АВ была короче радиуса окружности, точка В должна попасть на дугу В₁АВ₂, длина которой равна  длины окружности.

Вероятность того, что длина хорды АВ будет меньше радиуса окружности, равна:

.

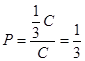III. Выбор точки из числового отрезка

Геометрическую вероятность можно применять к числовым промежуткам. Предположим, что случайным образом выбирается число Х, удовлетворяющее условию . Этот опыт можно заменить опытом, в котором из отрезка [m;n] на числовой прямой выбирается точка с координатой Х.

Рассмотрим событие, состоящее в том, что точка с координатой Х выбрана из отрезка [a;b], содержащегося в отрезке [m;n]. Это событие обозначим  . Его вероятность равна отношению длин отрезков [a;b] и  [m;n].

.

Пример 1.  Найти вероятность того, что точка, случайно выбранная из отрезка [0;1], принадлежит отрезку .

Решение:  По формуле геометрической вероятности находим:

.

Пример 2.  Согласно правилам дорожного движения, пешеход может перейти улицу в неустановленном месте, если в пределах видимости нет пешеходных переходов. В городе Миргороде расстояние между пешеходными переходами на улице Солнечной равно 1 км. Пешеход переходит улицу Солнечную где-то между двумя переходами. Он может видеть знак перехода не дальше чем за 100 м от себя. Найдите вероятность того, что пешеход не нарушает правила.

Решение:  Воспользуемся геометрическим методом. Расположим числовую прямую так, что участок улицы между переходами окажется отрезком [0;1]. Пусть пешеход подходит к улице в некоторой точке с координатой Х. Пешеход не нарушает правила, если он находится на расстоянии более чем 0,1 км от каждого перехода, т.е. 0,1<X<0,9. Найдем вероятность этого события:

.

Пример 3.  Поезд проходит мимо платформы за полминуты. В какой-то момент, совершенно случайно выглянув из своего купе в окно, Иван Иванович увидел, что поезд идет мимо платформы. Иван Иванович смотрел в окно ровно 10 секунд, а затем отвернулся. Найдите вероятность того, что он видел Ивана Никифоровича, который стоял ровно посередине платформы.

Решение:  Воспользуемся геометрическим методом. Будем вести отсчет в секундах. За 0 секунд примем момент, когда Иван Иванович поравнялся с началом платформы. Тогда конца платформы он достиг в момент 30 секунд. За Х сек. Обозначим момент, когда Иван Иванович выглянул в окно. Следовательно, число Х случайным образом выбирается из отрезка [0;30]. С Иваном Никифоровичем Иван Иванович поравнялся в момент 15 секунд. Он увидел Ивана Никифоровича, только если он выглянул в окно не позже этого момента, но не раньше, чем за 10 секунд до этого. Таким образом, нужно найти геометрическую вероятность события  . По формуле находим

.

«Вероятностная подоплека»

В самом начале поэмы Н. В. Гоголя «Мертвые души» два мужика спорят относительно того, как далеко доедет колесо в экипаже Чичикова:

«…два русских мужика, стоявших у дверей кабака против гостиницы, сделали кое-какие замечания, относившиеся впрочем, более к экипажу, чем к сидевшему в нем. «Вишь ты», сказал один другому: «вон какое колесо! Что ты думаешь, доедет то колесо, если б случилось, в Москву, или не доедет?» - «Доедет», отвечал другой. «А в Казань-то, я думаю, не доедет?» «В Казань не доедет», отвечал другой».

Задачи для решения.

1.     Найти вероятность того, что точка случайным образом брошенная в квадрат       ABCD со стороной 4 попадет в квадрат A₁B₁C₁D₁ со стороной 3, находящийся внутри квадрата ABCD.

Ответ. 9/16.

2.     Два лица А и В договорились встретиться в определенном месте в промежутке времени от 9⁰⁰ до 10⁰⁰. Каждый из них приходит наудачу (в указанный промежуток времени), независимо от другого и ожидает 10 минут. Какова вероятность того, что они встретятся?

Ответ. 11/36.

3.     В отрезке АВ длины 3 случайно появляется точка С. Определить вероятность того, что расстояние от точки С до В превосходит 1.

Ответ. 2/3.

4.     В круг радиусом 5 вписан треугольник наибольшей площади. Определите вероятность попадания в треугольник точки, случайно брошенной в круг.

Ответ.

5.     Буратино посадил на прямоугольный лист размером 20 см на 25 см круглую кляксу радиусом 1 см. Сразу после этого Буратино посадил еще одну такую же кляксу, которая целиком оказалась на листе. Найдите вероятность того, что эти две кляксы не соприкасаются.

Ответ.

6.     В окружность вписан квадрат ABCD. На этой окружности случайным образом выбирается точка М. Найдите вероятность того, что эта точка лежит на:            а) меньшей дуге АВ; б) большей дуге АВ.

Ответ. а) 1/4; б) 3/4.

7.     На отрезок [3;6] случайным образом бросается точка Х. С какой вероятностью выполняется неравенство: а) ;  б) ;  в) ?

Ответ. а) 1/3; б) 1/3; в) 1/3.

8.     Про село Иваново известно только, что оно находится где-то на шоссе между Миргородом и Старгородом. Длина шоссе равна 200 км. Найдите вероятность того, что: 

             а) от Миргорода  до Иваново по шоссе меньше 20 км;

             б) от Старгорода до Иваново по шоссе больше 130 км;

             в) Иваново находится менее чем в 5 км от середины пути между городами.

Ответ. а) 0,1; б) 0,35; в) 0,05.

Дополнительный материал

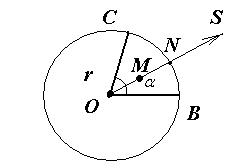Геометрический подход к вероятности события не зависит от вида измерений геометрического пространства: важно только, чтобы множество элементарных событий F и множество G, представляющее событие А, были бы одинакового вида и одинаковых измерений.

Пусть на плоскости задан круг и определен его сектор ВОС.  .

Рассмотрим вероятность трех событий А₁, А₂ и А₃, состоящих в следующем.

1)  В круг наудачу бросается точка М.  А₁ – «попадание М в сектор ВОС».

2)  На дугу окружности наугад бросается точка N. А₂ – «попадание N на дугу BDC».

3)  На рисунок наудачу бросается вектор , начало которого закреплено в точке О. А₃ – «попадание   в угол ».

Пусть ОС=r – радиус круга. Тогда

;

;

.

Задачи для решения:

1.              Случайная точка Х имеет равномерное распределение в квадрате . Найти вероятность того, что квадрат с центром Х и сторонами длины b (0<b<2a), параллельными осями координат, целиком содержится в квадрате А.                                                                     

Ответ.  .

2.              Случайная точка Х равномерно распределена в квадрате . Найти вероятность того, что квадрат с центром Х и сторонами длины b, параллельными осям координат, целиком содержится в квадрате А.

 Ответ.  .

Литература:

1.     Теория вероятностей и статистика / Ю. Н. Тюрин, А. А. Макаров, И. Р. Высоцкий, И. В. Ященко. – 2-е изд., переработанное. – М.: МЦНМО: ОАО «Московские учебники», 2008. – 256 с.: ил.

2.     Теории вероятностей и математическая статистика в примерах и задачах с применением Excel / Г. В. Горелова, И. А. Кацко. – Изд. 4-е. – Ростов н/Д: Феникс, 2006. – 475 с.: ил. – (Высшее образование).

3.     Пятьдесят занимательных вероятностных задач с решениями. Пер. с англ./Под ред. Ю. В. Линника. 3-е изд. – М.: Наука, Главная редакция физико-математической литературы, 1985. – 88 с.

4.     Сборник задач по теории вероятностей: Учеб. Пособие для вузов./Зубков А. М., Севастьянов Б. А., Чистяков В.П. – 2-е изд., испр. И доп. – М.: Наука. Гл. ред. Физ.-мат. Лит. – 1989. – 320с.

5.     Факультативный курс по математике: Теория вероятностей: Учеб. Пособие для 9-11 кл. сред. шк./Лютикас В.С. – 3-е изд. перераб. – М.: Просвещение, 1990. – 160 с.