Дидактикалық материал №4_Формативты бағалау

Формативное оценивание  №  4    (4 четверть)

                                                                         Ф.И. ученика______________________________

        Задача 1. В прямоугольник 5*4 см² находится круг радиуса 1,5 см. Найти

      вероятность того, что точка, взятая случайным образом, не попадёт в данный  круг.

      Ответ дайте с точностью до сотых.

      Задача 2. В круге случайным образом берется точка. Найдите вероятность того,

       что эта точка принадлежит вписанному в этот круг квадрату.

Задача 3. Вася и Оля условились о свидании у памятника Пушкину между девятью и   

десятью часами. Они договорились, что каждый ждет другого в течение 20 минут, а

затем уходит. Какова вероятность, что они встретятся?

Задача 4. В квадрате АВСД случайным образом выбирается точка Х. Найдите вероятность того, что эта точка принадлежит трапеции АМСД, где точка М  делит отрезок СB в отношении, 1: 3, считая от точки B.

      Задача 5. Оконная решетка состоит из клеток со стороной  25 см. В решетку 70 раз     

      бросили наугад один и тот же мяч. В 30 случаях он пролетел через решетку, не задев

      ее. Найдите радиус мяча.

Задача о встрече. Вася и Оля условились о свидании у памятника Пушкину между девятью и десятью часами. Они договорились, что каждый ждет другого в течение 15 минут, а затем уходит. Какова вероятность, что они встретятся?

Пусть х – момент прихода Васи (отсчитываем его от девяти часов в долях часа: например, если он пришел полдесятого, то х = 0,5), у – момент Олиного прихода. Исход эксперимента можно описать парой чисел {х, у} или точкой на плоскости с такими координатами. При этом обе координаты могут принимать любые значения от 0 до 1. Таким образом, область Ω, соответствующая всем возможным исходам,– это единичный квадрат (рис. 11.6). Благоприятный исход (когда Вася и Оля встретятся) означает, что между моментами х и у прошло не больше 15 минут, или четверти часа. Это описывается неравенством |х – у| ≤ ¹/₄. Раскрывая модуль, получим х – ¹/₄ ≤ у ≤ х + ¼.Этому неравенству удовлетворяют точки, лежащие между прямыми у = х – ¹/₄ и у = х + ¹/₄ (заштрихованная область А на рис. 11.6). Нетрудно посчитать площадь благоприятной области. Она равна площади квадрата минус площадь двух незаштрихованных прямоугольных треугольников. Катеты треугольников равны ³/₄, и их суммарная площадь равна (³/₄)² = ⁹/₁₆. Значит, искомая площадь S(A) = 1 – ⁹/₁₆ = ⁷/₁₆. Вероятность встречи

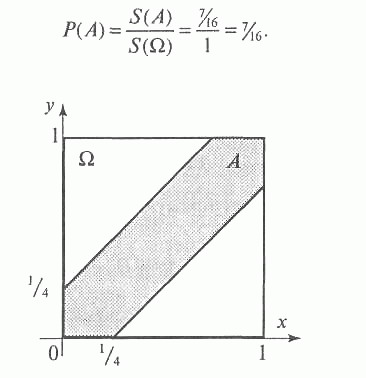
Рис. 11.6

 Тест

Вопрос 1. Выберите верное утверждение о геометрической вероятности.

1)  Геометрическая вероятность используется при вычислении объемов тел. 

2)  При использовании формул  геометрической вероятности всегда нужно находить площади фигур. 

3)  Формулы геометрической вероятности могут применяться тогда, когда число исходов опыта бесконечно. 

4)  Формулы геометрической вероятности используются при нахождении длин отрезков. 

Ответ:  3) 

Вопрос 2. На отрезке длиной 20 см случайным образом выбирается точка. Какова вероятность, что точка окажется серединой отрезка?

 1)  0 

2)  0,1 

3)  0,2 

4)  1 

Ответ: 1) 

Вопрос 3. В квадрате  со стороной 4 см выбирается случайная точка. Какова вероятность, что эта точка лежит на диагонали квадрата?

 1)  0 

2)  0,125 

3)  0,5 

4)  1 

Ответ: 1) 

Вопрос 4. В круге с радиусом 10 см наугад выбирается точка. С какой вероятностью расстояние от этой точки до центра круга будет меньше 5 см?

 1)  0,5 

2)  0,1 

3)  0,2 

4)  0,25 

Ответ: 4) 

Вопрос 5. В прошлом веке в Америке была популярна следующая игра. Игрок бросает монету на поверхность стола, разграфленную на однодюймовые квадраты. Если монета (диаметром 3/4 дюйма) попадает полностью внутрь квадрата, то игрок получает награду, в противном случае игрок теряет свою монету. Каковы шансы выиграть?

 1)  0 

2)  0,0625 

3)  0,5 

4)  0,75 

Ответ: 2) 

Обменяйтесь листком с соседом по парте. Проверим ответы. (учитель записывает верные ответы на доске).

Учащимся, справившимся с тестом без ошибок, а также активно работавшим на уроке выставляются оценки.

7. Домашнее задание.

Домашнее задание записано на рабочем листке, который учащиеся забирают с собой.

1. Оконная решетка состоит из клеток со стороной 20 см. Какова вероятность того, что попавший в окно мяч пролетит через решетку, не задев ее, если радиус мяча равен: а) 10 см, б) 5 см.

2. В решетку из предыдущей задачи 100 раз бросали наугад один и тот же мяч. В 50 случаях он пролетел через решетку, не задев ее. Оцените приближенно радиус мяча.

Задача о встрече. Вася и Оля условились о свидании у памятника Пушкину между девятью и десятью часами. Они договорились, что каждый ждет другого в течение 25 минут, а затем уходит. Какова вероятность, что они встретятся?

3.

Ответы: 1. а) 0; б) .   2. Если обозначить R радиус мяча, то  R3.

8. Рефлексия.

Учащиеся, используя слова, записанные в рабочем листе,  дают ответы: что узнали, что поняли, чему научились, что вызывает затруднения.