Длина отрезка

Тема урока; Длина отрезка

 

(урок изучения и первичного закрепления новых знаний)

Цель урока:

·  Познакомить учащихся с процедурой измерения отрезков, рассмотреть свойства измерения отрезка;

·  познакомить с различными единицами измерения и инструментами для измерения отрезков;

·  узнать, как приблизительно уметь измерять без инструментов.

Планируемые результаты

(предметные, личностные метапредметные УУД):

Личностные: формирование устойчивой мотивации к индивидуальной деятельности по самостоятельно составленному плану

Предметные: знать определение отрезка, длины отрезка

Метапредметные УУД

Коммуникативные: слушать других, пытаться принимать другую точку зрения, быть готовым изменить свою точку зрения.

Регуляционные: проводить контроль в форме сравнения способа действия и его результат с заданным эталоном с целью обнаружения отклонений от эталона и внесения необходимых коррективов.

Познавательные: сравнивать, делать выводы; выделять существенную информацию из текстов разных видов

 

Тип урока: урок изучения и первичного закрепления новых знаний

Формы работы: групповая, индивидуальная, фронтальная.

Учебник: Никольский С.М., Потапов М. К., Решетников Н. Н. и др. «Математика. 6 класс», − М.: Просвещение, 2014г.

Оборудование: учебник, проектор, компьютер, карточки с заданиями в парах, презентация, словарь, информация из энциклопедии, листы самооценки.

 

ХОД УРОКА:

1. Организационный момент.

- Здравствуйте, ребята!

Разложите по порядку

Книжки, ручки и тетрадки!

Начинаем наш урок,

Он пойдет, конечно, впрок.

Будем знанья открывать!

Постарайтесь всё понять!

2. Актуализация опорных знаний.

1. Устный счёт:

1) 3,2 * 2 5) 8,4 : 0,2 9) 2,5 : 0,01 13) – 6 + 10

2.10 : 0,5 6) 25 * 0,4 10) 10 : 2,5 14) 7 – 11

3.12 * 0,3 7) 15 : 1,5 11) 0,3 * 0,4 15) - 7 + 7

4) 4,2 * 2 8) 24 : 0,8 12) – 5 – 4

2. Да или нет?

1.Целое число является рациональным.

2.Конечные десятичные дроби являются иррациональным.

3.Иррациональное число является действительным.

4.Рациональное число является действительным.

5.Периодическая десятичная дробь является рациональным.

Ответы:

1) Да;

2) Нет;

3) Да;

4) Да;

5) Да.

Производится взаимопроверка.

 

3. Подготовка и мотивация

 

РЕБЯТА, ПЕРЕД ВАМИ ГЕОМЕТРИЧЕСКАЯ ФИГУРА, НАЗОВИТЕ ЕЁ:

 

А

 В АВ = 4 см 6 мм

Как вы думаете, ребята, какая тема сегодняшнего урока?

(Дети высказывают свои предположения о теме урока)

Значит, тема урока «Длина отрезка»

 

Далее учитель предлагает записать в тетрадях тему урока, сформулировать цель и задачи урока.

Цель урока:

·  Познакомить учащихся с процедурой измерения отрезков, рассмотреть свойства измерения отрезка;

·  познакомить с различными единицами измерения и инструментами для измерения отрезков;

·  узнать, как приблизительно уметь измерять без инструментов.

 

4. Изучение нового материала.

 

Однажды два друга пошли на рыбалку и на удочку попался кувшин, а в кувшине карта. А в карте было указано, где зарыт клад!

В карте указано, что клад зарыт от старого дуба на расстоянии 20 …, остальную часть смыло водой.

Что же делать? В чём измерять?

Первый встречный предложил им измерить в аршинах:

Аршин – длина всей руки

1 аршин = 71,12 см

 

Второй предложил в саженях:

Маховая сажень – расстояние между кончиками пальцев раскинутых рук

1 маховая сажень = 151,4 см

 

И друзья намерили так, что забрели далеко в дремучий лес. Это всё потому, что не знали в чём измерять!

Просмотр видеофильма из передачиАБВГДейка о системе единиц измерения расстояния.(С 13.51-16.02 и 21.24-21.51)

 

Метр (русское обозначение: м; международное: m; от др.-греч. μέτρον — мера, измеритель) — единица измерения длины и расстояния в Международной системе единиц (СИ), одна из семи основных единиц СИ.

Двое друзей узнав в чем измеряется расстояние и измерив на основе инструкции на карте, нашли клад.

 

 

 

- А чем мы обычно измеряем? Сравниваем?

  

Линейка Рулетка Штангенциркуль

Свойства измерения отрезка:
1. Каждый отрезок имеет определенную длину, большую нуля.
2. Длина отрезка равняется сумме длин частей, на которые он разбивается любой своей внутренней точкой.
3. Расстоянием между двумя точками A и B называется длина отрезка AB .
4. При этом, если точки A и B совпадают, будем считать, что расстояние между ними равно нулю.
5. Два отрезка называются равными, если равны их длины.

6.Физминутка

 

7.Закрепление.

А теперь познакомимся с самой маленькой древней мерой в странах Европы:

(эта мера очень часто используется в нашей жизни)

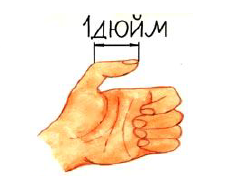
Дюйм – мера, равная длине верхней фаланги большого пальца.

1 дюйм ≈ 2, 54 см

Задание 1

Два друга поспорили, у кого из них диагональ телевизора длинней. Первый говорит, что диагональ его телевизора равна 81 см, а второй утверждает, что у него – 32 дюйма. Кто из друзей прав?

32.              * 2,54 =81,28 см

81 см < 81,28 см

Ответ: второй друг прав.

Задание 2

№1026

Длина отрезка АВ выражена числом 5,375. Запишите приближённую длину отрезка с точностью до 1 ; до 0,1.

5,375 ≈ 5

5,375 ≈ 5,4

Задание 3

На прямой отмечены точки А, В, С.

Длина отрезка АВ выражена числом 7,345 , а длина отрезка ВС выражена числом 2, 48 . Запишите приближённую длину отрезка АС (рассмотрите всевозможные случаи) с точностью до 0,01.

 

1.случай АС= 7,345 +2,48=9,825≈9,83

2.случай АС=7,345 – 2,48=4,865≈4,87

 

8.Практическое применение.

Каждой паре раздаются отрезки равных длин – 61 см. Выполнить следующие задания:

1.Измерьте длину отрезка на глаз, ответ запишите в тетрадь;

2.Вам совет:

Должно быть известно вам наибольшее расстояние между концами указательного и большого пальцев. Или расстояние между концами мизинца и большого пальцев .
Вооружившись всеми этими сведениями, вы сможете довольно удовлетворительно выполнять разнообразные измерения буквально голыми руками, даже в темноте.

А теперь проверьте этим методом, ответ запишите в тетрадь;

3.Теперь длину измерьте линейкой, ответ запишите в тетрадь.

Ну как ребята, научились примерно измерять длину отрезка без линейки?

Надеюсь, эти знания пригодятся в будущем!

 

9.Домашнее задание:

 

1.повт. п. 5.1-5.5;№1022, №1027 (б)

2.Вспомните пословицы, поговорки, в которых фигурируют меры длины.

3.Найти еще единицы измерения длины, которые не были перечислены на уроке.

 

10.              Подведение итога урока:

 

Учащиеся оценивают друг друга, обсуждаются типичные ошибки.

 

Скачано с www.znanio.ru