ДОКАЗАТЕЛЬСТВО ТОЖДЕСТВ

Доказательство тождеств

Цели: продолжить  формирование  умения  умножать  многочлены; применять  это  умение  для  доказательства  тождеств  и  некоторых утверждений.

Ход урока

I. Устная работа.

1. Выполните умножение.

а) x² · 7x⁵;                                          г) 2х (х² – 7х);

б) –8а · 4а⁴;                                          д) –4p⁴ ;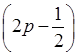

в) –6y³ · 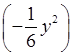;                             е) –3п⁵ (п³ – 2п).

2. Сколько слагаемых получится со знаком «+» и сколько со знаком «–» при умножении многочленов:

а) (a + 2) (b + 5);                                  в) (n² – 3) (m – 5);

б) (х – 3) (у + 7);                                  г) (–а – 2) (с – 4)?

II. Формирование умений и навыков.

Все задания можно разбить на две группы. В 1-ю группу войдут задания на доказательство тождеств, а во 2-ю группу – на доказательство утверждений о делимости, кратности и др.

1-я группа

Прежде чем приступить к выполнению заданий этой группы, нужно вспомнить логику доказательства тождеств.

Для наглядности можно вынести на доску схему:

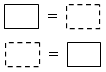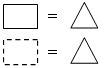1)              2)               3) 

То есть существует три основных приема доказательства тождеств:

1) преобразовать левую часть тождества в правую или правую часть тождества в левую;

2) показать, что левая и правая части исходного равенства тождественно равны одному и тому же выражению;

3) показать, что разность левой и правой части исходного равенства тождественно равна нулю.

1. № 690 (а), № 691 (а).

При доказательстве этих тождеств используется первый прием, то есть мы будем преобразовывать одну часть равенства до тех пор, пока она не станет тождественно равной другой части равенства.

2. № 692 (а).

При доказательстве этого тождества используется второй прием.

Решение:

а) (x – 3) (x + 7) – 13 = (x + 8) (x – 4) – 2.

Преобразуем левую часть равенства:

Преобразуем правую часть равенства:

Получаем следующее: левая и правая части равенства тождественно равны одному и тому же выражению, значит, исходное равенство является тождеством.

2-я группа

1. № 693.

Решение:

а) Упростим данное выражение:

Получаем, что исходное выражение равно числу –36, значит, не зависит от переменной х.

б)

2. № 699 (а).

Решение:

а) Упростим данное выражение:

Поскольку каждое слагаемое суммы 6п + 6 кратно 6, то и вся сумма кратна 6.

3. № 696.

Решение:Четыре последовательных нечётных числа можно записать в следующем виде:

а = 2п + 1,   b = 2п + 3,   с = 2п + 5   и   d = 2п + 7.

Составим разность cd – ab:

(2n + 5) (2n + 7) – (2n + 1) (2n + 3).

Преобразуем это выражение:

– 6n – 2n – 3 = 16n + 32 = 16 (n + 2).

Очевидно, что полученное выражение кратно 16.

III. Итоги урока. Домашнее задание:  № 690 (б);  № 691 (б);  № 692 (б);  № 694;
№ 695 (б).