Доклад "Использование межпредметных связей при подготовке к ОГЭ и ЕГЭ по математике"

 Доклад на тему :

«Использование межпредметных связей при подготовке

к ОГЭ И ЕГЭ по математике».

Подготовила

Бондаренко Надежда Ивановна,

 учитель математики

 ГБОУ РО «Новочеркасская школа-интернат» .

I.                  Вступительная часть: обоснование актуальности проблемы.

   Реализация межпредметных связей в учебном процессе создает условия для целостного восприятия единой научной картины мира. Использование межпредметных связей при подготовке к единому государственному экзамену (далее – ЕГЭ) обусловлено несколькими аспектами: во-первых, повышением научного уровня содержания образования, во-вторых, увеличением объема информации, подлежащей усвоению учащимися, в-третьих, возросшими требованиями к уровню предметных компетенций выпускников средней школы. Согласно ФГОС среднего (полного) общего образования метапредметные результаты освоения основной образовательной программы должны отражать:

·        Владение навыками познавательной, учебно-исследовательской и проектной деятельности, навыками разрешения проблем; способность и готовность к самостоятельному поиску методов решения практических задач, применению различных методов познания;

·        Умение самостоятельно определять цели деятельности и составлять планы деятельности; самостоятельно осуществлять, контролировать и корректировать деятельность; использовать все возможные ресурсы для достижения поставленных целей и реализации планов деятельности; выбирать успешные стратегии в различных ситуациях;

Межпредметные связи развивают у школьников логическое и критическое мышление, творческие способности. Использование таких связей в учебном процессе уменьшает дублирования при изучении нового материала, формирует навыки и умения у учащихся применять в практике свои знания.

II.               Теоретические основания данной темы.

   Характерной особенностью КИМов по предмету: «Математика» является наличие задач прикладного характера, в которых прослеживается межпредметная связь с рядом дисциплин: биологией ,физикой, химией,  экономикой. Следует отметить, что данные задания не являются типовыми ни для математики; ни для физики, химии, биологии, поскольку для решения данных задач необходим как математический аппарат (интерпретация графиков, работа с диаграммами, понимание прикладного значения производной, вероятности), так и понятийный аппарат дисциплин естественнонаучного и социально-экономического профиля. Предлагая учащемуся задачу прикладного характера, учитель должен представлять, какую цель преследует данная задача и какие именно знания или понятия других дисциплин необходимо использовать для решения подобных задач. Следует стремиться выдерживать общий дидактический принцип, основанный на идее посильности каждой задачи в общей цепи упражнений, постепенном нарастании трудности, взаимосвязи нового и пройденного материала. С помощью таблицы можно увидеть связь предметов:

Данная таблица поможет учителю определить, на какие навыки и умения по другим предметам он может опираться при изучении тех или иных тем своего предмета. Не случайно в заданиях ЕГЭ по математике много задач с прикладным содержанием, как при сдаче профильного уровня, так и базового. В вариантах базового  уровня это задачи 4, 9, 11, 14, профильного 2,8,10.

III.          Практикоориентированный материал

   Подготовка к ОГЭ  и  ЕГЭ осуществляется на уроках, элективных курсах и консультациях.

   Задачи на установление соответствия величин, на определение зависимости использую, как устный счет в начале урока, ориентирую учащихся на то, что в этом задании необходимы знания географии, биологии и физики:

Пример1. Установите со­от­вет­ствие между ве­ли­чи­на­ми и их воз­мож­ны­ми значениями: к каж­до­му эле­мен­ту пер­во­го столб­ца под­бе­ри­те со­от­вет­ству­ю­щий эле­мент из вто­ро­го столбца.

   Пример2. В ходе химической реакции количество исходного вещества (реагента), которое еще не вступило в реакцию, со временем постепенно уменьшается. На рисунке эта зависимость представлена графиком. На оси абсцисс откладывается время в минутах, прошедшее с момента начала реакции, на оси ординат – масса оставшегося реагента, который еще не вступил в реакцию (в граммах). Определите по графику, сколько граммов реагента вступило в реакцию за три минуты?

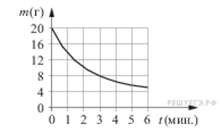
   Не секрет, что большие трудности у учащихся вызывают текстовые задачи. Как правило, с текстовыми задачами справляются 35 - 40% учащихся. Для решения текстовых задач используем следующий алгоритм:

1.     Прочитать текст задачи;

2.     Определить все неизвестные величины;

3.     Сопоставить каждой неизвестной величине свою математическую переменную (неизвестную);

4.     Связать все неизвестные величины с данными задачи (т.е. составить уравнение);

5.     Решить полученное уравнение;

6.    Записать ответ задачи.

    В первую очередь необходимо перевести задачу на математический язык. Текстовые задачи делятся на: задачи на движение, на сплавы и смеси, на совместную работу, на проценты. Чтобы рассмотреть как можно больше видов задач, класс делиться на группы. Первая группа решает задачу на движение, вторая на совместную работу, третья на смеси и сплавы, четвертая на проценты. Для удобства каждая группа должна заполнить предложенную таблицу, решить задачу и предложить решение задачи остальным ученикам. Приведу примеры:

    Задача на движение. (1 группа)

Основная формула S=v∙t

Два велосипедиста одновременно отправились в 240-километровый пробег. Первый ехал со скоростью, на 1 км/ч большей, чем скорость второго, и прибыл к финишу на 1 час раньше второго. Найти скорость велосипедиста, пришедшего к финишу первым. Ответ дайте в км/ч.

1.     Заполнить таблицу:

(вторую строчку группа заполняет самостоятельно)

2.     Составить уравнение и решить его.

3.     Записать ответ.

   Задача на совместную работу. (2 группа)

Основная формула: A=F∙s (физика) A=n∙t, где n-количество деталей в час, t-время.

На изготовление 475 деталей первый рабочий тратит на 6 часов меньше, чем второй рабочий на изготовление 550 таких же деталей. Известно, что первый рабочий за час делает на 3 детали больше, чем второй. Сколько деталей в час делает первый рабочий?

1.     Заполнить таблицу:

(вторую строчку группа заполняет самостоятельно)

2.     Составить уравнение и решить его.

3.     Записать ответ.

   Задача на смеси и сплавы. (3 группа)

Основная формула: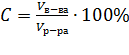

Смешали 4 литра 15–процентного водного раствора некоторого вещества с 6 литрами 25–процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?

1.     Заполнить таблицу:

(вторую строчку группа заполняет самостоятельно)

2.     Составить выражение и решить его.

3.     Записать ответ.

После рассмотрения всех задач ученикам предлагается  выполнить самостоятельную работу.

IV.            Заключение.

    При рассмотрении интегрированных задачи по математике и физике, математике и химии, математики и географии и т.д, можно раскрыть все особенности их решения с позиции различных предметов, и дать цельное представление. Цель интегрированного подхода к решению задач – воспитание личности с нестандартным мышлением. Интегрированный подход способствуют развитию речи, абстрактному и логическому мышлению, произвольному вниманию, побуждают к активности и самостоятельности. Чтобы выполнить задание, которое подбирает учитель, ученик должен знать программный материал, уметь делать выводы на основе сравнений, выявлять закономерность, уметь воображать. Каждый ученик работает в меру своих сил, поднимаясь, на свою, только ему посильную ступеньку.