ЭФФЕКТИВНОСТЬ И ПРАВИЛЬНОСТЬ.docx

ЭФФЕКТИВНОСТЬ И ПРАВИЛЬНОСТЬ

В этом разделе мы обсудим понятия, которые являются частью данного формального введения в теорию алгоритмов. О

них всегда нужно помнить при самостоятельной разработке алгоритмов. Первое из них – эффективность, а второе – пра- вильность.

Эффективность алгоритма. Хотя современные машины способны выполнять миллионы операций в секунду, эффек- тивность по-прежнему остается важнейшим аспектом разработки алгоритмов. Зачастую выбор между эффективным и неэф- фективным решением задачи может на самом деле означать выбор между реализуемым и нереализуемым способом ее реше- ния.

Рассмотрим задачу, с которой сталкивается секретарь университета при поиске личных дел студентов и их заполнении. Хотя в университете на протяжении любого семестра фактически числится около 10 000 студентов, секретарю в действи- тельности приходится иметь дело с более чем 30 000 личных дел, поскольку за несколько предыдущих лет многие из студен- тов зарегистрировались для изучения хотя бы одной из преподаваемых в университете дисциплин, но не смогли закончить цикл обучения. Теперь предположим, что все личные дела хранятся в компьютере секретаря в виде списка, упорядоченного по идентификационным номерам каждого из студентов. Чтобы найти личное дело некоторого студента, секретарь должен выполнить поиск по его идентификационному номеру в общем списке.

Мы уже познакомились с двумя алгоритмами поиска в подобных списках последовательным и двоичным поиском. Сейчас нам нужно дать ответ на вопрос, почувствует ли секретарь разницу между этими двумя алгоритмами? Начнем с рассмот- рения последовательного поиска.

При заданном идентификационном номере студента алгоритм последовательного поиска начинает работу с начала спи- ска и последовательно сравнивает каждый выбираемый элемент с искомым числом. Не зная, что представляет собой искомое число, мы не можем определить, насколько далеко потребуется просматривать список. Все же можно утверждать, что для множества выполненных операций поиска их средняя глубина будет равна приблизительно половине длины списка, хотя в отдельных случаях поиск потребует меньшего числа операций, а в других – большего. Можно сделать вывод, что при много- кратном выполнении последовательного поиска на каждый случай в среднем приходится приблизительно 15 000 просмот- ренных личных дел. Если выборка каждого личного дела из памяти и сравнение его номера с искомым выполняется за де- сять миллисекунд (десять тысячных долей секунды), то среднее время поиска будет составлять 150 с или две с половиной минуты. Если секретарю придется так долго ожидать появления на экране монитора личного дела интересующего его сту- дента, несомненно, что этот вариант совершенно неприемлем. Даже если время выборки и проверки каждой записи сокра- тить до одной миллисекунды, на поиск личного дела студента все равно потребуется в среднем около 15 с – все еще слиш- ком много для среднего времени ожидания ответа, которое можно считать приемлемым.

В противоположность этому, алгоритм двоичного поиска начинает работу со сравнения искомого значения со средним элементом списка. Если это не искомый элемент, то область поиска сразу же сужается до половины исходного списка, т.е. после проверки среднего элемента списка из 30 000 личных дел алгоритм двоичного поиска в большинстве случаев выберет для дальнейшего рассмотрения только 15 000 дел. После второго этапа область поиска в большинстве случаев сократится до 7500 дел, после третьего – до 3750 и т.д. В результате искомое значение будет найдено при выборе, самое большее, 15 эле- ментов списка, состоящего из 30 000 дел. Таким образом, если каждое выбранное значение обрабатывается за 10 миллисе- кунд, процесс поиска нужного личного дела потребует не более 0,15 с, а это означает, что с точки зрения секретаря личное дело любого студента будет появляться на экране практически мгновенно. Можно сделать обоснованное заключение, что выбор между алгоритмом последовательного поиска и алгоритмом двоичного поиска в данном случае имеет большое значе- ние².

Этот пример иллюстрирует важность той области компьютерных наук, которую называют анализом алгоритмов. Эта область связана с изучением необходимых алгоритмам ресурсов, таких, как время или используемый объем памяти. Основ- ным практическим применением результатов подобных исследований является оценка относительных достоинств альтерна- тивных алгоритмов. В нашем случае мы проанализировали время, требующееся алгоритмам последовательного и двоичного поиска, что позволило нам определить, какой из них больше подходит в данном конкретном случае. В общем случае такой анализ осуществляется в более широком контексте. Это означает, что при рассмотрении алгоритмов, выполняющих поиск в списке, мы не ограничимся списком фиксированной длины, но пытаемся вывести формулу эффективности алгоритма для списков произвольной длины. Такой анализ включает изучение ситуаций, в которых алгоритм демонстрирует свои наилуч- шие свойства, ситуаций, когда его эффективность минимальна, а также оценку его средней производительности.

В предыдущем случае выполненный нами анализ заключался в оценке средней производительности алгоритма после-

довательного поиска, а также определении той производительности, которую алгоритм двоичного поиска продемонстрирует в наихудшем случае. Хотя мы рассматривали список определенной длины, несложно обобщить наши рассуждения на случай списка произвольной длины. В частности, при применении к списку из п элементов алгоритму последовательного поиска в среднем потребуется проверить n/2 элементов, тогда как алгоритму двоичного поиска в самом худшем случае потребуется проверить только log₂n элементов. (В данном случае выражение log₂n представляет логарифм числа п по основанию 2, кото- рый показывает, сколько раз число n можно разделить на два.)

Давайте попробуем проанализировать аналогичным образом алгоритм сортировки методом вставки. Поскольку основ- ным действием в реализации данного алгоритма является сравнение двух имен, наш подход будет состоять в подсчете коли- чества таких сравнений, которые потребуется выполнить при сортировке списка длиной п элементов.

Вспомним, что при сортировке методом вставки осуществляется выбор некоторого элемента, называемого опорным; после этого он сравнивается с предшествующими ему элементами, пока для него не будет найдено надлежащее место, после чего опорный элемент вставляется в соответствующую позицию. Алгоритм начинается с выбора второго элемента списка в качестве опорного. По мере его выполнения в качестве опорных выбираются следующие элементы – пока не будет достиг-

² Чтобы воспользоваться преимуществами алгоритма двоичного поиска, личные дела студентов должны располагаться в памяти машины таким образом, чтобы можно было извлекать средние записи последовательно уменьшающихся подсписков без чрезмерных усилий. Это можно осуществить, запоминая личные дела в индексированных файлах-структурах, которые будут обсуждаться в главе 8. Кроме того, тех же результа- тов можно достичь и с использованием хешированных файловых структур, которые также описываются в главе 8.

нут конец списка. В самом лучшем случае каждый опорный элемент уже находится на положенном ему месте. Следователь- но, чтобы это было обнаружено, его потребуется сравнить только с одним именем. Поэтому в наилучшем случае применение

алгоритма сортировки методом вставки к списку из п элементов потребует выполнения

n -1

сравнений. (Второй элемент

сравнивается с одним элементом (первым), третий элемент – с одним элементом (вторым) и т.д.).

И наоборот, наихудший сценарий имеет место в том случае, когда каждый опорный элемент потребуется сравнивать со всеми впереди стоящими элементами, прежде чем удастся найти правильное место его расположения. Очевидно, что в этом случае исходный список упорядочен в обратном порядке. Первый опорный элемент (второй элемент списка) сравнивается с

одним элементом, второй опорный элемент (третий элемент списка) – с двумя элементами и т.д. (рис. 4.17). Следовательно,

общее  количество  сравнений  при  сортировке  списка  из  n  элементов  составит   1+ 2 + 3 + ... + (n -1) ,  что эквивалентно

n(n -1)/ 2 или 1/2(n² – n). В частности, для списка из 10 элементов алгоритму сортировки методом вставки в наихудшем слу- чае потребуется выполнить 45 сравнений.

В среднем при сортировке методом вставки можно ожидать, что каждый опорный элемент потребуется сравнить с по-

ловиной предшествующих ему элементов. В этом случае общее количество выполненных сравнений будет вдвое меньше, чем в наихудшем случае, т.е. (1/4)(п² – п) сравнений для списка длины п. Например, если использовать сортировку методом вставки для упорядочения множества списков из 10 элементов, то среднее число производимых в каждом случае сравнений будет равно 22,5.

Рис. 4.17. Работа алгоритма сортировки методом вставки в наихудшем случае

Данный график построен по оценкам работы алгоритма в наихудшем случае, когда, исходя из результатов наших исследова- ний, для списка длиной п требуется выполнить не менее 1/ 2 n² - n сравнений элементов. На графике отмечено несколько

конкретных значений длины списка и указано время, необходимое в каждом случае. Обратите внимание, при увеличении длины списка на одно и то же количество элементов время, необходимое для сортировки списка, все больше и больше возрастает. Таким образом, с увеличением длины списка эффективность данного алгоритма уменьшается.

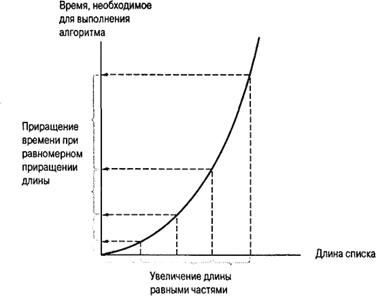Рис. 4.18. График зависимости времени сортировки от длины списка при сортировке методом вставки

Выполним аналогичный анализ работы алгоритма двоичного поиска в наихудшем случае. Как было установлено выше, при использовании этого алгоритма для поиска в списке из п элементов потребуется проанализировать не более log₂ n эле- ментов. Это позволяет оценить время, необходимое для выполнения алгоритма при различной длине сортируемого списка. На рис. 4.19 представлен график, построенный по результатам данного анализа. На этом графике также отмечены конкрет- ные значения длины списка, возрастающие на одну и ту же величину, и указано соответствующее время выполнения алго- ритма. Обратите внимание, что темпы роста времени выполнения алгоритма снижаются по мере увеличения длины списка, т.е. эффективность алгоритма двоичного поиска возрастает с увеличением длины списка.

Основным отличием между графиками, представленными на рис. 4.18 и 4.19, безусловно, является их общая форма. Именно форма графика, а не его индивидуальные особенности, демонстрирует, насколько хорошо данный алгоритм будет справлять- ся с все возрастающими объемами данных. Заметим, что общая форма графика определяется типом отображаемого выраже- ния, а не его конкретными особенностями: все линейные выражения изображаются прямой линией, все квадратичные выраже- ния – параболической кривой, а все логарифмические выражения порождают логарифмическую кривую, подобную пред- ставленной на рис. 4.19. Общую форму кривой принято определять простейшим выражением, порождающим кривую данной формы. В частности, параболическая форма обычно определяется выражением n², а логарифмическая – выражением lgn.

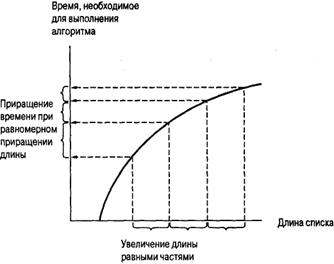Рис. 4.19. График зависимости времени поиска от длины списка для алгоритма двоичного поиска

Выше было показано, что форма графика, представляющего зависимость времени выполнения алгоритма от объема входных данных, отражает общие характеристики эффективности алгоритма. Поэтому принято классифицировать алгорит- мы согласно форме их графиков, построенных для самого неблагоприятного случая. Способ обозначения, используемый для определения этих классов, иногда называют тета-классами. Алгоритмы, графики которых имеют параболическую форму (например, сортировка методом вставки), относятся к классу Q(n²), алгоритмы, графики которых имеют логарифмическую форму (например, двоичный поиск), – к классу Q(lgn). Любой алгоритм из тета-класса Q(lgn) по самой свой сути всегда бо- лее эффективен, чем алгоритм из тета-класса Q(n²).

Верификация программ. Вспомним, что четвертая фаза процедуры решения задачи, согласно схеме, предложенной математиком Полиа (см. раздел 4.3), заключается в оценке точности работы программы или верификации (verification) и определении его потенциала как инструмента для решения других задач. Важность первой части этой фазы мы проиллюст- рируем следующим примером.

Путешественник, у которого есть золотая цепочка из семи звеньев, должен остановиться в уединенном отеле на семь ночей. Плата за каждую проведенную в отеле ночь составляет одно звено его цепочки. Какое наименьшее число звеньев не- обходимо разрезать, чтобы путешественник мог платить владельцу отеля одно звено каждое утро, не внося плату заранее?

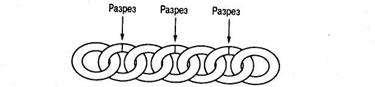
Первым делом уясним себе, что нет необходимости разрезать все звенья. Если мы разрежем только второе звено, то и первое, и второе будут отделены от остальных пяти звеньев. Следуя этому, можно прийти к решению разрезать только вто- рое, четвертое и шестое звенья цепочки. В результате все звенья окажутся свободными, причем только три из них будут раз- резанными (рис. 4.20). Более того, любое меньшее число разрезов оставит два звена соединенными, поэтому мы заключаем, что правильный ответ для этой задачи – три звена.

Однако, рассмотрев задачу более внимательно, можно заметить, что если разрезать только третье звено, то получится три фрагмента цепочки, состоящие из одного, двух и четырех звеньев (рис. 4.21). С этими фрагментами мы можем поступить следующим образом.

Первое утро. Отдать владельцу отеля одно звено.

Второе утро. Забрать у владельца отеля одно звено и отдать ему фрагмент цепочки из двух звеньев.

Рис. 4.20. Разделение всех звеньев цепочки с помощью лишь трех разрезов

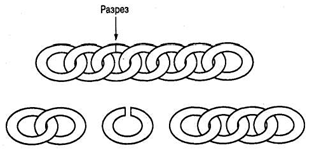
Рис. 4.21. Решение задачи с помощью лишь одного разреза

Третье утро. Отдать владельцу отеля одно звено.

Четвертое утро. Забрать у владельца отеля три отданные ему ранее звена и отдать ему фрагмент цепочки из четырех звеньев.

Пятое утро. Отдать владельцу отеля одно звено.

Шестое утро. Забрать у владельца отеля одно звено и отдать ему фрагмент цепочки из двух звеньев.

Седьмое утро. Отдать владельцу отеля одно звено.

Следовательно, тот ответ, который мы считали правильным, на самом деле неверен. Как же убедиться, что новое реше- ние действительно правильно? В качестве доказательства можно привести следующее рассуждение. Поскольку в первое ут- ро необходимо отдать владельцу отеля одно звено, придется разрезать, по крайней мере, одно звено цепочки. Но так как в новом варианте решения требуется разрезать только одно звено, то это решение должно быть оптимальным.

Применительно к программированию этот пример демонстрирует различия между программой, которая выглядит пра- вильной, и программой, которая действительно является правильной. Это не всегда одно и то же. Специалистам в области обработки данных известно множество ужасных историй о том, как программное обеспечение, которое считалось безуслов- но правильным, все же отказывало в критический момент, поскольку возникшая ситуация оказывалась для него совершенно непредвиденной. Следовательно, верификация программного обеспечения – это важное и необходимое дело, а поиск эффек- тивных методов верификации является активным направлением исследований в области компьютерных наук.

Одно из самых современных направлений в этой области заключается в использовании методов формальной логики для доказательства корректности программ. Это означает, что цель проводимых исследований состоит в применении формаль- ной логики для доказательства того факта, что реализованный данной программой алгоритм делает именно то, для чего он предназначен. Основополагающий тезис заключается в том, что при сведении процесса верификации к формальной проце- дуре мы застрахованы от некорректных умозаключений, вытекающих из интуитивной аргументации, как это было в случае с задачей о золотой цепочке. Давайте рассмотрим данный подход к верификации программ более подробно.

Подобно тому, как формальное математическое доказательство основывается на аксиомах (геометрические доказатель- ства часто базируются на аксиомах Евклидовой геометрии, тогда как доказательства других утверждений – на аксиомах тео- рии множеств), формальное доказательство правильности программы основывается на спецификациях, в соответствии с ко- торыми эта программа разрабатывалась. Чтобы доказать, что программа правильно сортирует списки имен, мы можем на- чать с предположения о том, что на вход программы подается список имен. Если программа создана для вычисления средне- го значения одного или более положительных чисел, мы можем предположить, что исходными данными для программы яв- ляется одно или несколько положительных чисел. Короче говоря, доказательство корректности начинается с предположения о том, что в начале работы программы удовлетворены некоторые условия, называемые предварительными условиями (pre- condition), или предусловиями.

Следующий этап доказательства корректности заключается в рассмотрении того, как следствия из этих предусловий распространяются по программе. С этой целью исследователи изучили различные программные структуры, пытаясь устано- вить, как выполнение данной структуры влияет на утверждение, о котором до выполнения этой структуры было известно, что оно истинно. Например, пусть определенное утверждение о значении переменной Y перед выполнением приведенной ниже инструкции было истинно:

X ← Y

После выполнения этой инструкции то же утверждение можно сделать о значении переменной X. Например, если перед выполнением инструкции значение переменной Y отличалось от 0, то можно сделать заключение, что после выполнения этой инструкции значение переменной X также будет отличаться от 0.

Несколько более сложным случаем является выполнение оператора if-then-else, например, следующего вида:

if (условие) then {инструкция 1} else {инструкция 2}.

Если в этом примере известно, что некоторое утверждение было истинно перед выполнением данной структуры, то не- посредственно перед выполнением инструкции 1 мы знаем, что истинны как это утверждение, так и проверяемое условие. В то же время, если должна выполняться инструкция 2, мы знаем, что должны быть истинны исходное утверждение и отрица- ние проверяемого условия.

Верификация требуется не только программному обеспечению. Обсуждаемые в тексте проблемы верификации касаются не толь- ко программного обеспечения. Столь же важно получить гарантии, что выполняющая программу аппаратура также не содержит ошибок. Это подразумевает верификацию как разрабатываемых схем, так и конструкции всей машины. И в этом случае полученные результаты в значительной степени зависят от тестирования, задача которого, как и в случае с программным обеспечением, – выявить скрытые ошибки. Показателен пример машины Mark 1, созданной в Гарвардском университете в 1940 г., монтажные ошибки в которой оставались необна- руженными в течение многих лет. Более "свежий" пример – ошибки в блоке выполнения операций с плавающей точкой, имевшие место в первых микропроцессорах типа Pentium. В обоих случаях существующие ошибки были выявлены до каких-либо серьезных последствий.

Если следовать правилам, приведенным выше, доказательство корректности программы осуществляется путем опреде- ления положений, называемых утверждениями, которые устанавливаются в различных точках программы. В результате по- лучается набор утверждений, каждое из которых является следствием предусловий программы и последовательности инст- рукций, приводящей к той точке программы, где установлено данное утверждение. Если утверждение, установленное по- добным образом в конце программы, соответствует спецификациям того, что требуется получить на ее выходе, то можно сделать заключение о правильности программы.

В качестве примера рассмотрим типичную циклическую структуру while-do, представленную на рис. 4.22. Предпо- ложим, как следствие предусловий, заданных в точке А, мы можем установить, что определенное утверждение истинно при каждой проверке условия окончания цикла (точка В) на протяжении всего процесса повторения. Такое утверждение внутри цикла называется инвариантом цикла (loop invariant). Как только повторение завершается, выполнение переходит к точке С, где мы можем заключить, что истинны как инвариант цикла, так и условие его окончания. (Инвариант цикла остается истин- ным, поскольку проверка условия окончания не изменяет никаких величин в программе, а условие окончания истинно, по- скольку в противном случае цикл бы просто не завершился.) Если комбинация этих положений означает то, что мы хотим видеть на выходе, наше доказательство корректности можно завершить, просто показав, что компоненты инициализации и модификации цикла в конечном счете приводят к условию окончания.

Этот метод анализа можно применить к приведенному выше алгоритму сортировки методом вставки (см. рис. 4.11).

Внешний цикл в этой программе основан на следующем инварианте цикла:

Каждый раз при выполнении проверки условия окончания цикла имена, предшествующие N-му элементу, образуют от- сортированный список.

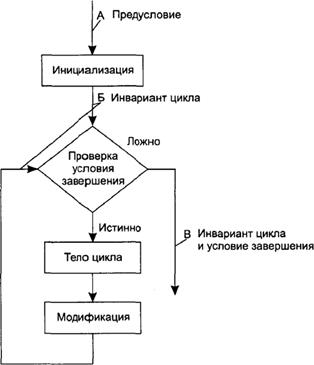Рис. 4.22. Использование формального утверждения для проверки правильности оператора цикла while-do

Условие окончания этого цикла формулируется следующим образом:

Значение N больше, чем длина списка.

Таким образом, как только цикл завершится, мы будем знать, что оба условия должны быть выполнены, а это означает, что весь список будет отсортирован.

К сожалению, методы формальной верификации программ не настолько хорошо разработаны, чтобы их можно было использовать в приложениях общего типа. Сегодня в большинстве случаев "верификация" программного обеспечения про- изводится посредством его тестирования при различных исходных условиях, что весьма ненадежно. Верификация с помо- щью тестирования не доказывает ничего иного, кроме того, что программа правильно работает в тех условиях, в которых ее проверяли. Любые дополнительные заключения – это всего лишь предположения. Ошибки, содержащиеся в программе, ча- ще всего являются следствием оплошности и недосмотра, что может произойти и при тестировании. В результате ошибки в программе, такие, как в задаче с золотой цепочкой, могут остаться и часто остаются незамеченными, хотя были потрачены значительные усилия, чтобы этого избежать. Драматический случай произошел в компании AT&T. Ошибка в программном обеспечении, управляющем 114 телефонными станциями, оставалась незамеченной с момента его установки в декабре 1989 г. и вплоть до 15 января 1990 г., когда исключительное стечение обстоятельств привело к тому, что за девять часов было беспричинно заблокировано примерно 5 миллионов телефонных звонков.

Вопросы для самопроверки

1.  Предположим, было установлено, что при использовании алгоритма сортировки методом вставки машине требуется в среднем одна секунда для сортировки списка из 100 элементов. Оцените, сколько времени ей понадобится для сортировки списков из 1000 и 10 000 элементов?

2.  Приведите примеры алгоритмов, относящихся к каждому из следующих классов: Q(lgn), Q(n), Q(n²).

3.  Перечислите следующие классы в порядке убывания их эффективности: Q(n²), Q(lgn), Q(n), Q(n³).

4.  Проанализируйте следующую задачу и предлагаемый ответ. Является ли этот ответ правильным? Поясните свои вы- воды.

Задача. Предположим, что в коробке находятся три карточки. У одной из них обе стороны черного цвета, у второй обе стороны красного цвета, а у третьей одна сторона черного цвета, а другая – красного. Из коробки вынимают одну карточку,  и вам разрешается посмотреть на одну из ее сторон. Какова вероятность того, что вторая сторона этой карточки того же цве- та, что и та, которую вам показали?

Предлагаемый ответ. Одна вторая. Предположим, что показанная вам сторона карточки была красного цвета. (Рассу- ждения будут аналогичны и в том случае, если она будет черного цвета, так как задача симметрична.) Из трех карточек толь- ко у двух есть красная сторона. Следовательно, карточка, которую вы увидели, – одна из этих двух. У одной из этой пары карточек вторая сторона красная, а у другой – черная. Следовательно, вторая сторона у выбранной из коробки карточки с равной вероятностью может быть как черной, так и красной.

5.   Приведенный ниже программный сегмент используется, чтобы вычислить частное (не принимая во внимание оста- ток) двух целых положительных чисел (делимого и делителя) путем подсчета, сколько раз делитель можно вычесть из дели- мого, пока оставшаяся часть станет меньше делителя. Например, при делении по этому методу числа 7 на 3 получится 2, так как число 3 можно вычесть из 7 дважды. Правильно ли составлена эта программа? Обоснуйте свои выводы.

Счетчик ← 0;

Остаток ← Делимое;

repeat {Остаток ← Остаток – Делитель; Счетчик ← Счетчик + 1}

until (Остаток < Делитель) Частное ← Счетчик

6.  Приведенный ниже программный сегмент предназначен для определения произведения двух неотрицательных целых чисел X и Y посредством вычисления суммы X копий числа Y. Другими словами, выражение 3 ´ 4 вычисляется как сумма трех четверок. Правильно ли составлена эта программа? Обоснуйте это.

Произведение ← Y;

Счетчик ← 1;

while (Счетчик < X) do

{Произведение ← Произведение + Y;

Счетчик ← Счетчик + 1}

7.  Приняв как предусловие, что значение N – целое положительное число, установите инвариант цикла, который приво- дит к заключению, что по окончании приведенной ниже программы переменной Сумма будет присвоено значение, равное 0

+ 1 + ... + N.

Сумма ← 0;

I ← 0;

while (I < N) do

{I ← I + 1;

Сумма ← Сумма + I}

Приведите аргументы в пользу того, что эта программа действительно завершится.

8.   Предположим, что программа и выполняющая ее аппаратура были формально проверены на корректность. Гаранти- рует ли это правильность их работы?

Упражнения

1.    Приведите примеры последовательности этапов, удовлетворяющей неформальному определению алгоритма, приве- денному в начале раздела 4.1, но не удовлетворяющей определению, приведенному на рис. 4.1.

2.    Объясните различие между неоднозначностью в предложенном алгоритме и неоднозначностью в представлении ал- горитма.

3.    Поясните, как использование примитивов помогает устранить неоднозначность в представлении алгоритмов?

4.    Представляет ли следующая программа алгоритм в строгом смысле этого слова? Поясните свой ответ.

Счетчик ← 0;

while (Счетчик ¹ 5) do

{Счетчик ← Счетчик + 2}

5.    По какой причине приведенная ниже последовательность этапов не образует алгоритм? Этап 1. Провести отрезок прямой линии, соединяющий точки с координатами (2, 5) и (6, 11). Этап 2. Провести отрезок прямой линии, соединяющий точки с координатами (1, 3) и (3, 6).

Этап 3. Провести окружность с радиусом 2 и центром в точке пересечения проведенных отрезков.

6.   Перепишите следующий сегмент программы, используя структуру repeat-until вместо while-do. Убедитесь, что новая версия программы печатает те же значения, что и исходная.

Счетчик ← 2;

while (Счетчик < 7) do

{напечатать значение переменной Счетчик; Счетчик ← Счетчик +1}

7.  Перепишите следующий фрагмент программы, используя структуру while-do вместо repeat-until. Убедитесь, что новая версия печатает те же значения, что и исходная.

Счетчик ← 1;

repeat {напечатать значение переменной Счетчик; Счетчик ← Счетчик + 1}

until (Счетчик = 5)

8.  Разработайте алгоритм, который получает на входе некую конфигурацию из цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 и перестав- ляет полученные цифры таким образом, чтобы новая конфигурация представляла собой значение, следующее по величине за исходным, из числа тех, которые могут быть составлены из этих цифр (или сообщает, что такой перестановки не существует, если никакие перестановки не приводят к большему значению). Например, для исходной конфигурации 5 647 382 901 таким числом будет 5 647 382 910.

9.  В чем отличие формального языка программирования от псевдокода?

10.  В чем отличие между синтаксисом и семантикой?

11.  Четыре шахтера, которые имеют один фонарь, должны пройти через шахту. Одновременно по шахте могут двигаться не больше двух человек, и каждый шахтер, двигаясь в шахте, должен иметь фонарь. Шахтеры, имена которых Эндрю, Блэйк, Джонсон и Келли, могут пройти шахту за одну, две, три и четыре минуты, соответственно. Когда два шахтера идут вместе, они движутся со скоростью более медленного из них. Каким образом шахтеры могут пройти через шахту за 15 минут? После того как вы решите задачу, объясните, с чего вы начали решение.

12.  Допустим, у нас есть большой и маленький стаканчики для вина. Сначала наполним вином маленький стаканчик и перельем его в большой стакан. Затем наполним водой маленький стакан, перельем некоторое количество воды в большой стакан и смешаем его с вином. Теперь будем переливать смесь обратно в маленький стакан, пока он не наполнится. Чего те- перь больше в маленьком стакане – воды в вине или вина в воде? После того как вы решите задачу, объясните ход ваших рассуждений.

13.  Две пчелы, Ромео и Джульетта, живут в разных ульях, но они встретились и полюбили друг друга. Однажды безвет- ренным весенним утром они одновременно вылетели из своих ульев, чтобы слетать друг к другу в гости. В 50-ти метрах от ближайшего улья они встретились, но не заметили друг друга и полетели дальше. Прибыв к месту своего назначения, они потратили одинаковое время, чтобы выяснить, что того, к кому они прилетели, нет дома, и повернуть назад. На обратном пути они встретились в точке, находящейся на расстоянии 20 метров от ближайшего улья. На этот раз они увидели друг дру- га и устроили пикник, прежде чем возвратиться домой. На каком расстоянии друг от друга расположены их улья? Решив задачу, объясните, с чего вы начали свои рассуждения.

14.  Разработайте алгоритм, который получает на входе две строки символов и проверяет, является ли первая строка ча- стью второй.

15.  Следующий алгоритм разработан для того, чтобы напечатать несколько первых чисел Фибоначчи. Определите, что является телом цикла. Где выполняется операция инициализации управления циклом? Где выполняется операция модифика- ции? Какая инструкция реализует операцию проверки? Какой список чисел получится в результате работы алгоритма?

Последнее ← 0;

Текущее ← 1;

while (Текущее < 100) do

{напечатать значение переменной Текущее; Временное ← Последнее;

Последнее ← Текущее;

Текущее ← Последнее + Временное}

16.  Какую последовательность чисел напечатает следующий алгоритм, если на входе задать значения 0 и 1?

procedure MysteryWrite (Последний, Текущий)

if (Текущий < 100) then

{напечатать значение переменной Текущий; Временный ← Текущий + Последний;

применить процедуру MysteryWrite к значениям Текущий и Временный}

17.   Преобразуйте процедуру MysteryWrite из предыдущего задания так, чтобы она печатала числа в обратном по- рядке.

18.  Какие буквы будут проверяться, если применить двоичный поиск (см. рис. 4.13) для поиска значения J в списке А, В, С, D, E, F, G, H, I, J, К, L, M, N, О? А в случае поиска значения Z?

19.   Сколько раз в среднем потребуется сравнивать между собой два элемента при поиске значения в списке из 6000

элементов с помощью метода последовательного поиска? А что можно сказать о методе двоичного поиска?

20.   Определите тело цикла в следующей структуре и подсчитайте, сколько раз оно будет выполнено. Что произойдет, если проверяемое условие заменить на выражение "while (Счетчик ≠ 6)"?

Счетчик ← 1;

while (Счетчик ≠ 7) do

{напечатать значение переменной Cчетчик;

Счетчик ← Счетчик + 3}

21.  Какие проблемы могут возникнуть при реализации на компьютере следующей программы? (Подсказка. Вспомните об ошибках округления при выполнении арифметических операций с плавающей точкой.)

Счетчик ← 0.1;

repeat {напечатать значение переменной Счетчик; Счетчик ← Счетчик + 0.1}

until (Счетчик = 1)

22.  Разработайте рекурсивную версию алгоритма Евклида (вопрос 3 к разделу 4.2).

23.   Предположим, что на вход процедур Testl и Test2, приведенных ниже, передано значение 1. Чем будут отли- чаться напечатанные этими процедурами результаты?

procedure Test1 (Счетчик)

if (Счетчик ≠ 5)

then {напечатать значение параметра Счетчик; выполнить процедуру Test1(Счетчик + 1)}

procedure Test2 (Счетчик)

if (Счетчик ≠ 5)

then {выполнить процедуру Test2(Счетчик + 1);

напечатать значение параметра Счетчик}

24.   Определите основные составляющие механизма управления в предыдущей задаче. В частности, какое условие вы- зывает окончание процесса? Где происходит модификация состояния процесса, приближающая его к условию завершения? Где инициализируется состояние управляющего процесса?

25.   Разработайте алгоритм генерации последовательности целых положительных чисел (в возрастающем порядке), ко- торые имеют только два простых множителя – 2 и 3, т.е. программа должна генерировать последовательность чисел 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 27, Представляет ли эта программа алгоритм в строгом смысле этого слова?

26.   Ответьте на следующие вопросы применительно к списку имен Alice, Byron, Carol, Duane, Elaine, Floyd, Gene, Henry, Iris.

а) Какой алгоритм поиска (последовательный или двоичный) позволит быстрее найти имя Gene?

б) Какой алгоритм поиска (последовательный или двоичный) позволит быстрее найти имя Alice?

в) Какой алгоритм поиска (последовательный или двоичный) позволит быстрее обнаружить отсутствие в списке имени

Bruce?

г) Какой алгоритм поиска (последовательный или двоичный) позволит быстрее обнаружить отсутствие в списке имени

Sue?

д) Сколько элементов будет рассмотрено при поиске имени Elaine с использованием метода последовательного поиска?

Сколько элементов будет рассмотрено при поиске этого имени с использованием метода двоичного поиска?

27.   По определению факториал числа 0 равен 1. Факториал целого положительного числа – это произведение данного целого положительного числа и факториала предшествующего ему целого положительного числа. Для обозначения факто- риала целого положительного числа п используется запись п!. Таким образом, факториал числа 3 (обозначается как 3!) – это 3!= 3*(2!)= 3*(2*(1!))= 3*(2*(1*(0!))) = 3*(2*(1*(1))) = 6. Разработайте рекурсивный алгоритм вычисления факториала задан- ного числа.

28.   а) Предположим, что вам необходимо отсортировать список из пяти имен и что вы уже разработали раньше алго- ритм для сортировки списка из четырех имен. Разработайте алгоритм сортировки списка из пяти имен, использующий ранее разработанный алгоритм.

б) Разработайте рекурсивный алгоритм сортировки списка произвольной длины, основанный на методе, используемом для решения предыдущей задачи.

29.  Головоломка "Ханойская башня" состоит из трех вертикальных стержней, на один из которых надето несколько ко- лец последовательно уменьшающихся (в направлении снизу вверх) размеров. Задача состоит в том, чтобы переместить набор колец на другой стержень. Разрешается перемещать только одно кольцо за один ход, причем нельзя надевать большее коль- цо поверх меньшего. Заметим, что головоломка с одним кольцом решается предельно просто. Если колец несколько, то, пе- реместив на другой стержень все кольца, кроме наибольшего, наибольшее кольцо можно было бы перенести на третий стер- жень. После этого задача была бы сведена к перемещению всех остальных колец на наибольшее. Исходя из этого, разрабо- тайте рекурсивный алгоритм для решения головоломки "Ханойская башня" с произвольным числом колец.

30. 

31.  Разработайте циклический и рекурсивный алгоритмы для распечатки дневной заработной платы рабочего, который в каждый последующий день получает вдвое больше, чем в предыдущий (первый платеж равен одному пенни), за 30 дней работы. С какими проблемами, касающимися хранения данных, вам придется столкнуться при реализации вашего решения

на реальной машине?

32.   Разработайте алгоритм для нахождения значения квадратного корня из положительного числа с помощью следую- щего метода. В качестве первого приближения выбирается само это число, а последующие приближения получаются из пре- дыдущих путем вычисления среднего арифметического для предыдущего приближения и числа, полученного при делении ис- ходного числа на предыдущее приближение. Проанализируйте возможности управления этим повторяющимся процессом. В част- ности, какое условие должно использоваться для его окончания?

33.  Разработайте алгоритм, который печатает все возможные варианты перестановки символов в строке из пяти различ- ных символов.

34.  Разработайте алгоритм, который в заданном списке имен находит самое длинное имя. Определите, как поведет себя алгоритм, предложенный вами в качестве решения, если "самых длинных" имен в списке будет несколько. В частности, как поведет себя ваш алгоритм, если все имена в списке будут одной длины?

35.  Разработайте алгоритм, который в заданном списке из пяти или более чисел находит пять наименьших и пять наи- больших чисел, не сортируя полностью весь список.

36.  Расположите имена Brenda, Doris, Raymond, Steve, Timothy и William в таком порядке, который при использовании алгоритма сортировки методом вставки потребует выполнения наименьшего числа сравнений (рис. 4.11).

37.   Какое максимальное количество элементов может быть проверено при применении алгоритма двоичного поиска (рис. 4.13) к списку, содержащему 4000 строк? Как оно соотносится с аналогичным значением для метода последовательного поиска (рис. 4.6)?

38.  Используя нотацию тета-классов, классифицируйте традиционные школьные алгоритмы для сложения и умножения в столбик. Другими словами, определите, сколько отдельных операций сложения необходимо выполнить при суммировании двух чисел значностью п и сколько отдельных операций умножения потребуется для их перемножения.

39.  Иногда небольшое изменение условия задачи может вызвать существенные изменения в способе ее решения. Например, найдите простой алгоритм решения следующей задачи и определите его тета-класс.

Разделите группу людей на две непересекающиеся подгруппы (произвольных размеров), такие, чтобы разность между суммами возрастов членов этих подгрупп была максимальной. Теперь измените условие задачи так, чтобы требуемая раз- ность была минимальной, и вновь классифицируйте ваше решение.

40.  Из следующего списка выделите несколько чисел, сумма которых равна 3165. Насколько эффективен ваш метод ре- шения задачи?

26, 39, 104, 195, 403, 504, 793, 995, 1156, 1673

41.  Завершится ли цикл в следующей программе? Поясните свой ответ. Объясните, что могло бы случиться, если бы эта программа в действительности выполнялась машиной (см. раздел 1.7)

X ← 0;

Y ← 1/2;

while (X ≠ 1) do

{X ← X+Y;

Y ← Y-2}

42.  Следующий фрагмент программы разработан для вычисления произведения двух неотрицательных целых чисел X и Y путем вычисления суммы X копий числа Y. Выражение 3 ´ 4 вычисляется посредством нахождения суммы трех четверок. Правильно ли составлен данный фрагмент? Поясните свой ответ.

Произведение ← 0;

Счетчик ← 0;

repeat {Произведение ← Произведение + Y;

Счетчик ← Счетчик + 1}

until (Счетчик = X)

43.  Следующий фрагмент программы составлен для определения, какое из двух целых чисел X и Y является большим. Является ли этот фрагмент правильным? Поясните свой ответ.

Разность ← X—Y;

if (Разность положительна)

then {напечатать "X больше Y"}

else {напечатать "Y больше X"}

44.  Следующий фрагмент программы должен находить наибольший элемент в непустом списке целых чисел. Правиль- но ли он составлен? Поясните свой ответ.

Значение ← значение первого элемента списка; Текущий ← значение первого элемента списка; while (Текущий ≠ последнему элементу списка) do

{if (Текущий > Значение)

then {Значение ← Текущий}

Текущий ← значение следующего элемента списка}

45.   а) Определите предусловия для алгоритма последовательного поиска. Установите инвариант цикла для структуры while в этой программе, который, будучи объединен с условием окончания цикла, предполагает, что по окончании этого цикла алгоритм правильно сообщит об успехе или неудаче.

б) Приведите аргументы в пользу того, что цикл while действительно завершается.

46.  Опираясь на предусловие для приведенной ниже программы, утверждающее, что параметрам X и Y присвоены не- отрицательные целые значения, определите инвариант цикла ее структуры while, который, будучи объединен с указанным условием окончания, предполагает, что значение переменной Z по завершении цикла будет X – Y.

Z ← X;

J ← 0;

while (J < Y) do

{Z ← Z-1;

J ← J+l}

Скачано с www.znanio.ru