ФЕДЕРАЛЬНЫЙ ИНСТИТУТ ПЕДАГОГИЧЕСКИХ ИЗМЕРЕНИЙ

В.Р. Лещинер, М.А. Ройтберг

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ  для учителей, подготовленные на

основе анализа типичных ошибок участников ЕГЭ 2015 года 

по ИНФОРМАТИКЕ и ИКТ

Москва, 2015

Контрольные измерительные материалы единого государственного экзамена по информатике и ИКТ позволяют установить уровень освоения выпускниками федерального компонента государственного образовательного стандарта среднего (полного) общего образования (приказ Минобразования России от 05.03.2004 № 1089). В то же время результаты ЕГЭ признаются образовательными учреждениями высшего профессионального образования как результаты вступительных испытаний по информатике и ИКТ. Именно это двойное назначение экзамена определяет специфику КИМ ЕГЭ как инструмента педагогического измерения.

Содержанием экзаменационной работы охватывается основное содержание курса информатики, важнейшие его темы, наиболее значимый в них материал, однозначно трактуемый в большинстве преподаваемых в школе вариантов курса информатики. Работа содержит как задания базового уровня сложности, проверяющие знания и умения, предусмотренные стандартами базового уровня подготовки по предмету, так и задания повышенного и высокого уровней, проверяющие знания и умения, предусмотренные профильным стандартом. Количество заданий в тесте должно, с одной стороны, обеспечить всестороннюю проверку знаний и умений выпускников, приобретенных за весь период обучения по предмету, и, с другой стороны, обеспечить адекватное ранжирование абитуриентов вузов по уровню подготовки к получению образования по выбранной специальности высшего профессионального образования. С этой целью в тесте используются задания двух типов: с кратким ответом и с развернутым ответом. Одной из разновидностей заданий с кратким ответом являются задания на выбор и запись одного или нескольких правильных ответов из предложенного перечня ответов. Такие задания, конечно, позволяют экзаменуемому угадать ответ, но зато они позволяют проверить выполнение таких заданий, краткий ответ по которым невозможен или затруднен в силу формата, а проверка развернутого ответа нецелесообразна из-за громоздкости процедуры. Заданий этой разновидности в экзаменационной работе 2015 г. было всего 3, в экзаменационной работе 2016 г. от заданий этого типа было решено отказаться. 

Задания с кратким ответом в виде числа или строки символов, распознаваемым и проверяемым компьютером, исключают возможность угадывания ответа, но увеличивают вероятность ошибки распознавания. Наконец, задания с развернутым ответом, наиболее трудоемкие и позволяющие экзаменуемым в полной мере проявить свою индивидуальность и приобретенные в процессе обучения умения, проверяются экспертами региональных экзаменационных комиссий на основании единых критериев проверки, являющихся частью контрольных измерительных материалов по предмету. В экзаменационной работе всего 4 таких задания, их выполнение требует значительного времени и в связи с наличием человеческого фактора при их проверке имеется определенная вероятность ошибки оценивания. 

Итак, каждый вариант экзаменационной работы состоит из двух частей и включает в себя 27 заданий, различающихся формой и уровнем сложности.

Часть 1 содержит 23 задания базового, повышенного и высокого уровней сложности. В этой части собраны задания с кратким ответом, подразумевающие самостоятельное формулирование и запись ответа в виде числа или последовательности символов. Задания проверяют материал всех тематических блоков. В первой части 12 заданий относится к базовому уровню, 10 заданий имеют повышенный уровень сложности, 1 задание – высокий уровень сложности.

Часть 2 содержит 4 задания, первое из которых повышенного уровня сложности, остальные 3 задания высокого уровня сложности. Задания этой части подразумевают запись развернутого ответа в произвольной форме. Они направлены на проверку сформированности важнейших умений записи и анализа алгоритмов, предусмотренных требованиями к обязательному уровню подготовки по информатике учащихся средних общеобразовательных учреждений. Последнее задание работы на высоком уровне сложности проверяет умения по теме «Технология программирования». 

Задания КИМ оцениваются разным количеством баллов в зависимости от их типа.

Выполнение каждого задания части 1 оценивается в 1 балл. Задание части 1 считается выполненным, если экзаменуемый дал ответ, соответствующий коду верного ответа. За выполнение каждого задания присваивается (в дихотомической системе оценивания) либо 0 баллов («задание не выполнено»), либо 1 балл («задание выполнено»). Ответы на задания части 1 автоматически обрабатываются после сканирования бланков ответов № 1. Максимальное количество первичных баллов, которое можно получить за выполнение заданий части 1, – 23.  Выполнение заданий части 2 оценивается от нуля до четырех баллов. Ответы на задания второй части проверяются и оцениваются экспертами (устанавливается соответствие ответов определенному перечню критериев). Максимальное количество баллов, которое можно получить за выполнение заданий части 2, – 12. 

Максимальное количество первичных баллов, которое можно получить за выполнение всех заданий экзаменационной работы, – 35. 

Оценка, фиксируемая в свидетельстве о результатах ЕГЭ для поступления в учреждения профессионального образования, подсчитывается по стобалльной шкале на основе выполнения всех заданий экзаменационной работы. В свидетельство выставляются результаты ЕГЭ при условии, если выпускник набрал количество баллов не ниже минимального.

Минимальное количество баллов ЕГЭ по информатике и ИКТ, подтверждающее освоение выпускником основных общеобразовательных программ среднего (полного) общего образования в соответствии с требованиями Федерального компонента государственного образовательного стандарта среднего (полного) общего образования, составляет 40 баллов по стобалльной шкале (установлено Распоряжением Рособрнадзора № 3499-10 от 29.08.2012 года).

КИМ 2015 г. претерпели значительные изменения по сравнению с КИМ 2014 г. Изменилось деление работы на части, сократилось общее количество заданий (с 32 до 27), соответственно уменьшилось с 40 до 35 максимальное количество первичных баллов. Изменился алгоритм перевода первичных баллов в тестовые. Также, в связи с сокращением количества заданий в варианте, уменьшилось с 8 до 6 минимальное количество первичных баллов ЕГЭ по информатике и ИКТ, подтверждающее освоение выпускником основных общеобразовательных программ среднего (полного) общего образования в соответствии с требованиями Федерального компонента государственного образовательного стандарта среднего (полного) общего образования (граница по стобалльной шкале осталась неизменной). 

Уменьшение количества заданий произведено за счет укрупнения тематики заданий, сведения близких по тематике и сложности заданий в одну позицию. Такими укрупненными стали позиции 3 (хранение информации в компьютере), 6 (формальное исполнение алгоритмов), 7 (технология вычислений и визуализации данных с помощью электронных таблиц) и 9 (скорость передачи звуковых и графических файлов). В КИМ ЕГЭ, использовавшихся на экзамене, в части вариантов были задания по одной из указанных в спецификации тем, в другой части – по смежной теме. Это сильно повысило вариативность вариантов, добавив элемент неопределенности. В спецификации КИМ ЕГЭ 2016 г. укрупненные позиции сохранены, этот факт необходимо учитывать при подготовке учащихся к экзамену.

В связи с уменьшением количества частей изменилась последовательность заданий в варианте. Вторая часть работы (задания с развернутым ответом) не изменилась, но относительный вес баллов, полученных за задания с развернутым ответом, увеличился за счет сокращения общего количества заданий в варианте. Последнее задание 27, проверяющее умение создавать самостоятельные программы, давалось в двух вариантах, более простом, оценивавшемся из 2 баллов, и более сложном, требующем создания эффективного по памяти и скорости выполнения алгоритма, оценивавшегося максимально 4 первичными баллами.

Общее количество участников экзамена в 2015 г  - 50394 чел. Доля участников экзамена среди всех выпускников на протяжении ряда лет составляет около 7,2%.  

Средний тестовый балл в 2015 г. составил 53,99 балла (в 2014 г. - 57,79 балла). Уменьшение среднего тестового балла объясняется уменьшением общего количества заданий в КИМ за счет исключения наиболее простых, обладавших низкой дифференцирующей способностью заданий. При этом доля участников, получивших высокие тестовые баллы (81-100) увеличилась (8,21% в 2015 г. против 7,15% в 2014 г.).

Тенденция распределения результатов экзамена 2014 г. сохранилась и в 2015 г., но в целом она иллюстрирует вывод 2014 г. о наложении двух нормальных распределений с модой в области чуть выше минимального балла (в 2015 г. минимальный балл составил 6 первичных баллов) и в области 19-20 первичных баллов в 2015 г (26 первичных баллов в 2014 г.). В 2015 г. сокращение количества простых заданий и практически полное исключение заданий с выбором ответа привело к консолидации результатов в области низких баллов и сдвигу обеих кривых распределения влево. В то же время более сбалансированное количество заданий повышенного и высокого уровня привело к менее резкому падению кривой распределения в области высоких баллов в 2015 г. Наложение на графике двух кривых нормального распределения показывает, что среди участников экзамена присутствуют две группы: первая - плохо подготовленные участники, для которых характерны низкие результаты, и вторая - мотивированные выпускники, нацеленные на получение максимального балла.

Доля выпускников, не набравших минимального количества баллов в 2015 г., составила 16,15%, в то время как в 2014 г. она составляла 10,36% Сказалось исключение заданий с выбором ответа и общее уменьшение количества заданий. Это изменение отражает профильный характер экзамена по выбору, требующего от участника целенаправленной подготовки.

Количество и доля стобалльников на ЕГЭ 2015 г. (105 чел., 0,21%) увеличились в 3 раза по сравнению с ЕГЭ 2014 г. (35 чел., 0,07%), но в любом случае эти значения невелики и находятся в границах статистической погрешности. Доля высокобалльников (81-100 тестовых баллов) в 2015 г. также увеличилась по сравнению с 2014 г. до 8,21% в 2015 г. против 7,15% в предыдущем году. Таким образом, уменьшение количества заданий привело к большей плотности результатов экзамена, что следует рассматривать как позитивное изменение в экзаменационной модели.

Спецификация КИМ ЕГЭ устанавливает три уровни сложности заданий: базовый, повышенный и высокий, при этом для заданий базового уровня примерный интервал выполнения задания предполагается 60–90%; для повышенного уровня результат выполнения должен быть в интервале 40– 60%; с заданиями высокого уровня сложности должны справляться менее

40% участников экзамена. Поэтому содержательный анализ результатов ЕГЭ следует начать с определения того, насколько результат выполнения отдельных заданий совпал с их прогнозируемой сложностью.

В общей сложности в работе было 27 заданий, из которых 12 заданий базового уровня сложности, 11 заданий повышенного уровня сложности и 4 задания высокого уровня сложности. В заданиях базового уровня сложности от экзаменуемого требовалось непосредственно применить конкретные знания, умения и навыки по одной из тем курса. В задачах повышенного уровня и, в большей степени, высокого уровня, требуется применять знания материала из различных областей и ориентироваться в более или менее новой для экзаменуемого обстановке задачи. Результат выполнения 16 заданий (59% заданий) укладывается в границы, установленные для заданий соответствующего уровня сложности (от 60% выполнения для базового уровня, от 40 для повышенного, до 40% выполнения для высокого уровня). Из этих 16 заданий слишком легкими для своего уровня оказались 2 задания базового уровня (задания 5 и 3 с показателями выполнения 89% и 85% соответственно) и 2 задания повышенного уровня (№17 и 15 с показателями выполнения около 65%). В работе 2014 г. слишком легких заданий (особенно базового уровня) было гораздо больше, для варианта 2015 г. такой результат можно считать очень хорошим. 

На позиции 5 в ЕГЭ 2015 г. стояло задание на определение кратчайшего пути в графе, заданном таблицей длин ребер. В существующем виде это задание допускает простое переборное решение путем подсчета суммарных длин всех возможных путей. Понятно, что для более сложных графов такое решение будет иметь слишком большую вычислительную сложность. В варианте 2016 г. это задание будет стоять на позиции 3 и будет усложнено, его станет невозможно решить без построения графа, соответствующего таблице. 

Задание 3 в части вариантов требовало построения дерева на основании данных из двухтабличной реляционной базы данных, а в другой части вариантов проверяла умение выпускников работать с масками при поиске файлов средствами операционной системы. Оба варианта задания предполагали выбор одного варианта ответа из четырех предложенных. В 2016 г. заданий с выбором ответа в работе не будет, это задание (оно в демоверсии КИМ ЕГЭ 2016 г. стоит на 4 позиции) будет предполагать ответ в виде натурального числа. Вообще задания на работу с файловой системой всегда выполняются экзаменуемыми очень хорошо, а задания на работу с базами данных, первоначально вызывавшие затруднения у участников экзамена, последние годы выполняются также 80% и более участников экзамена.

Задания 15 и 17 относятся к категории заданий повышенной сложности. Их хорошее выполнение в 2015 году показывает, что содержание, которое они проверяют (поиск информации в Интернет для задания 17 и подсчет количества путей в графе для задания 15), прочно вошло в содержание школьного курса и хорошо усвоено основной массой участников экзамена.

Большую тревогу вызывают крайне низкие показатели выполнения двух заданий. Задание 11 базового уровня выполнено в среднем с показателем 25,7% (при разбросе по вариантам от 13% до 50%). Задание по этой теме (рекурсивные алгоритмы) вызывало затруднения и в прошлые годы. При том, что сам по себе способ его выполнения (формальное исполнение алгоритма, записанного на языке программирования) учащимися усвоен (это видно по результату выполнения других заданий, предполагающих тот же способ решения). Видимо, содержание этой темы (соответствующее базовому стандарту) недостаточно хорошо разъясняется учителями, отсюда эта тянущаяся год от года лакуна в подготовке участников экзамена. Разброс по вариантам связан как с разным уровнем подготовки в разных географических зонах, так и с тем, что на экзамене для различных групп вариантов использовались две модели формулировок задания, одна из которых оказалась проще для восприятия. В разделе 6 данных рекомендаций содержится детальный разбор решения задания 11 обоих типов. 

Задание 18 повышенного уровня выполнено в среднем с показателем 11,3% (при разбросе по вариантам от 5% до 19%). Задание, проверяющее это содержание (преобразование импликации в логических выражениях), существует в ЕГЭ с 2005 г., но начина с 2012 г. оно планомерно усложняется. До 2014 г. задание было в группе заданий с выбором ответа, его перенос в категорию заданий с кратким ответом в сочетании с вводом дополнительного содержания в ряде вариантов (функция поразрядной конъюнкции двоичных чисел) привел к существенному снижению результатов. Задание разобрано далее в разделе 6. То, что оно вызвало такие большие затруднения, связано с недостатками в подготовке участников экзамена: несмотря на предупреждения о том, что задания в вариантах, используемых на экзамене, могут по модели и формулировке отличаться от заданий, приведенных в демоверсии, формулировка задания, использованная в КИМ ЕГЭ, повидимому, заставила многих отказаться от попыток его решить.

Результат выполнения еще двух заданий базового уровня: 9 и 10 (39% и 36% соответственно) – также следует признать неудовлетворительным. В демоверсии 2015 г. задание 9 (тема – дискретизация аналогового сигнала) было представлено в двух вариантах: на определение объема или глубины палитры растровых графических изображений и на оценку размера звуковых файлов в зависимости от параметров записи звука. В течение ряда лет (с 2012 г.) задания на растровую графику в ЕГЭ не использовались и, видимо, это содержание ушло из поля зрения учителей. Возвращение в 2015 г. заданий на графику в варианты ЕГЭ оказалось, видимо, неожиданностью для многих участников экзамена.

Задание 10 продолжает линию заданий ЕГЭ, проверяющих знание учащимися комбинаторной формулы зависимости количества возможных кодовых слов от мощности алфавита и длины слова. Это фундаментальное базовое содержание, составляющее теоретическую основу курса и, безусловно, присутствующее во всех учебных программах и учебниках. Низкий результат выполнения этого задания (также тянущийся из года в год) показывает, что подготовка учащихся зачастую сводится к формальному решению задач известных моделей. Каждое небольшое изменение модели задания вызывает резкое снижение результатов. Задание 10 модели 2015 г. также разобрано в разделе 6 настоящих рекомендаций.

Еще 3 задания базового уровня (1, 6 и 12) и 4 задания повышенного уровня (14, 16, 21 и 22) были выполнены с низкими, но в целом приемлемыми результатами. Результат выполнения задания 1 (43,5% в среднем, разброс от 35 до 50%) показывает, что форма задания с выбором ответа в данном случае не прибавляет дополнительных процентов выполнения. Это задание проверяет знание по достаточно сложной для понимания теме неравномерного кодирования (которая, несмотря на сложность, относится к содержанию базового уровня) и, поэтому, вызывает определенные затруднения. В 2016 г. в связи с отказом от использования заданий с выбором ответа, задание аналогичного содержания будет на позиции 5, что больше соответствует его реальной сложности.

Затруднения с выполнением заданий 6 и 12 (42% и 40% соответственно) были связаны с новизной формулировок. Задание 12 впервые появилось в 2012 г. и вызвало шок своей новизной (процент выполнения был не выше 15%). Далее в 2013-2014 гг. оно было в неизменной формулировке, что привело к тому, что его стали выполнять более 60% участников. В 2015 г. оно было дано в новой формулировке, что опять привело к снижению результата.

Суммируя сказанное выше, можно отметить, что значительная часть экзаменуемых при подготовке ориентируется на тренировку решения конкретного типа заданий, приведенного в демоверсии КИМ ЕГЭ, а не на полноценное усвоение изучаемого материала. 

Остальные задания показали результат, более-менее соответствующий их ожидаемой сложности, хотя процент выполнения заданий повышенного уровня 14 (27,5%) и 16 (31%) не дотягивал до требуемых 40%. В задании 14 в 2015 г. был описан новый исполнитель Редактор, что, возможно, явилось причиной недостаточно высоких результатов. Задание 14 также было среди тех заданий, которые были перенесены из группы А (задания с выбором ответа). При том, что, согласно спецификации, это задание предполагает применение знаний в новой для экзаменующегося ситуации (практически это означает, что в задании может быть описан неизвестный экзаменуемым исполнитель, поэтому проверяется умение разобраться в системе команд исполнителя и исполнить алгоритм для него), ввод нового исполнителя зачастую ставит выпускников в тупик. Задание 16 было похоже на задание прошлого года, которое тоже вызвало затруднения, но было опубликовано в демоверсии экзамена 2015 г. и разобрано в методических рекомендациях. В этом году результаты были выше, чем в 2014, но пока не дотягивают до ожидаемого уровня.

Итоги ЕГЭ 2015 г. еще раз показали, что основной причиной провалов по отдельным заданиям является формализм в подготовке участников экзамена, перекос подготовки в сторону механистического решения известных моделей заданий в ущерб изучению фундаментального содержания. В случае отдельных тем (рекурсия, логические преобразования), возможно, затруднения экзаменуемых связаны с недостаточным пониманием содержания этих тем учителями.

Вся выборка участников статистически по результатам экзамена была разделена на 4 группы. В 1 группу вошли участники экзамена, получившие балл ниже минимального, в 4 группу – участники, получившие максимальные баллы. Группу 2 составили участники, набравшие больше минимального, но менее половины первичных баллов, группу 3, самую многочисленную – участники, набравшие более половины первичных баллов, но не входящие в группу 4. На рис. 1 показано распределение всех участников по группам.

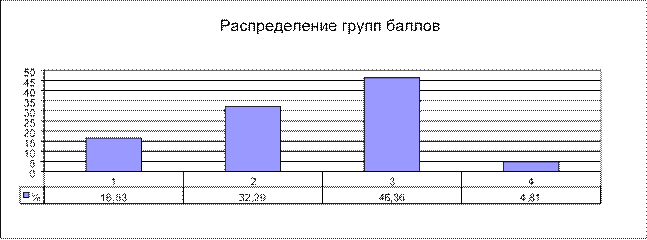
Рис. 1 Распределение участников по группам подготовки

Группу 1 в основном составляют участники, пришедшие на экзамен случайно, не готовившиеся к экзамену целенаправленно и плохо представляющие себе содержание экзаменационных заданий. Сравнительно лучше других эти участники выполняют задания 5 и 3, которые можно выполнить, опираясь на здравый смысл и следуя инструкции, содержащейся в формулировке задания. Задания простые, но требующие знания терминов и понятий информатики, такие как задания 2, 4, 7 и т.п., выполняются этими участниками экзамена неудовлетворительно. С заданием 8, требующим от экзаменующегося умения прочесть и формально исполнить базовые операторы языка программирования, справились только 27% экзаменующихся из этой группы. Примечательно, что 15% участников из этой группы справились с заданием повышенного уровня 15, проверяющим, наряду с освоением понятием графа, владение методом динамического программирования. Вместе с тем, это задание имеет чрезвычайно трудоемкое и требующее высокой внимательности переборное решение, которое можно осуществить, опираясь на здравый смысл и бытовое прочтение задания. Видимо, именно этот факт позволил наиболее упорным экзаменующимся данной группы получить верное решение. Вместе с тем, элементарное по содержанию задание 4, требующее, однако, знания правил записи натуральных чисел в двоичной и кратных системах счисления, осилили только 20% из этой группы. Также задание повышенного уровня 17, которое можно решить, опираясь на базовые теоретико-множественные представления, выполнили 11% экзаменуемых группы 1. Из заданий с развернутым ответом только задание 26 покорилось 5% участников группы с минимальным результатом в 1 балл (из 3 возможных).

Выявить учащихся с подобным уровнем подготовки в условиях школьного класса достаточно просто, это делается обычной контрольной работой. Учащиеся этой группы вряд ли смогут записать натуральное число в двоичной системе (и наоборот, прочесть двоичную запись числа), затруднятся исполнить алгоритм, записанный на алгоритмическом языке или языке программирования, содержащий оператор присваивания и конструкцию ветвления. Любое задание на воспроизведение школьных знаний будет выполнено учащимися этой группы, скорее всего, неудовлетворительно.

Для перехода из группы 1 в группу 2 этим учащимся требуется элементарная подготовка к экзамену, хотя бы знакомство с демоверсией КИМ ЕГЭ. Даже небольшой опыт решения заданий базового уровня, основанного на изучении соответствующего материала и освоении проверяемых умений, приведет этих учащихся к удовлетворительному результату и позволит им преодолеть минимальную границу баллов ЕГЭ.

Результаты экзаменующихся группы 2 гораздо кучнее и определеннее. По крайней мере 8 заданий выполняются этими участниками уверенно. К ним относятся задания 2,3,4,5,7 и 8 базового уровня (процент выполнения выше 60%) и задания 15 и 17 повышенного уровня (процент выполнения в диапазоне 50%-60%). Среди этих заданий находятся простые, но требующие знания терминов и понятий информатики задания 2, 4, 7, 8, а также задания 3, 5, 15 и 17, которые можно решить как специфическими методами информатики, так и опираясь на здравый смысл и общеучебные умения. Еще 6 заданий первой части экзаменационной работы выполняются примерно четвертью участников экзамена из этой группы. Это задания 1, 6, 9, 12 базового уровня и 19 и 20 повышенного уровня. Недостаточно уверенное выполнение этих заданий определяется определенными лакунами в подготовке выпускников, связанными с темами «Неравномерное кодирование», «Кодирование растровых изображений», «Адресация в сети Интернет», «Обработка массивов». Также определенные затруднения вызывала новизна формулировок заданий 6, 9 и 20.

Из четырех заданий с развернутым ответом каких-то значимых результатов участники этой группы достигают при выполнении только двух заданий: 24 и 26, но и там результат сильно ниже требуемого.

Участники экзамена из этой группы совсем не справляются с заданиями 11 (рекурсия в алгоритмах), 18 (преобразование импликации), 21 (функции в алгоритмах) и 22 (применение метода динамического программирования для анализа результатов исполнения алгоритма), а также заданиями высокого уровня сложности 23, 25 и 27.

Выделение этой группы учащихся в составе класса осуществляется посредством диагностических работ в формате ЕГЭ. Выше указаны аспекты содержания, по которым у учащихся данной группы имеются пробелы: «Неравномерное кодирование», «Кодирование растровых изображений», «Адресация в сети Интернет», «Обработка массивов», «Функции в алгоритмах». Учащиеся этой группы скорее всего затруднятся выполнить задание 20, так как не «узнают» реализованный там алгоритм. Они не очень уверенно будут оперировать с натуральными числами, записанными в позиционных системах счисления, отличных от десятичной, могут допускать ошибки при решении комбинаторных задач. В целом усвоение и воспроизведение знаний и умений этой группой учащихся осуществляется формально, без опоры на понимание фундаментальных основ предмета.

Важнейшей задачей учителя на этапе формирующего обучения является профилактика появления этой группы обучающихся. В отличие от участников экзамена из первой группы, которые просто не имеют интереса к предмету и в силу этого «пропускают материал мимо ушей», обучающиеся второй группы вполне мотивированы на изучение информатики. Учитель должен своевременно выявлять возможные лакуны в подготовке, не допуская их формирования. Важно добиться глубокого понимания со стороны учащихся каждой темы, каждого раздела учебного предмета, дать обучающимся достаточную практику применения полученных знаний и освоенных умений при решении заданий разных типов и моделей. Очень полезно на этом этапе использовать тематические сборники заданий в формате ЕГЭ, не отказываясь от решения заданий в формате экзаменов прежних лет, при том что заданий подобных моделей в экзамене 2016 г. точно не будет. Так, в открытом банке заданий ЕГЭ содержится огромный корпус заданий с выбором ответа, решение которых будет безусловно эффективно при изучении отдельных тем курса.

Если принадлежность учащегося ко второй группе выявилась в результате диагностической работы на этапе итогового повторения в 11 классе, оптимальным будет совместное составление учителем и учеником индивидуального плана ликвидации пробелов в подготовке. При этом задачей учителя должно быть добиться полного овладения учащимся содержания каждого узкого аспекта подготовки, научить учащихся решать не только конкретное задание, аналогичное имеющемуся в демоверсии, но весь корпус возможных заданий, проверяющих данное содержание. Важнее, чтобы выпускник пришел на экзамен, твердо зная, к решению каких заданий по спецификации он подготовлен полностью и какой первичный балл он должен получить в любом случае, независимо от того, насколько знакомыми ему будут те или иные формулировки заданий.

Конечно, педагогическое мастерство учителя в решении данной задачи играет не меньшую роль, чем уровень мотивации ученика. Именно учитель должен хорошо представлять себе, какие аспекты подготовки проверяет то или иное задание КИМ ЕГЭ, видеть весь корпус возможных типов и моделей заданий, отделять важное содержание от факультативного, показать учащемуся подходы, которые используют авторы КИМ ЕГЭ при конструировании заданий.

Надо понимать, что полного исчезновения группы 2 не произойдет никогда, тем более, что это и не требуется. Среди сдающих ЕГЭ по информатике и ИКТ есть прослойка учеников, изучающих информатику на базовом уровне и планирующих поступление в высшие учебные заведения с невысоким проходным баллом. Уровень подготовки, соответствующий второй группе, показывает, что экзаменуемые могут продолжить обучение в области, связанной с информатикой, при условии, что это обучение начнется с повторения основ. Поэтому они заслуженно получают по итогам ЕГЭ положительную оценку. 

Группа 3 является наиболее многочисленной. Это участники, готовившиеся к экзамену, изучавшие информатику на профильном или углубленном уровне, имеющие опыт решения задач в формате ЕГЭ. От группы 2 их отличает уверенное выполнение заданий 1, 6, 9, 10, 12, 13, 20, 21 первой части и заданий 24, 25 и 26 с развернутым ответом. Вызывают затруднения уже упоминавшиеся задания 11 и 22, а также задания повышенного уровня 14 (анализ результата исполнения алгоритма) и 16 (запись чисел в позиционных системах счисления) – с каждым из них справилось около 40% членов группы. Задания 18, 23 и 27 выполняются неудовлетворительно (процент выполнения ниже 15%).

Отличие этих учеников от учеников наиболее сильной, четвертой, группы – в уровне способности справляться с новыми для себя формулировками, именно решать задачи, а не выбирать решение среди заранее известных. Диагностика этих умений – важная задача ЕГЭ, который среди прочего, должен быть инструментом по отбору абитуриентов в ведущие ВУЗы страны. 

В то же время способность к творческому мышлению, свободному владению материалом тоже может быть предметом обучения. Эффективный способ повышения индивидуальных результатов для учащихся этой группы – это тренировка по решению заданий с нестандартными формулировками, заданий, требующих применения знаний в новой ситуации. Кроме того, следует ликвидировать лакуны в подготовке по отдельным темам (рекурсия, поразрядная конъюнкция двоичных чисел, динамическое программирование).

Основной резерв повышения результатов экзамена у этой группы выпускников находится на этапе итогового предэкзаменационного повторения в 11 классе, так как именно хорошая учебная работа на этапе формирующего обучения обеспечила их попадание в эту успешную группу. Учителю следует по результатам диагностики в формате ЕГЭ определить для каждого учащегося из группы имеющиеся пробелы в подготовке, а затем составить индивидуальные комплекты тренировочных заданий для ликвидации этих пробелов. Комплекты должны обеспечить формирование опыта применения знаний и умений в новой, нестандартной ситуации.

Учащимся из третьей группы надо четко оценивать свои силы и не ставить невыполнимых задач. Например, многие участники группы 4 испытывают затруднения при выполнении задания 27. Приобретение опыта самостоятельного программирования требует значительного времени, ставить эту задачу, не перейдя из третьей группы в четвертую, преждевременно.

Наконец, группа 4 – это наиболее подготовленные участники экзамена, самая малочисленная группа (менее 5% участников). Ими освоено проверяемое содержание и основные группы умений. Затруднения у участников из этой группы вызывают лишь задания 18, 23 и 27 – наиболее сложные в экзамене. Основным резервом повышения индивидуальных результатов для участников этой группы является тренировка по созданию оригинальных программ для решения практических задач – умение, проверяемое последним и наиболее трудоемким 27 заданием, правильное выполнение которого приносит экзаменующемуся 4 первичных балла.

Подобная тренировка должна осуществляться опытным учителем, так как самостоятельно проверить качество выполнения программы и ее эффективность учащийся обычно не в состоянии. Также важной является последовательность предъявления заданий на программирование, которая должна обеспечить формирование устойчивого умения писать правильные и эффективные программы для решения разнообразных задач тех типов, которые проверяются на ЕГЭ. Неоценимую помощь учителю в подборе таких заданий может оказать открытый банк заданий ЕГЭ прошлых лет.

Анализ результатов ЕГЭ по информатике из года в год показывает, что появление новой формулировки задания вызывает довольно резкое снижение результатов по сравнению с предыдущим годом. Однако уже в следующем году результаты идут вверх, и через пару лет, когда к формулировке все привыкают, оказываются на первоначальном уровне. С учетом того, что объективная сложность заданий не изменяется и основные характеристики совокупности участников ЕГЭ по информатике и ИКТ также остаются неизменными, логично предположить, что основной причиной этих падений результатов по отдельным заданиям являются недостатки в подготовке выпускников. Наша гипотеза состоит в том, что многие учителя при подготовке школьников к ЕГЭ сосредотачиваются на тренировке учащихся в решении заданий, аналогичных заданиям, опубликованным в демонстрационном варианте КИМ, в ущерб фундаментальному изучению предмета. Шок от необычной формулировки задания, получаемый экзаменующимся, приводит к потере баллов и недостаточно высоким результатам.

В этой связи напомним, что содержание курса информатики, проверяемое в ЕГЭ, включает три блока тем:

А.  Математические основы информатики (кодирование и передача данных, системы счисления, элементы математической логики, дискретные математические объекты).

Б.  Алгоритмы и программирование.

В.  Теоретические основы информационно-коммуникационных технологий.

Для каждой из тем каждого блока важно хорошо представлять себе круг понятий и фактов, которые проверяются в ЕГЭ. В процессе преподавания важно обеспечить овладение учащимися этими понятиями и знакомство их с фактами, а только затем показать им посредством каких заданий это может быть проверено на итоговой аттестации в формате ЕГЭ. 

Попробуем перечислить эти понятия и факты для одного раздела первого блока тем: «Элементы математической логики» (раздел 1.5 «Перечня элементов содержания, проверяемых на ЕГЭ» Кодификатора). Логические операции:

Отрицание (инверсия, логическое НЕ); конъюнкция (логическое умножение, логическое И); дизъюнкция (логическое сложение, логическое ИЛИ); следование (импликация); тождество (эквивалентность). 

Логические константы – ИСТИНА (1) и ЛОЖЬ (0).

Логическое выражение – выражение, составленное из символов логических переменных и констант с помощью знаков логических операций и скобок.  Приоритеты логических операций. Значение логического выражения при заданных значениях переменных. Таблица истинности. 

К слову, почти все, что перечислено выше, написано в списке обозначений и соглашений, предваряющих экзаменационную работу. В частности, там указаны приоритеты логических операций а также приведено преобразование импликации.

Понятно, что простое перечисление понятий на уроке явно недостаточно. Необходимо раскрыть свойства логических выражений. 

Рекомендуем при подготовке учеников обратить внимание на следующие свойства логических выражений (как и любой подобный список он НЕ является исчерпывающим).

Общие свойства

1. Для набора из n логических переменных существует ровно 2ⁿ различных набора значений. Таблица истинности для логического выражения от n переменных содержит n+1 столбец и  2ⁿ строк. Дизъюнкция

1.     Если хоть одно из подвыражений, к которым применяется дизъюнкция, истинно на некотором наборе значений переменных, то и вся дизъюнкция истинна для этого набора значений.

2.     Если все выражения из некоторого списка истинны на некотором наборе значений переменных, то дизъюнкция этих выражений тоже истинна.

3.     Если все выражения из некоторого списка ложны на некотором наборе значений переменных, то дизъюнкция этих выражений тоже ложна.

4.     Значение дизъюнкции не зависит от порядка записи подвыражений, к которым она применяется. Конъюнкция

1.     Если хоть одно из подвыражений, к которым применяется конъюнкция, ложно на некотором наборе значений переменных, то и вся конъюнкция ложна для этого набора значений.

2.     Если все выражения из некоторого списка истинны на некотором наборе значений переменных, то конъюнкция этих выражений тоже истинна.

3.     Если все выражения из некоторого списка ложны на некотором наборе значений переменных, то конъюнкция этих выражений тоже ложна.

4.     Значение конюнкции не зависит от порядка записи подвыражений, к которым она применяется.

Простые дизъюнкции и конъюнкции

Назовем (для удобства) конъюнкцию простой,  если подвыражения, к которым применяется конъюнкция, – различные переменные или их отрицания. Аналогично, дизъюнкция называется простой,  если подвыражения, к которым применяется дизъюнкция, – различные переменные или их отрицания.

1.     Простая конъюнкция принимает значение 1 (истина) ровно на одном наборе значений переменных.

2.     Простая дизъюнкция принимает значение 0 (ложь) ровно на одном наборе значений переменных.

Дизъюнкция простых конъюнкций 

Для любого множества наборов значений переменных можно построить выражение, которое истинно на всех наборах из заданного множества и только на них. Это выражение удобно записать в виде дизъюнкции простых конъюнкций.

Пример. На рисунке приведены все строки таблицы истинности функции F(x, y, z), при которых F(x, y, z) истинно.

Тогда функция F может быть задана таким выражением:

(¬x/\y/\z) \/ (x/\¬y/\z) \/ (x/\y/\¬z)

Здесь первый член дизъюнкции соответствует первой строке таблицы фрагмента истинности; второй член – второй строке; третий член – третьей строке

Импликация

1.     Импликация A →B равносильна дизъюнкции (¬А)  \/ В. Эту дизъюнкцию можно записать и так: ¬А \/ В.

2.     Импликация A →B принимает значение 0 (ложь) только если  A=1 и B=0. Если A=0, то импликация A →B истинна при любом значении B.

Посмотрим теперь как перечисленные свойства логических выражений используются при решении заданий ЕГЭ.

Задание 2 базового уровня сложности проверяет знание экзаменующимся понятия таблицы истинности и умение построить таблицу истинности для выражений, содержащих отрицание, конъюнкцию и дизъюнкцию. До 2015 года включительно задание представляло собой фрагмент таблицы истинности. Необходимо было выбрать из предложенных выражение, этой таблице соответствующее. Задание выполнялось участниками экзамена с хорошим результатом, представляло собой одно из тех заданий, с которыми справлялось большинство участников экзамена из группы 2 (см. раздел 5 рекомендаций). В 2016 году задание впервые будет предполагать краткий ответ в виде строки символов. Приведем здесь разбор этого задания в новой модели. Задание 2.1

Логическая функция F задаётся выражением (¬z)/\x \/ x/\y. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных  x, y, z. 

В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая 1-му столбцу; затем – буква, соответствующая 2-му столбцу; затем – буква, соответствующая 3-му столбцу). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.

Пример. Пусть задано выражение x → y, зависящее от двух переменных x  и y, и таблица истинности:

Тогда 1-му столбцу соответствует переменная y, а 2-му столбцу соответствует переменная x. В ответе нужно написать: yx.

Решение. Заметим, что при x=0 значение F(x, y, z)=0 независимо от значений аргументов y и z. В таблице этому свойству удовлетворяет 3-я переменная. Значит, это x. Чтобы понять, какой столбец таблицы соответствует переменной y, а какой – переменной z, рассмотрим строку, в которой x=1 (то есть в третьем столбце стоит 1), а F(x, y, z) = 0 . Это происходит,  если y=0, а z=1. В нужной строке (это 3-я строка снизу) 1 стоит в 1-м столбце, а 0 – во втором. Значит, 1-й столбец соответствует z, а второй соответствует y.

Ответ: zyx

Заметим, что задача допускает в принципе и переборное решение «в лоб»: можно составить таблицы истинности для всех 6 перестановок переменных x, y, z и посмотреть, какая из них соответствует условию задачи. Однако, это переборное решение существенно более трудоемкое, чем переборное решение задания 2 прежней модели, когда было достаточно подставить значения переменных из таблицы в выражения в ответах и проверить значения функции. При разборе этого задания можно построить для тренировки если не все 6 таблиц, то хотя бы 2-3, но объяснять надо, конечно, приведенное выше простое и быстрое решение.

Еще один пример задания 2 нового типа. Задание 2.2

Логическая функция F задается выражением 

                              (x /\ y /\¬z) \/ (x /\ y /\ z) \/ (x /\¬y /\¬z).   

На рисунке приведен фрагмент таблицы истинности функции F, содержащий все наборы аргументов, при которых функция F истинна.

Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных  x, y, z. 

В ответе напишите буквы x, y, z  в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая 1-му столбцу, затем – буква, соответствующая 2-му столбцу и т.д.)  Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно. Пример. Пусть задано выражение ¬x \/ y, зависящее от двух переменных  x и y, и фрагмент её таблицы  истинности, содержащий все наборы аргументов, при ко которых функция F истинна.

Тогда    1-му    столбцу    соответствует    переменная    y,    а    2-му   столбцу

соответствует переменная  x. В ответе нужно написать: yx

Решение. В этом случае также при x=0 значение F(x, y, z)=0 независимо от значений аргументов y и z. В таблице только второй столбец содержит только единицы. Значит, второй столбец соответствует x. Чтобы понять, какой столбец таблицы соответствует переменной y, а какой – переменной z, надо найти строку, в которой у переменных y и z разные значения. В этом случае  x /\ y /\ z = 0 и x /\¬y /\¬z = 0. Значит, так как F(x, y, z) = 1, x /\ y /\¬z = 1.  Это происходит,  если y=1, а z=0. В нужной строке (это 3-я строка снизу) 1 стоит в 1-м столбце, а 0 – во втором. Значит, 1-й столбец соответствует y, а третий столбец соответствует z. Ответ: yxz

Задание 18 повышенного уровня сложности проверяет знание экзаменующимся таблицы истинности для импликации и умение осуществить преобразование импликации в сложных выражениях. В этом году задание в ряде вариантов заодно проверяло умение осуществить поразрядную конъюнкцию двоичных чисел. Оно вызвало у экзаменующихся серьезные затруднения.

Пример задания 18.

Обозначим через m&n поразрядную конъюнкцию неотрицательных целых чисел m и n. Так, например, 14&5 = 1110₂&0101₂ = 0100₂ = 4. Для какого наименьшего неотрицательного целого числа А формула

x&25 ≠ 0 → (x&17 = 0 → x&А ≠ 0)

тождественно истинна (т.е. принимает значение 1 при любом неотрицательном целом значении переменной х)?

Решение. Для начала требуется применить преобразование импликации два раза и получить выражение без импликации:

x&25 ≠ 0 → (x&17 = 0 → x&А ≠ 0) ≡ x&25 = 0 \/ (x&17 = 0 → x&А ≠ 0) ≡  x&25 = 0 \/ (x&17 ≠ 0 \/ x&А ≠ 0) ≡ x&25 = 0 \/ x&17 ≠ 0 \/ x&А ≠ 0

Запишем числа 25 и 17 в двоичной системе: 25₁₀ = 11001₂, 17₁₀ = 10001₂. Различие между ними только в одном разряде – четвертом. Поэтому число A = 1000₂ =8₁₀ обеспечит тождественную истинность выражения x&25 = 0 \/ (x&17 ≠ 0 \/ x&8 ≠ 0)

Ответ:8

Как видно из приведенного примера, задание не тредует для своего выполнения каких-то знаний и умений. Выходящих за рамки перечисленных выше свойств логических выражений.

Задание 23 высокого уровня сложности, предполагающее краткий ответ в виде натурального числа, является едва ли не самым сложным заданием КИМ ЕГЭ по информатике и ИКТ. С ним, как правило, справляются не более 5% экзаменуемых. Задание проверяет умение преобразовывать выражения, содержащие логические переменные, умение описать на естественном языке множество значений логических переменных, при которых заданный набор логических выражений истинен. 

Для того, чтобы выполнить задание, ученик должен уметь:   - преобразовывать логические выражения (включая выполнение замены переменных); 

-                     переводить формальное описание, в виде системы логических условий, на нормальный, "человеческий" язык;

-                     подсчитать число          двоичных   наборов,     удовлетворяющих заданным условиям. 

После того, как выяснено, что за наборы удовлетворяют системе, подсчет их числа относительно прост. Наиболее трудным для усвоения, видимо, является второе из перечисленных требований – оно не формализуется, от ученика, как правило, требуется догадка.

Стоит привести здесь разбор этого задания.

Пример №1 формулировки задания 23:

          Сколько существует различных наборов значений логических переменных x₁, x₂, ... x₉, x₁₀, которые удовлетворяют всем перечисленным ниже условиям?

((x₁ ≡ x₂) \/ (x₃ ≡ x₄)) /\ (¬(x₁ ≡ x₂) \/ ¬(x₃ ≡ x₄)) =1

((x₃ ≡ x₄) \/ (x₅ ≡ x₆)) /\ (¬(x₃ ≡ x₄) \/ ¬(x₅ ≡ x₆)) =1

((x₅ ≡ x₆) \/ (x₇ ≡ x₈)) /\ (¬(x₅ ≡ x₇) \/ ¬(x₇ ≡ x₈)) =1

((x₇ ≡ x₈) \/ (x₉ ≡ x₁₀)) /\ (¬(x₇ ≡ x₈) \/ ¬(x₉ ≡ x₁₀)) =1

В ответе не нужно перечислять все различные наборы значений x₁, x₂, ... x₉, x₁₀, при которых выполнена данная система равенств. В качестве ответа вам нужно указать количество таких наборов.

Набросок решения:

Решение состоит из двух этапов. Сначала попытаемся описать, как устроены все наборы значений переменных, удовлетворяющие данной системе. Далее   подсчитаем число таких наборов.

          Этап 1. Как устроено множество решений     А. Предварительный этап – упрощаем уравнения.

 В системе фигурируют логические функции от следующих выражений:

(x₁ ≡ x₂),  (x₃ ≡ x₄), (x₅ ≡ x₆), (x₇ ≡ x₈),  (x₉ ≡ x₁₀)

 Подобно тому, как это делается при решении алгебраических уравнений, сделаем замену переменных:

                   t₁ =    x₁ ≡ x₂                 t₂ =    x₃ ≡ x₄                               t₃ =     x₅ ≡ x₆                           t₄ =     x₇ ≡ x₈          t₅ =     x₉ ≡ x₁₀

                Общая формула замены (k=1, 2, 3, 4, 5):

                                tk = (x2k-1 ≡ x2k)     Получим:

(t₁  \/  t₂) /\ (¬t₁  \/ ¬ t₂ ) =1

(t₂  \/  t₃) /\ (¬t₂  \/ ¬ t₃ ) =1

(t₃  \/  t₄) /\ (¬t₃  \/ ¬ t₄ ) =1

(t₄  \/  t₅) /\ (¬t₄  \/ ¬ t₅ ) =1

          Уравнения полученной системы имеют вид (k=1, 2, 3, 4):

(t_k  \/  t_k+1) /\ (¬t_k  \/ ¬ t_k+1 ) =1

 Это означает, что из каждых двух переменных t_k  и  t_k+1 ровно одна равна 1 и ровно одна равна нулю, т.е. эти переменные имеют разные значения. Таким образом, систему можно еще немного упростить и записать ее так:

 ¬(t₁  ≡   t₂ ) =1

¬(t₂  ≡   t₃ ) =1

¬(t₃  ≡   t₄ ) =1

¬(t₄  ≡   t₅ ) =1

          Б. Анализ системы.

 В любом решении последней системы значения переменных чередуются. Поэтому такая система имеет ровно два решения: 01010 и

10101 (первая цифра – значение переменной t₁,  вторая - значение   t₂ и т.д.).

          Далее, т.к. 

                                      tk = x2k-1 ≡ x2k

(здесь k=1, 2, 3, 4, 5), то каждому значению t_k соответствуют две пары значений переменных  x_2k-1 и x_2k. Например, t_k = 1 в двух случаях: { x_2k-1 = x_2k=1 } и { x_2k-1 = x_2k=0 }.

          Этап 2. Подсчет числа решений.

          Каждому    из      двух решений     системы      для    переменных         t соответствует 2⁵ = 32 решения исходной системы. Поэтому исходная система имеет 2∙32 = 64 решения. Ответ: 64

Пример №2 формулировки задания 23:

Сколько     существует          различных наборов      значений    логических переменных x₁, x₂, ..., x₁₀, которые удовлетворяют всем перечисленным ниже условиям?

¬(x₁ ≡ x₂) /\  (x₁ \/ x₃) /\ (¬x₁ \/ ¬x₃) =0

¬(x₂ ≡ x₃) /\  (x₂ \/ x₄) /\ (¬x₂ \/ ¬x₄) =0

...

¬(x₈ ≡ x₉) /\  (x₈ \/ x₁₀) /\ (¬x₈ \/ ¬x₁₀) =0

В ответе не нужно перечислять все различные наборы значений x₁, x₂, ..., x₁₀, при которых выполнена данная система равенств. В качестве ответа вам нужно указать количество таких наборов.

Набросок решения:

Решение состоит из двух этапов. Сначала попытаемся описать, как устроены все наборы значений переменных, удовлетворяющие данной системе. Далее   подсчитаем число таких наборов.

Этап 1. Как устроено множество решений

А. Предварительный этап – упрощаем уравнения.

Заметим, что выражение (a \/ b) /\ (¬a \/ ¬b) равносильно тому, что ровно одна из переменных a и b равна 1, то есть равносильно выражению ¬(a ≡ b). Поэтому каждое выражение вида (x_k \/ x_k+2) /\ (¬x_k \/ ¬x_k+2), где k=1, …, 8, в наших уравнениях можно заменить выражением   ¬(x_k ≡ x_k+2).   Таким образом, наша система эквивалентна системе

¬(x₁ ≡ x₂) /\  ¬(x₁ ≡ x₃) =0

¬(x₂ ≡ x₃) /\  ¬(x₂ ≡ x₄) =0

...

¬(x₈ ≡ x₉) /\  ¬(x₈ ≡ x₁₀) =0

 Далее,  ¬a  /\  ¬b = 0 означает, что, если  ¬a   истинно, то ¬b  истинным быть не может. Т.е. ¬a  /\  ¬b = 0 эквивалентно ¬a  → b = 1. Поэтому систему можно записать в следующем виде

¬(x₁ ≡ x₂)  → (x₁ ≡ x₃) =1

¬(x₂ ≡ x₃)  → (x₂ ≡ x₄) =1

...

¬(x₈ ≡ x₉) → (x₈ ≡ x₁₀) =1

          Б. Анализ системы.

     Каждое из уравнений полученной системы имеет вид (k = 1, …, 8): ¬(x_k ≡ x_k+1)  → (x_k ≡ x_k+2) =1

Иными словами, если два соседних элемента набора x_k и x_k+1 не равны между собой, то x_k=x_k+2, то есть элементы x_k+1 и x_k+2 также не равны между собой. Таким образом, набор удовлетворяет системе, тогда и только тогда, когда он обладает следующими свойствами. В начале набора стоит несколько (может быть, одно) одинаковых значений (назовем это"головой" набора). Затем (после первого появления нового числа) значения в наборе чередуются ("хвост" набора). 

Пример решения: 1111010101 (в  этой последовательности первая цифра

– значение переменной x₁, вторая цифра – значение переменной x₂, и т.д.) 

Здесь голова набора состоит из четырех единиц, а хвост – это последовательность  01010101. в данном примере длина головы равна 4.

Важное наблюдение. Для каждой непустой головы есть ровно один хвост, образующий вместе с ней решение. Действительно, первая цифра такого хвоста – это цифра, противоположная цифрам головы. А дальше цифры в хвосте чередуются.

Этап 2. Подсчет числа решений

В соответствии с важным наблюдением, количество решений совпадает с количеством возможных голов. Очевидно, существует 10 голов, состоящих из единиц (1, 11, 111, …, 1111111111) и столько же голов, состоящих из нулей. 

Ответ: 20

Как видим, сложность решения задачи не зависит от числа переменных и уравнений. Если понятно, как устроено множество решений, подсчитать количество решений для аналогичной системы, скажем, с 20-ю переменными, не сложнее, чем в уже рассмотренном случае.

Отметим, что разбирать эту задачу стоит только с учениками, которые достаточно свободно владеют преобразованиями логических выражений. Стоит выписать несколько полезных преобразований (они встречались в разобранных примерах):

          ¬a \/ b                            равносильно        a→ b

          (a→ b) /\ (a→ b) равносильно          a ≡ b  (¬a \/ b) /\ (a\/¬b) равносильно      a ≡ b

          (a \/ b) /\ (¬a \/ ¬b)          равносильно        ¬(a ≡ b).

Кроме того, полезно потренироваться в выполнении замен в логических выражениях. Отметим, что это делается точно так же, как и замены в уравнениях, которые встречаются в курсе математики.

Первая цель при выполнении задания 23 - понять, что собой представляет множество решений системы. Для этого систему бывает полезно преобразовать (упростить) систему, используя тождественные преобразования и замены переменных. Затем – подсчитать количество элементов во множестве решений. Во многих случаях система состоит из однотипных уравнений, каждое из которых связывает небольшое число переменных (две-три-четыре), при том, что в системе может быть 10 и более переменных. Обычно, количество переменных не является источником сложности, оно является параметром решения. Если не получается решить задачу в общем виде, можно попробовать перебрать все решения для системы с небольшим количеством переменных. Это может подсказать, как выглядит решение в общем виде.

Если понятно, как выглядит множество решений, подсчет их количества – несложная комбинаторная задача. Сильные ученики могут сообразить, как провести подсчет, даже не обладая специальными знаниями. Стоит повторить формулы произведения возможностей и формулу суммы арифметической прогрессии. 

Серьезное затруднение в этом году вызвало задание базового уровня 11 из раздела «Теория алгоритмов», при том, что выполняется оно методом формального исполнения алгоритма. Приведем здесь его разбор.

Задание 11 проверяет владение экзаменуемыми понятием рекурсии в алгоритмах и связанных с этим понятием умений и навыков. Оно как в 2014 г., так и в 2015 г. было выполнено плохо (средний процент выполнения: 13,2% в 2014 г., 25,7% в 2015 г.). В 2014 году задание представляло собой фрагмент рекурсивного алгоритма, содержащего оператор вывода (печати) внутри вызываемой рекурсивной функции. Вопрос формулировался просто: какое количество символов (чисел) будет напечатано, то есть сколько раз будет выполнена команда вывода. В 2015 г. эта модель задания была слегка модифицирована, вопрос формулировался в виде «Какая строка символов будет напечатана?». По идее, это задание решается методом формального исполнения (трассировки) алгоритма, то есть в результате репродуктивной деятельности, знакомой учащимся. Низкий показатель выполнения этого задания говорит о том, что понятие рекурсии многими учащимися в процессе обучения так и не было освоено.

В связи с тем, что это задание вызывает систематические затруднение, приведем здесь разбор двух различных образцов данного задания из вариантов КИМ ЕГЭ 2015 г. Задание 11.1

Ниже на пяти языках программирования записана рекурсивная функция (процедура) F.

Что выведет программа при вызове F(9)? В ответе запишите последовательность выведенных цифр слитно (без пробелов).

Решение: Взгляд на текст процедуры показывает, что печать происходит сразу после вызова, при этом печатается аргумент, с которым процедура была вызвана. После этого в алгоритме содержится условный оператор, который при условии, что алгоритм больше либо равен семи осуществляет еще два последовательных рекурсивных вызова той же процедуры с аргументом на 3 и на 1 меньше, чем первоначальный аргумент. Исполним алгоритм для указанного аргумента.

Ответ: 9685746 Задание 11.2

Ниже на пяти языках программирования записаны две рекурсивные функции (процедуры): F и G.

Сколько символов «звёздочка» будет напечатано на экране при выполнении вызова F(11)?

Решение: Взгляд на текст задания показывает, что печать происходит только внутри процедуры G сразу после вызова, при этом печатается один символ «звёздочка». Записаны две процедуры F и G, при этом из процедуры F осуществляется вызов G(n-1), а из процедуры G осуществляется вызов  F(n-2). Рекурсия заканчивается, когда аргумент становится равным 1 (в процедуре G) или 0 (в процедуре F). 

Исполним алгоритм для указанного аргумента (11).

Таким образом, символ «звёздочка» будет напечатан 4 раза.

Ответ: 4

Как видно из приведенных решений к образцам заданий, от экзаменующихся не требовалось ничего больше, чем исполнить приведенный алгоритм. Видимо, проблема заключается в том, что разъяснению понятия рекурсии и механизма осуществления рекурсивного вызова было уделено недостаточно внимания. Понять и почувствовать конструкцию рекурсии не проще, чем конструкцию оператора присваивания a := a +1, основной способ добиться этого понимания – решать больше практических заданий. 

Например, можно добавить в описанные две процедуры еще один оператор вывода. Для экономии места приведем алгоритмы на двух языках:

К данному алгоритму можно задать несколько вопросов. Первый: «Сколько символов «плюс» будет напечатано?» – достаточно прост и эквивалентен по сложности заданию 11.2, а другой: «Какая последовательность символов будет напечатана?» - требует глубокого понимания сущности рекурсии и ближе по сложности к заданию 11.1. (Ответ: при выполнении вызова F(11) будет напечатана строка «****++++».)

Эффективным способом организации занятий по данной теме может быть разбор заданий у доски с объяснением учителя, а затем самостоятельная работа учащихся с теми же алгоритмами, реализованными в среде программирования (например, в среде «КуМир»), когда учащиеся могут запустить эти алгоритмы с разными аргументами (например модифицированное задание 11.2 с аргументами 9 и 8) и обсудить, в чем причина совпадения или несовпадения результатов. Далее учащиеся могут попробовать модифицировать алгоритмы (например, переместить операторы вывода) и спрогнозировать результаты их выполнения, а затем проверить гипотезу.

В любом случае, рекурсия относится к фундаментальным понятиям информатики, ее изучение в школе необходимо и важно в плане общего образования.

Модель КИМ 2016 г. по сравнению с КИМ 2015 г. изменилась незначительно. Прежде всего, в первой части больше совсем не будет заданий с выбором одного ответа из множества предложенных, все ответы будут представлять собой либо число, либо строку символов, формируемую по определенному алгоритму. В связи с этим была изменена последовательность предъявления заданий 1–5: первым будет идти задание, проверяющее правила записи чисел в двоичной и кратных системах счисления, пятым – эквивалент стоявшего в 2015 г. на первом месте задания на определение оптимального кода при неравномерном кодировании. Количество заданий и максимальный первичный балл остались без изменений.

Несмотря на то, что в КИМ ЕГЭ 2016 г. не будет заданий с выбором ответа, не следует игнорировать задания открытого банка ЕГЭ этого типа. Решение заданий ЕГЭ прошлых лет поможет учащимся представить разнообразие сюжетов и проверяемых элементов содержания по каждому из разделов содержания.

Приложение Основные характеристики экзаменационной работы ЕГЭ 2015 г.  по ИНФОРМАТИКЕ и ИКТ

Анализ надежности экзаменационных вариантов по информатике и ИКТ подтверждает, что качество разработанных КИМ соответствует требованиям, предъявляемым к стандартизированным тестам учебных достижений. Средняя надежность (коэффициент альфа Кронбаха)^[1] КИМ по информатике и ИКТ - 0,9.