Электромагнитная природа света. Скорость света. Интерференция света. Дифракция света. Дифракционные решетки

50 №Сабақ / Урок № 50

Сабақ жоспары / План урока

Сабақтың тақырыбы / Тема урока

Электромагнитная природа света. Скорость света. Интерференция света. Дифракция света. Дифракционные решетки

Природа света

Первые представления древних ученых о свете:

-     из глаз выходят тонкие щупальца, и зрительные впечатления возникают при ощупывании ими предметов;

-     источник света→свет распространяется→глаз, вызывая зрительное ощущение→мы видим!

Передача воздействий:

1 способ: посредством переноса вещества;

2 способ: посредством изменения состояния среды между телами (без переноса вещества).

Возникли две теории света(≈17 век)

СВЕТ ОБЛАДАЕТ КОРПУСКУЛЯРНО-ВОЛНОВЫМ ДУАЛИЗМОМ

В 60-е годы XIX века Максвеллом были установлены общие законы электромагнитного поля, которые привели его к заключению, что свет – это электромагнитные волны. Важным подтверждением такой точки зрения послужило совпадение скорости света в вакууме с электродинамической постоянной.

Электромагнитная природа света получила признание после опытов Г. Герца по исследованию электромагнитных волн (1887–1888 гг.). В начале XX века после опытов П. Н. Лебедева по измерению светового давления (1901 г.) электромагнитная теория света превратилась в твердо установленный факт.

Электромагнитная теория света позволила объяснить многие оптические явления, такие как интерференция, дифракция, поляризация и т. д. Однако, эта теория не завершила понимание природы света. Уже в начале XX века выяснилось, что эта теория недостаточна для истолкования явлений атомного масштаба, возникающих при взаимодействии света с веществом. Для объяснения таких явлений, как излучение черного тела, фотоэффект и др. потребовалось введение квантовых представлений. Наука вновь вернулась к идее корпускул – световых квантов. Тот факт, что свет в одних опытах обнаруживает волновые свойства, а в других – корпускулярные, означает, что он имеет сложную двойственную природу, которую принято характеризовать термином корпускулярно-волновой дуализм.

Квантовая природа света - основоположник - Макс Планк

Планк пришел к выводу, что процессы излучения и поглощения электромагнитной энергии нагретым телом происходят не непрерывно, как это принимала классическая физика, а конечными порциями – квантами. Квант – это минимальная порция энергии, излучаемой или поглощаемой телом. По теории Планка, энергия кванта E прямо пропорциональна частоте света:

где h – так называемая постоянная Планка. h = 6,626·10^–34 Дж·с.

Постоянная Планка – это универсальная константа, которая в квантовой физике играет ту же роль, что и скорость света в СТО.

1.        СВЕТ- видимое излучение. Электромагнитные волны, имеющие длину волны от 4_*10^-7до 8*10^-7 метра (Рисунок 1).

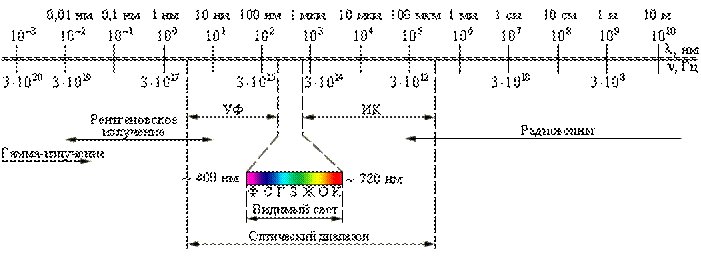Рисунок 1 – Шкала электромагнитных излучений

2.        Оптика - раздел физики изучающий световые явления.

3.        Световой пучок - узкий световой пучок, диаметр которого значительно больше длины волны

4.        Световой луч – линия, вдоль которой распространяется энергия световых электромагнитных волн.

Скорость света является фундаментальной, конечной, предельной величиной

Способы определения скорости света

1.                  прямой с=l/t косвенный (лазер) с=λν, В основе косвенного способа измерения скорости света лежит представление о свете как об электромагнитной волне и ее скорость находится путем умножения длины волны на частоту колебаний волны - астрономический (опыт Рёмера). Во времена Рёмера диаметр орбиты Земли считался равным примерно 182 000 000 миль (292 000 000 км). Разделив это расстояние на 1320 секунд, Рёмер получил, что скорость света равна 138 000 миль (222 000 км) в секунду. Теперь мы знаем, что максимальное запаздывание затмения спутника равно не 22 минутам, как думал Рёмер, а примерно 16 минутам 36 секундам, а диаметр орбиты Земли приближенно равен не 292 000 000 км, а 300 000 000 км. Если внести эти поправки в расчет Рёмера, получается, что скорость света равна 300 000 км/с.

2.                  лабораторный (метод Физо) - скорость света равна около 312 000 км в секунду.

Принцип суперпозиции

Наблюдения за распространением волн на поверхности воды показывают, что волны от двух или более источников проходят одна через другую, не влияя друг на друга. Не влияют друг на друга и звуковые волны. Когда оркестр играет, то звуки от скрипки не мешают распространяться звукам от трубы и барабана, звуки от каждого инструмента оркестра приходят к нам точно такими же, как от одного отдельно звучащего инструмента. Итак, распространение волн от одного источника не оказывает никакого влияния на распространение, какого угодно числа волн от любых других источников.

Принцип суперпозиции гласит:  В каждой точке, которой достигают волны от разных источников, амплитуда колебаний, вызванных действием нескольких волн, в любой момент времени равна векторной сумме амплитуд каждой волны в отдельности.

Интерференция волн

Если в волновой ванне на одном вибраторе укрепить два стержня, то они служат двумя точечными источниками волн с одинаковой частотой колебаний. Сложение этих волн приводит к появлению особой картины: на водной поверхности видны области, где колебания не происходят, и области с интенсивными колебаниями. Создается впечатление, что в некоторых местах волны от других источников при встрече как бы гасят друг друга, в других – усиливают (Рисунок 2).

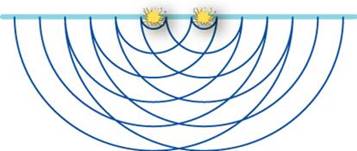
Рисунок 2 – Пример интерференции волн

Подобное явление можно обнаружить и в опытах со звуковыми волнами. Установим два громкоговорителя и подключим их к выходу одного звукового генератора. При перемещениях на небольшие расстояния в классной комнате можно обнаружить на слух, что в одних точках пространства звучание громкое, а в других – тихое. Опять результат таков, как будто звуковые волны от двух источников в одних точках пространства усиливают, а в других ослабляют друг друга.

При интерференции амплитуда результирующих колебаний в разных точках пространства имеет различные значения, а расположение в пространстве максимумов и минимумов с течением времени не изменяется.

Явление интерференции волн не противоречит принципу суперпозиции. В точках с нулевой амплитудой колебаний две встречные волны не гасят друг друга, обе они без изменений распространяются далее. Точно так же в точках с максимумами амплитуды волны не усиливают друг друга, после встречи волны распространяются независимо. Меняется лишь суммарная амплитуда в месте встречи этих волн.

Проблема когерентности волн. Повседневный опыт учит, что интерференцию света в действительности наблюдать не просто. Если в комнате горят две одинаковые лампочки, то в любой точке складываются интенсивности света и никакой интерференции не наблюдается. Возникает вопрос, в каких случаях нужно складывать напряженности (с учетом фазовых соотношений), в каких – интенсивности волн? Теория интерференции монохроматических волн не может дать ответа на этот вопрос.

Реальные световые волны не являются строго монохроматическими. В силу фундаментальных физических причин излучение всегда имеет статистический (или случайный) характер.

Интерференция может возникнуть только при сложении когерентных колебаний, т. е. колебаний, относящихся к одному и тому же цугу. Фаза волны, излучаемой реальным источником света, остается приблизительно постоянной только на интервалах времени порядка τ (τ ≤ 10^–8 с). Отдельные «обрывки» излучения длительности τ называются цугами. Цуги имеют пространственную длину, равную cτ, где c – скорость света.

Хотя фазы каждого из этих колебаний также подвержены случайным изменениям во времени, но эти изменения одинаковы, поэтому разность фаз когерентных колебаний остается постоянной. В этом случае наблюдается устойчивая интерференционная картина и, следовательно, выполняется принцип суперпозиции полей.

Таким образом, интерференция может возникнуть только при сложении когерентных колебаний. Волны, создающие в точке наблюдения когерентные колебания, также называются когерентными.

Волны от двух независимых источников некогерентны и не могут дать интерференции, для получения интерференции света нужно волну от источника разделить на две когерентные волны и затем наблюдать на экране результат их сложения. Так делается во всех интерференционных схемах. Однако, даже в этом случае интерференционная картина исчезает, если разность хода Δd превысит длину когерентности c_*τ.

Условие интерференционного минимума и максимума

Допустим, что имеются два когерентных источника волн S₁ и S₂ (Рисунок 3), которые возбуждают колебания в точке C, расположенной от источников на расстояниях d₁ и d₂ соответственно. Предположим, что источники S₁ и S₂ являются когерентными. Найдем результирующую амплитуду в точке C.

Амплитуда в точке C зависит от разности расстояния d₂ – d₁, которую называют разностью хода - Δd=d₂-d₁  

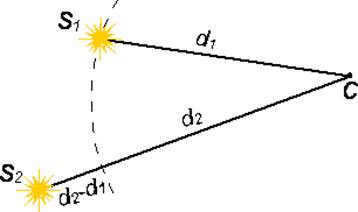
Рисунок 3 – Разность хода двух волн от когерентных источников света

Возможны три случая:

1.      Условие интерференционного максимума.

Если разность хода волн Δd=d₂ - d₁  равна четному числу полуволн (Рисунок 4):

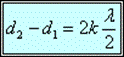
, где k – количество полуволн.

Данное выражение называется условие интерференционного максимума. В этом случае будет происходить увеличение результирующей амплитуды.

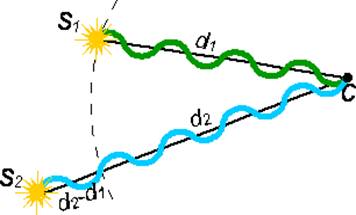
Рисунок 4 - Условие интерференционного максимума

2.      Условие интерференционного минимума.

Если разность хода волн Δd=d₂ - d₁ равна нечетному числу полуволн:

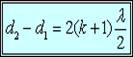
Данное выражение называется условие интерференционного минимума. В этом случае будет происходить уменьшение результирующей амплитуды (Рисунок 5).

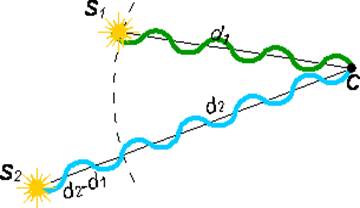
Рисунок 5 - Условие интерференционного минимума

3.      Если же разность хода волн рана не целому числу полуволн, то в этом случае может происходить как увеличение, так и уменьшение результирующей амплитуды.

Интерференция света.

Любуясь радужными цветами мыльных пленок или цветными пятнами масла на асфальте (Рисунок 6, а), мы, как правило, не задумываемся о причине этих явлений. Хотя с причиной – интерференцией – мы знакомы.

Уже отмечалось, что интерференция — одно из наиболее убедительных доказательств волновых свойств. Значит, если мы сможем осуществить интерференцию света, то докажем, что он обладает волновыми свойствами.

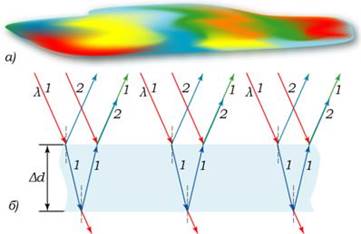
Рисунок 6 – Пример интерференции света

Цвета тонких пленок

Вернемся к выяснению причин возникновения радужных пятен па асфальте или радужных мыльных пленок. Белый свет падает на тонкую пленку (Рисунок 6, б). Частично свет отражается от верхней поверхности пленки, частично, пройдя через пленку, отражается от ее нижней поверхности. Обе отраженные волны (1' и 2') отличаются разностью хода. Естественно, что больший путь проходит волна, отраженная от нижней поверхности пленки, хотя разность хода невелика – немногим превышает удвоенную толщину пленки.

Белый свет не монохроматичен, он содержит электромагнитные волны разной длины — от 400 до 760 нм. Из-за того, что разность хода зависит от длины волны, максимумы интерференционной картины для разных длин волн получаются в разных точках приемника (например, на сетчатке глаза). Именно поэтому пленки имеют радужную окраску.

Явление дифракции

Волны способны огибать края препятствий. Когда размеры препятствий малы, волны огибая края препятствий, смыкаются за ними. Так, морские волны свободно огибают выступающие из воды камни (Рисунок 7), если его размеры меньше длины волны или сравнимы с ней. За камнем волны распространяются так, как если бы его не было совсем (маленькие камни). Точно так же волны от брошенного в пруд камня огибает торчащий из воды прутик. Только за препятствием большого по сравнению с длиной волны размера образуется «тень»: волны за него не проникают.

Рисунок 7 – Дифракция морских волн

            Способностью огибать препятствия обладают и звуковые волны. Вы можете услышать сигнал машины за углом дома, когда самой машины не видно, или если крикнуть в лесу, то звуковые волны будут огибать, в отличие от света, стволы деревьев.

            Дифракция световых волн – это явление отклонения от прямолинейного распространения волн, т.е. огибание волнами препятствий сравнимых с длинной волны.

Дифракция присуща любому волновому процессу в той же мере, как и интерференция. При дифракции происходит искривление волновых поверхностей у краев препятствий.

Дифракция волн проявляется особенно отчетливо в случаях, когда размеры препятствий меньше длины волны или сравнимы с ней.

Явление дифракции волн на поверхности воды можно наблюдать, если поставить на пути волн экран с узкой щелью, размеры которой меньше длины волны (Рисунок 8, а). Хорошо будет видно, что за экраном распространяется круговая волна, как если бы в отверстии экрана располагалось колеблющееся тело – источник волн. Если размеры щели велики по сравнению с длинной волны, то картина распространения волн за экраном совершенно иная (Рисунок 8, б). Волна проходит сквозь щель, почти не меняя своей формы.

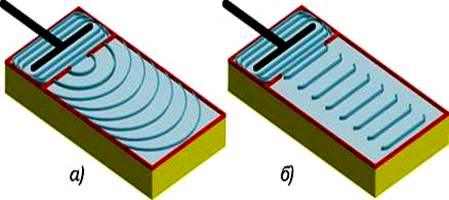
Рисунок 8 - Явление дифракции волн на поверхности воды

Принцип Гюйгенса – Френеля

Для более полного понимания протекания явления дифракции целесообразно познакомится с принципом Гюйгенса – Френеля, который гласит:

·                    каждая точка пространства, которой достигла в данный момент распространяющаяся волна, становится источником элементарных сферических волн.

·                    результат интерференции этих волн — огибающая элементарных сферических волн, образующая волновую поверхность.

Как Вам известно, принцип Гюйгенса утверждал, что каждая точка среды, до которой дошло возмущение, сама становится источником вторичных волн (Рисунок 9). Принцип Гюйгенса первоначально был сформулирован как геометрический прием для нахождения фронта волны. При чисто геометрическом подходе Гюйгенс не учитывал интерференцию вторичных волн. Позже, после изучения явления интерференции, принцип Гюйгенса был дополнен Френелем представлением об интерференции вторичных волн.

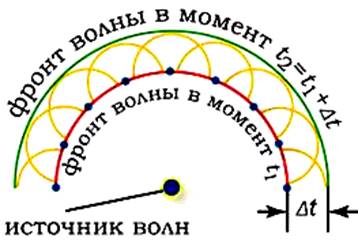
Рисунок 9 - Принцип Гюйгенса

Дифракция света

Поскольку длины волн света малы, дифракцию можно наблюдать только на значительном расстоянии от препятствия или отверстия. Пусть на пути лучей помещен маленький диск AB (Рисунок 10), а дифракция наблюдается на экране CD. В случае если диск находится на небольшом расстоянии d от экрана, мы можем наблюдать тень, чуть меньшую диаметра диска AB (Рисунок 10, а). Однако, когда расстояние от диска до экрана достаточно велико, то на экране получается дифракционная картина из чередующихся темных и светлых колец (Рисунок 10, б), а в центре экрана оказывается светлый кружок.

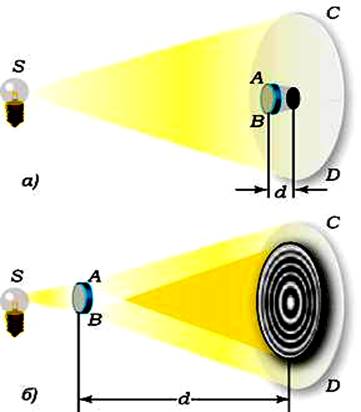
Рисунок 10 – Наблюдение дифракции света

            Для наблюдения дифракции от узкой щели проведет следующий опыт. На пути параллельных лучей света ставят непрозрачный экран с узкой щелью, а на некотором расстоянии от него помещают второй экран, на котором наблюдают дифракционную картину, показанную на Рисунке 11.  При этом против щели видна светлая полоса, ширина которой оказывается тем больше, чем уже щель, а за светлой полосой чередуются полосы радужной окраски.

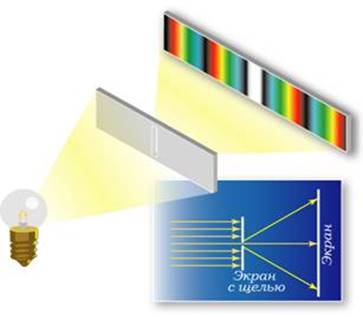
Рисунок 11 - Наблюдения дифракции от узкой щели

При освящении экрана со щелью монохроматическим светом на втором экране будут наблюдаться чередование светлых и темных полос.

Дифракционная решетка

Для наблюдения явления дифракции света используется специальный прибор, называемый дифракционной решеткой. Решетки представляют собой периодические структуры, выгравированные специальной делительной машиной на поверхности стеклянной или металлической пластинки (Рисунок 12). У хороших решеток параллельные друг другу штрихи имеют длину порядка 10 см, а на каждый миллиметр приходится до 2000 штрихов. При этом общая длина решетки достигает 10–15 см. Изготовление таких решеток требует применения самых высоких технологий. На практике применяются также и более грубые решетки с 50 – 100 штрихами на миллиметр, нанесенными на поверхность прозрачной пленки. В качестве дифракционной решетки может быть использован кусочек компакт-диска или даже осколок граммофонной пластинки.

Она представляет собой совокупность большого числа очень большого числа щелей, разделенных непрозрачными промежутками (Рисунок 12).

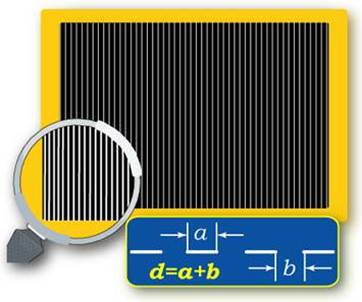
Рисунок 12 - Дифракционная решетка

Число непрозрачных промежутков доходит до нескольких тысяч на 1 мм. Если ширину прозрачного промежутка равно a, а ширина непрозрачного – b, то их сумма равна:

d=a+b

, где величина d называется периодом решетки.

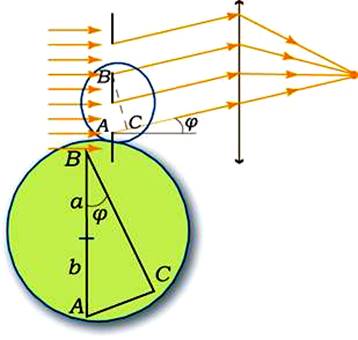
Рисунок 13 – Пример дифракции света

Рассмотрим пример, представим, что на решетку с периодом d падает монохроматическая волна длинной λ (Рисунок 13). Разность хода между щелей равна длине отрезка AC.  Если на этом отрезке укладывается целое число длин волн, то волны от всех щелей, складываясь, будут усиливать друг друга.

Из треугольника ABC можно найти длину катета AC:

Максимумы будут наблюдаться под углом φ, определяемым условием:

, где k – порядок максимума дифракционной решетки

Простейшую дифракционную решетку можно получить, если посмотреть, прищурившись, на яркий источник света. При этом мы наблюдаем радужные цвета. Белый свет разлагается в спектр при дифракции вокруг глаз.

А для наблюдения дифракции рентгеновских лучей необходимо использовать кристаллы. Вследствие малой длины волны препятствием сравнимым с ней могут быть только молекулы, находящиеся в узлах кристаллической решетки.

С помощью теории дифракции решают такие проблемы, как защита от шумов с помощью акустических экранов, распространение радиоволн над поверхностью Земли, работа оптических приборов (так как изображение, даваемое объективом, - всегда дифракционная картина), измерения качества поверхности, изучение строения вещества и многие другие.

На Рисунке 14 приведены спектры, полученные с помощью дифракционной решетки.

Рисунок 14 – Спектры различных источников

Дифракционные картины от различных препятствий

Из-за того, что длина световой волны очень мала, угол отклонения света от направления прямолинейного распространения невелик. Поэтому для отчетливого наблюдения дифракции нужно либо использовать очень маленькие препятствия, либо же располагать экран далеко от препятствий. При расстоянии между препятствием и экраном порядка метра размеры препятствии не должны превышать сотых долей миллиметра. Если же расстояние до экрана достигает сотен метров или нескольких километров, то дифракцию можно наблюдать на препятствиях размером в несколько сантиметров и даже метров.

На Рисунке 15 показано, как выглядят на фотографиях дифракционные картины от различных препятствий: а) от тонкой проволочки; б) от круглого отверстия; в) от круглого экрана.   

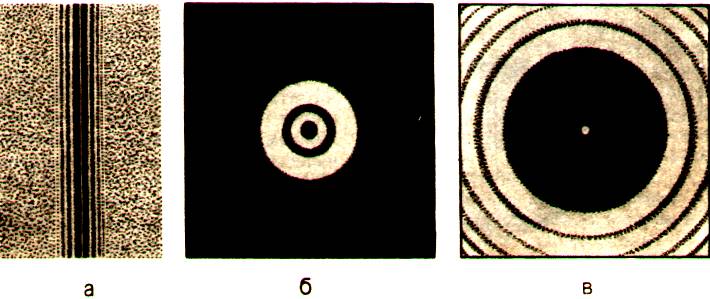
Рисунок 15 - Дифракционные картины от различных препятствий

Вместо тени от проволочки видна группа светлых и темных полос; в центре дифракционной картины от отверстия появляется темное пятно, окруженное светлыми и темными кольцами (изменяя диаметр отверстия, можно в центре дифракционной картины получить и светлое пятно, окруженное темными и светлыми кольцами); в центре тени, образованной круглым экраном, видно светлое пятнышко, а сама тень окружена темными концентрическими кольцами.

Границы применимости геометрической оптики

Дифракция налагает также предел на разрешающую способность телескопа. Вследствие дифракции волн у края оправы объектива изображением звезды будет не точка, а система светлых и темных колец. Если две звезды находятся на малом угловом расстоянии друг от друга, то эти кольца налагаются друг на друга и глаз не в состоянии различить, имеются ли две светящиеся точки или одна. Предельное угловое расстояние между светящимися точками, при которых их можно различать, определяется отношением длины волны к диаметру объектива.

 Этот пример показывает, что дифракция происходит всегда, на любых препятствиях. И при очень тонких наблюдениях ею нельзя пренебречь и для препятствий, по размеру значительно больших длины волны.

Дифракция света определяет границы применимости геометрической оптики. Огибание светом препятствий налагает предел на разрешающую способность важнейших оптических инструментов – телескопа и микроскопа.

Домашнее задание:

1. Прочесть Учебник «Физика 11 класс. 1 часть» с. 161-180

2. Составить опорный конспект из материала 50.docx

3. Создать презентацию по плану (приложен ниже) на тему, соответствующую вашему варианту ОБЪЕМОМ НЕ МЕНЕЕ 10 слайдов и прикрепить на портал

ПЛАН ПРЕЗЕНТАЦИИ:

1.      Название (Фото)

2.      Определение

3.      Описание установки

4.      Принцип работы (описание и иллюстрации)

5.      Применение

6.      *Особенности

ТЕМЫ Презентаций:

1. Интерференция света в природе
2. Применение интерференции в технике
3. Интерферометры
4. Проверка качества обработки поверхностей
5. Просветление оптики
6. Голография
7.  Голографическая интерферометрия
8. Голографический анализ вибраций
9. Объемные голографические изображения высокого качества
10. Голографические оптические элементы
11. Качество шлифовки поверхностей
12. Измерение углового размера источников излучения
13. Измерение показателя преломления веществ
14. Интерферометр Жамена
15. Интерферометр Майкельсон
16. Интерферометр Фабри—Перо
17. Интерферометр Рэлея
18. Интерферометр Маха—Цендера
19. Защита от шумов с помощью акустических экранов (дифракция)
20. Распространение радиоволн над поверхностью Земли (дифракция)
21. Работа оптических приборов (так как изображение, даваемое объективом, - всегда дифракционная картина)
22. Измерения качества поверхности (дифракция)
23. Изучение строения вещества (дифракция)
24. Дифракция рентгеновских лучей
25. Определение длины волны с помощью дифракционной решетки
26. Практическое применение дифракционной решетки в спектроскопии


27. Скачано с www.znanio.ru