Добавить материал

и получить 10 документов
и свидетельство автора

Ковалева Марина Ивановна

Электронная книга "Олимпиада по математике" 3 класс

pdf
20.05.2021

Публикация педагогических разработок

Бесплатное участие. Свидетельство автора сразу.
Мгновенные 10 документов в портфолио.

Добавить материал

Олимпиада по математике 3 класс.pdf

Х. О. Орту Н. Г. Белицкая ОЛИМПИАДЫ

математи з

класс

Издание восьмое, переработанное и Дополненное

Издательство

«ЭКЗАМЕН»

МОСКВА

2016

УДКЗ7З:5ЦО75.2) ББК 22.1я71 о 64

Орг А. О.

064 Олимпиады по математике. 3 класс. ФГОС / А. О. Орг, Н. Г. Белицкая. 8-е изд., перераб. и доп. — М. : Издательство «Экзамен», 2016. 94, [2] с.

ISBN 978-5-377-10678-4

Данное пособие полностью соответствует федеральному государственному образовательному стандарту (второго поколения) для начальной школы.

Олимпиады по математике содержат варианты заданий для проведения школьных туров. В книге собраны занимательные и нестандартные задания, соответствующие возрастным особенностям детей и требованиям учебной программы.

Данные материалы призваны привить любовь к предмету, сформировать умение самостоятельно добывать знания, научить логически мыслить, а также помочь учителю в организации внеурочной деятельности по предмету.

Приказом № 729 Министерства образования и науки Российской Федерации учебные пособия издательства «Экзамен» допущены к использованию в общеобразовательных организациях.

удк

ББК 22.1я71

Подписано в печать 26.02.2016. Формат 70х100/16. Гарнитура «TextBookC». Бумага офсетная.

Уч.-изд. л. 1,8. Усл. печ. л. 7,8.

Тираж 6 ООО экз. Заказ № 7132/16.

ISBN 978-5477-10678-4 © Орг А. О., Белицкая Н. Г., 2016

СОДЕРЖАНИЕ

Предисловие

Вариант	1
Вариант Вариант Вариант	2 з 4		11
Вариант	5		17
Вариант	6		19
Вариант	7		21
Вариант Вариант	8 9		23
Вариант	10		27
Вариант	11		29
Вариант	12	• • • • •	31
Вариант	13		33
Вариант	14		35
Вариант	15	• • • •
Вариант	16		39
Вариант	17		41
Вариант	18		43
Вариант	19		45

Вариант	20	47
Вариант	21	49
Вариант	22	51
Вариант	23	53
Вариант	24	55
Вариант	25
Вариант	26 • • •	59
Вариант	27	61
Вариант	28	63
Вариант	29 • •	65
Вариант	зо • •
Вариант	31 • • • а • • •	69
Вариант	32	71
Вариант	33	73
Вариант	34	75
Вариант	35 в • • •	77
Ответы		79

ПРЕДИСЛОВИЕ

Внеклассная работа по предметам, изучаемым в ШКОле первой ступени образования, является неотъемлемой частью учебно-воспитательного процесса и представляет собой обязательный элемент нормально организованной работы школы.

Окружающая действительность, с которой ребёнок постоянно контактирует, вызывает у него интерес (СГЕЦИфическую направленность личности), формируемый в зависимости от склонностей учащихся. Чем разнообразнее вопросы, над которыми приходится размышлять ребёнку, тем устойчивее его познавательный интерес.

Основная форма обучения в школе — урок. Но в настоящее время актуальным стало проведение внеклассных занятий, внеурочных мероприятий, призванных систематизировать и углублять знания, развивать умения, совершенствовать навыки. Одной из форм внеклассной работы, способствующей формированию познавательного интереса, является предметная олимпиада, помогающая выявить не только уровень обученности учащихся, но и их начитанность, кругозор, общий культурный уровень.

Привить любовь к предмету, научить самостоятельно добывать знания, логически и нестандартно мыслить — это основная задача творчески работающего учителя, реализующаяся посредством внеурочной деятельности по предмету, примером которой может служить олимпиада.

Олимпиада — это и соревнование, и праздник одновременно, Ученики начальной школы — благодарные слушатели и активные участники учебного процесса; они с энтузиазмом принимают участие в различных мероприятиях, в том числе и в предметных олимпиадах.

По времени олимпиада, проводимая в начальных классах, не должна занимать более одного урока (40-45 минут). При проведении олимпиады необходимо создать для учащихся комфортную атмосферу: чётко организовать работу, проследить за тем, чтобы задания были сформулированы понятным языком (с учётом возрастных психологических особенностей детей). Необходимо обязательно предупредить участников олимпиады, что они вправе выполнять задания не по порядку, а в удобной для них последовательности. Если учитель раздаёт готовые варианты, куда участникам олимпиады необходимо вписать ответы, рекомендуется предложить школьникам листы для черновых записей.

Данное пособие содержит варианты заданий для проведения школьного тура олимпиады по математике. Сборник состоит из занимательных и нестандартных заданий, которые подобраны в соответствии с возрастными особенностями школьников, требованиями учебной программы и ОГОС ноо.

Как оценивать задания

Критерии оценивания зависят от сложности конкретных заданий. Данные олимпиады предлагается оценивать, используя максимально гибкую систему. В каждом варианте 10 заданий.

Подведение итогов не следует откладывать на длительное время. Методическим комиссиям необходимо провести анализ допущенных ошибок. Победители и призёры поощряются на уроке или на занятии предметного кружка, объединения.

1. Запиши два числа, произведение и частное которых равно 24.

2. Мама купила 100 г перца, 2 кг сыра, 1 кг 500 г масла, 600 г конфет. Сколько муки должна купить мама, чтобы общий вес продуктов равнялся 5 кг?

З. Вставь знаки и однозначные числа так, чтобы получились верные равенства.

16 + + 16 +

9 + 9 + 9 + 9 + 9 + 9 + 19 = 9

4. Определи массу лисы, белочки и обезьянки, если известно: масса зайца 3 кг; масса двух одинаковых зайцев на 1 кг меньше массы лисы; масса двух обезьян равна массе одного зайца и одной лисы; масса обезьяны на 1 кг больше массы одного зайца и одной белочки.

6. Девочка занимается теннисом 2 раза в неделю. Какие два дня может выбрать девочка для тренировок, если в понедельник и в воскресенье нет занятий? Опиши все возможные варианты.

7. Укажи ряд чисел, расположенных в порядке убывания.

а) 728, 725, 672, 214, 518, 424, 365, 275 6) 935, 928, 876, 729, 627, 604, 546, 324

в) 357, 507, 613, 784, 838, 864, 905, 989

8. Бабушка сплела кружево длиной 84 см. Она решила обшить этим кружевом платок квадратной формы. Какого размера платок (сторона квадрата) она может обшить кружевом, если на каждый уголок нужно добавить по 1 см?

1. На стоянке стоят 10 легковых и грузовых автомобилей. У легкового 4 колеса, у грузового 6 колёс, а всего у этих автомобилей 46 колёс. Сколько каких автомобилей на стоянке?

2. У девочки день рождения то ли 10, то ли 11, то ли 12, то ли 13 октября. Как узнать день рождения девочки, задав только два вопроса, если в ответ она будет говорить только «да» или «нет»?

З. Первая обезьяна съела 8 бананов, вторая третья 6, а четвёртая 9. Сколько бананов съели две обезьяны?

4. Сумма чисел, обозначающих номера трёх соседних домов на одной стороне улицы, равна 21. Запиши номера этих домов.

5. Поставь знаки действия и скобки так, чтобы получилось верное равенство.

а) 8 8 8 8 8 8

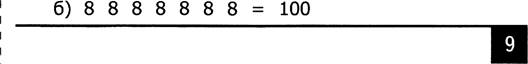6) 8 8 8 8 8 8 8 - 100

6. Пудель на 2 кг тяжелее таксы и на 9 кг легче овчарки. На сколько килограммов такса легче, чем овчарка?

7. Начерти З прямые так, чтобы на каждой прямой было отмечено по З точки, а всего было отмече-

но 6 точек.

8. Укажи числа, которые и на З.

а) 38 6) 42

д) 18 е) 54

9. Миша, Сергей, Юра, очереди за билетами делятся одновременно на 6

в) 9 27

ж) 63 з) 66

Даня и Кирилл стояли в в кинотеатре. Кто за кем

1. Количество богатырей в сказке АС. Пушкина «Сказка о мёртвой царевне...» раздели на порядковый номер средней ступеньки у лестницы в 15 ступенек. Запиши ответ.

2. Найди принцип, по которому расставлены числа, и вставь пропущенные числа.


11	21		41	51

З. Мальчик начертил на отдельных листочках З треугольника и 2 четырёхугольника. Сколько отрезков ему пришлось начертить?

4. Около магазина стоят 10 мотоциклов и двухколёсные велосипеды. Всего у них 30 колёс. Сколько на стоянке велосипедов? Укажи правильный ответ.

5. Вставь такую цифру, чтобы неравенство стало

верным.

а) 275 < 229 б) 251 >

в) 000 > 800 г) 801 < 832

6. Какими будут номера трёх соседних домов, если их сумма равна 42?

7. Матвей, Виктор, Борис и Илья на уроке труда смастерили кораблики: зелёные, синие, красные и жёлтые. Каждый складывал кораблики только одного цвета. Кораблики Ильи и Матвея не красные. Борис и Илья не захотели мастерить синие, Матвей не делал ни синие, ни жёлтые. Кто из мальчиков какие кораблики смастерил?

8. Число километров, которые проехала машина, равно числу минут, которые она была в пути. Сколько километров проезжала машина за 1 ч?

5 брёвен одинаковой толщины длиной по 4 м надо распилить так, чтобы получилось 20 брёвен длиной по 1 м. Один распил занимает 1 мин. Сколько времени потребуется на эту работу? Укажи верный ответ.

а) 20 мин б) 15 мин в) 10 мин

10. В четырёхугольнике проведи один отрезок так, чтобы получился 1 треугольник и 1 пятиугольник.

1. Раскрась кружочки в жёлтый, красный, синий и зелёный цвета в соответствии с подписями. (Цвета не должны повторяться.)

не ЖёЛТЫ Й

не ЗеЛёНЫЙ, не жёлтый

не красный, не зелёный

не синий, не ЗеЛёНЫЙ,

2. Расставь знаки -е, и скобки так, чтобы получились верные равенства.

а) 9 8 7 6 5 4 3 2 1 _ 45 6) 9 8 7 6 5 4 3 2 1 70

З. Три брата купили 9 тетрадей и распределили их таким образом: младший получил на 1 тетрадь меньше, чем средний, а старший на 1 тетрадь больше, чем средний. Сколько тетрадей получил средний брат?

4. Купили печенье круглой и квадратной формы. Сколько весит отдельно 1 печенье круглой формы и 1 печенье квадратной формы, если 2 квадратных печенья и 1 круглое весят вместе 80 г, а 1 круглое и 1 квадратное 50 г?

5. Какое число получится, если количество точек, которые надо взять на прямой, чтобы получить 5 равных отрезков, разделить на наименьшее количество линий, которыми можно разделить квадрат на 4 равные части?

1. Сколькими способами Винни-Пух может сделать подарки друзьям Пятачку, Тигре и ослику Иа-Иа, если он хочет одному из них подарить баночку с вареньем, а двум другим по баночке с мёдом? Укажи правильный ответ.

2. Укажи номера чисел, которые одновременно делятся на 6 и на З.

а) 38 6) 42 ^г) 27

д) 54 е) 63 ж) 66 з) 18

З. Количество углов многоугольника умножили на 19 и получили 171. О каком многоугольнике идёт речь? Запиши ответ.

4. Нарисуй З одинаковых квадрата таким образом, чтобы получилось 7 квадратов.

5. Какое число на циферблате часов расположено напротив числа 5? Запиши ответ.

6. Вставь такую цифру, чтобы неравенство было вер-

НЫМ.

а) > 329; 6) > 420

в) < 934 г) 501 > 549

7. Укажи самый тяжёлый и самый лёгкий фрукт, если известно, что груша тяжелее яблока, но легче апельсина; яблоко тяжелее персика, а апельсин легче ананаса.

8. У Виктора 10 марок, а у Николая столько же марок, сколько у Виктора, и ещё половина всех его марок. Сколько марок у Николая?

9. Сколько ёлочек потребуется для посадки вдоль забора, длина которого 12 м, если расстояние между саженцами будет равно З м? Укажи верный ответ.

10. Расставь в выражениях скобки так, чтобы равенства были верными.

9	12	з	2	- 23
9	12			75
9	12	З	2	47
9	12	з		— 77

1. Соедини пары выражений, в которых значение одного в З раза больше значения другого.

12 : 4

42 2

Крышка стола имеет четыре угла. Как, отпилив 1 угол, получить треугольную, пятиугольную и четырёхугольную крышки? Ответ начерти.

З. Миша, Коля, Вера, Надя и Толя должны спуститься с горы на санках. Запиши, в каком порядке дети могут спуститься с горы, если Толя поедет первым, а за ним поедут Миша и Коля.

6. Максим шёл по дороге и нашёл монету в 5 р. Сколько бы рублей нашли 2 его друга, если бы шли по той же дороге?

7. Все ли из приведённых утверждений верны? Укажи правильный ответ.

а) Сумма трёх нечётных чисел есть число чёт-

ное.

б) Единица измерения углов — градус.

в) У трёх кошек 12 лап, З хвоста и 8 ушей.

1. Расставь фигуры так, чтобы в каждой строке и в каждом столбце не было одинаковых фигур.

оодшпдопд

2. Расставь знаки арифметических действий так, чтобы равенства были верными.

а) 5 5 5 5 16

6. У девочки 2 вида ручек и 4 вида карандашей. Сколько различных комплектов, состоящих из одного вида ручки и одного вида карандаша, можно из них составить?

7. Найди закономерность, запиши в каждом столбике следующее уравнение.

17 х - 10 13 34 — х — 31

19 х - 8 15 36 — х 33

21 х - 6 17 38 - х 35

1. Расставь знаки арифметических действий и скобки так, чтобы равенство было верным.

5 4 0 6 7 - 63

2. Дорисуй фигуру, соблюдая закономерность.

З. Все ли утверждения верны? Укажи правильный ответ.

	21

а) Все числа, кратные четырём, делятся на 2.

б) У куба шесть граней.

в) Окружность это замкнутая кривая, все точки которой одинаково удалены от одной точки.

1) да 2) нет

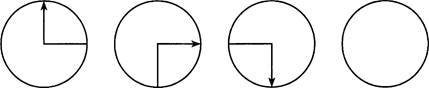
4. Сколько прошло времени, если минутная стрелка повернулась на прямой угол?

5. Запиши, как трём туристам переправиться на другой берег реки в одной лодке, если лодка вмещает только двух человек.

6. От 5 чемоданов перепутали ключи. Какое наибольшее число проб понадобится, чтобы подобрать к каждому чемодану свой ключ? Запиши

1. Сумма однозначного, двузначного и трёхзначного чисел, записанных одной и той же цифрой, представляет собой трёхзначное число, последняя цифра которого такая же, как и в записи данных чисел. Запиши данные числа и их сумму.

2. Расставь знаки арифметических действий так, чтобы получились верные равенства.

а) 40 20 2001000 6) 60 20 2001000 в) 60 зо 8001000

З. Какова масса курицы, если рядом с ней на чаше весов стоят гири массой в 1 кг и 500 г, а на другой чаше 2 гири по 2 кг каждая?

4. Как можно разместить на скамейке Настю, Таню, Мишу и Серёжу, чтобы мальчики и девочки чередовались? Запиши возможные варианты.

5. У Миши есть песочные часы двух видов. Часы одного вида отмеряют З мин, а другого вида 7 мин. Как Мише с их помощью отмерить ровно

6. Периметр прямоугольника 32 м. Какую наибольшую площадь может иметь прямоугольник?

7. Все ли утверждения верны? Укажи верный ответ.

а) Если сложить трио и дуэт, получится октет.

б) Римская цифра, обозначающая одиннадцать, состоит из трёх палочек.

в) У прямоугольника четыре стороны.

1) да 2) нет

8. Посчитай и запиши количество групп из трёх последовательно расположенных чисел, которые дают в сумме 15.

9. 60 мандаринов разложили в З пакета: в первый положили на 5 мандаринов больше, чем во второй, а во второй на 10 мандаринов меньше, чем в третий. Сколько мандаринов в каждом пакете?

10. Проведи в четырёхугольниках по одному отрезку так, чтобы получилось:

1) 2 разносторонних треугольника

2) 2 равнобедренных треугольника

1. Используя не более двух знаков действия и, если надо, скобки, составь верные равенства.

а) 8 8 8 8 8 8

6) 8 8 8 8 8 8 - 100

2. Какая занавеска шире и на сколько сантиметров, если к тюлевой занавеске пришили 8 колец на расстоянии 12 см одно от другого, а к гобеленовой 17 колец на расстоянии 5 см?

а) тюлевая б) гобеленовая

З. Будет ли значение выражения а — В чётным числом, если известно, что значение выражения а + В чётное ЧИСЛ о

а) да б) нет

4. Для участия в концерте нужны двое ведущих (мальчик и девочка). На роль ведущих претендуют Миша, Коля, Сергей, Надя, Рита, Лена и Вера. Запиши все возможные варианты пар ведущих.

5. Расположи точку так, чтобы она находилась внутри окружности и внутри треугольника. Сделай чертёж. Предложи разные варианты решения.

8.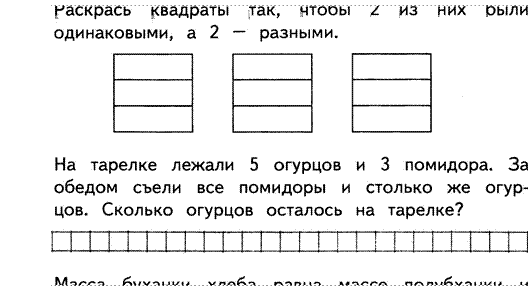 Масса буханки хлеба равна массе полубханки и ещё полкилограмма. Какова масса целой буханки?

Если сейчас на часах без десяти минут три, то сколько будет времени, когда минутная стрелка повернётся на прямой угол?

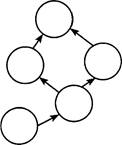10. Расставь любые числа в кружочки так, чтобы соблюдалось правило: стрелка направлена всегда от кружка с большим числом к кружку с меньшим.

1 1

1. Сколько здесь групп из трёх последовательных чисел, которые дают в сумме 10?

3 2 4 6 9 1 7 2 5 3 4 1 6 4 2 4

Расставь любые числа в кружочки так, чтобы соблюдалось правило: стрелка направлена всегда от кружка с большим числом к кружку с меньшим.

З. Расположи 4 равных равнобедренных прямоугольных треугольника таким образом, чтобы образовались восемь равнобедренных прямоугольных треугольников и квадрат. Сделай чертёж.

Один из двух множителей равен 12. Как изменится произведение, если второй множитель увели чить на 5?

8. Мальчик решил в каникулы навестить бабушку, своего друга Петю и старшего брата Сергея. Запиши все возможные варианты последовательности данных визитов.

1. Все ли утверждения верны? Укажи правильный ответ.

1) Числа З, 6, 9, 12 — кратные 3.

2) Двузначных чисел всего 100,

3) При делении числа на 0 получается 0.

а) да б) нет

2. Расставь скобки так, чтобы равенства были верными.

а) 75 15 + 17 20

• 9 + 12 : 3 - 2 23

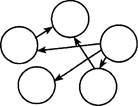
З. Расставь любые числа в кружочки так, чтобы соблюдалось правило: стрелка направлена всегда от кружка с большим числом к кружку с меньшим.

4. Выбери признак и разбей числа на две группы:

23, 61, 14, 25, 32, 50, 16, 52

5. Запиши сумму, используя только три числа:

12 + 4 + 12 + 5 + 12 12 + 7 + 12 + 8

шения их значений.

2 • 19; 19 • 4; 19 • 7; 8 • 19; 19 • 5; 10 19;

19 • з; 19 • 9; 19 • 6

1. У девочки есть книги сказок А. Пушкина, Г. Ан дерсена, братьев Гримм и К. Чуковского. На урок внеклассного чтения она взяла книги двух авторов. Книги каких авторов могла взять на урок девочка? Укажи все возможные варианты.

2. Начерти все возможные отрезки, если точки А, В, С, Д являются их концами.

д,

З. Все ли утверждения верны?

а) Если уменьшаемое и вычитаемое чётные числа, то и разность будет чётным числом.

б) Если уменьшаемое и вычитаемое нечёт— ные числа, то и разность будет нечётным

числом.

в) Если уменьшаемое и вычитаемое равные числа, то разность будет равна О.

1) да 2) нет

4. Составь и запиши все возможные равенства из чисел 400, 50, 8.

5. Вдоль участка, сумма длин сторон которого рав- на 20 м, расставили колышки на расстоянии 5 м было первона-

Если провести стеклом по мрамору, на мраморе останется след. Если провести алмазом по стеклу, царапина останется на стекле. Что самое твёрдое? Укажи верный ответ.

а) стекло б) алмаз в) мрамор

2. Вставь пропущенные цифры, реши примеры.

а) 397 + =

б) 156 + 344 =

в) 470 - = 041

З. Портной ежедневно отрезает по 2 м от куска сукна длиной 16 м. На какой день портной отрежет последний кусок?

4. Миша, Коля, Вера, Надя и Толя должны спуститься с горы на санках. В каком порядке дети могут спуститься с горы, если Толя поедет первым, а за ним поедут Вера и Надя? Укажи все возможные варианты.

5. Запиши сумму произведений, используя только два числа.

6 • 2, 6 • з, 6 , 4, 6 • 5, 6 • 6, 6 • 7

6. В каждой записи поставь, где надо, знак чтобы равенства стали верными.

а) 1 2 3 4 5 6 7 - 100

6) 9 8 7 6 5 4 3 2 1 - 90

7. Трое ребят собирали грибы. Каждый из них шёл разное нечётное количество белых грибов. Игорь и Олег вместе нашли 8 грибов, а Олег и Саша 6. Сколько грибов нашёл Игорь, если известно, что у него грибов больше всех?

8. Расставь любые числа в кружочки так, чтобы соблюдалось правило: стрелка направлена всегда от кружка с большим числом к кружку с меньшим.

30 кубиков уложили в З коробки: одну большую и две маленькие. В большую коробку положили на 9 кубиков больше, чем в каждую маленькую. Сколько кубиков в большой коробке?

скобки в выражениях так, чтобы равенства были верными.

8 + 12

8 + 12 74

8 + 12 23

. 8 + 12 47

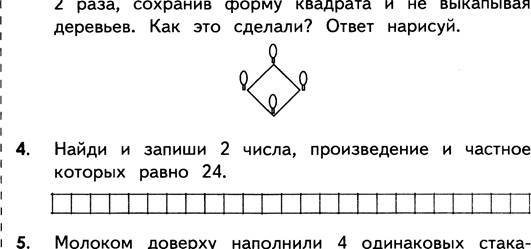По углам пруда, имеющего форму квадрата, растут 4 дерева. Площадь этого пруда увеличили в 2 раза, сохранив форму квадрата и не выкапывая деревьев. Как это сделали? Ответ нарисуй.

Молоком доверху наполнили 4 одинаковых стакана. Во всех стаканах столько молока, сколько в банке. В стакане и в банке 1 кг 200 г молока. Сколько граммов молока в стакане?

1. Сколько здесь групп из трёх последовательных чисел, которые в сумме дают 12?

2. В шахматном турнире участвовали 7 человек. Каждый с каждым сыграл по одной партии. Сколько всего партий они сыграли? Укажи верный ответ.

6) 14 в) 21 г) 28

З. На одной чаше весов находятся 2 одинаковые банки с вареньем и гиря в 5 кг, а на другой чаше весов З такие же банки с вареньем и З гири по 1 кг. Какова масса банки с вареньем, если весы находятся в равновесии?

4. Доктор Пилюлькин прописал Незнайке принимать по 1 ложке лекарства через каждые 20 мин. На какое время хватит Незнайке лекарства, если в пузырьке его ровно на З приёма?

5. Из куска проволоки согнули квадрат, площадь которого 81 см ². Затем проволоку разогнули и из неё согнули треугольник с равными сторонами. Какова длина стороны треугольника?

6. Составь из цифр 2, 5, 9 все возможные трёх- числе не долж-

8. В класс пришли 4 новых ученика:

Саша и Петя. Сколькими способами учитель сможет рассадить детей за две свободные

1. Поставь знаки арифметических действий так, ЧТО— бы равенства были верными.

а) 30 20 40

6) ш 30 п 1000

2. Как пожарить 6 котлет за 15 мин, если на сковороде помещается только 4 котлеты и каждую котлету нужно жарить по 5 мин с каждой стороны?

З. В прямоугольник длиной 8 см и шириной 6 см вписали другой прямоугольник, стороны которого на 1 см отстоят от сторон первого прямоугольника. На сколько сантиметров периметр одного прямоугольника больше другого?

4. Все ли утверждения верны? Укажи верный ответ.

1) Периметр сумма длин сторон многоугольника.

2) Вычитаемое компонент действия деления. 3) Центнер единица массы.

а) да б) нет

5. Проведи З отрезка так, чтобы стало 15 треугольников.

6. Прилетели галки, сели на палки. Если на каждой палке сядет по одной галке, то для одной галки не хватит палки. Если же на каждой палке сядут по две галки, то одна палка останется без галок. Сколько было галок и сколько палок?

7. Расшифруй комбинацию кодового замка, если:

1) третья цифра на З больше, чем первая;

2) вторая цифра на 2 больше, чем четвёртая;

З) в сумме все цифры дают число 17;

4) вторая цифра З

8. Какое число получится, если количество двузначных чисел с нулём на конце умножить на однозначное число, которое побуждает к действию?

9. Представь 20 в виде суммы двух слагаемых так, что если к первому прибавить 4, а от второго отнять 4, то оба слагаемых будут равными.

10. Четырёх мальчиков зовут Дима, Иван, Антон и Валерий. Распредели имена мальчиков в соответствии с их ростом (в порядке возрастания), если известно, что Иван не самый высокий, но всё же он выше Димы и Валерия, а Дима выше Валерия.

1. Представь данные числа в виде произведения трёх одинаковых множителеи.

б) 27

в) 64

2. Все ли утверждения верны? Укажи правильный ответ.

1) При умножении двух нечётных чисел в произведении получится нечётное число.

2) Квадрат это фигура, у которой все стороны равны.

3) Сумму одинаковых слагаемых можно заменить умножением.

а) да б) нет

З. Что тяжелее: яблоко или груша, если на одной чаше весов 2 одинаковые сливы и груша, а на дру гой яблоко и слива с такой же массой? Весы находятся в равновесии. Укажи верный ответ.

а) груша б) яблоко

4. Используя знаки арифметических действий, восстанови равенства.

а) 11

б) 28

в) 20 24

5. Начерти квадрат и треугольник, поставь внутри данных фигур 4 точки так, чтобы в квадрате оказалось З точки, а в треугольнике 2 точки.

6. Укажи ряд чисел, растания.

а) 728, 729, 772, 6) 935, 928, 876, в) 357, 503, 615,

расположенных в порядке воз-

814, 818, 824, 965, 907

732, 691, 603, 548, 321

789, 845, 867, 905, 991

7. Из Москвы в Вологду был послан человек, лено ему было в хождении своём совершать по 40 вёрст всякий день. На следующий день вслед ему был послан второй человек и приказано ему было проходить по 45 вёрст в день. На какой день второй человек догонит первого?

8. Расшифруй и запиши пример на сложение трёх двузначных чисел (буква А обозначает одну цифру). 1А + И + ЗА = ЕЕЕГЕЕЕШ:ЕШЗ

9. Запиши решение задачи математическим выражением.

Гуляли по аллейке куриные семейки.

У каждой мамы-квочки три сына и две дочки. Сколько всех цыплят, мы спросим, Если квочек ровно восемь?

10. Сорок дынь разложили на З полки сначала так, что на нижней полке дынь было столько, сколько на двух других. Затем З дыни с верхней полки переложили на среднюю, и на этих двух полках дынь стало поровну. Сколько дынь было на каждой полке сначала?

1. В маленькой клетке было на З кролика меньше, чем в большой. Сколько кроликов было в малень кой клетке, если в большой их было в 2 раза больше, чем в маленькой?

6. Верблюд, проживший неделю без воды, выпивает за несколько минут 100 л. На сколько дней хватит этого количества воды человеку, чья суточная норма потребления два с половиной литра?

7. Расставь математические знаки (можно использовать и скобки) так, чтобы равенства были верными.

2 в) 14

9. Все ли утверждения верны? Укажи правильный ответ.

1) Чтобы найти уменьшаемое, надо к разности прибавить вычитаемое.

2) Произведение длины и ширины прямоуголь- ника это его площадь.

З) Единицы первого разряда называются единицами.

а) да б) нет

10. Какая из перечисленных стран самая большая по численности населения, если в Китае людей живёт больше, чем в Индии, а в Индии больше, чем в России?

а) Китай б) Индия в) Россия

1. Какая страна из перечисленных самая большая по площади, если Китай занимает больше места на Земле, чем Индия, но меньше, чем Россия?

а) Китай б) Индия в) Россия

2. Какова масса гуся, если на одной чаше весов гиря в 5 кг, а на другой гусь и гиря в 1 кг? Весы находятся в равновесии.

З. Вдоль границы квадратного участка со стороной 5 м надо расставить столбы на расстоянии

1 м друг от друга так, чтобы с каждой стороны

участка было по 6 столбов. Сколько для этого потребуется столбов?

4. Один термометр показывает —5 ^ос. Сколько градусов мороза покажут 2 термометра?

а) 5 градусов б) 10 градусов в) О градусов

5. Запиши решение задачи математическим выраже-

К двум зайчатам в час обеда Прискакали три соседа.

В огороде зайцы сели

И по семь морковок съели. Кто считать, ребята, ловок, Сколько съедено морковок?

8. Мальчик до реки шёл пешком, а обратно ехал на велосипеде. На весь путь он затратил 40 мин. В следующий раз он ехал до реки и обратно на велосипеде и затратил всего 20 мин. Сколько времени понадобится мальчику, чтобы проделать путь в оба конца пешком?

9. На столе было 12 книг. Сколько книг убрали со стола, если их осталось в З раза меньше, чем было? Укажи правильный ответ.

в) 10

10. Поставь знаки действий и, если надо, скобки, чтобы равенства были верными.

а) 5 5 5 5 - 50 6

в) 5 5 5 5

1. По периметру участка земли прямоугольной формы длиной 10 м и шириной 4 м натянули проволоку. Через каждые 2 м вбили колышки. Сколько колышков вбили, чтобы огородить этот участок?

Раздели квадрат на равные части так, чтобы из полученных частей можно было сложить два равных квадрата. Линии разреза укажи на чертеже.

Реши задачу, составив математическое выражение.

Модница сороконожка стала примерять сапожки:

Чёрных 8 пар надела и 4 пары белых.

Сколько остаётся ножек для коричневых сапожек?

5. Как-то в 1997 г. у девочки спросили: «Когда ты родилась?» «Позавчера мне было ещё 9 лет, а в будущем году мне уже исполнится 12», ответила девочка. Запиши дату рождения девочки и дату, когда ей был задан вопрос.

6. Вставь пропущенный множитель.

• 2 - 8 _ 55

• 25 56

7. Чему равна половина третьей части числа 12? Запиши число.

8. На календаре 2009 год. Сумма цифр этого числа равна 11. Через сколько лет повторится такая же сумма цифр?

9. У клоуна 4 берета: красный, чёрный, жёлтый, зелёный и З рубашки: клетчатая, полосатая, в горошек. Сколько вариантов выбора комплекта «берет рубашка» может получиться?

10. Все ли утверждения верны? Укажи правильный ответ.

1) Отрезок это часть прямой, ограниченная двумя точками.

2) У треугольника вершин, как и сторон, три.

З) Отрезок, соединяющий любую точку на окружности с её центром, называется диаметром.

а) да б) нет

1. Все ли утверждения верны? Укажи правильный ответ.

1) Действие, результат которого называют частным, называется делением.

2) Если одно число не делится нацело на другое, то получится остаток.

3) Числа, которые делятся на 2 без остатка, называются чётными.

а) да б) нет

2. Начерти все возможные отрезки, для обозначения которых надо использовать буквы А, В, С, D так, чтобы среди них не было отрезков, обозначенных одинаковыми буквами.

З. Два туриста вышли навстречу друг другу из двух населённых пунктов. Первый за 1 час проходил 5 км. Второй вышел на 2 ч позже первого и за 1 час проходил 6 км. Сколько времени до встре чи шёл второй турист, если расстояние между пунктами 43 км?

4. Ученики класса построились в колонну по одному. Сзади Светы стоят 16 детей, включая Иру, а перед Ирой стоят 14 детей. Сколько ребят в классе, если между Светой и Ирой стоят 7 детей?

стало верным.

8 + 20 : 4 - 2 - 76

это число

При этом сделали пять разрезов. Какой длины получилась каждая часть?

одного грейпфрута. Масса яблока и грейпфрута 750 г. Какова масса яблока?

число десятка меньше предыдущего.

а) 110, 140, 170, 180, 6) 930, 910, 900, 880, в) 232, 902, 872, 842,

г) 232, 252, 272, 292,

д) 211, 241, 271, 301,

е) 824, 804, 784, 764,

выражения и

Запиши ещё 2 выражения. Вычисли.

а) 36 6) 32

в) 28 4 - 5 - 2

1. Среди 9 монет достоинством 1 к. одна монета тяжелее каждой из 8 остальных. Как найти её двумя взвешиваниями на чашечных весах, не используя никаких гирь?

2. Сколько здесь групп из трёх последовательных чисел, которые в сумме дают 19?

З. С помощью цифр З, 5, 7 запиши все возможные двузначные числа (цифры в записи чисел не повторяются) в порядке возрастания.

4. Поросята Ниф-Ниф, Нуф-Нуф и Наф-Наф надели куртки жёлтого, сиреневого и оранжевого цветов и такого же цвета шапки. Ниф-Ниф надел куртку и шапку одного цвета. Нуф-Нуф не носит одежду жёлтого цвета, а Наф-Наф надел сиреневую шапку и куртку другого цвета. Как одеты поросята?

8. Вставь числа так, чтобы равенства были верны.

а) 100 19 49 +

в) 63 г) 81

9. Все ли утверждения верны? Укажи правильный ответ.

1) Сумма длин всех сторон многоугольника периметр.

2) Литр единица измерения объёма жидко- сти,

а) да

п - х = 58

11	24		20	з
4	12	25
		13	21
10	18		14	22
23				15

1. Заполни пустые клетки в квадрате так, чтобы он стал магическим.

2. Переставь в каждом выражении числа так, чтобы значения выражения можно было вычислить. Запиши получившиеся выражения и реши их.

72 6 18 ЕППЗГП-Е:ППГП

З. Проведи в квадрате 2 отрезка так, чтобы получилось З треугольника, 1 четырёхугольник и 1 пятиугольник.

4. Нарисуй пирамидку, в которой красное кольцо меньше зелёного, но больше синего; жёлтое кольцо больше зелёного.

5. На сколько увеличится число 12, если цифры переставить местами?

6. Вставь числа, чтобы равенства были верными.

а) 13 + 14

в) 76 - 27 _ 7 , а г) 42

7. Реши задачу, записав математическое выражение. В летний полдень под сосной Ёж нашёл сюрприз лесной: две лисички, пять опят Под сосной в лесу стоят.

Ну а дальше у опушки

Сыроежки, все подружки, По три в три ряда стоят, На ежа они глядят.

Кто ответ нам дать готов:

Сколько ёж нашёл грибов?

8. В трёхзначном числе отсутствует разряд десятков, а сотен в 2 раза больше, чем единиц. Известно, что оно делится на 9. Укажи это число.

а) 306 6) 603 в) 201 ^г) 804

9. Масса 5 одинаковых яблок и З одинаковых груш такая же, как и масса 4 таких же яблок и 4 таких же груш. Что легче: яблоко или груша?

10. Жираф пробежал 100 м за 7 с. Сможет ли он пробежать 1 км за 1 мин, если будет двигаться так же быстро? Укажи верный ответ.

а) да б) нет

54

1. В бочку налили 16 вёдер воды по 12 л каждое. Если наливать в эту бочку воду кастрюлей, то кастрюль понадобится в 2 раза больше. Сколько литров воды вмещает кастрюля?

2. Орёл за 1 мин пролетает 1800 м, а сокол за 23 м. Сможет ли орёл догнать сокола, если между ними расстояние 15 м? Укажи верный ответ.

а) да б) нет

З. Реши задачу, записав математическое выражение.

У мамы-квочки восемь сынков и две дочки. Каждому мама купила по два кусочка мыла, Чтоб чистыми были, опрятными, Красивыми и аккуратными.

Сколько кусочков мыла мама детишкам купила?

4. Вставь числа, чтобы получились верные равенства.

а) З + З + З + З + = 21 6

100 + 100 + + 100

в) 15 + 15 + 15 + 15 + 15 15

г) 12 + 12 + 12 7

5. Если девочка купит 4 конфеты, то у неё оста нется 20 р., а если девочка купит 6 конфет, то останется 14 р. Сколько денег у девочки?

1. Проведи 2 прямые. На одной отметь З точки, на другой 5. Всего 7 точек. Покажи на чертеже, как это возможно сделать.

2. Счётчик автомобиля показывал 616 км. Через 1 ч на счётчике опять появилось число, которое читалось одинаково в обоих направлениях. Сколько километров мог проехал автомобиль?

З. Как из 4 палочек сделать 15? (Палочки ломать нельзя.) Ответ нарисуй.

4. Винни-Пуху подарили в день рождения бочонок с мёдом массой 7 кг. Когда Винни-Пух съел поло вину мёда, то бочонок с оставшимся мёдом стал иметь массу 4 кг. Сколько килограммов мёда было первоначально в бочонке?

5. Одни часы отстают на 25 мин и показывают время 1 ч 50 мин. Какое время показывают другие часы, если они спешат на 15 мин?

1. Расставь пропущенные числа так, чтобы равенства были верны.

18 24

в) 8 + о = 34

Расположи два одинаковых равносторонних треугольника так, чтобы получились 6 одинаковых равносторонних треугольников и шестиугольник.

По данному уравнению, не меняя знака, составь новое уравнение с таким же значением неизвестного. Реши уравнения.

4. Вставь пропущенное число.

Брат родился на 2 года раньше сестры. Сейчас ему 5 лет. Сколько лет сестре?

6. Запиши решение задачи с помощью математиче- ского выражения.

Чип и Дейл на помощь к кому-то спешили,

Сто километров на лодке проплыли,

Меньше в 2 раза прошагали пешком,

Ещё двадцать пять на верблюде верхом.

Спасли кого нужно, устали чуть-чуть. Какой же они проделали путь?

7. Беседка длиной З м, шириной 2 м обнесена бортиком высотой 1 м. Сколько краски потребуется для нанесения на бортик с внешней стороны, если расход краски на 1 м ²составляет 90 г?

8. Какие З числа, если их перемножить или сложить, дают один и тот же результат? Запиши сумму и произведение данных чисел.

9. Как, имея З сосуда ёмкостью 8 л, 5 л, З л, налить в котёл 7 л?

10. Когда в Риге 9 ч, в Перми 11 ч. Когда в Перми 11 ч, в Якутске 17 ч. Какое время показывают часы в Якутске, когда в Риге 12 ч?

62

1. Расставь пропущенные числа так, чтобы равенства были верны.

а) 28 +

в) 56 12

Заштрихуй 4 клетки так, чтобы в каждом из горизонтальных и вертикальных рядов было по

одной заштрихованной клетке, и никакие из них

попарно не соприкасались.

З. На прямой поставили 4 точки. Сколько получилось отрезков, концами которых являются эти точки? Укажи верный ответ.

4. Масса ящика с лимонами 25 кг. После продажи половины всех лимонов ящик взвесили. Весы по казали 15 кг. Какова масса пустого ящика?

5. Уроки в школе начинаются в 9 ч. В 8 ч 40 мин мальчик проехал половину пути. Продолжая путь с прежней скоростью, мальчик приедет в школу за 10 мин до начала уроков. Сколько времени мальчик потратит на дорогу в школу?

1. Оставляя на месте знаки действий, переставь чис ла в выражении так, чтобы результат увеличился в 9 раз. Предложи два варианта решения.

2. Квадрат разделили на 4 равные части. Составь из полученных частей 1 треугольник.

З. Поставь знаки действий и, если надо скобки, так, чтобы равенства были верны.

а) 5 5 5 5 16 6) 5 5 5 5 45

4. По какому правилу составлен ряд чисел? Запиши ещё два числа.

40, 39, 37, 34, 30,

Машина за 40 мин проехала 40 км, а катер за 30 мин прошёл 35 км. Что быстрее? Укажи верный ответ.

а) машина б) катер

Запиши два числа, сумма которых равна 15, а произведение 54.

1. Поставь между некоторыми цифрами знак сложе ния так, чтобы получилось выражение, значение которого равно 1000.

8 8 8 8 8 8 8 8 1000

2. Для решения задачи составь математическое вы-

У маЛЫШКИ-МУРаВЬИШКИ муравьиная семья: Семь братишек-шалунишек, Рыжеватых муравьишек, дядек ровно двадцать пять.

А сестрёнок-муравьишек

Вдвое больше, чем братишек.

Догадайся, какова муравьиная семья?

З. Запиши все двузначные числа, в которых число десятков в 2 раза больше числа единиц.

4. Квадрат со стороной 1 м разрезали на квадраты со стороной 1 см и выстроили их в один ряд в виде полосы шириной 1 см. Какой длины получилась полоса?

4 2 8 6 3 7 5 9

1. Используя цифру 9 и знаки действий, составь выражение, значение которого равно 90.

2. Определи, как из чисел верхнего ряда получили числа нижнего ряда. Запиши ещё 2 числа.

З. Запиши данные выражения, разделив их на группы. Вычисли.

4. Проведи в прямоугольниках по одному отрезку так, чтобы получились треугольник, пятиугольник и

Запиши два числа, сумма которых равна 11, а произведение равно 28.

1. В корзине было 12 помидоров. Когда из неё пе реложили в тарелку З помидора, то в корзине стало на 5 помидоров меньше, чем в тарелке. Сколько помидоров было в тарелке?

2. Как с помощью двух бидонов ёмкостью 5 л и 8 л отлить из молочной цистерны 7 л молока?

	71

З. За 20 с заяц пробежит 60 м. Сколько метров он успеет пробежать за 1 мин?

4. Бюро прогнозов сообщило в З ч дня, что в ближайшую неделю сохранится безоблачная погода. Можно ли ожидать, что через 60 ч будет светить солнце? Укажи верный ответ.

а) да б) нет

5. В третьем классе в среду должно быть четыре урока: математика, русский язык, музыка, физкультура. Сколько различных вариантов расписания уроков можно составить на этот день?

6. Расставь скобки в данном выражении так, чтобы его значение равнялось 14.

9 8 + 12 : 4 + 2 14

9. В квадрате проведи 2 отрезка так, чтобы получилось 2 треугольника и 2 четырёхугольника.

10. Не вычисляя, запиши данные выражения в порядке увеличения их значений.

96 : 6 96 12 96 : 4 96 : 8 96 : з

96 : 2 96 • 24 96 : 48 96 : 32 96 : 16

1. В двух корзинах 85 мандаринов. Когда из первой корзины взяли З мандарина, в обеих корзинах мандаринов стало поровну. Сколько мандаринов было в каждой корзине первоначально?

Собака погналась за лисицей, находящейся от неё на расстоянии 120 м. Через сколько времени собака догонит лисицу, если лисица пробегает в минуту 320 м, а собака — 350 м?

4. В пятиугольнике проведи 2 отрезка так, чтобы получилось З треугольника и 5 четырёхугольников.

Используя числа 6, 9, 5, 72, 90, 2, 4, 36, 54, З, составь все возможные произведения и частные так, чтобы значение каждого было равно 18.

3 7 4 6 8 5

10 22 13 19

6. Шестью девятками запиши число 20.

9 9 9 9 9 9 20

7. Определи правило, по которому из чисел верхней строчки получены числа нижней строчки, и допиши ещё З числа.

8. К ситцевой занавеске шириной 96 см пришили кольца на расстоянии 12 см одно от другого, а к шёлковой занавеске шириной 90 см пришили кольца на расстоянии 10 см одно от другого. На какой занавеске колец больше и на сколько?

а) на ситцевой

1. Сколько всего можно составить четырёхзначных чисел, сумма цифр которых равна З?

2. В представлении участвовали З клоуна: Джон, Ганс, Иван. Им дали З колпака красный, жёлтый, зелёный, З рубахи красную, жёлтую и зелёную и З пары шаровар красные, жёлтые и зелёные. Клоуны оделись так, что у каждого колпак, рубаха и брюки были разных цветов. Ганс взял зелёную рубаху, а Джон красные шаровары. Как был одет Иван?

З. В столовую привезли коробку печенья массой 19 кг. Когда съели половину печенья, то коробка с остатками печенья стала весить 10 кг. Сколько килограммов печенья было в коробке первоначально?

4. Во дворе были куры и овцы. Всего З головы и 8 ног. Сколько было кур и сколько овец?

5. Расставь скобки так, чтобы равенство было верным.

2 + 7 - 14

ОТ В ЕТ Ы

Вариант 1

24 И 1

2, 800 г

З. 16 • б + 4

4. лиса — 7 кг, белочка 1 кг, обезьянка — 5 кг

5. 6 отрезков

6. Вторник — среда; вторник — четверг; вторник — пятница; вторник — суббота; среда — четверг; среда — пятница; среда — суббота; четверг — пятница; четверг — суббота; пятница — суббота.

7. 6)

8. 20 см

9. 66 лет

10. 5 землекопов

Вариант 2

1. 7 легковых; З грузовых

2. Перв ы й вариант. 1-й вопрос: «У тебя день рождения 10 или 11?» Если «да», то 2-й вопрос: «10 октября?» Если «да», то 10 октября, если «нет», то 11 октября.

Второй вариант. Если на 1-й вопрос первого варианта ответ «нет», то 2-й вопрос: «День рождения 12 октября?» Если «да», то 12 октября, если «нет»,

	то 13 октября.
з.	15	1	и	з - 14
	17	2		з - 13
	16	з	и	4 - 15

5, 8) 8)0 (в/в возможны варианты);

(888 • 8) - (88 100

	77

6. на 11 кг легче

7. Точки расположены на пересечении прямых (3 точки) и по 1 точке на каждой прямой всего 6 точек, а на каждой прямой по З точки.

9. СКМДЮ

10. 6

Вариант З

1. 1

2. 6, 31

17 отрезков

4. а)

а) 175 < 229

в) 900 > 800 12, 14, 16

6) 251 > 249 (в/в)

г) 821 < 832 (в/в)

зелёные; тые 60 км

синие;

Б красные; И

жёл-

10.

Вар иант 4

2. (98 - 76) + (54

- 32) + 1

_ 45

(98 - 76) + 54

з. 3 тетради

70 (в/в)

4. круглое — 20 г; квадратное

5. З

6. 11 ч 55 мин

7, 231

8. АВ•, АС; ВС

9. 7 трёхколёсных; 3 двухколёсных

10. а)

Вар и ант 5

1. в) 2.

З. девятиугольник

6. 2; г) 5 (в/в) самый тяжёлый ананас; самый лёгкий персик

8. 15 марок

9. в)

(7 12)- 2 - 23

12- 75

7 12)3 - 2 = 47

7 • (9 + 122) — 77

Вариант 6

1. 5 б и з

з. ТМКНВ; тмквн; ткмнв; ТКМВН 4, 8 (в/в) 5.

6. Вопрос шуточный. (в/в)

7. 2)

8. Вариант 1. 1 группа: 10, 14, 21, 5, 15.

28, 30, 42; 2 группа:

Вариант 2. 1 группа: 10, 5, 21, 28, 42.

9. 90

15, 30; 2 группа: 14,

10. 2 кружочка — одним цветом, 1

Вари ант 7

кружочек — другим

2. а) 55 167

З. Из 5-литровой кастрюли дважды отлить воду в З-литровую банку, получая по 2 л, которые надо перелить в ведро.

4. 595

5. в)

6. 8 комплектов

7. Х + 11 23; х — 4 — 40 — х = 37

8. б)

9. гусей — 7; лошадей 10, 6)

Вар иант 8

1. (54 + 0)63

з. 1)

4. 15 мин

5. Сначала переправляются 2 человека, один возвращается и забирает третьего.

6. 10 проб

7. 4 и 6 порций

8. Нали^ть в кувшин 5 л из 5-литрового сосуда, затем из 5-литоового отлить в 3-литровый сосуд, а оставшиеся 2 л долить в кувшин.

9. 4 кг 10.

Вариант 9

1. 5, 55, 555; 615 — сумма

2. а) 40 • 20 + 200 — 1000 6) 60 • 20 - 200 - 1000 в) 60 • зо - 800 - 1000

з. 2 кг 500 г

4, НМТС•, мтсн; ТСНМ; снмт; ТМНС•, мнст; нстм; СТМН

5. Яйцо в кипящую воду нужно положить только после того, как просыпется песок в 3-минутных часах (обе пары часов необходимо перевернуть одновременно).

64 м2 (квадрат, каждая сторона

7. 2)

9, — 25

Вариант 10

1. а) 888 • 888 1 6) (888 - 88) 8 100 2. а), на 4 см

з. а)

4.мл, мв; кн, кв КЛ, кв; сн, ср, сл, св

		с
ж	ж
з	з	б

6.(в/в)

7. 2 огурца

8. 1 кг

9. 3 ч 5 мин

10. в/в

Вариант 1 1

1, З группы (1, 2,4,

2. 4 (в/в)

4, 2 см

5. увеличится на 60

а) 36 2 126) 24 2

В) 48 2 -— 24 • 4

7. Сначала налить воду в котёл из 5-литрового сосуда, затем из 5-литрового отлить в З-литровый сосуд, и оставшиеся 2 л добавить в котёл. (в/в)

8. яС; ПСЫ, СЫТ, СПБ; БСТ, ПБС

9. 31 х 7 + 2

10. Петухи яйца не несут. Вариант 12

2. (75 30) 15 + 17 - 20

(7 • 9 + 12) - 2 - 23

з. (в/в)

4. 1 группа: 23, 61, 25; 2 группа: 14, 32, 50, 16, 52

5. 12 6.

7. Девочки могли быть в белых кофточках и с косичками

одновременно.

8. г)

9. 21 треугольник

10. 10 19; 19 19;

19 • 4; 19 19

Вариант 13

1. ПА, ПГ, ПЧ, дг, АЧ, ГЧ 2. дв, АС, АД, ВД, ДС, ВС

з. 2)

7; 19

4. 400 : 5 - 80 400 • 80

5. 14 КОЛЫШКОВ

а) 34 х 5 + 4 6) 8 х 8 + 2

7. 60 десятков

8. 3 группы (2, 4, 6; 5,

- 5

5 -

400

10. 24 . 2 - 12 80

55 : 5 = 11

Вариант 14

1. 6)

20 45 : З = 15 12 х 5 = 60

2. а) 397 + 549 = 946

6) 156 + 344 _- 500

в) 470 — 29 441

г) 700 - 323 - 377

З. на седьмой

4. твнмк•, твнкм•, тнвмк•, тнвкм

6 • 27

6, 6 2 + 34 + 56 + 7 _ 100

6 + 54 + З + 2 + 1 _ 90

7. и — 7 грибов, о — 1 гриб, С — 5 грибов

8. (в/в)

9. Вариант 1. 1 группа: 15, 5, 55, 10; 2 группа: 2, 12, 51, 21, 19, 59. Вариант 2. 1 группа: 2, 12, 10; 2 группа: 15, 51,

21, 19, 55, 59. 10.

Вариант 15

1. 16 кубиков

2, 1274

З,

4. 24 и 1

5. 240 г молока

6. Авсм, АВМЕ, АМЕК•, АВСМЕ, ВМЕКА

7. Катя Маша — № 3, Петя

8. 6)

9, 800 зрителей

10. о (870)

Вариант 16

1. 7 групп (3, 5, 4; 5, 4, з; 7, Ф, з,7, 4, 1;

2. в)

З. 2 кг

4, 40 МИН

5. сторона треугольника — 12 см

84

6. 1) 952, 925, 592, 529, 295, 259

2) 259, 295, 529, 592, 925, 952

7, а) 40 20 + 200 — 1000

6) 60 20 - 200 = 1000

8. 24 способа

14 -диаметр; радиус

10. 22 человека

Вариант 17

1. а) 600 зо + 20 - 40 6) 60 • зо - 800 = 1000

2, Обжарить 4 котлеты с одной стороны (5 мин), 2 котлеты снять со сковороды, 2 другие перевернуть, добавив 2 сырые, обжарить (5 мин). 2 полностью обжаренные котлеты выложить, оставшиеся 2 котлеты перевернуть и с двумя недожаренными котлетами обжарить с другой стороны (5 мин). Итого 15 мин.

З. 8 см

4. 6) 5.

6. 4 галки и З палки

7. 5381

8. 27, (9

9. 20 - 6 + 14

10. Валерий, Дима, Иван, Антон

Вариант 18

1. а) 8 - 2 6) 27 • З в) 64 = 4 2. а)

з. 6)

4. 11

2 28

в) 20 24 (в/в)

7. на восьмой день

8, 15 + 25 + 35 = 75

9. — 40 (цыплят)

10. верхняя — 13; средняя

Вариант 19

1. 3 кролика

2. см и 4 см;

З. 4 группы (3, 8, 6;

4. 201

5. На одной чаше весов гири

нижняя — 20 ДЫНЬ

3 см и 3 см

в 8 кг и 3 кг, на дру—

гой пакет с крупой и гиря в 5 кг, Весы — в рав-

новесии.

6. 40 дней

7. 1

в) 2 • 4 + б = 14

8. (в/в)

9, а)

10. а)

Вариант 20

1. в)

2, 4 кг

З. 20 столбов

4. а)

7— 35 (морковок)

7. 160 кг саха а

86

8. 1 час

9. 6)

10. а) 5 5 50 6) 55 6

в) 55 - 5 5

Вариант 21

1. 14 КОЛЫШКОВ

З. 99 + 9 - 100

4. 16 ножек

5. дата 31.12.1986 г вопрос задан: 01.01.1997 г.

6, 70 7 - 8 - 55

. З + 27 — 54 25 - 56

7, 2

8, через 9 лет

9. 12 вариантов

10. 6)

Вариант 22

1. а)

2.	дв, АС, AD,	ВС, Во, CD
4,	23 человека
5,	6 . (8 + 20	- 2 = 76
6.	55552

8. 150 г

10. а) 36 4Г) 24

6) 321 д) 20

Вариант 23

1. 9 монет делят на З тройки. две тройки раскладывают на чаши весов. Выявляется та тройка монет, в которой находится тяжёлая монета. Из выявленной тройки берутся 2 монеты и раскладываются на чаши весов.

выявляется фальшивая монета.

2. 5 групп (4,

з. 35, 37, 53, 57, 73, 75

4, Ниф-Ниф — курточка и шапочка жёлтого цвета. Наф-Наф — курточка оранжевая, шапочка сиреневая.

Нуф-Нуф — курточка сиреневая, шапочка оранжевая.

5. 1 + 1 + 1 + 1 — 1 З (в/в)

6. 7 четырёхугольников

7. 8 - 45 (цветов)

8. а) 100 - 19 - 9											8 — 49 + 7
в) 63 — 9. а) 10. 35 - х = 21 Вариант 24 1.							(в/в)		г) 81
		11	24		7	20		З
		4	12		25	8		16
		17	5		13	21		9
		10	18		1	14		22
		23	6		19	2		15
	2. 4, 5.	32 снизу		вверх:			64 з ж		72	18		- 24
	6.	а) 13		+ 14 —			З			б) 4		6
		в) 76 - 27								г) 42	• 6 = 14		2

88

7, 16 (грибов)

8. 6)

9, Масса яблока и груши одинаковая.

10. 6)

Вариант 25

1. 6 л воды 2. а)

з. 2— 20 (кусочков мыла)

4.21

6) 100 100 + 100 + 100 + 100

в) 15 + 15 + 15 + 15 + 15 - 15 5

Г) 12 + 12 + 12 — 7 - 12 5.

7,— 31 вариант

8, а)

9, 6)

10. З числа (20, 60, 100)

Вар иант 26

1. 9 + 12 75

6) (36 - 12) • 6 — 2 = 2

в) 23 - 12 2. 8

з.

1	2		з	6
4 7 5		8		9	12

5, 6.

4 способа

33 337 зо кг 500 г

9. — 50 (МЫШеЙ и мышат)

10. в 11 раз

Вар и ант 27 1.

2. 60 км (676), 70 км (686), 80 км (696), 91 км (707)

з. xv

4. 6 кг мёда

5. 2 ч 30 мин

6. 6)

7. 2 яблока

8. а) 72

в) 89 - 68 - 7 + 14

9. 2)

10. (в/в)

Вариант 28

1.		18	24
	6) (13 -	9)	_ 40
		34	2
з.	х - 52 -	21	(в/в); х = 73

4. 11

5, 3 года

6. 100 + 100 • 2 + 25 175 (км)

7. 900 г краски

8.о; 1 2 9.

10, в Якутске 20 ч

Вариант 29

1. а) 28 — 32 : 4 20 З = 30

в) 56 12

з. г) 4. 5. 20 мин 6. 24 см
7. 15 вариантов 8. 9.	троек лошадей
10. 12 • 4 Вар иант 1, 18 6 6 • 18 =	8 54		4	12 -	2 (в/в)
18 • 6 = 54 2.
з. а) 55 4. 25, 19 5. 6) 6,		16			5 = 45
7. — рыжий;		— белый;		— чёрный

8. 14 (птиц) 9.

10. 10 см; 8 см

Вариант 31

1. 888 + 88 + 8 1000

2. 1 + 7 + 25 + 8 = 49 (муравьёв)

з. 21, 42, 63, 84

4. 10 000 см 5.

6. 21 партия

7. 12

10. 10, 6, з

Вариант 32

• 9 + 9

2. 15 27

5. 7 см и 4 см

6, ширина — 4 см; длина — 7 см

8.- 29

- 12

— - 48

10. 6 машинок

Вариант 33

1. 11 помидоров

2. В 8-литровый бидон 2 раза вылить молоко из 5-литрового бидона. Один раз полностью, а второй раз останется 2 л в 5-литровом бидоне. Объединить оставшиеся 2 л и 5 л из 5-литрового бидона. Получим 7 л молока.

з. 180 м

4. 6)

5. 24 варианта

6.2) — 14

7, - 65

68 з = 69

8, 4 см, 18 см

10. 96 : 48; 96 : 32; 96 24; 96 • 16; 96 : 12; 96 : 8; 96 : 6; 96 : 4; 96 : з; 96 : 2

Вариант 34

1. 1 корзина — 44 мандарина; 2 корзина — 41 мандарин

2. Налить в ведро 2 раза по З л и ещё долить из банки до 7 л, в банке останется 2 л, их вылить в кастрюлю и добавить ещё З л. З. Через 4 мин

9 • з; 36 54 , 4; 90

6, (9 9) 20

7. 25, 16, 28

8. б); на 1 кольцо

10. 7 кукол

Вариант 3 5

1, 10 чисел (1110, 1011, 1101, 1200, 1020, 1002, 2100,

2010, 2001, 3000)

2. У Ивана красная рубаха, жёлтый колпак, зелёные брюки.

За 18 кг печенья

4, 2 курицы и 1 овца

5. 2 + 7 - 14

а)

в)

19 - 13 = 36 6

19 + 7 2 = 33

6) 13

см и 1 см; 8 см и см и з см; 6 см и

2 см

4 см

10.

Учебное изДание

Орг Александр Оскарович

Белицкая Наталия Георгиевна

Олимпиады по математике

З класс

Издательство «ЭКЗАМЕН»

Гигиенический сертификат

№ РОСС RU. АЕ51. Н 16678 от 20.05.2015 г.

Главный редактор Л. Д. Лаппо

Редактор М. А. Козлова

Технический редактор Л. В. Павлова

Художественный редактор Л. В. Демьянова

Корректоры Т. И. Шитикова, Л. В. Дьячкова

Дизайн обложки А. Ю. Беляева

Компьютерная вёрстка М В. Дёмина

107045, Москва, Луков пер., д. 8. www.examen.biz

E-mail: по общим вопросам: info@examen.biz; по вопросам реализации: sale@examen.biz тел./факс 8 (495) 641-00-30 (многоканальный)

Общероссийский классификатор продукции ок 005-93, том 2; 953005 книги, брошюры, литература учебная

Отпечатано в соответствии с предоставленными материалами в ООО «ИПК Парето-Принт», г. Тверь, www.pareto-print.ru

По вопросам реализации обращаться по тел.: 8 (495) 641-00-30 (многоканальный).

Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

Посмотрите также