Электронные состояния в манганитах

Перенос заряда в La_0,7Sr_0,3MnO₃. Двойной обмен.

Появление металлической ферромагнитной фазы в манганитах впервые объяснено Зенером [39, 40]. – Благодаря сильному внутриатомному обмену между локализованным спином и делокализованным электроном спин последнего всегда выстраивается параллельно спину иона. Если все спины ионов выстроены в одном направлении, электрон может свободно передвигаться от узла к узлу решетки по цепочке Mn⁺³(e_g)→O(2p)→Mn⁺⁴(e_g). Такое реальное межионное туннелирование носителя названо двойным обменом (ДО), что подчёркивает двухэтапный характер процесса (Рис. 1.4).

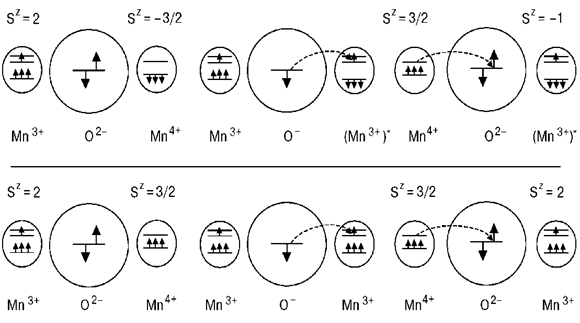
Рис. 1.4. Схема двухэтапного переноса электронной конфигурации (носителя) между ионами ПМ, имеющими противоположные (a) либо одинаковые (б) направления спинов. В обоих случаях межионный переход электрона разрешен и не лимитируется законом сохранения спина, однако в первом случае один из ионов в конечном состоянии оказывается в возбужденном (Mn³⁺)^* состоянии (нерезонансный перенос) либо такой переход сопровождается рождением спинового возбуждения в кристалле [39, 40].

Модель ДО позволяет на качественном уровне интерпретировать металлизацию манганитов как индуцированную носителями заряда и самосогласованную перестройку спинов от коллинеарного антиферромагнитного (АФМ) состояния в насыщенную ферромагнитную (ФМ) фазу, которая благодаря появлению в ней зоны проводимости конечной ширины, понижает общую энергию системы. То есть, ферромагнитное состояние в манганитах возникает не за счет обычного обменного взаимодействия между ионами, а в результате кинетического эффекта.

В отличие от обычных ФМ металлов, манганиты в ФМ состоянии обладают зоной проводимости с носителями только одной спиновой поляризации, так как противоположная отвечает высоколежащему -состоянию иона ПМ и, следовательно, другой зоне этого металла. Такие проводящие системы носят название половинных металлов (half metals) (например, [16, 64-67]) и входят в группу так называемых «плохих» металлов. Также манганиты относят к классу сильно коррелированных электронных систем, так как ДО является одним из корреляционных эффектов.

Роль ян-теллеровских деформаций

Исходный антиферромегнетный порядок является лишь одним из факторов, не позволяющих носителю свободно перемещаться по решетке манганитов в условиях слабого легирования. Другим, не менее существенным фактором, служит ЯТ характер иона Mn³⁺ в кубическом кристаллическом поле [61, 68]. Миллис, Литтлвуд и Шрайман [41, 69] первыми привлекли эффект ЯТ к описанию электрических и магнитных свойств манганитов. Они показали, что использование одной лишь модели ДО приводит к значительному количественному несоответствию между вычисляемыми и измеряемыми величинами. Так, температура Кюри Lа_1−xСа_xMnO₃ при х ≈ 0,2 в модели ДО практически на порядок превышает известные из экспериментов значения К, а вклад спиновых флуктуаций в электрическое сопротивление системы не может обеспечить наблюдаемой величины магниторезистивного эффекта вблизи Т_C. В итоге, в работе [41] сделан вывод о принципиальной необходимости привлечения новых механизмов КМС, одним из которых является деформационный механизм, основанный на эффекте ЯТ. Ещё одним подтверждением влияния колебательных степеней свободы на транспортные и магнитные свойства манганитов валяется колоссальный изотопический эффект – сдвиг T_C при полном замещении ¹⁶О ← ¹⁸O составляет порядка 20 К, в различных составах Lа-А-Mn-O [70, 71].

Для описания основного состояния нелегированного соединения LаMnO₃ в принципе можно использовать модель зонного диэлектрика (при этом необходимо учитывать факт ЯТ удвоения решетки) [12, 72-95].

Ширина зоны проводимости в результате поляронного сужения оказывается зависящей от температуры Т; при этом, вблизи носителя возможно неоднородное распределение углов подворотов спинов [96, 97]. Таким образом, носитель в кристалле одет в фононную и магнонную «шубы», т.е. является заряженным магнитоупругим поляроном, что непосредственно сказываются на его эффективной массе. Тем самым модель ДО обобщается включением в нее неоднородных статических смещений ионов и подворотов их спинов.

Помимо ЯТ деформации на ширине зоны проводимости манганитов эффективно сказываются средняя амплитуда термических поворотов октаэдров [98, 99] и также расширения решетки. Эти факторы приводят к дополнительному сужению зоны, и способствует локализации носителей с образованием поляронов, время жизни которых из-за их термического развала должно уменьшаться [10].

Полярон малого радиуса.

Поляроном называется квазичастица, представляющая собой электрон, окруженный деформированной областью решетки. Поляризации среды приводит к формированию вокруг такого электрона потенциальной ямы, что приводит к его автолокализации. Для выхода из этого состояния, электрону необходимо преодолеть потенциальный барьер. В зависимости от размеров области локализации различают поляроны большого (порядка сотен и тысяч периодов решетки) и малого (порядка одного-двух периодов) радиуса.

Теория электропроводности на поляронах малого радиуса описана в классических работах [100-102]. Вклад поляронов малого радиуса в электропроводность возникает благодаря надбарьерными перескоками поляронов между соседними узлами кристаллической решетки [102]. Поскольку длительность этого процесса значительно меньше обратной частоты фононов , перескок “происходит так быстро, что электрон выскакивает из созданной им поляризационной ямы, стряхивает с себя “тяжелый груз атомных смещений” и прекращает свое существование как полярон [102]. Но поскольку время между перескоками гораздо больше, чем то, после попадания на следующий узел решётки, электрон вновь успевает создать поляризационную яму и опуститься в нее. Т.е. прежде чем электрон перескочит на другой узел, он вновь возвращается в поляронное состояние. При этом, за время между перескоками, электроны не успевают туннелировать на соседний узел. Однако, в случае сильной связи переход носителя с узла на узел возможен только путём туннелирования, и происходит быстро [103].

Перескок электрона на соседний узел (как и процесс оптического разрушения полярона) приводит к увеличению энергии системы, как минимум, на величину равную энергии излучения фононов. Но это возрастание энергии должно компенсироваться работой внешнего электрического поля над электроном. Без этого перескок электрона запрещён законом сохранения энергии в данном микропроцессе.

В случае полярона большого радиуса, превышение им критической скорости (минимальной фазовой скорости фононов) приводит к очень эффективному торможению его движения за счёт излучения реальных когерентных фононов [104].

Скачано с www.znanio.ru