физика

Физика - Поурочные разработки 11 класс - 2017 год

Корпускулярно-волновой дуализм свойств микрочастиц - АТОМНАЯ ФИЗИКА - КВАНТОВАЯ ФИЗИКА

При планировании уроков рекомендуем, во-первых, выделить урок для закрепления представлений о корпускулярно-волновом дуализме; во-вторых, рассмотреть спектры на основе квантования энергии атома; в-третьих, на уроке обобщения раскрыть значимость идеи квантования в современной физике.

С нашей точки зрения, следует логику современного теоретического познания довести до следствий — спектров и химического действия света. Очевидно, что на решении задач также не стоит экономить время.

Урок 1*. Корпускулярно-волновой дуализм свойств микрочастиц

Задачи урока: расширить понятие о корпускулярно-волновом дуализме микрочастиц.

Ход урока

I. Постановка задач урока.

II. Примерное содержание рассказа учителя о дуализме свойств света приведено ниже (см. также с. 190).

1. Ранее мы узнали, что электромагнитные волны состоят из элементарных частиц — фотонов. В одних явлениях, таких как интерференция и дифракция, свет проявляет себя как волны. В этих явлениях участвует очень большое число фотонов, и мы наблюдаем их суммарное действие на макроскопические тела, причём отдельные фотоны незаметны. В других явлениях, например в фотоэффекте, на первый план выступает взаимодействие отдельного фотона с микрочастицей — электроном и проявляются квантовые свойства света. Наличие у одного и того же объекта — света — свойств непрерывных волн и свойств потока дискретных частиц (корпускул) называется корпускулярно-волновым дуализмом (двойственностью) свойств света.

Кроме фотонов, имеются и другие микрочастицы, они входят в состав вещества. Это известные нам лёгкие электроны и более тяжёлые протоны. Они в отличие от фотонов имеют массу покоя m₀ ≠ 0. Как же обстоит дело с этими микрочастицами, обладают ли они дуализмом свойств?

2. В 1928 г. физики Дж. П. Томсон и П. С. Тартаковский независимо друг от друга поставили эксперименты, в которых поток электронов взаимодействовал с поверхностью кристаллических тел. Правильное чередование атомов в кристалле создаёт условия для дифракции коротких волн. Так, при отражении от кристаллических поверхностей наблюдается дифракция рентгеновских лучей, которые представляют собой электромагнитные волны.

Но и для электронов в названных опытах наблюдалась дифракционная картина! Электроны вели себя как волны длиной волны порядка 1 А. Рассмотрим явление дифракции электронов. Принципиальная схема установки изображена на рисунке 127.

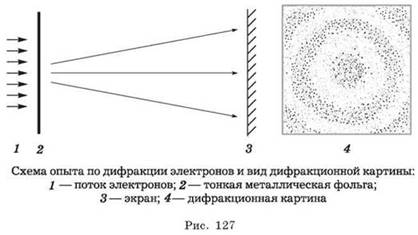
Электроны, попадая на фотопластинку, “засвечивают” её (подобно свету). После проявления пластинки обычным способом на ней обнаруживаются тёмные области, такие же, какие получаются в результате дифракции волн.

Причём по расстоянию между кольцами определяют длину волны. На рисунке 128 представлен результат дифракции рентгеновских лучей (рис. 128, а) и электронов (рис. 128, б) на поликристалле алюминия. Фотография на рисунке а получена с помощью рентгеновских лучей с длиной волны 0,71 А, на рисунке б — с помощью пучка электронов с энергией 60 эВ (λ = 0,50 Ă). Для сопоставления обоих снимков фотография на рисунке б увеличена в 1,6 раза.

3. Как объяснить результаты эксперимента? Какой вывод следует сделать из наблюдаемого явления дифракции электронов? На эти вопросы попытался ответить французский физик Луи де Бройль. Ещё в 1923 г. он высказал предположение о том, что любые микрочастицы обладают волновыми свойствами. По гипотезе де Бройля состояние движения любой свободной микрочастицы характеризуется волной, частота и длина волны которой определяются по формулам

где р = mv — импульс частицы, а  - её энергия. Поэтому электроны в опытах и проявляют волновые свойства. Зная скорость электрона, можно вычислить длину его волны. Результат совпадает с измеренной длиной волны по расстояниям между дифракционными кольцами. (Школьники зарисовывают принципиальную схему опыта, записывают формулы, зарисовывают схематическую картину дифракции. Важно логически последовательно и ясно изложить материал, не увлекаясь деталями.)

4. Полезно заметить, что формулы де Бройля и формулы Планка—Эйнштейна аналогичны, т. е. связь между волновыми и корпускулярными величинами для фотонов, частиц без массы, и микрочастиц с массой одна и та же. При этом фотонам соответствует макроскопическое электромагнитное поле, а волны де Бройля для электронов и других микрочастиц такого поля не образуют, не являются они и волнами в какой-либо материальной среде, подобно звуковым. В настоящее время установлено, что волны, связанные с микрочастицами, имеют вероятностный смысл: вероятность нахождения микрочастицы в том или ином месте пространства пропорциональна квадрату амплитуды волны.

Это положение непосредственно было подтверждено опытами известного физика В. А. Фабриканта (совместно с Л. М. Биберманом, Н. Г. Сушкиным) по дифракции одиночных, поочерёдно летящих электронов. Отдельный электрон, проходя через дифракционную решётку, попадает в отдельную точку фотопластинки и вызывает на ней потемнение в виде отдельного пятнышка. Однако после прохождения через решётку множества отдельно летящих электронов получается дифракционная картина (рис. 129). Она вполне аналогична картине, которую дают потоки фотонов.

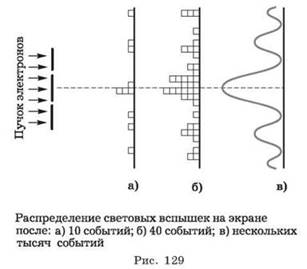
Вероятность попадания электрона в разные точки пластинки различна. Там, где образуется дифракционный максимум, вероятность попадания больше, электроны чаще оказываются на пластинке. А там, где минимум, электроны очень редко попадают на пластинку. Это и значит, что электроны движутся в пространстве и взаимодействуют с дифракционной решёткой, как волны.

Итак, электроны (и другие микрочастицы) обладают двойственностью, т. е. корпускулярными и волновыми свойствами. Электроны и протоны имеют очень малые размеры (радиус протона ~ 10¹⁵ м, а электрона ещё меньше) и ведут себя при столкновении друг с другом и микрочастицами как маленькие тела — корпускулы, проявляя при этом корпускулярные свойства. Волновые свойства микрочастиц проявляются в том, что положение их в пространстве и взаимодействие с макроскопическими телами определяются соответствующей частице волной. Волновые свойства приводят к тому, что для микрочастиц оказываются неприменимыми понятие движения по траектории и законы классической механики.

Граница между квантовой и классической картиной движения определяется на основании формул де Бройля: если длина волны частицы значительно меньше размеров тел, с которыми она взаимодействует, то волновая картина несущественна — частица движется по законам классической механики; если же длина волны сравнима с размерами тел, то проявляются волновые закономерности движения частицы.

III. Закрепление материала можно осуществить, решая задачи. Приведём примеры задач.

1. Определите длину волны электрона, движущегося со скоростью 6 ∙ 10⁵ м/с.

2. Определите длину волны нейтрона, движущегося со скоростью 2 ∙ 10³ м/с.

3. Пылинка массой 10^-5 кг движется со скоростью 10 м/с. Проявляет ли она при своём движении волновые свойства?

Решение. Формулы де Бройля справедливы для любого тела. Определим длину волны пылинки:

Длина волны так мала, что размеры частицы во много раз больше её, поэтому волновые свойства пылинки не проявляются.

IV. Домашнее задание: решение задач.

1. В опыте по дифракции электроны ускорялись разностью потенциалов 100 В. Определите длину волны де Бройля электронов. На каких объектах можно наблюдать их дифракцию?

2. В каком случае проще наблюдать дифракцию электронов: при скорости электронов 10³ м/с или 10⁵ м/с?