Физика

 

Уроки № 88-95 обобщающее повторение

Уроки № 94 обобщающее повторение темы «Электростатика»

Тема урока: обобщающее повторение темы «Электростатика»

Цели работы для учащегося:

- понимание основных понятий и формул;

- формирование навыков решения задач

Краткая теория

Электрический заряд и его свойства

Электрический заряд – это физическая величина, характеризующая способность частиц или тел вступать в электромагнитные взаимодействия. Электрический заряд обладает следующими свойствами:

 Существует минимально возможный (по модулю) электрический заряд, называемый элементарным зарядом. Его значение:

e = 1,602177·10^–19 Кл ≈ 1,6·10^–19 Кл.

Электрический заряд любого тела всегда кратен элементарному заряду:

где: N – целое число. Обратите внимание, невозможно существование заряда, равного 0,5е; 1,7е; 22,7е и так далее. Физические величины, которые могут принимать только дискретный (не непрерывный) ряд значений, называются квантованными. Элементарный заряд e является квантом (наименьшей порцией) электрического заряда.

7. Закон сохранения электрического заряда. В изолированной системе алгебраическая сумма зарядов всех тел остается постоянной:

Иногда в задачах электрический заряд распределен по некоторому телу. Для описания этого распределения вводятся следующие величины:

 Закон Кулона

Точечным зарядом называют заряженное тело, размерами которого в условиях данной задачи можно пренебречь. На основании многочисленных опытов Кулон установил следующий закон:

Силы взаимодействия неподвижных точечных зарядов прямо пропорциональны произведению модулей зарядов и обратно пропорциональны квадрату расстояния между ними:

где: ε – диэлектрическая проницаемость среды – безразмерная физическая величина, показывающая, во сколько раз сила электростатического взаимодействия в данной среде будет меньше, чем в вакууме (то есть во сколько раз среда ослабляет взаимодействие). Здесь k – коэффициент в законе Кулона, величина, определяющая численное значение силы взаимодействия зарядов. В системе СИ его значение принимается равным:

k = 9∙10⁹ м/Ф.

Коэффициент k в системе СИ иногда записывают в виде:

где: ε₀ = 8,85∙10^–12 Ф/м – электрическая постоянная.

Для диэлектрической проницаемости вещества верно следующее (о том, что такое электрическое поле чуть ниже):

 Электрическое поле и его напряженность

По современным представлениям, электрические заряды не действуют друг на друга непосредственно. Каждое заряженное тело создает в окружающем пространстве электрическое поле. Это поле оказывает силовое действие на другие заряженные тела. Главное свойство электрического поля – действие на электрические заряды с некоторой силой. Таким образом, взаимодействие заряженных тел осуществляется не непосредственным их воздействием друг на друга, а через электрические поля, окружающие заряженные тела.

Электрическое поле, окружающее заряженное тело, можно исследовать с помощью так называемого пробного заряда – небольшого по величине точечного заряда, который не вносит заметного перераспределения исследуемых зарядов. Для количественного определения электрического поля вводится силовая характеристика - напряженность электрического поля E.

Напряженностью электрического поля называют физическую величину, равную отношению силы, с которой поле действует на пробный заряд, помещенный в данную точку поля, к величине этого заряда:

Напряженность электрического поля – векторная физическая величина. Направление вектора напряженности совпадает в каждой точке пространства с направлением силы, действующей на положительный пробный заряд. Электрическое поле неподвижных и не меняющихся со временем зарядов называется электростатическим.

Для наглядного представления электрического поля используют силовые линии. Эти линии проводятся так, чтобы направление вектора напряженности в каждой точке совпадало с направлением касательной к силовой линии. Силовые линии обладают следующими свойствами.

·         Силовые линии электростатического поля никогда не пересекаются.

·         Силовые линии электростатического поля всегда направлены от положительных зарядов к отрицательным.

·         При изображении электрического поля с помощью силовых линий их густота должна быть пропорциональна модулю вектора напряженности поля.

·         Силовые линии начинаются на положительном заряде или бесконечности, а заканчиваются на отрицательном или бесконечности. Густота линий тем больше, чем больше напряжённость.

·         В данной точке пространства может проходить только одна силовая линия, т.к. напряжённость электрического поля в данной точке пространства задаётся однозначно.

Силовые линии кулоновских полей положительных и отрицательных точечных зарядов изображены на рисунке:

 

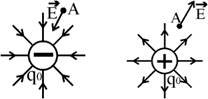
Если с помощью пробного заряда исследуется электрическое поле, создаваемое несколькими заряженными телами, то результирующая сила оказывается равной геометрической сумме сил, действующих на пробный заряд со стороны каждого заряженного тела в отдельности. Следовательно, напряженность электрического поля, создаваемого системой зарядов в данной точке пространства, равна векторной сумме напряжённостей электрических полей, создаваемых в той же точке зарядами в отдельности:

Это свойство электрического поля означает, что поле подчиняется принципу суперпозиции. В соответствии с законом Кулона, напряженность электростатического поля, создаваемого точечным зарядом Q на расстоянии r от него, равна по модулю:

Напряженность электрического поля, которую создает заряженная плоскость вблизи своей поверхности:

Потенциальная энергия взаимодействия зарядов

Электрические заряды взаимодействуют друг с другом и с электрическим полем. Любое взаимодействие описывает потенциальной энергией. Потенциальная энергия взаимодействия двух точечных электрических зарядов рассчитывается по формуле:

Электростатическое поле обладает важным свойством: работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только положением начальной и конечной точек и величиной заряда.

Следствием независимости работы от формы траектории является следующее утверждение: работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю.

Свойство потенциальности (независимости работы от формы траектории) электростатического поля позволяет ввести понятие потенциальной энергии заряда в электрическом поле. А физическую величину, равную отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда, называют потенциалом φ электрического поля:

Потенциал φ является энергетической характеристикой электростатического поля. В Международной системе единиц (СИ) единицей потенциала (а значит и разности потенциалов, т.е. напряжения) является вольт [В]. Потенциал - скалярная величина.

Электрическое напряжение это просто разность потенциалов, т.е. определение электрического напряжения может быть задано формулой:

В однородном электрическом поле существует связь между напряженностью поля и напряжением:

Работа электрического поля может быть вычислена как разность начальной и конечной потенциальной энергии системы зарядов:

Работа электрического поля в общем случае может быть вычислена также и по одной из формул:

В однородном поле при перемещении заряда вдоль его силовых линий работа поля может быть также рассчитана по следующей формуле:

В этих формулах:

·         φ – потенциал электрического поля.

·         ∆φ – разность потенциалов.

·         W – потенциальная энергия заряда во внешнем электрическом поле.

·         A – работа электрического поля по перемещению заряда (зарядов).

·         q – заряд, который перемещают во внешнем электрическом поле.

·         U – напряжение.

·         E – напряженность электрического поля.

·         d или ∆l – расстояние на которое перемещают заряд вдоль силовых линий.

Из принципа суперпозиции напряженностей полей, создаваемых электрическими зарядами, следует принцип суперпозиции для потенциалов (при этом знак потенциала поля зависит от знака заряда, создавшего поле):

Обратите внимание, насколько легче применять принцип суперпозиции потенциала, чем напряженности. Потенциал – скалярная величина, не имеющая направления. Складывать потенциалы – это просто суммировать численные значения.

 Электрическая емкость. Плоский конденсатор

При сообщении проводнику заряда всегда существует некоторый предел, более которого зарядить тело не удастся. Для характеристики способности тела накапливать электрический заряд вводят понятие электрической емкости. Емкостью уединенного проводника называют отношение его заряда к потенциалу:

В системе СИ емкость измеряется в Фарадах [Ф]. 1 Фарад – чрезвычайно большая емкость. Для сравнения, емкость всего земного шара значительно меньше одного фарада. Емкость проводника не зависит ни от его заряда, ни от потенциала тела. Аналогично, плотность не зависит ни от массы, ни от объема тела. Емкость зависит лишь от формы тела, его размеров и свойств окружающей его среды.

Электроемкостью системы из двух проводников называется физическая величина, определяемая как отношение заряда q одного из проводников к разности потенциалов Δφ между ними:

Величина электроемкости проводников зависит от формы и размеров проводников и от свойств диэлектрика, разделяющего проводники. Существуют такие конфигурации проводников, при которых электрическое поле оказывается сосредоточенным (локализованным) лишь в некоторой области пространства. Такие системы называются конденсаторами, а проводники, составляющие конденсатор, называются обкладками.

Простейший конденсатор – система из двух плоских проводящих пластин, расположенных параллельно друг другу на малом по сравнению с размерами пластин расстоянии и разделенных слоем диэлектрика. Такой конденсатор называется плоским. Электрическое поле плоского конденсатора в основном локализовано между пластинами.

Каждая из заряженных пластин плоского конденсатора создает вблизи своей поверхности электрическое поле, модуль напряженности которого выражается соотношением уже приводившимся выше. Тогда модуль напряженности итогового поля внутри конденсатора, создаваемого двумя пластинами, равен:

За пределами конденсатора, электрические поля двух пластин направлены в разные стороны, и поэтому результирующее электростатическое поле E = 0. Электроёмкость плоского конденсатора может быть рассчитана по формуле:

Энергия конденсатора. Ее же называют энергией электрического поля внутри конденсатора. Опыт показывает, что заряженный конденсатор содержит запас энергии. Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор. Существует три эквивалентные формы записи формулы для энергии конденсатора (они следуют одна из другой если воспользоваться соотношением q = CU):

Особое внимание обращайте на фразу: «Конденсатор подключён к источнику». Это означает, что напряжение на конденсаторе не изменяется. А фраза «Конденсатор зарядили и отключили от источника» означает, что заряд конденсатора не изменится.

 Соединения конденсаторов

Параллельное соединение конденсаторов – для увеличения ёмкости. Конденсаторы соединены одноименно заряженными обкладками, как бы увеличивая площадь одинаково заряженных пластин. Напряжение на всех конденсаторах одинаковое, общий заряд равен сумме зарядов каждого из конденсаторов, и общая ёмкость также равна сумме емкостей всех конденсаторов соединенных параллельно. Выпишем формулы для параллельного соединения конденсаторов:

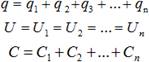
При последовательном соединении конденсаторов общая ёмкость батареи конденсаторов всегда меньше, чем ёмкость наименьшего конденсатора, входящего в батарею. Применяется последовательное соединение для увеличения напряжения пробоя конденсаторов. Выпишем формулы для последовательного соединения конденсаторов. Общая емкость последовательно соединенных конденсаторов находится из соотношения:

Из закона сохранения заряда следует, что заряды на соседних обкладках равны:

Напряжение равно сумме напряжений на отдельных конденсаторах.

Для двух последовательно соединённых конденсаторов формула выше даст нам следующее выражение для общей емкости:

 

  Ссылки на интернет-ресурс: https://educon.by/index.php/materials/phys/elektrostatika

 

Задания для самостоятельного решения

Электродинамика. Закон Кулона

Задание #1

Вопрос:

Электродинамика - это...

 

Выберите один из 4 вариантов ответа:

1) Ветвь электростатики

2) Ветвь физики

3) Наука о поведении электрических полей

4) Наука, изучающая электрические заряды

 

Задание #2

Вопрос:

Сколько родов электрических зарядов существует?

 

Выберите один из 4 вариантов ответа:

1) 1

2) 2

3) 3

4) 4

 

Задание #3

Вопрос:

Выберете верные утверждения об элементарном заряде

 

Выберите несколько из 5 вариантов ответа:

1) Численно равен заряду электрона

2) Это заряд любой субатомной частицы

3) Это наименьший заряд в природе

4) Это заряд, который не переносится

5) Это заряд, который не делится

 

Задание #4

Вопрос:

Первый шарик имеет заряд 120 нКл, а второй шарик имеет заряд -200 нКл. Шарики абсолютно одинаковые. При их соприкосновении, какой заряд окажется на втором шарике?

 

Выберите один из 5 вариантов ответа:

1) -40 нКл

2) -80 нКл

3) -320 нКл

4) 120 нКл

5) 320 нКл

 

Задание #5

Вопрос:

Электростатика - это...

 

Выберите один из 4 вариантов ответа:

1) Ветвь электродинамики, изучающая взаимодействие между движущимися зарядами

2) Ветвь электродинамики, изучающая взаимодействие между покоящимися зарядами

3) Ветвь электродинамики, статистически обосновывающая взаимодействие между электрическими зарядами

4) Правильного ответа нет

 

Задание #6

Вопрос:

Сопоставьте величины в электродинамике с аналогичными величинами в механике

 

Укажите соответствие для всех 3 вариантов ответа:

1) G

2) m

3) r

 

__ q

__ k

__ r

 

Задание #7

Вопрос:

В каких единицах измеряется коэффициент пропорциональности в законе Кулона?

 

Выберите один из 4 вариантов ответа:

1)

2)

3)

4)

 

Задание #8

Вопрос:

Сила взаимодействия между двумя разноименно заряженными шариками равна 25 Н. Шарики имеют одинаковый по модулю заряд и находятся на расстоянии 15 см друг от друга. Найдите модуль заряда шариков (в мкКл).

 

Запишите число:

 ___________________________

 

Задание #9

Вопрос:

На рисунке указаны два разноименно заряженных шарика, модуль заряда которых равен 120 нКл. Масса шарика, подвешенного на нерастяжимой нити равна 20 мг. Найдите силу натяжения нити (в мкН), если расстояние между центрами шариков составляет 50 см.

Изображение:

 

Запишите число:

 ___________________________

 

Задание #10

Вопрос:

Найдите модуль силы (в Н) взаимодействия между зарядами 2 мкКл и 3 мкКл, если расстояние между ними равно 40 см.

 

Запишите число:

 ___________________________

 

Конденсаторы

 

 

Задание #1

Вопрос:

Выберете верные утверждения

 

Укажите истинность или ложность вариантов ответа:

__ Электроёмкость - это отношение заряда тела к его объёму

__ Электроёмкость характеризует способность тела накапливать заряд

__ Электроёмкость двух проводников - это отношение напряженность поля между ними к модулю заряда на одном из них

__ Электроёмкость конденсаторов определенного типа может являться переменной

 

Задание #2

Вопрос:

Для изготовления плоского конденсатора необходимо иметь две обкладки и диэлектрик. При этом...

 

Выберите один из 3 вариантов ответа:

1) Толщина диэлектрика должна быть значительно больше размеров обкладок

2) Толщина диэлектрика должна быть значительно меньше размеров обкладок

3) Толщина диэлектрика должна быть сравнима с размерами обкладок

 

Задание #3

Вопрос:

Каким образом можно увеличить ёмкость конденсатора?

 

Выберите несколько из 4 вариантов ответа:

1) Заменить используемый диэлектрик, на диэлектрик с меньшей диэлектрической проницаемостью

2) Увеличить размер конденсатора

3) Увеличить площадь обкладок

4) Уменьшить расстояние между обкладками

 

Задание #4

Вопрос:

Из предложенных вариантов выберете единственное корректное описание конденсатора

 

Выберите один из 4 вариантов ответа:

1) Плоский, цилиндрический с переменной ёмкостью

2) Цилиндрический, электролитический с постоянной емкостью

3) Керамический электролитический с переменной емкостью

4) Бумажный сферический с ёмкостью

 

Задание #5

Вопрос:

Заряд на одной из обкладок конденсатора равен 400 мкКл. Какова ёмкость этого конденсатора (в мкФ), если напряжение между пластинами равно 80 В?

 

Запишите число:

 ___________________________

 

Задание #6

Вопрос:

В конденсаторе с ёмкостью 20 пкФ используются обкладки площадью 5 мм². Найдите диэлектрическую проницаемость используемого диэлектрика, если расстояние между обкладками равно 0,1 мм.

 

Запишите число:

 ___________________________

 

Задание #7

Вопрос:

Энергия заряженного конденсатора...

 

Выберите один из 4 вариантов ответа:

1) Рассредоточена вокруг него

2) Сосредоточена на пластинах конденсатора

3) Сосредоточена в электрическом поле

4) Нигде не сосредоточена

 

Задание #8

Вопрос:

В некоторых видах клавиатур используются конденсаторы для регистрации нажатия на клавишу. Для этого используется следующее свойство конденсатора

 

Выберите один из 4 вариантов ответа:

1) Изменение ёмкости при изменении расстояния между обкладками

2) Изменение ёмкости при изменении площади обкладок

3) Способность быстрой разрядки

4) Наличие диэлектрика между обкладками

 

Задание #9

Вопрос:

Энергия конденсатора равна 30 Дж. Если заряд на обкладках этого конденсатора равен 300 мкКл, какова его электроёмкость (в нФ)?

 

Запишите число:

 ___________________________

 

Задание #10

Вопрос:

Конденсатор с ёмкостью 300 мкФ накопил энергию, равную 45 мДж. Найдите напряжение между пластинами этого конденсатора (в В).

 

Запишите число:

 ___________________________

 

Скачано с www.znanio.ru