
ФОНД ОЦЕНОЧНЫХ СРЕДСТВ
ПО УЧЕБНОЙ ДИСЦИПЛИНЕ
ЕН.01 Математика
для специальности
08.02.02 Строительство и эксплуатация инженерных сооружений
уровень подготовки базовый
форма обучения очная
Содержание
1. Паспорт комплекта оценочных средств
2. Результаты освоения дисциплины, подлежащие контролю
3. Система контроля и оценки освоения программы дисциплины
4. ОЦЕНОЧНЫЕ СРЕДСТВА для текущего контроля
5. ОЦЕНОЧНЫЕ СРЕДСТВА для промежуточной аттестации
6. Литература для подготовки к текущей и промежуточной аттестации
1. ПАСПОРТ КОМПЛЕКТА КОНТРОЛЬНО-ОЦЕНОЧНЫХ СРЕДСТВ
Фонд оценочных средств (ФОС) предназначен для проверки результатов освоения дисциплины «Математика» образовательной программы специальности 08.02.02 Строительство и эксплуатация инженерных сооружений.
ФОС включает контрольные материалы для проведения текущего контроля успеваемости, промежуточной аттестации в форме дифференцированного зачета.
ФОС позволяет оценивать уровень освоения знаний и умений по дисциплине.
2. Результаты освоения дисциплины, подлежащие контролю
В результате контроля и оценки по дисциплине осуществляется комплексная проверка следующих знаний и умений по показателям, а также динамика формирования общих и профессиональных компетенций:
Общие компетенции:
v ОК 01. Выбирать способы решения задач профессиональной деятельности применительно к различным контекстам;
v ОК 02. Осуществлять поиск, анализ и интерпретацию информации, необходимой для выполнения задач профессиональной деятельности;
v ОК 03. Планировать и реализовывать собственное профессиональное и личностное развитие;
v ОК 04. Работать в коллективе и команде, эффективно взаимодействовать с коллегами, руководством, клиентами;
v ОК 05. Осуществлять устную и письменную коммуникацию на государственном языке Российской Федерации с учетом особенностей социального и культурного контекста;
v ОК 06. Проявлять гражданско-патриотическую позицию, демонстрировать осознанное поведение на основе традиционных общечеловеческих ценностей;
v ОК 07. Содействовать сохранению окружающей среды, ресурсосбережению, эффективно действовать в чрезвычайных ситуациях;
v ОК 08. Использовать средства физической культуры для сохранения и укрепления здоровья в процессе профессиональной деятельности и поддержания необходимого уровня физической подготовленности;
v ОК 09. Использовать информационные технологии в профессиональной деятельности;
v ОК 10. Пользоваться профессиональной документацией на государственном и иностранном языках;
v ОК 11. Использовать знания по финансовой грамотности, планировать предпринимательскую деятельность в профессиональной сфере.
Профессиональные компетенции:
v ПК 1.1. Участвовать в подготовке и проведении инженерных изысканий;
v ПК 1.2. Участвовать в разработке конструктивных и объемно-планировочных решений инженерного сооружения;
v ПК 1.3. Составлять проектно-сметную документацию на строительство инженерных сооружений;
v ПК 1.4. Использовать системы автоматизированного проектирования инженерных сооружений.
v ПК 2.1. Участвовать в разработке проекта организации строительства и составления технологических решений инженерных сооружений;
v ПК 2.2. Организовывать и контролировать производство однотипных работ при строительстве и эксплуатации инженерных сооружений;
v ПК 2.3. Участвовать в строительных и организационно-производственных мероприятиях по эксплуатации инженерных сооружений;
v ПК 2.4. Обеспечивать рациональное использование строительных машин, механизмов, транспортных средств на участке (объекте).
v ПК 3.1. Участвовать в разработке проекта производства работ на строительство инженерных сооружений;
v ПК 3.2. Организовывать и контролировать работы по производственно-техническому и технологическому обеспечению строительного производства при возведении инженерных сооружений.
v ПК 4.1. Обеспечивать строительное производство строительными материалами, изделиями, оборудованием, инструментами, вспомогательными расходными материалами и защитными средствами, требуемыми для охраны труда;
v ПК 4.2. Организовывать работу складского хозяйства.
|
Результаты обучения (освоенные умения, усвоенные знания) |
Основные показатели оценки результатов |
Формируемые общие и профессиональные компетенции |
|
У1. Умение решать задачи математического анализа, линейной алгебры и аналитической геометрии |
- Выполнение действий над матрицами - Вычисление определителей - Решение систем линейных уравнений методом обратной матрицы - Решение систем линейных уравнений по формулам Крамера - Решение систем линейных уравнений методом Гаусса - Выполнение действий над векторами - Нахождение скалярного, векторного и смешанного произведения векторов - Построение точек и нахождение их координат в прямоугольной декартовой и полярной системах координат - Вычисление предела функции в точке и в бесконечности - Исследование функции на непрерывность в точке - Нахождение производной функции - Нахождение производных высших порядков - Исследование функции и построение графика - Нахождение неопределенных интегралов - Вычисление определенных интегралов - Нахождение частных производных |
ОК1-ОК11, ПК1.1-1.4, ПК2.1-2.4, ПК3.1, ПК3.2, ПК4.1, ПК4.2 |
|
З1. Знание основных методов математического анализа, аналитической геометрии, линейной алгебры, элементарной теории вероятностей |
- Перечисление последовательности действий при решении систем линейных уравнений методом обратной матрицы, по формулам Крамера, методом Гаусса - Формулировка определений и перечисление свойств скалярного, векторного и смешанного произведения векторов - Классификация точек разрыва - Формулировка правил дифференцирования и перечисление производных основных элементарных функций - Перечисление табличных интегралов - Формулировка классического определения вероятности |
ОК1-ОК11, ПК1.1-1.4, ПК2.1-2.4, ПК3.1, ПК3.2, ПК4.1, ПК4.2 |
|
З2. Знание математических моделей простейших систем и процессов в естествознании и технике |
- Формулировка геометрического и механического смысла производной - Приложение определенного интеграла к вычислению площадей плоских фигур, объемов тел вращения, пути, пройденного точкой |
ОК1-ОК11, ПК1.1-1.4, ПК2.1-2.4, ПК3.1, ПК3.2, ПК4.1, ПК4.2 |
3. Система контроля и оценки освоения программы дисциплины
3.1. Формы промежуточной аттестации по образовательной программе при освоении программы дисциплины
|
Наименование дисциплины |
Семестр на базе основного общего образования / среднего общего образования |
Формы промежуточной аттестации |
|
Математика |
3 семестр |
Дифференцированный зачет |
3.2. Организация контроля и оценки освоения программы дисциплины
Основными формами проведения текущего контроля знаний на занятиях являются входной контроль, выполнение практических работ.
Промежуточная аттестация проводится в сроки, установленные учебным планом и определяемые календарным учебным графиком образовательного процесса, в форме дифференцированного зачета.
|
Содержание учебного материала по программе УД |
Формы и методы контроля |
|
|
Текущий контроль |
||
|
Форма контроля |
Проверяемые З, У, ОК, ПК |
|
|
Раздел 1. Элементы линейной алгебры |
|
З1, У1, ОК1-ОК11, ПК1.1-1.4, ПК2.1-2.4, ПК3.1, ПК3.2, ПК4.1, ПК4.2 |
|
Тема 1.1.Определители и их свойства |
Входной (тестовый) контроль |
З1, У1 |
|
Практическое занятие №1. Вычисление определителей |
тестирование, практическая работа
|
З1, У1 |
|
Практическое занятие №2. Вычисление определителей |
практическая работа
|
З1, У1 |
|
Тема 1.2. Системы линейных уравнений |
|
З1, У1, ОК1-ОК11, ПК1.1-1.4, ПК2.1-2.4, ПК3.1, ПК3.2, ПК4.1, ПК4.2 |
|
Практическое занятие № 3. Решение систем уравнений методом Крамера |
практическая работа
|
З1, У1 |
|
Практическое занятие № 4. Решение систем уравнений методом Гаусса |
практическая работа
|
З1, У1 |
|
Практическое занятие № 5. Решение систем уравнений методом обратной матрицы |
практическая работа |
З1, У1 |
|
Раздел 2. Элементы векторной алгебры |
|
З1, У1, ОК1-ОК11, ПК1.1-1.4, ПК2.1-2.4, ПК3.1, ПК3.2, ПК4.1, ПК4.2 |
|
Тема 2.1. Основные понятия векторной алгебры |
|
|
|
Практическое занятие № 6. Действия над векторами |
практическая работа
|
З1, У1 |
|
Практическое занятие № 7. Действия над векторами |
практическая работа
|
З1, У1 |
|
Тема 2.2. Скалярное и векторное произведение векторов |
|
З1, У1 |
|
Практическое занятие № 8. Решение задач на приложения скалярного произведения |
практическая работа
|
З1, У1 |
|
Практическое занятие № 9. Решение задач на приложения векторного произведения |
практическая работа
|
З1, У1 |
|
Раздел 3. Аналитическая геометрия на плоскости |
|
З1, У1, ОК1-ОК11, ПК1.1-1.4, ПК2.1-2.4, ПК3.1, ПК3.2, ПК4.1, ПК4.2 |
|
Тема 3.1. Прямоугольная система координат |
|
|
|
Практическое занятие № 10. Приложения метода координат на плоскости |
практическая работа
|
З1, У1 |
|
Практическое занятие № 11. Приложения метода координат на плоскости |
практическая работа
|
З1, У1 |
|
Тема 3.2. Линии на плоскости |
|
|
|
Практическое занятие № 12. Уравнения прямой |
практическая работа
|
З1, У1 |
|
Практическое занятие № 13. Линии второго порядка |
практическая работа
|
З1, У1 |
|
Раздел 4. Аналитическая геометрия в пространстве |
|
З1, У1, ОК1-ОК11, ПК1.1-1.4, ПК2.1-2.4, ПК3.1, ПК3.2, ПК4.1, ПК4.2 |
|
Тема 4.1. Прямая и плоскость в пространстве |
|
|
|
Практическое занятие № 14. Решение задач на прямую и плоскость |
практическая работа
|
З1, У1 |
|
Практическое занятие № 15. Решение задач на прямую и плоскость |
практическая работа
|
З1, У1 |
|
Тема 4.2. Поверхности в пространстве |
|
|
|
Практическое занятие № 16. Поверхности второго порядка. Эллипсоид. |
практическая работа
|
З1, У1 |
|
Практическое занятие № 17. Поверхности второго порядка. Гиперболоид. |
практическая работа
|
З1, У1 |
|
Практическое занятие № 18. Поверхности второго порядка. Конус второго порядка. Эллиптический цилиндр. |
практическая работа
|
З1, У1 |
|
Раздел 5. Элементы математического анализа |
|
З1, З2, У1, ОК1-ОК11, ПК1.1-1.4, ПК2.1-2.4, ПК3.1, ПК3.2, ПК4.1, ПК4.2 |
|
Тема 5.1. Дифференциальное исчисление |
|
|
|
Практическое занятие №19. Вычисление производной |
практическая работа
|
З1, У1 |
|
Практическое занятие № 20. Производная и ее применение |
практическая работа
|
З2, У1 |
|
Практическое занятие № 21. Производная и ее применение |
практическая работа
|
З2, У1 |
|
Тема 5.2. Интегральное исчисление |
|
|
|
Практическое занятие № 22. Неопределенный интеграл |
практическая работа
|
З1, У1 |
|
Практическое занятие № 23. Определенный интеграл |
практическая работа
|
З1, У1 |
|
Практическое занятие № 24. Приложения интеграла |
практическая работа
|
З2, У1 |
|
Итоговый контроль: дифференцированный зачет |
З1, З2, У1, ОК1-ОК11, ПК1.1-1.4, ПК2.1-2.4, ПК3.1, ПК3.2, ПК4.1, ПК4.2 |
|
4. ОЦЕНОЧНЫЕ СРЕДСТВА для текущего контроля
4.1. Входной контроль
Тест для входного контроля по математике
для студентов 2 курса
1 вариант
1. Найти сумму корней уравнения
![]()
а) -2 б) 2 в) 1,5 г) 0,5
2. Решить неравенство 2х – 3 (х + 1) > 3 – 7 (2 - х)
а) x < 1 б) x>1 в) x<-1 г) x>-2
3. Найти область определения
функции ![]()
а) ![]() б)
б) ![]() в)
в) ![]() г)
г) ![]()
4. Функция задана графически. Определить чётную функцию.
а) б) в) г)

5. Вычислить значение выражения ![]()
а) -34 б) 30 в) -30 г) 28
6. Вычислить значение выражения ![]()
а) 7 б) -2 в) 3 г) -1
7. Решить показательное
неравенство ![]()
а) ![]() б)
б) ![]() в)
в) ![]() г)
г) ![]()
8. Решить логарифмическое
уравнение ![]()
а) 2 б) -0,5 в) корней нет г) 0,5
9. Упростить выражение и вычислить
его значение при ![]()
![]()
а)
0 б) ![]() в)
в) ![]() г) 1
г) 1
10. Упростить выражение с помощью формул приведения
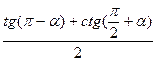
а)
-2 б) ![]() в) -
в) -![]() г) 1
г) 1
11. Вычислить предел ![]()
а) 0,5 б) -0,5 в) 2 г) -4
12. Найти значение производной функции
в точке х = 0 ![]()
а) 5 б) -8 в) 4 г) 0
13. Указать промежутки возрастания
функции ![]()
а) ![]() б)
б) ![]() в)
в)
![]() г)
г) ![]()
14. Вычислить определённый
интеграл 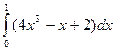
а) -1,5 б) 0,5 в) -3,5 г) 2,5
15. Сторона основания правильной 4-угольной призмы равна 3 см, высота призмы равна 7 см. Найти объём призмы.
а) 63 см3 б) 21 см3 в) 147 см3 г) 42 см3
2 вариант
1. Найти произведение корней
уравнения ![]()
а)
-3 б) ![]() в)
3 г)
в)
3 г) ![]()
2. Решить неравенство 20 – 4 (x - 1) < 5 - (2x - 3)
а) x<8 б) x>-4 в) x<-7 г) x>8
3. Найти область определения
функции ![]()
а) ![]() б)
б) ![]() в)
в) ![]() г)
г)
![]()
4. Функция задана графически. Определить нечётную функцию.
а) б) в) г)

5. Вычислить значение выражения ![]()
а) 9 б) -9 в) -15 г) 11
6. Вычислить значение выражения ![]()
а) 7 б) -2 в) 3 г) -1
7. Решить показательное
неравенство ![]()
а) ![]() б)
б) ![]() в)
в) ![]() г)
г) ![]()
8. Решить логарифмическое
уравнение ![]()
а) -3 б) корней нет в) -2 г) 1
9. Упростить выражение и вычислить его
значение при ![]()
![]()
а)
0 б) 3 в) -3 г) ![]()
10. Упростить выражение с помощью формул приведения
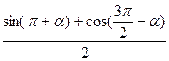
а)
2 б) -![]() в) 1 г)
в) 1 г) ![]()
11. Вычислить предел ![]()
а) 1 б) 2 в) -2 г) -4
12. Найти значение производной функции
в точке х = 0 ![]()
а) -1 б) -5 в) -2 г) 8
13. Указать промежутки убывания
функции ![]()
а) ![]() б)
б) ![]() в)
в)
![]() г)
г) ![]()
14. Вычислить определённый
интеграл 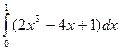
а) 0 б) 1,5 в) 3,5 г) -0,5
15. Радиус основания цилиндра равен 2 см, высота цилиндра равна 4 см. Найти объём цилиндра.
а) 32![]() см3 б) 16 см3
в) 16
см3 б) 16 см3
в) 16![]() см3 г) 64
см3 г) 64![]() см3
см3
Оценка индивидуальных образовательных достижений по результатам текущего контроля и промежуточной аттестации производится в соответствии с универсальной шкалой (таблица).
|
Процент результативности (правильных ответов) |
Качественная оценка индивидуальных образовательных достижений |
|
|
балл (отметка) |
вербальный аналог |
|
|
90 ÷ 100 |
5 |
отлично |
|
80 ÷ 89 |
4 |
хорошо |
|
70 ÷ 79 |
3 |
удовлетворительно |
|
менее 70 |
2 |
неудовлетворительно |
Практическая работа №1
Вычисление определителей
Цель: Сформировать умение вычислять определители второго, третьего и n-го порядка.
Задание: Вычислить определители.
Порядок выполнения:
1. Выполнить задания;
2. Ответить на вопросы.
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() ; 5)
; 5) 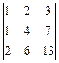 ;
;
6) 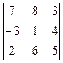 ; 7)
; 7) 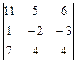 ; 8)
; 8) 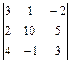 ; 9)
; 9) 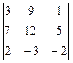 ;
;
10) 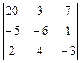 ; 11)
; 11) 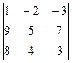 ; 12)
; 12) 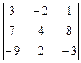 ;
;
13) 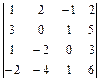 ; 14)
; 14) 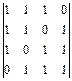 ;15)
;15) 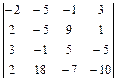 ;
;
16) 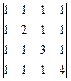 ; 17)
; 17) 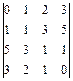 ; 18)
; 18) 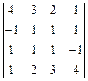 .
.
Контрольные вопросы:
1. Что называется определителем второго порядка?
2. Свойства определителей.
3. Какие способы вычисления определителей вам известны?
4. Что называется определителем матрицы?
Практическое занятие №2
Операции над матрицами. Вычисление определителей
Цель занятия: Научиться выполнять действия с матрицами, вычислять определители.
Порядок выполнения:
1. Выполнить задания;
2. Ответить на вопросы.
Задание:
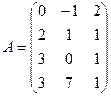 и
и 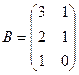 . Найти матрицу С = А·В.
. Найти матрицу С = А·В.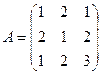 и
и 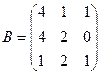 . Найти матрицу С = А·В – В·А.
. Найти матрицу С = А·В – В·А.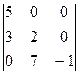 .
.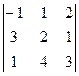 .
. .
.
Контрольные вопросы:
1. Что называется матрицей?
2. Что называется суммой матриц?
3. Что называется произведением матрицы на число?
4. Какая матрица называется транспонированной к матрице А?
5. Как найти произведение двух матриц?
Практическая работа №3
Решение систем линейных уравнений методом Крамера
Цель занятия: Научиться решать системы линейных уравнений различными методами.
Порядок выполнения:
1. Выполнить задания;
2. Ответить на вопросы.
Задание:
Решить системы линейных уравнений методом Крамера.
1) 
2) 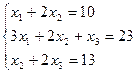
3) 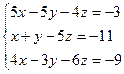
4) 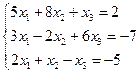
5)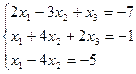
Контрольные вопросы:
1. Сформулируйте теорему Крамера.
2. Запишите формулы Крамера.
Практическое занятие №4
Решение систем линейных уравнений методом Гаусса
Цель занятия: Научиться решать системы линейных уравнений методом Гаусса.
Порядок выполнения:
3. Выполнить задания;
4. Ответить на вопросы.
Задание:
1) 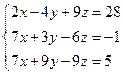
2) 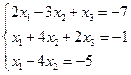
4) 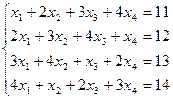
5) 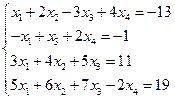
3) 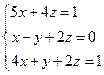
6) 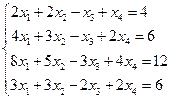
Контрольные вопросы:
1. Какие преобразования систем линейных уравнений являются эквивалентными?
2. Опишите алгоритм решения системы линейных уравнений методом Гаусса.
Практическая работа №5
Решение систем линейных уравнений методом обратной матрицы (матричным методом)
Цель занятия: Научиться решать системы линейных уравнений различными методами.
Порядок выполнения:
1. Выполнить задания;
2. Ответить на вопросы.
Задание:
1) 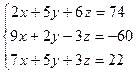
2) 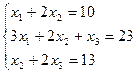
3) 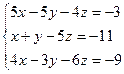
4) 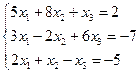
5)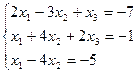
Контрольные вопросы:
1. Как записать простейшее матричное уравнение?
2. Укажите алгоритм решения простейшего матричного уравнения.
3. Как проверить правильность решения простейшего матричного уравнения?
Практическое занятие №6
Операции над векторами
Цель занятия: Научиться выполнять действия с векторами.
Порядок выполнения:
1. Выполнить задания;
2. Ответить на вопросы.
Задание на занятие:
Вариант 1
Даны векторы ![]() и
и ![]() (для № 1-5).
(для № 1-5).
1. Найти ![]() .
.
2. Найти ![]() .
.
3. Найти ![]() .
.
4. Найти ![]() .
.
5. Найти координаты
векторов ![]() ,
, ![]() ,
,
![]() .
.
6. В прямоугольной
декартовой системе координат построить точки A (0; 0),
B (3; -4), C (-3; 4). Определить расстояние между точками A и B, B и C, A и C.
7. Построить точки,
заданные полярными координатами: A (2; p/2), B (3; p/4),
C (3; 3p/4).
8. Даны точки в полярной системе координат A (2; p/4), B (4; p/2). Найти их прямоугольные координаты.
Вариант 2
Даны векторы ![]() и
и ![]() (для
№ 1-5).
(для
№ 1-5).
1. Найти ![]() .
.
2. Найти ![]() .
.
3. Найти ![]() .
.
4. Найти ![]() .
.
5. Найти координаты
векторов ![]() ,
, ![]() ,
,
![]() .
.
6. В прямоугольной
декартовой системе координат построить точки A (0; 0),
C (-3; 4), D (-2; 2) E (10; -3). Определить расстояние между точками C и D, A и D, D и E.
7. Построить точки,
заданные полярными координатами: A (4; 0), B (2; 3p/2),
C (3; p).
8. Даны точки в
прямоугольной системе координат A (0; 5), B (-3; 0), C (![]() ; 1). Найти их полярные координаты.
; 1). Найти их полярные координаты.
Контрольные вопросы:
1. Что называется вектором? Длиной вектора?
2. Как сложить два вектора?
3. Как найти разность двух векторов?
4. Как умножить вектор на число?
5. Как найти координаты вектора, заданного двумя точками?
Практическое занятие №7
Операции над векторами
Цель занятия: Научиться выполнять действия с векторами.
Порядок выполнения:
1. Выполнить задания;
2. Ответить на вопросы.
Задание:
1. Даны векторы ![]() и
и
![]() .
Построить векторы
.
Построить векторы ![]() ,
, ![]() .
.
2. Найти координаты векторов ![]() ,
, ![]() ,
,
![]() , если А(2; 3), В(-1;
-3), С(-7; 5).
, если А(2; 3), В(-1;
-3), С(-7; 5).
3. Даны векторы ![]() =
(-2; 4) и
=
(-2; 4) и ![]() = (3; 1). Найти:
= (3; 1). Найти: ![]() ,
, ![]() ,
, ![]() ,
,
![]() .
.
4. Найти длину вектора ![]() ,
если А(5; 2), В(8; -2).
,
если А(5; 2), В(8; -2).
5. Дан треугольник с вершинами А (7; 7), В (4; 3), С (3; 4). Найти его периметр.
6. Отрезок АВ задан точками А (2;
3), В (10; 11). Найти координаты точки С, если известно, что ![]() .
.
7. Найти длину медианы АМ треугольника с вершинами А (7; -4), В (-1; 8), С (-12; -1).
8. Найти скалярное произведение
векторов ![]() = (5; 7) и
= (5; 7) и ![]() = (4; 3).
= (4; 3).
9. Найти угол между векторами ![]() =
(4; 0) и
=
(4; 0) и ![]() = (2; -2).
= (2; -2).
10. Найти углы треугольника с вершинами А (6; 7), В (3; 3), С (1; -5).
Контрольные вопросы:
1. Как найти длину вектора, заданного двумя точками?
2. Как найти длину вектора, заданного своими координатами?
3. Как вычисляется скалярное произведение векторов, заданных своими координатами?
4. Как найти угол между векторами?
Практическое занятие №8
Применение скалярного произведения векторов при решении задач
Цель занятия: Научиться выполнять действия с векторами.
Порядок выполнения:
1. Выполнить задания;
2. Ответить на вопросы.
Задание:
1.Найти скалярное произведение
векторов ![]() = (5; 7) и
= (5; 7) и ![]() =
(4; 3).
=
(4; 3).
2.Найти угол между векторами ![]() = (4; 0) и
= (4; 0) и ![]() =
(2; -2).
=
(2; -2).
3.Найти углы треугольника с вершинами А (6; 7), В (3; 3), С (1; -5).
Контрольные вопросы:
1.Как найти длину вектора, заданного своими координатами?
2.Как вычисляется скалярное произведение векторов, заданных своими координатами?
3.Как найти угол между векторами?
Практическое занятие №9
Применение векторного произведения векторов при решении задач
Цель занятия: Научиться выполнять действия с векторами.
Порядок выполнения:
1. Выполнить задания;
2. Ответить на вопросы.
Задание:
1.Даны вершины параллелограмма АВСД: А(2;3;1),В(4;1;-2),С(6;3;7),Д(-1;2;4).
Вычислить: 1) площадь АВСД
2) площадь треугольника АВС
3) углы параллелограмма АВСД
4) уравнения сторон параллелограмма
Контрольные вопросы:
1.Как вычисляется векторное произведение векторов, заданных своими координатами?
2.Как применяется векторное произведение векторов при решении задач векторной алгебры?
Практическое занятие №10
Применение смешанного произведения векторов при решении задач.
Цель занятия: Научиться выполнять действия с векторами.
Порядок выполнения:
1. Выполнить задания;
2. Ответить на вопросы.
Задание на занятие:
Даны вершины пирамиды АВСД: А (2;3;1), В (4;1; -2), С (6;3;7), Д (-1;2;4).
Вычислить: 1) объем пирамиды АВСД
2) площадь треугольника АВС
3) углы параллелограмма АВСД
4) уравнения сторон параллелограмма
Контрольные вопросы:
1.Как вычисляется смешанное произведение векторов?
2.Как применяется смешанное произведение векторов при решении задач векторной алгебры?
Практическое занятие №11
Приложения метода координат на плоскости
Цель занятия: Научиться составлять уравнения прямых.
Порядок выполнения:
1. Выполнить задания;
2. Ответить на вопросы.
Задание:
1. Диаметры AB и CD окружности перпендикулярны. Хорда ЕА пересекает диаметр СD в точке К, хорда ЕС пересекает диаметр АВ в точке L. Докажите, что если СК: KD так же как 2:1, то AL: LB так же как 3:1.
2. Доказать, что сумма квадратов длин сторон четырехугольника равна сумме квадратов длин его диагоналей, сложенной с учетверенным квадратом расстояния между серединами диагоналей. (Теорема Эйлера)
3. Найти угол между прямыми Зх-4у+6=0 и 12х+5у+8=0
4. Определите расстояние от точки А (-3,4) до прямой у=х+2.
5. Вычислите площадь треугольника, вершины которого имеют следующие координаты: А (0,-2), В (6,2) и С (2,4).
Контрольные вопросы:
1. Каким уравнением описывается прямая на плоскости?
2. Записать уравнение прямой, проходящей через точку и имеющей нормальный вектор.
Практическое занятие №12
Уравнения прямых на плоскости
Цель занятия: Научиться составлять уравнения прямых.
Порядок выполнения:
3. Выполнить задания;
4. Ответить на вопросы.
Задание:
1.Составить уравнение прямой, проходящей через точки А(2;-3) и D(-3;7) и привести его к виду: а) каноническому
б) параметрическому
в) общему
г) в отрезках
д) с угловыми коэффициентами.
2. Составить уравнение прямой, проходящей через точку (2; 3) и перпендикулярной прямой 4х + 3у - 12 = 0.
3. Записать уравнения прямых в отрезках и построить их:
а) 2х + 5у + 20 = 0;
б) х – 8у + 4 = 0.
Контрольные вопросы для зачета:
1. Записать уравнение прямой, проходящей через точку и имеющей направляющий вектор.
2. Записать уравнение прямой, проходящей через две точки.
Практическое занятие №13
Уравнение прямой и плоскости в пространстве
Цель занятия: Научиться составлять уравнения прямых и плоскости.
Порядок выполнения:
1. Выполнить задания;
2. Ответить на вопросы.
Задание:
1. Составить уравнение прямой,
проходящей через точку В(5; 3) и имеющей нормальный вектор ![]() (5; 0).
(5; 0).
2. Составить уравнение прямой,
проходящей через точку А(3; -2) и имеющей направляющий вектор ![]() (-5; 3).
(-5; 3).
3. Треугольник задан точками А(5; 2), В(-1; -4), С(-5; -3). Составить уравнение прямой, проходящей через точку В параллельно АС.
4. Составить уравнение прямой, проходящей через точки А(1; 3), В(4; 1).
5. Составить уравнения медиан треугольника с вершинами А(7; 0), В(3; 6), С(-1; 1).
Контрольные вопросы:
1. Каким уравнением описывается прямая на плоскости?
2. Записать уравнение прямой, проходящей через точку и имеющей нормальный вектор.
3. Записать уравнение прямой, проходящей через точку и имеющей направляющий вектор.
Практическое занятие № 14
Составление канонического уравнения эллипса и окружности
Цель занятия: Научиться составлять уравнения эллипса и окружности, строить их.
Порядок выполнения:
1. Выполнить задания;
2. Ответить на вопросы.
Задание:
Контрольные вопросы для зачета:
Практическое занятие № 15
Составление канонического уравнения гиперболы и параболы
Цель занятия: Научиться составлять уравнения гиперболы и параболы, строить их.
Порядок выполнения:
1. Выполнить задания;
2. Ответить на вопросы.
Задание:
1.Найти координаты фокусов, длины осей и эксцентриситет эллипса, заданного уравнением 16х2 + 25у2 = 400.
2.Найти координаты фокусов, длины осей, эксцентриситет и уравнения асимптот гиперболы, заданной уравнением 16х2 – 25у2 = 400.
3.Составить каноническое уравнение
гиперболы, действительная ось которой 2b = 10, а уравнения асимптот имеют вид: ![]() .
.
4.Найти координаты фокуса и уравнение директрисы параболы, заданной уравнением у2 = 8х.
5.Составить уравнение параболы с вершиной в начале координат, если уравнение ее директрисы х + 3 = 0.
Контрольные вопросы для зачета:
1.Дать определение кривых второго порядка (гиперболы, параболы), записать их канонические уравнения.
2.Что называется эксцентриситетом гиперболы? Как его найти?
3.Записать уравнение равносторонней гиперболы.
Практическое занятие № 16
Уравнение сферы и цилиндрических поверхностей
Цель занятия: Научиться составлять уравнения сферы и цилиндрической поверхности.
Порядок выполнения:
1. Выполнить задания;
2. Ответить на вопросы.
Задание:
1.Составить уравнение сферы, если:
1)центр ее находится в точке
О(0;0;0),а радиус равен ![]() ;
;
2)центр ее находится в точке С (4;1; -3), а радиус равен 2;
3) центр сферы находится в точке С (-3;3;7), а она проходит через точку О (0;0;0);
4) точки А (1;4) и D (-1;2; -1) находятся на концах одного диаметра.
2.Найти радиус и центр сферы:
1)![]() +
+![]() +
+![]() =36
=36
2)![]() +4х+
+4х+![]() -2у+
-2у+![]() -4=0
-4=0
3) 2![]() +2
+2![]() +4у+2
+4у+2![]() -3z+2=0
-3z+2=0
3.Установить, какие цилиндрические поверхности задаются следующими уравнениями; какой оси параллельны их образующие; сделать чертеж:
1)![]() +
+![]() =9
=9
2) 2![]() +3
+3![]() =6
=6
3) 5![]() -3
-3![]() =15
=15
4)![]() =4z
=4z
Контрольные вопросы:
1.Дать определение поверхностей второго порядка (сферы, цилиндрической поверхности), записать их канонические уравнения.
2.Записать уравнение эллиптического цилиндра, гиперболического цилиндра, параболического цилиндра.
Практическое занятие № 17
Уравнение конической поверхности и поверхности вращения
Цель занятия: Научиться составлять уравнения поверхностей вращения и конических поверхностей.
Порядок выполнения:
1. Выполнить задания;
2. Ответить на вопросы.
Задание:
1.Найти уравнение поверхности, полученной при вращении:
1) эллипса![]() =1
=1
2) гиперболы![]()
3) параболы ![]()
4) прямой ![]()
Контрольные вопросы для зачета:
1.Дать определение поверхностям вращения (эллипсоид, однополостный гиперболоид, двуполостный гиперболоид, эллиптический параболоид), коническим поверхностям (конус 2 порядка).
2.Записать уравнение эллипсоида, однополостного гиперболоида, двуполостного гиперболоида, эллиптического параболоида, конуса 2 порядка.
Практическое занятие № 18
Поверхности второго порядка
Цель занятия: Научиться определять поверхность второго порядка по ее уравнению.
Порядок выполнения:
1. Выполнить задания;
2. Ответить на вопросы.
Задание:
1. Определить вид и параметры
поверхности второго порядка, заданной уравнением ![]()
2. Определить вид и параметры поверхности
![]()
3. Доказать, что уравнение ![]() Определяет гиперболический
параболоид.
Определяет гиперболический
параболоид.
4. Доказать что уравнение ![]() определяет конус.
определяет конус.
Контрольные вопросы:
1.Дать определение поверхностей второго порядка и записать их канонические уравнения.
Практическое занятие № 19
Вычисление производной
Цель занятия: Научиться пользоваться правилами и формулами дифференцирования.
Порядок выполнения:
1. Выполнить задания;
2. Ответить на вопросы.
Задания:
1. Найти производную
функции ![]() .
.
2.
Найти
производную третьего порядка функции ![]() .
.
3.
Найти
производную функции ![]() .
.
4.
Найти
производную третьего порядка функции ![]() .
.
5. Найти производную функции ![]() .
.
6. Найти производную третьего порядка
функции ![]() .
.
7. Найти производную функции ![]() .
.
8. Найти производную третьего порядка
функции ![]() .
.
Контрольные вопросы:
1. Сформулировать правила дифференцирования и записать производные основных элементарных функций.
2. Геометрический смысл производной.
Практическое занятие № 20
Приложение производной
Цель занятия: Научиться исследовать функцию с помощью производной и строить ее график.
Порядок выполнения:
1. Выполнить задания;
2. Ответить на вопросы.
Задание:
Исследовать функцию и построить ее график.
1.
![]() ;
;
2.
![]() ;
;
3.
![]() .
.
Контрольные вопросы:
1. Геометрический смысл производной.
2. Производная сложной функции.
Практическое занятие № 21
Приложение производной
Цель занятия: Научиться составлять уравнения сферы и цилиндрической поверхности.
Порядок выполнения:
1. Выполнить задания;
2. Ответить на вопросы.
1.
Написать
уравнение касательной к графику функции ![]() в точке с
абсциссой
в точке с
абсциссой ![]()
2.
Материальная
точка движется по закону ![]() . Найти скорость и
ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
. Найти скорость и
ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
3.
Написать
уравнение касательной к графику функции ![]() в точке с
абсциссой
в точке с
абсциссой ![]() ,
, ![]() .
.
4.
Материальная
точка движется по закону ![]() . Найти скорость и
ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
. Найти скорость и
ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
5. Написать уравнение касательной к
графику функции ![]() в точке с абсциссой
в точке с абсциссой ![]() ,
, ![]() .
.
6. Материальная точка движется по
закону ![]() . Найти скорость и ускорение в
момент времени t=5 с. (Перемещение измеряется в
метрах.)
. Найти скорость и ускорение в
момент времени t=5 с. (Перемещение измеряется в
метрах.)
Контрольные вопросы:
1.Физический смысл производной.
Практическое занятие № 22
Неопределенный интеграл
Цель занятия: Научиться вычислять неопределенный интеграл.
Порядок выполнения:
1. Выполнить задания;
2. Ответить на вопросы.
Задание:
1. Найти неопределенные интегралы методом непосредственного интегрирования (для № 1-5).
1. ![]() .
.
2. ![]() .
.
3. ![]() .
.
4.  .
.
5. ![]() .
.
2. Найти неопределенные интегралы методом подстановки (для № 6-8).
6. ![]() .
.
7. ![]() .
.
8. ![]() .
.
3.Найти
неопределенный интеграл методом интегрирования по частям: ![]() .
.
Контрольные вопросы:
1. Записать табличные интегралы.
2. Свойства неопределенного интеграла.
Практическое занятие № 23
Определенный интеграл
Цель занятия: Научиться вычислять определенный интеграл.
Порядок выполнения:
1. Выполнить задания;
2. Ответить на вопросы.
Задание:
1. Вычислить
определенный интеграл: 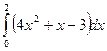 .
.
2. Вычислить
определенный интеграл методом подстановки: ![]() .
.
3. Вычислить определенный интеграл: 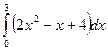 .
.
4. Вычислить определенный интеграл
методом подстановки: 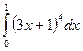 .
.
5. Найти
неопределенный интеграл методом интегрирования по частям:![]()
Контрольные вопросы:
1. Определение определенного интеграла.
2. Свойства определенного интеграла.
Практическое занятие № 24
Приложения интеграла
Цель занятия: Научиться вычислять площади и объемы тел вращения с помощью определенного интеграла.
Порядок выполнения:
1. Выполнить задания;
2. Ответить на вопросы.
Задание:
1. Вычислить,
предварительно сделав рисунок, площадь фигуры, ограниченной линиями: ![]() .
.
2. Найти объем тела,
полученного при вращении вокруг оси абсцисс криволинейной трапеции, ограниченной
линиями: ![]() .
.
3. Скорость движения
точки изменяется по закону ![]() (м/с). Найти
путь S, пройденный точкой за 10 с от начала движения.
(м/с). Найти
путь S, пройденный точкой за 10 с от начала движения.
4. Вычислить, предварительно сделав
рисунок, площадь фигуры, ограниченной линиями: ![]() .
.
5. Скорость движения точки изменяется
по закону ![]() (м/с). Найти путь S,
пройденный точкой за четвертую секунду.
(м/с). Найти путь S,
пройденный точкой за четвертую секунду.
Контрольные вопросы:
1. Дать определение поверхностей второго порядка (сферы, цилиндрической поверхности), записать их канонические уравнения.
2. Записать уравнение эллиптического цилиндра, гиперболического цилиндра, параболического цилиндра.
4.3. Порядок оформления заданий (практических работ):
Решения заданий оформляются в отдельной тетради в соответствии с требованиями, предъявляемыми к практическим работам.
Приступать к выполнению практического задания следует только после проработки теоретического материала на занятиях, по материалам конспектов и рекомендуемым учебникам «Математика» для СПО.
Критерий оценивания практической работы:
|
Процент результативности (правильных ответов) |
Качественная оценка индивидуальных образовательных достижений |
|
|
балл (отметка) |
вербальный аналог |
|
|
90 ÷ 100 |
5 |
отлично |
|
80 ÷ 89 |
4 |
хорошо |
|
70 ÷ 79 |
3 |
удовлетворительно |
|
менее 70 |
2 |
неудовлетворительно |
5. ОЦЕНОЧНЫЕ СРЕДСТВА для промежуточной аттестации
5.1. Вопросы для подготовки к дифференцируемому зачету:
1. Определители. Способы их вычисления.
2. Матрицы. Операции над матрицами. Обратные матрицы.
3. Решение систем линейных уравнений методом Крамера.
4. Решение систем линейных уравнений матричным методом.
5. Решение систем линейных уравнений методом Гаусса.
6. Векторы в пространстве. Операции над векторами.
7. Скалярное произведение векторов. Применение скалярного произведения векторов.
8. Векторное произведение векторов. Применение векторного произведения векторов.
9. Смешанное произведение векторов. Применение смешанного произведения векторов.
10. Прямая на плоскости. Уравнения прямых. Расстояние от точки до прямой.
11. Плоскость и прямая в пространстве. Уравнения прямых на плоскости. Уравнение плоскости. Расстояние от точки до плоскости.
12. Линии второго порядка.
13. Поверхности второго порядка.
14. Производная функции.
15. Геометрический смысл производной. Механический смысл производной.
16. Таблица производных. Понятие сложной функции. Производная сложной функции.
17. Схема исследования функции. Область определения функции. Множество значений функции. Четность и нечетность функции. Нули функции. Промежутки знакопостоянства функции. Возрастание и убывание функции, правило нахождения промежутков монотонности. Точки экстремума функции, правило нахождения экстремумов функции.
18. Производные высших порядков. Физический смысл второй производной. Исследование функции с помощью второй производной.
19. Первообразная. Неопределенный интеграл. Основные свойства неопределенного интеграла.
20. Таблица неопределенных интегралов.
21. Методы интегрирования: метод непосредственного интегрирования; метод замены переменной (метод подстановки); метод интегрирования по частям.
22. Определенный интеграл. Понятие интегральной суммы. Достаточное условие существования определенного интеграла (интегрируемости функции).
23. Основные свойства определенного интеграла. Геометрический смысл определенного интеграла.
24. Методы вычисления определенных интегралов. Формула Ньютона-Лейбница.
25. Геометрические и физические приложения определенного интеграла.
1.
Тело движется
прямолинейно со скоростью ![]() м/с. Вычислить
путь, пройденный телом за 10 сек.
м/с. Вычислить
путь, пройденный телом за 10 сек.
2. Вычислить площадь фигуры, ограниченной линиями y=2x2; x=1 и x=2
3. Скорость движения точки изменяется
по закону ![]()
![]()
![]() м/с. Найдите путь, пройденный
точкой за 10 с от начала движения
м/с. Найдите путь, пройденный
точкой за 10 с от начала движения
4. Решить систему линейных уравнений методом Крамера
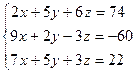
5.Решить систему линейных уравнений методом Крамера
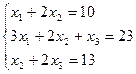
6. Решить систему уравнений методом Гаусса
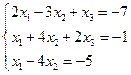
7.Решить систему уравнений методом Гаусса
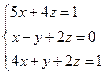
8.Решить систему уравнений методом обратной матрицы (матричным способом)
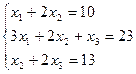
9. Решить систему уравнений матричным способом
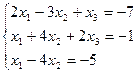
10. Даны матрицы ![]() и
и ![]()
Найти матрицу С = 5А – 2В
11. Даны матрицы 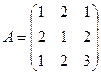 и
и 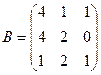 .
Найти матрицу С = А·В – В·А
.
Найти матрицу С = А·В – В·А
12. Вычислить определитель 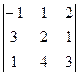
13. Составить каноническое
уравнение эллипса, у которого малая ось 2b = 6, а расстояние между фокусами ![]() = 8.
= 8.
14. Найти координаты фокусов, длины осей и эксцентриситет эллипса, заданного уравнением 16х2 + 25у2 = 400.
15. Найти координаты фокусов, длины осей, эксцентриситет и уравнения асимптот гиперболы, заданной уравнением 16х2 – 25у2 = 400.
16. Составить каноническое
уравнение гиперболы, действительная ось которой 2b = 10, а уравнения асимптот имеют вид: ![]() .
.
17. Найти координаты фокуса и уравнение директрисы параболы, заданной уравнением
у2 = 8х.
18. Составить уравнение параболы с вершиной в начале координат, если уравнение ее директрисы х.
19. Найти производную
функции ![]() .
.
20. Найти производную
функции ![]() .
.
21. Найти производную
функции ![]() .
.
22. Найти производную
функции ![]() .
.
23. Найти
неопределенный интеграл ![]() .
.
24. Найти
неопределенный интеграл методом замены переменной ![]() .
.
25. Найти
неопределенный интеграл методом замены переменной ![]() .
.
26. Найти
неопределенный интеграл методом замены переменной ![]() .
.
27. Найти
неопределенный интеграл методом замены переменной ![]() .
.
28. Вычислить
определенный интеграл 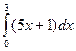 .
.
29. Вычислить
определенный интеграл 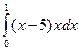 .
.
30. Вычислить
определенный интеграл 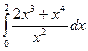 .
.
31. Скорость движения
точки изменяется по закону ![]() (м/с). Найти путь
s, пройденный точкой за 4 с от начала движения.
(м/с). Найти путь
s, пройденный точкой за 4 с от начала движения.
32. Вычислить объем
тела, полученного от вращения фигуры, ограниченной линиями ![]() ,
, ![]() ,
, ![]() ,
, ![]() , вокруг оси Ox.
, вокруг оси Ox.
33. Вычислить площадь
фигуры, ограниченной линиями ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
5.3. Билеты к дифференцированному зачету
Билет № 1
Специальность 08.02.02 Строительство и эксплуатация инженерных сооружений
Курс 2, группа ___, дисциплина Математика
1. Первообразная. Неопределенный интеграл и его свойства.
2.Решить систему линейных уравнений методом Крамера.
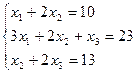
3.Найти координаты фокусов, длины осей, эксцентриситет и уравнения асимптот гиперболы, заданной уравнением 16х2 – 25у2 = 400.
В комплекте - 30 билетов.
К комплекту билетов для дифференцируемому зачету прилагаются разработанные преподавателем и утвержденные на заседании цикловой комиссии оценки по дисциплине.
Критерии оценки:
- оценка «отлично» выставляется студенту, если отражены в ответе все вопросы в полном объёме и решены задачи;
- оценка «хорошо», если отражены в ответе все вопросы, имеются неточности и решены задачи;
- оценка «удовлетворительно», если отражён в ответе только теоретический вопрос и решена одна задача;
- оценка «неудовлетворительно» не в полном объёме отражены ответы на вопросы и не решены задач.
6. ШКАЛА ОЦЕНКИ ОБРАЗОВАТЕЛЬНЫХ ДОСТИЖЕНИЙ
|
Процент результативности (правильных ответов) |
Оценка уровня подготовки |
|
|
балл (отметка) |
вербальный аналог |
|
|
90 ÷ 100 |
5 |
отлично |
|
80 ÷ 89 |
4 |
хорошо |
|
70 ÷ 79 |
3 |
удовлетворительно |
|
менее 70 |
2 |
неудовлетворительно |
7. Литература для подготовки к текущей и промежуточной аттестации
7.1. Печатные издания
1. Баврин И.И. «Математический анализ. Учебник и практикум для СПО. М. – Юрайт, 2016
2. Богомолов Н.В. практические занятия по математике; учебное пособие по математике для средних специальных учебных заведений. - М. Высшая школа, 2013.
3. Ивашев-Мусатов О.С. «Теория вероятностей и математическая статистика. Учебник и практикум для СПО. М. – Юрайт, 2016.
4. Татарников О.В. Элементы линейной алгебры. Учебники практикум для СПО. М. – Юрайт, 2016.
5. Попов А.М. Теория вероятностей и математическая статистика. Учебник для СПО. М. – Юрайт, 2017.
7.2. Электронные издания (электронные ресурсы):
1. Дадаян, А. А. Математика: учебник / А.А. Дадаян. — 3-е изд., испр. и доп. — Москва: ИНФРА-М, 2019. — 544 с. — (Cреднее профессиональное образование). - ISBN 978-5-16-102338-9. - Текст: электронный. - URL: https://new.znanium.com/catalog/product/1006658.
2. Шипова, Л. И. Математика: учеб. пособие / Л.И. Шипова, А.Е. Шипов. — Москва: ИНФРА-М, 2019. — 238 с. — (Среднее профессиональное образование). - ISBN 978-5-16-107059-8. - Текст: электронный. - URL: https://new.znanium.com/catalog/product/990024.
3. Фоминых, Е. И. Математика: Практикум / Фоминых Е.И. - Минск: РИПО, 2017. - 438 с.: ISBN 978-985-503-702-7. - Текст: электронный. - URL: https://new.znanium.com/catalog/product/977677 .
4. Кочеткова, И. А. Математика. Практикум: учеб. пособие / И. А. Кочеткова, Ж. И. Тимошко, С. Л. Селезень. - Минск: РИПО, 2018. - 503 с.: ил. ISBN 978-985-503-773-7. - Текст: электронный. - URL: https://new.znanium.com/catalog/product/1018898 .
5. Гусева, А. И. Дискретная математика: учебник / А.И. Гусева, В.С. Киреев, А.Н. Тихомирова. — Москва: КУРС: ИНФРА-М, 2019. — 208 с. — (Среднее профессиональное образование). - ISBN 978-5-16-105603-5. - Текст: электронный. - URL: https://new.znanium.com/catalog/product/978936.
6. Фоминых, Е. И. Математика. Практикум: учебное пособие / Е. И. Фоминых. - 2-е изд., испр. - Минск: РИПО, 2019. - 440 с. - ISBN 978-985-503-936-6. - Текст: электронный. - URL: https://new.znanium.com/catalog/product/1088275.
7. Бардушкин, В. В. Математика. Элементы высшей математики: учебник: в 2 т. Т. 2 / В.В. Бардушкин, А.А. Прокофьев. — Москва: КУРС, НИЦ ИНФРА-М, 2020. — 368 с. — (Среднее профессиональное образование). - ISBN 978-5-16-104732-3. - Текст: электронный. - URL: https://new.znanium.com/catalog/product/1047417.
8. Бардушкин, В. В. Математика. Элементы высшей математики: учебник: в 2 т. Т. 1 / В.В. Бардушкин, А.А. Прокофьев. — Москва: КУРС: ИНФРА-М, 2020. — 304 с. — (Среднее профессиональное образование). - ISBN 978-5-16-105427-7. - Текст: электронный. - URL: https://new.znanium.com/catalog/product/1079342.
9. Пенчанский, С. Б. Основы начального курса математики в примерах и залачах: учеб. пособие / С. Б. Пенчанский. — Минск: РИПО, 2018. — 239 с. - ISBN 978-985-503-830-7. - Текст: электронный. - URL: https://new.znanium.com/catalog/product/1020270.
10. Дадаян, А. А. Сборник задач по математике: Учебное пособие/Дадаян А. А., 3-е изд. - Москва: Форум, ИНФРА-М. Издательский Дом, 2018. - 352 с.: - (Профессиональное образование). - ISBN. - Текст: электронный. - URL: https://new.znanium.com/catalog/product/970454.
11. Жавнерчик, В. Э. Справочник по математике и физике / Жавнерчик В.Э., Майсеня Л.И., Савилова Ю.И., - 2-е изд. - Мн: Вышэйшая школа, 2014. - 399 с.: ISBN 978-985-06-2458-1. - Текст: электронный. - URL: https://new.znanium.com/catalog/product/509603.
12. Майсеня, Л. И. Справочник по математике: основные понятия и формулы / Майсеня Л.И., - 2-е изд. - Мн: Вышэйшая школа, 2012. - 399 с.: ISBN 978-985-06-2035-4. - Текст: электронный. - URL: https://new.znanium.com/catalog/product/508021.
13. Зельдович, Я. Б. Элементы прикладной математики / Зельдович Я.Б., Мышкис А.Д. - Москва: ФИЗМАТЛИТ, 2008. - 592 с.: ISBN 978-5-9221-0775-. - Текст: электронный. - URL: https://new.znanium.com/catalog/product/944876.
14. http://window.edu.ru/window/catalog Каталог Российского общеобразовательного портала.
15. http://www.school.edu.ru Каталог «Образовательные ресурсы сети Интернет для общего образования».
16. http://www.math.ru Материалы по математике в Единой коллекции цифровых образовательных ресурсов.
17. http://edu.of.ru/computermathМатематика в «Открытом колледже».
18. http://wwwkvant.infohttp://kvant.mccme.ru Образовательный математический сайт Exponenta.ru.
19. http://www.exponenta.ru Портал Allmath.ru — Вся математика в одном месте.
20. http://www.allmath.ru Прикладная математике: справочник математических формул, примеры и задачи с решениями.
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.