Министерство образования и науки Донецкой Народной Республики

Государственное бюджетное профессиональное образовательное учреждение

«ТОРЕЗСКИЙ ИНДУСТРИАЛЬНЫЙ ТЕХНИКУМ ИМ. А.Ф.ЗАСЯДЬКО»

ФОНДЫ ОЦЕНОЧНЫХ СРЕДСТВ

по дисциплине

ЕН.01 МАТЕМАТИКА

для специальностей:

13.02.11 Техническая эксплуатация и обслуживание электрического и электромеханического оборудования (горная отрасль)

2024

СОДЕРЖАНИЕ

1. ПАСПОРТ фонда оценочных средств. 3

2. Результаты освоения учебной дисциплины, подлежащие проверке.. 3

3. Оценка освоения учебной дисциплины... …4

3.1. Формы и методы оценивания………………………………………..4

3.2. задания для оценки освоения дисциплины (ПРИЛОЖЕНИЕ 1).6

4. ПЕРЕЧЕНЬ ТИПОВЫХ ЗАДАНИЙ/ВОПРОСОВ ДЛЯ ПРОМЕЖУТОЧНОЙ аттестации по учебной дисциплине..7

приложение 1.……………………………………………………………….9

1. ПаСПОрт фонда оценочных средств

В результате освоения учебной дисциплины ЕН.01 Математика обучающийся должен обладать предусмотренными ФГОС по специальности СПО 13.02.11 Техническая эксплуатация и обслуживание электрического и электромеханического оборудования (горная отрасль) следующими умениями, знаниями, которые формируют профессиональную компетенцию, и общими компетенциями:

ОК 01. Выбирать способы решения задач профессиональной деятельности применительно к различным контекстам;

ОК 02. Осуществлять поиск, анализ и интерпретацию информации, необходимой для выполнения задач профессиональной деятельности;

ОК 03. Планировать и реализовывать собственное профессиональное и личностное развитие;

ОК 10. Пользоваться профессиональной документацией на государственном и иностранном языках;

ОК 11. Использовать знания по финансовой грамотности, планировать предпринимательскую деятельность в профессиональной сфере;

ПК1.4 Составлять отчетную документацию по техническому обслуживанию и ремонту электрического и электромеханического оборудования;

ПК3.1 Участвовать в планировании работы персонала производственного подразделения;

ПК3.2 Организовывать работу коллектива исполнителей;

ПК3.3 Анализировать результаты деятельности коллектива исполнителей.

Формой аттестации по учебной дисциплине является экзамен.

2.Результаты освоения учебной дисциплины,

подлежащие проверке

В результате аттестации по учебной дисциплине осуществляется комплексная проверка следующих умений и знаний, а также динамика формирования общих компетенций:

Таблица 1

Результаты обучения: умения, знания и общие компетенции	Форма контроля и оценивания
Уметь:
.решать прикладные задачи в области профессиональной деятельности	Оценка в ходе проведения и защиты практических работ Интерпретация результатов наблюдения за деятельностью обучающихся в процессе групповой дискуссии
Знать:
значение математики в профессиональной деятельности и при освоении ППССЗ	Оценка выполненных домашних работ Оценка выполненных практических работ Оценка результатов контрольных работ Оценка результатов устных опросов
основные математические методы решения прикладных задач в области профессиональной деятельности
основные понятия и методы математического анализа, дискретной математики, линейной алгебры, теории комплексных чисел, теории вероятностей и математической статистики
основы интегрального и дифференциального исчисления

3.Оценка освоения учебной дисциплины

3.1. Формы и методы оценивания

Предметом оценки служат умения и знания, предусмотренные ФГОС по дисциплине ЕН.01 Математика, направленные на формирование общих и профессиональных компетенций.

Контроль и оценка освоения учебной дисциплины по темам (разделам)

Таблица 2

Элемент учебной дисциплины

Формы и методы контроля

Текущий контроль

Форма контроля

Проверяемые У, З, ОК, ПК

Раздел 1. Элементы теории комплексных чисел

Тема 1.1 Комплексные числа и действия над ними

Устный опрос

Практическая работа №1

У1, З3, З 1, З2

ОК2, ОК4, ОК5, ОК 8

Раздел 2. Основные понятия и методы линейной алгебры

Тема 2.1 Матрицы и определители

Устный опрос

Математический диктант

Практическая работа №2

У1, З 1, З2, З3,

ОК2, ОК4, ОК5, ОК8

Тема 2.2 Решение систем линейных алгебраических

уравнений

Устный опрос

Практическая работа №3

Контрольная работа

У1, З 1, З2, З3,

ОК2, ОК4, ОК5, ОК8

Раздел 3. Математический анализ

Тема 3.1 Предел функции. Непрерывность функции

Устный опрос

У1, З2, З4, З1, З3

ОК2, ОК4, ОК5, ОК8

Тема 3.2 Производная, исследование функций с помощью производных

Устный опрос

Практическая работа №4

Практическая работа №5

У1, З2, З4 З1, З3

ОК2, ОК4, ОК5, ОК8

Тема 3.3. Интеграл и его приложения

Устный опрос

Практическая работа №6

Практическая работа №7

У1, З2, З4, З1, З3

ОК2, ОК4, ОК5, ОК8

Тема 3.4. Дифференциальные уравнения

Устный опрос

Практическая работа №8

Контрольная работа

У1, З2, З4, З1,З3

ОК2, ОК4, ОК5, ОК8

Раздел 4. Основы теории вероятностей и математической статистики

Тема 4.1 Элементы теории вероятностей

Устный опрос

Практическая работа №9

У1, З2, З3,З1

ОК2, ОК4, ОК5, ОК8

Тема 4.2 Элементы математической статистики

Устный опрос

Практическая работа №18

У1, З2, З3,З1

ОК2, ОК4, ОК5, ОК8

3.2. задания для оценки освоения дисциплины (ПРИЛОЖЕНИЕ 1)

Таблица 3

Оценивающий инструмент

Критерии оценки

Тест

Проводится письменно. Время, отведенное на процедуру - 40 минут.

Неявка – 0 баллов.

Критерии оценки определяются процентным соотношением.

Удовлетворительно - от 56% правильных ответов.

Хорошо - от 75% правильных ответов.

Отлично – от 90% правильных ответов.

Максимальная оценка – 5 баллов.

Доклад

(сообщение)

Проводится в письменной и/или устной форме

Критерии оценки:

1.Соответствие содержания доклада заявленной тематике (1 балл).

2.Качество источников и их количество при подготовке работы(1 балл).

3.Владение информацией и способность отвечать на вопросы аудитории (1 балл).

4.Качество самой представленной работы (1 балл).

5.Оригинальность подхода и всестороннее раскрытие выбранной тематики (1 балл).

Максимальная сумма баллов - 5 баллов.

Задачи

Проводится в письменной форме.

1. Выбор оптимального метода решения задачи -(1 балл)

2. Умение применить выбранный метод –(1 балл)

3. Логический ход решения правильный, но имеются арифметические ошибки в расчетах –(1 балл).

4. Решения задачи и получение правильного результата –(2 балла)

5.Задача не решена вообще –(0 баллов)

Максимальная оценка – 5 баллов.

Контрольная работа

Проводится в письменной форме. Время, отведённое на выполнение работы – 60 минут.

Оценивается правильность результатов, верность графического изображения фигуры и выбора формулы для выполнения задания.

Критерии оценки определяются процентным соотношением:

Неудовлетворительно – менее 51% правильных результатов.

Удовлетворительно - от 51% правильных результатов.

Хорошо - от 70% правильных результатов.

Отлично – от 90% правильных результатов.

Максимальная оценка – 5 баллов.

Практическая

работа

1. Оформление в соответствии с требованиями – (1 балл)

2. Выбор методов для выполнения заданий – (1 балл)

3.Умение применять выбранные методы – (1 балл)

4. Выполнение заданий и получение верных результатов – (2 балла)

Максимальная оценка – 5 баллов.

4.ПЕРЕЧЕНЬ ТИПОВЫХ ЗАДАНИЙ ДЛЯ

аттестации по учебной дисциплине

1. Комплексные числа и изобразить на плоскости и найти их модули

2. Записать в тригонометрической форме комплексное число

3. Записать комплексное число в алгебраической и тригонометрической формах

4. Записать комплексное число в алгебраической и показательных формах:

5. Решить уравнение

6. Решить уравнение

7. Выполнить действия над матрицами , если

8. Вычислить определитель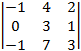

9. Найти линейную комбинацию , если

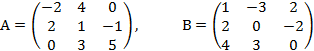
10. Найти матрицу, обратную заданной:

11. Решить систему уравнений методом Крамера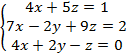

12. Решить матричным способом систему уравнений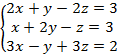

13. Вычислить предел функции

14. Вычислить предел функции

15. Вычислить производную функции

16. Тело движется по закону 𝑆(𝑡) = 2𝑡³ − 12𝑡² − 5 (м). Найти момент времени 𝑡 (с), когда тело остановится.

17. Тело движется по закону 𝑆(𝑡) = 𝑡³ + 2𝑡² − 5 (м). Найти скорость движения тела в момент времени 𝑡 = 2 (с).

18. Найти производную 2-ого порядка для функции

19. Найти критические точки функции

20. Тело движется по закону 𝑆(𝑡) = 4𝑡³ + 2𝑡² − 3 (м). Найти ускорение движения тела.

21. Тело массой 5 кг движется по закону S(t)=5t²+2t-4. Найти кинетическую энергию тела через 3 секунды после начала движения

22. Вычислить площадь фигуры, ограниченной графиком функции и осью абсцисс

23. Количество электричества, протекшего через проводник, начиная с момента времени t=0, дается формулой q=t²+3t+1. Найдите силу тока в конце десятой секунды.

24. Вычислить производную функции

25. Для функции составить уравнение касательной в точке 𝑥₀=−1

26. Найти количество электричества, проходящего через поперечное сечение проволоки за 20 с, если сила тока изменяется по закону І( t) = 5t³ - 4t² + t + 8( А).

27. Найти значение определенного интеграла

28. Найти значение определенного интеграла

29. Вычислить интеграл

30. Вычислить неопределенный интеграл . Результат проверить дифференцированием

31. Вычислить определенный интеграл

32. Скорость движения тела изменяется по закону V(t)=(3t²+t+1)м/с. Найдите путь, пройденный телом за 6с от начала движения.

33. Скорость движения точки выражается формулой V=(15t -5t²)м/с. Найдите путь, пройденный точкой от начала движения до ее остановки.

34. Найдите путь, пройденный телом за 5-ю секунду, зная, что скорость его прямолинейного движения выражается формулой V =3t²-4t -2 м/с.

35. Найти общее решение уравнения

36. Решить уравнение

37. Найти частные решения дифференциального уравнения если при

38. В урне 10 белых и 16 черных шаров. Наудачу берут 8 шаров. Какая вероятность того, что среди них будет ровно 5 белых шаров?

39. Вероятность попадания стрелка в мишень при первом выстреле – 0,8, при втором – 0,6. Сделано два выстрела. Какова вероятность того, что в мишени будет ровно одна пробоина?

40. Абонент забыл две последние цифры номера телефона и помнит лишь, что они разные. Какова вероятность правильного набора номера?

41. Сколько матчей будет сыграно на футбольном чемпионате с участием 12 команд, если каждые две команды встречаются между собой один раз?

42. В отделе работают 5 экономистов и 9 инженеров. Сколькими способами можно отобрать 2 экономистов и 3 инженеров, если специалисты считаются равноценными?

43. Дискретная случайная величина задана рядом распределения. Найти р₁, М(Х), D(X)

Х	0	2	3	4	5
Р	р₁	0,3	0,3	0,1	0,1

44. Дискретная случайная величина задана рядом распределения. Найти р₁, М(Х), D(X)

Х	1	5	7	8	10
Р	р₁	0,2	0,1	0,3	0,1

ПРИЛОЖЕНИЕ 1

Задания для оценки освоения дисциплины

Контрольная работа по теме «Линейная алгебра»

Вариант 1	Вариант 2
1. Найдите 2А+3В, если 2. Найти матрицу, обратную заданной: 3. Решите систему уравнений матричным методом и методом Крамера:	1. Найдите 3А-2В, если 2. Найти матрицу, обратную заданной: 3. Решите систему уравнений методом Крамера и методом Гаусса:
Вариант 3	Вариант 4
1. Найдите 3А+2В, если 2. Найти матрицу, обратную заданной: 3. Решите систему уравнений матричным методом и методом Крамера:	1. Найдите 2А-3В, если 2. Найти матрицу, обратную заданной: 3. Решите систему уравнений методом Крамера и методом Гаусса:

Контрольная работа по теме «Основы математического анализа»

Вариант 1

1. Найдите первообразную функции , если график первообразной

проходит через точку А( 0; 3).

2. Найдите неопределённый интеграл:

а) ; б)

в).

Выполните проверку дифференцированием.

3. Вычислить:

а) ; б) .

4. Вычислить площадь фигуры, ограниченной линиями :

; у=0.

Вариант 2

1. Найдите первообразную функции , если график первообразной проходит через точку А( 0; 3).

2. Найдите неопределённый интеграл:

а) ; б)

в).

Выполните проверку дифференцированием.

3. Вычислить:

а) ; б) .

4. Вычислить площадь фигуры, ограниченной

линиями :

Вариант 3

1. Для функции укажите первообразную F, график которой проходит через точку .

2. Найдите неопределённый интеграл:

а) ; б)

в)..

Выполните проверку дифференцированием.

3. Вычислить:

а) ; б) .

4. Вычислить площадь фигуры, ограниченной

линиями :

Вариант 4

1. Найдите первообразную функции , если график первообразной проходит через точку .

2. Найдите неопределённый интеграл:

а) ; б)

в).

Выполните проверку дифференцированием.

3. Вычислить:

а) ; б) .

4. Вычислить площадь фигуры, ограниченной

линиями :

Перечень практических работ

№ п/п	Наименование работы	Время выполнения
1	Действия над комплексными числами. Переход из одной формы в другую. Решение квадратных уравнений с отрицательным дискриминантом	2
2	Выполнение действий над матрицами	2
3	Решение систем линейных уравнений различными методами	2
4	Полное исследование функции и построение графиков	2
5	Применение производной к решению практических задач	2
6	Вычисление площадей фигур с помощью определенного интеграла	2
7	Вычисление определенных и неопределенных интегралов	2
8	Решение дифференциальных уравнений	2
9	Решение задач на определение вероятности события	2
10	Определение числовых характеристик выборок; геометрическое изображение: полигоны частот, гистограммы	2
Итого		20

Перечень докладов (сообщений)

1. Развитие понятия числа.

2. Применение комплексных чисел в естествознании и технике.

3. История возникновения дифференциального исчисления.

4. История возникновения и развития теории вероятностей.

Скачано с www.znanio.ru

Министерство образования и науки

СОДЕРЖАНИЕ 1. ПАСПОРТ фонда оценочных средств

ПаСПОрт фонда оценочных средств

Знать: значение математики в профессиональной деятельности и при освоении

Контроль и оценка освоения учебной дисциплины по темам (разделам)

ПРИЛОЖЕНИЕ 1) Таблица 3

ПЕРЕЧЕНЬ ТИПОВЫХ ЗАДАНИЙ ДЛЯ аттестации по учебной дисциплине 1

Найти значение определенного интеграла 29

ПРИЛОЖЕНИЕ 1 Задания для оценки освоения дисциплины

Контрольная работа по теме «Основы математического анализа»

Перечень практических работ № п/п

Материалы на данной страницы взяты из открытых истончиков либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

09.11.2024