5. Медиация и разрешение конфликтов. Умение урегулировать конфликтные ситуации и осуществлять медиацию поможет укрепить позитивные межличностные отношения, Применение методов, используемых для разрешения конфликтов, таких как активное слушание, постановка вопросов и поиск компромиссных решений.

Таким образом, проанализированное проблемное поле данной статьи позволяет сформулировать следующие выводы: научные предложения основаны на исследованиях и могут помочь обучающимся ИТ-классов развивать позитивные межличностные отношения и чувствовать себя лучше в образовательной среде. Необходимо помнить, что каждый человек уникален, поэтому может потребоваться время и терпение, чтобы наладить отношения с окружающими людьми. Развитие навыков саморегуляции и эмпатии помогает улучшить качество взаимоотношений и преодолеть конфликты.

Список литературы

1.           Атаманов Г.А. Информационная безопасность: сущность и содержание / Г.А. Атаманов // Бизнес и безопасность в России. – 2007. – №47. – С. 106–115.

2.           Бичева И.Б. Безопасность образовательной среды как категория современного профессионально-педагогического знания / И.Б. Бичева, О.М. Филатова // Вестник Мининского университета. – 2017. – №1. – С. 48 [Электронный ресурс]. – Режим доступа: https://vestnik.mininuniver.ru/jour/article/view/326/327 (дата обращения: 16.10.2023).

3.           Долина Н.В. Я – лидер нового поколения: учебное пособие / Н.В. Долина. – М.: Просвещение, 2023.

4.           Непрокина И.В. Безопасная образовательная среда: моделирование, проектирование, мониторинг: учебное пособие / И.В. Непрокина. – Тольятти: ТГУ, 2012. – EDN TMAAWB

5.           Чирков В.И. Самодетерминация и внутренняя мотивация поведения человека / В.И. Чирков // Вопросы психологии. – 1996. – №3. – С. 116–117.

6.           Ясвин В.А. Образовательная среда: от моделирования к проектированию / А.А. Ясвин. – М.: Смысл, 2001. – EDN OFJKFI

Снигирева Людмила Николаевна магистр, учитель

МКОУ «Лицей №7 имени Шуры Козуб с. Ново-Ивановского» с. Ново-Ивановское, Кабардино-Балкарская Республика

ФОРМИРОВАНИЕ ЭМОЦИОНАЛЬНОГО ИНТЕЛЛЕКТА ОБУЧАЮЩИХСЯ В ПРОЦЕССЕ ОРГАНИЗАЦИИ  ЗАНЯТИЙ ПО МАТЕМАТИКЕ

Аннотация: в статье рассматривается вопрос формирования эмоционального интеллекта обучающихся в процессе организации занятий по математике как в урочной, так и внеурочной деятельности путём решения заданий метапредметной направленности. Автор приходит к выводу, что система заданий способствует созданию учебных ситуаций, обеспечивающих плодотворное начало, протекание и завершение познавательной деятельности учащихся. В заданиях четко и понятно определяются адекватные учебные действия, создаются условия благополучной мотивации деятельности, предусматривается усложнение операционной ее стороны, корректируются процесс и результаты, прогнозируются последующие виды деятельности. Таким образом, образовательная задача математического образования – формирования эмоционального интеллекта обучающихся выполняется наличием познавательной стороны этой эмоции, т.е. радостью познания, которая обеспечивает системное включение ребенка в процесс самостоятельного построения им нового знания и позволяет проводить поэтапное обучение на уровне познавательного интереса к науке.

Ключевые слова: последовательности, прогрессии, эмоциональный интеллект, дополнительные занятия.

Изучение арифметической и геометрической прогрессии является одной из самых сложных тем школьного курса математики. Вместе с тем рассматриваемые прогрессии являются эффективным средством решения ряда текстовых задач и находят свое применение в теории чисел, физике, геодезии, информатике, социально-экономических и геометрических задачах. Тем не менее, знакомство с этим материалом дает представление учащимся об общих идеях и методах математической науки, таких как метод математической индукции для вывода формул, доказательства равенств и неравенств, решения задач на делимость. Задачи и задания способствуют развитию критического мышления, овладению приёмами анализа, синтеза, отбора и систематизации материала, формируют умение учиться и организовывать свою деятельность, формируют политехническое мышление.

Прогрессии изучаются в курсе алгебры 9 класса. Всего на тему «Арифметическая и геометрическая прогрессии» в Федеральной Рабочей Программе (ФРП) отводится 15 часов (5 недель) из 30 часов в третьей четверти. Существенным отличием изучения этой темы от традиционной подачи материала является параллельное изучение арифметической и геометрической прогрессии [3], а это способствует формированию познавательного интереса посредствам профессиональной направленности предмета математики. В ФРП СООв 10 классе на базовомуровне изучению темы «Последовательности и прогрессии» отводится 5 часов (2,5 нед.), на углубленном уровне^* 10 часов (2,5 нед.) по содержанию: Последовательности, способы задания последовательностей. Метод математической индукции^*. Монотонные и ограниченные^* последовательности. История возникновения математического анализа как анализа бесконечно малых^*. Арифметическая и геометрическая прогрессии. Бесконечно убывающая геометрическая прогрессия. Сумма бесконечно убывающей геометрической прогрессии. Линейный и экспоненциальный рост^*. Число е*. Формула сложных процентов. Использование прогрессии для решения реальных задач прикладного характера [4]. Также в работах Филатова Е.Н. предлагается углубить на дополнительных занятиях эту тему, уделяя решению заданий от средней трудности до олимпиадного уровня [5] в среднем 7–8 занятий. Материал темы учебника составляет 180 стр., что позволяет самостоятельно подробно изучить его ученику.

Одним из путей изучения сложных тем курса является организация рефлексивного обучения математики. Рефлексивное обучение математике определяется, как обучение, главный акцент которого делается на умении учащегося осмысливать математическую деятельность, её цели, структуру и результат. Данный метод обучения нацелен на активизацию имеющихся знаний учащихся, их обобщение и систематизацию, применение знаковых математических методов в незнакомых ситуациях, ликвидацию познавательных пробелов на основе рефлексивных стратегий, позволяет обогатить ментальный опыт учащихся [1, c.45]. При этом методическая схема изучения прогрессий в старших классах системно выстраивается по этапам.

1 Этап изучения. Мотивация. На уроке предлагается рассмотреть типое задание на исследование последовательностей с помощью информационного листка (рис.1).

Цель учителя: выявить область интересов исследования темы учащихся и применения её в будущей профессии.

Цель ученика: прочитать текст и ответить на вопрос: «В каких профессиях (науках) применяются Последовательности?» Ожидаемый ответ.

На интерактивной доске составляется список профессий (наук). Можно открывать по типу игры «Сто к одному», а можно огласить весь список и попросить учащихся расставить названия по своим приориетатм «Что мне интересно».

Рис. 1. Информационный листок «Последовательности» [1, с. 170]

Далее обсуждается, в каких современных статьях эта тема приведена. Учащимся домой раздают статьи по их интересам (см. табл. 1) для определения темы исследовательского проекта во внеурочной деятельности. Исходя из опыта работы, на уроке вводного занятия по теме Последовательности, способы задания последовательностей, уделяется 15–20 минут, т.к. эта тема совмещена с анализом контрольной работы предыдущего блока. Хорошая эмоциональная разгрузка для учащихся во второй половине урока! В образовании выполняется один из новых компонентов формирования эмоционального интеллекта учащихся. А именно практическое внедрение основных идей Концепции и ФООП, где стоит одна из задач перед системой образования проблема формирования эмоционального интеллекта обучающихся (в принятых примерных рабочих программах по каждому предмету в разделе «Метапредметные результаты»).

Таблица 1 Россыпь фраз (игра «Сто к одному»)

В конце занятия учащиеся приходят к выводу, что прогрессии применяются во всех сферах деятельности человека.

2 Этап изучения. Введение. На уроке по теме «Арифметическая и геометрическая прогрессии» основных понятий, формул и алгоритмов учащимся предлагается вспомнить основной материал из  5–9 классов с помощью обобщенной схемы (рис. 2).

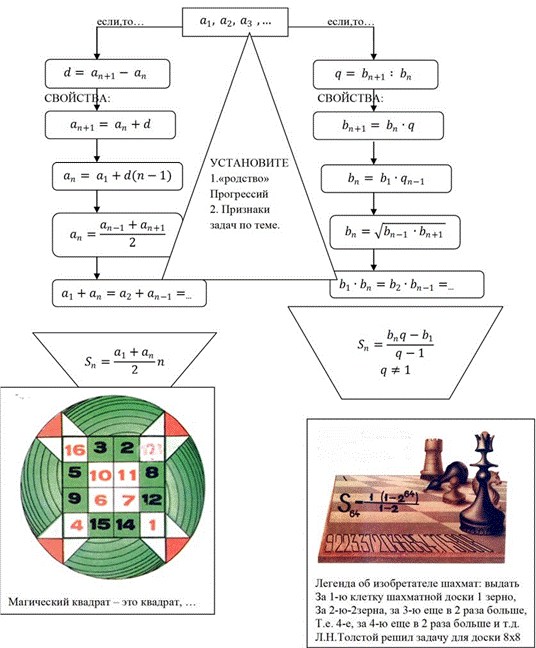
Рис. 2. Схема «Сравнение арифметической и геометрической прогрессий»

При этом обращаем внимания учащихся на то, что прогрессии – это последовательности чисел, которые обладают определенным законом изменения.

Ожидаемый результат. Перечислим пять основных признаков задач на прогрессию: 1) наличие последовательности чисел или величин;

2)    изменение значений последовательности с некоторым закономерным шагом;

3)    наличие задачи на нахождение суммы или среднего арифметического элементов последовательности;

4)    наличие задачи на нахождение неизвестного элемента последовательности;

5)    ^* наличие задачи на нахождение суммы или произведения корней уравнения. Если мы имеем дело с квадратным уравнением, которое можно представить в виде произведения двух скобок, то сумма корней будет являться коэффициентом перед старшей степенью уравнения, а произведение корней – свободным коэффициентом. Если коэффициенты можно выразить через последовательности, то это может быть задача на прогрессию.

3      этап. Усвоение. На этапе усвоения темы на дополнительных занятиях решаются задачи методом интеграции последовательностей, таким образом, устанавливается взаимосвязь между числовой последовательностью и различными видами прогрессий, таких как геометрическая и алгебраическая прогрессия. Также особое внимание уделяется различным формам записи числовых последовательностей и решению задач с применением формул алгебраических и геометрических прогрессий.

Задание. Задать последовательность разными способами.

      Последовательность:      = 4n -1.

Решение: Последовательность задана формулой общего члена. Можем задать ее числовой последовательностью. Для этого подставим вместо n натуральные числа n =1, 2, 3, 4…. Получим: ₁, ₂, ₃, 4… или 3, 7, 11, 15,…. d1: 4 4 4.

Определим, будет ли разность               ₁ 1 одинаковой для всех пар чисел. В данном случае, d1 – постоянная величина. Следовательно, наша последовательность является арифметической прогрессией. Можем применить реккурентную формулу арифметической прогрессии:

                                                                                            1 .

      А в нашем случае        ₁ 1, или            ₁ =          + 4.

Вывод: числовую последовательность можно задать разными способами. Как правило, почти всегда можно из последовательности вывести новую последовательность, которая будет являться геометрической или арифметической прогрессией. Отметим также, что задать числовую последовательность формулой общего члена не всегда возможно – иногда последовательность задаётся путём перечисления её членов (например, последовательность простых чисел).

4      этап. Обобщения и систематизации.

В учебнике Е.Н. Филатова предлагается рассмотреть текстовые задачи по пяти направлениям:

1.  Числовые последовательности – применение последовательностей в экспериментах и быту.

2.  Текстовые задачи на применение арифметической прогрессии.

3.  Геометрическая прогрессия в геометрических задачах.

4.  Текстовые задачи на применение геометрической прогрессии.

5.  Комбинированные задания.

Целями этого этапа являются использование умений диагностики и коррекции собственной деятельности при решении задач. Таким образом, в учебнике рассмотрены этапы и условия использования учебно-познавательных задач.

Проиллюстрируем все выше сказанное, разбором задачи по методике Е.Н. Филатова в текстовой беседе Автора и Читателя (можно на уроке зачитать по ролям).

Задача: 15 января планируется взять кредит в банке на 10 месяцев. Условия его возврата таковы: – 1-го числа каждого месяца долг возрастает на 4% по сравнению с концом предыдущего месяца; – со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; – 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15 -е число предыдущего месяца. Сколько процентов от суммы кредита составляет общая сумма денег, которую нужно выплатить банку за весь срок кредитования?

Автор: обозначим сумму кредита через . Данную сумму взяли на 10 месяцев, как это запишем?

                             10        9         8              2         1

        Читатель: S,      S,    S,…          S,            S, 0.

                                10 10 10                   10 10

Автор: читаем первое условие возврата: – 1-го числа каждого месяца долг возрастает на 4% по сравнению с концом предыдущего месяца. Это что значит?

Читатель: начисляем процент на основной долг: S·0,04 +      S·0,04 +             S·0,04+…+ S·0,04 +

S·0,04 + 0·0,04.

Автор: выполняем преобразования.

Читатель: S +0,04· S· (1+ +…).

Автор: что записано в скобках?

Читатель: В скобках записана сумма членов арифметической прогрессии.

Автор: Правильно. Можно ли воспользоваться какой-либо формулой?

Читатель: можно использовать формулу суммы первых  членов арифметической прогрессии. Автор: что получим?

Читатель: получим:  + 0,04 ·  ·(            ·10)=  + 0,04 ·  ·=  · 1,22.

2

Автор: отсюда видно, что 122% от суммы кредита составляет общая сумма денег, которую нужно выплатить банку за весь срок кредитования.

Очевидно, что человек, увидевший в теоретической формуле ясный ответ на заинтересовавшийся его вопрос, проблему, трудность, эту теоретическую формулу не забудет, т.к. каждая мыслительная операция сопровождается у учащихся определенными эмоциональными эффектами, на которые преподаватель может влиять. Это обеспечивает более осознанное овладение математической теорией, обучает учащихся самостоятельному выполнению заданий, учит новым приемам поиска, исследования и методов доказательства.

5 этап. Применение.

На этом этапе необходимо научить учащихся применению формул арифметической и геометрической прогрессий в задачах современной математики и олимпиадных задачах.

1. Теория чисел.

Теорема Дирихле в теории чисел называется теоремой о простых числах Дирихле и гласит, что «для любых двух взаимнопростых положительных чисел m и n (m и n не имеют нетривиальных общих множителей) существует бесконечно много простых чисел вида m + αn, где значения α – положительные целые числа». Более точно, теорема Дирихле утверждает, что последовательность m, m + n, m + 2n, m + 3n, …, m + αn, … содержит бесконечно много простых чисел. Напомним одно важное свойство простых чисел, заключающееся в том, что если натуральное число d является составным, то для наименьшего простого делителя g числа d выполняется неравенство g²≤ d. Детально с «общими свойствами рядов Дирихле» можно ознакомиться в научной литературе [2, с. 331], а мы рассмотрим применение столь важной теоремы при решении школьных математических задач.

Задача. Найдите не менее пяти чисел из бесконечного множества простых чисел.

Решение. Рассмотрим прогрессию вида 4α + 3 (при целом α). Заметим, что всякое простое число больше 2 обязательно нечетное (иначе оно делилось бы на число 2). Возьмем несколько целых чисел

1= 0, ₂= 1, ₃= 2, ₄= 4, ₅= 5 и т. д. Теперь подставим в нашу прогрессию: 4 · 0 + 3 = 3; 4 · 1 + 3 = 7; 4 · 2 + 3 = 11; 4 · 4 + 3 = 19; 4 · 5 + 3 = 23. Итак, мы получили пять чисел из бесконечного множества простых чисел. По такому же принципу можно найти первые десять чисел из бесконечного множества простых чисел в прогрессиях: 1) 8α + 1, 2) 10α + 9.

Теорема Дирихле, кроме всего прочего, дает возможность решать логические и геометрические задачи, а также задачи, содержащие числовые последовательности, является весьма эффективным методом решения задач, дающим во многих случаях наиболее простое и изящное решение.

2. Упрощение алгебраических выражений с помощью формул суммы прогрессий.

Числовая последовательность – частный случай числовой функции, а именно функция натурального аргумента. В школьном курсе математики понятие последовательности объясняют на определённых примерах, демонстрируя, что последовательность может быть задана словесно, аналитически или рекуррентно. Приведем пример из учебника Е.Н. Филатова олимпиадного задания, решаемого с помощью свойств геометрической прогрессии. Задача. Упростить выражение: х²- х⁴+ х⁶+…+ х²⁰.

х²- х⁴+ х⁶+…+ х²⁰ – это сумма геометрической прогрессии, где ₁ = х², q = – х². Заметим, что пока-

затели степеней задаются формулой 2n. Если 2n = 20, то n = 10, т.е. в данной сумме 10 слагаемых. Тогда

.

6 этап. Контроля.

На этапе контроля проверяется сформированные умения учащихся применять аппарат арифметической и геометрической прогрессии как метод решения математических задач. На дополнительных занятиях предлагается провести Расчетную работу по технологии тренинга (см. рис.3). Такие виды работ на уроке сформировывают политехнические навыки учащихся, а именно вырабатывают умение правильно, аккуратно и чётко выполнять чертежи, проводить вычисления. Причём, само оформление работы и предоставление её результатов полностью зависит от творческого подхода учащегося. Это даёт возможность школьникам совершенствовать приобретённые познавательные универсальные учебные действия в процессе изучения темы «Последовательности и прогрессии».

Рис. 3. Схема расчетной работы

Проанализировав этапы изучения темы «Последовательности и прогрессии», можно сказать, что система заданий способствует созданию учебных ситуаций, обеспечивающих плодотворное начало, протекание и завершение познавательной деятельности учащихся. В заданиях четко и понятно определяются адекватные учебные действия, создаются условия благополучной мотивации деятельности, предусматривается усложнение операционной ее стороны, корректируются процесс и результаты, прогнозируются последующие виды деятельности. Таким образом, образовательная задача математического образования – формирования эмоционального интеллекта обучающихся выполняется наличием познавательной стороны этой эмоции, т.е. радостью познания, которая обеспечивает системное включение ребенка в процесс самостоятельного построения им нового знания и позволяет проводить поэтапное обучение на уровне познавательного интереса к науке.

Список литературы

1.      Вордерман Кэрол Как объяснить ребенку математику / Кэрол Вордерман. – М.: Манн, Иванов и Фербер, 2016.

2.      Воронин С.М. Дзета-функция Римана / С.М. Воронин. – М.: Физматлит, 1994. – 376 с.

3.      Мишина В.Ю. Формирование познавательного интереса посредством профессиональной направленности предмета математики / В.Ю. Мишина, Е.Н. Эрентраут // Актуальные проблемы развития среднего и высшего образования: XIII межвузовский сборник научных трудов. – Челябинск: Край Ра, 2017. – С. 112–115. EDN YUGFAT

4.      Федеральная рабочая программа среднего общего образования. Математика. Углубленный уровень. – М., 2023. – С. 81. 5. Филатов Е.Н. Алгебра. 10 класс: учебное пособие / Е.Н. Филатов. – Ч. 2. – М.: Авангард; НИЯУ МИФИ, 2018.

Сычева Марина Николаевна преподаватель

Колледж ФГБОУ ВО «Южно-Уральский государственный  гуманитарно-педагогический университет» г. Челябинск, Челябинская область

ПРОБЛЕМА СОЦИАЛЬНО-ПСИХОЛОГИЧЕСКОЙ АДАПТАЦИИ ПЕРВОКУРСНИКОВ К ПРОЦЕССУ ОБУЧЕНИЯ  В ПЕДАГОГИЧЕСКОМ КОЛЛЕДЖЕ

Аннотация: в статье обсуждается проблема адаптации студентов первого курса к условиям обучения в педагогическом колледже. Автором рассматриваются трудности, с которыми сталкиваются первокурсники на начальном этапе процесса обучения, анализируются сложности иногородних студентов, описываются способы решения проблемы социально-психологической адаптации студентов в колледже ФГБОУ ВО «Южно-Уральский государственный гуманитарно-педагогический университет».

Ключевые слова: адаптация, студент-первокурсник, куратор, студент-наставник, студенческий коллектив.

В настоящее время в российском обществе наблюдается повышение престижа среднего профессионального образования. Это, на наш взгляд, обусловлено рядом причин.

1.          Выпускники настороженно относятся к необходимости сдачи Единого государственного экзамена после окончания средней школы, не чувствуют уверенности в уровне своих знаний для успешной сдачи экзамена.

2.          Молодые люди стремятся как можно быстрее получить профессию, начать трудовую деятельность и, как результат, стать финансово независимыми от своих родителей.

3.          Статус студента колледжа для подростков более значителен, чем статус школьника.

В образовательных учреждениях СПО отмечается повышение количества абитуриентов, что позволяет произвести набор студентов с более высоким уровнем знаний. Как правило, эти студенты уже замотивированы на обучение и дальнейшее трудоустройство по выбранной специальности. Это особенно актуально для колледжей педагогической направленности, так как перед ними стоит задача не только подготовить специалиста разносторонне образованного, профессионально зрелого с активной жизненной позицией, но и умеющего воспитать ученика с широким кругозором, гражданина современного российского общества.

Чем быстрее вчерашний абитуриент адаптируется к процессу обучения в колледже, его особенностям, тем продуктивнее будет этот процесс, тем скорее и эффективнее будут сформированы его профессиональные компетенции.

Проблема адаптации первокурсников к процессу обучения представляется очень актуальной. В разное время ее исследованием занимались Ж. Пиаже, Р.С. Немов, В.А. Емельянов, А.А. Горяйнов,