Формирование функциональной грамотности как условие повышения качества образовательных результатов на уроках ЕМЦ

Формирование функциональной грамотности как условие повышения качества образовательных результатов на уроках ЕМЦ

Функциональная грамотность - явление метапредметное, и поэтому она формируется при изучении всех школьных дисциплин и имеет разнообразные формы проявления. 

Типы задач:

·        Предметные задачи: в условии описывается предметная ситуация, для решения которой требуется установление и использование знаний конкретного учебного предмета, изучаемых на разных этапах и в разных его разделах; в ходе анализа условия необходимо «считать информацию», представленную в разных формах, сконструировать способ решения.

·        Межпредметные задачи: в условии описана ситуация на языке одной из предметных областей с явным или неявным использованием языка другой предметной области. Для решения нужно применять знания из соответствующих областей; требуется исследование условия с точки зрения выделенных предметных областей, а также поиск недостающих данных, причем решение и ответ могут зависеть от исходных данных, выбранных (найденных) самими обучающимися.

·        Практико-ориентированные задачи: в условии описана такая ситуация, с которой подросток встречается в повседневной своей жизненной практике. Для решения задачи нужно мобилизовать не только теоретические знания из конкретной или разных предметных областей, но и применить знания, приобретенные из повседневного опыта самого обучающегося. Данные в задаче должны быть взяты из реальной действительности.

·        Ситуационные задачи: не связаны с непосредственным повседневным опытом обучающегося, но они помогают обучающимся увидеть и понять, как и где могут быть полезны ему в будущем знания из различных предметных областей. Решение ситуационных задач стимулирует развитие познавательной мотивации обучающихся, формируют способы переноса знания в широкий социально-культурный контекст.

Задача №1. Менеджер одной компании по продаже газированных напитков заметил, что летом при повышении температуры на один градус продажа напитков увеличивается примерно на 200 литров в день и на столько же она уменьшается на каждый градус понижения температуры. Сегодня он продал 4 600 литров напитка.

·                       Сколько он может продать завтра, если а) температура повысится на 1^оС; б) станет жарче на 2^оС; в) температура упадет на 1^оС; г) температура не изменится?

·                       При каком изменении температуры объем продаж напитка не будет превышать 3 000 литров?

·                       На складе хранится 6 400 литров продукции. К какому наибольшему повышению температуры готова компания?

I этап. Построение математической модели.

Как видно из вопросов задачи, нам необходимо не только определить, сколько менеджер сможет продать завтра газированных напитков при четырех различных условиях (вопрос № 1), но и исследовать различные варианты продажи (вопросы № 2 и № 3). Для решения этой задачи составим общую формулу, которая бы учитывала количество проданного напитка в зависимости от колебания температуры.

Пусть у — количество литров напитка, которое может быть продано завтра. Будем считать, что завтра температура изменится на х градусов. Заметим, что если температура повышается, то х — величина положительная, а если понижается — то отрицательная. Тогда объем продаж изменится на 200х и составит:
у = 4 600 + 200х.
Таким образом, для каждого вопроса задачи можно составить математическую модель:

·        «Найти величину у по формуле у = 4 600 + 200х при х равном а)1; б)2; в)–1; г)0».

·        «Решить неравенство 4 600 + 200х  3 000».

·        «Решить уравнение 4 600 + 200х = 6 400».
II этап. Исследование математической модели.

·        Подставляем в формулу у = 4 600 + 200х различные значения для х и находим у. Результаты удобно заносить в таблицу.

а) у = 4 600 + 200(+1) = 4 800, 
б) у = 4 600 + 200(+2) = 5 000,
в) у = 4 600 + 200(–1) = 4 400,
г) у = 4 600 + 2000 = 4 600.

·        Решаем неравенство 4 600 + 200х  3 000. Получаем 200х  –1 600 или 
х  –8.

·        Решаем уравнение 4 600 + 200х = 6 400. После преобразований получаем 
200х = 1 800 или х = 9.

III этап. Анализ (интерпретация) результатов.

·        Этот этап для этой задачи не вызывает затруднений. Если температура повысится на 1^оС, то можно рассчитывать на продажу 4 800 литров напитка. Если температура повысится на 2^оС, то продажи за следующий день могут достичь 5 000 литров. Понижение температуры на 1^оС сулит сокращение продаж до 4 400 литров. Объемы продаж не изменятся, если завтра не изменится температура.

·        Так как х — это изменение температуры, то из полученного нами результата х  –8 можно сделать вывод, что объем продаж не превысит 3 000 литров при понижении (об этом говорит знак минус) температуры на 8 ^оС и более.

·        Компания не будет испытывать недостатка в товаре, даже если температура завтра поднимется на 9 ^оС. Однако, это наибольшее повышение температуры, к которому готова компания по складским запасам.

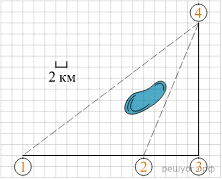
Задача №2. Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. 

Полина летом отдыхает у дедушки в деревне Ясная. В четверг они собираются съездить на велосипедах в село Майское в магазин. Из деревни Ясная в село Майское можно проехать по прямой лесной дорожке. Есть более длинный путь: по прямолинейному шоссе через деревню Камышёвка до деревни Хомяково, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в село Майское. Есть и третий маршрут: в деревне Камышёвка можно свернуть на прямую тропинку в село Майское, которая идёт мимо пруда.

Лесная дорожка и тропинка образуют с шоссе прямоугольные треугольники.

Задача №3. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме.

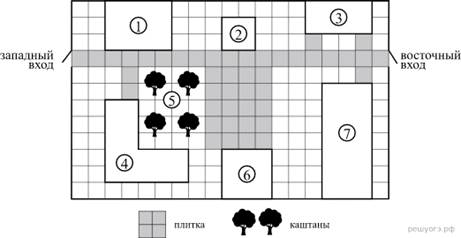
На плане (см. рисунок) изображён парк культуры и отдыха города Малый. Сторона каждой клетки равна 2 м. Парк имеет прямоугольную форму. Зайти в парк можно через один из двух входов: западный или восточный.

Если зайти в парк через западный вход, то слева будет расположено кафе «Полдник», а справа — детская площадка. Рядом с детской площадкой посажены каштаны. Рядом с восточным входом располагаются общественные туалеты и бадминтонная площадка, обозначенная на плане цифрой 7. Помимо указанных объектов, в парке имеются фонтан (отмечен цифрой 2) и сцена. Все дорожки в парке имеют ширину 2 м и вымощены тротуарной плиткой 1 м × 1 м. Между фонтаном и сценой имеется площадка, вымощенная такой же плиткой.

Задача №4.   Найдите объём парного отделения строящейся бани (в куб. м).

Хозяин дачного участка строит баню с парным отделением. Парное отделение имеет размеры: длина 3,9 м, ширина 2,1 м, высота 2 м. Для разогрева парного помещения можно использовать электрическую или дровяную печь. Три возможных варианта даны в таблице.

Для установки дровяной печи дополнительных затрат не потребуется. Установка электрической печи потребует подведения специального кабеля, что обойдётся в 6200 руб. Кроме того, хозяин подсчитал, что за год электрическая печь израсходует 2300 киловатт-часов электроэнергии по 3,5 руб. за 1 киловатт-час, а дровяная печь за год израсходует 1,6 куб. м дров, которые обойдутся по 1700 руб. за 1 куб. м.

Задача №5.  Какое наименьшее количество дуг нужно заказать, чтобы расстояние между соседними дугами было не более 60 см?

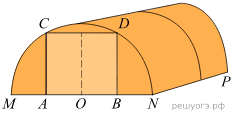
Алексей Юрьевич решил построить на дачном участке теплицу длиной NP = 5,5 м. Для этого он сделал прямоугольный фундамент. Для каркаса теплицы Алексей Юрьевич заказывает металлические дуги в форме полуокружностей длиной 5,8 м каждая и плёнку для обтяжки. В передней стенке планируется вход, показанный на рисунке прямоугольником ACDB .

Точки A и B — середины отрезков MO и ON соответственно.

Задача №6. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. 

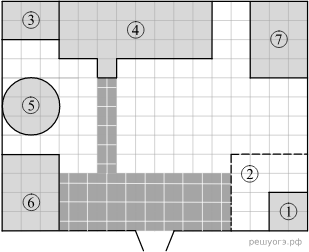
На плане изображено домохозяйство по адресу: с. Коткино, улица Садовая, д. 7 (сторона каждой клетки на плане равна 1 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота.

При входе на участок слева от ворот находится овчарня, отмеченная на плане цифрой 6. Площадь, занятая овчарней, равна 12 кв. м.

Жилой дом находится в глубине территории. Помимо овчарни и жилого дома, на участке имеются пристройка к дому и теплица, построенная на территории огорода (огород отмечен цифрой 2). Между пристройкой и овчарней расположен пруд. Также на участке есть курятник, расположенный рядом с домом.

Все дорожки внутри участка вымощены тротуарной плиткой размером 0,5 м × 0,5 м. Между овчарней и огородом имеется площадка, вымощенная такой же плиткой.

На участке планируется провести электричество.

Задача №7. Света отправила SMS-cообщения с новогодними поздравлениями своим 19 друзьям. Стоимость одного SMS-сообщения 1 рубль 90 копеек. Перед отправкой сообщения на счету у Светы было 37 рублей. Сколько рублей останется у Светы после отправки всех сообщений?

Задача №8. Летом килограмм клубники стоит 80 рублей. Маша купила 2 кг 500 г клубники. Сколько рублей сдачи она должна была получить с 1000 рублей?

Задача №9. Для покраски 1 кв. м потолка требуется 150 г краски. Краска продаётся в банках по 2,5 кг. Какое наименьшее количество банок краски нужно для покраски потолка площадью 41 кв. М?

Задача №10. На день рождения полагается дарить букет из нечётного числа цветов. Тюльпаны стоят 45 рублей за штуку. У Вани есть 300 рублей. Из какого наибольшего числа тюльпанов он может купить букет Маше на день рождения?

Задача №11. При взвешивании животных в зоопарке выяснилось, что буйвол тяжелее льва, медведь легче буйвола, а рысь легче льва. Выберите утверждения, которые следуют из приведённых данных.

1) Рысь легче медведя.

2) Буйвол самый тяжёлый из всех этих животных.

3) Медведь тяжелее льва.

4) Рысь легче буйвола.

Задача №12. Грузчик на складе может поднять упаковку размером 3×3×3 литровых пакетов молока. Смогут ли три грузчика поднять упаковку 9×9×9 пакетов?

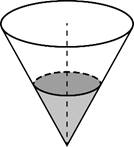
Задача №13. В сосуд, имеющий форму конуса, налили 25 мл жидкости до половины высоты сосуда (см. рисунок). Сколько миллилитров жидкости нужно долить в сосуд, чтобы заполнить его доверху?

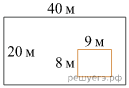
Задача №15. Дачный участок имеет форму прямоугольника, стороны которого равны 40м и 20м. Дом, расположенный на участке, на плане также имеет форму прямоугольника, стороны которого равны 9 м и 8 м. Найдите площадь оставшейся части участка, не занятой домом. Ответ дайте в квадратных метрах.

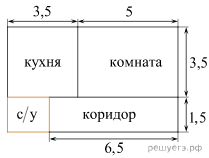
Задача №16. Квартира состоит из комнаты, кухни, коридора и санузла (см. чертёж). Комната имеет размеры 5 м × 3,5 м, коридор — 1,5 м × 6,5 м , длина кухни — 3,5 м. Найдите площадь санузла (в квадратных метрах).

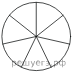
Задача №17. На рисунке показано, как выглядит колесо с 7 спицами. Сколько будет спиц в колесе, если угол между соседними спицами в нём будет равен 12°?

Проблема формирования функциональной грамотности актуальна для школьников. В обществе, осуществляющем переход к экономике знаний, процесс овладения компонентами функциональной грамотности продолжается всю жизнь.