Формирование логического мышления обучающихся на уроках математики и информатики в условиях внедрения нового ГОС

Сценарий мастер-класса

«Формирование логического мышления обучающихся на уроках математики и информатики в условиях внедрения нового ГОС»

 

Учитель информатики

МБОУ «Специализированная школа  № 35 г. Донецка»

 Кузнецова Ирина Васильевна

 

 

Всё наше достоинство заключено в мысли

Б.Паскаль

 

Тема:  Формирование логического мышления обучающихся на уроках математики и информатики в условиях внедрения нового ГОС

Цель: создание условий для развития мыслительных операций путём использования нестандартных заданий.

 Задачи:

• Способствовать развитию мыслительных операций: сравнение, анализ, синтез, классификация, абстрагирование и обобщение.
• Познакомить с приёмами решения нестандартных заданий.
• Способствовать развитию интеллектуальных способностей.
• Повысить интерес к решению нестандартных логических задач по информатике и  математике.
• Задействовать участников в работе на мастер-классе.

Результаты:

- Разработать модель использования нестандартных заданий по информатике и  математике, которая способствует развитию мыслительных операций, таких как обобщение, анализ, синтез, сравнение, классификация, абстрагирование.

- Создать методический продукт: банк логических нестандартных заданий по информатике и  математике.

- Разместить информацию о проведении мастер-класса и рабочие материалы в сети Интернет.

План проведения

 

№	Содержание работы
I.	Теоретическая часть Мастер-класс «Формирование логического мышления  обучающихся на уроках математики и информатики в условиях внедрения нового ГОС».
II.	Практическая часть Обзор и решение развивающих нестандартных заданий по информатике, с целью развития мыслительных операций (обобщение, анализ, синтез, сравнение, классификация, абстрагирование).
III.	Практическая часть Обзор и решение развивающих нестандартных заданий по  математике.
IV.	Рефлексия. Подведение итогов
І. Теоретическая часть. Формирование логического мышления  обучающихся на уроках математики и информатики в условиях внедрения нового ГОС
		Всё наше достоинство заключено в мысли, - писал французский математик и философ 17 века Б. Паскаль. Не пространство, не время, которых мы не можем заполнить, возвышает нас, а именно она, наша мысль. Почему же так важно научить детей мыслить?
		Мотивационное видео, ввод в тему.
		В Государственном образовательном стандарте основного общего образования на 2015-2017 год сказано, что в результате изучения образовательной отрасли «Математика и информатика» обучающиеся развивают логическое и математическое мышление, получают представление о математических моделях; овладевают математическими рассуждениями; учатся применять математические знания при решении различных задач и оценивать полученные результаты; овладевают умениями решения учебных задач; развивают математическую интуицию; получают представление об основных информационных процессах в реальных ситуациях.
		Мышление расширяет границы познания, даёт возможность выйти за пределы непосредственного опыта ощущений и восприятия. Мышление даёт возможность знать и судить о том, что человек непосредственно не наблюдает, не воспринимает. Оно позволяет предвидеть наступление таких явлений, которые в данный момент не существуют.
		Различают два вида мышления: продуктивное и репродуктивное.
		Условием развития репродуктивного мышления является наличие у школьника необходимого минимума знаний.
		Условием возникновения продуктивного мышления – наличие проблемной ситуации, способствующей осознанию потребности в открытии новых знаний, стимулирующей высокую активность решающего проблему субъекта.
		Возможность оперировать в голове отвлеченными понятиями развивает саму способность к мышлению.  Известно всем, для того, чтобы способность к мышлению развивалась, мозгу надо постоянно подбрасывать новые оригинальные проблемы и задания. В процессе их решения мыслительные способности улучшаются. Действительно, мышление учащегося проявляется в умении анализировать и синтезировать, сравнивать и находить закономерности, классифицировать, обобщать, рассуждать, конкретизировать, т.е. в умении применять различные приемы мыслительной деятельности к изучаемому материалу, к решению задачи, к любой жизненной ситуации.  Мышление человека, и в частности школьника, наиболее ярко проявляется при решении задач.  Любая мыслительная деятельность начинается с вопроса, который ставит перед собой человек, не имея готового ответа на него. Иногда этот вопрос ставят другие люди, но всегда акт мышления начинается с формулировки вопроса, на который надо ответить, задачи, которую надо решить, с осознания чего-то неизвестного, что надо понять, уяснить.
		Мышление представляет собой процессы познания человеком объектов и явлений окружающего мира и их связей, решения жизненно важных задач, поиска неизвестного, предвидения будущего.  Логическое же мышление – основа школьного образования, залог успешного понимания технических и гуманитарных дисциплин.
		Одним из основных метапредметных результатов, формируемых при изучении информатики в основной школе является владение информационно-логическими умениями:  определять понятия, создавать обобщения, устанавливать аналогии, классифицировать, самостоятельно выбирать основания и критерии для классификации, устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение  и делать выводы.
		В основе системы знаний учащихся лежит сформированность системы понятий изучаемой предметной области. Владение понятийным аппаратом в большей степени определяет понимание учебного материала, его использование для решения прикладных задач. Мышление у человека происходит понятиями и ассоциациями с ними связанными, понимание учебного материала расширяет понятийную базу учащегося, в следствии расширяя масштабы и потенциал его мышления. Каждое новое вводимое понятие должно быть четко определено, раскрыта суть изучаемого понятия, кроме того, должны быть определены связи данного понятия с другими понятиями, как уже введенными, так и еще неизвестными учащимся.
		Включенность понятия в совокупность взаимосвязей помогает появлению дополнительных ассоциаций, закреплению понятия в схемах мышления учащихся, переносу знаний о понятии из одной области на знания из других областей, и как следствие формирование универсальных учебных действий, прописанных в Государственном образовательном стандарте основного общего образования.
		Формирование логических приемов мышления у школьников способствует развитию у них познавательной деятельности и продуктивных мыслительных процессов.  Логические приемы мышления результативно формируются и развиваются, если их процесс становления отвечает следующим методическим требованиям:  -учет возрастных особенностей школьников;  -последовательность формирования логических приемов мышления; системность; - непрерывность и преемственность в методике формирования и развития логических приемов мышления на различных этапах обучения.
		Логическое мышление не является врожденным, поэтому его можно и нужно развивать. Решение логических задач на уроках информатики в начальной школе как раз и представляет собой один из приемов развития мышления. Это дает возможность развить внимание, память и привить навыки правильного мышления. Однако нужно помнить, что решение задач – это только один из приемов достижения цели.
		Для формирования логического мышления в среднем звене можно применить тесты, которые можно разделить на три основные группы: словесные, символико-графические и комбинированные и логические задачи. К первой группе относятся анаграммы и вербальные тесты.  К комбинированным логическим тестам относятся задания, содержащие как вербальную версию, так и символико-графическую. Таким образом, осуществляется связь информатики с языковым развитием учащихся. Такие упражнения требуют не только наблюдательности, но и умения устанавливать необычные связи между объектами. Примерами таких упражнений могут быть  «Вставь пропущенное слово»,  «Исключи лишнее», «Переставь буквы» и др.
		После усвоения таких заданий можно приступить к освоению эвристических методов решения логических задач. Человек, владеющий эвристикой, мыслит уже не хаотично, как это бывает, а, применяя эвристические приемы, что позволяет ему решать, казалось бы, неразрешимые задачи. Освоение эвристических приемов – это умение применять их при решении трудных задач, что дается лишь упорной тренировкой.
		Развитию логического мышления способствует формирование навыков решения логических задач. Поэтому в курс информатики включен раздел «Алгебра логики». Основная цель раздела – формирование у школьников основ логического мышления. При решении логических задач учащиеся учатся анализировать, сравнивать, описывать планы действий, делать выводы; у них вырабатываются навыки излагать свои мысли в строгой логической последовательности.
		Подбирая задания необходимо учитывать следующие аспекты: Какие мыслительные операции будут «работать» при ее решении; Будет ли сама постановка задачи способствовать активизации мышления учащихся; Какие критерии развития мышления можно применить в ходе решения этой задачи.
		Логическое мышление не является врожденным, значит, на протяжении всех лет обучения в школе необходимо всесторонне развивать мышление учащихся, учить их логически мыслить. Логика необходима там, где имеется потребность систематизировать и классифицировать различные понятия, дать им четкое определение. Решение логических задач позволяет улучшить логическое мышление учащихся, развить способность рационально мыслить упорядочить и систематизировать мыслительные процессы.
		Видео 10 класс «бросает вызов» участникам мастер-класса.

 

 

ІІ. Практическая часть. Информатика.

Развивающие упражнения

 

1.     Найдите лишнее в каждой строке:

  

 

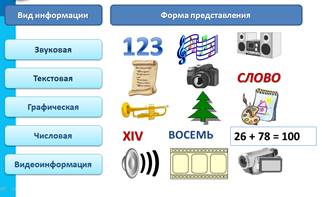
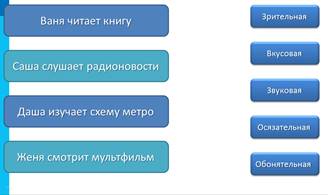
2.     Установите соответствие:

 

3.     Заполните таблицу:

       

 

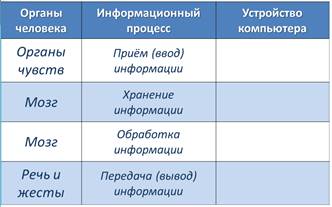
4.     Разгадайте ребус:

 

5.     Найдите лишнее в каждой группе:

  

 

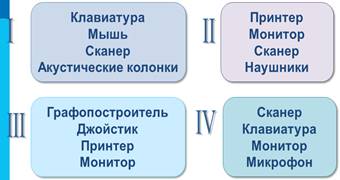
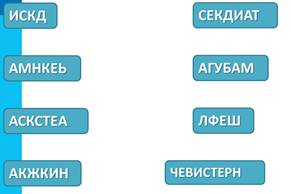
6.     Анаграммы:

 

7.     Интерактивные упражнения на работу с множествами:

             

 

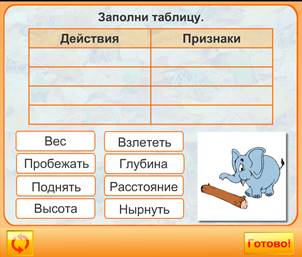
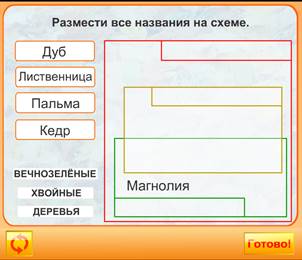
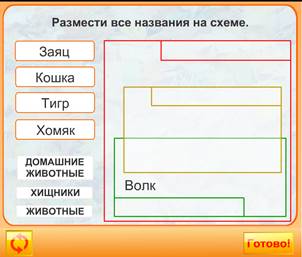
8.                     Решите задачу методом последовательного уточнения:

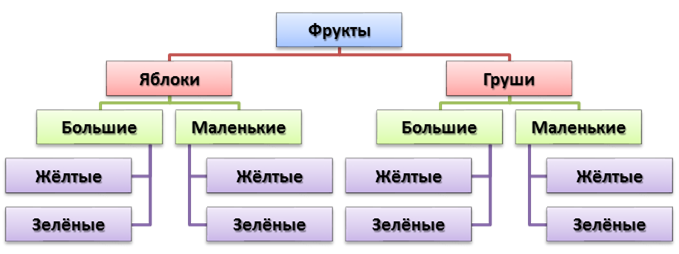
Бабушка прислала Ивану посылку с яблоками и грушами. Некоторые из этих плодов были большими, остальные – маленькими. По цвету плоды тоже различались: часть плодов была жёлтого цвета, остальные – зелёного. Среди плодов не было ни маленьких груш, ни маленьких зелёных яблок. Яблок было 25, а груш – 17. Больших плодов было 32. Жёлтых плодов было 28. Зелёных яблок было на 2 больше, чем зелёных груш. Иван угостил этими плодами своих друзей. Больше всего ребятам понравились  большие жёлтые яблоки.

Сколько было таких яблок?

Практическая часть. Информатика. Задачи

 

1.                     Пятеро одноклассников: Аня, Саша, Лена, Вася и Миша стали победителями школьных олимпиад по физике, математике, информатике, литературе и географии. Известно, что:

Победитель по информатике учит Аню и Сашу работать на компьютере;

Лена и Вася тоже заинтересовались информатикой;

Саша всегда побаивался физики;

Лена, Саша и победитель по литературе занимаются плаванием;

Саша и Лена поздравили победителя по математике;

Аня сожалеет, что у нее мало времени на литературу.

 

2.                     Квадрат, круг, ромб и треугольник вырезаны из белой, синей, красной и зелёной бумаги. Известно, что круг не белый и не зелёный; синяя фигура лежит между ромбом и красной фигурой; треугольник не синий и не зелёный; квадрат лежит между треугольником и белой фигурой. Из бумаги какого цвета вырезаны фигуры?

	белая	синяя	красная	зелёная
квадрат
круг
ромб
треугольник

 

3.            В детском саду 52 ребёнка. Каждый из них любит конфеты или мороженое. Половина детей любит конфеты, а 20 человек – конфеты и мороженое. Сколько детей любит мороженое? Сколько детей любит только мороженое?

 

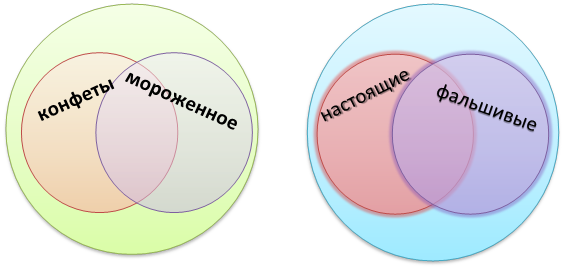
4.                     Одноногий Сильвер со своей шайкой обнаружил клад, спрятанный самим Флинтом. Пираты были крайне нетерпеливы – всем хотелось скорее получить свою долю. 52-м пиратам  достались настоящие пиастры, а 30-ть пиратов получили  фальшивые. 12-ти  достались и фальшивые и настоящие.

Сколько всего пиратов нашло сокровища?

5.                     Коля, Вася и Серёжа гостили летом у бабушки. Однажды один из мальчиков нечаянно разбил любимую бабушкину вазу.

На вопрос, кто разбил вазу, они дали такие ответы:

Серёжа: Я не разбивал. Вася не разбивал.

Вася: Серёжа не разбивал. Вазу разбил Коля.

Коля: Я не разбивал. Вазу разбил Серёжа.

Бабушка знала, что один из её внуков (правдивый), оба раза сказал правду; второй (шутник) оба раза сказал неправду; третий (хитрец) один раз сказал правду, а другой раз - неправду. Назовите имена правдивого, шутника и хитреца.

Кто из внуков разбил вазу?

 

6.                   Разбирается дело Джона, Брауна и Смита. Известно, что один из них нашёл и утаил клад. На следствии каждый из подозреваемых сделал два заявления:

Смит: «Я не делал этого. Браун сделал это».

Джон: «Браун не виновен. Смит сделал это».

Браун: «Я не делал этого. Джон не делал этого».

Суд установил, что один из них дважды солгал, другой дважды сказал правду, третий один раз солгал, один раз сказал правду.

Кто из подозреваемых должен быть оправдан?

 

7.                   Составить расписание занятий так, чтобы математика была первым или вторым уроком, информатика первым или третьим уроком, а физика – вторым или третьим. В расписании всего три урока. Сколько вариантов расписания с такими условиями можно составить?

 

ІІІ. Теоретическая часть.

Развитие логического мышления на уроках математики

	Меняется жизнь: претерпевают изменения её социальная и нравственная сферы. В связи с этим возникает много проблем, какая должна быть экономика, политика, как обеспечить достойный уровень жизни всех граждан государства. Общество не может стоять на месте, оно развивается, и для прогресса нужны люди свободные, высокообразованные, творческие, обладающие высоким уровнем развития разных видов мышления.   Вряд ли вы достигнете высот в любой из точных наук, не зная математику на достаточно высоком уровне. Это невозможно, точно так же, как взять первый приз на конкурсе имени Чайковского человеку, который лишен слуха. Занятие физикой, химией, астрономией и большинством других наук, без досконального знания математики (причем высшей), совершенно нереально. В этих дисциплинах недостаточно просто поставить эксперимент, его нужно еще и описать и сделать выводы. Все это делается с помощью уравнений и математических формул. Очень часто сначала строится математическая модель определенного явления, а уж потом она проверяется на практике.
	Одним из важнейших условий построения обучения, которое способствует развитию мыслительной деятельности школьников на уроках математики, является пробуждение их к самостоятельной мысли. Развитие у школьников теоретического сознания и мышления есть следствие того, что соответствующими знаниями, умениями и навыками учащиеся овладевают в форме учебной деятельности. Это овладение теоретическими знаниями происходит в диалоге, дискуссии, в их сознании постоянно функционирует анализ, обобщение, планирование, рефлексия.
	Согласно государственному образовательному стандарту основного общего образования предметные результаты изучения предмета Математика в образовательной отрасли «Математика и информатика» должны отражать: развитие умений работать с учебным математическим текстом (анализировать, извлекать необходимую информацию), точно и грамотно выражать свои мысли с применением математической терминологии и символики, проводить классификации, логические обоснования, доказательства математических утверждений.        Поэтому, важнейшей задачей математического образования является вооружение учащихся общими приёмами мышления, развитие способности понимать смысл поставленной задачи, умение логически рассуждать. Каждому важно научиться анализировать, отличать гипотезу от факта, отчётливо выражать свои мысли. Большие развивающие возможности в этом плане имеют уроки математики. В современной ситуации обучения математике ставятся задачи, связанные не только вооружением младших школьников математическими знаниями, умениями и навыками, но и развитием познавательных способностей на математическом материале. Большое внимание решению последней задачи уделяют развивающие программы математического образования.
	Математика проникает почти во все области деятельности человека, что положительно сказалось на темпе роста научно-технического прогресса. В связи с этим стало жизненно необходимым усовершенствовать математическую подготовку подрастающего поколения. В качестве развития познавательных процессов при этом используются различные методы и средства. Наиболее эффективным средством развития логического мышления младших школьников выступает игра. Наилучшим образом используются логико-математические игры, в которых смоделированы математические отношения, закономерности, предполагающие выполнение логических операций.
	В.А. Сухомлинский писал: «…Не обрушивайте на ребёнка лавину знаний… под лавиной знаний могут быть погребены пытливость и любознательность. Умейте открыть перед ребёнком в окружающем мире что-то одно, но открыть так, чтобы кусочек жизни заиграл перед детьми всеми цветами радуги. Открывайте всегда что-то неизведанное, чтобы хотелось ещё и ещё раз возвратиться к тому, что он узнал». Поэтому обучение, воспитание и развитие ребёнка должны быть непринужденными, осуществляться через свойственные конкретному возрасту виды деятельности и педагогические средства.
	Роль математики в развитии логического мышления исключительно велика. Причина столь исключительной роли математики в том, что это самая теоретическая наука из всех изучаемых в школе. Выдающийся отечественный математик А.Н. Колмогоров писал: «Математика не просто один из языков. Математика – это язык плюс рассуждения, это как бы язык и логика вместе. Математика – орудие размышления. В ней сконцентрированы результаты точного мышления многих людей. При помощи математики можно связать одно рассуждение за другим, очевидные сложности природы с её странными законами и правилами, каждое из которых допускает отдельное очень подробное объяснение, на самом деле тесно связаны. Таким образом, математика позволяет сформировать определённые формы мышления, необходимые для изучения окружающего нас мира.
	В любой творческой деятельности, в учёбе, в труде, в игре, да и просто в жизни – везде внимание, смышлёность, умение логически мыслить – необходимы человеку, они помогают решать проблемы, находить выход из сложных ситуаций и полезны для здоровья: поддерживают тонус головного мозга, смекалку можно развить, упражняясь в решении занимательных задач, головоломок, разбирая математические игры, шутки и фокусы, то есть любые задания, требующие работы ума.
	Важнейшей задачей математического образования является вооружение учащихся общими приёмами мышления, пространственного воображения, развитие способности понимать смысл поставленной задачи, умение логично рассуждать, усвоить навыки алгоритмического мышления. Каждому важно научиться анализировать, отличать гипотезу от факта, отчётливо выражать свои мысли, а с другой стороны развить мысли и интуицию (пространственное представление, способность предвидеть результат и предугадать путь решения). Именно математика предоставляет благоприятные возможности для решения этих задач.

 

 

IV. Практическая часть. Математика

 

Задача 1. Землекопы.

Пять землекопов за 5 часов выкапывают 5 метров канавы. Сколько землекопов выкопают 100 метров канавы за 100 часов?

 

Задача 2. Станок.

За один час станок разрезает 300 шестиметровых досок на одинаковые куски, по 2 метра в каждом. Сколько времени потребуется, чтобы на этом же станке разрезать 200 восьмиметровых досок такой же ширины и толщины на такие же куски?

 

Задача 3. Переливание

Восьмиведерный бочонок заполнен доверху квасом. Двое должны разделить квас поровну. Но у них только два пустых бочонка, в один из которых входит 5 ведер, а в другой – 3 ведра. Как они могут разделить квас, пользуясь только этими тремя бочонками?

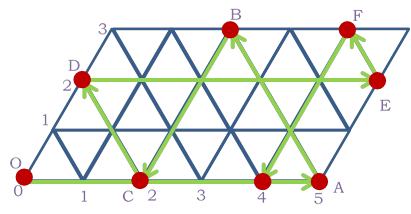
Решение (метод бильярда).

1. Наливаем молоко в 5-ведерный бочонок (переходим в точку А(5;0)).

2. Из 5-ведрного переливаем в 3-ведерный, в 5-ведерном остается 2 литра (точка В(2;3)).

3. Из 3-ведерного переливаем в 8-ведерный (точка С(2;0)).

4. Из 5-ведрного переливаем 2 ведра в 3-ведерный (точка D(0;2)).

5. В 5 – ведерный наливаем из 8-ведерного (точка E(5;2)). В 8-ведерном останется 1 ведро.

6. Из 5-ведерного переливаем в 3-ведерный (точка F(4;3)). В 5-ведерном осталось 4 ведра, из 3-ведерного переливаем в 8-ведерный, в котором теперь тоже 4 ведра.

Задача 4. Кошки и котята.

Четыре кошки и 3 котенка весят 15 килограммов, а 3 кошки и 4 котенка весят 13 килограммов. Предполагается, что все взрослые кошки весят одинаково и котята также весят одинаково. Сколько весит каждая кошка и каждый котенок в отдельности?

 

Задача 5. В вашем распоряжении пять двоек и любые знаки математических операций. Вы должны с помощью только этого цифрового материала, используя его полностью и применяя знаки математических операций, выразить числа 15, 11, 12321.

 

Задача 6. Парень пригласил девушку на свидание в кафе. А чтобы проверить, что это судьба, они договорились прийти туда в любое время с 12 до 13 часов. Тот, кто придет первым, будет ждать 20 минут, после чего уйдет. Какова вероятность, что это настоящая любовь и они встретятся? Учтите, что моменты их прихода независимы, и связаться друг с другом они никак не могут.

 

Задача 7.  На 2-х крышах сидят 16 голубей. С первой на вторую крышу перелетело пять голубей, а со 2-ой на первую два голубя, то на обеих крышах стало равное количество птиц. Вопрос: сколько изначально голубей было на каждой из крыш?

 

Задача 8. Саша ходит в бассейн один раз в три дня, а Вася один раз в четыре дня, Ваня – в 5 дней. Они встретились в бассейне в этот понедельник.
Через сколько дней и в какой день недели они встретятся снова?

 

Задача 9. После семи стирок измерения куска хозяйственного мыла, имеющего форму прямоугольного параллелепипеда, уменьшились в двое. На сколько еще стирок хватит оставшегося куска мыла? 

 

Задача 10.  Найти все пары целых чисел х и у, удовлетворяющих уравнению .

 

Задача 11. Найдите, какую цифру обозначает каждая буква в следующем равенстве: АХ^А=БАХ.

 

 

                                                                                                     V.            Рефлексия. Подведение итогов.

Давайте подведем итоги нашей работы. Сегодня прозвучало много важных слов о мышлении, логике, творчестве…

Давайте создадим НАШЕ облако слов. Помоги нам в этом! Мы воспользуемся облачным сервисом WORDLE. Какие слова вам кажутся наиболее важными и весомыми?

 

Разместим это облако слов вместе с фото-материалами нашей встречи на платформе программы «Время жить ярко!» и на странице учителей информатики Калининского района. Тут же вы найдете все презентационные и видеоматериалы нашей встречи.

 

Спасибо за плодотворную работу. Сегодня нами совместно была  разработана   модель использования нестандартных заданий по информатике и  математике, которая способствует развитию мыслительных операций, таких как обобщение, анализ, синтез, сравнение, классификация, абстрагирование.

Также у каждого из вас теперь есть методический продукт: банк логических нестандартных заданий по информатике и  математике, который вы сможете использовать как для работы на уроках, так и для построения индивидуальных образовательных траекторий обучающихся.

И еще, хотелось бы сказать….

Демонстрация финального видеофильма-мотиватора «Живи ярко!»

 

 

Приложение 1

Библиотека учителя информатики

 

1.                     Девочки Вика, Валя и Ксения зашли в кафе. Выяснилось, что каждая девочка заказала самое любимое блюдо. Девочки заметили, что они заказали три различных блюда в кафе: борщ, мороженное и овощной салат. Валя сказала, что ей не нравятся супы, т.к. мама их готовит каждый день. Вика предпочитает сладкое и не понимает своих подружек, которые в кафе заказывают первые или вторые блюда. Кто какое блюдо заказал?

2.                     Три одноклассника — Олег, Тимур и Том, встретились спустя 14 лет после окончания школы. Выяснилось, что один из них стал актёром, другой физиком, а третий юристом. Том сказал, что на туризм ему не хватает времени, хотя его сестра — единственный юрист в семье, заядлый турист. Одноклассники вспомнили, что Олег всегда увлекался точными науками, а профессию выбрал не связанную с точной наукой. Зато Тимур никогда не любил точные науки, т.к. является очень творческим человеком и связал свою жизнь с театром. Определи профессию каждого.

3.                     В симфонический оркестр приняли на работу трёх музыкантов: Вадима, Олега и Артёма, умеющих играть на скрипке, флейте, альте, кларнете, гобое и трубе. Известно, что: Олег самый высокий;  играющий на скрипке меньше ростом играющего на флейте; играющие на скрипке и флейте и Вадим любят пиццу; когда между альтистом и трубачом возникает ссора, Олег мирит их;  Вадим не умеет играть ни на трубе, ни на гобое. На каких инструментах играет Вадим, если каждый музыкант владеет двумя инструментами?

4.                     Работники банка Сидоров, Петрова и Федосеев приобрели себе автомобили Renault, BMW и Suzuki. Петрова рассказала хозяину Suzuki, что с детства мечтала о немецкой машине. Но её мечта не сбылась. Сидоров мечтал о французской машине, но его мечта тоже не сбылась. Только у Федосеева мечта сбылась о немецкой машине. Какую машину он приобрёл?

5.                     Четверо друзей – Алик, Володя, Миша и Юра – собрались в доме  у Миши. Мальчики оживленно беседовали о том, как они провели лето. Ну, Балашов, ты, наконец, научился плавать? – спросил Володя. О, еще как, - ответил Балашов – могу теперь потягаться в плавании с тобой и Аликом. Посмотрим, какой я гербарий собрал – сказал Петров, прерывая разговор друзей, и достал из шкафа большую папку. Всем, особенно Лунину и Алику, гербарий очень понравился. А Симонов обещал показать товарищам собранную им коллекцию минералов. Назови имя и фамилию каждого мальчика?

6.                     В рабочем поселке живут и работают девушки: Валя, Галя, Сима и Женя. Две из них - Валя и Галя – живут вместе и на работу утром тоже ходят вместе, так как места их  работы расположены вблизи друг от друга. Специальности у девушек разные – ткачиха, врач, секретарь, шофер. Женя и Валя участвуют в хоре при Дворце культуры. Врач решила познакомить Галю со своей подругой, чудесной девушкой – шофером, с которой Галя раньше не встречалась. Девушка, которая работает секретаршей, на работу  ходит одна. Она вообще любит уединение и книги, зато не любит музыку. Как оказалось Женя значительно старше ткачихи и врача. В задаче необходимо определить специальности каждой девушки.

7.                     Однажды пираты взяли на абордаж испанский галион. Они взяли в плен трех моряков. Их фамилии были Белов, Чернов, Рыжов. Один из них был блондин, другой – брюнет, третий – рыжий. Брюнет сказал Белову: «Ни у одного из нас цвет волос не соответствует фамилии». Какой цвет волос у каждого из них, если брюнеты всегда говорят правду?

8.                     Пусть А = «На Web-странице встречается слово "крейсер"», В = «На Web-странице встречается слово "линкор"». В некотором сегменте сети Интернет 5000000 Web-страниц. В нём высказывание А истинно для 4800 страниц, высказывание В - для 4500 страниц, а высказывание А∪В - для 7000 страниц.

Для какого количества Web-страниц в этом случае будут истинны следующие выражения и высказывание: НЕ (А ИЛИ В);  А И B; На Web-странице встречается слово "крейсер" И НЕ встречается слово "линкор".

9.                     На бригантине живут 60 пиратов. 37 из них вечером пьют чай. 33 – курят трубку, 42 – играют в кости. При этом 21 из них  пьют чай и курят трубку. 23 – играют в кости и курят трубку, 22 – играют в кости и пьют чай. Только 20 пиратов занимаются одновременно тремя делами: пьют чай, играют в кости и курят трубку. Так ли это. Сколько пиратов было на бригантине?

10.                 Лучший попугай капитана Флинта изучил 52 слова на разных языках. Он знал 35 слов на английском, а 23 на французском. 16 слов он знал и на французском и на английском. Остальные слова он почерпнул из могучего русского языка. Сколько слов попугай произносил из русского языка?

11.                 Несколько пиратов высадились на берег, чтобы подкрепиться. Из них 9 –любят бананы, 8 – ананасы, 7 – кокос. 5 – любят и бананы и ананасы, 4 – ананасы и кокос, 3 – бананы и кокос. И только двое охотно ели бананы, кокос и ананасы. Сколько пиратов высадилось на берег?

12.              Алёша, Боря и Гриша нашли в земле старинный сосуд. Рассматривая удивительную находку, каждый высказал по два предположения:  Алеша: «Это сосуд греческий и изготовлен в V веке».  Боря: «Это сосуд финикийский и изготовлен в III веке».  Гриша: «Это сосуд не греческий и изготовлен в IV веке».

Учитель истории сказал ребятам, что каждый из них прав только в одном из двух предположений. Где и в каком веке изготовлен сосуд?

13.              Команды четырех соседних школ соревновались в волейбольном турнире. Болельщики поделились своими предположениями:

1-й болельщик: 556-я победит, а 450-я — будет второй.

2-й болельщик: Нет, 556-я будет последней, а вот победит 324-я.

3-й болельщик: Уверен, что первой будет 445-я, а 450-я —третьей.

Когда соревнования закончились, выяснилось, что каждый болельщик был не прав в одном из своих прогнозов. Какое место заняли команды школы № 324, школы № 445, школы № 450 и школы № 556?

14.              Следователь допрашивает Клода, Жака и Дика.  Клод утверждает, что Жак лжет, Жак обвинял во лжи Дика, а Дик призывает не слушать ни того, ни другого. Кто из допрашиваемых говорил правду?

15.                 По обвинению в ограблении перед судом предстали три человека – Иванов,  Петров и Сидоров. Установлено следующее: Если Иванов невиновен, или Петров виновен, то Сидоров виновен. Если Иванов невиновен, то Сидоров невиновен. Установить, виновен ли Иванов.

Приложение 2

 

Библиотека учителя математики

 

Задача 1. Три друга

Три друга – Алеша, Коля и Саша – сели на скамейку в один ряд. Сколькими способами они могли это сделать?

 

Задача 2. Кубики, раковина и бусины.

На чашечных весах 3 кубика и 1 морская раковина уравновешиваются 12 бусинами, а 1 раковина уравновешивается 1 кубиком и 8 бусинами. Сколько бусин надо положить на свободную чашку весов, чтобы уравновесить раковину на другой чашке?

 

Задача 3. Вес фруктов.

Три яблока и 1 груша весят столько же, сколько 10 персиков, а 6 персиков и 1 яблоко весят столько же, сколько 1 груша. Сколько же персиков надо взять, чтобы уравновесить 1 грушу?

 

Задача 4. Пятью тройками.

Вы, конечно, знаете, что пятью тройками и знаками математических операций можно записать число 100:

.

Но можно ли записать пятью тройками число 10?

 

Задача 5. У филателиста Бори большое количество марок. Однажды он решил разместить их в большом альбоме, состоящем из 1000 страниц, так, чтобы на всех заполненных страницах марок было поровну (какие-то страницы в конце альбома могут остаться пустыми). Но когда Боря попробовал раскладывать по 7 марок на странице, то у него 5 марок осталось (но не все страницы были заполнены). Тогда он стал раскладывать сначала по 11 марок на странице, затем – по 13 марок на странице. Но снова у него оба раза осталось 5 марок. Наконец, когда Боря решил разложить по 23 марки на странице, то на этот раз у него осталось 6 марок. Сколько марок в коллекции у Бори? 

 

Задача 6.

В маленькой школе учится столько мальчиков, сколько и девочек. Однажды учитель принёс  234 ореха и разделил их. Каждому мальчику досталось по 5 орехов, а каждой девочке по  - 4. Но так как девочки обиделись, учителю пришлось ещё принести орехи и разделить их так, чтобы в конце концов всем досталось поровну, а именно по 6. сколько орехов принёс учитель во второй раз?

 

Задача 7.

В оранжерее было срезано 360 гвоздик. Причем красных на 80 больше, чем белых, а розовых на 160 штук меньше, чем красных. Какое наибольшее число одинаковых букетов можно составить из этого количества цветов? Сколько и каких цветов было в каждом букете?

 

Задача 8.

Докажите, что произведение четырех последовательных целых чисел, сложенное с единицей, есть точный квадрат. 

 

Задача 9. Рейс через океан.

Каждый день в полдень из Гавра в Нью-Йорк отправляется пароход через Атлантический океан, и в то же самое время пароход той же компании отправляется из Нью-Йорка в Гавр. Переезд в том и другом направлении совершается ровно за семь, дней. Сколько судов своей компании, идущих в противоположном направлении, встречает пароход на пути из Гавра в Нью-Йорк?

 

Задача 10. Почем дюжина лимонов?

Три дюжины лимонов стоят столько рублей, сколько дают лимонов на 16 рублей. Сколько стоит дюжина лимонов? (Одна дюжина =12.)

 

Задача 11. Мед и керосин.

Банка с медом весит 500 граммов. Та же банка с керосином весит 350 граммов. Керосин легче меда в 2 раза. Сколько весит пустая банка?

 

Задача 12. Кто разбил окно?

Один из пяти братьев – Андрей, Витя, Дима, Толя или Юра разбил окно. Андрей сказал: “Это сделал или Витя, или Толя”. Витя сказал: “Это сделал не я и не Юра”. Дима сказал: “Нет, один из них сказал правду, а другой – неправду”. Юра сказал: “Нет, Дима, ты не прав”. Их отец, которому, конечно, можно доверять, уверен, что не менее трех братьев сказали правду. Кто же из братьев разбил окно?

 

Задача 13. Попробуйте сложить.

Возьмите все цифры от 1 до 9, расположите их в две колонки так, чтобы сумма чисел в каждой колонке была одинаковой. Эта задача требует нестандартного мышления.

 

Задача 14. Сколько кошек?

В комнате четыре угла. В каждом углу сидит кошка. Напротив каждой кошки по три кошки. На хвосте каждой кошки по одной кошке. Сколько всего кошек в комнате?

 

Задача 15.

Футбольный мяч сшит из 32 лоскутков: белых шестиугольников и черных пятиугольников. Каждый черный лоскуток граничит только с белыми, а каждый белый – с тремя черными и тремя белыми. Сколько лоскутков белого цвета?

 

 

 

Скачано с www.znanio.ru