Формулы n-го члена и суммы первых n членов арифметической прогрессии

Тема: С Формулы n-го члена арифметической и геометрической прогрессий, суммы первых n членов (сумма арифметической прогрессии)

2.Тип урока: Урок освоения новых знаний и умений

3.Планируемые результаты:

Личностные:

Готовность к разнообразной совместной деятельности, стремление к взаимопониманию и взаимопомощи, активное участие в школьном самоуправлении. Овладение языковой и читательской культурой как средством познания мира. Овладение основными навыками исследовательской деятельности, установка на осмысление опыта, наблюдений, поступков и стремление совершенствовать пути достижения индивидуального и коллективного благополучия

Предметные:  Решать задачи с применением формул общего члена и суммы прогрессий. Распознавать арифметические и геометрические прогрессии

Метапредметные ориентироваться в своей системе знаний (определять границы знания/незнания);анализ объектов с целью выделения признаков; самостоятельное выделение – формулирование познавательной цели; построение логической цепи рассуждений; умение структуризировать знания, выбор наиболее эффективных способов решения задач;

Ключевые слова: формула суммы первых нескольких членов арифметической прогрессии

Краткое описание: На уроке предусмотрено использование следующих типов электронных образовательных материалов: «Диагностическая работа», «Самостоятельная работа».

                                Блочно-модульное описание урока

БЛОК1. Вхождение  в тему урока и создание условий для осознанного восприятия нового материала.

1.Мотивирование на учебную деятельность

Эпиграф урока: Математика есть единая симфония бесконечного. Д. Гильберт.

Термин «прогрессия» имеет латинское происхождение, что  «движение вперед», «успех» .

 Не будем останавливаться и мы, а пойдем вперед в направлении изучения прогрессий.

Чтобы идти вперед, чаще оглядывайтесь назад, ибо вы забудете, откуда вы вышли и куда вам нужно идти. Давайте оглянемся, что на данный момент мы знаем о прогрессиях.

Как называется прогрессия, которую мы изучаем?

Что мы о ней знаем, выясним в ходе устной работы

2. Актуализация опорных знаний

1.Являются ли арифметическими прогрессиями последовательности чисел:

    3, 7, 12, … (нет)                28, 31,34…  (да)                    

2.Дайте определение арифметической прогрессии. Запишите это определение с помощью формулы   на доске и в тетради.

(a_n+1 = a_n + d. Арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом)

3.Как называется каждый компонент этой формулы? 

4.Как найти разность арифметической прогрессии? ( d = a_n+1 - a_n )

5.Скажите, а какой еще формулой можно задать арифметическую прогрессию? Запишите эту формулу. (  a_n = kn + b. Любая арифметическая прогрессия может быть задана формулой вида a_n = kn + b, где k и b – некоторые числа)

6.Какие из формул задают арифметическую прогрессию: a_n = 5n + 7, a_n = 3n²+1,  a_n = 4 – n³   , a_n = 3 – 4n  ?

3. Целеполагание (Назовите цель: ты узнаешь, ты научишься……) познакомишься  с формулой суммы n-первых членов арифметической прогрессии, развить представления учащихся об использовании прогрессии в окружающей их жизни.

БЛОК 2. Освоение нового материала

1.Осуществление учебных действий по освоению нового материала

Скажите, сколько времени вам понадобится для того, чтобы сложить, к примеру, все натуральные числа от 1 до 100?

Совершенно не сомневаюсь в ваших способностях.

Истории математики известны случаи очень раннего проявления математических способностей. С формулой суммы n первых членов арифметической прогрессии был связан эпизод из жизни немецкого математика К. Ф. Гаусса (1777 – 1855).

 Когда Карлу было 9 лет, учитель задал на уроке следующую задачу: «Сосчитать сумму натуральных чисел от 1 до 100 включительно». Через 1 минуту Карл произнес: «Я уже решил... – и сдал работу, в которой была записана формула и верный ответ. К концу урока сумму вычислили и остальные.

Юный Гаусс сам того, не подозревая, вывел формулу суммы первых 100 членов арифметической прогрессии.

На этом уроке, подобно Гауссу, мы выведем в общем виде формулы суммы n-первых членов арифметической прогрессии и рассмотрим некоторое их применение к практическим задачам.

Задача эта не проста,

Как сделать, чтобы быстро

От единицы и до ста

Сложить в уме все числа.

Пять первых связок рассмотри,

Найдёшь к решению ключи.

Давным-давно сказал один мудрец

Что прежде надо

Связать начало и конец

У численного ряда.

S = 1 + 2 + 3+ …+98 + 99 + 100,

S = 100 + 99 + 98+ …+3 +2 +1,

2S = 101∙100, S =  =5050.

Сумму п первых членов арифметической прогрессии принято обозначать как Sn.. Вывод формулы проведем в ходе решения задачи «Найти сумму п первых членов арифметической прогрессии, если известны ее первый и n-ый члены.» 

(а_n) – арифметическая прогрессия.
S_n = a₁ + a₂ + a₃ + … + a_n-2 + a_n-1 + a_n,
S_n = a_n + a_n-1 + a_n-2 + …+ a₃ + a₂ + a_1.
a₂ + a_n-1 = (a₁ + d) + (a_n – d) = a₁ + a_n,
a₃ + a_n-2 = (a₁ + 2d) + (a_n – 2d) = a₁ + a_n,
a₄ + a_n-3 = (a₁ + 3d) + (a_n – 3d) = a₁ + a_n и т.д.
2S_n = (a₁ + a_n)∙n. 

БЛОК 3.  Применение изученного  материала

1.Применение знаний,  в том числе в новых ситуациях

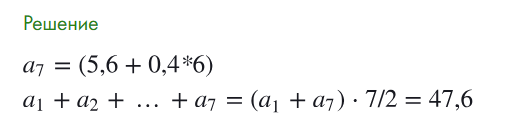
2.

3.

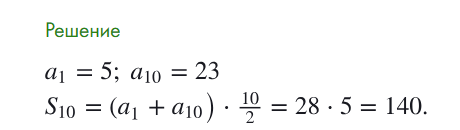
№605(а)

S₉ =  ∙9 =  ∙ 9 =  ∙ 9 = 7 ∙ 9 = 63.

1.      2.Выполнение межпредметных заданий из реальной жизни.

3.Задание ЕГЭ и ОГЭ

Ответ:-25,2

БЛОК 5. Подведение итогов, домашнее задание.

1. Рефлексия  (достигнуто или не достигнуто по образовательным результатам)

Обсуждаем итоги урока, выставляем оценки в журнал.

Я запомнил, что…

 Я понял, что…

Мне на уроке …

Думаю, что

2. Домашнее задание.

Рекомендации по ДЗ. №603 стр.158

   Ответ:53,2

2.     

Ответ:    -36

3.     

   Ответ: 550