
ЕВ. Ромашкова
Функции и шатки
в 8-11 классах
E.B. POMau1KOBa
 OY爿『P
OY爿『P
![]() 1
1
MOCKBa
20 Ⅱ
БЖ 74262+22.161
Рб9
Научный редактор и рецензент:
доцент кафедры алгебры и геометрии РГПУ им. СА. Есенина, кандидат педагогических наук Денисова Мария Ивановна
Ромашкова Е.В.
Р69 Функции и графики в 8—11 классах. М.: ИЛЕКСА,
![]()
ISBN 978-5-89237-314-2
В пособии систематизированы материалы всех разделов, посвященных функциям и графикам, которые изучают на протяжении школьного курса математики. Задачи относятся к линейным, квадратичным, тригонометрическим, показательным и логарифмическим функциям, рассмотрены различные методы анализа функций и построения графиков; задачам предшествуют примеры решения и построения графиков. Приведены задания для самостоятельной обучающей и контролирующей работ, для теоретического зачета, устной и обобщающей контрольных работ, а также составленная автором Программа по изучению темы «Функции и графики» для 8—11 классов с углубленным изучением математики.
Пособие предназначено для учителей математики, студентов педагогических вузов, может использоваться учащимися для самостоятельной работы, а также абитуриентами при подготовке к вступительным эк-
заменам в вузы.
ББК 74262+22.161
© Ромашкова Е.В.,2011
ISBN 978-5-89237414-2 ©
ИЛЕКСА,![]()
Изучению функций и построению их графиков отводится важное место в программе школьного курса обучения математике. Здесь закладываются основы аналитического мышления, развивается логика, формируются математическая интуиция и навыки уверенного владения методами графического решения уравнений.
В пособии представлены задачи на исследование функций и построение их графиков по всем разделам школьного курса математики.
Материал пособия расположен в последовательности, при которой сначала изучается линейная функция, затем на основе рассмотренных в 7 классе функций изучается тема «Построение графиков преобразований».
В теме «Квадратные уравнения» вводится определение квадратичной функции, график которой строится с использованием метода выделения полного квадрата с помощью алгебраических преобразований. Углублено изучение других функций.
Особое внимание уделяется заданиям, формирующим математическое мышление, способствующим обучению школьников графическому языку. В число таких упражнений, кроме задач на геометрические преобразования графиков, входят задания на построение графиков функций элементарными методами, упражнения по переводу со словесного описания поведения функций на графический язык и обратно.
В книгу включены устные упражнения, таблицы, отражающие зависимость вида графика от параметров функции, вопросы к теоретическим зачетам, устные контрольные работы, различные самостоятельные работы, а также задания на построение графиков функций.
Приводятся задачи повышенной трудности, рекомендуемые для рассмотрения на занятиях математического кружка. К большинству задач даны ответы.
Автор выражает благодарность Зубкову В. А., Ромашковой В. А., Рязанцевой Г. К. и рецензенту Денисовой М. И., замечания которых способствовали улучшению качества пособия.
Приступая к изучению функций, следует иметь в виду, что график функции должен строиться на основе предварительного исследования.
Пусть дана функция у = х ![]()
До построения графика необходимо получить максимальное количество свойств этой функции. Для этого нужно составить таблицу и использовать ее не как средство построения точек, а для изучения свойств функции.
Итак, у = х 2 . Зададим значения аргумента и занесем их в таблицу. Вычислим значения функции и также занесем их в таблицу.
|
|
-3 |
-2 |
-1 |
|
|
2 |
|
|
у |
9 |
4 |
|
0 |
|
4 |
9 |
Свойства:
1) функция принимает только неотрицательные значения;
2) проходит через точку О (О; 0);
3) противоположным значениям аргумента соответствуют одинаковые значения функции;
4) до нуля значения функции убывают, после нуля — возрастают.
Показывается, как вьшњленные свойства отразятся на графике. После этого строятся точки, соединяются плавной линией. С учащимися обсуждается вопрос, почему это можно сделать. Получив график функции, используем его как средство для изучения свойств функции.
Далее идут задания следующих типов:
1) на распознавание функции по ее графику;
2) на установление соответствия аналитическому заданию различных функций графического изображения;
3) на установление связи между параметрами функции и видом ее графика;
4) на определение аналитического выражения линии, изображенной на графике.
Построив график функции, используем его для установления свойств функции и для составления таблицы в двух взаимно обратных задачах: 1) перевести свойства функции на графический язык; 2) по имеющемуся графику сформулировать свойства, а также для решения уравнений и неравенств. Для этого необходимо ввести графические понятия «равно», «больше», «меньше». Владея такими понятиями, уже ученик 7 класса может графически решать уравнения вида х 2 = 2 и неравенства типа х 2 < 2х.
С первых уроков 8 класса необходимо формировать у учащихся понимание того, что существуют два метода построения графиков функций: 1) на основе исследования свойств функции, 2) с помощью геометрических преобразований, а также умения применять эти методы для построения графиков.
После изучения темы «Исследование свойств функции с помощью производной» необходимо снова вернуться к рассмотрению свойств элементарных функций, но уже с новых позиций.
Живой интерес у учащихся вызывают вопросы типа: почему параболу — график квадратной функции у = х2 — рисуют так, как показано на рисунке 1, а? Почему ее не рисуют так, как показано на рисунках 1, б или 1, в?
|
|
|
а б 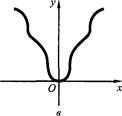
Правильно ответить на поставленный вопрос позволяют как алгебраическое, так и аналитическое рассуждения.
Средства контроля
1. Математический диктант. Например, по теме «Линейная функция» учащиеся должны ответить на следующие вопросы:
1) Как называется линейная функция у = ,lcr + Ь, у которой К = 0,
2) Изобразите схематически график этой функции.
З) Запишите уравнение оси ординат.
4) Является ли ось ординат графиком функции?
5) Дана функция у = Кх + Ь. Известно, что К >0, b> 0. Постройте схематично график этой функции. Какой угол составляет эта прямая с положительным направлением оси Ох?
6) Постройте схематично график функции у = Кх + Ь, где К< 0,
2. Карточки с печатной основой.
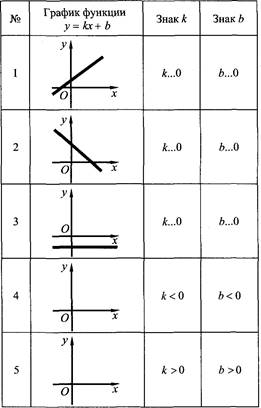
З. Обучающая самостоятельная работа.
4. Контролирующая самостоятельная работа.
5. Теоретический зачет.
6. Устная контрольная работа.
7. Обобщающая контрольная работа.
8 КЛАСС
1 . ЛИНЕЙНАЯ ФУНКЦИЯ
1. Какие из данных функций являются линейными:
1) у=—х +2; 2) у=3х 2 — (х +3х — 4); З) у— — + х +1; 4) _y= lxl•,
![]() х
х
2
1
2. Даны функции: 1) у=2х2. 2) у=Зх -2•, 3) у-![]()
2
![]()
Укажите, графики каких функций — прямые. Какие из прямых проходят через начало координат; образуют острый (тупой) угол с осью абсцисс, пересекают ось ординат в точке с отрицательной ординатой?
З. На рисунке 1.1 изображены графики линейной функции у = Кх + Ь. Укажите знаки коэффициента К и свободного члена Ь для
![]()
|
|
|
|
|
О |
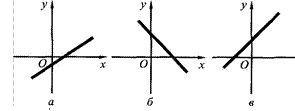 г
г
4. Что можно сказать о коэффициентах К и Ь функций, графики которых изображены на рисунке 1.2?
|
|
|
а
5. Найдите координаты точек пересечения с осями координат графиков функций: 1) у = х —2; 2) у=0,5х —3; 3) у= —2х —2.
6. Три функции выражены аналитически одной и той же формулой у = 2х, причем одна из них имеет областью определения все действительные числа, другая натуральные числа от 1 до 10, а третья — все отрицательные числа. Чем отличаются графики этих функций?
7. Что представляет собой график функции у = —х, если х принадлежит промежутку [—5; —2]?
8. Приведите пример линейной функции, областью определения которой служат все действительные числа, кроме х = —3?
9. При каком значении К график функции у = —Е — 7 проходит через точку (2; 6)?
10.Дана функция у = Кх + Ь, график которой проходит через точки (0; 6) и (3; 0). Найдите значения К и Ь.
11.График функции, заданной формулой у = + 3, проходит через точку Щ— 1 ; 5). Найдите коэффициент К. Является ли эта функция возрастающей или убывающей? Найдите 0 этой функции.
12.При каких значениях х функция у = 2х + 1: 1) равна 0; 2) положительна; 3) отрицательна?
13.Каким свойством обладает линейная функция, если ее график для х< —3 лежит ниже оси абсцисс, а для х > —3 выше оси
14.Приведите пример функции, графиком которой является прямая, проходящая через начало координат и составляющая с осью абсцисс:
1) тупой угол (больше, меньше 135 0 );
2) острый угол (больше, меньше, равный 45 0 ).
15.Укажите знаки коэффициентов К и Ь функции, график которой изображен на рисунке 1 З:
|
|
|
а
16.Вершина прямого утла равнобедренного треугольника имеет координаты (0; 1). Основание треугольника лежит на оси Ох.
а) найти координаты двух других вершин треугольника;
б) напишите уравнения прямых, на которых лежат боковые стороны.
17.а) Вершина прямого угла треугольника находится в точке (—1; 1). Прямая, содержащая один из катетов, имеет уравнение у = 1. Каким уравнением задается прямая, содержащая другой катет?
б) (—5; 1) и (—1; 5) — координаты вершин острых углов прямоугольного треугольника из задания 1.17, а. Найдите угловой коэффициент гипотенузы треугольника.
18.Центр квадрата совпадает с началом координат, а оси координат параллельны соответствующим сторонам квадрата. Напишите уравнения прямых, содержащих диагонали квадрата.
19.Центр квадрата совпадает с началом координат, а диагонали лежат на осях. Одна из вершин квадрата имеет координаты (0; З). Напишите уравнения прямых, содержащих стороны квадрата.
20.График функции у = 2х параллельно перенесен на две единицы в положительном направлении вдоль оси (П. Какое уравнение соответствует новому графику?
2 Функции и графики в 8-11 кл.
21. Найдите уравнение прямой, параллельной биссектрисе первого координатного угла и проходящей через точку (0; —5).
22. Точка А(0,2; 0,2) принадлежит графику функции у = Кх. Найти коэффициент К1 функции у = к1х — 4, график которой параллелен графику у = Кх.
23.
Напишите уравнение прямой, параллельной прямой у = 2х + 1 и проходящей:
а) через точку (0; 2); б) через точку (1.![]()
24. Под каким углом пересекаются графики функций у = х
![]()
25. Найдите координаты точек пересечения графиков функций у = 2х и у = х + 1.
26. При каком условии графики функций у = К 1х + , у— к2х + Ц, у = Кзх + Ьз пройдут через точку (О; 4)?
27. При каком значении а графики функций у = 2 и у = 2х + а имеют одну общую точку?
Одним из методов систематизации и обобщения знаний учащихся является работа по составлению таблиц. Ниже приведена таблица линейной функции у = kr + Ь для различных сочетаний знаков коэффициентов К и Ь.
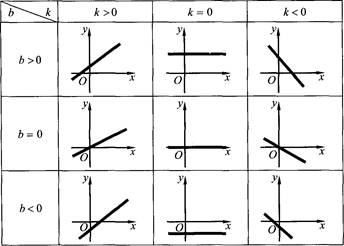
1 . Какая функция называется линейной?
2. Исследуйте функцию у = Кх + Ь по плану:
а) область определения;
б) множество значений;
в) точки пересечения с осями координат;
г) промежутки знакопостоянства функции;
д) промежутки возрастания и убывания функции.
З. Можно ли считать линейную функцию четной, нечетной? Подберите значения К и Ь так, чтобы функция у = Кх + Ь была: а) четной; б) нечетной; в) четной и нечетной.
4. Что является графиком линейной функции? Сколько точек на плоскости, координаты которых удовлетворяют уравнению у = + Ь, достаточно иметь, чтобы построить график функции?
5. Каковы частные случаи линейной функции и как расположены на координатной плоскости их графики? Является ли ось ординат графиком линейной функции?
6. Как зависит расположение графика функции у = Кх + Ь от величины Ь?
7. Как влияет коэффициент К на график функции у = Кх + Ь?
8. Постройте график функции: а) у = 2х — 4; б) у=/а + Ь. Используя график, выясните:
1) при каких значениях х значения у равны нулю;
2) при каких значениях х значения у отрицательны и при каких — положительны;
З) при каких значениях х величины х и у имеют одинаковые знаки;
4) при каких значениях х величины х и у имеют разные знаки;
5) промежутки возрастания и убывания функции.
9. Напишите формулы из курсов геометрии, физики, содержащие прямо пропорциональные величины.
10. Напишите формулы из курса физики, содержащие величины, находящиеся в линейной зависимости.
1.3. Устная контрольная работа по теме
Контроль знаний учащихся непосредственно в ходе урока всегда является непростой задачей. Одной из эффективных форм проверки знания теории являются устные контрольные работы, предлагаемые всему классу. Работы рассчитаны на один урок, причем ученики записывают только ответы. Предлагается два варианта контрольной работы.
1 вариант
1. При каком условии график линейной функции пересекает ось абсцисс в точке, имеющей отрицательную абсциссу?
2. Приведите пример линейной функции: а) положительной на всей числовой прямой; б) положительной при х< хо, где хо ноль функции.
3. При каком значении а функция у = (а — 2)х + За — 4 является четной?
4. Найдите значения К, при которых функция f(x) = (К — + +k 2 —3 монотонно возрастает.
5. Как изменяется график линейной функции у = kr + Ь с изменением Ь при постоянном К?
6. Изобразите схематически график функции у = kr + Ь, если:
![]()
7. Известно, что К < 0. Определите вид утла, образованного графиком функции у = + Ь с осью абсцисс.
8. Напишите уравнения: а) прямой, содержащей биссектрису
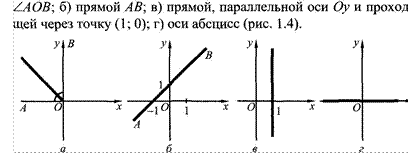
2 вариант
1. При каком условии график линейной функции пересекает ось абсцисс в точке, имеющей положительную абсциссу?
2. Приведите пример линейной функции: а) отрицательной на всей числовой прямой; б) положительной при х > хо, где хо — ноль функции.
З. При каком значении а функция у = (а — 2)х + За — 4 является нечетной?
4. Найдите значения К, при которых функция f(x) = (К — 1)х + +k 2 —3 монотонно убывает.
5. Как изменяется график линейной функции у = Кх + Ь с изменением К при постоянном Ь?
6. Изобразите схематически график функции у = kr + Ь, если:
а) КО, кО; 6) 00, b< 0•, в) КО, Ь =О.
7. Известно, что К > 0. Определите вид угла, образованного rpaфиком функции у = Кх + Ь с осью абсцисс.
8. Напишите уравнения: а) прямой, содержащей биссектрису ZAOB; б) прямой АВ; в) прямой, проходящей через точку (О; 1), параллельной оси Ох; г) оси ординат (рис. 1.5)
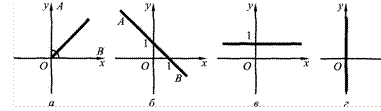 х
х
Рис. 1.5
2. УРАВНЕНИЯ, СОДЕРЖАЩИЕ ЗНАК МОДУЛЯ
Пример. Решите уравнение: ' х —3' +2' = 7.
Решение. Исследуем поведение функции у = ' х —3' -+|х +2' на интервалах х Э З; х З; х < —2 и изобразим результат графически.
13
Решим данное уравнение на каждом из указанных промежутков.
![]()
неверно, корней нет;
3) -(х 3) - (х +2) = 7, х = -3; -3<-2. Ответ: —3; 4.
2.1. Решите уравнения:
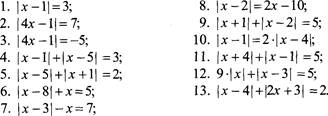
З. ФУНКЦИИ, СОДЕРЖАЩИЕ ЗНАК МОДУЛЯ
Пример. Постройте график функции у х: Н х + Ц.
Решение. Исследуем поведение функции на интервалах х >0; —К х х< —l и изобразим результат графически:
![]() х З) х< —1, у = —2х — 1.
х З) х< —1, у = —2х — 1.
По найденным значениям строим график функции (рис. З. 1).
|
|
|
|
|
-1 0 |
х |
3,1, Постройте графики функций:
х
![]() 14
•
14
• ![]() х
х
![]()
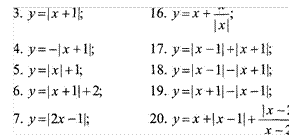
|
—2х1; 3 |
|
24.  y=lx +ll —Д —2xl х —21—х —1;
y=lx +ll —Д —2xl х —21—х —1;
25. y=lx — Ц —lxl +|2х + 4).
Позднее учащихся можно познакомить и с другими способами построения подобных графиков. Например, графиком функции у = ' х 1+1 х + Ц является ломаная линия с вершинами в точках с абсциссами х = —1; х = 0.
Найдем ординаты этих точек:
![]()
Итак, вершинами ломаной являются точки (—1; 1); (О; 1). Используя две дополнительные точки, например, (—3; 5) и (1; З), строим график функции.
15
«Разложение многочлена на множители»
1 вариант
1. Разложите на множители многочлен:
а) ![]() + 7ab 2
+ 7ab 2![]()
![]() +b+a2 — b2.,
+b+a2 — b2.,
16
|
г) 2х 2 +3х +1. |
|
|
2. Постройте график функции у = 2х +1 х 2 вариант 1. Разложите на множители многочлен: |
Ц. |
![]() +12ac 2
+12ac 2![]()
|
Г) Х 2 + 8х + 12. |
|
|
2. Постройте график функции у = [х + |
—2х. |
1 вариант
1. Сократите дроби:
 а)
а)
г)
2 вариант
1. Сократите дроби:
а) 2'

Задача для математического кружка
При каких К уравнение 1 х + Ц— х — Ц = Кх +1 имеет единственное решение?
а. ПОСТРОЕНИЕ ГРАФИКОВ ФУНКЦИЙ ВИДА:
![]()
У = —f(x); у = а f(x).
Пример. Постройте график функции у = (х + ![]() 1 способ
(рис. 4.1).
1 способ
(рис. 4.1).  llW
llW
![]()
2 способ (рис. 4.2). Построим новую систему координат с началом в точке —3); в ней строим график функции у = х 2 . Таким образом, график получается не преобразованием самих графиков, а преобразованием системы координат.

4.1. Постройте графики функций:
 3х +2; б) у = 3х +4; в) у = 3х —3; г) у =
3х —5;
3х +2; б) у = 3х +4; в) у = 3х —3; г) у =
3х —5;
15. а) y=lx +61; б) y=lx — 7';
16. а) у = (х +2) 2 ; б) у = (х +2) 2 +1; в) у = (З — х) 2 + 1;
г) у = 9 — (х +2) 2 ; д) у = 2 • (х —2)![]()
17. а) у = (х — 1) 3 ; б) у = (х +3) 3 ; в) (х —2) з +1;
![]()
5. ПОСТРОЕНИЕ ПО ГРАФИКАМ ФУНКЦИЙ у = Л(х) И ![]() ГРАФИКОВ
ФУНКЦИЙ:
ГРАФИКОВ
ФУНКЦИЙ:
![]()
Построение графика функции метоДом алгебраических операций
Пример 1. Постройте график функции у = xl +1х + Ц.
Строим графики функций и y=lx + Ц, затем находим суммы ординат точек графиков этих функций при одних и тех же значениях х; так как сумма линейных функций есть линейная функция, то достаточно найти суммы ординат угловых точек, т.е. при х =0их = —1, и по одной точке при х Яи х< —1 (рис. 5.1).

Пример
2. Постройте график функции у х +![]()
Обычно не прибегают к вычитанию графиков, а строят два графика: у = 1 .rl и у = х + 1, искомый график строится как график суммы этих функций (рис. 5.2).
Примечание. При сложении (вычитании) графиков можно пользоваться циркулем.
19
При умножении (делении) надо предварительно переводить отрезки (ординаты) в числа, а потом, перемножая (деля) эти числа, наносить на плоскость соответствующие им точки. При делении следует помнить, что у = f2 (х) не должно обращаться в нуль.
Построение графика функции метоДом геометрических преобразований
Существует графический способ сложения, умножения и деления функций, который дает учащимся представление о новых для них примерах использования простейших геометрических преобразований.
Рассмотрим приемы построения точки Щ, принадлежащей искомым графикам. Построение будем выполнять для тех значений аргумента, при которых определены обе функции, причем в случае деления Л (х) 0.
Пример 1. Постройте график функции у +f2(x) (рис. 5.3).
|
|
|
|
в
|
|
|
|
||
|
м |
|
|
х |
1) Возьмем на оси Ох произвольную точку М и проведем через нее вертикаль MN.
2)
Через произвольную точку А, принадлежащую графику у ![]() проведем
вертикаль; точку ее пересечения с графиком функции У = fl (х) обозначим через
В.
проведем
вертикаль; точку ее пересечения с графиком функции У = fl (х) обозначим через
В.
З) Построим отрезок АМ.
4) Из точки В опустим перпендикуляр на прямую MN, основание перпендикуляра обозначим через К.
5) Через точку К проведем прямую, параллельную прямой МА, до ее пересечения с прямой АВ. Точка пересечения — обозначим ее А 1 — и будет искомой.
Пример 2. Постройте график функции у •f2(x) (рис. 5.4).
1) Через произвольную точку А, принадлежащую графику функции у = f2 (х), проведем вертикаль до ее пересечения с графиком функции у = Л (х). Точку пересечения обозначим буквой В.

2) Через точку А проведем горизонталь до ее пересечения с прямой х = 1; точку пересечения обозначим через ЛЩ. З) Проведем прямую ОЛЩ.
4) Через точку В проведем горизонталь до ее пересечения с биссектрисой первого (или третьего) координатного угла; эту точку обозначим через М2.
5) Через точку проведем вертикаль до ее пересечения с прямой ОМР эту точку обозначим через мз.
6) Точка А [ пересечения прямой АВ с горизонталью, проведенной через точку Му— искомая.
Пример З. Постройте график функции у ![]() (рис. 5.5).
(рис. 5.5).
1) Через произвольную точку А, принадлежащую графику функции у = (х), проведем горизонталь до ее пересечения с прямой х = 1; полученную точку обозначим через Мг
2) Через точку А проведем вертикаль, точку ее пересечения с графиком функции у = Л (х) обозначим через В.
3) Проведем прямую ОЛЩ.
4) Через точку В, принадлежащую графику у = Л (х), проведем горизонталь до ее пересечения с прямой ОМЕ Точку пересечения обозначим мз .
5)
Через точку Мз проведем вертикаль до пересечения с прямой у = х. Точку
пересечения обозначим![]()
6)
Искомая точка А] находится как точка пересечения прямой АВ с
горизонталью, проведенной через точку![]()
21
Примечание. С графическим способом построения целесообразно знакомить учащихся после прохождения темы «Подобие треугольников», так как доказательство того, что точка А 1 — искомая, строится на основе подобия соответствующих треугольников.
1 вариант
1 . Выполните действия: а) (—тб
/ 3) 3 , б)![]()
14171 3 5а — 5b' 38
в)![]() г) 2тп • 2' 4771 з • п c+d 7c+7d
г) 2тп • 2' 4771 з • п c+d 7c+7d
д) 2 ![]()
х х
2. Разложите на множители многочлена +2а 2 —3.
2 вариант
1. Выполните действия:

2. Разложите на множители многочлен а з + а 2 + 4.
Дополнительное заДание
Постройте график функции
![]()
6. ПОСТРОЕНИЕ ГРАФИКОВ ФУНКЦИЙ ВИДА:
![]()
Пример. Постройте график функции у = xl + 7l.

Примечание. Используя свойства модуля, можно было строить график у= — 7i.
6.1. Постройте графики функций:

6.2. Обобщающий урок по теме ![]()
Примечание. Перед уроком на стенд «Сегодня на уроке» прикрепляется таблица «Построение графиков функций с помощью геометрических преобразований известных графиков». Этой таблицей учащиеся могут пользоваться, отвечая на вопросы о преобразовании графиков.
Цель урока: систематизировать различные приемы построения графиков функций, определить область их применения, закрепить полученные знания с помощью упражнений.
Все упражнения выполняются устно.
1. Упростить выражения:
![]()

2. На доске нарисованы графики семи функций (рис. 6.2) и написаны семь формул. Определить, какая формула к какому графику относится.

1 вариант Постройте графики функций:
![]()
2 вариант
Постройте графики функций:


З Функции и графики в 8-11 кл.
На внутренней части доски заранее, перед уроком, нарисованы графики этих функций (рис. 6.3, 6.4).
2 вариант

Рис. 6.4
В ходе взаимопроверки выясняются ошибки и проводится работа по их устранению.
6.4. Фронтальная работа с классом Строятся графики функций:
![]()
1) х >2, у=2х +1; 2) «2, у=2х —1 (рис. 6.5).

Рис. 6.6
2. у=х![]()

1) хы, у = х —1; 2) —1< х< 1, у = х
+1; З) х< —1, у = ![]() (рис. 6.7).
(рис. 6.7).
Группы формируются из четырех учащихся, один из которых назначается «консультантом».
Задание группам: постройте графики функций:
 1 -1 -1 1 - 1 .
1 -1 -1 1 - 1 .
Учитель проверяет все задание у каждого консультанта, консультант организует проверку работы каждого члена группы.
В ходе обсуждения каждого задания выявляются ошибки и проводится коллективная работа над ними, оказывается взаимопомощь.
Самое интересное задание обсуждается у доски. Решение.
1) —2, у=—х +3; 2) х< —2, у = х —3 (рис. 6.8).
27

Рис. 6.9 Рис. 6.10

Рис. 6.11 Рис. 6.12
 +1) (рис. 6.9).
+1) (рис. 6.9).
-1.
После выполненных преобразований у = 2х +1 (рис. 6.10). ![]() D(y):
х $2; х $3.
D(y):
х $2; х $3.
1) х>з, у=2; 2) 2< х< З, у З)
«2, у = —2 (рис. 6.11). ![]() —1 —1 (рис. 6.12).
—1 —1 (рис. 6.12).
6.6. Подведение итогов урока
Выставляются оценки за две самостоятельные работы.
6.7. Задание на дом
Подготовиться к контрольной работе,
повторив правила действий с дробями и способы построения графиков функций;
построить (3х +1) •lx — Ц +3х 2 —2х —1 график функции у =![]()
7. ФУНКЦИЯ у- х

7.1. Постройте графики функций:

![]() —х;
—х;
29
8. ФУНКЦИИ, ПРИ ПОСТРОЕНИИ ГРАФИКОВ КОТОРЫХ ИСПОЛЬЗУЕТСЯ ПРЕОБРАЗОВАНИЕ ВЫРАЖЕНИЙ, СОДЕРЖАЩИХ КВАДРАТНЫЕ КОРНИ
Пример. Постройте график функции у =![]()

8.1. Постройте графики функций:


9. ПОСТРОЕНИЕ ГРАФИКОВ
КВАДРАТИЧНЫХ ФУНКЦИЙ,
ИСПОЛЬЗУЯ МЕтод ВЫДЕЛЕНИЯ
ПОЛНОГО КВАДРАТА И ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ ГРАФИКОВ
Пример. Постройте график функции у = — х 2 — 3х + 6.
Выполним необходимые преобразования:

9.1. Постройте графики функций:
 1. у=х2 —4х+4;
1. у=х2 —4х+4; 
4
5. +6х—9;
1 вариант
1. На рис. 9.2 изображен график квадратичной функции. Внимательно прочитайте вопрос и, пользуясь чертежом, определите, какой из ответов (а — г) является правильным?
1)
 При каких значениях аргумента х значения у равны 0:
При каких значениях аргумента х значения у равны 0:
а) при х = 3;
б) при х —![]()
в) при х = 1;
г) «не знаю»?
2) При каких значениях аргумента х значения функции у положительны:
а) при х > 0;
б) при х< —1 их > З;
Рис. 9.2 в) при х > —3;
![]() г) «не знаю»?
г) «не знаю»?
3) При каких значениях аргумента х значения функции у отри-
цательны:
а) при 3; в) при х< 0;
б) при —4< х< 0; г) «не знаю»?
4) При каких значениях аргумента х функция у возрастает:
а) при х > —4; в) при х > 1;
б) при х > 0; г) «не знаю»?
5) При каких значениях аргумента х функция у убывает:
а) при х< 1; в) при х< З;
б) при х > —1; г) «не знаю»?
6) При каких значениях аргумента х функция у имеет наименьшее значение:
а) при х< —1; в) при х = 1;
б) при х > —4; г) «не знаю»?
7) Какое из перечисленных значений может принимать функция у:
![]()
![]() г) «не знаю»?
г) «не знаю»?
8) График какой из перечисленных функций изображен на рисунке 9.2:
2
![]()
б) у= (х +1)2 — 4; г) «не знаю»,
![]() Примечание. Ответы к
устным самостоятельным работам № и № 2 ученики представляют в заранее
составленной таблице, что дает возможность быстро осуществить обратную связь.
Примечание. Ответы к
устным самостоятельным работам № и № 2 ученики представляют в заранее
составленной таблице, что дает возможность быстро осуществить обратную связь.
Карточка для ответов
Незаполненная карточка Ответы
на задачи из варианта ![]()
|
|
|
Незаполненную (слева) карточку ученик получает перед уроком, заполненную (справа) сдает учителю после выполнения работы.
2. Установите, какое уравнение соответствует каждому из графиков, изображенных на рис. 9.3, если: а > 0; b> 0.
![]()


2 вариант
1. На рис. 9.4 изображен график квадратичной функции. Внимательно прочитайте вопрос и, пользуясь чертежом, определите, какой из ответов (а — г) является правильным.
|
|
|
|
—3 |
1 |
1)
![]()
![]() При каких значениях аргумента х значения функции у равны
О:
При каких значениях аргумента х значения функции у равны
О:
г) «не знаю»?
2) При каких значениях аргумента х значения функции у положительны:
г) «не знаю»?
З) При каких значениях аргумента х значения функции у отрицательны:
![]() г) «не знаю»?
г) «не знаю»?
4) При каких значениях аргумента х функция у возрастает:
![]()
г) «не знаю»?
5) При каких значениях аргумента х функция у убывает:
![]()
![]() г) «не знаю»?
г) «не знаю»?
6) При каких значениях аргумента х функция у имеет наибольшее значение:
а) при х — в) при х = 1;
б) при х = 2; г) «не знаю»? 7) Какое из перечисленных значений может принимать функция:
![]()
г) «не знаю»?
8) График какой из перечисленных функций изображен на рис. 9.4:
![]() в) у = —(х +1)2 +4;
в) у = —(х +1)2 +4;
г) «не знаю»?
2. Установите, какое уравнение соответствует каждому из графиков, изображенных на рис. 9.5 (а > 0, Ь > 0):
![]()
а)
|
|
|
О |
|
д) |
у |
|
|
|
|
у |
|
|
 г)е)
г)е)
10. ФУНКЦИИ,
ПРИ ПОСТРОЕНИИ ГРАФИКОВ КОТОРЫХ ИСПОЛЬЗУЕТСЯ РАЗЛОЖЕНИЕ КВАДРАТНОГО ТРЕХЧЛЕНА НА ЛИНЕЙНЫЕ МНОЖИТЕЛИ
Пример. Постройте график функции у =![]()

Рис. 10.1
10.1. Постройте графики функций:
 4х
2 -1
4х
2 -1  2
2
10,2. Вопросы к теоретическому зачету по теме
1 . Дайте определение квадратного трехчлена.
2. Изложите способ выделения из квадратного трехчлена полного квадрата двучлена.
3. Дайте определение корня, или нуля, квадратного трехчлена. Выведите формулу нахождения корней (нулей) квадратного трехчлена.
4. Дайте определение дискриминанта квадратного трехчлена. Изложите исследование корней квадратного трехчлена по его дискриминанту .
5. Докажите теорему Виета.
6.
Докажите теорему: Если и корни квадратного трехчлена ах 2 +
bx + с, то ах 2 + bx + с = а(х — х 1 )(х![]()
7. Дайте определение квадратичной функции. Рассмотрите функцию у = ах 2 , а 0. Изложите ее свойства и постройте график, рассмотрите различные значения коэффициента.
8. Рассмотрите функцию у = а (х + b) 2 , а * О. Изложите и обоснуйте способ построения графика этой функции по имеющемуся графику функции у = ах 2 . Приведите примеры.
9. Рассмотрите функцию у = ах 2 + с, а 0. Изложите и обоснуйте способ построения графика такой функции по имеющемуся графику функции у = ах 2 . Приведите примеры.
10. Рассмотрите функцию у=а(х + Ь) 2 + с, а $0. Изложите и обоснуйте способ построения графика такой функции по имеющемуся графику функции у = ах 2 . Приведите примеры.
11. Как из графика функции у = ах 2 получить график функции
![]()
12.
Докажите теорему: Если Дискриминант квадратного трехиена отрицателен, то
знак кваДратного трехчлена при всех значениях х совпаДает со знаком
коэффициента при х ![]()
13. Приведите примеры квадратных трехчленов, имеющих:
а) наибольшее значение; б) наименьшее значение.
14. Приведите примеры квадратичных функций: а) положительных при всех х; б) положительных при всех х, кроме одного; в) отрицательных при всех х; г) отрицательных при всех х, кроме одного', д) положительных при (К х< 1; е) отрицательных при х< —2 и х > 0; ж) положительных при х< —1 и х> З; з) отрицательных при
15. Приведите примеры квадратичных функций: а) возрастающих при х > 2; б) убывающих при х < —3.
16. Приведите примеры четных квадратичных функций.
17. Приведите примеры квадратичных функций вида у ах2 и у = а (х + Ь) 2 + с. Где на практике встречаются кривые, имеющие вид параболы?
10.3. Задачи
1. На координатной плоскости Оху изобразили график функции у = х 2 . Потом оси стерли на рисунке осталась только парабола. Как при помощи циркуля и линейки восстановить оси координат и единицу длины?
2.
Почему параболу — график квадратичной функции у = х2 ![]() рисуют на
координатной плоскости так, как показано на рисунке
рисуют на
координатной плоскости так, как показано на рисунке
10.2? Почему ее не рисуют так, как на рисунках 10.3 и 10.4?
|
|
|
 Рис. 10.4
Рис. 10.4
1 1 . ДРОБНО-ЛИНЕЙНЫЕ ФУНКЦИИ
К Обратно пропорциональная зависимость: у = ![]() х
х


Пример 1. Постройте график функции у =![]()

![]()
Используем правило построения графика функции у![]()
(рис. 11.2)
Пример З. Постройте график функции у =![]() • D(y): х $1.
• D(y): х $1.

Рис. 11.1 Рис. 11.2 Рис. 11.3

11,2, Постройте графики функций:

25.![]()
11.3. Вопросы к теоретическому зачету
1. Дайте определение дробно-линейной функции. Рассмотрите функцию у = —. Изложите свойства этой функции, проиллюстри-
х руйте свойства графически. Как изменяется положение ветвей гиперболы относительно осей координат: а) в зависимости от знака параметра К; б) при изменении абсолютной величины К?
2. Изложите и обоснуйте способ построения графика функции
К К
![]() по имеющемуся графику функции у = —-.
по имеющемуся графику функции у = —-.
х
З. Изложите и обоснуйте способ построения
графика функции к К ![]() + Ь по имеющемуся графику функции у = —.
+ Ь по имеющемуся графику функции у = —.
х х
4. Изложите и обоснуйте способ построения графика функции к К
![]() + Ь по имеющемуся графику функции у = .
+ Ь по имеющемуся графику функции у = .
х
5. Изложите и обоснуйте способ построения графика функции ах + Ь
![]()
6. Приведите формулы из геометрии и физики, содержащие обратно пропорциональные величины.
4 функции и графики в 8-11 кл. 41
12. КВАДРАТИЧНАЯ ФУНКЦИЯ

1. Принадлежат ли точки ( 2; 2) и (2; 2 +45) графику функции
2 ![]()
2. При каком значении с проходят через точку (2; 1) графики функций: а) у=х 2 +5х + с, б) у = х 2 + сх +1?
З. Найдите точки пересечения с координатными осями графиков функций: а) у=х 2 +6х + 8, б) у = х 2 — х — 42.
4. Найдите те значения К, при которых график функции у = х 2 +2х +21 + К имеет одну общую точку с осью Ох.
5. Найдите уравнение оси параболы у = (х + —3), а также координаты ее вершины.
6. При каких значениях а ось симметрии параболы у=х 2 +2ах + а 2 + Ь задается уравнением: 1) х - — -1, • 2) х=3? как влияет на вид уравнения оси параболы значение параметра Ь?
7. Найдите расстояние между осью параболы у = х — х —6 и осью Оу.
8. Найдите расстояние между осями симметрии парабол у = х 2 —5х+6 иу=х 2 +х +—х.
9. На
каком расстоянии от начала координат находится вершина параболы у = (х + 1)![]()
10. По виду графиков функции у = ах 2 + bx + с сделайте выводы о знаках коэффициентов а, Ь, с (рис. 12.1).
|
|
|
|
|
Рис. 12.1
43
11. Не строя графиков функций, поясните, как они расположены на координатной плоскости:
![]() г) у = х 2 +9х
+20;
г) у = х 2 +9х
+20;
в) у=х 2 —2х
+1; ![]()
![]()
12. График какой функции выглядит так, как показано на рисунке 12.2: а) у=х 2 +2х—3; б) у=х 2 —2х +3; в) —2х +1;
г) у = —х 2 +2х + 1; д) у = —х 2 +2х —1?
|
|
|
Рис. 12.2 Рис. 12.3
13. Задайте аналитически функции, которые соответствуют графикам, являющимся результатом параллельного переноса графика функции у = х 2 : а) вдоль оси Оу на а единиц; б) вдоль оси Ох на —3 и вдоль оси Оу на единицу.
14. Какая из указанных формул задает параболу, изображенную на рисунке 12.3: а) +2; б) +2х; в) —2х; г) у = —(х —1) 2 ; д) у = —(х —2) 2 ?
15. Напишите уравнения парабол, изображенных на рисунке
12.4, если они получены из параболы у = х ![]()
16. Найдите множество значений функции у = х 2 —2х + З.
17. При каких значениях х равняются нулю, положительны или отрицательны следующие квадратные трехчлены:
![]() в)
—х 2 —5х + 66;
в)
—х 2 —5х + 66;
![]() г) -х 2 +3х
-20, д)
г) -х 2 +3х
-20, д)
18. При каком значении с функция у = х 2 —2х + с принимает только положительные значения?
19. Назовите промежутки возрастания и убывания функции у = —х 2 + 2х — 9. Каково множество значений функции?


Рис. 12.4
20. Найдите множество значений аргумента функции у = 5 + 4х — х 2 , при котором функция: а) убывает (возрастает); б) положительна (отрицательна).
2.1. При каких значениях х достигают наименьшего и наибольшего значения функции: а) у=х 2 +3; б) —3х; в) у = —х 2 — 5;
г) у = х 2 — 5х; д) у = х“ —6х +9; е) у = —.r 2 +8х +12?
22. При каких значениях а графики функций у = х 2 +2х + 4 и у = а имеют: 1) две общие точки; 2) одну общую точку; 3) не имеют общих точек?
23. Как располагается относительно осей Ох и Оу график функции: 1) y=x 2 +3lxl+2; 2) у = [х 2 —5х + Щ?
1 вариант
1. При каком условии квадратичная функция у = ах 2 + bx + с положительна при всех действительных значениях х?
2. При каком условии квадратичная функция у = ах 2 + bx + с имеет упих = Т
З. При каком условии неравенство ах 2 + bx + с выполняется при .Xl < ху где .Xl И корни соответствующего квадратного трехчлена?
4. При каком условии неравенство (ах 2 + bx + с)(х + — 5) > 0 справедливо только при —2< х< 5?
5. Определите
знак параметра а квадратичной функции у = ах 2 +bx + с , если >
при < х 1 <![]()
6. При каком условии график квадратичной функции у = х 2 + рх +q пересекает ось Ох в точках, абсциссы которых отличны от нуля и имеют одинаковые знаки?
7. При каком значении т прямая у = т пересекает параболу у = ах 2 + bx + с (а < 0) в двух точках?
8. При каком условии парабола у = ах 2 и прямая у = —bx — с не имеют общих точек?
9. Постройте схематически график функции у = ах 2 + blxl + с , если а Я), с Я), b< 0, D > 0.
2 вариант
1. При каком условии квадратичная функция у = ах 2 + bx + с отрицательна при всех действительных значениях х?
2. При каком условии квадратичная функция у = ах 2 + bx + с имеет упт.п = Т
З. При каком условии неравенство ах 2 + bx + с< 0 выполняется при х 1 < х< , где и х2 — корни соответствующего квадратного трехчлена?
4. При каком условии неравенство (у — 2)(у + by + с) < 0 справедливо при —7< у< 2?
5.
Определите знак параметра а квадратичной функции у=ах 2 +bx+c
, если при » —![]()
6. При каком условии график квадратичной функции у = х + рх + q пересекает ось Ох в точках, абсциссы которых отличны от нуля и имеют разные знаки?
7. При каком значении т прямая у = т пересекает параболу у = ах 2 + bx + с (а в двух точках?
8. При каком условии парабола у = ах 2 и прямая у = bx + с имеют только одну общую точку?
9.
Постройте схематически график функции у = ах 2 + blxl + с,
если а< 0, с< 0, b< 0, D![]()
В. КВАДРАТИЧНЫЕ ФУНКЦИИ,
СОДЕРЖАЩИЕ ЗНАК МОДУЛЯ
Постройте графики функций:

![]()

![]() б) у = lxl2—7 lxl+6;
б) у = lxl2—7 lxl+6; ![]() у = 1 х 1 (х —2);
у = 1 х 1 (х —2);
47
2

![]() 13.2. Самостоятельная работа по теме
13.2. Самостоятельная работа по теме
Предлагается следующая форма проведения этой самостоятельной работы. Каждый ученик рисует 5 клеток (по числу заданий, см. эскиз) и приступает к построению графиков. Как только построен первый график, то учащийся сразу же подходит к учителю. При правильно выполненном первом задании в первую клетку учитель
![]()
ставит «-е», при неправильном — «—». Ученик строит второй график и снова ПОДХОДИТ к учителю и т. д. У учителя свой список учеников, в который заносится результат работы. После заполнения таблицы сразу становится ясно, какое задание нужно разбирать у доски. Кроме того, каждый ученик получает оценку.
1 вариант
1. Постройте графики функций:

![]() 1) у = 1х 2
—4х+3|;
1) у = 1х 2
—4х+3|;
2. Постройте график уравнения
Ответ. Графики функций:


График уравнения:

Рис. 13.2
2 вариант
1. Постройте графики функций:

![]() —3.
—3.
2. Постройте график уравнения
|
|
24 12 |
|
|
|
-3
|
|
4) |
12 |
|
2) |
|
|
|
|
|
|
-3 |
|
Ответ. Графики функций:
1) См. рис. 13.1(1).
3) См. рис. 13.1(3).
4)
2)
Рис. 13.3 График уравнения:
|
З |
|
|
-3 |
|
14. ФУНКЦИИ, ПРИ ПОСТРОЕНИИ ГРАФИКОВ
КОТОРЫХ ИСПОЛЬЗУЕТСЯ РЕШЕНИЕ НЕРАВЕНСТВ ВТОРОЙ СТЕПЕНИ С ОДНОЙ ПЕРЕМЕННОЙ
Пример. Постройте график функции у = 1 х![]()

Постройте графики функций:

15. ФУНКЦИИ,
ПРИ ПОСТРОЕНИИ ГРАФИКОВ КОТОРЫХ
ИСПОЛЬЗУЮТСЯ СВОЙСТВА АРИФМЕТИЧЕСКОГО КОРНЯ п-ой СТЕПЕНИ

 Пример.
Постройте график функции
Пример.
Постройте график функции
Постройте графики функций:

2

16, КУСОЧНО-НЕПРЕРЫВНЫЕ ФУНКЦИИ
![]() = sign х.
= sign х.
![]() 1, если х >0,
signx —0, если х = 0,
1, если х >0,
signx —0, если х = 0,
—1, если х< 0 (рис. 16.1).
![]()
[х]= К, если х = К + а, где Ке Z и0<а![]()
(т. е. у равен наибольшему целому числу, не превосходящему х) (рис. 16.2).
![]()
{х} = х — [х]. Если х = К + а, где К е Z и (Ка то {х} = а
(рис. 16.3).
|
|
|
|
Рис. 16.1 Рис. 16.2 Рис. 16.3
Пример 1. Постройте график функции у = [х 2 ].
Проведем прямые у= р, где ![]() (рис.
16.4). Они разобьют исходный график на части. Рассмотрим каждую часть графика,
лежащую в полуоткрытой полосе, для которой у < р +1, и спроектируем ее на
прямую у= р. Получим отрезки, в каждом из которых исключены либо левые (при х
< 0), либо правые (при х > О) концы. Множество полученных таким образом
«открытых»
(рис.
16.4). Они разобьют исходный график на части. Рассмотрим каждую часть графика,
лежащую в полуоткрытой полосе, для которой у < р +1, и спроектируем ее на
прямую у= р. Получим отрезки, в каждом из которых исключены либо левые (при х
< 0), либо правые (при х > О) концы. Множество полученных таким образом
«открытых»

![]() и
«полуоткрытых» отрезков является графиком функции у = [х 2 ] (рис.
16.4).
и
«полуоткрытых» отрезков является графиком функции у = [х 2 ] (рис.
16.4).
Пример 2. Постройте график функции
2
|
у
|
|
|
|
х |
Заметим, что все точки этого графика
лежат внутри полосы у < 1. Проведем прямые у = р, где ![]() Из точек
пересечения исходного графика с этими прямыми Рис. 16.4 проведем перпендикуляры
к прямой Ох. Прямые у = р разбивают исходный график на ряд участков. Так как
{р+ и СК а то для построения графика функции у = {х 2 } нужно ту
часть графика, которая попадает в полосу р < у < р + 1, параллельно
перенести нар единиц вниз, ту же часть графика, кото-
Из точек
пересечения исходного графика с этими прямыми Рис. 16.4 проведем перпендикуляры
к прямой Ох. Прямые у = р разбивают исходный график на ряд участков. Так как
{р+ и СК а то для построения графика функции у = {х 2 } нужно ту
часть графика, которая попадает в полосу р < у < р + 1, параллельно
перенести нар единиц вниз, ту же часть графика, кото-
Рис. 16.5 рая находится в полосе у < 1, следует оставить без изменения. Исключив в каждой из этих кривых точку, принадлежащую прямой у = 1, получим график данной функции (рис. 16.5).
Постройте графики функций:

2- 4 —lxl, lxl< 4,
13. у = 8 ![]() l x
l '
l x
l '

![]()
![]()
![]() signx;
signx;
15. signx — З;
18 . у-— {х} +signx;
19![]()
20 у:
21. ![]()
22.![]()
23.
39 •![]()
24.
![]()
![]()
![]() = {х}2,
= {х}2,  2
2
![]() 44. у = sig
[х].
44. у = sig
[х].
17. МЕТОДЫ построения ГРАФИКОВ ФУНКЦИЙ
Преобразование графиков функций
|
Функция |
Преобразование графика функции f(x) |
|
|
Параллельный перенос вдоль оси Оу на Ь единиц вверх, если Ь > 0; на lbl единиц вниз, если Ь 0. (рис. 17.1) |
|
|
Параллельный перенос вдоль оси Ох на а единиц вправо, если а < 0; на а единиц влево, если а Я). (рис. 17.2) |
|
|
Растяжение вдоль оси Оу относительно оси Ох в К раз, если К > l; сжатие в раз, если 1. К (рис. 17:3) |
|
У = f(kr) |
Сжатие вдоль оси Ох относительно оси Оу в К раз, если К Я; растяжение в — раз, если 0 < К < 1. (рис. 17.4) |
|
|
Симметричное отражение графика относительно оси Ох. (рис. 17.5) |
|
|
Часть графика, расположенная ниже оси Ох, симметрично отражается относительно этой оси, остальная его часть остается без изменения. (рис. 17.6) |
|
|
Симметричное отражение графика относительно оси Оу. (рис. 17.7) |
|
|
Часть графика, расположенная в области х > 0, остается без изменения, а его часть для области х < 0 заменяется симметричным отображением относительно оси Оу части графика для х > 0. (рис. 17.8) |
 |


5 (DYHKUMH M rpa(þHKV1 B 8-1 1![]()
![]()


![]()


Рассмотренные выше геометрические преобразования графиков функций могут использоваться в различных комбинациях. Так, построение графиков функций вида у = Af(k + а) + Ь по графику функции у = .f(x) может быть проведено по следующей схеме:
![]()
Может быть использована и другая схема:
![]()
Во избежание ошибок обращаем внимание на то, что длина отрезка, на которую производится параллельный перенос графика вдоль оси Ох (т. е. величина — ), определяется той константой, которая прибавляется к аргументу х, а не к выражению К; именно поэто-
а му выражение Кх + а сначала приводится к виду К х + — К
18. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
Пример 1. Постройте график функции у = — sin 2х — cos 2х.
4
1. Выполним преобразования: у = — sin 2х — cos2x = 4
![]() —
sin2x — —- cos 2х • sin2x — sin — • cos2x
—
sin2x — —- cos 2х • sin2x — sin — • cos2x![]()
![]()
![]() —sin 2х—— —sin2 х
—sin 2х—— —sin2 х
2 з 2
2. Построим график функции у = —sin2 х ——![]()
6

Рис. 18.1
Пример 2, Постройте график функции
У = cos2x — — sin2x • (sinx + cos х).
После упрощения получаем:  у cos2x —lcosx — sin
у cos2x —lcosx — sin
Рис. 18.2
1)
![]() Если х е+ 2пК•, +2лК , К eZ, то y=2cos2x.
Если х е+ 2пК•, +2лК , К eZ, то y=2cos2x.
2) Если х е+ 2лК; — +2лК , К eZ, то у =0.

Рис.18.З
18.2. 3ana11H
Ha nocTpoeHue rpa(þHK0B TPHTOHOMeTpwqecKHX![]()
IlocTpoï1Te rpad)HKH (þYHKUHü:
![]() y = Sin x + I;
y = Sin x + I;
![]()
![]() y = 3 sin x;
y = 3 sin x;
![]()
9. y=cos2x;
![]() . y=cos 2x——
. y=cos 2x—— ![]() 2
2
1
![]() — cos x
— cos x![]()
2 6
1
![]()
2

3

27 • y = x • sin x;
29 • y = sin x + cosx; ![]() sin 4 x —
cos x;
sin 4 x —
cos x;
1
![]()
3

y = cosx — 2;
![]() COS X + _
COS X + _ ![]() 4
4
. y = —cos x;
![]()
1
![]()
3
![]()
22 • y = ctg 3x;
24 • y ![]() 3 ctg x;
3 ctg x;
![]() y = x + sin x;
y = x + sin x;
28 • y = x — cosx; . y=sin x+cos x; y = tgx • ctgx • sin x;
33. y=ctg— • sin x; tgx
35. y = ![]()
37. y =3cos 2 x +2
34. ![]() tg— • sin x;
tg— • sin x;
![]() 36.
36.![]() sin 2 x —cos x;
sin 2 x —cos x;
3 sin x • cosx + sin 2 x;
38. y = I sin x l;
40. ![]() Sin IX + ll;
Sin IX + ll;
42.
![]() 44. (sin | x | — cos x); 2
44. (sin | x | — cos x); 2
![]()
sin x

54. y=sinx • Icosxl;
cos x 56.![]()
58. y = tgx + tglxl;
39. sin 1x1;

sin x
![]()
sin 2x
55 • y![]()
![]() . y=lsinxl + x;
. y=lsinxl + x;
|
60. 2
62. Y =sin x cos x +cosx sin 2 x; 63. Y = I —cos 2 x + 1 —sin 2 x; |
59. y = 1 x1 +lsinxl —cosx;
cosx sinx 64 • ![]()
lcosx| +
lsinxl +1 ![]()
![]() cosxl + lsinxl
cosxl + lsinxl
68 • у— {cosx};
![]() у = [2 sin х];
у = [2 sin х];
![]() 1 72 •
1 72 •
76. у = arctgx + Ц; ![]() у — sin
(arccos х);
у — sin
(arccos х); ![]() у = cos (arcsin х);
у = cos (arcsin х);
82. у = ctg (arctg х);
84 • у = arcsin (sin х);
86 • у = arctg (tg х); ![]() у = arccos
(sin х);
у = arccos
(sin х);
90 • у = sin (6 arccos х). cosx + lcosxl ![]() sinx + ) sin
.xl
sinx + ) sin
.xl
67 • у— {sin х};
69 •![]()
71 . у— - arcsin(2x![]()
73 • arctg
3х —![]()
![]() у = arctg lxl;
у = arctg lxl;
. y=larcsintxl —1; ![]()
79 • у— arccos х![]()
4
81. у = tg (arcctgx);
![]() . у = sin (arcsin х);
. у = sin (arcsin х);
85 • у = cos (2 arccos х); ![]() у = arccos (cos х);
у = arccos (cos х); ![]() у =
cos (2 arcsin х);
у =
cos (2 arcsin х);
18.3. Математические диктанты
1 вариант
На рисунке изображен график функции v= sinx (рис. 18.2). Пользуясь графиком, найдите:
1) Один из промежутков возрастания и один из промежутков убывания этой функции.
2) Координаты трех точек, которые соответствуют экстремальным значениям.
З) Один из промежутков знакопостоянства.
4)
Промежуток значений функции у, если —— х — ![]()
![]() 6
6
1
5)
Те значения х из промежутка [п; 2л], для которых sin х — ![]() 2
2
6)
Те значения х из промежутка [0; л], для которых выполняетЗ ся
неравенство sin х <![]()
2
7) Такие значения а, при которых прямая у = а имеет с графиком общие точки.
2 вариант
На рисунке изображен график функции у = cosx (рис. 18.2).
Требуется ответить на все вопросы задания первого варианта.
1 вариант
Постройте схематично графики функций:
![]() — sin х на промежутке [—180 0 ;
—90 0 1;
— sin х на промежутке [—180 0 ;
—90 0 1;
2) у = tgx на промежутке![]()
![]() — sin х! на промежутке [0; 2п];
— sin х! на промежутке [0; 2п];
![]()
![]() —cosx на промежутке О;
—cosx на промежутке О;
![]() — — ' cosxl на промежутке
— — ' cosxl на промежутке
2 вариант
Постройте схематично графики функций:
1) у = cosx на промежутке [—90 0 ; 90 0 ];
2)
y=ctgx на промежутке 0;![]()
4
![]()
![]() — lcosxl на
промежутке
— lcosxl на
промежутке
![]() 2sinx на промежутке 0;
2sinx на промежутке 0;
![]() sin х 1 на промежутке 0;
sin х 1 на промежутке 0;
18.4. Самостоятельная работа по теме
1 вариант
1
1) Найдите область определения
функции у = ![]() cos2x
cos2x
2) Постройте график функции у = — sinx — 1 и найдите область
ее значений.
3) Исследуйте на четность и нечетность функцию у = sin х 1.
4) Постройте график функции у = 4cos х + — и укажите точки
экстремума.
5) Постройте графики функций:
sin х
![]() б)
cosx — cos х; в) y=cos 2 х.
б)
cosx — cos х; в) y=cos 2 х.
2 вариант
1)
Найдите область определения функции у =![]()
2 sin 3х
2) Постройте график функции у = — cosx +1 и найдите область
ее значений.
З) Исследуйте на четность и нечетность функцию у = cos х![]()
4) Постройте график функции у = 2sin х — — и укажите точки 4
экстремума.
66
5) Постройте графики функций:
cosx
![]() б) у = sinxl —sinx; в) у = sin 2 х.
б) у = sinxl —sinx; в) у = sin 2 х.
Пример варианта
Постройте график функции у = —ctg +1 с помощью
геометрических преобразований и проведите исследование функции по схеме:
а) область определения;
б) четность — нечетность; периодичность;
в) точки пересечения с осями координат;
г) промежутки знакопостоянства;
д) промежутки возрастания и убывания;
е) точки экстремума и значения функции в этих точках.
19. ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ
1. На рис. 19.1 изображены графики некоторых функций. Достройте их, если можно, до графиков: 1) четных; 2) нечетных функций, заданных на промежутке [—1; 1].
|
|
|
|
|
а б г
Рис. 19.1
2. Достройте графики функций, изображенных на рисунке 19.2, до графиков всюду определенных, непрерывных на R и 1) четных функций; 2) нечетных функций.
|
|
|
|
а 
Рис. 19.2
В каких случаях это невозможно? В каких случаях это можно сделать несколькими способами?
З. Известно, что функция f (х) всюду определена, четна, периодична с периодом Т = 4. Восстановите ее график по участку, изображенному на рисунках 19.3. В каких случаях этого сделать нельзя'? В каких случаях это можно сделать, но неоднозначно?
|
у |
|
|
О |
2 3 4 х |
|
|
|
|
|
о |
2 |
х |
аг
Рис. 19.3
Докажите (1 — 8):
1. а) График четной функции на координатной плоскости Оху симметричен относительно оси ординат.
б) Если график функции f (х) симметричен относительно оси ординат, то функция .f(x) четная.
2. а) График нечетной функции на координатной плоскости Оху симметричен относительно начала координат.
б) Если график функции f (х) симметричен относительно начала координат О, то функция f(x) нечетная.
68
З. Сумма, разность и произведение двух четных функций тоже являются четными функциями.
4. Сумма и разность двух нечетных функций, а также произведение нечетной функции на число являются нечетными функциями.
5. Произведение двух нечетных функций есть функция четная на их общей области определения.
6. Произведение четной функции на нечетную есть функция нечетная на их общей области определения.
7. Любую функцию с симметричной областью определения можно представить в виде суммы четной и нечетной функций. Такое представление единственно.
8. Если некоторый многочлен является:
а) четной функцией, то он содержит одночлены лишь с четными степенями х; б) нечетной функцией, то он содержит многочлены с нечетными степенями х.
9. Приведите пример функций, которые являются одновременно четными и нечетными.
10. Какое значение может принимать нечетная функция в точке
11. Существуют ли всюду определенные функции, являющиеся одновременно:
а) четными и возрастающими на К;
б) нечетными и убывающими на К;
в) нечетными и положительными на R?
12. Может ли четная (нечетная) функция иметь в точности:
1) одну; 2) две; 3) три точки экстремума?
13. Может ли четная функция иметь обратную функцию?
14. Всегда ли нечетная функция имеет обратную функцию?
15. Найдите все четные и все нечетные функции среди:
а) линейных функций f(x) = ах + Ь; б) квадратичных функций f(x) = ах 2 + bx + с, в) функций вида f(x) = а cosx + bsin х.
16.
f(x) произвольная функция, заданная на симметричном множестве. Что можно
утверждать о четности и нечетности функций: а) +f(—x); б) y=f(x) —f(—x); в)![]()
г) у = f(x2![]()
17.
Функция у = f(x) четная (нечетная). Каковы функции: y=—f(x); y=f(—x);
y=f(x) + Ь; y=kf(x); y=f(kr);![]()
![]()
20. НУЛИ И ИЗМЕНЕНИЯ ЗНАКА. НЕПРЕРЫВНОСТЬ. АСИМПТОТЫ
Тест
1. Для каждого из графиков, изображенных на рисунках
20.1 — 20.3, сконструируйте формулу, задающую график.

Рис. 20.1

Рис. 20.2

2. Для каждого из графиков, изображенных на рисунке 20.4, подберите в списке формул 1— 22 ту, которая задает этот график.
70

Рис. 20.4
![]()
![]()
![]()
![]()
![]()
![]()
![]() 2. —l)(x
—1);
2. —l)(x
—1);
5. —l)(x +1);
6. у, (х + 1) 2 ,
7. —l)(x +1);
![]() х)3,
х)3,
21. ВОЗРАСТАНИЕ И УБЫВАНИЕ ФУНКЦИЙ. ЭКСТРЕМУМЫ ФУНКЦИЙ
21.1. Задачи на исследование функций
1. Укажите промежутки возрастания и убывания функций, графики которых изображены на рисунке 21.1.
|
|
|
Рис. 21.1
2, Известно, что функция f(x) убывает на промежутках: а) [О; 1) и [1; 2); б) [0; 1] и [1; 2). Можно ли утверждать, что функция f(x) убывает:
1) на объединении этих промежутков на полуинтервале [0; 2)?
2)
на промежутке 0; ![]()
2
3. Нарисуйте график функции f(x) так, чтобы она:
1) убывала на промежутках (—с, —2] и [1; 4] и возрастала на промежутках [—2; 1] и [4; +00);
2) имела бы бесконечное число промежутков возрастания и убывания.
4. Нарисуйте график всюду определенной и всюду непрерывной функции так, чтобы у нее было ровно: а) 0; б) 1; в) 2; г) З; д) 10; е) бесконечно много точек экстремума.
5. Нарисуйте график всюду определенной и всюду непрерывной функции так, чтобы на отрезке [0; 1] она имела бесконечно много точек экстремума.
6. Нарисуйте график функции, которая определена и непрерывна на отрезке [0; 1] и имеет бесконечно много экстремумов на этом отрезке.
7. Для функций, графики которых изображены на рисунке 21.2, укажите все точки максимума и минимума, если они есть.
|
|
|
|
а 
|
|
|
|
|
Рис. 21.2
1. Какова геометрическая интерпретация монотонности функ-
2. Запишите условие, которому удовлетворяет любая функция Г (х), не являющаяся строго возрастающей на множестве Х?
З. Если функция определена на всей числовой прямой и принимает только конечное множество различных значений, то может ли она быть монотонной на всей числовой оси? Строго монотонной?
4. Докажите, что всякая строго монотонная функция имеет обратную, причем, последняя возрастает (убывает), если взятая функция возрастающая (убывающая).
5. Может ли иметь обратную функцию монотонная, но не строго монотонная?
6. Функция f(x) всюду определена и убывает на всей числовой оси. Может ли при этом функция (х) быть: а) всюду положительной; б) всюду отрицательной; в) четной; г) нечетной; д) периодической?
7. Функции Д g возрастают на множестве Х, а (Р и у убывают на множестве Х. Что можно утверждать относительно монотонно-
6 Функции и графики в 8-l I кл.
сти функций: а) —f; 6)f± g; (Р :± y;f+ (р; в) а •f; а * О; г)Г g; (Р • у; f• (Р? Если нельзя утверждать монотонность в общем случае, то при каких дополнительных условиях можно?
8.
Функция f(x) является возрастающей (убывающей) на всей области
определения. Какие из функций у = kf(x — а) + Ь; у =f(kr); y=f(—x); у = ![]() будут:
а) монотонными при любом выборе функции f(x); б) немонотонными при любом выборе
функции f(x); в) монотонными при одних f(x) и немонотонными при других?
будут:
а) монотонными при любом выборе функции f(x); б) немонотонными при любом выборе
функции f(x); в) монотонными при одних f(x) и немонотонными при других?
9. Может ли функция, определенная на отрезке, не иметь на этом отрезке ни максимума, ни минимума? Иметь более одного максимума?
10.Может ли минимум функции превосходить ее максимум?
11.Может ли иметь экстремумы монотонная функция?
12.Может ли иметь только один экстремум периодическая функция?
13.Точка хо является точкой максимума четной (нечетной) функции. Является ли точка —хо точкой экстремума?
14.Может ли нечетная функция, заданная на [—с, а], иметь экстремум в точке х = О?
15.Может ли многочлен третьей степени иметь: 1) три экстремума; 2) два экстремума; 3) два максимума (минимума)? тах min тах min min
![]()
Рис. 21.3 Рис. 21.4
16.Существует ли всюду определенная и непрерывная функция, у которой: а) было бы ровно две точки максимума .Xl и .хз и ровно одна точка минимума, расположенные, как на рис. 21 З? б) было бы ровно две точки минимума и х2 (рис.21 А) и не было бы больше ни одной точки экстремума (ни максимума, ни минимума)?
17.Может ли функция, имеющая экстремум, иметь обратную функцию?
22. ВЫПУКЛОСТЬ И ВОГНУТОСТЬ ФУНКЦИЙ
Докажите следующие утверждения:
1. Функция f(x) = ах 2 + bx + с выпукла при а< Ои вогнута при
К 2. Функция f(x) = выпукла на (0; +00) и вогнута на (—оо; 0) х
З . Функция .f (х) = cos х выпукла на отрезках +2К1Ђ +2Кл 2 и вогнута на отрезках — +2Кт; — +2Кл , где К eZ.
4. Функция Г (х) = tgx вогнута на отрезках Кл _+Кл и вы-
пукла на отрезках — + Кт, Кл , где К eZ.
2
5.Функция Г (х) — вогнута на отрезке (2; +00) и выпукла
на (—оо; 2).
6. Если к выпуклой на [а; Ь] функции прибавить линейную функцию у = Кх + Ь, то полученная сумма выпуклая на [а; Ь].
1. Каков геометрический смысл понятий: выпуклая функция, вогнутая функция?
2. Существует ли четная функция, выпуклая (вогнутая) на всей области определения? Такой же вопрос для нечетной функции.
3. Функция у = f(x) выпукла (вогнута) на всей числовой оси. Каковы:
![]()
![]()
г) у = f(—x);
![]()
ж) у = f(kx + а) + Ь?
4. Функции Д q выпуклы, а функции (Р и ЧЈ вогнуты на [0; 1].
Каковыј± q ;f± (р; (Р ± y;f• q;f• (р; (Р • у?
5. Может ли возрастающая функция иметь точки перегиба?
6. Может ли многочлен третьей степени иметь:
![]() ) две точки перегиба;
) две точки перегиба;
2) два экстремума и ни одной точки перегиба.
7. Какую наименьшую степень могут иметь многочлены, графики которых изображены на рис. 22.1 ?

а
Рис. 22.1
8. Какое наибольшее число точек экстремума и точек перегиба может иметь многочлен 10-й степени?
23. ПРОИЗВОДНАЯ
Задачи на исследование производной
1. Можно ли утверждать, что:
а) производная любой четной функции является: 1) четной; 2) нечетной;
б) производная любой нечетной функции является: 1) нечетной; 2) четной;
в) производная периодической функции является периодической?
2. Может ли:
а) производная всюду положительной функции быть всюду отрицательной;
б) производная всюду определенной
непериодической ![]() функции быть периодической;
функции быть периодической;
в) производная всюду определенной функции, не являющейся ни четной, ни нечетной, быть: 1) четной: 2) нечетной?
З. Какая из указанных функций имеет производную, график которой изображен на рис. 23.1 ?
![]()
![]()
![]() 2)
f(x) = х 2 — х;
2)
f(x) = х 2 — х;
х
2 х
2
4. Какие промежутки возрастания имеет функция f(x) , если график ее производной выглядит так, как изображен на рис. 23 2?
![]() Рис.
23.2
Рис.
23.2 
5. На рис. 23.3 изображены графики функций y=f(x), в том числе квадратичной (а). Какие из расположенных под ними графиков (рис. 23.4) могут являться графиками производных этих функции?
|
|
|

Рис. 23.4
6. На рис. 23.5 изображены графики функций у = f(x). В тех же системах координат (или же под графиками функций у = f(x)) нарисуйте примерные графики производных у = f'(x).

7. По графикам производных y=f'(x) , изображенных на рис. 23.6, восстановите примерные графики функций у = f(x).

Рис. 23.6

Рис. 23.6 (продолжение)
24. ИССЛЕДОВАНИЕ СВОЙСТВ ФУНКЦИЙ
И ПОСТРОЕНИЕ ГРАФИКОВ С ПОМОЩЬЮ ПРОИЗВОДНОЙ
24.1. Задачи на построение графиков функций Постройте графики функций:
![]()
![]()
 (х
+ 1)(х — 2)
(х
+ 1)(х — 2)
![]()
![]() х
х
19. У = 2' 1—х
20.
21. ![]()
х х
![]() 22. У = 26.
22. У = 26.
2
![]() Примечание. По одной задаче каждый ученик
класса по-
Примечание. По одной задаче каждый ученик
класса по-
лучал в качестве индивидуального задания на дом на длительный срок (2 недели).
Каждая группа получает задание на карточке: постройте график функции, проведя полное исследование:
![]()
![]() 2х
2х
З
![]() х
х ![]()
По окончании работы ученики проверяют правильность построения графиков по эскизам, заранее построенным на внутренней части доски. В ходе проверки выявляются ошибки и проводится работа по их устранению.
Класс делится на 6 групп, каждая группа получает задание провести полное исследование функции и построить ее график (каждый учащийся выполняет задание дома, самостоятельно). В классе по группам обсуждаются результаты работы.
Примеры заданий:
1. y=sinx
+ cosx; ![]()
2. у = sin2x —2cos 2 х;![]()
у= cos х ![]() cos х
cos х
у= sinx + ![]() smx
smx
у = sinx — —sin2x.
После проверки обсуждается вопрос: «Нельзя ли построить графики этих функций без применения производной»?
24.4. Экзаменационная контрольная работа по алгебре и началам анализа за 10-й класс
1 вариант
1. Дан многочлен Р (х) = х(х — — а) + 12. Известно, что число (—1) является корнем этого многочлена. Разложите многочлен на множители.
2.
Решите неравенство: ![]()
199
3. Решите уравнение: sin 5х + 6cosx • sin 3х = 2 sin 3х — sin х.
4. Установите промежутки монотонности, экстремумы, нули
3 —х2
функции у = Найдите асимптоты и постройте график функ-
ции.
5. Напишите уравнение касательной к графику функции
тс
у = sin 2 3х в точке с абсциссой хо = .
2
2 вариант
1. Дан многочлен Р (х) = х(х + l)(x — а) — 12. Известно, что число 1 является корнем этого многочлена. Разложите многочлен на множители.
81
2.
Решите неравенство: ![]()
3. Решите уравнение: 10sinx • cos 3х — cosx = 4cos3x + cos 5х.
4. Установите промежутки монотонности, экстремумы, нули функции у = — (З — х) з . Найдите промежутки выпуклости и вогну9 тости, точки перегиба.
5. Напишите
уравнение касательной к графику функции у = cos 2 3х в точке с
абсциссой хо![]()
3
25. ПОСТРОЕНИЕ ГРАФИКОВ ПОКАЗАТЕЛЬНОЙ ФУНКЦИИ
Пример. Постройте график функции у = 4 x — 2x+
1 +1 +2 х![]()
|
|
|
Рис. 25.1 Рис. 25.2
25.1. Задачи на построение графиков показательной функции
Постройте графики функций:
![]()
![]()
![]() 4. y=2'xl •,
4. y=2'xl •, 

83
1
17. _.22 —2—2х—4
![]()
З З

26. ПОСТРОЕНИЕ ГРАФИКОВ ЛОГАРИФМИЧЕСКОЙ И ПОКАЗАТЕЛЬНОЙ ФУНКЦИЙ С ПОМОЩЬЮ
ГЕОМЕТРИЧЕСКИХ ПРЕОБРАЗОВАНИЙ
Пример. Постройте график функции у = log2 (lxl — 1) .

Рис. 26.1
26.1. Задачи на построение графиков
Постройте графики функций:
1.
![]() у = log2
(х —2);
у = log2
(х —2);
2. у = log2 (l — х);
 З. log3(3
З. log3(3

13 . * y =0,5 log2(x —1) 2 ;
14. log 127X — 541;
![]()
16. y = logx 2;
![]()
![]()
![]() log (x—3) .
log (x—3) .
![]()
—x + log3
+ log i
![]()
![]()
![]()
 9x 2 —6x +l;
9x 2 —6x +l;
— 4x +1.,
y = logo (16 — 8x + x 2 ) + log2(2x — 8);
![]() y=
log3 2 log (X" -12x +36);
y=
log3 2 log (X" -12x +36);
33. ![]() (x —2)) + log3 (3x
(x —2)) + log3 (3x![]()
34 • y — log (x —5x2 + 8x — 4) — log (x —l); log2(x —2) 2![]()
![]() — logo 5
(x —2) 2
— logo 5
(x —2) 2![]()
27. ПОСТРОЕНИЕ ГРАФИКОВ
ПОКАЗАТЕЛЬНОЙ И лог»иОмикской ФУНКЦИЙ МЕТОДОМ ПРОИЗВОДНОЙ
27.1. Примеры на построение графиков показательной и логарифмической функций
Пример 1. Постройте график функции у = 2 ![]() Исследование
функции. D(y): х 0.
Исследование
функции. D(y): х 0.

![]() Построение графика:
Построение графика:

Рис. 27.1
Пример 2. Постройте график функции у =![]()
х
Исследование функции. 1) = + 00).
2) Функция общего вида. З) Асимптоты:
а) вертикальные ![]() lim = —оо, х вертикаль-
lim = —оо, х вертикаль-
ная асимптота;
б) наклонные асимптоты: ![]() где К = lim
где К = lim![]()
х
![]()
![]() lnx — 1
lnx — 1
= lim ![]()
![]() х 2х
х 2х
у = 0 — горизонтальная асимптота.
![]()
![]() . На (О; е2
] функция возрастает; х на [еж, +00) функция убывает; х = е
точка макси-
. На (О; е2
] функция возрастает; х на [еж, +00) функция убывает; х = е
точка макси-
![]()
 . На (0; е 2 е) график функции
х выпуклый; на [е 2 е; + х) график функции вогну-
. На (0; е 2 е) график функции
х выпуклый; на [е 2 е; + х) график функции вогну-
тый; е  точка перегиба.
точка перегиба.

Рис. 27.2
27.1. Задачи на построение графиков показательной и логарифмической функций
Постройте графики функций:

![]()
2
х
![]()
1пх
10.![]()
х-
![]()
12. ln(l -cos х);
![]()
х

х
19. у =![]()
![]()
х“
![]()
![]()
х
![]()
2
![]() у = ln(x
у = ln(x ![]()
lnx2 27 •
![]() 2
2
28 • у = ln 2 х — ln х; ![]() у = х — ln(x +1);
у = х — ln(x +1); ![]() ln(X 2 + 1);
ln(X 2 + 1);
![]()
16 —х
32. v=-x(lnx +1).
Примечание. Одна из этих задач предлагается каждому учени-
ку класса в качестве индивидуального домашнего задания на длительный срок (2 недели).
27.3. Контрольная работа по теме
1 вариант
1.
Решите уравнение: 125 5 ![]()
2. Решите неравенства:
![]() х+ 2
х+ 2
а) б) log (3 ![]() log2
(х + 4) 2
log2
(х + 4) 2
3. Найдите площадь фигуры, ограниченной графиком функции
![]() , касательной к графику этой функции,
проведенной в точх ке хо = 1, и прямой х = 5.
, касательной к графику этой функции,
проведенной в точх ке хо = 1, и прямой х = 5.
4. Постройте график функции:
х
![]()
2 вариант
1.
Решите уравнение: 2![]()
2. Решите неравенства: log (х + 6)
а)
![]() б)
log (2
б)
log (2![]()
3.
Найдите площадь фигуры, ограниченной графиком функции ![]() касательной
к графику этой функции, проведенной в точх ке хо = 1, и прямой х = 5.
касательной
к графику этой функции, проведенной в точх ке хо = 1, и прямой х = 5.
4. Постройте график функции:
![]()
х
![]() 28. ЗАДАЧИ С РЕШЕНИЯМИ
28. ЗАДАЧИ С РЕШЕНИЯМИ
1. у= cos(arcsin х), х 1
![]()
З. lxl tg(arccosx), ![]() 4, У = +sin2 х;
4, У = +sin2 х;
![]() —cos х •
—cos х •
2
![]()
—2 log I sin x
![]()
 cosxf sinx(;
cosxf sinx(; 13.
2 sin 2x +
14.
log i x +1 ; ![]() sin x
sin x
![]()
 cosx
cosx
PeuœH11H
1. y = cos(arcsinx), 1x1 <1.
1
![]()
TIycTb y = arcsinx, Torna sin (2 arcsinx) = sin 2 y =2 sin y • cos y =
|
y |
1 |
|
|
-1 |

|
-1 |
1 |
|
|
1 -1 |
Puc. 28.2
3. y= lxl tg(arccosx), 1 x 1 < l.
![]() sin (arccos x) tg(arccosx) =
sin (arccos x) tg(arccosx) =
cos (arccosx) x x
![]()
4. v = I + sin 2 x. ![]() ržeTHaH.
ržeTHaH.
x > 0, y =
1 + sin - x; y = ——cos2x +1 ![]() T —
T —![]()

Puc. 28.4
![]() —cos 2x .
—cos 2x .



Puc. 28.6
—2 log sin x
![]()
![]() v): sinx>(); 2nk< x< n. +2Ttk, k
e Z.
v): sinx>(); 2nk< x< n. +2Ttk, k
e Z.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() —210g
I sin x log (sin x) •
—210g
I sin x log (sin x) •
![]() log
log ![]() 2 (sin 2 x)
2 (sin 2 x) ![]() cos 2x.
cos 2x.
 y = cos 2.x
y = cos 2.x
 ± ltk, k e Z.
± ltk, k e Z.
Y = sin 2x.
|
|
Y = sin |
|
|
|
x![]()
2x ![]()
Puc. 28.8
![]()
PIccJ1eA0BaHHe (þYHKUHH:


Puc. 28.9
![]() DO): x + Ttk, k e Z; y =cos 2x
DO): x + Ttk, k e Z; y =cos 2x

Рис. 28.10

Рис. 28.11
2log (х+ 1)

Рис.
13. y = 2 sin
2x + — ![]()
![]()
![]() — = 2 sin
2 x + —
— = 2 sin
2 x + — ![]()
Y = sin x ![]() y = sin 2x —
y = sin 2x — ![]() Y = sin + 6)
Y = sin + 6)![]()
Y = Isin 2(x+ v = asin 2(x+
Puc. 28.13
![]() log l X + ll.
log l X + ll.
Puc. 28.14

Puc.
![]()

Рис. 28.16


Рис. 28.17
![]()

Рис.
![]()
Преобразуем исходную функцию к виду: у = х 2 —8 lxl + 15 .
Строим график функции у = х 2 —
8х + 15 = (х — 4) 2 —1 и используем правила построения графиков
функций у = .f(l х] ) и у =![]()

Рис. 28.19 Рис. 28.20
![]()
Строим график функции у = (х![]() — 2,25 и
далее действуем аналогично задаче 19 (рис. 2820).
— 2,25 и
далее действуем аналогично задаче 19 (рис. 2820).
![]()
Функция четная.

Рис.
![]()


Puc. 28.22


Puc.
![]()
y = sin x •Icosxt; T = 2m

![]()
![]()
![]()
![]() Puc. 28.24
Puc. 28.24
y = cosx ![]() v = cos2x
v = cos2x![]()
![]() — — cos2x
— — cos2x![]()
— cos2x+—![]()
—( — cos2x + —) — — •
Puc.
1.
Планирование учебного материала для VII класса с углубленным изучением
математики. Методические рекомендации. ![]()
м., 1988.
2. Планирование учебного материала для IX класса с углубленным изучением математики. Методические рекомендации. — М., 1990.
З. Планирование учебного материала для Х класса с углубленным изучением математики. Методические рекомендации. — М.,
4. Галицкий М. Л. и др. Углубленное изучение курса алгебры и математического анализа. Методические рекомендации и дидактические материалы: Пособие для учителя [ М. Л. Галицкий, М. М. Мошкович, С. И. Шварцбурд. Изд. 2-е, дораб. — М., 1990.
5. Абрамов М. И., Стародубцев М. Т. Математика (алгебра и элементарные функции). Учебное пособие. — М., 1976.
6. Алгебра и начала анализа в 9—10 классах. Пособие для учителей / А. М. Абрамов, Б. М. Ивлев, З. И. Моисеева и др. — М., 1982.
7. Алгебра и элементарные функции. Справочник (Ф. П. Яремчук, Т. А. Рудченко). Изд. 3-е, пер. и доп. — Киев, 1987.
8. Афанасьева О. Н., Бродский Я. С., Гуткин И. И., Павлов А. Л. Сборник задач по математике для техникумов на базе средней школы. Учебное пособие для техникумов. — М., 1987.
9. Башмаков М. И., Беккер Б. М., Гольховой В. М. Задачи по математике. Алгебра и анализ / Под ред. Д. К. Фаддеева. — М., 1982.
10. Берман Г. Н. Сборник задач по курсу математического анализа. — м., 1972.
11. Блошкин Б. Ф. Самостоятельные и контрольные работы по математике для 9 и 10 классов. — М., 1969.
12. Болтянский В. Г. Как развивать «графическое мышление» // Математика в школе. 1978, № з.
13. Болтянский В. Г. Квадратное уравнение /l Квант. 1992, № 6.
14. Бородуля И. Т. Показательная и логарифмическая функции (задачи и упражнения): Пособие для учителя. — М, 1984.
15. Виленкин Н. Я. Функции в природе и технике: Книга для внекл. чтения 9—10 классов. 2-е изд., испр. — М., 1985.
16. Виленкин К. Я., Мордкович А. Г. Производная и интеграл. Пособие для учителей. — М., 1976.
17. Гельфанд И. М., Глаголева В. Г., Э. З. Шноль. Функции и графики (основные приемы). — М., 1965.
18. Гельфанд И. М., Глаголева Е. Г., Кириллов А. А. Метод координат. — м., 1973.
19. Гнеденко Б. В. Важные аспекты качества обучения // Математика в школе. 1976, № 1.
20. Графики функций: Учебное пособие для поступающих в вузы. — м., 1972.
21. Грицаенко Н. П. Устные упражнения по математике для 8—10 классов: Пособие для учителя. — Киев, 1988.
22. Гулимова Г. А. Обратные тригонометрические функции // Математика. (Сб. ст.) — М., 1975.
23.
Дворянинов С. В. О построении графиков сложных функций на основе
свойства монотонности Математика в школе. ![]() 1986. — № 4.
1986. — № 4.
24. Демидович Б. П. Сборник задач и упражнений по математическому анализу. — М., 1962.
25. Детская энциклопедия. Т.2., изд. 3-е. — М., 1972.
26. Дополнительные главы по курсу математики: Учебное пособие по факультативному курсу для учащихся 10 кл: Сборник статей. Сост. З. А. Скопец. Изд. 2-е, перераб. и доп. — М., 1974.
27. Дорофеев Г. В., Потапов М. К., Розов Н. Х. пособие по математике для поступающих в вузы. — М., 1962.
28. Егерев В. К. и др. Методика построения графиков функций: Учебное пособие для студентов вузов. Изд. 2-е. — М., 1970.
29. Задачи повышенной трудности по алгебре и началам анализа: Учебное пособие для 10—11 кл. средней школы / Б. М. Ивлев, А. М. Абрамов, Ю. П. Дудницын, С. И. Шварцбурд. — М., 1990.
30.
Задачи по математике. Начала анализа: Справочное пособие ![]() В. В.
Вавилов, И. И. Мельников, С. Н. Олехник, Т. Н. Пасиченко. — м., 1990.
В. В.
Вавилов, И. И. Мельников, С. Н. Олехник, Т. Н. Пасиченко. — м., 1990.
31.
Земляков А., Ивлев Б. 17 задач по анализу /l Квант. 1977. ![]()
32.
Земляков А. Четные и нечетные функции // Квант.![]()
33. Земляков А., Ивлев Б. Вопросы по алгебре и анализу // Квант. — 1978. — № 2.
34.
Земляков А., Орлов В. Вопросы для выпускников // Квант. ![]() 1978. — № 7.
1978. — № 7.
35. Земляков А. Еще 17 вопросов // Квант. 1978. — № 12.
36. Земляков А. Проверьте себя // Квант. 1980. — № 9.
37.
Канин Е. С., Канина Е. М., Чернявский М. Д. Упражнения по началам
математического анализа в 9—10 классах. — М., 1986. 38. Колмогоров А. Н. Что
такое функция? // Квант.![]()
39.
Колмогоров А. Н. Что такое график функции // Квант. ![]() 1970. — № 2.
1970. — № 2.
40. Кондратьева Л. А., Соломоник В. С. Сборник вопросов и задач по математике для поступающих в техникумы: Учебное пособие. — м., 1983.
41. Кочетков Е. С., Кочеткова Е. С. Алгебра и начала анализа. 10 класс. Пробный учебник. Издание 2-е, перераб. — М., 1974.
42. Крамор В. С., Михайлов П. А. Тригонометрические функции: Система упражнений для самостоятельного изучения: Пособие для учащихся. — М., 1979.
43.
Кузнецова Е. П. Об одном методе построения графиков тригонометрических
функций (метод рамок) // Математика в школе. ![]() 1990. — № 4.
1990. — № 4.
44. Методика преподавания математики в средней школе: Общ. методика: Учебн. пособие для пед. институтов по спец. 2104 «Математика» и 2105 «Физика» / А. Я. Блох, Е. С. Канин, Н. Г. Килина и др.; Сост. Р. С. Черкасов, А. А. Столяр. — М., 1985.
45. Методическое пособие по математике для поступающих в вузы / В. А. Васильева, Т. Д. Курина, Р. Н. Молодожникова. Под ред.
Р. Н. Молодожниковой. — М., 1991.
46. Мордкович А. Г. Алгебра и начала анализа. — М., 1979.
47. Мордкович А. Г., Солодовников А. С. Математический анализ: Учебное пособие для техникумов. — М., 1990.
48.
Мышкин А. Д., Сатьянов П. Г. О формировании культуры построения графиков
функций // Математика в школе. — 1985.![]()
49. Новоселов С. И. Обратные тригонометрические функции. Пособие для учителей. Изд. 3-е. — М., 1950.
50. Павленкова И. А. Об изучении функционального материала // Математика в школе. 1970. — № 1.
51. Панчишкин А. А., Шавгулидзе Е. Т. Тригонометрические функции в задачах. — М., 1986.
52. Повышение эффективности обучения математике в средней школе: Пособие для учителей / Под ред. Г. Г. Масловой. — М.,
53.
Подольский В. А., Суходольский А. М. Сборник задач по математике для
техникумов: Учебное пособие для техникумов. ![]()
м., 1978.
54. Пособие по математике для поступающих в вузы: Учебное пособие / А. Д. Кутасов, Г. С. Пиголкина, В. И. Чехлов, Т. Х. Яковлева. Под ред. Г. Н. Яковлева. 3-е изд., перераб. — М., 1988.
55. Пособие по математике для техникумов. Алгебра и началд анализа. Часть 1 / М. И. Каченовский, Ю. М. Колягин, Г. Л. Луканин, Г. Н. Яковлев. Под ред. Г. Н. Яковлева. — М., 1977.
56. Практикум з розв'язувания задач з математики: Сборник задач. Изд. 3-е. — Киев, 1989.
57.
Ошмарина Т. К., Федорова Н. Е. Из опыта проведения итогового повторения
курса алгебры 7 класса // Математика в школе. ![]() 1970. — № 2.
1970. — № 2.
58.
Райхмист Р. Б. Графики функций: Справ. пособие для вузов. ![]()
м., 1991.
59.
Сатьянов П. Г. Задачи графического содержания при обучении алгебре и
началам анализа // Математика в школе.![]()
60. Сборник задач по алгебре и началам анализа для 9 и 10 классов. Пособие для учителей. — М., 1978.
61. Сборник задач по математике для поступающих в вузы: Учебн. пособие / П. Г. Дыбов, А. И. Зибаев, А. С. Иванов и др. Под ред. А. И. Прилепенко. 2-е изд., испр. и доп. — М., 1989.
62. Сборник конкурсных задач по математике для поступающих во втузы. Учебное пособие / Под ред. М. И. Сканави. 3-е изд., доп. — М., 1976.
63. Сефибеков С. Р. Внеклассная работа по математике: Книга для учителя. — М., 1988.
64. Сивашинский Ч. Х. Элементарные функции и графики. Изд. 2-е. — м., 1968.
65. Соломоник В. С. Сборник вопросов и задач по математике (для поступающих в техникумы): Учебн. пособие. 2-е изд., перераб. и доп. — М., 1978.
66. Справочник «Элементарные функции». Формулы, таблицы, графики / В. Д, Рыбасенко, И. Д. Рыбасенко. Под ред. Е. В. Шикина. — м., 1987.
67. Факультативный курс. Избранные вопросы математики. (7—8 класс). — М., 1978.
68. Худобин А. И. и др. Сборник задач по алгебре и элементарным функциям. Пособие для учителей. Изд. 3-е. — М., 1973.
69. Шварцбурд С. И., Ивашов-Мусатов О. С. Алгебра и начала анализа: Учебное пособие для средн. проф. техн. училищ. — М.,
70. Энциклопедический словарь юного математика. Сост. А. П. СаВИЧ. — М., 1989.
71. Яшина И. В. Приемы построения графиков // Математика в школе. 1994. — № з.
ПРОГРАММА ЦЕЛОСТНОГО ИЗУЧЕНИЯ темы
«ФУНКЦИИ И ГРАФИКИ» В 8-1 1 КЛАССАХ
С УГЛУБЛЕННЫМ ИЗУЧЕНИЕМ
МАТЕМАТИКИ
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Тема «Функции и графики» является важной составляющей программы средней школы по математическим дисциплинам, так как именно здесь закладываются основы аналитического мышления, формируется математическая интуиция, развивается логика и приобретаются навыки использования функциональных обозначений и методов.
Понятие функции важно для школьного курса математики- еще и потому, что оно тесно связано с понятием тождества, уравнения и неравенства.
Понятие функции для математики и ее приложений, связанных с изучением переменных величин, столь же фундаментально, как понятие числа при изучении количественных соотношений реального мира. Каждая область знаний: физика, химия, биология, социология, лингвистика и т. д.— имеет свои объекты изучения, устанавливает свойства и, что особенно важно, взаимосвязи этих объектов. Математика рассматривает абстрактные переменные величины и изучает законы их взаимодействия, т. е. функции.
На первых ступенях обучения математике главная трудность для учащихся состоит в том, чтобы уметь отвлечься от конкретных объектов и овладеть абстрактными понятиями. При изучении же элементов математического анализа главная трудность состоит уже не в обобщении, а в конкретизации, т. е. умении видеть за математическими терминами и их определениями конкретные образы, представлять себе достаточно полно изучаемое понятие.
Данная программа ставит целью развитие конструктивных способностей и графического мышления учащихся.
Для школьного курса алгебры и начал анализа можно выделить З основных языка: естественный, словесный язык; язык аналитических выражений; язык графических изображений, или «графический язык».
Графический язык — особый язык математики, график — один из ее методов. Эффективное применение графического языка в курсе математики невозможно без обучения правилам этого языка и сопутствующей терминологии. Обучение всякому языку включает в себя составление функционально-графического словаря и обучение переводу. Перевод предполагает два взаимно обратных вида деятельности:
1) перевод свойства функции на графический язык,
2) умение по заданному графику сформулировать свойства функции.
Графический язык является важным средством преодоления формализма в знаниях школьников, развития геометрической интуиции, необходимой для понимания основных фактов анализа и их применения на практике, способствует формированию прикладных и политехнических умений.
Важный класс задач, связанных с использованием графического языка на внутреннем этапе решения, образуют достаточно широко используемые в школьном курсе задания на графическое решение уравнений и неравенств. Здесь графические образы могут быть или наглядной опорой, позволяющей упростить аналитическое решение, или являться основным и даже единственным средством решения.
Определенные трудности в усвоении графиков в значительной степени объясняются тем, что тема разбросана по разным разделам алгебры и тригонометрии стандартной программы, функции изучаются в несколько этапов, причем вначале рассматриваются частные случаи, без обобщения и систематизации.
Включение в программу углубленного изучения математики разделов «Построение графиков функций методом геометрических преобразований», «Построение графиков функций, содержащих знак модуля», «Построение графиков функций методом алгебраических преобразований», «Исследование свойств элементарных функций с помощью производной» и ряда других имеет целью систематизировать изложение методов исследования функций и построения графиков, сформировать у учащихся понимание того, что кроме метода построения графиков на основе исследования свойств функции существует метод геометрических преобразований, применяемый в тех случаях, когда график функции может быть получен из уже имеющегося графика; способствовать повышению общей математической культуры учащихся.
Обучение по этой программе вводится в 8 классе и рассчитано на 4 года обучения.
8-9 КЛАССЫ
В результате обучения учащиеся должны:
Знать определение функции, различные способы задания функции (табличный, графический, аналитический, словесный); терминологию (аргумент, значение функции, график функций, область определения и др.); свойства функций; определения линейной, прямой и обратной пропорциональности, квадратичной, степенной функции и способы их графического представления; алгоритмы построения графиков различных функций; роль элементарных функций в изучении явлений реальной действительности в практической деятельности человека.
Уметь правильно употреблять функциональную терминологико и символику, понимать ее при чтении текста, в речи учителя, в формулировке задач; находить значение функций, заданных формулой, таблицей, графиком, решать обратную задачу; строить графики функций — линейной, прямой и обратной пропорциональности, квадратичной функции, степенной функции; исследовать расположение графиков в координатной плоскости в зависимости от значений параметров, входящих в формулу; по графику функции устанавливать ее свойства: указывать промежутки возрастания и убывания, знакопостоянства и др.; свободно применять правила преобразований графиков (параллельный перенос, деформация, симметрия) для построения графиков функций; строить эскизы графиков функций с предварительным исследованием; применять аппарат алгебры к задачам построения графиков различных функций; оперировать графическими моделями; применять опыт, полученный при изучении функций, к решению несложных практических задач.
8 класс
1. Повторение и обобщение темы «Функции», изученной в 7 классе (6 ч.)
Числовые функции. Область определения и область значений функции. Способы задания функции. График функции.
Свойства функции: четность, нечетность, нули, интервалы знакопостоянства, возрастание и убывание, наибольшее и наименьшее значения. Схема исследования функции. Линейная функция, ее свойства и график. Функции, содержащие знак модуля. Функции у = и у = х з , их свойства, графики.
2. Графики функций и их преобразования (10 ч.)
Построение графиков функций вида: у =f(x) + Ь, у =f(x + а) + Ь, У = У = —.f(x), у = • х), у = af(x).
Построение по графикам функций вида: у = Л (х) и y=.f2 (х) графиков функций: y=fl (х) + Л (х), у = Л (х) — Л (х), у = Л (х) х хл ЕЛ (х) / f2(x).
Построение графиков функций вида: ![]()
![]()
З. Изучение НОВЫХ функций. Использование аппарата алгебры при построении графиков различных функций (13 ч.)
Функция у = х, ее свойства, график. ![]()
Функции, при построении графиков которых используются преобразования выражений, содержащих квадратные корни.
Функция у = ах 2 + 6х + с. Построение графика квадратной
функции с использованием метода выделения полного квадрата и геометрических преобразований графиков.
Функции, при построении графиков которых используется раз-
ложение квадратного трехчлена на линейные множители. к
Функция у = — ее свойства и график. Дробно-рациональные
![]() х функции. Непрерывность. Вертикальные и
горизонтальные асимптоты.
х функции. Непрерывность. Вертикальные и
горизонтальные асимптоты.
4. Повторение. Систематизация изученного материала (З ч.)
9 класс
1. КваДратичная функция
(повторение) (12 ч.)![]()
Определение и свойства функции. Построение графиков функций с помощью геометрических преобразований. Функции, содержащие модуль.
Квадратичная функция. Ее свойства и график.
Графики уравнений.
Функции, при построении графиков которых используется решение неравенств второй степени с одной переменной.
Применение свойств квадратичной функции к решению задач с параметрами.
2. Степень с рациональным показателем (6 ч.)
Функция у = х п , ее свойства и график.
Функция у = х, ее свойства и график.
Функции, при построении графиков которых используются свойства арифметического корня п-ой степени.
З. МетоДы построения графиков функций без использования производной (6 ч.)
Понятие о пределе функции.
Построение графиков функций вида у = .f(la + Ь).
Построение графиков функций вида у = .f (ах 2 + bx + с).
Построение графиков функций вида у = f(ax + Ь/сх + Ь). Эскизирование графиков функций.
4. Простейшие неэлементарные функции (6 ч.)
Кусочно-непрерывные функции.
Функции у = sin х; у = [х! у = {х}.
Построение графиков функций двух видов:
![]()
5. Обобщающее повторение темы
«Функции и их графики» (З ч.)
10-1 1 КЛАССЫ
В результате обучения учащиеся должны:
Знать определения и основные свойства числовых функций (монотонность, сохранение знака, экстремумы, наибольшее и наименьшее значения, ограниченность, периодичность и др.) и их графическую интерпретацию; свойства и графики тригонометрических, показательной, логарифмической и степенной функции; схему исследования функций; содержание и прикладное значение задачи исследования функции.
Уметь изображать графики основных элементарных функций, по виду графика описывать свойства этих функций; строить графики функций, включающие в себя тригонометрические, показательную, логарифмическую и степенную функции методом геометрических преобразований; использовать свойства функций для сравнения и оценки ее значений; применять первую производную для исследования функций на монотонность и экстремумы; применять вторую производную для исследования функций на выпуклость, вогнутость, точки перегиба; строить графики функций, используя исследование с помощью производной; применять различные методы построения графиков функций, свойства изученных функций при решении задач с параметром и практических задач.
1. (повторение) (4 ч.)
Числовые функции. Способы задания. График функции. Композиция функций. Преобразование графиков функций. Схема исследования функций.
2. Тригонометрические функции (14 ч.)
Функции синус, косинус, тангенс и котангенс числового аргумента. Свойства функций и их графики.
Приемы построения графиков тригонометрических функций.
Гармонические колебания. Графики гармонических колебаний.
Функции, при построении графиков которых используются преобразования тригонометрических выражений.
Функции, содержащие модуль, и их графики.
Обратные тригонометрические функции, их свойства, графики. Использование для построения графиков функций, содержащих обратные тригонометрические функции.
З. Применение ПРОИЗВОДНЫХ к исследованию функций и построению графиков (10 ч.)
Общая схема исследования функций с помощью производной.
Построение графиков различных функций с предварительным их исследованием по общей схеме.
Исследование линейной функции с помощью производной.
Исследование квадратичной функции с помощью производной.
Исследование дробно-рациональной функции с помощью производной.
Исследование свойств тригонометрических функций с помощью производной.
Использование общей схемы для построения графиков функций, содержащих тригонометрические функции.
Применение производной при решении задач с параметром.
4. Повторение, систематизация изученного материала (З ч.)
1. Показательная, логарифмическая и степенная функции (14 ч.)
Показательная функция, ее свойства и график. Построение графиков функций, содержащих показательную функцию, с помощью геометрических преобразований.
Логарифмическая функция, ее свойства и график. Построение графиков функций, содержащих логарифмическую функцию, с помощью геометрических преобразований.
112
Построение графиков функций, содержащих логарифмическую и показательную функции.
Производная логарифмической и показательной функций. Построение графиков функций с использованием схемы исследования функций с помощью производной.
Свойства показательной, логарифмической и степенной функций в задачах с параметром.
Графические приемы при решении задач с параметрами.
2. Полярная система коорДинат (4 ч.)
Полярная система координат.
Кривые, заданные уравнениями в полярных координатах. Примеры спиралей, роз и других кривых.
З. Алгебраические кривые 2-го поряДка (4 ч.)
Эллипс, окружность. Гипербола. Парабола.
4. Повторение (10 ч.)
ПЗ
OTBETbl



![]()
3.1 .23. Il -x! x-31


![]()

4.1.16д.


122
![]()






9.1.7. у = —х2 + 4х — 1 9.1.8.![]() —2х2 + 4х +
—2х2 + 4х +


![]()
![]()










![]() 16.3.18.
y {x} + signx
16.3.18.
y {x} + signx



16.3.27. 16.3.28.
{х} < 1, то
![]() Следовательно,
D(y) = {Z}.
Следовательно,
D(y) = {Z}.



16.3.43.![]() 16.3.44. y
= sign [x]
16.3.44. y
= sign [x]

142





|
|
|

 —
—



|
|
|
|
|
|
|
O |
27C |
311 x |
18.2.57. y = Isinx|+x 




![]() 18.2.81. y
= sin(arcsin x) 18.2.82.
18.2.81. y
= sin(arcsin x) 18.2.82.

18.2.83. y = cos(2arccos x) 18.2.84.
 —21t
_ 37t
—21t
_ 37t
|
|
|
|
|
|
O |
1t 31t 27t X |
y = arcsin(sin x)
y = arccos(sin x)
18.2.87. y = cos(2arcsinx) 18.2.88. y = sin(6arccos x)













![]()

 27.1.29.
27.1.29.
От автора![]()
Методика изучения темы «Функции и
графики в 8—11 классах» . ![]() 4
4
Задачи. . ![]() 7
7
8 класс
1. Линейная функция . ![]() 7
7
|
2. Уравнения, содержащие
знак модуля |
13 |
|
3.
Функции, содержащие знак модуля 4. Построение графиков функций вида: у = f(x) + Ь; |
14 |
![]()
|
У = а f(x). 5.
Построение по графикам функций у = Л (х) и у = Л (х) графиков функций:
у = .fl (х) + f2 (х); у = Л (х) — .f2 (х); у = Л (х) • Л y=f1 6. Построение графиков функций вида: у = f(lxl ), |
19 |
![]() 23
23
29
|
8.
Функции, при построении графиков которых используется преобразование
выражений, содержащих квадратные корни . 9. Построение графиков квадратичных функций, используя метод выделения полного квадрата |
|
|
и геометрические
преобразования графиков 10. Функции, при построении графиков которых используется разложение квадратного трехчлена |
31 |
|
на линейные множители |
36 |
|
11. Дробно-линейные функции. 9 класс |
38 |
|
12. Квадратичная функция . |
42 |
|
13. Квадратичные
функции, содержащие знак модуля 14. Функции, при построении графиков которых используется решение неравенств второй степени |
47 |
|
с одной переменной .
. |
51 |
169
|
15. Функции, при построении графиков которых используются свойства арифметического корня |
|
|
п-ой степени . |
52 |
|
16. Кусочно-непрерывные функции . |
52 |
|
17. Методы построения
графиков функций . |
56 |
|
18. Тригонометрические
функции . |
60 |
|
19. Четные и нечетные
функции |
67 |
|
20. Нули и изменения знака.
Непрерывность. Асимптоты |
70 |
|
21. Возрастание и убывание
функций. Экстремумы функций |
72 |
|
22. Выпуклость и вогнутость
функций. |
75 |
|
23.
Производная . 24. Исследование свойств функций и построение графиков |
76 |
|
с помощью производной
|
79 |
|
25. Построение
графиков показательной функции 26. Построение графиков логарифмической и показательной функций с помощью |
83 |
|
геометрических преобразований. . |
84 |
|
и логарифмической
функций методом производной . |
86 |
|
28. Задачи с решениями . Литература . Программа целостного изучения темы «Функции и графики» в 8—11 классах |
89 |
|
с углубленным изучением математики . Ответы |
106 |
Ромашкова Елена Васильевна
Редактор Л. В. Вахуркина
Подписано в печать 07.04.2010. Формат 60х88/16. Усл. печ. л. 10,45. Тираж 3000 экз. Заказ 5492.
ООО «Илекса», 105187, г. Москва, Измайловское шоссе, 48а, сайт: www.ilexa.ru, E-mail: real@ilexa.ru, факс 8(495) 365-30-55, телефон 8(495) 984-70-83
Отпечатано в полном соответствии с качеством предоставленных издательством материалов в ОАО «Тверской ордена Трудового Красного Знамени полиграфкомбинат детской литературы им. 50-летия СССР». 170040, г. Тверь, проспект 50 лет Октября, 46.
НОВЫЕ КНИГИ ПО МАТЕМАТИКЕ
Е.П. Нелин, В.А. Лазарев
Алгебра и начала анализа. 10 класс Учебник
Учебник является первым в линейке учебников по курсу «Алгебра и начала анализа. lO-11 классы». Содержание учебника соответствует федеральным компонентам государственного стандарта общего образования по математике и содержит материал как базового, так и профильного уровня. По нему можно работать независимо от того, по каким учебникам учились школьники в предыдущие годы. Учебник нацелен на подготовку учащихся к успешной сдаче ЕГЭ и поступленико в вузы.
КОМПЛЕКСНАЯ ПОДГОТОВКА К ЕГЭ И Гп
![]() Е.П. Нелин
Е.П. Нелин
Алгебра. 7-11 классы I Геометрия. 7-11 классы
ОпреДиения, свойства, метоДы решения задач — в таблицах.
В пособиях логически упорядочен и систематизирован минимум основных и дополнительных сведений из школьных курсов алгебры и начал анализа и геометрии, который позволяет решать всевозможные задачи, предлагаемые на выпускных или вступительных экзаменах, а также в заданиях ЕГЭ и ГИА по математике.
АП. Ершова, ВВ. Голобородько
ВСЯ ШКОЛЬНАЯ МАТЕМАТИКА в самостоятельных и контрольных работах
![]()
![]() 1 . Математика 5-6
1 . Математика 5-6
2. Алгебра 7-11
З. Геометрия 7-9
4. Геометрия 10-11
Сборники содержат полный набор самостоятельных и контрольных работ по всему курсу математики 5-11 классов. В конце книг приводятся ответы ко всем работам, а к некоторым задачам приведены решения и указания. Материалы книг можно использовать при работе с любыми учебниками.
Шевкин А.В.
Текстовые задачи по математике: 5-6 7-11
![]() Сборники включают текстовые задачи по
курсу школьной математики 5-6 и 7-11 классов. Наряду с интересными задачами
современных авторов (в том числе, олимпиадными) в сборники включены известные
старинные задачи, задачи из «Арифметики» Л.Ф. Магницкого и «Арифметики» А.П.
Киселева, других дореволюционных сборников. Ко многим задачам даны ответы и
советы, помогающие найти правильное решение. Сборники можно использовать как
дополнение к любым учебникам 5-6 и 7-11 классов. Сборник 7-11 классов содержит
материал для подготовки к итоговой аттестации (ГИА-9 и ЕГЭ- 1 1 ).
Сборники включают текстовые задачи по
курсу школьной математики 5-6 и 7-11 классов. Наряду с интересными задачами
современных авторов (в том числе, олимпиадными) в сборники включены известные
старинные задачи, задачи из «Арифметики» Л.Ф. Магницкого и «Арифметики» А.П.
Киселева, других дореволюционных сборников. Ко многим задачам даны ответы и
советы, помогающие найти правильное решение. Сборники можно использовать как
дополнение к любым учебникам 5-6 и 7-11 классов. Сборник 7-11 классов содержит
материал для подготовки к итоговой аттестации (ГИА-9 и ЕГЭ- 1 1 ).
Хлевнюк Н.Н., Иванова М.В.
Формирование вычислительных навыков на уроках математики 5-9 классы
![]() Представлена не имеющая аналогов
методика формирования вычислительных навыков и развития математических
способностей у ижольников. Приведен полный пакет контролирующих уровневых
тестов для проверки умений и навыков оперирования числами и выражениями.
Содержание тестов полностью соответствует гос. стандарту математического
образования. Пособие позволяет организовать системную работу с учащимися по
формированию базовых математических знаний, начиная
Представлена не имеющая аналогов
методика формирования вычислительных навыков и развития математических
способностей у ижольников. Приведен полный пакет контролирующих уровневых
тестов для проверки умений и навыков оперирования числами и выражениями.
Содержание тестов полностью соответствует гос. стандарту математического
образования. Пособие позволяет организовать системную работу с учащимися по
формированию базовых математических знаний, начиная
с класса.
Самсонов П.И.
Обучающие контрольные работы по алгебре и началам математического анализа 10-11
Представлены практические материалы для организации текущего и итогового контроля знаний учащихся в форме обучающих разноуровневых контрольных работ. Ко всем текстам предложенных работ приводятся пояснения, касаюЩИеСЯ компоновки варианта, ответы, а к некоторым заданиям и решения.
Лисичкин В. Т.
![]() Производная и ее приложение в задачах
Производная и ее приложение в задачах
Книга позволяет самостоятельно научиться решать задачи по одному из главных разделов математики и подготовиться к ЕГЭ. Краткие теоретические сведения сопровождаются подробными решениями задач. Самостоятельные упражнения снабжены ответами, указаниями и пояснениями.
МАТЕМАТИКА: ЭЛЕКТИВНЫЕ КУРСЫ
Новая серия книг издательства ориентирована на углубленное изучение различных тем школьного курса математики. Книги будут интересны и полезны учителям математики, учащимся старших классов, абитуриентам, студентам педагогических ВУЗов. Их целесообразно использовать при подготовке к ЕГЭ (особенно для решения задач части С). Уже вышли или подготовлены к печати следующие книги серии:
1. Мякишев А.Г. Теория вероятностей.
2. Субханкулова СА. Задачи с параметрами.
З. Полякова Е.А. Уравнения и неравенства с параметрами.
4. Калугина Е.Е. Уравнения, содержащие знак модуля. 5. Гилев ВГ. Исследование рациональных функций на монотонность и экстремумы.
В.И. Голубев
Решение сложных и нестандартных задач по математике
![]() Пособие содержит задачи по алгебре и
началам анализа повышенной сложности. Основные варианты решения рассматриваются
с подробными комментариями, а объяснения подкреплены упражнениями. Основной
акцент сделан на изложении малоизвестных эффективных технологий решения
нестандартных задач, таких, например, как метод трех точек, метод замены
множителей и др. Даны развернутые комментарии и указания на возможность решения
очень трудных задач простыми методами.
Пособие содержит задачи по алгебре и
началам анализа повышенной сложности. Основные варианты решения рассматриваются
с подробными комментариями, а объяснения подкреплены упражнениями. Основной
акцент сделан на изложении малоизвестных эффективных технологий решения
нестандартных задач, таких, например, как метод трех точек, метод замены
множителей и др. Даны развернутые комментарии и указания на возможность решения
очень трудных задач простыми методами.
Левитас ГГ.
МАТЕМАТИКА материалы для уроков
5-6, 7, 8, 9 классы

Книги этой группы содержат
дидактические материалы, позволяющие интенсифицировать работу каждого ученика.
Материалы подготовлены на основе технологии учебных циклов (ТУЦ). Эта
технология отличается большой простотой и доступностью для каждого учителя.
Взамен трудно осуществляемой ![]() дифференциации учащихся здесь применяется легко осуществляемая «лесенка»
сложности и трудности заданий. Компьютер используется лишь в качестве помощника
учителя, а не как основное средство обучения. Если же компьютера нет, то это
совершенно не препятствует использованию ТУЦ.
дифференциации учащихся здесь применяется легко осуществляемая «лесенка»
сложности и трудности заданий. Компьютер используется лишь в качестве помощника
учителя, а не как основное средство обучения. Если же компьютера нет, то это
совершенно не препятствует использованию ТУЦ.
По этой технологии преподавание ведется однородными учебными циклами. В том варианте ТУЦ, который реализован, например, в книге для 7 класса, каждый учебный цикл состоит из шести уроков. На первых двух уроках вводится новый материал и проверяется, понят ли он учащимися. На следующих четырех уроках этот материал включается в общую систему знаний. Применение ТУЦ к преподаванию математики проходит особенно успешно, если видоизменить планирование курса. При этом особенно важно резко увеличить число задач, решаемых детьми в классе.
Для работы по ТУЦ предлагается новое планирование учебного материала. За основу взяты учебники «Алгебра 7» под ред. СА. Теляковского, «Геометрия 7-9» под ред. Л.С. Атанасяна и «Геометрия 7-9» А.В. Погорелова как наиболее массовые. Однако книги можно использовать и при работе по другим учебникам.
В пособии приведены методические рекомендации для работы по данной технологии.
В книгах даны тексты диктантов для первых уроков цикла (диктанты по материалам предыдущих циклов) и диктантов для третьих и четвертых уроков цикла (диктанты по всему пройденному курсу математики). В ней содержатся конспекты к каждому циклу. Даны полные тексты ТПО. Приводятся рекомендации для проведения самостоятельных и проверочных работ, и для коррекции знаний.
Пособия предназначены для учащихся и учителей общеобразовательных школ, студентов педагогических вузов, преподавателей центров повышения квалификации учителей.
Ивашев-Мусатов ОС.
Начала анализа для школьников

В пособие включены темы в соответствии с программой курса математики в средней школе. Это непрерывность функции; производная функция; понятие о пределе функции; первообразная функции. По каждой теме есть теоретический материал и упражнения. Имеется блок рисунков. В конце книги ответы к задачам и указания к решению, а к некоторым задачам даются решения. В приложении к основному материалу содержатся доказательства правил вычисления производных (в соответствии с определением, данным в этой работе); объяснено взаимоотношение определений предела функции, данного в этой работе, и традиционного; приведены материалы, посвященные числу Эйлера е.
Это пособие подготовлено в соответствии с дифференцированным подходом к обучению математике. Оно рассчитано на учащихся, воспринимающих математику только как предмет, без которого нельзя получить школьный аттестат и поступить в вуз. Эти учащиеся математику просто должны «терпеть».
Поэтому в пособии нет сложных рассуждений. Внимание автора сосредоточено на формировании основных понятий; они объяснятся на доступном языке с опорой на простые, геометрические ясные и наглядные соображения. Сложные доказательства опускаются с оговоркой: «в математике это доказано».
Например, понятие степени числа с целым показателем несложно, и правила действий здесь доказываются просто. Все сложности начинаются при обобщении понятия числа. И тогда достаточно сказать: математики доказали, что любое положительное число можно возвести в любую степень (не тОлЬКО целую), при этом получается положительное число, которое ВЫЧИСЛЯСТСЯ на компьютере, а все правила вычислений со степенями (доказанные для целых показателей степени) полностью сохраняются. Остается сообщить, что при натуральном п > 1 степень а пп называют корнем п-й степени из числа а и обозначают ” а.
Весь традиционный набор упражнений сохраняется, а времени при этом экономится достаточно .
В книге дается краткий экскурс в историю преподавания математики, что поможет лучше представить современные проблемы, в том числе связанные с дифференцированным подходом в обучении математике.
Пособие предназначено для учителей математики и учащихся общеобразовательных школ. Его можно использовать и в системе довузовской подготовки в тех случаях, когда экзамен по математике есть, и нужно поднять уровень знаний, но математика не будет главной профессиональной составляющей.
Ивашев-Мусатов ОС.
![]()

При броске монеты ничего определенного нельзя сказать о том, что вы увидите, когда монета ляжет на землю одной стороной вверх. Это может оказаться цифра, а может оказаться и герб. А последствия более сложных действий (две монеты, три монеты, бросили игральную кость или две, стрельба по цели и т.п.) и более многообразны и гораздо сложнее для прогнозирования. В этом основная трудность при изучении теории вероятностей: нужна психологическая перестройка на восприятие многообразия возможностей.
В пособии представлен учебный материал, соответствующий
темам по теории вероятностей в математической программе общеобразовательной
школы. Приведены термины, базовые теоретические материалы, примеры определения
вероятности событий, упражнения, а также ответы и упражнения к решению задач. ![]()
Материал пособия отражает методические приемы преподавания математики, практическое применение теории вероятностей.
Пособие предназначено для учителей общеобразовательной школы, студентов физико-математических факультетов педагогических вузов. Его могут использовать и ученики старших классов для самостоятельной работы в школе и дома.
ИЛЕКСА
ЕЕ Ромашкова
В пособии представлены задачи на исследование функций и построение их графиков по всем разделам школьного курса математики.
Задачи относятся к линейным, квадратичным, тригонометрическим, показательным и логарифмическим функциям, рассмотрены различные методы анализа функций и построения графиков; задачам предшествуют примеры решения и построения графиков. Материал пособия расположен в последовательности, при которой сначала изучается линейная функция, затем на основе рассмотренных в 7 классе функций изучается тема «Построение графиков преобразований».
огон ги
978-5-89237-314-2
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.