Геометрия 7 класс. Зачет по теме треугольники

Карточка 1

1.     Объясните, какой отрезок называется перпендикуляром, проведенным из данной точки к данной прямой.

2.     Докажите, что углы при основании равнобедренного треугольника равны.

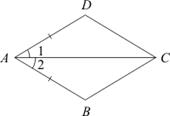
3.     Докажите равенство треугольников ADC и ABC, изображенных на рисунке, если AD = AB и ∠1 = ∠2. Найдите углы ADC и ACD, если ∠АСВ = 38°, ∠ABC = 102°.

4.     В треугольниках ABC и А₁В₁С₁ АВ = А₁В₁, ∠A = ∠A₁, ∠B = ∠B₁. На сторонах ВС и B₁C₁ отмечены точки D и D₁ так, что ∠CAD = ∠C₁A₁D₁. Докажите, что: a) ∆ADC = ∆A₁D₁C₁; б) ∆ADB = ∆A₁D₁B₁.

__________________________________________________________________

Карточка 2

1.     Какой отрезок называется медианой треугольника? Сколько медиан имеет треугольник?

2.     Сформулируйте и докажите теорему, выражающую первый признак равенства треугольников.

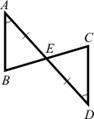
3.     Докажите равенство треугольников ABE и DCE на рисунке, если AE = ED, ∠A = ∠D. Найдите стороны треугольника ABE, если DE = 3 см, DС = 4 см, EС = 5 см.

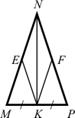
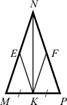
4.     На рисунке треугольник MNP равнобедренный с основанием МР, точка К – середина отрезка МР, ME = PF. Докажите, что луч KN – биссектриса угла EKF.

Карточка 3

1.     Какой отрезок называется биссектрисой треугольника? Сколько биссектрис имеет треугольник?

2.     Сформулируйте и докажите теорему, выражающую второй признак равенства треугольников.

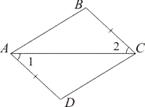
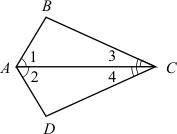
3.     Докажите равенство треугольников ABC и ADC, изображенных на рисунке, если BC = AD и ∠1 = ∠2. Найдите углы ACD и ADC, если ∠АВС = 108°, ∠BAC = 32°.

4.     На рисунке треугольник MNP равнобедренный с основанием МР, точка К – середина отрезка МР, ∠МКЕ = ∠PKF. Докажите, что ∆NEK = ∆NFK.

__________________________________________________________________

Карточка 4

1.     Какой отрезок называется высотой треугольника? Сколько высот имеет треугольник?

2.     Сформулируйте и докажите теорему о биссектрисе равнобедренного треугольника.

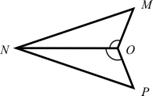
3.     Докажите равенство треугольников MON и PON на рисунке, если ∠MON = ∠PON, а луч N0 – биссектриса угла MNP. Найдите углы треугольника NOP, если ∠MNO = 42°, ∠NMO = 28°, ∠NOM = 110°.

4.     В треугольниках DEC и D₁E₁C₁ DE = D₁E₁, ∠D = ∠D₁, ∠E = ∠E₁. На сторонах DE и D₁E₁ отмечены точки Р и P₁ так, что ∠DCP = ∠D₁C₁P₁. Докажите, что: a) ∆DCP = ∆D₁C₁P₁; б) ∆СРЕ = ∆С₁Р₁Е₁.

Карточка 5

1.     Какой треугольник называется равнобедренным? Как называются его стороны?

2.     Сформулируйте и докажите теорему, выражающую третий признак равенства треугольников.

3.     На рисунке AB = AD, BC = CD. Докажите, что луч АС – биссектриса угла BAD.

4.      На стороне АС как на основании построены по разные стороны от него два равнобедренных треугольника АВС и ADC. Докажите, что BD перпендикулярен АС.

__________________________________________________________________