
Постройте и упростите логические выражения, соответствующие приведённым таблицам истинности. В каждом случае выбирайте наиболее простой способ синтеза. В вашем решении опишите все шаги алгоритма.
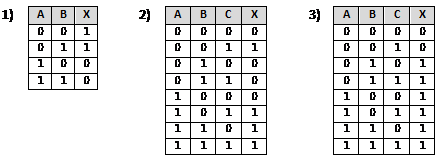
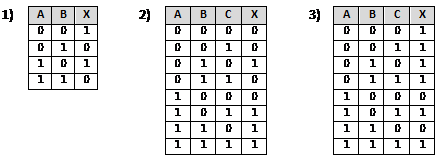
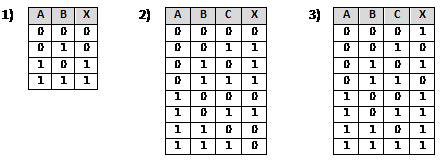
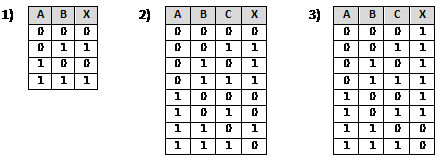
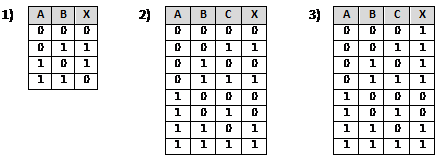
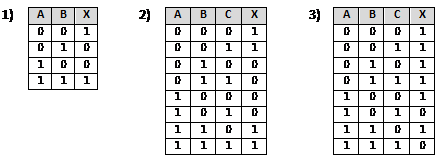
Ответы по вариантам:
|
Ваpиант 1 1. 2. 3. |
Ваpиант 2 1. 2. 3. |
Ваpиант 3 1. 2. 3. |
|
Ваpиант 4 1. 2. 3. |
Ваpиант 5 1. 2. 3. |
Ваpиант 6 1. 2. 3. |
1-4.
Задайте с помощью предиката ![]() множество
точек, соответствующее заштрихованной области на плоскости.
множество
точек, соответствующее заштрихованной области на плоскости.
5. Введите предикат и запишите заданное высказывание, используя кванторы.
6. Запишите отрицание высказывания, записанного в п. 5, в словесной форме и с помощью кванторов и введённого предиката.
|
|
Вариант 1 |
Вариант 2 |
Вариант 3 |
|
1. |
|
|
|
|
2. |
|
|
|
|
3. |
|
|
|
|
4. |
|
|
|
|
5. |
«Для любой реки существует море, в которое она впадает». |
«Для любого моря существует река, которая в него впадает». |
«Существует река, которая впадает во все моря». |
|
|
Вариант 4 |
Вариант 5 |
Вариант 6 |
|
1. |
|
|
|
|
2. |
|
|
|
|
3. |
|
|
|
|
4. |
|
|
|
|
5. |
«Существует море, в которое впадают все реки». |
«Найдется такая гора, что ни одна птица не может подняться выше неё». |
«Для каждой горы найдется птица, которая не может подняться выше неё». |
Ответы по вариантам:
Ваpиант 1
1. ![]()
2. ![]()
3. ![]()
4. ![]()
5. ![]() , где
, где ![]() : «река
: «река ![]() впадает в море
впадает в море ![]() »
»
6. «Найдется такая река, для которой не существует моря, в которое она впадает».
![]()
Ваpиант 2
1. ![]()
2. ![]()
3. ![]()
4. ![]()
5. ![]() , где
, где ![]() : «река
: «река ![]() впадает в море
впадает в море ![]() »
»
6. «Найдётся такое море, для которого
нет рек, которые в него впадают».
![]()
Ваpиант 3
1. ![]()
2. ![]()
3. ![]()
4. ![]()
5. ![]() , где
, где ![]() : «река
: «река ![]() впадает в море
впадает в море ![]() »
»
6. «Нет такой реки, которая впадает во
все моря».
![]()
Ваpиант 4
1. ![]()
2. ![]()
3. ![]()
4. ![]()
5. ![]() , где
, где ![]() : «река
: «река ![]() впадает в море
впадает в море ![]() »
»
6. «Нет такого моря, в которое впадают
все реки».
![]()
Ваpиант 5
1. ![]()
2. ![]()
3. ![]()
4. ![]()
5. ![]() , где
, где ![]() : «птица
: «птица ![]() может подняться выше горы
может подняться выше горы ![]() »
»
6. «Не существует такой горы, что ни
одна птица не может подняться выше неё».
![]()
Ваpиант 6
1. ![]()
2. ![]()
3. ![]()
4. ![]()
5. ![]() , где
, где ![]() : «птица
: «птица ![]() может подняться выше горы
может подняться выше горы ![]() »
»
6. «Существует такая гора, что любая
птица может подняться выше неё».
![]()
1. Постройте схему, соответствующую заданной логической функции, на логических элементах «И», «ИЛИ» и «НЕ». Предварительно преобразуйте выражение так, чтобы количество использованных логических элементов было минимальным.
2. Постройте схему, соответствующую заданной логической функции, на логических элементах «И», «ИЛИ» и «НЕ» (в базисе «И-ИЛИ-НЕ»). Предварительно преобразуйте выражение так, чтобы количество использованных логических элементов было минимальным.
3. * Используя формулу ![]() (она следует из закона двойного
отрицания и закона де Моргана), постройте схему, соответствующую логической функции
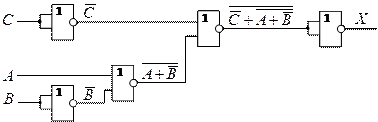
из п. 1, используя только логические элементы «И-НЕ» (в базисе «И-НЕ»).
(она следует из закона двойного
отрицания и закона де Моргана), постройте схему, соответствующую логической функции
из п. 1, используя только логические элементы «И-НЕ» (в базисе «И-НЕ»).
4. * Используя формулу ![]() (она следует из закона двойного
отрицания и закона де Моргана), постройте схему, соответствующую логической
функции из п. 1, используя только логические элементы «ИЛИ-НЕ» (в базисе
«ИЛИ-НЕ»).
(она следует из закона двойного
отрицания и закона де Моргана), постройте схему, соответствующую логической
функции из п. 1, используя только логические элементы «ИЛИ-НЕ» (в базисе
«ИЛИ-НЕ»).
|
Вариант 1 1. 2. |
Вариант 2 1. 2. |
|
Вариант 3 1. 2. |
Вариант 4 1. 2. |
|
Вариант 5 1. 2. |
Вариант 6 1. 2. |
Ответы по вариантам:
Вариант 1
1. ![]()
2. ![]()
3. ![]()


4. ![]()
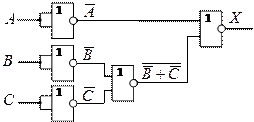

Вариант 2
1. ![]()
2. ![]()
3. ![]()
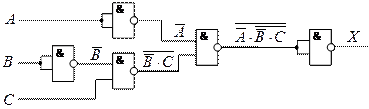

4. ![]()
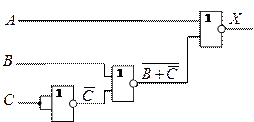

Вариант 3
1. ![]()
2. ![]()
3. ![]()
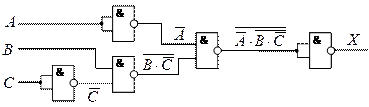

4. ![]()
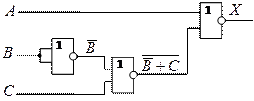

Вариант 4
1. ![]()
2. ![]()
3. ![]()
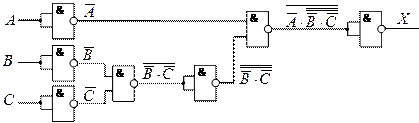

4. ![]()
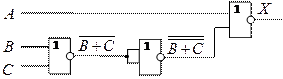

Вариант 5
1. ![]()
2. ![]()
3. ![]()
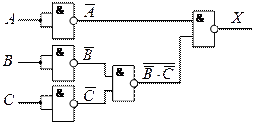

4. ![]()
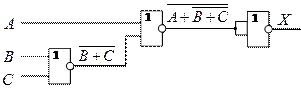

Вариант 6
1. ![]()
2. ![]()
3. ![]()
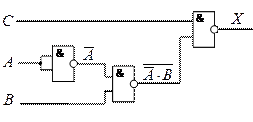

4. ![]()

Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.