Графические изображения скорости резания

             4. Графическое изображение скорости резания                                                                                        Обрез

Для быстрого определения скорости резания υ по известным диаметру d и частоте вращения n шпинделя и, наоборот, для определения при известных n и d скорости резания υ и сравнения, полученного значения с рекомендуемым в справочнике, используют лучевую или логарифмическую диаграмму.

Лучевая диаграмма. В основу построения лучевой диаграммы положено уравнение скорости резания (м/мин)

Скорость резания прямо пропорциональна диаметру d обрабатываемой заготовки и при постоянной частоте вращения n будет зависеть только от диаметра этой заготовки. Графически эта зависимость изображается прямой, проходящей через начало координат, потому что при d = 0 скорость резания υ = 0. Для построения диаграммы масштабы для скоростей и диаметров обрабатываемых изделий с учетом их максимальных значений на станке выбираются независимо друг от друга.

Уравнение скорости резания можно представить в виде:

то при d = 318 мм скорость резания будет равна частоте вращения шпинделя.

Для станка с рядом частот вращения шпинделя 12,5; 16; 20; 25; 31,5; 40; 50; 63; 80; 100; 125; 160; 200; 250 и т. д. до 2000 об/мин. С диаметром до 400 мм и скоростями резания ≤130 м/мин диаграмма строится следующим образом (рис. 26, а). По оси абсцисс откладываем размеры обрабатываемых диаметров детали, а по оси ординат скорости резания. При диаметре обрабатываемой детали d = 318 мм на прямой I—I, параллельной оси ординат, находим точки n, соответствующие ряду частот вращения шпинделя, которые численно равны значениям скоростей и через них из начала координат проводим лучи; эти лучи и будут отражать соответствующие частоты вращения шпинделя для разных диаметров и скоростей резания. Например, для частот n₁ = 12,5, n₂ = 16, n₃ = 20 соответствующие значения скорости резания будут υ₁ = 12,5, υ₂ = 16, υ₃ = 20 м/мин.

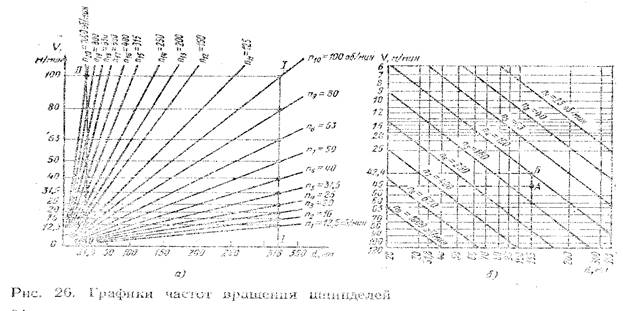
Лучи, соответствующие n > 125 об/мин, построить затруднительно из-за ограниченных размеров диаграммы. Для построения их принимаем n = 31,8 мм, тогда υ = n/31,8 = n/10. На прямой II—II находим точки для частот вращения, численно в 10 раз больших, чем значения скорости. Таким образом, например, лучи n₁₂ = 160 об/мин из начала координат пройдет через точку α, соответствующую υ_P = 16 м/мин. Если точка не лежит ни на одном луче диаграммы, а находится между лучами, то в этом случае обычно берут меньшую частоту, так как увеличение скорости резания по сравнению с заданной нежелательно. Оно приводит к преждевременному выходу инструмента из строя. Лучевая диаграмма имеет тот недостаток, что лучи для больших частот вращения поднимаются слишком круто, а вблизи начала координат расположены очень тесно, это влечет за собой ошибки в подсчетах. От этого недостатка свободна логарифмическая диаграмма.

Логарифмическая диаграмма строится па логарифмической сетке (рис. 26, б). Для построения диаграммы уравнение скорости υ = πdn/1000 (м/мин) представим в виде:

Это уравнение в двойной логарифмической системе координат lg υ и lg d при различных значениях n представляет ряд параллельных линий, наклоненных к осям координат под углом 45°. Например, пусть частоты вращения шпинделя станка имеют следующий ряд: n₁ = 25, n₂ = 40, n₃ = 63, n₄ = 100, n₅ = 160, n₆ = 250, n₇ = 400, n₈ = 630 и n₉ = 1000 об/мин.Пределы скоростей резания υ = 6 ÷ 120 м/мин, пределы изменения диаметров d = 20 ÷ 318 мм. Принимаем масштаб М = 125 мм, тогда размер шкалы, на которой откладываются скорости S_υ = М (lg υ_MAX ‒ lg υ_MIN),

S_υ = 125 (2,0792 — 0,7781) = 125*1,3011 = 162,6 мм; размер шкалы, на которой откладываются диаметры:

По этим данным на осях координат производим разбивку шкал. По оси ординат откладываем логарифмы скоростей резания в убывающем порядке, а по оси абсцисс — логарифмы диаметров в возрастающем порядке. Цифровые обозначения па осях абсцисс и ординат соответствуют самим числам. Так как числа на осях составляют геометрическую прогрессию, расстояния между всеми прямыми n одинаковы.

Построение прямых частот вращения n можно производить следующим способом. При точно выдержанном знаменателе ϕ прямая n₁ может быть определена при пересечении диаметра (d = 318 мм и прямой, проходящей через скорость υ₁, которая равна υ₁ = n₁. Масштабы одинаковы и прямые n расположены под углом 45° к осям. Прямые остальных частот вращения определяются из уравнений: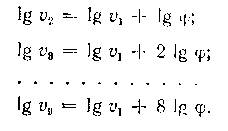

Все прямые n₁, n₃, …, n₉ находятся друг от друга на расстоянии ϕ принятого масштаба.

Пример. Определить частоту вращения шпинделя и относительную потерю скорости резания при выборе действительной частоты его вращения, если диаметр обрабатываемой заготовки d = 135 мм; скорость резания υ = 45 м/мин. На логарифмической диаграмме проводим прямую из точки υ = 45 м/мин, перпендикулярную к оси ординат, а из точки, соответствующей диаметру d = 135 мм, проводим вторую прямую, перпендикулярную к оси абсцисс. Пересечение этих двух прямых в точке А определит положение требуемой частоты вращения шпинделя. Так как точка A не совпадает с прямыми, характеризующими частоту вращения n₄ и n₅, принимаем ближайшую меньшую частоту вращения шпинделя n₄= 100 об/мин.

Чтобы определить действительную скорость при частоте вращения n₄, прямую, проведенную из точки d = 135 мм, продолжаем до пересечения с n₄, получаем точку Б, из которой проводим перпендикуляр на ось ординат, и при пересечении с этой осью получим искомую действительную скорость υ_Д = 42,4 м/мил.

Для определения потерн скорости резания вследствие уменьшения частоты вращения, найденные значения подставляем в формулу:

Скачано с www.znanio.ru