химия

Интегрированный урок по математике и химии в 11 классе.

Тема урока: «Задачи на смеси и сплавы».

Цели  урока:

1.      Подготовка к ЕГЭ по математике (задача В13) и химии (задача В9) .

2.       Обобщение  и закрепление знаний учащихся по теме «Задачи на смеси и сплавы».

3.      Формирование умений переноса знаний  с одного предмета на другой.

4.   Развивать познавательный интерес, реализуя межпредметные связи курсов химии и

      математики. 

Задачи урока :

      1.   Рассмотреть в сравнении химический и математический  способ решения задач с

           использованием понятия концентрация.

      2.   Применить способы решения задач на практических опытах.

      3.   Вывести новый метод решения задач на смеси и сплавы , рассматривать его

            применение на уроках математики и химии.

Оборудование: экран, проектор, презентация, раздаточный материал, аптечные весы ,

            дистиллированная  вода, кристаллизатор, фенолфталеин, металлический натрий, 

            этиловый спирт, кристаллический йод, хлорид натрия, физиологический раствор.     

Ход урока.

Учитель математики: Сегодня у нас необычный урок, это интегрированный урок математики и химии и вести его будут два учителя. На этом уроке мы посмотрим с вами на задачи с двух точек зрения – с химической и математической, и выясним: как математика помогает в решении химических задач и как химия решает некоторые математические задачи.

Тема урока «Задачи на смеси и сплавы». (Слайд №  )

Задачи  урока

1. Рассмотреть в сравнении химический и математический способ решения задач с использованием понятия концентрация.
2. Применить способы решения задач на практических опытах.
3. Вывести новый метод решения задач на смеси и сплавы и рассмотреть его применение на уроках математики и химии.

  (Слайд №  )

В задачах на смеси и сплавы ключевым понятием является понятие концентрации. Как найти концентрацию вещества в растворе или сплаве?  ( Отношение массы (или объема) чистого вещества к общей массе (или объему). Концентрация может быть выражена дробью k =    или в процентах, тогда эта дробь умножается на 100%. (Слайд №  ).   Во многих текстовых задачах понятие «концентрация» может быть заменено на:

«жирность» (масло, творог, молоко), «крепость» (уксус), «проба» (золото). ( Слайд №   ). Как понимать, что жирность молока равна 3,2%, крепость уксуса 9%, проба золота 583 ?

Используя формулу для вычисления концентрации, решим устно задачи:

v  К 1 части сахара добавили 4 части воды. Какова процентная концентрация полученного раствора?  ( 20%)

v  1 кг соли растворили в 9 литрах воды. Какова процентная концентрация полученного раствора? (10%)

v  Смешали 3 литра 14% раствора соли с 3 литрами воды. Какова процентная концентрация полученного раствора? (7%)

v  Сколько граммов сахара содержится в 2 кг 10% сахарного сиропа? (200 г)

Учитель химии:

Задача 1. Смешали 150 г раствора нитрата калия с массовой долей 12% и 300 г раствора этой же соли с массовой долей 7%. Какой стала массовая доля соли в полученном растворе? (9%)

Решение:

m₁ (в-ва)=m(р-ра) ∙w(в-ва)

m₁(в-ва)= 150 ∙ 0,12=18 г

m₂(в-ва)=300∙ 0,07= 21 г

W₃(в-ва) = 18+21/150+300= 0,09 ( 9%)

Учитель математики: А  вот как прозвучала бы эта задача на уроке математики.

Смешали 150 г 12% водного раствора некоторого вещества с 300 г 7% раствора  этого же  вещества. Сколько процентов составляет концентрация получившегося раствора? (Результат округлить до единиц)

Решим эту задачу с помощью таблицы. (Таблица заполняется постепенно)

Учитель химии:

Задания для практической работы

1. Приготовить 55,5 г физиологического раствора, содержащего  0,9% по массе поваренной соли.

  Решение:

  m(в-ва)= 55,5 ∙ 0,009=0,5 г

 m(H₂O)= 55,5 – 0,5 = 55 г

2. Приготовить 30 г 5% раствора йодной настойки.

m(в-ва)= 30∙ 0,05=1,5 г

m(H2O)=30- 1,5= 28,5 г

Учитель математики: 

Задача 2.

Один раствор содержит 30% по объему  HNO₃  , а второй 55% HNO₃ .Сколько нужно взять первого и второго  раствора, что бы получить 100 литров 50% раствора  HNO₃?

Получаем уравнение: 0,3х + 0,55(100 – х) = 50;

                                      0,3х + 55 – 0,55х = 50;

                                      х = 20.

Значит, первого раствора надо взять 20 литров, а второго 80 литров.

Учитель химии: Проверим решение практических задач( у доски учащиеся рассказывают решение практических задач.

Задача 3 .

Определить массу воды, которую надо добавить к 20 г раствора уксусной кислоты с массовой долей 70% для получения раствора уксусной кислоты с массовой долей 5%.

Решение: ( учащиеся выполняют у доски).

m 1(в-ва)= 20∙ 0,7= 14 г

0,05= 14/ 20+х

х=260 г

 Учитель математики: 

Решим задачу в общем виде.

Задача 4.

Смешали два водных раствора некоторого вещества с концентрацией k₁ %  и k₂ %_.  Получили раствор с концентрацией k %. В каком отношении нужно взять массы этих растворов? Рассмотрим случай, когда k₁  < k  < k₂

Если мы обозначим массы растворов т₁  и   т₂, то надо выразить  через k₁, k₂ и k.

Получаем уравнение:   k(m₁ + m₂ ) = k ₁m₁ + k ₂m₂

                                                                =

			k-k1

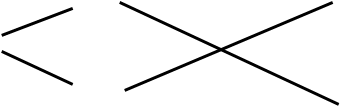
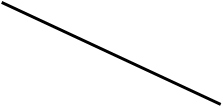
Эта схема похожа на рыбку, поэтому такой способ решения задач называется способ «рыбки». Этот способ справедлив не только, когда выполняется условие k₁  < k  < k₂, просто надо из большего вычитать меньшее. Впервые в России такой способ решения задач был описан в арифметике 18 века, автором которой был Леонтий Филиппович          Магницкий  (1669-1739) . эта арифметика так и называется «Арифметика Магницкого». Этот учебник М. В. Ломоносов назвал «вратами учености».

Решим этим способом задачу.

Задача 5

К 15 г 10% раствора соли добавили 5% раствор соли и получили 8% раствор. Сколько добавили граммов 5% раствора соли?

                                    , х = 10

Решим таким же способом задачу 3. Будем считать, что вода имеет концентрацию равную 0.

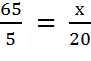 ; х = 260.

Задача 4

Имеется два сплава с разным содержанием меди: в первом содержится 70%, а во втором – 40% меди. В каком отношении надо взять первый и второй сплавы, чтобы получить из них новый сплав, содержащий 50% меди?

Учащиеся решают самостоятельно. Ответ:  .

     Учитель химии: Демонстрационный опыт( показывает учитель): в кристаллизатор с  

     водой опускаем кусочек металлического натрия. Что за газ выделяется? Почему вода

    изменила окраску на малиновую?

    Согласно поставленному опыту нам надо решить следующую задачу:

Задача 5

10 г Na провзаимодействовали со 100 г воды. Найти массовую долю гидроксида натрия  в растворе.

Решение:

2Na + 2НОН =2NaOH +H₂

n (Na)= 10:23=0,43 моль

n (HOH)=100 : 18= 5,56 моль ( избыток)

n (NaOH) = 0,43 моль

m (NaOH)= 40∙ 0,43= 17,2 г

n (H₂) = 0,43:2= 0,215 моль

m (H₂)=0,215 ∙2=0,43г

w (NaOH)= 17,2/ 10+100- 0,43=0,157( 15,7%)

Итог урока:Сегодня мы на уроке повторили химические и математические способы решения задач, а так же рассмотрели новый способ , который подойдет для решения задач как по математике так и по химии с использованием понятия концентрация ( массовая и объемная доля вещества).Все это поможет на ЕГЭ.

Урок окончен. Успехов вам на экзамене.

Литература:

1. А. В. Шевкин ,,Текстовые задачи по математике,, Москва, Илекса,2011 г.                              

            http://schoolmathematics.ru/prakticheskie-rekomendacii-zadanie-v13-chast-3.

      2. А.А.Кушнарев ,,Учимся решать задачи по химии,, Москва , Школа- пресс, 1996г.

Скачано с www.znanio.ru