Индивидуальные домашние задания

ВАРИАНТ №19

. Задание 1 № 367680

Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырёх цифр.

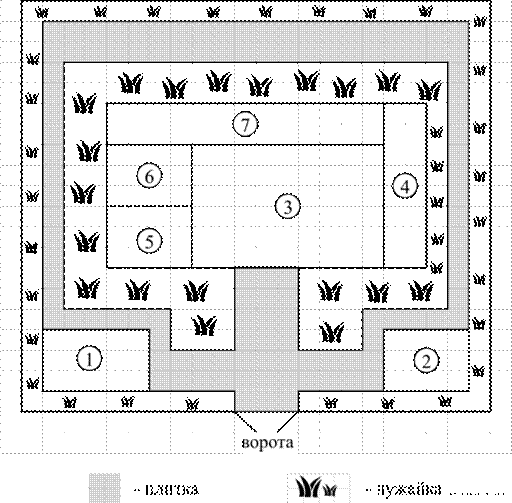
Инна Сергеевна имеет дом с участком. На рисунке приведён план этого участка.

При входе на участок слева находится гараж площадью 15 м², справа расположена баня. Дом находится внутри участка, имеет форму прямоугольника. Сторона каждой клетки на плане равна 1 метру.

Вход в дом осуществляется через стеклянную дверь. Внутри дома расположены: кухня, гостиная, спальня, детская комната, подсобные помещения.

В центре дома находится гостиная, справа — кухня. Спальня и детская имеют равные площади, подсобные помещения обозначены на плане цифрой 7.

Площадка около входа и дорожки вокруг дома выложены плитками размером 1 м × 1 м, на остальной территории посеяна трава.

2. Задание 2 № 367682

Тротуарная плитка продаётся в упаковках по 4 штуки. Сколько упаковок понадобилось купить, чтобы выложить все дорожки участка и площадку около входа?

3. Задание 3 № 367683

Найдите площадь (в м²), которую занимает жилой дом.

4. Задание 4 № 367686

Найдите расстояние от гаража до бани (расстояние между двумя ближайшими точками по прямой) в метрах.

5. Задание 5 № 367687

Инна Сергеевна планирует произвести оклейку стен помещений: детской комнаты и спальни — обоями. Она рассмотрела два варианта: флизелиновые и текстильные обои. Данные о стоимости рулона, площади комнат, расходе обоев на комнаты представлены в таблице. Обдумав оба варианта, Инна Сергеевна решила наклеить текстильные обои. На сколько рублей выгоднее наклеить текстильные обои, чем флизелиновые?

6. Задание 6 № 340581

Найдите значение выражения 

7. Задание 7 № 316987

Какое из приведенных ниже неравенств является верным при любых значениях a и b, удовлетворяющих условию a > b?

В ответе укажите номер правильного варианта.

1) b − a < −2

2) a − b > −1

3) a − b < 3

4) b − a > −3

8. Задание 8 № 369527

Найдите значение выражения 

9. Задание 9 № 338937

Решите уравнение 

10. Задание 10 № 325460

Валя выбирает случайное трехзначное число. Найдите вероятность того, что оно делится на 51.

11. Задание 11 № 349441

На рисунках изображены графики функций вида . Установите соответствие между знаками коэффициентов k и b и графиками функций.

КОЭФФИЦИЕНТЫ

А) 

Б) 

В) 

ГРАФИКИ

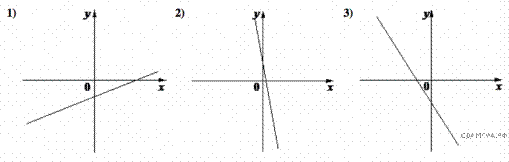
В таблице под каждой буквой укажите соответствующий номер.

Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:

12. Задание 12 № 352770

Перевести значение температуры по шкале Фаренгейта в шкалу Цельсия позволяет формула , где — температура в градусах Цельсия,— температура в градусах Фаренгейта. Скольким градусам по шкале Цельсия соответствует 23 градуса по шкале Фаренгейта?

13. Задание 13 № 350790

Укажите решение неравенства 

1)

2)

3)

4)

14. Задание 14 № 392691

В фирме «Чистая вода» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле C = 6500 + 4000n, где n — число колец, установленных в колодце. Пользуясь этой формулой, рассчитайте стоимость колодца из 12 колец. Ответ дайте в рублях.

15. Задание 15 № 339450

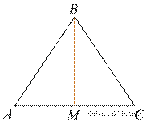
В треугольнике ABC AB = BC = 53, AC = 56. Найдите длину медианы BM.

16. Задание 16 № 351256

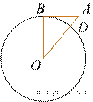
Отрезок AB = 21 касается окружности радиуса 72 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.

17. Задание 17 № 349920

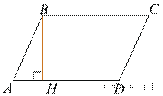Высота BH ромба ABCD делит его сторону AD на отрезки  и . Найдите площадь ромба.

18. Задание 18 № 311495

Найдите тангенс угла  A  треугольника  ABC, изображённого на рисунке.

19. Задание 19 № 369741

Какое из следующих утверждений верно?

1) Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой.

2) В любой прямоугольник можно вписать окружность.

3) Каждая из биссектрис равнобедренного треугольника является его медианой.

В ответе запишите номер выбранного утверждения.

20. Задание 20 № 316330

Решите уравнение 

21. Задание 21 № 341393

Два бегуна одновременно стартовали в одном направлении из одного и того же места круговой трассы в беге на несколько кругов. Спустя один час, когда одному из них оставалось 3 км до окончания первого круга, ему сообщили, что второй бегун прошёл первый круг 9 минут назад. Найдите скорость первого бегуна, если известно, что она на 6 км/ч меньше скорости второго.

22. Задание 22 № 338253

Постройте график функции  и определите, при каких значениях m прямая  имеет с графиком ровно три общие точки.

23. Задание 23 № 206

Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна 140°.

24. Задание

В параллелограмме ABCD диагонали AC и BD пересекаются в точке K. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника CKD.

25. Задание

Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 96, тангенс угла BAC равен  Найдите радиус окружности, вписанной в треугольник ABC.

Скачано с www.znanio.ru