

ЗАДАЧНИК![]()
 ПРАКТИКУМ
ПРАКТИКУМ
$ИЗДАТЕЛЬСТВО Б НОМ
![]()
Задачник-практикум
В двух томах
Под редакцией И. Семакина, Е. Хеннера
Москва
БИНОМ. Лаборатория знаний
ущс 004.9 ББК 32.97
ин
Авт ор ы:
Л. А. Залогова, М. А. Плаксин, С. В. Русаков, О. Л. Русакова,
И. Г. Семакин, Е. К. Хеннер, Т. Ю. Шеина, А. П. Шестаков,
Л. В. Шестакова, М. А. Южаков
Информатика и ИКТ. Задачник-практикум![]()
ИИ Т. 1 / Л. А. Залогова [и др.] ; под ред. И. Г. Семакина, Е. К. Хеннера. — 3-е изд. — М. : БИНОМ. Лаборатория знаний, 2011. — 309 с. : ил.
ISBN ![]() (Т. 1)
(Т. 1)
ISBN 978-5-99630475-2
Задачник-практикум входит в состав учебно-методических комплектов «Информатика и ИКТ» для 8—9 и 10—11 классов. В практикум включены разноуровневые задания, которые подобраны в соответствии с темами основного курса информатики и ИКТ (8—9 массы) и курса для старшей школы (базовый уровень).
удк 004.9 ББК 32.97
По вопросам приобретения обращаться:
«БИНОМ. Лаборатория знаний» Телефон: (499) 157-5272 e-mail: binom@Lbz.ru, http://www.Lbz.ru
ISBN 978,5-9963-0476-9 (Т. 1) ISBN 978-5-9963-0475=2
(Э БИНОМ. Лаборатория знаний,
2011
Введение . . . . ![]()
Раздел 1. Представление
![]() 1.1. Информация и
языки . .
1.1. Информация и
языки . .
1.2. Кодирование информации. .![]() . 10
. 10
1.3. Измерение информации .![]() . 15
. 15
1.4. Количество информации и вероятность. . . . .![]() .
23
.
23
1.5. Представление числовой информации. . . . . . . . . . . . . . . 28
1.5.1. Системы счисления . . . .. 28
![]()
1.5.2. Перевод десятичных чисел в другие системы счисления . . 33
1.5.3. Системы счисления,
используемые в компьютере (с основанием 2 п ) . . ![]() . 36
. 36
1.5.4. Арифметика в позиционных системах счисления![]()
1.6. Логическая информация и основы логики 44
1.6.1. Высказывания
1.6.2. Логические величины, операции, выражения . . .
1.6.3. Логические схемы и логические выражения . ![]() . 50
. 50
1.6.4. Импликация и эквивалентность ![]() . 54
. 54
1.6.5. Преобразование логических выражений . . . ![]() . 56
. 56
Раздел 2. Информационные модели:
системы
и структуры данных ![]() . 61 2.1. Введение в системологию . . . .
. 61 2.1. Введение в системологию . . . .
![]() . 61
. 61
2.1.1. Понятие «система»; системный эффект . ![]() . 61
. 61
2.1.2. Среда. Вход и выход системы. «Черный ящик» . . . . . . . . . 63
2.1.3. Состав и структура системы. Информационная модель . . . 67
2.1.4. Систематизация![]() . 72
. 72
2.2. Информационные модели на графах . . ![]() . 79
. 79
2.2.1. Основные понятия: теоретическое введение . . . . . . . . . . . . 79
2.2.2. Классификация и наследование![]() . 88
. 88
2.2.3. Блок-схемы . . . .![]() . 94
. 94
2.3. Табличные
информационные модели .![]() 97 2.3.1. Основные понятия . . . . . . . .
. .
97 2.3.1. Основные понятия . . . . . . . .
. .![]()
2.3.2. Таблицы типа «объекты—свойства»![]() . 102
. 102
2.3.3. Таблицы типа «объекты—объекты». . . . . . . . . . . . . . . . . 105
|
2.3.4. Более сложные типы таблиц |
|
|
2.3.5.
Вычислительные таблицы . |
|
|
и архитектура ЭВМ |
. 128 |
|
3.1. Представление информации в компьютере
. |
. 128 |
|
З. 1.1. Структура внутренней памяти . . . . . . . . |
|
|
З. 1.2. Структура дисков; файлы и каталоги |
|
|
З. 1.3. Представление символьной информации |
|
Содержание
![]()
З. 1.4. Представление числовой информации . ![]() . 139
. 139
3.1.4.1. Целые числа . . . . . . . . ![]() . 139
. 139
Работа № 1 ![]() . 141
. 141
3.1.4.2. Вещественные числа. . . . . . . ![]() . 142
. 142
Работа № 2 ![]() . 146
. 146
З. 1.5. Представление графической
информации ![]() . 147 3.1.5.1. Растровое представление. . . .
. 147 3.1.5.1. Растровое представление. . . . ![]() . 147
. 147
3.1.5.2. Векторное представление . ![]() . 154
. 154
З. 1.6. Звук в памяти компьютера. . ![]() . 160
. 160
3.2. Архитектура ЭВМ
(на моделях учебных компьютеров) ![]() . 163
. 163
3.2.1. Формат
машинной команды. . ![]() . 164 3.2.2. Язык машинных команд .. 167
. 164 3.2.2. Язык машинных команд .. 167
![]()
3.2.3. Машинно-ориентированные языки
(Автокод —
Ассемблер) . ![]() . 177
. 177
Раздел 4. Алгоритмизация и программирование. . ![]() . 183
. 183
4.1. Алгоритм и его свойства. 183
![]()
4.2. Алгоритмы управления учебными исполнителями . . . . 185
4.2.1. Машина Поста. 185
![]()
4.2.2. «Умный мячик». . . . . .. 190
![]()
4.2.3. Графический исполнитель (ГРИС) .. 196
![]()
4.2.4. ЛОГО — Черепашка. 200
![]()
4.3. Алгоритмы работы с величинами .. 209
![]()
4.4. Программирование на языках высокого уровня![]() .
218
.
218
4.4.1. Программирование линейных алгоритмов . . . . .. 218
![]()
4.4.2. Программирование ветвящихся алгоритмов .![]() . 233
. 233
|
4.4.3. Программирование циклических алгоритмов . |
|
|
|
4.4.4. Работа с массивами |
|
|
|
4.4.5. Подпрограммы |
|
|
|
4.4.6. Обработка строк . |
|
|
|
Приложение 1 |
|
. 299 |
|
Приложение 2 . |
|
. зоо |
|
Ответы к разделу 1 . . |
|
. 302 |
|
Ответы к разделу 3.1 |
|
. 304 |
|
Ответы к разделу 3.2 |
|
. 307 |
|
Ответы к работе .N2 1 |
|
. 308 |
|
Ответы к работе N2 2 |
|
. 308 |
|
Литература для дополнительного чтения. . .
. . . |
. 309 |
|
Настоящее учебное пособие является переработанным изданием задачника-практикума по информатике, выпускавшегося издательством «Лаборатория Базовых Знаний» начиная с 1999 года. В новом издании учтены требования федерального компонента Государственного образовательного стандарта по информатике и ИКТ для основной школы, принятого в 2004 году. В частности, в соответствии с содержанием ГОС, в пособии появился новый раздел «5.6. Компьютерные презентации». Внесены и другие изменения. В некоторые разделы включены новые задания, переработаны тексты теоретической части, добавлены примеры решения задач. Учтены некоторые замечания и предложения, отмеченные учителями в процессе использования предыдущего издания.
В предметной области информатики выделяются две составляющие: научная (теоретическая) и прикладная (технологическая). Обе они отражаются в школьном курсе информатики и поддержаны содержанием настоящего задачника-практикума.
Основные принципы, использованные при построении пособия (задачника-практикума), таковы.
1. Содержание пособия избыточно по отношению к большинству курсов информатики, но обеспечивает их в совокупности. Избыточность понимается в двояком смысле: по набору тематических разделов и по подбору задач в каждом разделе, позволяющему реализовать многоуровневость образовательных программ по информатике.
2. Пособие предназначено как для изучения базового курса информатики, так и для нескольких часто встречающихся профильно-ориентированных курсов. Материалы некоторых разделов могут быть использованы при изучении информатики в младших классах (пропедевтический курс). В каждом из шести разделов можно найти задачи разного уровня сложности, в том числе рассчитанные на углубленное изучение информатики.
З. Пособие, кроме основной части — задач и заданий — содержит для удобства читателей краткие теоретические описания по каждой теме и примеры решения задач, что делает его пригодным и для самообразования.
4. Пособие содержит практические материалы разного назначения. Это:
а задачи для
теоретического решения (без компьютера); ![]() задачи для решения с
помощью компьютера;
задачи для решения с
помощью компьютера; ![]() задания для лабораторного практикума; а
упражнения на отработку отдельных практических навыков работы за компьютером; а
творческие задания и проекты.
задания для лабораторного практикума; а
упражнения на отработку отдельных практических навыков работы за компьютером; а
творческие задания и проекты.
Задачник-шрактикум по информатике
![]()
5. Пособие не ориентировано на конкретный тип компьютера и определенные версии программного обеспечения.
6. В ряде разделов, связанных с применением средств информационных технологий (базы данных, электронные таблицы и др.), в пояснительной части для идентификации команд и режимов применяется псевдоязык (русские термины), который легко переложить на язык любой конкретной версии программного обеспечения.
Современное представление о структуре информатики
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
![]()
Информация — сведения, знания, содержащиеся в сообщении.
![]() Информация хранится, передается,
обрабатывается в
Информация хранится, передается,
обрабатывается в ![]() символьной (знаковой) форме. Одна и та же
информация может быть представлена в разной форме, с помощью раз-
символьной (знаковой) форме. Одна и та же
информация может быть представлена в разной форме, с помощью раз-
личных знаковых систем.
Язык — это определенная знаковая система представления информации.
Существуют естественные (разговорные) языки и формальные языки. Примеры формальных языков: язык музыки (нотная грамота), язык математики (цифры и математические знаки) и др. В некоторых случаях разговорную речь может заменять язык мимики и жестов, язык специальных знаков (например, дорожные знаки).
К какому языку относятся знаки на рис. 1.1 и что они обозначают?

Объясните, что обозначают жесты на рис. 1.2.


Предположим, что на «марсианском» языке выражение «lot do тау» означает «кот съел мышь»; «тау si» «серая мышв»; «ro do» — «он съел». Как написать на «марсианском» языке «серый кот» ?
Выразите в виде предложения на русском языке смысл математического выражения
( 1 О + 11 + 12 + 1 З + 14 + 1 • 19 2
5
Представьте в математической форме следующее утверждение:
Если сумму чисел от одного до пяти разделить на разность чисел десять и семь, то в результате получится пять. Какая форма записи удобнее?
Составьте таблицу способов символьного представления информации в перечисленных областях. Если знаков много, то запишите или нарисуйте некоторые из них.

Фраза на некотором иностранном языке «каля маля» в переводе на русский означает «красное солнышко», «фаля маля баля» — «большая красная груша», «цаля баля» — «большое яблоко». Как на этом языке записать слова: «груша», «яблоко», «солнышко»?
1.1. Информация и языки 9
![]()
Перечислите не менее пяти способов приветствия друг друга, используя разговорные языки, язык жестов и мимики.
Придумайте графический способ представления известной поговорки «повторение — мать учения».
Опишите вашу классную комнату. Какие языки вы при этом использовали?
Что может обозначать запись 18-15 с точки зрения продавца в магазине, машиниста электропоезда, ученика на уроке математики?
ЛЕ 13
Что может обозначать запись 141198?
Запишите на языке музыки (нотами) семь нот первой октавы до, ре, ми, фа, соль, ля, си.
Запишите на языке музыки (нотами) следующий музыкальный фрагмент: фа, до, ми, до, фа, ми, ре.
Л) 16
Придумайте и нарисуйте удобные знаки — пиктограммы для обозначения кабинета музыки, химии, информатики, спортивного зала.
![]()
![]() Кодирование
информации процесс формирования определенного представления информации. В более
узком смысле под термином «кодирование» часто понимают переход от одной формы
представления информации к другой, более удобной для хранения, передачи или
обработкси. Обратное преобразование называется декодированием.
Кодирование
информации процесс формирования определенного представления информации. В более
узком смысле под термином «кодирование» часто понимают переход от одной формы
представления информации к другой, более удобной для хранения, передачи или
обработкси. Обратное преобразование называется декодированием.
Способ кодирования зависит от цели, ради которой оно осуществляется. Такой целью может быть сокращение записи, засекречивание (шифровка) информации, удобство обработки и т. п.
Чаще всего кодированию подвергаются тексты на естественных языках (русском, английском и пр.). Существуют три основных способа кодирования текста:
1) графический — с помощью специальных рисунков или значков;
2) числовой — с помощью чисел;
З) символьный — с помощью символов того же алфавита, что и исходный текст.
Полный набор символов, используемый для кодирования текста, называется алфавитом или азбукой.
Дана кодовая таблица флажковой азбуки (рис. 1.3):
|
|
|
|
|
д |
|
|
||
|
ж |
|
|
|
|
|
|
||
|
|
О |
п |
р |
с |
|
У |
||
|
|
х |
ц |
|
ш |
щ |
|
||
|
|
|
|
|
|
||||
|
Ы |
Ь |
|
ю |
я |
|
|||
![]()
Старший помощник Лом сдает экзамен капитану Врунгелю. Помогите ему прочитать следующий текст (рис. 1.4):
![]()

С помощью флажковой азбуки (рис. 1.3) зашифруйте фразу «Учение да труд к славе ведут» .
С помощью флажковой азбуки (рис. 1.3) запишите свое имя и фамилию.
Дана кодовая таблица азбуки Морзе (рис. 1.5).

Расшифруйте (декодируйте), что здесь написано (буквы отделены друг от друга пробелами)?
![]()
Закодируйте с помощью азбуки Морзе слова:
ИНФОРМАТИКА, ДАННЫЕ, АЛГОРИТМ.
![]()
Закодируйте с помощью азбуки Морзе свое имя и фамилию.
Мальчик заменил каждую букву своего имени ее номером в алфавите. Получилось 4 6 15 1. Как зовут мальчика?
Зашифрованная пословица.
![]()
Чтобы рубить дрова, нужен 14, 2, З, 2, 7: , а чтобы полить ого-
![]()
Рыбаки сделали во льду З, 7, 2, 7, 8, 9, 11 и стали ловить
рыбу.
Самый колючий зверь в лесу - ЭТО t 12, 33 .
|
1, 2, З, 4, 5, 1, 6 7, 8, 9, 10, 11 9, 4, 7, 4, 13, 12, 14 |
А теперь прочитайте пословицу:
.
Заменяя каждую букву ее порядковым номером в алфавите, зашифруйте фразу: Я УМЕЮ КОДИРОВАТЬ ИНФОРМАЦИК). Что необходимо предусмотреть, чтобы зашифрованный текст был записан без пропусков?
.N2 10
Дана кодировочная таблица (первая цифра кода ![]() номер
строки, вторая — номер столбца) (рис. 1.6).
номер
строки, вторая — номер столбца) (рис. 1.6).
|
|
О с |
1 Б й Ы |
2 в к |
л |
д м |
5 Е Н |
6 Ё о |
7 |
|
|
|
ж |
||||||||
|
п |
р |
||||||||
|
|
Ч |
|
|
||||||
|
з |
|
|
|||||||
|
|
|
||||||||
С помощью этой кодировочной таблицы зашифруйте фразу: Я УМЕЮ РАБОТАТЬ С ИНФОРМАЦИЕЙ: А ТЫ?
Используя кодировочную таблицу на рис. 1.6, расшифруйте текст: 26211640360304054036121603040040.
ЛЕ 12
Придумайте свою кодировочную таблицу и зашифруйте с ее помощью свой домашний адрес.
Кодирование информации
![]()
Шифры замены. Каждая буква алфавита может быть заменена любым числом из соответствующего столбика кодировочной таблицы (рис. 1.7).
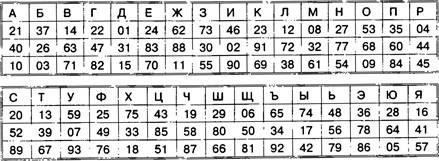
![]()
Какие сообщения закодированы с помощью этой таблицы?
|
16 |
55 |
54 1 10 .69 |
09 68 |
61 |
1 89 i29 |
49 44 10 |
02 |
73 |
32 |
1 83 «54 ; 74 |
||||||||
|
41 |
55 |
• 77 |
10 23 |
08 |
20 «66 |
76 |
44 61 |
90 |
55 |
21 |
61 |
83 254 |
42 |
|||||
|
57 |
зо |
27 |
10 |
91 |
68 |
32 |
20 |
80 |
02 |
49 45 40 |
32 |
46 |
55 |
40 |
08 |
83 27 |
17 |
|
Используя кодировочную таблицу, приведенную на рис. 1.7, зашифруйте свое имя и фамилию.
.М 15
Шифр Цезаря. Этот шифр реализует следующее преобразование текста: каждая буква исходного текста заменяется идущей после нее с некоторым сдвигом буквой в алфавите, который считается написанным по кругу. Пусть этот сдвиг равен З. Используя этот шифр, зашифруйте слова: ИНФОРМАЦИЯ, КОМПЬЮТЕР, ЧЕЛОВЕК.
Расшифруйте слово НУЛТХСЁУГЧЛВ, закодированное с помощью шифра Цезаря (см. задачу 15).
.М 17
Шифр Виженера. Этот шифр представляет собой шифр Цезаря с переменной величиной сдвига. Величину сдвига задают ключевым словом. Например, ключевое слово ВАЗА означает следующую последовательность сдвигов букв исходного текста: З 1 9 1 З 1 9 1 и т. д. Используя в качестве ключевого слово ВАГОН, закодируйте слова: АЛГОРИТМ, ПРАВИЛА, ИНФОРМАЦИЯ.
![]()
Слово НССРХПЛСГХСА получено с помощью шифра Винсенера (см. задачу № 17) с ключевым словом ВАЗА. Восстановите исходное слово.
Шифр перестановки. Кодирование осуществляется перестановкой букв в слове по одному и тому же общему правилу. Восстановите слова и определите правило перестановки: ЛЫСО, ЕРАВШН, умызмс, АШНРРИ, РКДЕТИ.
![]() 20
20
Зашифруйте по правилу из задачи № 19 слова: ИНФОРМАЦИЯ, ПРАВИЛА, АЛГОРИТМ.
Придумайте свой шифр перестановки и с его помощью зашифруйте свое имя и фамилию.
![]() 22
22
Какому или каким из перечисленных ниже слов соответствует
код ![]() Слова: ОРНАМЕНТ, ДОМИНИОН, РИФЛЕНИЕ,
СТРОЕНИЕ, СМЕКАЛКА.
Слова: ОРНАМЕНТ, ДОМИНИОН, РИФЛЕНИЕ,
СТРОЕНИЕ, СМЕКАЛКА.
.N2 23
Задано правило кодирования: после каждой гласной буквы вставляется буква А, а после согласной — Т. Расшифруйте слова: ИАНТФТОАРТМТААТГИАКТАА, ПТРТИАНТТГЕАРТ.
![]() 24
24
Угадайте правило шифровки и расшифруйте слова: ТКАФЕТРА, ткнитсни, ТИЦАРТНА, ЛАНИГИРО.
![]() 25
25
Пользуясь правилом из задачи № 24, зашифруйте фразу:
ИНФОРМАТИКА — ЭТО НАУКА О СПОСОБАХ ПОЛУЧЕНИЯ, НАКОПЛЕНИЯ, ОБРАБОТКИ, ПЕРЕДАЧИ И ПРЕДСТАВЛЕНИЯ ИНФОРМАЦИИ.
![]() 26
26
Определите правило шифровки и расшифруйте слова:
АКРОЛДИИТРБОФВНАЗНГИЦЕШ, ЩИКНГФЗОЕРУМЦАЫЦГИХИ
![]() 27
27
Для точности передачи сообщений и ликвидации «шумов» в сообщениях используется принцип двукратной последовательной передачи каждого символа. В результате сбоя при передаче информации приемником принята символьная последовательность: ПРРРАОССПТОО. Какое осмысленное сообщение передавалось?
![]() Содержательный
подход. Количество информации, заключенное в сообщении, определяется объемом
знаний, который это сообщение несет получающему его человеку. Сообщение
содержит информацию для человека, если заключенные в нем сведения являются для
этого человека новыми и понятными и, следовательно, пополняют его знания.
Содержательный
подход. Количество информации, заключенное в сообщении, определяется объемом
знаний, который это сообщение несет получающему его человеку. Сообщение
содержит информацию для человека, если заключенные в нем сведения являются для
этого человека новыми и понятными и, следовательно, пополняют его знания.
При содержательном подходе возможна
качественная оценка информации: полезная, безразличная, важная, вредная . ![]() Одну
и ту же информацию разные люди могут оценить по разному.
Одну
и ту же информацию разные люди могут оценить по разному.
Единица измерения количества информации называется битом. Сообщение, уменьшающее неопределенность знания человека в два раза, несет для него 1 бит информации.
![]()
Данная формула является показательным уравнением относительно неизвестного х. Из математики известно, что решение такого уравнения имеет вид:
х = log2N
— логарифм ЛУ по основанию 2. Если ЛУ равно целой степени двойки (2, 4, 8, 16 и т. д.), то такое уравнение можно решить «в уме». В противном случае количество информации становится нецелой величиной, и для решения задачи придется воспользоваться таблицей логарифмов, которая приведена в Приложении 1.
Пример 1. При
бросании монеты сообщение о резуль![]() тате жребия (например, выпал орел) несет
1 бит информации, поскольку количество возможных вариантов результата равно 2
(орел или решка). Оба эти варианта равновероятны.
тате жребия (например, выпал орел) несет
1 бит информации, поскольку количество возможных вариантов результата равно 2
(орел или решка). Оба эти варианта равновероятны.
Ответ может быть получен из решения уравнения: = 2, откуда, очевидно, следует: х = 1 бит.
Вывод: в любом случае сообщение об одном событии из двух равновероятных несет 1 бит информации.
Пример 2. В барабане для розыгрыша лотереи находится 32 шара. Сколько информации содержит сообщение о первом выпавшем номере (например, выпал номер 15)?
Решение. Поскольку вытаскивание любого из 32 шаров равновероятно, то количество информации об одном выпавшем номере находится из уравнения:
![]()
но 32 = 2 5 . Следовательно, х = 5 битов. Очевидно, ответ не зависит от того, какой именно выпал номер.
![]() Пример З. При игре в
кости используется кубик с
Пример З. При игре в
кости используется кубик с ![]() шестью гранями. Сколько битов информации
получает
шестью гранями. Сколько битов информации
получает ![]() игрок при каждом бросании кубика?
игрок при каждом бросании кубика?
Решение. Выпадение каждой грани кубика равновероятно. Поэтому количество информации от одного результата бросания находится из уравнения:
![]() 6.
6.
Решение этого уравнения: х = log2 6.
Из таблицы в Приложении 1 следует (с точностью до 3-х знаков после запятой):
х = 2,585 бита.
![]()
Определите, какое из сообщений содержит для вас информацию.
— Площадь Тихого океана — 179 млн кв. км. — Москва — столица России.
— Вчера весь день шел дождь.
![]() Завтра ожидается солнечная погода.
Завтра ожидается солнечная погода.
— Дивергенция однородного векторного поля равна нулю.
— Dog — собака (по-английски).
— Ro do, тау si, lot do тау. ![]() 4.
4.
Дайте следующим сообщениям оценки «важная», «полезная», «безразличная», «вредная» информация.
— Сейчас идет дождь.
— Занятия факультатива по информатике проводятся каждый вторник.
— IBM — это первые буквы английских слов, которые звучат как «интернешнел бизнес мэшинз», что по-русски означаег «машины для международного бизнеса» . — Завтра будет контрольная работа по химии.
— Чтобы родители не узнали про двойку, надо вырвать страницу из дневника.
— Лед — это твердое состояние воды.
— Первым человеком, полетевшим в космос, был Юрий Гагарин.
— Номер телефона скорой помощи 02.
«Вы выходите на следующей остановке? » — спросили человека в автобусе. «Нет», — ответил он. Сколько информации содержит ответ?
Какой объем информации содержит сообщение, уменьшающее неопределенность знания в 4 раза?
Вы подошли к светофору, когда горел красный свет. После этого загорелся желтый свет. Сколько информации вы при этом получили?
Группа школьников пришла в бассейн, в котором 4 дорожки для плавания. Тренер сообщил, что группа будет плавать на дорожке номер З. Сколько информации получили школьники из этого сообщения?
В корзине лежат 8 шаров. Все шары разного цвета. Сколько информации несет сообщение о том, что из корзины достали красный шар?
Была получена телеграмма: «Встречайте, вагон 7». Известно, что в составе поезда 16 вагонов. Какое количество информации было получено?
![]()
В школьной библиотеке 16 стеллажей с книгами. На каждом стеллаже 8 полок. Библиотекарь сообщил Пете, что нужная ему книга находится на пятом стеллаже на третьей сверху полке. Какое количество информации библиотекарь передал Пете?
При угадывании целого числа в диапазоне от 1 до было получено 7 битов информации. Чему равно N?
При угадывании целого числа в некотором диапазоне было получено 6 битов информации. Сколько чисел содержит этот диапазон?
Сообщение о том, что ваш друг живет на 10 этаже, несет 4 бита информации. Сколько этажей в доме?
Сообщение о том, что Петя живет во втором подъезде, несет З бита информации. Сколько подъездов в доме?
В коробке лежат 7 разноцветных карандашей. Какое количество информации содержит сообщение, что из коробки достали красный карандаш?
Какое количество информации несет сообщение: « Встреча назначена на сентябрь» ?
Какое количество информации несет сообщение о том, что встреча назначена на 15-е число?
Какое количество информации несет сообщение о том, что встреча назначена на 23 октября в 15.00?
![]() Алфавитный подход к
измерению информации позволяет определить количество информации, заключенной в
тексте. Алфавитный подход является объективным,
Алфавитный подход к
измерению информации позволяет определить количество информации, заключенной в
тексте. Алфавитный подход является объективным,
т. е. он не зависит от субъекта (человека), воспринимающего текст.
Множество символов, используемых при записи текста, называется алфавитом. Полное количество символов в алфавите называется мощностью (размером) алфавита. Если допустить, что все символы алфавита встречаются в тексте с одинаковой частотой (равновероятно), то количество информации, которое несет каждый символ, вычисляется по формуле:
![]() = logzN,
= logzN,
где N — мощность алфавита. Следовательно, в
2-символьном алфавите каждый символ «весит» 1 бит (logp = 1); в 4-символьном
алфавите каждый символ несет 2 бита информации ![]() 2); в 8-символьном —
З бита (log28 —
2); в 8-символьном —
З бита (log28 —![]()
Один символ из алфавита мощностью 256 (28 ) несет в тексте 8 битов информации. Такое количество информации называется байтом. Алфавит из 256 символов используется для представления текстов в компьютере.
1 байт = 8 битов.
Если весь текст состоит из К символов, то при алфавитном подходе размер содержащейся в нем информации равен:
где i — информационный вес одного символа в используемом алфавите.
![]() Пример 4. Книга,
набранная с помощью компьютера, содержит 150 страниц; на каждой странице — 40
строк, в каждой строке — 60 символов. Каков объем информации в книге?
Пример 4. Книга,
набранная с помощью компьютера, содержит 150 страниц; на каждой странице — 40
строк, в каждой строке — 60 символов. Каков объем информации в книге?
Решение. Мощность компьютерного алфавита равна 256. Один символ несет 1 байт информации. Значит, страница содержит 40 • 60 = 2400 байт информации. Объем всей информации в книге (в разных единицах): 2400 150 = 360 000 байт.
360000/1024 - 351,5625 Кбайт.
351,5625/1024 - 0,34332275 Мбайт.
![]()
Л) 19
Алфавит племени Мульти состоит из 8 букв. Какое количество информации несет одна буква этого алфавита?
Сообщение, записанное буквами из 64-символьного алфавита, содержит 20 символов. Какой объем информации оно несет?
Племя Мульти имеет 32-символьный алфавит. Племя Пульти использует 64-символьный алфавит. Вожди племен обменялись письмами. Письмо племени Мульти содержало 80 символов, а письмо племени Пульти — 70 символов. Сравните объемы информации, содержащейся в письмах.
М 22
Алфавит племени Мульти состоит из 32 символов. Члены племени используют в своей речи и письме только слова длиной 8 символов, причем все слова начинаются или с символа А, или с символа О, остальные буквы в слове могут быть любыми. Какое количество информации несёт одно слово этого племени?
Словарный запас племени Пульти составляют 256 слов одинаковой длины. Каждая буква алфавита несет 2 бита информации. Какова длина слова этого племени?
Словарный запас племени Пульти составляют 1024 слова из 5 букв. Какое количество информации несет одна буква из алфавита этого племени?
![]() 26
26
Информационное сообщение объемом 1,5 Кбайт содержит 3072 символа. Сколько символов содержит алфавит, при помощи которого было записано это сообщение?
![]() 27
27
Объем сообщения, содержащего 1024 символа, составил 1/512 часть мегабайта. Каков размер алфавита, с помощью которого записано сообщение?
.М2 28
Сколько символов содержит сообщение, записанное с помощью 16-символьного алфавита, если объем его составил 1/16 часть мегабайта?
![]() 29
29
Сколько килобайт составляет сообщение, содержащее 12288 битов?
Сколько килобайт составит сообщение из 384 символов 16-символьного алфавита?
Для записи текста использовался 256-символьный алфавит. Каждая страница содержит 30 строк по 70 символов в строке. Какой объем информации содержат 5 страниц текста?
![]() 32
32
Сообщение занимает З страницы по 25 строк. В каждой строке записано по 60 символов. Сколько символов в использованном алфавите, если все сообщение содержит 1125 байт?
«М 33
«М 34
Сообщение занимает 2 страницы и содержит 1/16 Кбайт информации. На каждой станице записано 256 символов. Какова мощность использованного алфавита?
Два сообщения содержат одинаковое количество символов. Количество информации в первом тексте в 1,5 раза больше, чем во втором. Сколько символов содержат алфавиты, с помощью которых записаны сообщения, если известно, что число символов в каждом алфавите не превышает 10 и на каждый символ приходится целое число битов?
Два сообщения содержат одинаковое количество информации. Количество символов в первом тексте в 2,5 раза меньше, чем во втором. Сколько символов содержат алфавиты, с помощью которых записаны сообщения, если известно, что размер каждого алфавита не превышает 32 символов и на каждый символ приходится целое число битов?
.М2 37
Выяснить, сколько битов информации несет каждое двузначное
целое число (отвлекаясь от его конкретного числового значения).
![]() Рассмотрим несколько
примеров.
Рассмотрим несколько
примеров.
1. В коробке имеется 50 шаров. Из них 40 белых и 10 черных. Очевидно, вероятность того, что при вытаскивании «не глядя» попадется белый шар больше, чем ве-
роятность попадания черного.
2. Сережа — лучший ученик в классе. Вероятность того, что за контрольную по математике Сережа получит «5», больше, чем вероятность получения двойки.
З. В пруду живут 8000 карасей, 2000 щук и 40 ООО пескарей. Самая большая вероятность для рыбака — поймать в этом пруду пескаря, на втором месте стоит вылавливание карася, на третьем — щуки.
Выше сделаны качественные заключения о вероятностях событий, которые интуитивно понятны. Однако вероятность может быть выражена количественно.
![]() Пример 1. Обозначим
рч вероятность вытаскивания черного шара, вероятность вытаскивания белого шара.
Тогда:
Пример 1. Обозначим
рч вероятность вытаскивания черного шара, вероятность вытаскивания белого шара.
Тогда:
Рч 10/50 - 0,2; - 40/50 - 0,8.
![]()
![]() Пример
2. Представим себе, что мы изучили успеваемость Сережи за несколько лет учебы.
За это время он получил по математике 100 оценок. Из них: 60 пятерок, 30
четверок, 8 троек и 2 двойки, Допуская, что такое распределение оценок может
сохраниться и в дальнейшем, вычислим вероятность получения каждой из оценок.
60/100 = 0,6; Р4 - 30/100 = 0,3; 8/100 - 0,08; - 2/100 - 0,02.
Пример
2. Представим себе, что мы изучили успеваемость Сережи за несколько лет учебы.
За это время он получил по математике 100 оценок. Из них: 60 пятерок, 30
четверок, 8 троек и 2 двойки, Допуская, что такое распределение оценок может
сохраниться и в дальнейшем, вычислим вероятность получения каждой из оценок.
60/100 = 0,6; Р4 - 30/100 = 0,3; 8/100 - 0,08; - 2/100 - 0,02.
![]() Пример З. Всего в
пруду обитают 50000 рыб. Из предыдущих примеров можно догадаться, что
вероятность попадания на удочку рыбы каждого из видов равна доле этого вида в
общем количестве. Отсюда:
Пример З. Всего в
пруду обитают 50000 рыб. Из предыдущих примеров можно догадаться, что
вероятность попадания на удочку рыбы каждого из видов равна доле этого вида в
общем количестве. Отсюда:
- 8000/50000 = 0,16;
![]() - 2000/50000 0,04; - 40000/50000 - 0,8.
- 2000/50000 0,04; - 40000/50000 - 0,8.
![]() Из рассмотренных
примеров можно сделать вывод: если лт — это общее число возможных
исходов какого-то процесса (вытаскивание шара, получение оценки, ловля рыбы), и
из них интересующее нас событие (вытаскива-
Из рассмотренных
примеров можно сделать вывод: если лт — это общее число возможных
исходов какого-то процесса (вытаскивание шара, получение оценки, ловля рыбы), и
из них интересующее нас событие (вытаскива-
ние белого шара, получение пятерки, попадание щуки) может произойти К раз, то вероятность этого события равна k/N.
Вероятность выражается в долях единицы. В частном случае, вероятность достоверного события равна 1 (из 50 белых шаров вытащен белый шар); вероятность невозможного события равна нулю (из 50 белых шаров вытащен черный шар).
Качественную связь между вероятностью события и количеством информации в сообщении об этом событии можно выразить так: чем меньше вероятность некоторого события, тем больше информации содержит сообщение об этом событии.
Например, сообщение о том, что Сережа
получил двойку по математике, содержит больше информации для тех, кто его
знает, чем сообщение о пятерке. Сообщение, что рыбак поймал в пруду щуку, более
информативно, чем сообщение о том, что на удочку попался пескарь.
Количественная зависимость между вероятностью события ф) и количеством
информации в сообщении о нем (i) выражается формулой: ![]() log2(1/p).
log2(1/p).
![]() Пример 4. В задаче о
шарах определим количество ин
Пример 4. В задаче о
шарах определим количество ин![]() формации в сообщении о вытаскивании белого
шара и
формации в сообщении о вытаскивании белого
шара и ![]() черного шара:
черного шара:
1041/0,2) = 2 - 2,321928.
![]() Вероятностный метод
применим и для алфавитного подхода к измерению информации, заключенной в
тексте. Известно, что разные символы (буквы алфавита, знаки препинания и др.)
встречаются в тексте с разной частотой и, следовательно, имеют разную
вероятность. Значит, измерять информационный вес каждого символа в тексте так,
как это делалось раньше (в предположении равновероятности), нельзя.
Вероятностный метод
применим и для алфавитного подхода к измерению информации, заключенной в
тексте. Известно, что разные символы (буквы алфавита, знаки препинания и др.)
встречаются в тексте с разной частотой и, следовательно, имеют разную
вероятность. Значит, измерять информационный вес каждого символа в тексте так,
как это делалось раньше (в предположении равновероятности), нельзя.
![]() Пример 5. В алфавите
племени МУМУ всего 4 буквы (А,
Пример 5. В алфавите
племени МУМУ всего 4 буквы (А, ![]() У, М, К), один знак препинания (точка) и
для разделе
У, М, К), один знак препинания (точка) и
для разделе![]() ния слов используется пробел. Подсчитали,
что в популярном романе «Мумука» содержится всего 10000 знаков, из них: букв А
— 4000, букв У — 1000, букв М — 2000, букв К — 1500, точек — 500, пробелов
1000. Какой объем информации содержит книга?
ния слов используется пробел. Подсчитали,
что в популярном романе «Мумука» содержится всего 10000 знаков, из них: букв А
— 4000, букв У — 1000, букв М — 2000, букв К — 1500, точек — 500, пробелов
1000. Какой объем информации содержит книга?
Решение
Поскольку объем книги достаточно большой, то можно допустить, что вычисленная по ней частота встречаемости в тексте каждого из символов алфавита характерна для любого текста на языке МУМУ. Подсчитаем частоту встречаемости каждого символа во всем тексте книги (т. е. вероятность) и информационные веса символов:
буква А: 4000/10000 = 0,4; iA — 1041/0,4) = 1,321928; буква У: 1000/10000 = 0,1; iy 1041/0,1) - 3,1928; буква М: 2000/10000 = 0,2;2,321928; буква К: 1500/10000 - 0,15; - - 2,736966; точка: 500/10000 = 0,05' iточка 1041/0,05) - 4,321928; пробел: 1000/10000 - 0,1;- 3,321928.
Общий объем информации в книге вычислим как сумму произведений информационного веса каждого символа на число повторений этого символа в книге:
![]() 1,321928 • 4000
+ + 3,1928 • 1000 + 2,321928 • 2000 + 2,736966 1500 +
1,321928 • 4000
+ + 3,1928 • 1000 + 2,321928 • 2000 + 2,736966 1500 +
+ 4,321928 • 500 + 3,321928 • 100 = 22841,84 бита.
![]()
В корзине лежат 32 клубка шерсти. Среди них 4 красных. Сколько информации несет сообщение о том, что достали клубок красной шерсти?
В коробке лежат 64 цветных карандаша. Сообщение о том, что достали белый карандаш, несет 4 бита информации. Сколько белых карандапмей было в коробке?
В ящике лежат черные и белые перчатки. Среди них 2 пары черных. Сообщение о том, что из ящика достали пару черных перчаток, несет 4 бита информации. Сколько всего пар перчаток было в ящике?
В классе 30 человек. За контрольную работу по математике получено 6 пятерок, 15 четверок, 8 троек и 1 двойка. Какое количество информации в сообщении о том, что Иванов получил четверку?
Известно, что в ящике лежат 20 шаров. Из них 10 черных, 5 белых, 4 желтых и 1 красный. Какое количество информации несут сообщения о том, что из ящика случайным образом достали черный шар, белый шар, желтый шар, красный шар?
В течение четверти ученик получил 100 оценок. Сообщение о том, что он получил четверку, несет 2 бита информации. Сколысо четверок ученик получил за четверть?
Для ремонта школы использовали белую, синюю и коричневую краски. Израсходовали одинаковое количество банок белой и синей краски. Сообщение о том, что закончилась банка белой краски, несет 2 бита информации. Синей краски израсходовали 8 банок. Сколько банок коричневой краски израсходовали на ремонт школы?
В корзине лежат белые и черные шары. Среди них 18 черных шаров. Сообщение о том, что из корзины достали белый шар, несет 2 бита информации. Сколько всего в корзине шаров?
Частотный словарь русского языка — словарь вероятностей (частот) появления букв в произвольном тексте — приведен ниже. Определите, какое количество информации несет каждая буква этого словаря.
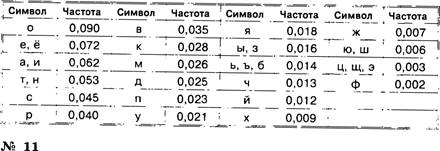
Используя результат решения предыдущей задачи, определите количество информации в слове ИНФОРМАТИКА.
Используя решение задачи № 10, определите количество инФормации в Фразе ПОВТОРЕНИЕ — МАТЬ УЧЕНИЯ.
Л) 13
Возьмите произвольный текст на английском языке (3—4 страницы) и составьте частотный словарь английского языка. Определите, какое количество информации несет каждая буква этого словаря.
.М 15
На остановке останавливаются автобусы с разными
номерами. Сообщение о том, что к остановке подошел автобус с номером N1 несет 4
бита информации. Вероятность появления на остановке автобуса с номером N2 в два
раза меньше, чем вероятность появления автобуса с номером N1. Сколько
информации несет сообщение о появлении на остановке автобуса с номером N2?
1.5.1. Системы счисления
![]() Система
счисления — это способ представления чисел и соответствующие ему правила
действия над числами. Разнообразные системы счисления, которые существовали
раньше и которые используются в наше время, можно разделить на непозиционные и
позиционные. Знаки, используемые при записи чисел, называются цифрами.
Система
счисления — это способ представления чисел и соответствующие ему правила
действия над числами. Разнообразные системы счисления, которые существовали
раньше и которые используются в наше время, можно разделить на непозиционные и
позиционные. Знаки, используемые при записи чисел, называются цифрами.
В непозиционных системах счисления от положения цифры в записи числа не зависит величина, которую она обозначает.
Примером непозиционной системы счисления является римская система (римские цифры). В римской системе в качестве цифр используются латинские буквы:
х С D м
1 5 10 50 100 500 1000
Пример 1. Число
CCXXXII складывается из двух сотен, ![]() трех десятков и двух единиц и равно
двумстам тридцати
трех десятков и двух единиц и равно
двумстам тридцати ![]() • двум.
• двум.
![]()
![]() Пример З
Пример З
MCMXCVIII - 1000
+ (-100 + 1000) + (-10 + 100) + ![]() - 1998.
- 1998.
![]() В позиционных
системах счисления величина, обозначаемая цифрой в записи числа, зависит от ее
позиции. Количество используемых цифр называется основанием позиционной системы
счисления.
В позиционных
системах счисления величина, обозначаемая цифрой в записи числа, зависит от ее
позиции. Количество используемых цифр называется основанием позиционной системы
счисления.
Система счисления, применяемая в современной математике, является позиционной десятичной системой. Ее основание равно десяти, так как запись любых чисел производится с помощью десяти цифр:
![]()
Позиционный характер этой системы легко понять на примере любого многозначного числа. Например, в числе 333 пер-
![]()
вая тройка означает три сотни, вторая — три десятка, третья — три единицы.
Для записи чисел в позиционной системе с основанием п нужно иметь алфавит из п цифр. Обычно для этого при п < 10 используют п первых арабских цифр, а при п 10 к десяти арабским цифрам добавляют буквы. Вот примеры алфавитов нескольких систем:

Если требуется указать основание системы, к которой относится число, то оно приписывается нижним индексом к этому числу. Например:
1011012, 36718, 3B8F16![]()
В системе счисления с основанием q ф-ичная система счисления) единицами разрядов служат последовательные степени числа q. q единиц какого-либо разряда образуют единицу следующего разряда. Для записи числа в вчной системе счисления требуется q различных знаков (цифр), изображающих числа О, 1, q—1. Запись числа q в фичной системе счисления имеет вид 10.
Развериутой формой записи числа называется запись в виде
![]()
-1 -2
![]()
Здесь А — само число, q — основание системы счисления,
а. — цифры данной системы счисления, п — число разрядов целой части числа, т число разрядов дробной части числа.
![]() Пример 4. Получить развернутую форму
десятичных
Пример 4. Получить развернутую форму
десятичных ![]() чисел 32478; 26,387.
чисел 32478; 26,387.
![]() Решение
Решение
3247810 = з
• 10000 + 2 , 1000 + 4 • 100 + 7 • 10 + 8 - 3 , + 2 • 103 + 4 • 10 2
+ 7 . 10 1 + 8 • 100![]()
26,38710 - 2 • 10 1 + 6 • 100 + 3 •
10-1 + 8 • 10-2 + 7 • 10 -3![]()

Решение
1123 - 1 • 10 2 + 1 • 10 1 + 2 • 100 .
1011012 1 • 10 101 + О •
10 100 + 1 • 10 11 + 1 • 10 10 + + О 10 1
+ 1 ' 100![]()
15FC16 - 1 • 10 3 + 10 2 + 10 1 + С • 100 .
101,112 1 • 10 10 + О • 10 1 + 1 • 100 + 1 • 10 —1 + 1 • 10—10 .
Обратите внимание, что в любой системе счисления ее основание записывается как 10.
Если все слагаемые в развернутой форме недесятичного числа представить в десятичной системе и вычислить полученное выражение по правилам десятичной арифметики, то получится число в десятичной системе, равное данному. По этому принципу производится перевод из недесятичной системы в десятичную.
![]() Пример 6. Все числа из предыдущего примера
перевести
Пример 6. Все числа из предыдущего примера
перевести ![]() в десятичную систему.
в десятичную систему. ![]() Решение
Решение
1123![]()
1011012 - 1 2 5![]() .
24 + 1 . 23 + 1 . 22 + О . 21 +
.
24 + 1 . 23 + 1 . 22 + О . 21 + ![]() — 4 51 .
— 4 51 .
15FC16 — 1 16 3
![]() 5 • 16 2 + 15 • 16 1 +
12 — 4096 + 1280 + 240 + 12 562810.
5 • 16 2 + 15 • 16 1 +
12 — 4096 + 1280 + 240 + 12 562810.
101,112
![]() - 5,7510.
- 5,7510.
![]()
Какие числа записаны с помощью римских цифр: MMMD, IV, XIX, мсмхсИх,Т п?
Запишите год, месяц и число своего рождения с помощью римских цифр.
![]()
В старину на Руси широко применялась система счисления, отдаленно напоминающая римскую. С ее помощью сборщики податей заполняли квитанции об уплате податей. Для записи чисел употреблялись следующие знаки:
звезда — тысяча рублей, колесо — сто рублей, квадрат
— десять рублей, Х — один рубль, II II — десять копеек, ![]() — копейка.
— копейка.
Запишите с помощью старинной русской системы счисления сумму 3452 рубля 43 копейки.
Какая сумма записана с помощью старинной русской системы счисления
![]()
Придумайте свою непозиционную систему счисления и запишите в ней числа 45, 769, 1001.
В некоторой системе счисления цифры имеют форму различных геометрических фигур. На рисунке 1.8 приведены некоторые числа, записанные в этой системе счисления:
![]() - 19
- 19
![]()
Какому числу соответствует следующая запись:
![]()
Выполните действия и запишите результат римскими цифра-
|
ми: |
|
|
|
|
ххп - vx |
cv - Ш; |
IC + xrx•, |
МСМ + VIII•, |
|
ХХ : vx |
|
LXVI : XI•, |
xxrv VII. |
32
![]()
Какое количество обозначает цифра 8 в десятичных числах 6538, 8356, 87 и 831?
Что вы можете сказать о числах 111 и 1?
.М2 10
Выпишите алфавиты в 5-ричной, 7-ричноЙ, 12-ричноЙ системах счисления.
.М2 11
Запишите первые 20 чисел натурального числового ряда в двоичной, 5-ричной, 8-ричноЙ, 16-ричноЙ системах счисления.
Запишите в развернутой форме числа:
1) = 25341; = 25341; 2) Аб - 25341; А16 -- 25341.
Запишите в развернутой форме числа:
1) Аш- 125,34; А— 125,34; 2) Аб = 125,34; А16= 125,34.
Г.Г2 14
Запишите в развернутой форме числа:
1) = 5341; А8 = 25,341; 2) Аб = 0,25341; = 341,54.
Г.Г2 15
Запишите в десятичной системе счисления числа:
1) А, - 341; А8 - 341; 2) Аб = 341; А16 = 341.
.М2 16
Запишите в десятичной системе счисления числа:
1) А5 - 34,1; Аз - 221; 2) А7 - 120; А16 - Е41А,12.
.М2 17
Запишите десятичный эквивалент числа 10101, если считать его написанным во всех системах счисления — от двоичной до девятеричной включительно.
Какое минимальное основание должна иметь система счисления, если в ней могут быть записаны числа: 10, 21, 201, 1201?
Какое минимальное основание должна иметь система счисления, если в ней могут быть записаны числа: 403, 561, 666, 125?
![]() 20
20
Какое минимальное основание должна иметь система счисления, если в ней могут быть записаны числа: 22, 984, 1010, А219?

1.5.2. Перевод десятичных чисел в другие системы счисления
![]() Перевод целых чисел.
Перевод целых чисел.
1) Основание новой системы счисления выразить в десятичной системе счисления и все последующие действия производить в десятичной системе счисления;
2) последовательно выполнять деление данного числа и получаемых неполных частных на основание новой системы счисления до тех пор, пока не получим неполное частное, меньшее делителя;
З) полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления;
4) составить число в новой системе счисления, записывая его, начиная с последнего частного.
Пример 1. Перевести число 3710 в двоичную
систему. ![]() Решение. Для обозначения цифр в записи
числа исполь
Решение. Для обозначения цифр в записи
числа исполь![]() зуем символику: а5а4аза2чао.
зуем символику: а5а4аза2чао.
37
|
2 |
2 |
2 |
2 |
||
|
18 18
|
|||||
|
9 8
|
|||||
|
4 4 |
|||||
|
2 |
2 |
||||
![]() Отсюда:
37 = 1001012 .
Отсюда:
37 = 1001012 .
![]() а,
а,
![]() Пример 2. Перевести
десятичное число 315 в восьмеричную и в шестнадцатеричную системы. Решение.
Пример 2. Перевести
десятичное число 315 в восьмеричную и в шестнадцатеричную системы. Решение.
![]() 315 16
315 16
16 19 16
155 16 1
72 7 з 11
Отсюда следует: 31510 4738 - 13В16. Напомним, что 1110 - В16.
2 Информатика и ИКТ. Т. I
![]()
![]() Перевод дробных
чисел.
Перевод дробных
чисел.
1) Основание новой системы счисления выразить в десятичной системе и все последующие действия производить в десятичной системе счисления;
2) последовательно умножать данное число и получаемые дробные части произведений на основание новой системы до тех пор, пока дробная часть произведения не станет равной нулю или не будет достигнута требуемая точность представления числа в новой системе счисления;
З) полученные целые части произведений, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления;
4) составить дробную часть числа в новой системе счисления, начиная с целой части первого произведения.
![]() Пример З. Перевести
десятичную дробь 0,1875 в двоич
Пример З. Перевести
десятичную дробь 0,1875 в двоич![]() ную, восьмеричную и шестнадцатеричную системы.
ную, восьмеричную и шестнадцатеричную системы.
|
|
|
|
|
Здесь вертикальная черта отделяет целые части чисел от дробных частей.
Отсюда: О, 187510 - 0,00112 - 0,148 - 0,316![]()
![]() Перевод смешанных
чисел, содержащих целую и дробную части, осуществляется в два этапа. Целая и
дробная части исходного числа переводятся отдельно по соответствующим
алгоритмам. В итоговой записи числа в новой системе счисления целая часть
отделяется от дробной запятой (точкой).
Перевод смешанных
чисел, содержащих целую и дробную части, осуществляется в два этапа. Целая и
дробная части исходного числа переводятся отдельно по соответствующим
алгоритмам. В итоговой записи числа в новой системе счисления целая часть
отделяется от дробной запятой (точкой).
Пример 4. Перевести десятичное число 315,1875 в восьмеричную и в шестнадцатеричную системы счисления.
![]() Решение.
Из рассмотренных выше примеров следует:
Решение.
Из рассмотренных выше примеров следует:
315,187510
- 473,148 13B,316![]()
![]()
![]()
.М2 23
Перевести целые числа из десятичной системы счисления в троичную:
1) 523; 65; 7000; 2307; 325; 2) 12; 524; 76; 121; 56.
![]() 24
24
Перевести целые числа из десятичной системы счисления в восьмеричную:
1) 856; 664; 5012; 6435; 78; 2) 214; 89; 998; 653; 111.
Л) 25
Перевести десятичные дроби в двоичную систему счисления. В двоичной записи числа сохранить шесть знаков. 1) 0,654; 0,321; 0,6135; 0,9876; 2) 0,555; 0,333; 0,1213; 0,453.
.М2 26
Перевести десятичные дроби в шестнадцатеричную систему счисления. В новой записи дроби сохранить шесть знаков.
1) 0,745; 0,101; 0,8453; 0,3451;
2) 0,8455; 0,225; 0,1234; 0,455.
Перевести смешанные десятичные числа в троичную и пятеричную системы счисления, оставив пять знаков в дробной части нового числа:
1) 40,5; 34,25; 124,44;
2) 78,333; 225,52; 90,99.
Перевести смешанные десятичные числа в двоичную и восьмеричную системы счисления, оставив пять знаков в дробной части нового числа:
1) 21,5; 432,54; 678,333; 2) 12,25; 97,444; 7896,2.
ЛЕ 29 Перевести из десятичной системы счисления следующие чис-
ла:
2) 675 -» Ан, 0,333 Аз, 23,15 -» А5.
![]()
.М2 зо Перевести из десятичной системы счисления следующие числа:
1) 1 , 25 А 16 , 675 0,355 А4 ;
2) 890 -» Аб, 0,675 -» АО 12,35 -» А?.
![]() 31
Перевести из десятичной системы счисления следующие числа:
31
Перевести из десятичной системы счисления следующие числа:
1) 425 Аб , 0,425 ![]() 98,45 Аз; 2) 0,55 Ау 765 -»
Аз, 765,75 -» Щ.
98,45 Аз; 2) 0,55 Ау 765 -»
Аз, 765,75 -» Щ.
![]() 32
Перевести из десятичной системы счисления следующие числа:
32
Перевести из десятичной системы счисления следующие числа:
2) 0,755 -» Аб , 907 -» Аб, 566,225 А16.
1.5.3. Системы счисления, используемые в компьютере (с основанием 2”)
![]() Для того чтобы целое
двоичное число записать в системе счисления с основанием q = 2 п (4,
8, 16 и т. д.), нужно:
Для того чтобы целое
двоичное число записать в системе счисления с основанием q = 2 п (4,
8, 16 и т. д.), нужно:
1) данное двоичное число разбить справа налево на группы по п цифр в каждой;
2) если в последней левой группе окажется меньше п разрядов, то ее надо дополнить слева нулями до нужного числа разрядов;
З) рассмотреть каждую группу как п-разрядное двоичное число и записать его соответствующей цифрой в системе счисления с основанием q = 2 п .
Для того чтобы дробное двоичное число записать в системе счисления с основанием q = 2 п , нужно:
1) данное двоичное число разбить слева направо на группы по п цифр в каждой;
2) если в последней правой группе окажется меньше п разрядов, то ее надо дополнить справа нулями до нужного числа разрядов;
З) рассмотреть каждую группу как п-разрядное двоичное число и записать его соответствующей цифрой в системе счисления с основанием q = 2 п .
Для того чтобы смешанное двоичное число записать в системе счисления с основанием q = 2 п , нужно:
1) целую и дробную части данного двоичного числа начиная от запятой разбить на группы по п цифр в каждой;
![]()
2) если в последних правой и левой группах окажется меньше п разрядов, то их надо дополнить соответственно справа и слева нулями до нужного числа разрядов;
З) рассмотреть каждую группу как п-разрядное двоичное число и записать его соответствующей цифрой в системе счисления с основанием q = 2 п .
Для того чтобы произвольное число, записанное в системе счисления с основанием q = 2 п , перевести в двоичную систему счисления, нужно каждую цифру этого числа заменить ее п-разрядным эквивалентом в двоичной системе счисления.
Применительно к компьютерной информации часто используются системы с основанием 8 (восьмеричная) и 16 (шестнадцатеричная).
Пример 5. Перевести число 15FC16 в
двоичную систему. ![]() Для решения задачи воспользуемся
приведенной ниже двоично-шестнадцатеричной таблицей:
Для решения задачи воспользуемся
приведенной ниже двоично-шестнадцатеричной таблицей:
Двоично-шестнадцатеричная таблица
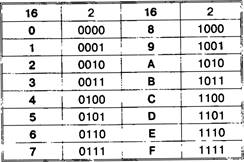
В одном столбце таблицы помещены шестнадцатеричные цифры, напротив, в соседнем столбце — равные им двоичные числа. Причем все двоичные числа записаны в четырехзначном виде (там, где знаков меньше четырех, слева добавлены нули).
А теперь проделаем следующее: каждую цифру в шестнадцатеричном числе 15FC заменим на соответствующую ей в таблице четверку двоичных знаков. Иначе говоря, перекодируем число 15FC по таблице в двоичную форму. Получается:
![]()
Если отбросить нули слева (в любой системе счисления они не влияют на значение целого числа), то получим искомое двоичное число. Таким образом:
![]()
В справедливости этого равенства можно убедиться, произведя тот же перевод через десятичную систему.
38
![]()
![]()
Решение. Разделим данное число на группы по четыре цифры, начиная справа. Так как в крайней левой группе меньше четырех цифр, дополним ее нулями:
![]()
А теперь, глядя на двоично-шестнадцатеричную таблицу,
заменим каждую двоичную группу на соответствующую шестнадцатеричную цифру.
Следовательно:
![]() - 37AEF
- 37AEF ![]()
![]() Пример 7. Перевести
смешанное число 1011101, 101112 в шестнадцатеричную систему.
Пример 7. Перевести
смешанное число 1011101, 101112 в шестнадцатеричную систему.
Решение. Перевод дробных чисел производится аналогично. Группы по четыре двоичных знака выделяются от запятой как влево так и вправо. Поэтому:
1011101,101112
0101 1101, 1011 1000 5D,B8 ![]()
Связь между двоичной и восьмеричной системами устанавливается аналогично. В этом случае используется двоичновосьмеричная таблица, приведенная ниже. Каждой восьмеричной цифре соответствует тройка двоичных цифр.
Двоично-восьмеричная таблица
|
8 |
2 |
|
|
000 |
|
1 |
001 010 |
|
2 |
|
|
з |
011 |
|
4 |
100 |
|
5 |
101 110 111 |
|
|
![]() Пример 8. Перевести
смешанное число 1011101,101112 в восьмеричную систему.
Пример 8. Перевести
смешанное число 1011101,101112 в восьмеричную систему.
Решение. Группы по три двоичных знака выделяются от запятой как влево так и вправо. Затем производится перекодировка по таблице:
1011101,101112 001 011 101, 101 110 135,568.
.М 33
Перевести двоичные числа в восьмеричную систему счисления:

Перевести двоичные числа в шестнадцатеричную систему счисления:
![]()
.М 35
Перевести смешанные двоичные числа в восьмеричную и шестнадцатеричную системы:
![]()
Перевести восьмеричные числа в двоичную систему счисления:
1) 256; 0,345; 24,025; 0,25;
2) 657; 76,025; 0,344; 345,77.
.М 37
Перевести шестнадцатеричные числа в двоичную систему счисления:
1) 1АС7•, 0,01; 2F,D8C•, FOC,FF•,
2) FACC; O,FFD; FDA,12F; DDFF,A.
Перевести числа из шестнадцатеричной системы счисления в восьмеричную:
1) А45; 24A,9F; 0,FDD5; F12,0457; 2) A24,F9; 54А; 0,DFD3; 20,567.
Л! 39
Перевести числа из восьмеричной системы счисления в шестнадцатеричную:
1) 774; 765,25; 0,5432; 654,763; 2) 665; 546,76; 0,7654; 432,347.
Перевести из одной указанной системы счисления в другую следующие числа:
1) 2316 -» „кг; 23,458 -» „кг;
1010,00111012 -» „кв; 1010,00111012 -» Х16,
![]()
2) АС116 -» Х8', 1010108 Щ;
1010102 -» х8; 23,5618 -» х 16.
Перевести следующие числа:
1) 10101,012 х8; 10101,018 х
10101,0116 -» х8; 10101,018 х
2) 11001,112 -» х8; 11001,118 — х
11001,1116 х8; 11001,118 х
Перевести следующие числа:
1) АВС,1А16 Х8; АВС,1А16 -» ь;
2) 123,568 -» х16; 123,568 щ;
3) 101011,1012 х8; 101011,1012 -» х 16', 4) 456,78 -» 456,716 х8.
Опишите четверичную систему. Постройте двоично-четверичную таблицу.
Перевести следующие числа:
2) 234 -» щ; 31,34 щ; 110011012+ х4; 111,1012 х4.
Перевести следующие числа:
1) 131,214 ха; 2348 -» х4; 321,124 А1В,Е16 х4;
2) 331,114 Ч; 3648 х4; 111,224 -» х16; 1А1,1Е16 -» х4.
1.5.4. Арифметика в позиционных системах счисления
![]() Любая позиционная
система счисления определяется основанием системы, алфавитом и правилами
выполнения арифметических операций. В основе правил арифметики лежат таблицы
сложения и умножения однозначных чисел. Например, таблицы сложения и умножения
в пятеричной системе счисления выглядят так:
Любая позиционная
система счисления определяется основанием системы, алфавитом и правилами
выполнения арифметических операций. В основе правил арифметики лежат таблицы
сложения и умножения однозначных чисел. Например, таблицы сложения и умножения
в пятеричной системе счисления выглядят так:
Пятеричная таблица сложения Пятеричная таблица умножения
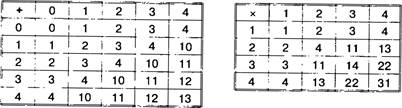
![]()
Пользуясь этими таблицами, можно выполнять арифметические операции с многозначными числами.
![]() Пример
9 342
Пример
9 342
23
Рассуждаем так: два плюс три равно 10 (по таблице); О пишем, 1 — в уме. Четыре плюс два равно 11 (по таблице), да еще один, — 12; 2 пишем, 1 — в уме. Три да один равно 4 (по таблице). Получаем в результате 420.
![]() Пример
10 213
Пример
10 213
х
з
Рассуждаем так: трижды три 14 (по таблице); 4 пишем, 1 — в уме. Один на три дает З, да плюс один, — пишем 4. Дважды три по таблице 11; 1 — пишем, 1 — переносим влево. Окончательный результат — 1144.
![]()
Л) 46
Составьте таблицы сложения и умножения в троичной системе счисления и выполните вычисления:
1)
12 + 22; 2) 221 - 11;![]()
Л) 47
Составьте таблицы сложения и умножения в двоичной системе счисления и выполните вычисления:
1) 1110 + 101; 2) 10101 - 11; 3) 101 • 11; 4) 1110 : 10.
Составьте таблицу сложения в восьмеричной системе счисления и выполните вычисления: 1) 3456 + 245; 2) 7631 - 456;
3) 77771 + 234; 4) 77777 - 237.
Л) 49
Составьте таблицу сложения в шестнадцатеричной системе счисления и выполните вычисления: 1) FFFF + 1; 2) 1996 + ВАВА; 3) ВОА - ВАС; 4) 1998 - A1F.
Л) 50
Вычислить выражения:
1) 101012 1012; 2) AFF116 - 19D16,
3)
1405 : 4) 1212113 + 221 з![]()
42
![]()
Может ли быть верным равенство 7 + 8 = 16?
![]() 52
52
Найти наименьшее основание системы счисления р и цифры т и п, если верно равенство:
ззт5п + 2п443 55424.
Пример выполнен в системе счисления с основанием р, т ![]() максимальная
цифра в этой системе.
максимальная
цифра в этой системе.
Найти основание системы счисления, в которой справедливо данное равенство; определить неизвестные цифры, отмеченные звездочками.
![]() +
* 235* 116678.
+
* 235* 116678.
.N2 54
Ей было 1100 лет.
Она в 101 класс ходила.
В портфеле по 100 книг носила.
Все это правда, а не бред.
Когда пыля десятком ног,
Она шагала по дороге,
За ней всегда бежал щенок
С одним хвостом, зато 100-ногий,
Она ловила каждый звук
Своими 10-ю ушами,
И 10 загорелых рук
Портфель и поводок держали.
И 10 темно-синих глаз
Оглядывали мир привычно.
Но станет все совсем обычным,
Когда поймете наш рассказ,
А. Стариков. «Странная девочка»
Чем объяснить противоречия в числах этого стихотворения? ЛЬ 55
В саду 100 фруктовых деревьев — 14 яблонь и 42 груши. В какой системе счисления посчитаны деревья?
Загадочная автобиография. В бумагах одного чудака математика найдена была его автобиография. Она начиналась следующими удивительными словами:
«Я окончил курс университета 44 лет от роду. Спустя год, 100-летним молодым человеком, я женился на 34-летней девушке. Незначительная разница в возрасте — всего 11 лет — способствовала тому, что мы жили общими интересами и мечтами. Спустя немного лет у меня была уже и маленькая семья
![]()
из 10 детей. Жалованья я получал в месяц всего 200 рублей, из которых 1/10 приходилось отдавать сестре, так что мы с детьми жили на 130 руб. в месяц» и т. д. Чем объяснить противоречия в числах этого отрывка?
Л) 57
В какой системе счисления выполнено следующее сложение?
756
307
2456
24
3767
.М2 58
В какой системе счисления выполнено умножение? 213 • з - 1144.
В какой системе счисления выполнено деление? 4415400 : 4532 - 543
![]()
34100
31412
22440
22440
Известно правило: чтобы перевести число из двоичной системы счисления в восьмеричную, нужно сгруппировать подряд по три цифры, считая от запятой, отделяющей целую часть от дробной, и отдельно перевести двоичные числа, полученные из цифр каждой группы, в восьмеричные числа, каждое из которых выражается только одной восьмеричной цифрой. Записанные в том же порядке эти восьмеричные цифры образуют искомую восьмеричную запись числа. Можно ли сформулировать похожее правило для перевода чисел из троичной системы в систему счисления с основанием 9?
Л) 61
Сумму восьмеричных чисел
17 + 1700 + 170000 + . . . + 1700 000 000 перевели в шестнадцатеричную систему счисления. Найдите в записи числа, равного этой сумме, пятую цифру слева.
Записать наибольшее и наименьшее п-разрядные числа, представимые в системе счисления с основанием р и перевести эти числа в десятичную систему:
а) п = 2, р — 2; б) п = З, р = 8; в) п — 4, р = 16.
44
![]()
1.6.1. Высказывания
![]() Высказывание
(суждение) это повествовательное предложение, в котором что-либо утверждается
или отрицается. По поводу любого высказывания можно сказать, истинно оно или
ложно.
Высказывание
(суждение) это повествовательное предложение, в котором что-либо утверждается
или отрицается. По поводу любого высказывания можно сказать, истинно оно или
ложно.
Высказывания бывают общими, частными или единичными. Общее высказывание начинается (или можно начать) со слов: все, всякий, каждый, ни один. Частное высказывание начинается (или можно начать) со слов: некоторые, большинство и т. п. Во всех других случаях высказывание является единичным.
![]() Пример 1. Определить
значения истинности для следую
Пример 1. Определить
значения истинности для следую![]() щих высказываний.
щих высказываний.
«Лед — твердое состояние Ответ: истинное воды» • высказывание. «Треугольник — это Ответ: истинное геометрическая фигура» . высказывание.
«Париж — столица Китая» . Ответ: ложное высказывание.
![]() Пример 2. Определить тип высказывания
(общее, част
Пример 2. Определить тип высказывания
(общее, част![]() ное, единичное).
ное, единичное).
«Все рыбы умеют плавать» . Ответ: общее высказывание. «Некоторые медведи — Ответ: частное бурые» . высказывание . «Буква А — гласная» . Ответ: единичное высказывание .
![]()
Какие из следующих предложений являются высказываниями? Определите их истинность.
1. Число 6 четное.
2. Посмотрите на доску.
З. Все роботы являются машинами.
4. У каждой лошади есть хвост.
5. Внимание!
6. Кто отсутствует?
7. Есть кошки, которые дружат с собаками.
8. Не все то золото, что блестит.
![]()
10. Некоторые люди являются художниками.
11, Выразите 1 час 15 минут в минутах.
12. Всякий моряк умеет плавать.
Какие из следующих предложений являются высказываниями? Определите их истинность.
1. Наполеон был французским императором.
2. Чему равно расстояние от Земли до Марса? З. Внимание! Посмотрите направо.
4. Электрон элементарная частица.
5. Не нарушайте правил дорожного движения!
6. Полярная Звезда находится в созвездии Малой Медведицы.
Какие из приведенных высказываний являются общими?
1. Не все книги содержат полезную информацию.
2. Кошка является домашним животным. З. Все солдаты храбрые.
4. Ни один внимательный человек не совершит оплошность.
5. Некоторые ученики двоечники.
6.
7. Мой кот страшный забияка.
8. Любой неразумный человек ходит на руках.
Какие из приведенных высказываний являются частными?
1. Некоторые мои друзья собирают марки.
2. Все лекарства неприятны на вкус. З. Некоторые лекарства приятны на вкус.
4. А — первая буква в алфавите.
5. Некоторые медведи — бурые.
6. Тигр хищное животное.
7. У некоторых змей нет ядовитых зубов.
8. Многие растения обладают целебными свойствами.
9. Все металлы проводят тепло.
Определите истинность высказываний.
1. Все ребята умеют плавать.
2. Киев — столица Украины. З. Некоторые кошки не любят рыбу.
4. Человек все может.
5. Невозможно создать вечный двигатель.
6. Каждый человек — художник.
7. Прямоугольник есть геометрическая фигура.
8. Некоторые рыбы хищники.
1.6.2. Логические величины, операции, выражения
![]() Логические величины —
это понятия, выражаемые словами: ИСТИНА, ЛОЖЬ (true, false). Следовательно,
истинность высказываний выражается через логические величины.
Логические величины —
это понятия, выражаемые словами: ИСТИНА, ЛОЖЬ (true, false). Следовательно,
истинность высказываний выражается через логические величины.
Логическая константа: ИСТИНА или ЛОЖЬ.
Логическая переменная: символически обозначенная логическая величина. Следовательно, если известно, что А,В,Х,У и пр. — переменные логические величины, то это значит, что они могут принимать значения только ИСТИНА или ЛОЖЬ.
Логическое выражение — простое или сложное высказывание. Сложное высказывание строится из простых с помощью логических операций (связок).
Логические операции
![]()
Дизъюнкция (логическое сложение). В русском языке этой связке соответствуют союз ИЛИ. В математической логике она обозначается знаком v. Дизъюнкция — двухместная операция; записывается в виде: А v В. Значение такого выражения будет ИСТИНА, если значение хотя бы одного из операндов истинно.
Отрицание. В русском языке этой связке соответствует частица НЕ (в некоторых высказываниях применяется оборот «неверно, что... Отрицание — унарная (одноместная) операция; записывается в виде: А или А.
Логическая формула (логическое выражение) — формула,
содержащая только логические величины и знаки логических операций. Результатом вычисления логической формулы является ИСТИНА или ЛОЖЬ.
![]() Пример З
Пример З
![]() А) Рассмотрим сложное
высказывание: «Число 6 делит
А) Рассмотрим сложное
высказывание: «Число 6 делит![]() ся на 2, и число 6 делится на З».
Представить данное высказывание в виде логической формулы.
ся на 2, и число 6 делится на З».
Представить данное высказывание в виде логической формулы.
Обозначта через А простое высказывание «число 6 делится на 2», а через В простое высказывание «число 6 делится на З». Тогда соответствующая логическая формула имеет вид: А & В. Очевидно, ее значение — ИСТИНА.
Б) Рассмотрим сложное высказывание: «Летом я поеду в деревню или в туристическую поездку» .
Обозначим через А простое высказывание «летом я поеду в деревню», а через В — простое высказывание «летом я поеду в туристическую поездку». Тогда логическая формула сложного высказывания имеет вид А х../ В.
В) Рассмотрим высказывание: «Неверно, что 4 делится на З».
Обозначим через А простое высказывание «4 делится на З». Тогда логическая формула отрицания этого высказывания имеет вид А.
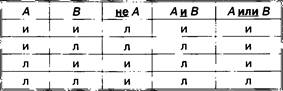
Последовательность выполнения операций в логических формулах определяется старшинством операций. В порядке убывания старшинства, логические операции расположены так: отрицание, конъюнкция, дизъюнкция. Кроме того, на порядок операции влияют скобки, которые можно использовать в логических формулах.
Например: (А и В) или (не А и В) или (не А и не В).
![]() Пример 4. Вычислить значение логической
формулы: не Х и У или Х и Z,
Пример 4. Вычислить значение логической
формулы: не Х и У или Х и Z,
если логические переменные имеют следующие значения: Х = ЛОЖЬ, У = ИСТИНА, Z - ИСТИНА.
Решение. Отметим цифрами сверху порядок выполнения операций в выражении: 1 2 4 з не Х и У или Х и Z.
Используя таблицу истинности, вычислим формулу по шагам:
1) не ЛОЖЬ - ИСТИНА; 2) ИСТИНА и ИСТИНА - ИСТИНА; 3) ЛОЖЬ и ИСТИНА - ЛОЖЬ; 4) ИСТИНА или ЛОЖЬ = ИСТИНА. Ответ: ИСТИНА.

Из двух простых высказываний постройте сложное высказывание, используя логические связки «И», «ИЛИ». Например:
|
|
Все ученики |
|
Все ученики изучают математику. |
изучают |
|
Все ученики изучают литературу. |
математику и |
литературу.
1. Марина старше Светы. Оля старше Светы.
2. Одна половина класса изучает английский язык. Вторая половина класса изучает немецкий язык.
З. В кабинете есть учебники. В кабинете есть справочники.
4. Слова в этом предложении начинаются на букву «Ч». Слова в этом предложении начинаются на букву «А» .
5. Часть туристов любит чай. Остальные туристы любят молоко.
6. Синий кубик меньше красного. Синий кубик меньше зеленого.
![]()
Определите значение истинности следующих высказываний:
1. Приставка — это часть слова, и она пишется раздельно со словом.
2. Суффикс — это часть слова, и он стоит после корня.
З. Родственные слова имеют общую часть, и они сходны по смыслу.
4. Рыбу ловят сачком или ловят крючком, или мухой приманивают, иль червячком.
5. Буква «а» — первая буква в слове «аист» или «сова».
6. Две прямые на плоскости параллельны или пересекаются.
7. Данное число четно или число, больше его на единицу, четно.
8. Луна планета или 2 + З = 5.
Используя логические операции, запишите высказывания, которые являются истинными при выполнении следующих условий:
1) неверно, что О < Х S З и У > 5;
2) Х является тах(Х, У);
З) Х не является min(X, У); 4) Z является min(X, У, а.
Используя логические операции, запишите высказывания, которые являются истинными при выполнении следующих условий:
1) У не является тах(Х, У, Z) и не является min(X, У, Z);
2) Х, У, Z равны между собой;
З) каждое из чисел Х, У, Z положительно; 4) каждое из чисел Х, У, Z отрицательно.
.М2 10
Используя логические операции, запишите высказывания, которые являются истинными при выполнении следующих условий:
1) хотя бы одно из чисел Х, У, Z положительно;
2) хотя бы одно из чисел Х, У, Z отрицательно;
З) хотя бы одно из чисел Х, У, Z не является положительным; 4) только одно из чисел Х, У, Z является отрицательным.
1) только одно из чисел Х, У, Z больше 10;
2) только одно из чисел Х, У, Z не больше 10; З) ни одно из чисел Х, У, Z не равно 104; 4) каждое из чисел Х, У, Z равно О.
.М2 12
Записать логические выражения (формулы), истинные при соблюдении следующих условий:
1) точка с координатами Х, У принадлежит первой четверти единичного круга с центром в начале координат;
2) точка с координатами Х, У не принадлежит единичному кругу с центром в начале координат и принадлежит кругу радиусом 2 и с центром в начале координат (изобразите это графически).
Сформулируйте высказывания на обычном языке для следующих логических выражений:
1) (Х > О и Х < 1) или (Х < 10 и Х > 5);
![]()
![]()
Сформулируйте высказывания на обычном языке для следующих логических выражений:
1) (Х = 12) и (У - 12) и (Z = 12);
2) (Х < 0) и (У > 0) или (У < 0) и (Х > 0);
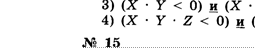
Определите значение логического выражения не (Х > Z) и не
![]()
(Х - У), если:
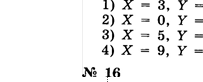
Определите значения логических переменных А, В, С, D, если:
1) А и (Марс — планета) — истинное высказывание;
2) В и (Марс — планета) — ложное высказывание;
З) С или (Солнце — спутник Земли) — истинное высказывание;
4) D или (Солнце — спутник Земли) — ложное высказывание.
Определите значения логических переменных А, В, С, D, если:
1) А или (1 литр молока дороже 1 кг сливочного масла) — истинно;
2) В и (1 литр молока дороже 1 кг сливочного масла) — ложно;
З) С или (масло дороже творога) — истинно; 4) D и (масло дороже творога) — ложно.
Пусть А = «эта ночь звездная», а В = «эта ночь холодная». Выразите следующие формулы на обычном языке:
|
2) А и не В; З) не А и не В; |
5) А и не В; 6) не А и не В. |
![]()
![]() 4)
не А или В;
4)
не А или В;
1.6.3. Логические схемы и логические выражения
Удобным способом представления
логических выражений являются логические схемы. Вот как изображают![]() ся
на таких схемах три основные логические операции:
ся
на таких схемах три основные логические операции:
Схематическое изображение логических операций
|
Конъюнкция |
Дизъюнкция |
Отрицание |
|
|
|
|
В этой таблице использованы следующие обозначения:
1 — ИСТИНА; о — ложь;
![]() логические операции
логические операции
Цифры в начале входящих стрелок — логические операнды; цифры в конце выходящих стрелок — результаты операций.
Данная таблица — та же таблица истинности, только представленная в форме логических схем. В такой форме удобно изображать цепочки логических операций и производить их вычисления.
![]() Пример 5. Для вычисления логического
выражения:
Пример 5. Для вычисления логического
выражения:
1 или О и 1 нарисовать схему, отражающую последовательность выполнения логических операций. По схеме вычислить значение логического выражения.
Решение
|
|
|
Здесь наглядно отражено то, что первой выполняется операция и, затем или. Теперь в порядке слева-направо припишем к выходящим стрелкам результаты операций:
|
или |
|
![]() 1
1
В результате получилась 1, т. е. «ИСТИНА».
Пример 6. Дано
выражение: не (1 и (О или 1) и 1). ![]() Вычислить значение
выражения с помощью логической схемы.
Вычислить значение
выражения с помощью логической схемы.
Решение. Логическая схема с результатами вычислений выглядит так:
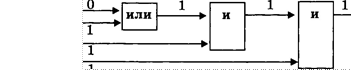
![]()
Пусть А, В, С — логические величины, которые имеют следующие значения: А = ИСТИНА, В = ЛОЖЬ, С = ИСТИНА. Нарисуйте логические схемы для следующих логических выражений и вычислите их значения:
![]() 4) А и В или С; 7) (А или В)
и (С или В);
4) А и В или С; 7) (А или В)
и (С или В);
![]() 20
20
Построить логические схемы по логическим выражениям:
1) .х1 и (не .х2 или хз);
2) х 1 и .х2 или не .х1 и хз;
З) х 4 и (х1 и .х2 и хз или не .х2 и не хз).
ЛЕ 21
Выполните вычисления по логическим схемам. Запишите соответствующие логические выражения:
1) 2)
|
или |
|
|
|
и |
|
|
или |
1
1 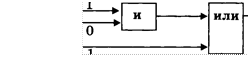
![]() 22
22
Дана логическая схема. Построить логическое выражение, соответствующее этой схеме. Вычислить значение выражения для:
![]()
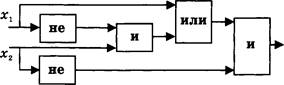
Упростить полученное в задаче № 22 выражение и построить для него новую логическую схему.
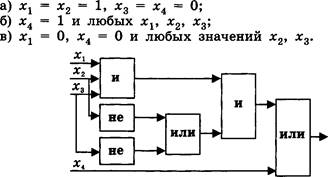
Упростить полученное в задаче № 24 логическое выражение и построить для него новую логическую схему.
Дана логическая схема. Построить соответствующее ей логическое выражение.
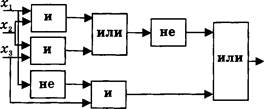
Вычислить значение выражения для:
![]() 1 и любых значений .х2
1 и любых значений .х2
![]()
ЛЕ 27
Упростить полученное в задаче № 26 логическое выражение и построить для него новую логическую схему.
1.6.4. Импликация и эквивалентность
![]() Импликация
(условное высказывание). В русском языке этой логической операции соответствуют
союзы если то; когда ..., тогда; коль скоро..., то и т. п. Выражение,
начинающееся после союзов если, когда, коль скоро, называется основанием
условного высказывания. Выражение, стоящее после слов то, тогда, называется
следствием. В логических формулах операция импликации обозначается знаком -».
Импликация — двухместная операция; записывается в
Импликация
(условное высказывание). В русском языке этой логической операции соответствуют
союзы если то; когда ..., тогда; коль скоро..., то и т. п. Выражение,
начинающееся после союзов если, когда, коль скоро, называется основанием
условного высказывания. Выражение, стоящее после слов то, тогда, называется
следствием. В логических формулах операция импликации обозначается знаком -».
Импликация — двухместная операция; записывается в
![]()
Эквивалентность. Языковой аналог — союзы если и только если; тогда и только тогда, когда ... Эквивалентность обозначается знаком или е.
Пример 7
![]() А) Дано
сложное высказывание: «Если выглянет солнце,
А) Дано
сложное высказывание: «Если выглянет солнце, ![]() • то станет тепло».
Преобразовать к логической формуле.
• то станет тепло».
Преобразовать к логической формуле.
Б) Дано сложное высказывание: «Людоед голоден тогда и только тогда, когда он давно не ел». Преобразовать к логической формуле.
Решение. Обозначим через А простое высказывание «людоед голоден», а через В — «он давно не ел». Тогда логическая формула сложного высказывания имеет вид А В.
![]() Таблица истинности операций импликации
Таблица истинности операций импликации ![]() и
эквивалентности
и
эквивалентности
Порядок всех пяти логических операций по убыванию старшинства следующий: отрицание, конъюнкция, дизъюнкция, импликация, эквивалентность.
![]()
![]()
Решение. Для решения задачи построим таблицу истинности этой формулы, перебрав все варианты значений логических переменных А, В, С. Введем числовые обозначения для логических величин: 1 — ИСТИНА, О — ЛОЖЬ.
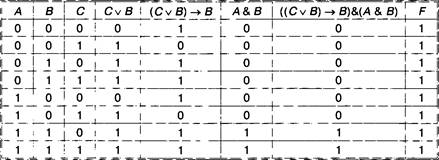
Ответ: формула является тождественно истинной.
![]()
Используя связку «ЕСЛИ... , ТО. » , измените высказывания.
Например: Человек, любящий животных, — Добрый. ![]()
Если человек любит животных, то он — Добрый.
1. Сделал дело — гуляй смело.
2. Знакомая дорога самая короткая. З. Тише едешь — дальше будешь.
4. Переходи улицу только на зеленый свет.
5. При встрече люди приветствуют друг друга.
6. В високосном году 366 дней.
7. Когда темнеет, зажигают фонари.
8. По стройке необходимо ходить в каске.
![]() 29
29
Могут ли быть истинными следующие высказывания?
1. Если солнце ярко светит, то на речку ты пойдешь.
2. Если утром тучи в небе, то к обеду будет дождь.
З. Если Костя — брат некто, то некто — брат Кости.
4. Если конь находится на поле СЗ, то поле Е2 находится под боем.
5. Если Х — сын или дочь У, то У — мать или отец Х.
6. Если он — ученый, то его сын — хороший ученик.
7. Если асфальт мокрый, то идет дождь.
8. Людоед голоден тогда и только тогда, когда он давно не ел.
.М2 зо
Запишите в виде логической формулы следующие высказывания:
1. Если Иванов здоров и богат, то он здоров.
2. Число является простым, если оно делится только на единицу и само на себя.
З. Если число делится на 4, оно делится на 2.
4. Произвольно взятое число либо делится на 2, либо делится на З.
5. Спортсмен подлежит дисквалификации, если он некорректно ведет себя по отношению к сопернику или судье, или если он принимал «допинг» .
Определить истинность формулы
![]()
![]()
Л) 33
Определить истинность формулы
![]()
1.6.5. Преобразование логических выражений
![]() Табличный способ
определения истинности сложного выражения имеет ограниченное применение, так
как при увеличении числа логических переменных приходится перебирать слишком
много вариантов. В таких случаях используют способ приведения формул к
нормальной форме. Формула имеет нормальную форму, если в ней используются
только знаки КОНъЮНКЦИИ, Дизъюнкции и отрицания, при этом знаки отрицания
находятся только при переменных, и Двойное отрицание отсутствует.
Табличный способ
определения истинности сложного выражения имеет ограниченное применение, так
как при увеличении числа логических переменных приходится перебирать слишком
много вариантов. В таких случаях используют способ приведения формул к
нормальной форме. Формула имеет нормальную форму, если в ней используются
только знаки КОНъЮНКЦИИ, Дизъюнкции и отрицания, при этом знаки отрицания
находятся только при переменных, и Двойное отрицание отсутствует.
Основные формулы преобразования логических выражений:
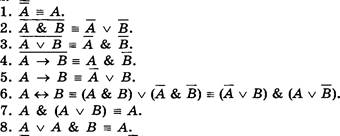

![]()
Решение

![]() Пример 10. Переведите
к виду логической формулы высказывание: «Неверно, что если погода пасмурная, то
дождь идет тогда и только тогда, когда нет ветра».
Пример 10. Переведите
к виду логической формулы высказывание: «Неверно, что если погода пасмурная, то
дождь идет тогда и только тогда, когда нет ветра».
Решение. Определим следующие простые высказывания:
П — «пасмурная погода»; Д — «идет дождь»; В — «дует ветер».
Тогда соответствующее логическое выражение запишется так:
![]()
Пример 11. Кто из
учеников А, В, С и D играет, а кто не ![]() играет в шахматы,
если известно следующее:
играет в шахматы,
если известно следующее:
а) если А или В играет, то С не играет;
б) если В не играет, то играют С и О,
в) С играет?
Решение. Определим следующие простые высказывания:
А «ученик А играет в шахматы»; В «ученик В играет в
шахматы»; ![]() «ученик С играет в шахматы»;
«ученик С играет в шахматы»;
D «ученик D играет в шахматы».
Запишем сложные высказывания, выражающие известные факты:
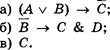
Запишем произведение указанных сложных высказываний:
![]()
Упростим эту формулу:
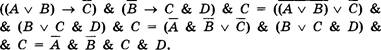
Отсюда А = О, В = О, С = 1, D = 1.
![]()
Упростите логические выражения, используя минимум законов преобразования:
![]()
![]()
Упростите логическую формулу и определите ее истинность:
![]()
Определите значения формул:
Заданы логические функции:
F1 = х1 8' х2 v х1 & хз v х2 8' хз и
F2 = (х1 8' х2 х2 8' хз v х1 8' хз) 8' (х1 8' х2 v х2 8' хз).
Необходимо упростить эти функции и проверить, являются ли они тождественными.
ОСНОВЫ
![]()
.М2 38
Переведите на язык логических выражений следующие высказывания:
1. Я поеду в Москву, и если встречу там друзей, то мы интересно проведем время.
2. Если будет солнечная погода, то ребята пойдут в лес, а если будет пасмурная погода, то ребята пойдут в кино.
З. Неверно, что если дует ветер, то солнце светит только тогда, когда нет дождя.
4. Если урок информатики будет интересным, то никто из школьников — Миша, Вика, Света — не будет смотреть в окно.
Определите, кто из подозреваемых участвовал в преступлении, если известно:
1) если Иванов не участвовал или Петров участвовал, то Сидоров участвовал;
2) если Иванов не участвовал, то Сидоров не участвовал.
Аня, Вика и Сергей решили пойти в кино. Учитель, хорошо знавший ребят, высказал предположения:
1) Аня пойдет в кино только тогда, когда пойдут Вика и Сергей;
2) Аня и Сергей пойдут в кино вместе или же оба останутся дома;
З) чтобы Сергей пошел в кино, необходимо, чтобы пошла Вика.
Когда ребята пошли в кино, оказалось, что учитель немного ошибся: из трех его утверждений истинными оказались только два. Кто из ребят пошел в кино?
.М2 41
На вопрос, какая завтра будет погода, синоптик ответил:
1) «если не будет ветра, то будет пасмурная погода без дождя» ;
2) «если будет дождь, то будет пасмурно и без ветра» ;
З) «если будет пасмурная погода, то будет дождь и не будет ветра» ,
Подумав немного, синоптик уточнил, что его три высказывания можно лаконично записать в виде одного составного высказывания. Сформулируйте его.
![]()
.М2 42
Виктор, Роман, Леонид и Сергей заняли на олимпиаде по физике четыре первых места. Когда их спросили о распределении мест, они дали три таких ответа: 1) Сергей — первый, Роман — второй;
2) Сергей — второй, Виктор — третий;
З) Леонид — второй, Виктор — четвертый.
Известно, что в каждом ответе только одно утверждение истинно. Как распределились места?
.М2 43
Меша, Боря и Гриша нашли в земле старинный сосуд. Рассматривая удивительную находку, каждый высказал по два предположения:
Алеша: «Это сосуд греческий и изготовлен в V веке».
Боря: «Это сосуд финикийский и изготовлен в III веке» .
Гриша: «Это сосуд не греческий и изготовлен в IV веке».
Учитель истории сказал ребятам, что каждый из них прав
только в одном из двух предположений. Где и в каком веке изготовлен сосуд?
.М2 44
В нарушении правил обмена валюты подозреваются четыре работника банка — А, В, С и D. Известно, что:
1. Если А нарушил, то и В нарушил правила обмена валюты.
2. Если В нарушил, то и С нарушил или А не нарушал.
З. Если D не нарушил, то А нарушил, а С не нарушал.
4. Если D нарушил, то и А нарушил.
Кто из подозреваемых нарушил правила обмена валюты?
Информационные моЭии:
системы и структуры Эаииых
![]()
2.1.1. Понятие «система»; системный эффект
![]() Объект — это то, о чем идет речь. Объектом может быть все,
что угодно: дом, если мы говорим о доме, звезды, если мы смотрим на звездное
небо, голод, если мы думаем о том, что проголодались.
Объект — это то, о чем идет речь. Объектом может быть все,
что угодно: дом, если мы говорим о доме, звезды, если мы смотрим на звездное
небо, голод, если мы думаем о том, что проголодались.
Системология это наука о системах.
Система — это целое, состоящее из частей, связанных между собой.
Примеры объектов, которые можно рассматривать в качестве систем: человек, дерево, дом, система обучения в школе (состоит из таких частей как школа, ученики, учителя, учебники и тетради, правила проведения уроков, школьные программы и многое другое), Солнечная система, книга, стол, науки математика, физика, химия и пр., человеческий язык.
Системы бывают материальные, нематериальные и смешанные. Примеры материальных систем: человек, дерево, дом. Примеры нематериальных: человеческий язык, математика. Пример смешанных — школьная система. Она включает в себя как материальные части (школьное здание, оборудование, портфели и учебники), так и нематериальные (расписание занятий, изучаемые темы и пр.).
Главное свойство любой системы — это возникновение системного эффекта или принцип эмерджентности. Заключается он в том, что при объединении частей в систему у системы появляются новые свойства, которыми не обладала ни оДна из частей в отдельности; при разрушении системы эти свойства пропадают. Другая формулировка принципа эмерджентности: целое — больше суммы своих частей.
Пример самолет. Главное его свойство способность к полету. Ни одна из составляющих его частей в отдельности (крылья, фюзеляж, двигатели и т. д.) этим свойством не обладает. Но если собрать их все вместе и соединить строго определенным способом, они полетят.
62 Раздел
![]()
Если теперь отнять у системы — у самолета — какую-нибудь часть, например, крыло, не только это крыло потеряет способность летать, но и вся система — весь самолет — тоже.
Еще одна замечательная иллюстрация принципа эмерджентности — мозаика. Набор составных частей мозаики — не более, чем груда кусочков картона. Однако соедините их строго определенным образом — и получите прекрасную картину.
![]()
Представьте себе перечисленные ниже объекты в виде системы взаимосвязанных частей и перечислите эти части: 1) гитара; 2) часы; З) шуба.
Представьте себе перечисленные ниже объекты в виде системы взамосвязанных частей и перечислите эти части: 1) веник; 2) велосипед; З) зубная щетка; 4) чайник.
Представьте себе перечисленные ниже объекты в виде системы взаимосвязанных частей и перечислите эти части:
1) телефон; 2) телевизор; З) телескоп; 4) конвейер на автозаводе.
Представьте себе перечисленные ниже объекты в виде системы взаимосвязанных частей и перечислите эти части:
1) пила; 2) железная дорога; З) библиотека; 4) больничная палата; 5) наука химия; 6) правила дорожного движения; 7) система счисления.
Какие из этих систем являются материальными, какие — нематериальными, какие — смешанными?
Придумайте 2—3 объекта и представьте их как части некоторой системы. Назовите эту систему. (Пример: брюки, пиджак — костюм; колеса, кузов, кабина — грузовик.)
Прочитайте условие задачи № 5, решите ее и ответьте на вопрос: в чем проявляется системный эффект (принцип эмерджентности) в придуманных вами системах?
Представьте себе школьную библиотеку как смешанную систему. Выделите в ней материальные и нематериальные части.
![]()
2.1.2. Среда. Вход и выход системы. Функции системы.
«Черный ящик»
![]() Всякая система представляет
собой некоторый объект, который можно выделить из окружающей среды.
Всякая система представляет
собой некоторый объект, который можно выделить из окружающей среды.
Система взаимодействует с окружающей средой: сре-
да оказывает влияние на систему, а
система — на среду. Воздействия среды на систему называют входами (или входом)
системы, а воздействия системы на среду — выходами (или выходом) системы. Здесь
«воздействие» понимается в самом широком смысле. Это могут быть материальные
объекты, которыми обмениваются среда и система, физическое воздействие,
информация. Например, автомат по продаже газет: на входе — монета, на выходе
газета; ручная мясорубка: на входе ![]() мясо и вращение ручки, на выходе — фарш;
сейф с кодовым замком: на входе — набор кода (информация), на выходе — доступ
внутрь.
мясо и вращение ручки, на выходе — фарш;
сейф с кодовым замком: на входе — набор кода (информация), на выходе — доступ
внутрь.
Для всякой системы можно перечислить множество входов и выходов, совсем не обязательно связанных с ее прямым назначением. Например, рассмотрим систему «ручные механические часы». Ее входы — это вращение верньера для завода часов и для перевода стрелок; но в то же время и пыль, грязь, вода, тряска, удары. Выходы — циферблат со стрелками, тиканье, вес, способ крепления на руке, способ изображения цифр на циферблате, точность хода и т. д. Для большинства реальных систем список входов/выходов бесконечен.
Когда система создается человеком, то она создается с определенной целью, для выполнения строго определенных действий. Пылесос собирает пыль, автомобиль перевозит людей и грузы, дом защищает от непогоды и врагов и т. д. Действие, которое выполняет система, называется функцией системы. Для искусственно созданной системы функция является ее главной характеристикой. Для примера рассмотрим систему «часы». Они могут быть ручные, настенные, настольные и башенные; механические, электронные, водяные, песочные, огневые, цветочные; с циферблатом и с табло; с арабскими цифрами, с римскими цифрами или вообще без цифр. Но все это часы. Почему? Потому что у них у всех одна общая функция: отмерять время.
Кроме главной функции система может иметь множество побочных. Например, автомобиль не только перевозит людей и грузы, но и сжигает топливо, вырабатывает выхлопные газы, может служить помещением для ночлега, освещает местность и т. д. Главная функция системы человеку всегда полезна (ради нее система и создается). Побочные функции могут быть как полезны, так и вредны или безразличны.
![]()
Подчеркнем, что понятия «цель системы» и «функция системы» применимы только к искусственным системам. Для естественных систем, созданных природой без участия человека, эти понятия бессмысленны.
Мы часто не знаем, как данный объект устроен «внутри». Нам важно лишь знать, к каким результатам на выходе приведут определенные воздействия на входе системы. В таких случаях говорят, что система рассматривается как «черный ящик » .
Представить некоторую систему в виде «черного ящика» — это значит указать ее входы и выходы, а также зависимости межДу ними. Такое описание позволяет целенаправленно использовать данную систему. Например, инструкции для пользователей сложной бытовой техники являются описаниями «черного ящика». В них объясняется, что нужно сделать на входе (включить, нажать, повернуть и пр.), чтобы достичь определенного результата на выходе (постирать белье, получить фруктовый сок, выполнить вычисления и пр.). Однако, что при этом происходит «внутри» не объясняется.
Для описания функционирования системы на формальном языке (математики, информатики) входы и выходы должны характеризоваться какими-то величинами. Чаще всего это числовые величины, но могут быть и символьные. Величины, характеризующие входы и выходы системы, называются параметрами. Например, в использованом выше примере с автоматом по продаже газет, в качестве входного параметра можно определить номинал монеты (например, 2 рубля). Но если учесть, что автомат сработает и при опускании в него любой металлической пластинки той же формы, размера и веса, что и двухрублевая монета, то в качестве входных параметров следует принять три числа: диаметр, толщину и вес пластинки.
Если входные и выходные параметры являются
числовыми величинами, то связь между ними может быть задана в виде
математической функции (формулы). Например, входные параметры: хр хг; выходной
— у. Связь между ними: у =![]()
![]()
Рассматривая каждый объект из перечисленных ниже как систему, выберите из списка подходящие входы и выходы. Укажите главную функцию системы и не менее 5 побочных функций.
Системы: 1) газовая плита; 2) электроплита; З) водопровод.
Рассматривая каждый из перечисленных ниже объектов как систему, выберите из списка и сопоставьте каждой системе подходящие входы и выходы (см. таблицу к задаче №8). Укажите главную функцию системы и не менее 5 побочных функций.
Системы: 1) утюг; 2) холодильник; З) механические часы.
Системы: 1) телевизор; 2) радиорепродуктор; З) транзисторный радиоприемник.
Рассматривая каждый из перечисленных ниже объектов как систему, выберите из списка и сопоставьте каждой системе
З Информатика и ИКТ. Т. I
подходящие входы и выходы (см. таблицу к задаче №8). Укажите главную функцию системы и не менее 5 побочных функций.
Системы: 1) магнитофон; 2) лазерный проигрыватель; З) граммофон.
В результате изучения работы «черного ящика» получен список соответствующих значений параметров на входе и на выходе. Определите, что делает система, т. е. по какому правилу значения входных параметров связаны с выходными. Попробуйте представить эту связь в виде математической функции (формулы).

![]() • Вход
• Вход
![]() Выход
Выход
В результате изучения работы «черного ящика» получен список соответствующих значений символьных параметров на входе и на выходе. Определите, что делает система, т. е. по какому правилу значения входных параметров связаны с выходными.
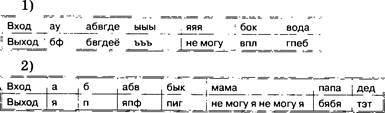

В результате изучения работы «черного ящика» получен список соответствующих значений числовых и символьных параметров на входе и на выходе. Определите, что делает система, т. е. по какому правилу значения входных параметров связаны с выходными.
![]()
![]() 4 2 з
4 2 з
вба ввв г бок
|
Вход ау Выход 1 |
абвгде ыыы яяя 666 б |
абв |
бва вба ввв 2 |
бок вода |
||
|
5 12 |
2 |
2l o |
2 |
|||
![]()
.М2 15
Известные вам системы (например: телевизор, радиоприемник, автомобиль, цветок, карандаш и т. д.) представьте в виде «черного ящика», т. е. укажите входы, выходы и связи между ними.
2.1.3. Состав и структура системы.
Информационная модель
![]() Составные части системы
называют компонентами. Компоненты бывают двух видов: элементы и подсистемы.
Элемент — это простейшая неделимая часть системы. Подсистема — это такая часть
системы, которая сама является системой. Какой компонент считать
Составные части системы
называют компонентами. Компоненты бывают двух видов: элементы и подсистемы.
Элемент — это простейшая неделимая часть системы. Подсистема — это такая часть
системы, которая сама является системой. Какой компонент считать
элементом, а какой подсистемой определяем мы сами, исходя из наших целей и возможностей. Например, при покупке компьютера его оперативную память можно рассматривать, как некую неделимую часть, предназначенную для хранения информации. Однако, если разбираться в вопросе о представлении в памяти различных типов данных, то приходится учитывать ее устройство (биты, байты).
Иногда слово «элемент» используют как синоним слова «компонент», т. е. называют элементами все составные части системы.
Состав системы — это перечень ее компонентов (составных частей).
Наряду с понятием «подсистема» существует понятие «надсистема». Надсистема — это система, частью которой является рассматриваемая нами система. Если система С1 является частью системы 02, то С1 для С2 — подсистема, а С2 для С1 — надсистема. Например, системный блок — компонент компьютера, процессор компонент системного блока. Это значит, что компьютер надсистема системного блока, а системный блок — подсистема компьютера. Системный блок — надсистема процессора, процессор подсистема системного блока.
Структура системы — это набор связей
(отношений) между компонентами системы. Связи могут быть любыми. Расположение
частей системы в пространстве определяется ОТНОШеНИями «над» / «под» , «левее»
/ «правее» , « впереди» / « позади » и т. п. Вложенность компонент отношениями
«состоит из» / «является частью». Подчиненность выражается отношениями
«начальник» / «подчиненный». Родственные связи ![]() отношениями «мать»,
«отец», «дочь», «сын», «сноха», «шурин» и т. д. При поступлении на работу
возникают отношения «работник» / «работодатель». При аренде помещения —
«арендатор»/«арендодатель». Последовательность событий описывается отношениями
«раньше» / «позже» / «одновременно». Алгоритм в зависимости от наличия или
отсутствия развилок и повторений будет иметь линейную, ветвящуюся или
циклическую структуру.
отношениями «мать»,
«отец», «дочь», «сын», «сноха», «шурин» и т. д. При поступлении на работу
возникают отношения «работник» / «работодатель». При аренде помещения —
«арендатор»/«арендодатель». Последовательность событий описывается отношениями
«раньше» / «позже» / «одновременно». Алгоритм в зависимости от наличия или
отсутствия развилок и повторений будет иметь линейную, ветвящуюся или
циклическую структуру.
Состав и структуру системы удобно описывать не словами (вербально), а специальными схемами — графами. Графам посвящен следующий раздел задачника.
Системный анализ — это процесс исследования объекта путем представления его в виде системы. Для проведения системного анализа необходимо:
1) определить главную функцию системы;
2)
четко определить границу системы, выделить ее из окруэкающей
среды (Например, пусть исследуемый объект ![]() это система городского
транспорта. Вопрос: входят ли в эту систему торговые павильоны, расположенные
на автобусных остановках?);
это система городского
транспорта. Вопрос: входят ли в эту систему торговые павильоны, расположенные
на автобусных остановках?);
З) определить входы/выходы системы, ее взаимосвязи с окруэкающей средой;
4) определить состав и структуру системы.
Информационная модель объекта — это его описание. Одному и тому же объекту можно поставить в соответствие разные информационные модели, все зависит от цели моделирования. Способы описания могут быть разными: вербальное (словесное), графическое, табличное, математическое и др.

Для каждого из объектов, перечисленных в задачах N2 8 ![]() 11,
проведите системный анализ. Какие из компонент следует считать элементами,
какие — подсистемами?
11,
проведите системный анализ. Какие из компонент следует считать элементами,
какие — подсистемами?
![]() 17
17
Выберите из данного списка элементы, входящие в состав сиСТеМЫ «Обед», если смотреть на нее с точки зрения мамы и с точки зрения сына.


Выберите из данного списка элементы системы «Фонтан», если смотреть на нее с точки зрения:
а) мальчишек, которые купаются в фонтане;
б) водопроводчика;
в) электрика;
г) архитектора.
1 бассейн 11 островок посреди
2 прожектора, бассейна освещающие фонтан 12 рубильник для
З вода в бассейне включения прожекторов
4 мостик над бассейном 1 13 • ласты
5 струи воды 14 сливные отверстия 6 трубы, подводящие 15 , насосы, качающие воду воду к фонтану 16 дерево на островке
7 бумажные кораблики 17 трубы, отводящие воду
8 украшения на бортиках от фонтана бассейна 18 рубильник для
9 ; электрические провода включения насосов
10 краны, перекрывающие 19 фигуры, из которых трубы бьют струи воды
.М 19
Попытайтесь провести анализ системы «Газета» и получить несколько вариантов информационных моделей с точки зрения разных людей:
а) читателя;
б) почтальона;
в) журналиста;
г) печатника;
д) уборщицы.
Элементы выберите из следующего списка:
|
и |
|
|
заго |
|
10 |
вод |
![]() 1 главный
редактор 11 стол журналиста печатный цех 12 рулоны бумаги з вес
газеты 13 стоимость газеты 4 кабинет главного 14 комната,
где стоит редактора стол журналиста
1 главный
редактор 11 стол журналиста печатный цех 12 рулоны бумаги з вес
газеты 13 стоимость газеты 4 кабинет главного 14 комната,
где стоит редактора стол журналиста
5 склад 15 директор типографии
6 начальник отдела, 16 компьютер, на котором в котором работает журналист готовит журналист хранит свои материалы
7 размер газеты 17 банки с краской
8
9 печатные машины (статей, фотографий, опроводловков и пр.).
![]() 20
20
Перечислите надсистемы для следующих систем:
1) дверной звонок;
2) переместительный закон умножения;
З) правила перехода улицы;
4) квартира;
5) колесо автомашины;
6) стрелка часов;
7) река;
8) Тихий океан;
9) планета Земля; 10) трамвай; 11) сердце.
![]() 21
21
Вы сами являетесь подсистемой многих надсистем и взаимодействуете с их элементами. Постарайтесь перечислить наибольшее число таких надсистем. Определите входы и выходы, через которые вы взаимодействуете с каждой надсистемой. Попробуйте описать (словами или схематически) структуру надсистемы и свое место в ней как элемента.
2.1.4. Систематизация
![]() Довольно
часто человеку приходится иметь дело с очень большими множествами объектов. Это
сложно. Для упрощения работы с большим количеством объектов был найден
следующий способ: все множество объектов надо поделить на несколько частей;
каждую из этих частей опять поделить на части; те, в свою очередь, еще раз; и
т. д. Таким образом можно очень быстро упростить ситуацию: свести большие
множества объектов к маленьким.
Довольно
часто человеку приходится иметь дело с очень большими множествами объектов. Это
сложно. Для упрощения работы с большим количеством объектов был найден
следующий способ: все множество объектов надо поделить на несколько частей;
каждую из этих частей опять поделить на части; те, в свою очередь, еще раз; и
т. д. Таким образом можно очень быстро упростить ситуацию: свести большие
множества объектов к маленьким.
Деление большого множества на подмножества удобно вести не беспорядочно, а по каким-то осмысленным признакам. Деление большого множества на подмножества объектов, имеющих общие признаки, называется классификацией. Подмножество объектов, имеющих общие признаки, называется классом. Признак, по которому один класс отличается от другого, называется основанием классификации.
Главное свойство системы возникновение системного эффекта — нового качества, которого не было у составных частей исходного набора. Какое же новое качество появляется в результате структурирования множества? Это свойство можно назвать обозримостью или познаваемостью. Разобраться в огромном неупорядоченном множестве объектов трудно или невозможно, а в систематизированном легко.
Классификацией (систематизацией) объектов каждый из нас занимается постоянно, когда разделяет одежду, посуду, книги и т. д., а внутри этих классов отделяет зимние пальто от летних платьев и костюмов, стаканы от кастрюль, учебники от сказок.
Систематизированы книги в библиотеке, экспонаты в музее, товары в магазине, поезда в расписании, дни в году.
Систематизация знаний — основа всех наук. Начало многих наук связано с именем великого древнегреческого ученого Аристотеля, который жил в 4 в. до н. э. Вместе со своими учениками Аристотель проделал колоссальную работу по классификации накопленных к тому времени знаний, разделил их на несколько частей и дал каждой свое название. Именно тогда появились на свет физика и биология, экономика и логика.
Другие известные научные классификации: систематизация математических знаний Евклидом (З в до н. э.), классификация живых существ Карлом Линнеем (1735 г.), классификация химических веществ Дмитрием Ивановичем Менделеевым (1869 г.), деление звездного неба на созвездия.
Последний пример интересен тем, по какому основанию проведена классификация звезд. Если в системах Евклида, Линнея, Менделеева деление объектов на классы проводилось по определенным существенным свойствам, то деление неба на участки-созвездия проводилось по признакам, которые к самим звездам явно не имели никакого отношения.
![]()
Повторите (хотя в неизмеримо меньшем масштабе) научный подвиг Аристотеля: систематизируйте перечисленные факты, разделите их по тем наукам, к которым они относятся.
![]()
2) «эки» «ши» пиши с буквой «и». З) Сосна хвойное дерево.
4)
5) Первый полет человека в космос состоялся в 1961 г.
6) Кит дышит легкими.
7) Многие болезни вызываются микробами.
8) Тела легче воды плавают.
9) Глагол выражает действие.
10) Серная кислота активно взаимодействует с металлами.
11) В банке можно получить кредит.
12) Курица несет яйца.
13) Остров Сицилия омывается Средиземным морем.
14) Яблоки — съедобны.
15) Экспорт — это вывоз товаров из страны.
16) Одноименные полюса магнита отталкиваются, разноименные притягиваются.
17) Реакция соединения с кислородом называется окислением.
18) Высочайшая вершина мира — Эверест (Джомолунгма).
19) Площадь прямоугольника равна произведению основания на высоту.
20) В арбузе есть семечки.
21) П Мировая война началась в 1939 г.
22) «Мама» существительное 1-го склонения. 23) Антарктида покрыта вечным льдом.
24) Чтобы предотвратить болезнь, делают прививки.
25) Для того чтобы подсчитать пройденный путь, надо скорость умножить на время.
26) Лев хищник.
27) Инфляция (т. е. обесценивание денег) ведет к росту цен.
28) В одной молекуле бензола 6 атомов углерода и 6 атомов водорода.
![]()
29) ![]() — а 2
— а 2![]()
30) Апельсин покрыт коркой.
31) Вода замерзает при температуре ноль градусов.
32) Из Тихого океана в Северный Ледовитый можно проплыть через Берингов пролив.
![]() При простуде помогает молоко с медом.
При простуде помогает молоко с медом.
34) Чем больше сжата пружина, тем сильнее она давит.
35) Птицы летают.
36) У розы есть шипы.
37) Для остановки кровотечения накладывают жгут.
38) Предприятие, которое не в состоянии заплатить свои долги, объявляется банкротом.
39) Числа, кратные 5, кончаются либо цифрой 5, либо цифрой О.
40)
41 ) Антибиотики сильные лекарства, применять которые надо очень осторожно.
42) Цена товара зависит от спроса и предложения.
43) Столицей древнерусского государства был город Киев.
44) В сложных словах используются соединительные гласные «о» и «е».
![]() Формула воды — Н2О.
Формула воды — Н2О.
46) Сумма внутренних углов треугольника 180 градусов.
47) В Грюнвальдской битве вместе сражались польские, литовские, русские, чешские и татарские полки.
48) Прилагательные бывают трех родов: мужского, женского и среднего.
49) Инертные газы не вступают в реакции с другими веществами.
50) У слона есть хобот.
Г.Г2 23
Сегодня зоологам известны около 2 млн видов различных животных. Разобраться в таком огромном множестве было бы невозможно, если бы не систематизация. В 1735 г. двадцативосьмилетний шведский биолог Карл Линней опубликовал книгу под названием «Система природы» в которой предложил свой способ классификации живых существ. Этот способ и сегодня является основой биологической классификации. Повторите, пожалуйста (хотя в неизмеримо меньшем масштабе), научный подвиг Линнея и систематизируйте перечисленные виды животных:
1) стрекоза; 26) мышь;
2) лиса; 27) оса;
З) лошадь; 28) крот;
4) тюлень; 29) пантера;
5) ерш; 30) корова;
6) гадюка; 31) горилла;
7) рысь; 32) кобра;
8) мартышка; 33) галка;
9) коза; 34) дельфин;
10) окунь; 35) гиена;
11)
уж![]() 36) буйвол;
36) буйвол;
12) синица; 37) питон;
13) волк; 38) ворон;
14)
16) кит; 41 ) ;
17) орел; 42) лев;
18) овца; 43) хомяк;
19) собака; 44) шимпанзе;
20) муравей; 45) комар;
21) кашалот; 46) плотва;
22) орангутан; 47) тигр;
23) щука; 48) гюрза;
24) кошка; 49) воробей; 25) жаба; 50) касатка.
![]() 24
24
Сегодня ботаникам известны более 500 тыс. видов различных растений. Разобраться в них помогает классификация, основы которой были заложены Карлом Линнеем. Повторите (хотя в неизмеримо меньшем масштабе) научный подвиг Линнея и систематизируйте перечисленные виды растений:
|
1) ель; |
9) лиственница; |
|
2) крыжовник; |
10) акация; |
|
З) ромашка; |
11) помидор; |
|
4) арбуз; |
12) подорожник; |
|
5) рожь; |
13) ячмень; |
|
6) дуб; |
14) картофель; |
|
7) репа; |
15) лимон; |
|
8) апельсин; |
16) малина; |
17) василек; 29) груша;
18) морковь; 30) кедр;
19) овес; 31) береза;
20) персик; 32) тыква;
21) кабачок; 33) смородина;
22) пихта; можжевельник;
23) грейпфрут; 35) огурец;
24 ) яблоня; 36) крапива;
25) пшеница; 37) свекла;
26) липа; 38) сосна; 27) дыня; 39) одуванчик; 28) мандарин; кукуруза.
![]() 25
25
В каждом пункте перечислены объекты, сгруппированные по классам. Например: стол, компьютер, лук / корова, ручка, кастрюля / село, знамя, перо — существительные, классифицированы по родам. Определить основания классификаций.
1) лев, лиса, заяц, еж / дуб, береза, клен, сосна;
2) волк, медведь, лиса, лось / корова, собака, кошка, лошадь;
4) рожь, тишь, ложь, рысь / пшеница, тишина, истина, кошка;
5) суп, щи, борщ, окрошка / котлеты, биточки, бифштекс, ростбиф;
6) рубашка, пиджак, платье, сарафан / сапоги, ботинки, калоши, валенки;
7) рубашка, пиджак, платье, сарафан / пальто, шуба, плащ, штормовка;
8) тарелка, нож, вилка, кастрюля / молоток, пила, гвоздь, плоскогубцы;
9) картофель, лук, огурцы, помидоры / яблоки, апельсины, груши, мандарины;
10) ель, сосна, кедр, пихта / береза, осина, липа, тополь;
11) килограмм, метр, минута, вольт / вес, длина, время, напряжение;
12) крот, комбайн, компьютер, кошка / мышь, мошка, молоток, мякоть.
![]() 26
26

Л) 27
Найдите лишнее слово в каждом из данных списков. Обоснуйте свой выбор. Ответы могут быть различны, но должны быть доказательны с точки зрения классификации:
1) дряхлый, старый, изношенный, маленький, ветхий;
2) смелый, храбрый, отважный, злой, решительный;
З) Вася, Федя, Коля, Оля, Саша;
4) колесо, телега, колокол, колодец, колбаса;
5) молоко, сливки, сыр, сало, сметана;
6) молчать, кричать, танцевать, рассказывать, шептать;
7) глубокий, высокий, светлый, низкий, мелкий;
8) дом, сарай, изба, хижина, мазанка;
9) длина, метр, килограмм, секунда, километр;
10) береза, сосна, дерево, дуб, ель;
11) канарейка, каблук, кабина, кабинет, кабан;
12) ненавидеть, презирать, возмущаться, негодовать, наказывать;
13) лопата, молоток, ботинок, грабли, стамеска;
14) гнездо, нора, муравейник, курятник, берлога;
15) молоток, гвоздь, топор, клещи, пила;
16) пилотка, берет, каска, шарф, шапка;
17) минута, секунда, час, вечер, сутки;
18) грабеж, кража, землетрясение, поджог, нападение;
19) длина, отрезок, круг, квадрат, треугольник;
20) кол, кот, нож, пол, кит;
21) Васильев, Федоров, Иван, Петров, Семенов;
22) стена, дверь, окно, картина, потолок;
23) комар, стрекоза, муха, сова, муравей;
24) тарелка, чашка, стол, кастрюля, чайник;
25) идти, прыгать, танцевать, сидеть, бежать;
26) бокал, ваза, чашка, стакан, кружка;
27) декабрь, понедельник, март, май, август;
28) длина, метр, масса, объем, скорость;
29) приставка, предлог, суффикс, окончание, корень;
30) горький, горячий, кислый, соленый, сладкий;
31)
32) треугольник, отрезок, круг, квадрат, прямоугольник.
.М2 28
Найдите закономерность и продолжите последовательность.
1) 1 3 6 9 12 15 18 21 .
4) б в г д ж з .
5)
20 17 14 11 .![]()
6)
а в д ё з й л .![]()
7)
15 13 16 12 17 11
.![]()
8)
а о о о а о о о о
а о о о о о а о .![]()
9) 1 2 4 8 16. . .
10)
Анна Борис Виолетта Георгий Дарья .![]()
11) 1 2 3 5 7 11 13 17 .![]()
12)
бегемот тигр горилла акула аллигатор рысь сайгак .![]()
13) 1 1 2 3 5 8 13 .![]()
14) а б е в ё г и .![]()
15)
як кот мышь кошка лошадь бегемот динозавр![]()
2.2.1. Основные понятия: теоретическое введение
![]() Граф — это средство для наглядного представления состава и
структуры системы.
Граф — это средство для наглядного представления состава и
структуры системы.
Граф состоит из вершин, связанных Дугами или ребрами. Вершины могут быть изображены кругами, овалами, точками, прямоугольниками и пр. Связи между вершинами изображаются линиями. Если линия направленная (т. е. со стрелкой), то она называется Дугой, если не направленная (без стрелки), то ребром. Принято считать, что одно ребро заменяет две дуги, направленные в противоположные стороны. Граф, в котором все линии направленные, называется ориентированным графом. Две вершины, соединенные дугой или ребром, называются смежными.
В случае представления информации о составе и структуре системы в виде графа компоненты системы изображаются вершинами, а связи между ними — линиями (дугами или ребрами).
Графы используются во многих областях человеческой деятельности.
|
МОСКОВСКИЙ МЕТРОПОЛИТЕН
|
|
многим
схему линий метрополитена можно рас ![]() сматривать как граф (рис. 2.1). Вершинами
являются станции метро, линии отражают рельсовую связь между станциями. Никакой
другой информации, кроме структуры мегрополитена, схема-граф не
содержит.
сматривать как граф (рис. 2.1). Вершинами
являются станции метро, линии отражают рельсовую связь между станциями. Никакой
другой информации, кроме структуры мегрополитена, схема-граф не
содержит.
Пример
2 ![]() Этот пример относится к органической
химии. Известно, что свойства химических
Этот пример относится к органической
химии. Известно, что свойства химических ![]()
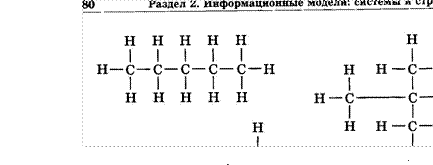
н—с—с— с—с—н
![]()
веществ, называемых углеводородами, зависят не только от того, из какого количества атомов углерода и водорода состоит молекула, но и от способа их соединения, т. е. от структуры молекулы. На рис. 2.2 изображена структура молекул трех разных веществ, состоящих из одинакового числа атомов углерода (С) и водорода (Н). Принятый в химии способ отображения структуры молекулы фактически является графом.
![]()
![]() Пример
З. Этот пример относится
Пример
З. Этот пример относится ![]() • к медицине.
• к медицине.
Как известно, у разных людей кровь отп пIII III
![]() личается по группе.
Всего групп крови четыре. В нормальных условиях номер группы роли не играет, а
вот при переливании играет, и весьма существенную. Дело в том, что не все
группы крови совместимы. Вливание человеку крови «не той» группы может иметь
весьма печальные последствия.
личается по группе.
Всего групп крови четыре. В нормальных условиях номер группы роли не играет, а
вот при переливании играет, и весьма существенную. Дело в том, что не все
группы крови совместимы. Вливание человеку крови «не той» группы может иметь
весьма печальные последствия.
Возможность переливания крови разных групп отражена на рис. 2.3. На этом графе соединяющие линии являются дугами (имеют стрелки). Глядя на рисунок, легко понять, что человек с первой группой крови может получить только кровь первой группы; человек со второй группой либо первой, либо второй; человек с третьей либо первой, либо третьей; и, наконец, человек с четвертой группой крови может получить кровь любой из четырех групп.
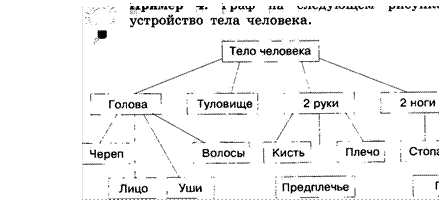 следующем
рисунке отражает
следующем
рисунке отражает
Рис. 2.4
Вес позволяет отобразить на графе не только структуру системы, но и различные свойства компонент и связей, КОЛИЧеСТвенные характеристики и пр.
![]() Пример 5. На рисунке
изображен взвешенный граф, представляющий информацию о дорогах между четырь
Пример 5. На рисунке
изображен взвешенный граф, представляющий информацию о дорогах между четырь![]() мя
деревнями. Веса вершин — названия деревень, веса линий — длина дорог в
километрах. И те, и другие задаются надписями.
мя
деревнями. Веса вершин — названия деревень, веса линий — длина дорог в
километрах. И те, и другие задаются надписями.
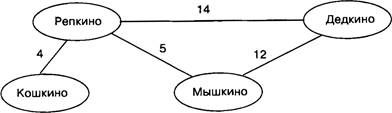
Рис. 2.5
82
![]()
Пример 6. Всем знакомые блок-схемы являются графами, выражающими структуру алгоритма. Вершины этих графов неравноправны. Они делятся на несколько типов (вычислительный блок, развилка, начало/конец). Информация о типе блока передается через его форму (прямоугольник, ромб, овал). Конкретное содержимое каждого блока задается надписью внутри этого блока. Дуги, выходящие из вершины-развилки, имеют пометки «да» и «нет».
![]() Дерево — это граф,
предназначенный для отображения таких связей между объектами, как вложенность,
подчиненность, наследование и т. п.
Дерево — это граф,
предназначенный для отображения таких связей между объектами, как вложенность,
подчиненность, наследование и т. п.
Строится он следующим образом. Сначала рисуем «главную» вершину, которая не зависит ни от одной другой вершины. Эта вершина называется корнем Дерева и является единственной вершиной 1-го уровня. Далее добавляем вершины 2-го уровня. Их может быть сколько угодно, и все они обязательно связаны с корнем — вершиной 1-го уровня, но не связаны между собой. На следующем шаге добавим вершины 3-го уровня. Каждая из них будет связана ровно с одной вершиной 2-го уровня (больше ни с одной другой вершиной). К любой вершине 2-го уровня может быть подсоединено сколько угодно вершин 3-го уровня (в том числе, ни одной). Следующий шаг — добавка вершин 4-го уровня, каждая из которых будет связана ровно с одной вершиной 3-го уровня (и не связана больше ни с чем). И так далее. На каждом шаге добавляем вершины очередного уровня, каждая из которых будет связана ровно с одной вершиной предыдущего уровня и не будет иметь никаких иных связей.
Полученный граф напоминает ветвящийся куст, который «растет сверху вниз»: верхние уровни имеют меньшие номера, нижние — большие. Граф из примера 4, отражающий состав тела человека, является деревом. Корень этого дерева — вершина «Тело человека». Графы из примеров З и 5 деревьями не являются.
Вообще говоря, дерево может быть и неориентированным графом, но чаще дерево ориентировано, причем дуги направлены от верхних вершин к нижним. Верхняя вершина называется преДком для связанных с ней нижних вершин, а нижние вершины потомками соответствующей верхней вершины. На любом дереве существует единственная вершина, не имеющая предка, — корень — и может быть сколько угодно вершин, не имеющих потомков, листьев. Все остальные вершины имеют ровно одного предка и сколько угодно потомков.
Если не принимать во внимание направленность связей, то в дереве из любой вершины можно по линиям дойти до любой другой вершины, причем по одному единственному пути.
![]()
В виде дерева удобно изображать системы, в которых нижние вершины в каком-то смысле «подчинены» верхним. Верхняя вершина может изображать начальника, нижние — подчиненных; верхняя систему, нижние ее компоненты; верхняя множество объектов, нижние входящие в него подмножества; верхняя вершина — предка, нижние — потомков и т. д.
![]() Пример 7. Родословное дерево первых
русских князей
Пример 7. Родословное дерево первых
русских князей ![]() (для каждого указан год смерти) (рис.
2.6).
(для каждого указан год смерти) (рис.
2.6).
Рюрик
879
Игорь
945
Святослав 972
![]()
Ярополк Владимир Св. Олег
![]() 977
977
ПОЛОЦКИЙ ![]() Тмутараканский
Тмутараканский
|
|
1076 |
1094 |
1056 |
1060 |
|
Всеслав Ростислав Святополк |
Олег |
Владимир |
Борис |
Давид |
|
|
Черниговский |
Мономах |
1078 |
|
![]()
![]() Северский
Северский
|
Владимиро |
Ростислав |
Святослав |
Игорь |
|
Галицкий |
|
|
1202 |
|
Ярослав
|
Иоанн Берладник |
Всеволод |
Святослав |
|
Владимир |
|
Михаил |
Олег Курский |
|
|
|
1246 |
1228 |
Рис. 2.6
По дереву легко восстановить всех предков каждого конкретного человека. Например, предки Владимира Мономаха (в обратной хронологии): Всеволод Переяславский, Ярослав, Владимир, Святослав, Игорь, Рюрик.
![]()
Пример 8. В виде дерева можно отразить иерархическую структуру разделов книги. На рис. 2.7 приведен пример изображенного в виде дерева содержания учебника географии за девятый класс.
География: население и народное хозяйство России
Часть 1. Общий обзор России
Россия на карте мира
Заселение территории
Сфера влияния России. Геополитическое влияние
![]() Экономическое влияние России человек и природа
Экономическое влияние России человек и природа
Природные условия и человек непосредственное влияние природных условий...
Население России
Часть 2. Районы России
— Подходы к районированию территории России...
Заключение. Россия: единство в многообразии
![]()
(ф З ад а ч и
![]()
Отразите в виде графа структуру следующих объектов, рассматривая их как системы:
1) велосипед; 6) учебник по русскому
2) кресло на колесиках; языку;
З) зонтик; 7) учебник по физике; 4) ботинок; 8) учебник по химии.
5) учебник по математике;
На рис. 2.8 изображена структурная формула нитробензола.
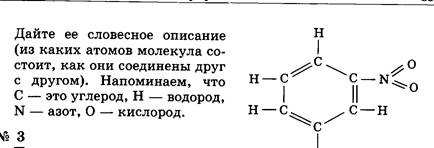
Пусть структура системы изоб- н ражается графом, приведенным на рис. 2.9. Рис. 2.8
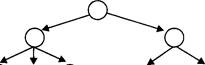
![]()
Назовите объекты, имеющие такую структуру.
Пусть структура системы изображается графом, приведенным на рис. 2.10.
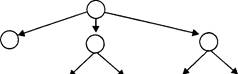
о о о о
Рис. 2.10
Назовите объекты, имеющие такую структуру.
Пусть структура системы изображается графом, приведенным на рис. 2.11.
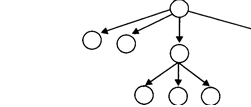
Рис. 2.11
Назовите объекты, имеющие такую структуру.
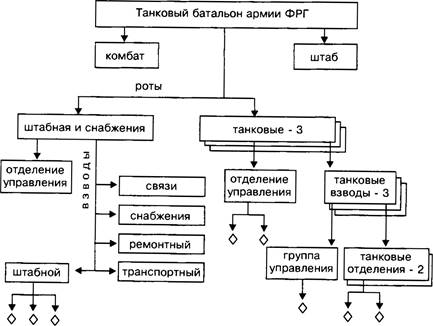
Рис. 2.12
Изобразить в виде графа информацию об организации мотострелковых (мотопехотных) батальонов разных армий.
1. Мотострелковый батальон армии СССР
В середине 70-х гг. ХХ в. мотострелковый батальон Советской Армии насчитывал 395 человек и имел следующую структуру. Во главе стоял командир батальона. Ему подчинялись управление, штаб, З мотострелковые роты, взвод связи, минометная батарея, противотанковый взвод, отделение технического обслуживания, взвод снабжения и батальонный медицинский пункт. В управление батальоном входили сам комбат, заместитель по политической части, заместитель по технической части и техник батальона. Штаб состоял из начальника штаба, начальника связи, инструктора-дозиметриста, писаря и водителя бронетранспортера. Начальник связи являлся командиром взвода связи (еще 12 чел.). Минометная батарея состояла из управления
(10 чел.) и двух взводов по 20 чел., в каждом — по З 120-мм миноме-
та. Противотанковый взвод состоял из отделения станковых противотанковых гранатометов (8 чел., 2 гранатомета СПГ-9) и двух отделений противотанковых управляемых ракет (по 6 чел. и по 2 ПТУРС в отделении). Отделение технического обслуживания: командир отделения, водитель-автослесарь и старший механик. Взвод снабжения: командир взвода, его заместитель, хозяйственная часть (З чел.) и автотранспортное отделение (4 чел.). Батальонный медицинский пункт: начальник пункта, шофер-санитар и 2 санитара.
Мотострелковая рота состояла из управления (командир роты, заместитель по политической части, старшина роты), пулеметного отделения и З мотострелковых взводов. Пулеметное отделение состояло из командира отделения, водителя бронетранспортера и двух пулеметных расчетов, в каждом пулеметчик и помощник пулеметчика. Мотострелковый взвод имел командира взвода, заместителя командира и З мотострелковых отделения. В каждом отделении: командир отделения, пулеметчик, гранатометчик, помощник гранатометчика, старший автоматчик, З автоматчика и водитель бронетранспортера.
2. Мотопехотный батальон армии США
Мотопехотная рота состояла из управления роты, минометного взвода и З мотопехотных взводов. Минометный взвод состоял из группы управления и трех минометных отделений, каждое из которых имело миномет калибра 81 мм. Мотопехотный взвод (47 чел.) состоял из группы управления (командир взвода, помощник командира и радист), отделения оружия (11 чел.) и З мотопехотных отделений (по 11 чел. в каждом). Отделение оружия состояло из командира отделения, двух пулеметных расчетов по 2 чел. в каждом, двух расчетов противотанковых ружей по 2 чел. в каждом и двух подносчиков. Мотопехотное отделение состояло из командира отделения, водителя бронетранспортера и двух групп: группы «А» (командир группы, гранатометчик и 2 стрелка) и группы «Б» (командир группы, гранатометчик и З стрелка).
З. Мотопехотный батальон армии ФРГ
В середине 70-х гг. ХХ в. в армии ФРГ были мотопехотные батальоны двух видов: на боевых машинах пехоты (БМП) «Мардер» и на бронетранспортерах (БТР) HS-30.
Батальон на БМП имел численность 764 чел. Во главе батальона стоял командир, которому подчинялись штаб и 5 рот: штабная и снабжения, минометная и З мотопехотные. Рота штабная и снабжения состояла из управления и З взводов: штабного, связи и снабжения. В штабном взводе было 4 отделения: штабное, мотоциклистов, транспортное и разведывательное. Во взводе связи было З отделения радиосвязи и 2 отделения проводной связи. Во взводе снабжения было 4 отделения: материально-технического обеспечения, продовольственного снабжения, транспортное и санитарное. Минометная рота состояла из управления, двух отделений передового наблюдения, отделения обеспечения и 6 расчетов 120-мм минометов.
Каждая мотопехотная рота (163 чел.) имела в своем составе З мотопехотных взвода по 48 чел. Каждый взвод состоял из группы управления и 4 мотопехотных отделений по 10 чел. Отделение делилось на две группы: первая — командир машины, наводчик-оператор (БМП «Мардер» оснащалась 20-мм пушкой и двумя пулеметами) и механик-водитель; вторая — командир отделения, пулеметчик, гранатометчик, огнеметчик и З стрелка.
Пример 9. Построить граф классификации геометрических объектов (рис. 2.13).
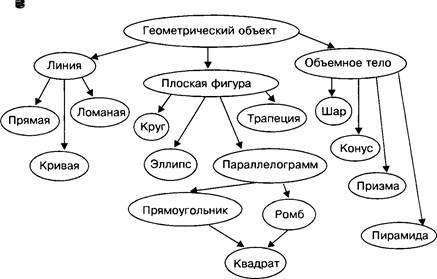
Рис. 2.13
Решение. Среди геометрических объектов можно выделить линии, плоские фигуры и объемные тела. Среди линий, в свою очередь, выделяются прямые, кривые и ломаные. Среди плоских фигур — круги, эллипсы, параллелограммы и трапеции и
Стоит отметить, что классификация, в данном случае, неполная. Например, отсутствует первичный геометрический объект, с которого все начинается, — точка. Обратим внимание на то, что приведенная классификация не является деревом. Объект «квадрат» имеет сразу двух предков — прямоугольник и ромб. Это означает, что любой квадрат обладает всеми свойствами прямоугольника и в то же время всеми свойствами ромба.
![]()
Биологическая классификация ![]()
Построить граф классификации. Является ли он деревом?
Биологическая классификация ![]()
Согласно биологической классификации царства делятся на типы, типы — на классы, классы — на семейства, семейства — на роды, роды — на виды.
Все существа царства животных не способны сами генерировать питательные вещества.
Все животные типа моллюсков двусторонне симметричны, имеют раковину, тело их делится на три отдела: голову, туловище и ногу. У моллюсков класса брюхоногих раковина цельная, спирально закрученная. У моллюсков класса двустворчатых раковины двустворчатые. У моллюсков класса головоногих нога имеет форму венца щупалец на голове, раковина скрыта под мантией (кроме наутилуса), все они хищники.
Все животные типа иглокожих радиально симметричны, имеют под кожей скелет из известковых пластинок с шипами, который может выступать наружу. Все иглокожие класса морских лилий имеют тело в форме «чашечки», от которой отходят 5 раздваивающихся «рук». Все иглокожие класса морских звезд имеют тело в форме звезды или правильного пятиугольника, скелетные пластинки у них соединены подвижно связками и мускулами, все они хищники. У иглокожих класса змеехвосток лучи четко обособлены от диска, членистые, подвижные, напоминают хвосты змей. Все иглокожие класса морских ежей имеют тело шарообразное или яйцевидное, заключенное в усаженный иглами панцирь из 20 рядов сросшихся пластинок. У иглокожих класса голотурий скелет сократился до отдельных элементов, за счет чего они могут менять форму; вокруг рта имеют венец из 8-30 щупалец.
Построить граф классификации. Используя граф, определить, какими признаками будут обладать следующие существа:
1) морской гребешок из класса двустворчатых;
2) трепанг из класса голотурий;
З) виноградная улитка из класса брюхоногих;
4) голова Горгоны из класса змеехвосток;
5) осьминог из класса головоногих;
6) мидия из класса двустворчатых;
7) теребра из класса брюхоногих;
8) каракатица из класса головоногих;
9) лилия стебельчатая из класса морских лилий;
10)
11)
устрица ![]() из класса двустворчатых; 12) кальмар
из класса двустворчатых; 12) кальмар ![]() из
класса головоногих.
из
класса головоногих.
Биологическая классификация![]()
Согласно биологической классификации царства делятся на типы, типы — на классы, классы — на семейства, семейства — на роды, роды — на виды.
Все существа царства животных не способны сами генерировать питательные вещества.
Все животные типа хордовых имеют хорду (спинную струну — ось внутреннего скелета), центральная нервная система у них проходит по спинной стороне.
Все хордовые класса птиц двуногие, имеют передние конечности в виде крыльев, откладывают яйца.
У всех птиц отряда аистообразных нет перьев между основанием клюва и глазами.
Все аистообразные семейства цаплевых имеют длинные острые когти. Цаплевые рода белых цапель имеют черно-белое оперение и белые маховые и рулевые перья. У цаплевых рода косматых цапель спина окрашена зимой и летом, ноги желтые или бурые. У цаплевых рода серые цапли маховые и рулевые перья темные или серые. Белые цапли вида белая цапля малая имеют черный клюв и хохолок на затылке из 2-3 длинных перьев. Белые цапли вида белая цапля боль-
шая не имеют хохолка на затылке. У косматых цапель вида цапля желтая на затылке 10 белых перьев с черными каемками. У косматых цапель вида цапля белокрылая на затылке 4-6 ржаво-коричневых перьев. У серых цапель вида цапля рыжая спина серая с рыжим налетом. У серых цапель вида цапля серая спина серая без рыжего налета.
Все аистообразные семейства аистовых имеют короткие тупые когти. Аистовые рода аистов имеют длинную шею и конический клюв. Аисты вида аист белый имеют оперение белое, кроме черных крыльев. Аисты вида аист черный имеют оперение черное, но грудь и брюхо белые.
У всех птиц отряда гусеобразных клюв прямой, по краям расположены роговые пластинки или зубчики.
Все гусеобразные семейства утиных имеют плотное оперение с
густым пухом.
У всех утиных подсемейства утиных цевка спереди покрыта крупными щитками. Утиные рода утки имеют крупные размеры (длина крыла — более 20 см). Утиные рода чирки имеют маховые крылья темные с белыми каемками. Утиные рода гоголи имеют широкий клюв. У уток вида широконоска клюв в конечной части почти в два раза шире, чем в основной. У уток вида шилохвость хвост длинный, клиновидный. У уток вида кряква обыкновенная клюв оливкового цвета. У чирков вида чирок-трескунок стержни маховых крыльев беловатые. У чирков вида чирок-клокотун стержни маховых перьев бурые. У гоголей вида гоголь обыкновенный длина крыла более 180 мм. У гоголей вида гоголь малый длина крыла менее 180 мм.
1. Представить указанную часть биологической классификации в виде графа.
2. Назвать все указанные в тексте признаки птиц следующих
видов:
|
1) белая цапля малая; |
9) лебедь-шипун; |
|
2) белая цапля большая; |
10) лебедь-кликун; |
|
З) цапля желтая; |
11) лебедь малый; |
|
4) цапля белокрылая; |
12) лебедь американский; |
|
5) цапля рыжая; |
13) гусь-гуменник; |
|
6) цапля серая; |
14) гусь серый; |
|
7) аист белый; |
15) гусь белолобый; |
|
8) аист черный; |
16) широконоска; |
17) шилохвость; 20) чирок-клокотун;
18) кряква обыкновенная; 21) гоголь обыкновенный; 19) чирок-трескунок; 22) гоголь малый.
Представить информацию о классификации в русском языке в виде графа. Является ли полученный граф деревом?
Классификации в русском языке
1. Местоимения в русском языке бывают трех лиц: 1-го, 2-го и 3-го. Во всех трех лицах они могут быть единственного и множественного числа. Местоимения 3-го лица единственного числа кроме того изменяются по родам. Местоимение 1-го лица единственного числа — я, местоимение 1-го лица множественного числа — мы. Местоимение 2-го лица единственного числа — ты, местоимение 2-го лица множественного числа — вы. Местоимения 3-го лица единственного числа: мужского рода — он, женского рода — она, среднего рода — оно. Местоимение 3-го лица множественного числа — они.
2.
![]()
З. Предложения в русском языке классифицируются по составу, по интонации и по цели высказывания.
По составу предложения делятся на нераспространенные и распространенные. Нераспространенные предложения состоят только из двух членов: подлежащего и сказуемого. Пример нераспространенного предложения: «Птицы прилетели». Распространенные предложения состоят из подлежащего, сказуемого и второстепенных членов предложения. Пример распространенного предложения: «Ранней весной прилетели первые птицы» .
По интонации предложения делятся на восклицательные («Пришла весна!» ) и невосклицательные («Пришла весна. »).
По цели высказывания предложения делятся на повествовательные, вопросительные и побудительные. Повествовательное предложение: «Мы собрали много грибов и ягод». Вопросительное предложение: «Вы собрали много грибов и ягод?». Побудительное предложение: «Собирайте грибы и ягоды!» .
4. Существительные бывают одушевленные и неодушевленные. Одушевленные отвечают на вопрос «кто?» , неодушевленные « что?». И одушевленные, и неодушевленные существительные относятся к одному из трех родов: мужскому, женскому или среднему. К мужскому роду относятся существительные, к которым можно поставить слова «он», «мой». К женскому роду относятся существительные, к которым можно поставить слова «она», «моя». К среднему роду относятся существительные, к которым можно поставить слова «оно», «моё». Пример одушевленных существительных мужского рода: мужчина, Иван. Пример одушевленных существительных женского рода: девушка, Мария. Пример одушевленного существительного среднего рода: Чудо-Юдо. Пример неодушевленных существительных мужского рода: праздник, огород. Пример неодушевленных существительных женского рода: улица, тетрадь. Пример неодушевленных существительных среднего рода: озеро, утро.
5. В русском языке существительные бывают трех склонений: 1-го, 2-го и 3-го. К 1-му склонению относятся существительные мужского и женского рода с окончаниями -а/-я. Ко 2-му склонению относятся существительные мужского рода с пустым окончанием и существительные среднего рода с окончаниями -0/-е. К 3-му склонению относятся существительные женского рода с пустым окончанием. Пример существительных 1-го склонения: женского рода — береза, земля; мужского рода — юноша, дядя.
Пример существительных 2-го склонения: мужского рода — ученик, день, трамвай; среднего рода — утро, сердце.
Пример супцествительных 3-го склонения: сирень, пристань.
12 Составить родословное дерево потомков Владимира Мономаха.
Потомки Владимира Мономаха
![]()
Классифицируйте своих знакомых (не менее 20 человек) по причине вашего знакомства (одноклассники, ребята из одного
двора, игроки одной команды и т. д.). Представьте результат в виде графа. Является ли полученный граф деревом? Есть ли такие люди, которые попали сразу в несколько классов?
Выберите из телепрограммы на текущую неделю передачи, которые представляют для вас интерес (не менее 20). Классифицируйте их:
1) по дате;
2) по телеканалам;
З) по категории (художественные фильмы, мультфильмы, спортивные передачи и т. п.).
Представьте результат в виде графа. Является ли полученный граф деревом? Есть ли такие передачи, которые попали сразу в несколько классов?
.М2 ЗА
Классифицируйте известные вам книги (не менее 20):
1) по жанру (учебники, приключения, фантастика, справочники и т. п.);
2)
Представьте результат в виде графа. Является ли полученный граф деревом? Есть ли такие книги, которые попали сразу в несколько классов?
1) Представьте в виде графа свою родословную по отцовской линии.
2) Представьте в виде графа свою родословную по материнСКОЙ линии.
2.2.3. Блок-схемы
![]() Пример 10.
Блок-схемы алгоритмов также являются
Пример 10.
Блок-схемы алгоритмов также являются ![]() примерами графов, отражающих процесс
выполнения некоторой работы, ход решения задачи. Вершины обозначают отдельные
действия, дуги указывают на последовательность выполнения действий.
примерами графов, отражающих процесс
выполнения некоторой работы, ход решения задачи. Вершины обозначают отдельные
действия, дуги указывают на последовательность выполнения действий.
Например, на рис. 2.14 дана блок-схема алгоритма вычислений. На входе любое целое число, на выходе — результат вычислений.

Какое значение получится на выходе схемы на рис. 2.14, если на вход подать: а) число З; б) число 1; в) число 25?
Рис. 2.14
Представьте в виде блок-схемы процесс принятия федеральных законов Российской Федерации. Вершины графа будут изображать действия, дуги — их последовательность.
Принятие Федеральных Законов Российской Федерации Согласно ст. 105, 107 конституции 1993 г. принятие федеральных законов регулируется следующими положениями:
1) В принятии закона принимают участие Государственная Дума, Совет Федерации и президент.
2) Закон принимает Государственная Дума.
З) Затем закон передается в Совет Федерации, который либо одобряет закон, либо отклоняет его (налагает вето).
4) Если Совет Федерации одобрил закон, закон направляется президенту .
5) Если Совет Федерации отклонил закон, закон возвращается в Государственную Думу.
6) Если Государственная Дума соглашается изменить закон, то все действия по принятию закона повторяются с самого начала. 7) Если Государственная Дума не согласна изменить закон, она проводит по нему повторное голосование.
8) Если при повторном голосовании в Думе закон получил менее 2/3 голосов, то Государственная Дума обязана внести в закон изменения и повторить все действия по принятию закона.
9) Если при повторном голосовании в Думе закон получил не менее 2/3 голосов, он считается принятым, несмотря на вето Совета Федерации (Государственная Дума преодолела вето Совета Федерации). В этом случае принятый закон направляется президенту.
10) Президент рассматривает полученный им закон и может одобрить его или отклонить (наложить вето).
11) В случае одобрения президент подписывает и обнародует закон, после чего закон вступает в силу.
12) В случае отклонения президентом закон возвращается в Государственную Думу.
13) Если Государственная Дума согласна изменить закон, то все действия по принятию закона повторяются с самого начала.
14) Если Государственная Дума не согласна изменить закон, она проводит по нему повторное голосование.
15)
16) Если при повторном голосовании в Думе закон получил не менее 2/3 голосов, он направляется в Совет Федерации (Государственная Дума преодолела вето президента). В этом случае Совет Федерации также проводит повторное голосование по закону.
17) Если при повторном голосовании в Совете Федерации закон получил менее 2/3 голосов, он возвращается в Думу.
18) Если при повторном голосовании в Совете Федерации закон получил не менее 2/3 голосов (Совет Федерации преодолел вето президента), закон направляется президенту. В этом случае президент обязан подписать и обнародовать закон.
![]()
2.3.1. Основные понятия
Пример 1. Рассмотрим следующий набор фактов:
Анаконда — длинная.
У электрички «глаза» горят. ![]() Человек бодрствует днем. На баранов коты
не охотятся. Сова покрыта перьями. Мышей ужи ловят, а баранов — нет. Человек не
длинный. Сова может передвигаться на двух ногах. Человек не ловит мышей.
Анаконды ловят баранов. Совы не длинные. Уж не может передвигаться на двух
ногах. Электричка когти не втягивает. Кот — животное не длинное. У совы глаза
горят. Кошки ловят мышей. Тело анаконды перьями не покрыто. Уж не имеет перьев.
Кот втягивает когти. Ночного образа жизни электрички не ведут. Глаза у кошек
горят. Люди баранов не ловят. Когти сова втягивать не умеет. Электрички —
длинные. Уж ведет ночной образ жизни. Кошки не умеют ходить на двух ногах. На
баранов сова не охотится. Анаконда ведет ночной образ жизни. Человек — без
перьев. Длинным уж не является. На двух ногах анаконда не передвигается.
Электричка не охотится ни на мышей, ни на баранов. Человек не относится к
существам, у которых горят глаза. Кошки ведут ночной образ жизни. На мышей
анаконда не охотится. Глаза у ужа не горят. Анаконда не имеет когтей. Днем сова
спит. Электрички не передвигаются на двух ногах. Когти у человека не
втягиваются. У кота перьев нет. У анаконды глаза горят. Уж не втягивает когти.
Человек передвигается на двух ногах. Сова ловит мышей. Перьями электричка не
покрыта.
Человек бодрствует днем. На баранов коты
не охотятся. Сова покрыта перьями. Мышей ужи ловят, а баранов — нет. Человек не
длинный. Сова может передвигаться на двух ногах. Человек не ловит мышей.
Анаконды ловят баранов. Совы не длинные. Уж не может передвигаться на двух
ногах. Электричка когти не втягивает. Кот — животное не длинное. У совы глаза
горят. Кошки ловят мышей. Тело анаконды перьями не покрыто. Уж не имеет перьев.
Кот втягивает когти. Ночного образа жизни электрички не ведут. Глаза у кошек
горят. Люди баранов не ловят. Когти сова втягивать не умеет. Электрички —
длинные. Уж ведет ночной образ жизни. Кошки не умеют ходить на двух ногах. На
баранов сова не охотится. Анаконда ведет ночной образ жизни. Человек — без
перьев. Длинным уж не является. На двух ногах анаконда не передвигается.
Электричка не охотится ни на мышей, ни на баранов. Человек не относится к
существам, у которых горят глаза. Кошки ведут ночной образ жизни. На мышей
анаконда не охотится. Глаза у ужа не горят. Анаконда не имеет когтей. Днем сова
спит. Электрички не передвигаются на двух ногах. Когти у человека не
втягиваются. У кота перьев нет. У анаконды глаза горят. Уж не втягивает когти.
Человек передвигается на двух ногах. Сова ловит мышей. Перьями электричка не
покрыта.
Попробуйте, пользуясь этим набором, ответить на следующие вопросы:
1) Кто ловит мышей?
2) Кто ведет ночной образ жизни?
З) Какие общие свойства у ужа и анаконды?
4) Кто (что) длинное и имеет горящие глаза?
Поиск ответов займет достаточно много времени. А теперь посмотрите на следующую таблицу, в которой представлена та же самая информация.
Таблица 1
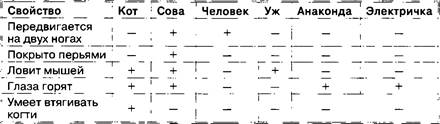
4 Информатика
и ИКТ. Т. ![]()
![]()
Таблица 1 (продолжение)
 Человек
I Уж Анаконд Элекуричка
Человек
I Уж Анаконд Элекуричка
Легко понять, что здесь плюсом отмечено наличие соответствующего признака, а минусом — его отсутствие. Глядя на эту таблицу, можно быстро найти ответы на перечисленные выше вопросы и любые другие на данную тему.
Этот пример иллюстрирует удобство табличной формы представления информации.
![]() Структура таблицы. Таблица состоит из следующих частеЙ:
головки, боковика и прографки. Кроме того, над таблицей могут располагаться
табличный номер и заголовок (которые могут и отсутствовать).
Структура таблицы. Таблица состоит из следующих частеЙ:
головки, боковика и прографки. Кроме того, над таблицей могут располагаться
табличный номер и заголовок (которые могут и отсутствовать).
Табличный номер
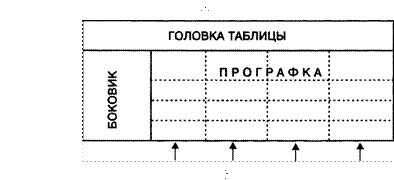
Рис. 2.15
Пример 2
Таблица 2
Моя семья

Таблица содержит четыре строки и четыре графы. Клетка на пересечении строки и графы называется ячейкой. Головка
информационные модели
![]()
состоит из заголовков отДедьных граф. Боковик содержит заголовки строк.
В некоторых сложных случаях головка таблицы и боковик могут оказаться многоуровневыми. Уровни головки называются ярусами, уровни боковика — ступенями.
Важное замечание! В таблице графа всегда подчиняется заголовку графы, а строка — заголовку строки. Это означает, что в графе не должно быть никакой информации, которая не соответствовала бы заголовку графы, а в строке не должно быть никакой информации, которая не соответствовала бы заголовку строки.
Пример З

Заголовки Заголовки
1-й ступени 2-й ступени
|
1) может отсутствовать; |
4) с большой буквы; |
|
2) имеет вид «Таблица |
5) знак «№» не пишет- |
|
Число-номер» ; |
ся; |
|
З) пишется справа вверху; 2. Заголовок таблицы: |
6) точка не ставится. |
|
1) может отсутствовать; |
З) с большой буквы; |
|
2) пишется посредине; |
4) точка не ставится. |
![]() Правила оформления таблицы.
Правила оформления таблицы.
1. Табличный номер:
З. Головка:
1) заголовок обязателен У ВСЕХ граф (в том числе у 60ковика!);
2) первый ярус — обязательно с большой буквы, остальные ярусы по смыслу;
З) точка не ставится;
4) заголовки пишутся в именительном падеже, единственном числе («Член семьи», а не «ЧленЫ семьи»);
5) заголовки одного яруса должны быть выровнены по верхнему уровню;
6) единицы измерения (если они есть) записываются после заголовка графы через запятую или в круглых скобках; единицы измерения следует поднимать как можно выше (с нижних ярусов головки на верхние или даже в заголовок таблицы).
4. Боковик:
1) первая ступень — обязательно с большой буквы, остальные ступени по смыслу; 2) точка не ставится.
5. Прографка:
1) как правило, с большой буквы, если только по смыслу таблицы не требуется маленькая буква как противопоставление большой;
2) точка не ставится;
З) данные одной строки должны быть выровнены по верхнему уровню;
4)
5) числа записываются посередине и выравниваются по разрядам (так, чтобы единицы всегда писались под единицами, десятки под десятками, сотни под сотнями и т. д.).
![]()
Построить таблицу «Домашняя библиотека». Таблица должна содержать не менее 6 книг. Для каждой книги должны быть указаны авторы, название, город и год издания, жанр (фантастика, детектив и пр.).
Построить таблицу «Существительные». Таблица должна содержать не менее 6 существительных. Для каждого должно быть указано не менее 5 характеристик.
Построить таблицу «Звери». Таблица должна содержать не менее 6 животных. Для каждого должно быть указано не менее 5 характеристик.
Объекты и свойства. Для правильного построения таблиц важными являются понятия «объект», «класс объектов», «свойство объекта».
Объект — это то, о чем идет речь.
Класс объектов — множество объектов, объединенных какими-то общими свойствами. Например, парты, домашние животные, планеты, сны.
Один и тот же объект может быть отнесен одновременно к нескольким классам. Например, кошка может быть отнесена к классу домашних животных, к классу кошачьих, к классу четвероногих.
Свойства — характеристики, признаки объекта. Например, говоря об объекте класса «человек», мы можем выделить такие его свойства: возраст, рост, вес, цвет глаз, образование, семейное положение.
У каждого свойства есть название и значение. Примеры названий: цвет, материал, форма. Примеры значений: зеленый, железный, прямоугольный.
Нас в первую очередь будут интересовать пары объектов, хотя можно рассматривать и тройки, четверки и т. д. Например, оценка в классном журнале является характеристикой сразу тройки объектов: «ученик—предмет—дата».
В дальнейшем при анализе текстов будем выделять объекты, названия и значения свойств с помощью подчеркиваний разного вида. Название объекта будем подчеркивать прямой линией, название свойства волнистой, значение — пунктиром: Мальчик весит 25 кг.
![]()
Если в фразе два объекта, то первый объект будем подчеркивать одной прямой, второй двумя. Название одиночного свойства будем подчеркивать одной волнистой линией, название парного свойства двумя волнистыми.
от П ерми ![]() до Питера
— 31 час.
до Питера
— 31 час.
Таблица универсальное средство представления информации. В таблице может содержаться информация о различных свойствах объектов, об объектах одного класса и разных классов, об отдельных объектах и группах объектов. Для простоты разделим все множество таблиц на несколько типов, укажем для каждого его отличительные черты и правила построения.
2.3.2. Таблицы типа «объекты—свойства»
![]() Если
Если ![]() рассматриваются
отдельные объекты (все свойства относятся не к группе объектов, а к какому-то
одному объекту) и
рассматриваются
отдельные объекты (все свойства относятся не к группе объектов, а к какому-то
одному объекту) и ![]() все объекты принадлежат одному классу, то
это таблица типа «объекты—свойства» (ОС). Схема таблиц типа ОС:
все объекты принадлежат одному классу, то
это таблица типа «объекты—свойства» (ОС). Схема таблиц типа ОС:
![]()
Пример 4
Таблица 4

Порядок построения таблицы типа ОС:
1)
![]() Выделить объекты и свойства. Для этого внимательно
прочитать текст. В каждой фразе подчеркнуть название объекта прямой линией,
название свойства объекта волнистой, значение свойства пунктирной.
Выделить объекты и свойства. Для этого внимательно
прочитать текст. В каждой фразе подчеркнуть название объекта прямой линией,
название свойства объекта волнистой, значение свойства пунктирной.
2) Назвать класс объектов. Название записать в заголовок таблицы и в заголовок боковика.
З) Названия объектов (они подчеркнуты прямой линией) записать в боковик.
4) Названия свойств (они подчеркнуты волнистой линией) записать в головку.
5) Значения свойств записать в прографку.
Пример 5. Пусть дан текст:
Полярная звезда находится в созвездии
Малая Медве![]() дица. Расстояние до Полярной звезды — 780
световых лет. Акрукс ярче Солнца в 2200 раз. Бетельгейзе находится в созвездии
Орион. Расстояние до Спики — 260 световых лет. Денеб находится в созвездии
Лебедь. Расстояние до Бетельгейзе — 650 световых лет. Ригель ярче Солнца в
55000 раз. Канопус находится в созвездии Стрекоза. Расстояние до Капеллы 46
световых лет. Спика находится в созвездии Дева. Антарес находится в созвездии
Скорпион. Расстояние до Арктура — 36 световых лет. Альдебаран ярче Солнца в 165
раз. Бетельгейзе ярче Солнца в 22000 раз. Расстояние до Акрукса — 260 световых
лет. Денеб ярче Солнца в 72500 раз. Расстояние до Антареса — 425 световых лет.
Альдебаран находится в созвездии Телец. Антарес ярче Солнца в 6600 раз.
Расстояние до Канопуса — 181 световой год. Арктур находится в созвездии
Волопас. Капелла ярче Солнца в 150 раз. Ригель находится в созвездии Орион.
Спика ярче Солнца в 2200 раз. Акрукс находится в созвездии Южный Крест.
Расстояние до Альдебарана — 70 световых лет. Арктур ярче Солнца в 105 раз.
Расстояние до Денеба — 1600 световых лет. Канопус ярче Солнца в 6600 раз.
дица. Расстояние до Полярной звезды — 780
световых лет. Акрукс ярче Солнца в 2200 раз. Бетельгейзе находится в созвездии
Орион. Расстояние до Спики — 260 световых лет. Денеб находится в созвездии
Лебедь. Расстояние до Бетельгейзе — 650 световых лет. Ригель ярче Солнца в
55000 раз. Канопус находится в созвездии Стрекоза. Расстояние до Капеллы 46
световых лет. Спика находится в созвездии Дева. Антарес находится в созвездии
Скорпион. Расстояние до Арктура — 36 световых лет. Альдебаран ярче Солнца в 165
раз. Бетельгейзе ярче Солнца в 22000 раз. Расстояние до Акрукса — 260 световых
лет. Денеб ярче Солнца в 72500 раз. Расстояние до Антареса — 425 световых лет.
Альдебаран находится в созвездии Телец. Антарес ярче Солнца в 6600 раз.
Расстояние до Канопуса — 181 световой год. Арктур находится в созвездии
Волопас. Капелла ярче Солнца в 150 раз. Ригель находится в созвездии Орион.
Спика ярче Солнца в 2200 раз. Акрукс находится в созвездии Южный Крест.
Расстояние до Альдебарана — 70 световых лет. Арктур ярче Солнца в 105 раз.
Расстояние до Денеба — 1600 световых лет. Канопус ярче Солнца в 6600 раз.
Читаем первую
фразу. Объект, о котором здесь говорится — Полярная звезда. Подчеркнем эти
слова прямой линией. Свойство объекта-звезды «находиться в созвездии».
Подчеркнем эти слова волнистой линией. Значение этого свойства ![]() лая
медведица» . Эти слова подчеркнем пунктиром. Получим:
лая
медведица» . Эти слова подчеркнем пунктиром. Получим:
Полярная
звезда ![]() Мала_я_ медведица._
Мала_я_ медведица._
Во второй фразе объект тот же — Полярная звезда. Подчеркнем его прямой линией. Свойство объекта-звезды «расстояние». Его подчеркнем волнистой линией. Значение свойства — «780 световых лет» подчеркнем пунктиром. Получим: Расстояние до Полярной звезды — 780 световых лет.
![]()
В каждой фразе описаны отдельные объекты. Все они принадлежат к одному классу — классу звезд. Значит, будем строить таблицу типа «объекты—свойства». Заголовок ее — название класса объектов: «Звезды». Поскольку речь идет не обо всех звездах, можно уточнить «Некоторые звезды» или «Яркие звезды», или еще как-нибудь. Заголовок боковика — «Звезда». В боковик будут записаны названия звезд (Полярная звезда, Бетельгейзе, Спика и т. д.), в головку — названия свойств («Созвездие», «Расстояние», «Во сколько раз ярче Солнца»). объектов в таблице много, то располагать их надо в некотором осмысленном порядке, согласно некоторому правилу. В частности, в табл. 4 ученики могут быть перечислены в алфавитном порядке их фамилий, по возрастанию или убыванию года рождения, роста или веса. Толысо в очень маленьких таблицах (из 3-4 строк) объекты можно перечислять без всякого порядка.
Таблица типа ОС может быть «повернута на бок» — строки превращены в графы, а графы в строки.
Например:
Таблица 5
Ученики 8-го «в»

Закончить работу над таблицей из примера 5. Обратить внимание на следующие моменты: правило упорядочения звезд в таблице (по алфавиту, по расстоянию, по яркости), единицы измерения.
Построить таблицу по следующим данным:
Столица, площадь, население и форма правления некоторых стран
Столица Франции — Париж. Площадь Франции — 552 тыс. кв. км. Население
Франции 52 млн чел. Форма правления Франции ![]() республика.
республика.
Столица Австрии — Вена. Площадь Австрии — 84 тыс. кв. км. Форма правления Австрии — федеративная республика.
Столица Великобритании — Лондон. Площадь Великобритании — 244 тыс. кв. км. Население Великобритании — 56 млн чел. Форма правления Великобритании — конституционная монархия (королевство).
Столица Швейцарии — Берн. Площадь Швейцарии — 41 тыс. кв. км. Население Швейцарии — 7 млн чел. Форма правления Швейцарии — конфедерация.
Площадь Италии — 301 тыс. кв. км. Население Италии — 55 млн чел. Форма правления Италии — республика.
Столица Канады — Оттава. Площадь Канады — 9974 тыс. кв. км. Население Канады — 22 млн чел. Канада — доминион в составе Британского содружества наций.
Столица Омана — Маскат. Население Омана — 1 млн чел. Форма правления Омана — абсолютная монархия (султанат).
Столица Японии — Токио. Площадь Японии — 370 тыс. кв. км. Население Японии — 108 млн чел. Форма правления Японии — конституционная монархия (империя).
Построить таблицу по следующим данным:
2.3.3. Таблицы типа «объекты—объекты»
![]() —
описываются пары объектов (свойства характеризуют не один объект, а пару) и
свойство только одно, то это таблица типа «объекты—объекты» (00).
—
описываются пары объектов (свойства характеризуют не один объект, а пару) и
свойство только одно, то это таблица типа «объекты—объекты» (00).
Схема таблиц типа 00:
Название свойства пары объектов и, возможно, название классов объектов

Здесь мы впервые сталкиваемся с многоуровневой — двухярусной головкой.
Пример 6
Таблица 6 Годовые оценки
![]()
Фамилия Предмет
![]()
Русский язык Математика Природоведение
![]()
Иванов Петя
Петров Ваня
![]()
Цветова Оксана
Порядок построения таблицы типа 00:
1)
Выделить объекты и свойства. Для этого внимательно прочитать
текст. В каждой фразе подчеркнуть ![]() название первого объекта в паре одной
прямой линией, название второго объекта в паре двумя прямыми, название
свойства пары объектов — двумя волнистыми линиями, значение свойства пунктиром.
название первого объекта в паре одной
прямой линией, название второго объекта в паре двумя прямыми, название
свойства пары объектов — двумя волнистыми линиями, значение свойства пунктиром.
2) Название свойства записать в заголовок таблицы.
4) Назвать класс вторых объектов в паре. Название записать в верхний ярус головки.
5) Названия первых объектов (они подчеркнуты одной прямой линией) записать в боковик.
6) Названия вторых объектов (они подчеркнуты двумя прямыми) записать в нижний ярус головки.
7) Значения свойства записать в прографку.
Пример 7. Пусть дан текст:
У Снегова по физике годовая оценка З. У Снегова по е географии годовая оценка 4. У Кошкина по географии годовая оценка З. У Петрова по химии годовая оценка 4. У Иванова по физике годовая оценка 5. У Сергеева по биологии годовая оценка 5. У Кузнецова по химии годовая оценка З. У Петрова по физике годовая оценка 4. У Сидорова по географии годовая оценка З. У Иванова по химии годовая оценка 4. У Кошкина по физике годовая оценка 4. У Кузнецова по биологии годовая оценка 5. У Иванова по географии годовая оценка 5. У Сергеева по химии годовая оценка 4. У Сидорова по физике годовая оценка 5. У Ветрова по химии годовая оценка 5. У Кузнецова по географии годовая оценка 5. У Петрова по биологии годовая оценка З. У Кошкина по химии годовая оценка 5. У Снегова по биологии годовая оценка З. У Сергеева по физике годовая оценка 5. У Сидорова по биологии годовая оценка 5. У Ветрова по географии годовая оценка 5. У Кузнецова по физике годовая оценка 4. У Иванова по биологии годовая оценка З. У Петрова по географии годовая оценка З. У Ветрова по биологии годовая оценка 4. У Снегова по химии годовая оценка 5. У Сергеева по географии годовая оценка 4. У Кошкина по биологии годовая оценка З. У Ветрова по физике годовая оценка 4. У Сидорова по химии годовая оценка 5.
Читаем первую фразу. В ней речь идет о паре объектов. Первый объект в паре — Снегов. Подчеркиваем его одной прямой. Второй объект — физика. Его подчеркиваем двумя прямыми. Свойство, которое объединяет эти два объекта, — годовая оценка. Его подчеркиваем двумя волнистыми. Значение свойства — тройка. Подчеркиваем пунктиром. Получим:
У Снегова по ![]() 3,
3,
Аналогично разбираем остальные фразы.
![]() Если объектов в
таблице много, располагать их надо согласно некоторому правилу. Для удобства
таблица типа 00 может быть «повернута на бок» — строки превращены в графы, а
графы в строки.
Если объектов в
таблице много, располагать их надо согласно некоторому правилу. Для удобства
таблица типа 00 может быть «повернута на бок» — строки превращены в графы, а
графы в строки.
![]()
Закончить работу над таблицей из примера 7. Обратить внимание на порядок объектов в таблице.
Построить таблицу «Мои четвертные оценки за прошлый год» .
Постройте таблицу по следующим данным:
Поголовье овец и коз на 1 января 1991 г. составляло 58,2 млн голов. Поголовье птицы на 1 января 1996 г. составляло 422,6 млн голов. Поголовье свиней на 1 января 1986 г. составляло 39 млн голов. Поголовье крупного рогатого скота на 1 января 1996 г. составляло 39,7 млн голов. Поголовье овец и коз на 1 января 1986 г. составляло 63,4 млн голов. Поголовье свиней на 1 января 1991 г. составляло 38,3 млн голов. Поголовье крупного рогатого скота на 1 января 1991 г. составляло 57 млн голов. Поголовье птицы на 1 января 1991 г. составляло 659,8 млн голов. Поголовье овец и коз на 1 января 1996 г. составляло 28 млн голов. Поголовье птицы на 1 января 1986 г. составляло 627,7 млн голов. Поголовье крупного рогатого скота на 1 января 1986 г. составляло 59,6 млн голов. Поголовье свиней на 1 января 1996 г. составляло 22,6 млн голов.
.М2 10
В следующем тексте речь идет о земельных ресурсах зарубежных стран. Постройте по этому тексту таблицу.
![]()
В следующем тексте речь идет о Московском метро. Постройте по этим данным таблицу:
Время в пути от станции Отрадное до станции Кутузовская составляет 37 мин. Время в пути от станции Театральная до станции Юго-Запиная составляет 24 мин. Время в пути от станции Октябрьская до станции Отрадное составляет 32 мин. Время в пути от станции Курская до станции Кутузовская составляет 23 мин. Время в пути от станции Октябрьская до станции Кутузовская составляет 16 мин. Время в пути от станции Юго-Западная до станции Отрадное составляет 46 мин. Время в пути от станции Театральная до станции Отрадное составляет 27 мин. Время в пути от станции Октябрьская до станции Театральная составляет 13 мин. Время в пути от станции Курская до станции Отрадное составляет 28 мин. Время в пути от станции Театральная до станции Кутузовская составляет 19 мин. Время в пути от станции Октябрьская до станции Юго-Западная составляет 23 мин. Время в пути от станции Юго-Западная до станции Кутузовская составляет 33 мин. Время в пути от станции Курская до станции Театральная составляет 10 мин. Время в пути от станции Октябрьская до станции Курская составляет 10 мин. Время в пути от станции Курская до станции Юго-Западная составляет 32 мин.
![]() — описываются пары
объектов (свойства характеризуют не один объект, а пару) и свойств пары
объектов несколько и
— описываются пары
объектов (свойства характеризуют не один объект, а пару) и свойств пары
объектов несколько и ![]() других свойств нет, то это таблица типа
«объекты-объекты-несколько» (ООН). Схема таблиц типа ООН:
других свойств нет, то это таблица типа
«объекты-объекты-несколько» (ООН). Схема таблиц типа ООН:
Общее название парных свойств или их перечисление
Название масса Название 2-го Название 2-го Название 2-го первых объекта из 1-й объекта из 2-й объекта из 3-й объектов пары пары пары
пары
Названия Названия Названия свойств пары свойств пары свойств пары объектов 1— объектов объектов
Названия первых Значения свойств пары объектов объектов
и, возможно, название классов объектов
Название масса вторых объектов пары
Порядок построения таблицы типа ООН:
1) Выделить объекты и
свойства. Для этого внимательно прочитать текст. В каждой фразе подчеркнуть
название первого объекта в паре одной прямой линией, название второго объекта в
паре — двумя прямыми, название свойства пары объектов двумя волнистыми линиями,
значение свойства ![]() пунктиром.
пунктиром.
2) Названия свойств записать в заголовок таблицы.
З) Назвать класс первых объектов в паре. Название записать в заголовок боковика.
4) Назвать класс вторых объектов в паре. Название записать в верхний ярус головки.
5) Названия первых объектов (они подчеркнуты одной прямой линией) записать в боковик.
6) Названия вторых объектов (они подчеркнуты двумя прямыми) записать в средний ярус головки.
7)
8) Значения свойств записать в прографку.
Пример 8
Таблица 7
Расписание движения поездов
![]() Станция
Станция
Глазов
Пример 9
Таблица 8
Оценки за полугодия и за год

В табл. 8 пары образуются из объектов, относящихся к классам «ученики» — «предметы», а свойствами являются оценки, полученные учениками по предметам за разные периоды учебы. Но та же информация может быть представлена иначе: пары могут быть образованы из объектов, относящихся к классам «ученики» «периоды обучения», а свойствами будут оценки, полученные по разным предметам в каждый период учебы. Тогда получится такая таблица:
Таблица 9
Оценки за полугодия и за год
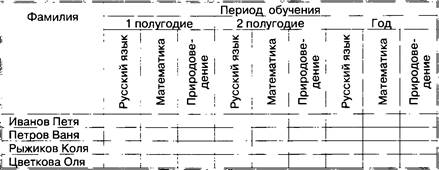
Для удобства таблица типа ООН может быть «повернута на бок» — строки превращены в графы, а графы — в строки. «Поворот» может касаться только объектов (боковик меняется местами с двумя верхними ярусами головки; нижний ярус (свойства) остается на месте), а может — всей головки. В последнем случае вместо многоярусной головки получим многоступенчатый боковик,
Если
— описываются пары объектов (существуют
свойства, которые характеризуют не один объект, а пару объектов) и ![]() существуют
свойства, которые характеризуют только один объект в паре и
существуют
свойства, которые характеризуют только один объект в паре и ![]() нет свойств,
которые характеризуют только другой объект в паре, то это таблица типа
«объекты—свойства—объекты» (ОСО).
нет свойств,
которые характеризуют только другой объект в паре, то это таблица типа
«объекты—свойства—объекты» (ОСО).
Схема таблиц типа ОСО:
Общее название парных свойст или их перечисление и, возможно, название классов объектов
![]()
|
|
|
![]()
![]() объектов, свойств
объектов, свойств ![]() Название Название Название
Название Название Название![]()
![]()
![]()
![]()
![]()
![]()
![]() для
которых (отдельная объекта из объекта из объекта из
для
которых (отдельная объекта из объекта из объекта из ![]() есть графа для 1-й
пары 2-й пары 3-й пары
есть графа для 1-й
пары 2-й пары 3-й пары ![]() одиночные каждого
одиночные каждого ![]() свойства
свойства ![]() свойства)
свойства) ![]() Названия Названия Названия
парных
Названия Названия Названия
парных![]() парных парных свойствсвойств свойств (отдельная
парных парных свойствсвойств свойств (отдельная![]() (отдельная (отдельная
(отдельная (отдельная ![]()
![]() графа для
графа для ![]() графа для графа для
каждого
графа для графа для
каждого ![]() каждого каждого
каждого каждого ![]() свойства)
свойства) ![]() свойства) свойства)
свойства) свойства)
![]()
li Названия Значения свойств объектов
![]()
В таблице перечислены: пары объектов, свойства, которые характеризуют каждую пару объектов, и свойства, которые относятся только к одному объекту в паре, но не относятся к дру-
При перечислении годовых оценок, полученных учее никами, для каждого предмета можно указать имя учителя и количество проведенных уроков. Оценка, полученная учеником по предмету, относится к паре объектов «ученик—предмет». А вот имя педагога и количество уроков — это характеристики только предмета, но никак не ученика.
Таблица 10
Успеваемость учеников 4 «в»
а Предмет Учитель Количество
уроков Иванов Петя Петров Ваня ![]()
 в учебном
в учебном
|
Русский ЯЗЫК |
Кошкина |
160 |
![]()
|
|
|
Природо- Сидорова 64 ведение
![]()
Таблица типа ОСО строится следующим способом. Берется таблица типа «объекты—объекты» и «раздвигается»: прографка «отодвигается» от боковика и в освободившееся место вставляются новые графы со свойствами, которые относятся только к объектам, которые «командуют» строками, но не относятся к объектам, которые «командуют» графами.
Порядок построения таблицы типа ОСО.
1) Выделить объекты и свойства. Для этого внимательно прочитать текст. В каждой фразе подчеркнуть название первого объекта в паре одной прямой линией, название второго объекта в паре двумя прямыми, название одиночного свойства волнистой линией, название парного свойства двумя волнистыми линиями, значение свойства пунктиром.
2) Название парных свойств записать в заголовок таблицы.
З) Определить и назвать класс объектов, для которых указаны одиночные свойства. Название этого класса записать в заголовок боковика.
4) Названия одиночных свойств (они подчеркнуты волнистой линией) записать в головку рядом с заголовком боковика. Каждое свойство записывается в отдельную графу.
В оставшейся части таблицы (правее одиночных свойств) головка будет трехъярусной. Будем называть эту часть таблицы III частью.
5) Назвать класс объектов, для которых указаны только парные свойства, но не указаны одиночные. Название записать в верхний ярус головки в III часть таблицы.
6) Названия объектов первого класса записать в боковик.
7) Названия объектов второго класса записать в средний ярус головки в III часть таблицы.
8) Названия парных свойств (они подчеркнуты двойной волнистой линией) записать в нижний ярус головки в III часть таблицы, повторив их для каждого объекта из среднего яруса. 9) Значения свойств записать в прографку.
Замечание. Если парных свойств несколько, то таблица типа ОСО строится из таблицы типа ООН. В этом случае в части III головка будет трехъярусной, как и в таблице типа ООН. Если парное свойство только одно, то таблица типа ОСО строится из таблицы типа 00. В этом случае в части III головка будет двухъярусной, как и в таблице типа 00.
Важное замечание! В отличие от таблиц предыдущих типов таблицы типа ОСО НЕЛЬЗЯ «повернуть на бок». Те объекты, для которых указаны индивидуальные свойства (свойства, характеризующие отдельный объект, а не пару объектов), обязательно должны находиться в боковике.
Сведения, приведенные в задачах №12 — N215, предствьте в виде таблиц типа ООН.
В следующем тексте речь идет о движении поезда от Перми до Москвы и обратно. Поезд N2 21 идет от Перми до Москвы, поезд N2 22 — от Москвы до Перми. Поездка в одну сторону занимает около суток (днем выехали — на следующее утро приехали). Во времени отправления и прибытия часы и минуты разделяются точкой.
Время отправления поезда № 21 из Перми —12.10. Время прибытия поезда № 22 в Нижний Новгород — 1.22. Время отправления поезда № 22 из Владимира — 22.06. Время стоянки поезда № 22 в Нижнем Новгороде — 12 мин. Время отправления поезда № 21 из Кирова — 19.56. Время стоянки поезда № 21 в Кирове — 17 мин. Время стоянки поезда № 21 во Владимире — 20 мин. Время отправления поезда № 22 из Кирова — 8.04. Время прибытия поезда N2 21 в Нижний Новгород — 2.33. Время отправления поезда № 22 из Москвы — 19.00. Время прибытия поезда N2 21 во Владимир — 6.00. Время прибытия поезда № 21 в Киров — 19.39. Время стоянки поезда № 21 в Нижнем Новгороде —12 мин. Время отправления поезда № 21 из Владимира 6.20. Время отправления поезда N2 21 из Нижнего Новгорода — 2.45. Время прибытия поезда N2 22 во Владимир — 21.48. Время прибытия поезда № 22 в Киров — 7.48. Время отправления поезда № 22 из Нижнего Новгорода 1.34. Время стоянки поезда № 22 во Владимире — 18 мин. Время прибытия поезда N2 21 в Москву — 9.20. Время стоянки поезда № 22 в Кирове — 16 мин. Время прибытия поезда N2 22 в Пермь — 16.01.
В 1970 г. в СССР было произведено бумаги всего 4,2 млн т. В 1970 г. в СССР было произведено бумаги на душу населения 17 кг. В 1970 г. в Австрии было произведено бумаги всего 0,9 млн т. В 1989 г. в Австрии было произведено бумаги всего 2,3 млн т. В 1980 г. в Бельгии было произведено бумаги на душу населения 81 кг. В 1970 г. в Болгарии было произведено бумаги всего 0,2 млн т. В 1989 г. в СССР было произведено бумаги на душу населения 22 кг. В 1980 г. в Болгарии было произведено бумаги всего 0,3 млн т. В 1970 г. в Австрии было произведено бумаги на душу населения 118 кг. В 1989 г. в Великобритании было произведено бумаги всего 3,6 млн т. В 1980 г. в СССР было произведено бумаги всего 5,3 млн т. В 1970 г. в Бельгии было произведено бумаги на душу населения 68 кг. В 1989 г. в Великобритании было произведено бумаги на душу населения 63 кг. В 1980 г. в Австрии было произведено бумаги всего 1,3 млн т. В 1989 г. в Бельгии было произведено бумаги всего 1,1 млн т. В 1980 г. в Болгарии было произведено бумаги на душу населения 36 кг. В 1970 г. в Великобритании было произведено бумаги всего 3,6 млн т. В 1989 г. в СССР было произведено бумаги всего 6,3 млн т. В 1970 г. в Великобритании было произведено бумаги на душу населения 65 кг. В 1980 г. в Бельгии было произведено бумаги всего 0,8 млн т. В 1970 г. в Болгарии было произведено бумаги на душу населения 24 кг. В 1980 г. в Великобритании было произведено бумаги всего 3,0 млн т. В 1989 г. в Болгарии было произведено бумаги на душу населения 42 кг. В 1989 г. в Бельгии было произведено бумаги на душу населения 112 кг. В 1980 г. в СССР было произведено бумаги на душу населения 20 кг. В 1980 г. в Австрии было произведено бумаги на душу населения 176 кг. В 1970 г. в Бельгии было произведено бумаги всего О, 7 млн т. В 1980 г. в Великобритании было произведено бумаги на душу населения 54 кг. В 1989 г. в Болгарии было произведено бумаги всего 0,4 млн т. В 1980 г. в Бельгии было произведено бумаги всего 0,8 млн т.
![]()
В следующем тексте речь идет об урожаях сельскохозяйственных культур в России. Урожайность — это урожай, собранный с одного гектара. Валовый сбор — это весь собранный урожай.
Урожайность картофеля в 1995 г. составила 117 ц с га. Валовый сбор зерновых культур в 1990 г. составил 116,7 млн т. Валовый сбор картофеля в 1995 г. составил 39,7 млн т. Урожайность сахарной свеклы в 1985 г. составила 211 ц с га. Валовый сбор овощей в 1985 г. составил 11,1 млн т. Валовый сбор сахарной свеклы в 1995 г. составил 19,1 млн т. Урожайность зерновых культур в 1995 г. составила 11,6 ц с га. Валовый сбор зерновых культур в 1995 г. составил 63,5 млн т. Урожайность овощей в 1990 г. составила 154 ц с га. Валовый сбор сахарной свеклы в 1990 г. составил 31,1 млн т. Валовый сбор картофеля в 1985 г. составил 33,9 млн т. Урожайность сахарной свеклы в 1995 г. составила 176 ц с га. Урожайность картофеля в 1990 г. составила 99 ц с га. Валовый сбор овощей в 1990 г. составил 10,3 млн т. Урожайность овощей в 1985 г. составила 153 ц с га. Урожайность сахарной свеклы в 1990 г. составила 213 ц с га. Валовый сбор зерновых культур в 1985 г. составил 98,6 млн т. Урожайность картофеля в 1985 г. составила 96 ц с га. Валовый сбор овощей в 1995 г. составил 11,2 млн т. Валовый сбор сахарной свеклы в 1985 г. составил 31,5 млн т. Урожайность овощей в 1995 г. составила 140 ц с га. Урожайность зерновых культур в 1985 г. составила 14,5 ц с га. Валовый сбор картофеля в 1990 г. составил 30,9 млн т. Урожайность зерновых культур в 1990 г. составила 18,5 ц с га.
Сведения, приведенные в задачах N2 16 — № 18, представьте в виде таблиц типа ОСО.
Г.Г2 16
Северное полушарие имеет общую площадь 255,1 млн кв. км. В северном полушарии суша занимает площадь в 100,5 млн кв. км. Доля северного полушария, занятая сушей, составляет 39,4 0/0 . В северном полушарии вода занимает площадь в 154,6 млн кв. км. Доля северного полушария, занятая водой, составляет 60,6 0/0 .
Южное полушарие имеет общую площадь 255,1 млн кв. км. В южном полушарии суша занимает площадь 48,5 млн кв. км. Доля южного полушария, занятая сушей, составляет 19,0 0/0 . В южном полушарии вода занимает площадь 206,6 млн кв. км. Доля южного полушария, занятая водой, составляет 81,0 0/0 .
Земля в целом имеет общую площадь 510,2 млн кв. км. На Земле в целом суша занимает площадь 149,0 млн кв. км. Доля Земли в целом, занятая сушей, составляет 29,2 % . На Земле в целом вода занимает площадь 361,2 млн кв. км. Доля Земли в целом, занятая водой, составляет 70,8 0/0 .
![]()
Территория Южной Америки — 17,8 млн кв. км. Население Европы в 1989 г. составило 701 млн человек. Плотность населения в Африке в 1989 г. была 21 человек на кв. км. Территория Австралии и Океании — 8,5 млн кв. км. Население Северной и Центральной Америки в 1989 г. составило 422 млн. человек. Плотность населения в Северной и Центральной Америке в 1970 г. была 13 человек на кв. км. Территория всего мира — 135,8 млн кв. км. Плотность населения в Австралии и Океании в 1989 г. была З человека на кв. км. Население Южной Америки в 1989 г. составило 291 млн человек. Территория Африки — 30,3 млн кв. км. Население Австралии и Океании в 1989 г. составило 26 млн человек. Плотность населения во всем мире в 1970 г. была 27 человек на кв. км. Территория Азии — 44,4 млн кв. км. Население всего мира в 1989 г. составило 5201 млн человек. Территория Северной и Центральной Америки — 24,3 млн кв. км. Население Азии в 1970 г. составило 2161 млн человек. Плотность населения в Европе в 1989 г. была 67 человек на кв. км. Плотность населения в Азии в 1970 г. была 49 человек на кв. км. Население Африки в 1970 г. составило 361 млн человек. Население Австралии и Океании в 1970 г. составило 19 млн человек. Население Южной Америки в 1970 г. составило 190 млн человек. Плотность населения в Африке в 1970 г. была 12 человек на кв. км. Население Северной и Центральной Америки в 1970 г. составило 320 млн человек. Плотность населения в Южной Америке в 1970 г. была 11 человек на кв. км. Население Африки в 1989 г. составило 628 млн человек. Плотность населения в Австралии и Океании в 1970 г. была 2 человека на кв. км. Население Европы в 1970 г. составило 642 млн человек. Плотность населения во всем мире в 1989 г. была 38 человек на кв. км. Территория Европы — 10,5 млн кв. км. Плотность населения в Северной и Центральной Америке в 1989 г. была 17 человек на кв. км. Плотность населения в Европе в 1970 г. была 61 человек на кв. км. Население Азии в 1989 г. составило 3133 млн человек. Плотность населения в Южной Америке в 1989 г. была 16 человек на кв. км. Население всего мира в 1970 г. составило 3693 млн человек. Плотность населения в Азии в 1989 г. была 71 человек на кв. км.
В следующем тексте речь идет о движении поездов от Перми до Москвы. Поездка занимает около суток (днем выехали — на следующее утро приехали). При указании времени часы и минуты разделяются точкой.
2.3.5. Вычислительные таблицы
![]() Вычислительными будем
называть такие таблицы, в которых значения некоторых свойств вычисляются с
использованием значений других свойств из этой же таблицы. Например, после
посещения магазина школьник составил «финансовый отчет» для своей мамы в форме
следующей таблицы:
Вычислительными будем
называть такие таблицы, в которых значения некоторых свойств вычисляются с
использованием значений других свойств из этой же таблицы. Например, после
посещения магазина школьник составил «финансовый отчет» для своей мамы в форме
следующей таблицы:
Таблица 11
Поход за покупками

Очевидно, что это таблица типа «объект—свойство». В ней значения в графе «Стоимость» вычислялись по формуле: Цена х Количество.
Пример 11. Незнайка, Торопыжка и Кнопочка
летом занялись выращиванием овощей. Когда собрали урожай, ![]() оказалось,
что Незнайка вырастил 40 кг капусты, 15 кг моркови, 10 кг огурцов и 18 кг лука.
Торопыжка вырастил 50 кг капусты, 25 кг моркови, 12 кг огурцов и 2 кг лука.
Кнопочка вырастила 30 кг капусты, 30 кг моркови, 20 кг огурцов и 5 кг лука.
Вопросы: Сколько всего овощей вырастил каждый из человечков? Какое общее
количество овощей одного вида вырастили все три человечка вместе? И, наконец,
сколько всего овощей было собрано?
оказалось,
что Незнайка вырастил 40 кг капусты, 15 кг моркови, 10 кг огурцов и 18 кг лука.
Торопыжка вырастил 50 кг капусты, 25 кг моркови, 12 кг огурцов и 2 кг лука.
Кнопочка вырастила 30 кг капусты, 30 кг моркови, 20 кг огурцов и 5 кг лука.
Вопросы: Сколько всего овощей вырастил каждый из человечков? Какое общее
количество овощей одного вида вырастили все три человечка вместе? И, наконец,
сколько всего овощей было собрано?
Решение. Первый этап решения задачи: занести всю исходную информацию в таблицу (это будет таблица типа «объект—объект» ).
Таблица 12 Урожай овощей, кг
![]()
![]() Человечек Овощи
Человечек Овощи
![]()
Капуста Морковь Огурцы лук
![]() 40
40 ![]() 15 18
15 18
![]()
![]()
![]()
![]()
Второй этап решения задачи: добавить в таблицу итоговую строку и итоговую графу.

Именно это последнее число удобно использовать для контроля правильности вычислений. Дело в том, что получить его можно двумя разными способами. Общий вес выращенных овощей можно определить, сложив веса овощей, выращенных каждым из человечков, т. е. вычислив сумму чисел, стоящих в итоговой графе: 83 + 89 + 85 = 257. А можно это же самое число получить, сложив веса овощей всех видов, выращенных всеми человечками, т. е. вычислив сумму чисел, стоящих в итоговой строке: 120 + 70 + 42 + 25 257. Понятно, что обе эти суммы должны совпадать. А произойдет это в том случае, если все вычисления были выполнены правильно. (Либо были допущены несколько ошибок, компенсирующих друг друга, но это представляется слишком маловероятным.) Следовательно, для контроля правильности вычислений достаточно посчитать число, стоящее в правом нижнем углу таблицы, дважды как сумму итоговой графы и как сумму итоговой строки.
Такое контрольное вычисление иногда называют «проверка уголком » .
.М2 19 Воздушный шар
Есть возможность отправиться в путешествие на воздушном шаре. Каждый аэронавт должен взять с собой вещи и продукты питания. Сформируйте из своих друзей экипаж шара (5 человек). Про каждого аэронавта нужно знать его вес (для каждого — свой), вес взятых им вещей и продуктов (пусть все веса будут разные). Составьте таблицу, по которой можно посчитать вес каждого аэронавта вместе с его вещами и продуктами, вес всех аэронавтов, всех вещей и всех продуктов, а также суммарный вес, который должен поднять шар. Проверьте последнюю величину, вычислив ее «уголком» .
.М2 20
Постройте таблицу, из которой будет видно, какое оборудование нужно закупить для каждого школьного кабинета и сколысо всего единиц оборудования каждого вида должна закупить школа.
Для кабинета математики нужен 1 шкаф. Для кабинета информатики нужно 30 столов. Для кабинета начальных классов нужен 1 стол. Для кабинета начальных классов нужно 4 шкафа. Для кабинета математики нужен 21 стол. Для кабинета начальных классов нужно 40 одноместных парт. Для кабинета математики нужен 21 стул. Для кабинета информатики нужно 2 шкафа. Для кабинета начальных классов нужно 2 доски. Для кабинета математики нужна 1 доска. Для кабинета информатики нужно 30 стульев. Для кабинета начальных классов нужен 1 стул. Для кабинета информатики нужно 11 компьютеров.
Вычисления в таблицах типа «объекты—свойства—объекты».
![]() Составим
таблицу «Поход за покупками» с информацией о покупке продуктов в течение не
одного дня (как в табл. 11), а трех (понедельника, вторника и среды).
Составим
таблицу «Поход за покупками» с информацией о покупке продуктов в течение не
одного дня (как в табл. 11), а трех (понедельника, вторника и среды).
Во-первых, определим тип таблицы. Здесь можно выделить объекты двух классов: товары и дни недели. Существуют свойСТВа, которые относятся к паре объектов «товар—день недели» (например, количество товара, купленное в этот день), а есть свойство, который относится только к товару, но не относится к дню недели — цена товара. Значит в данном случае мы имеем дело с таблицей типа ОСО — «объекты—свойства—объекты». Поскольку свойство, характеризующее объекты только одного класса (цена), относится к объектам класса «товар», товары придется разместить в боковике, а дни недели в головке. Для цены в этом случае следует выделить отдельную графу.
Следующий вопрос: а сколько имеется свойств, которые относятся сразу к паре объектов «товар—день»? Таких свойств два: количество товара, купленное в этот день, и стоимость этого товара. Проведенные рассуждения позволяют построить таблицу следующего вида:
Таблица 14
Поход за покупками
![]()
Товар![]() День недели
День недели
![]()
руб. Понедельник Вторник Среда
![]()
|
Кол-во |
Ст-ть, |
Кол-во |
Ст-ть, |
Кол-во |
Ст-ть, |
|
|
руб. |
|
руб. |
|
руб. |
![]() Масло
Масло
22
Творог 5 10 З кг 15
Добавив итоговую графу и итоговую строку, мы узнаем, сколько всего единиц товара каждого вида было куплено за три дня, сколько стоил этот товар, сколько денег было затрачено каждый день и за все время. Для удобства подсчета сумм по строкам несколько изменим запись. Пусть информация о каждом продукте занимает не одну строку, а две: это даст возможность при вычислениях «по строке» не путать рубли с килограммами.
Таблица 15
Поход за покупками
![]()
![]()
руб. Понедельник Вторник Среда Кол-во
Ст-ть, ![]()
![]()
Кол-во Ст-ть, Кол-во Ст-ть, Кол-во Ст-ть. руб. руб. руб. руб.
![]()
Масло 24 24 24 48
1 кг 2 кг
![]()
![]()
![]() 2 кг
2 кг
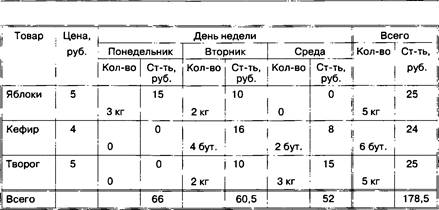
(Т ![]() З ад а ч и
З ад а ч и
В задачах 21 — 31 по текстам построить вычислительные таблицы, с помощью которых можно будет ответить на заданные вопросы.
.М2 21 Веселые человечки. Торты
Сладкоежка Пончик решил испечь на свой день рождения З торта: яблочный, ореховый и шоколадный. Для приготовления одного яблочного торта требуется 200 г сливочного масла, 200 г муки, 2 яйца, ЗОО г сахара и 8 яблок. Для приготовления одного орехового торта надо 200 г орехов, 400 г муки, ЗОО г сахара, ЗОО г масла и З яйца. На один шоколадный торт тратится З шоколадки, 2 яйца, ЗОО г муки, 200 г масла и 100 г сахара. Масло в Цветочном городе стоит 100 монет за кг, сахар — 20 монет за кг, яйца — 20 монет за десяток, мука — 30 монет за кг, орехи — 100 монет за кг, яблоки — 2 монеты за штуку, шоколадки — 10 монет за штуку.
Сколько будет стоить каждый торт? Сколько продуктов каждого вида Пончик должен купить и сколько это будет стоить? Сколько всего денег он должен взять с собой в магазин, отправляясь за продуктами?
М 22 Веселые человечки. Продажа газет
Во время каникул Незнайка решил поработать продавцом газет и проработал целую неделю. За каждый проданный экземпляр газеты «Известия Цветочного города» он получал 10 монет. За каждый экземпляр «Технической газеты Винтика и Шпунтика» — 7 монет. За каждый экземпляр «Медицинских новостей доктора Медуницы» — 8 монет.
В понедельник он продал 8 экземпляров «Известий», 7 экземпляров «Технической газеты» и 5 экземпляров «Медицинских новостей». Во вторник было продано 13 экземпляров «Известий», 4 экземпляра «Технической газеты» и 8 экземпляров «Новостей». В среду — 10
![]()
«Известий», 10 «Технических» и 12 «Новостей». В четверг — 8 «Известий», 7 «Технических газет» и 15 «Медицинских новостей». В пятницу — 10 штук «Известий», 5 штук «Технических» и 8 штук «Медицинских». В субботу — 9 «Известий», 13 «Технических газет» и 8 «Медицинских новостей». В воскресенье — 5 экземпляров «Известий», 6 экземпляров «Технической» и 9 экземпляров «Медицинской » .
Сколько экземпляров каждой газеты Незнайка продавал за каждый день недели и сколько — за всю неделю; сколько денег он зарабатывал за каждый день недели и сколько — за всю неделю; сколько денег он получал за продажу каждой газеты за всю неделю?
Л) 23 Веселые человечки. Напитки
Собираясь на пляж, веселые человечки решили запастись питьем. Незнайка
взял с собой 2 литра кваса и литр газировки, Пончик ![]() литр газировки и З литра малинового
сиропа, Винтик и Шпунтик вместе взяли З литра кваса и 2 литра газировки,
Торопыжка
литр газировки и З литра малинового
сиропа, Винтик и Шпунтик вместе взяли З литра кваса и 2 литра газировки,
Торопыжка ![]() З литра газировки, доктор Пилюлькин — 1 литр кваса и 1 литр касторки. 1
литр кваса в Цветочном городе стоит 1 монету, 1 литр газировки — З монеты, 1
литр касторки — 2 монеты, 1 литр сиропа — 6 монет.
З литра газировки, доктор Пилюлькин — 1 литр кваса и 1 литр касторки. 1
литр кваса в Цветочном городе стоит 1 монету, 1 литр газировки — З монеты, 1
литр касторки — 2 монеты, 1 литр сиропа — 6 монет.
Сколько всего напитков взял с собой каждый из человечков и сколько это ему стоило; какое количество напитка каждого вида взяли все человечки вместе и сколько это стоило; сколько всего было взято жидкости и сколько потрачено денег всеми человечками вместе?
![]() 24 Веселые
человечки. Охота
24 Веселые
человечки. Охота
Охотник Пулька всегда берет с собой на охоту собаку Бульку, которая загоняет для него зверя. Для того, чтобы загнать зайца, Булька должна пробежать 8 км, чтобы загнать волка — 15, лису — 10. За декабрь Пулька добыл 5 зайцев и одного волка, за январь — 8 зайцев, 2 волков и 2 лис, за февраль — лису, 6 зайцев и 2 волков, за март — 4 волков, З лис и 5 зайцев.
Сколько зверей каждого вида добыл Пулька за сезон; сколько
всего зверей он добывал каждый месяц и сколько — за весь сезон; сколько
километров пришлось Бульке пробежать на охоте за каждый месяц, сколько — за
весь сезон и сколько ![]() в погоне за зверями одного вида?
в погоне за зверями одного вида?
![]() 25 Веселые
человечки. Путешествия
25 Веселые
человечки. Путешествия
Во время каникул веселые человечки отправились путешествовать на разных видах транспорта. Незнайка проплыл 50 км на пароходе, проехал 40 км на поезде и пролетел 100 км на самолете. Поэт Цветик проплыл на пароходе 100 км и проехал на поезде 20 км. Торопыжка пролетел на самолете 200 км и проехал поездом 10 км. Доктор Медуница проехала на поезде 30 км и проплыла на пароходе 60 км. Стоимость проезда на поезде составляет 1 монету за км, на пароходе — 2 монеты за км, на самолете — 4 монеты за км.
информационные модели
![]()
Какое расстояние проехал каждый из человечков и сколько денег он заплатил за дорогу; какое расстояние все человечки вместе проехали на каждом виде транспорта и сколько им это стоило; сколько денег все человечки вместе заплатили за все виды транспорта?
Л) 26 Веселые человечки. Пирожки
Веселые человечки решили сходить в поход. Пончик испек для всех пирожки с мясом, яблоками, капустой и повидлом и разложил их по пакетам, кулькам и коробкам. Пирожков с мясом оказалось З коробки, 2 кулька и З пакета. Пирожков с яблоками — 5 пакетов, 1 кулек и 2 коробки. Пирожков с повидлом — 6 кульков и 1 коробка. Пирожков с капустой — 2 пакета, 1 коробка и 1 кулек. В коробку вмещается 20 пирожков, в пакет — 25, в кулек — 15.
Сколько всего пирожков испек Пончик и сколько среди них было пирожков каждого сорта; сколько пирожков было уложено в упаковку каждого вида; сколько всего упаковок понадобилось Пончику и сколько среди них было упаковок каждого вида?
.М2 27 Веселые человечки. Горючее
Как известно, автомобиль, изобретенный Винтиком и Шпунтиком, работает не на бензине, а на газировке разных сортов. На одном литре лимонада он проезжает 120 км, на одном литре кока-колы — 100 км, на одном литре фанты — 150 км. Цена одного литра фанты в Цветочном городе З монеты за литр, лимонада 1 монета за литр, кока-колы — 2 монеты за литр.
Готовясь к путешествию, Незнайка закупил 10 литров кока-колы, 5 литров лимонада и 10 литров фанты. Винтик и Шпунтик вместе купили 10 јштров лимонада и 10 литров фанты. Торопыжка — 5 литров фанты, 10 — кока-колы и 10 — лимонада. Поэт Цветик — 20 литров фанты. Сколько всего литров горючего купил каждый из человечков, сколько ему это стоило и какое расстояние он может проехать на этом горючем; сколько всего было куплено горючего каждого вида всеми человечками вместе, сколько это стоило и какое расстояние можно проехать на этом горючем; сколько всего горючего всех видов было куплено всеми человечками и сколько оно стоило?
ЛЕ 28 Калорийность обеда
Из одного грамма углеводов человек получает 4,1 ккал, из одного грамма жиров — 9,3 ккал, из одного грамма белков — 4,2 ккал. Порция борща со свежей капустой содержит 3,6 г белков, 12 г жиров и 24 г углеводов.
Порция гуляша — 24,3 г белков, 24 г жиров, 7 г углеводов.
Порция картофеля с маслом — 2,7 г белков, 7 г жиров и 39 г углеводов.
![]()
Порция компота из свежих фруктов содержит 0,4 г белков, 36 г углеводов и не содержит жиров. Сколько энергии вы получите
— из белков, жиров и углеводов, содержащихся в каждом блюде;
— из каждого блюда;
— отдельно из белков, жиров и углеводов, входящих в обед; — из всего обеда?
![]() 29 Дракон
Сергей Михайлович
29 Дракон
Сергей Михайлович
В пещере у реки поселился огнедышащий дракон по имени Сергей Михайлович. Всех, кто пытался его прогнать, он прогонял сам, полыхая на них огнем. Количество полыханий зависело от того, на кого надо полыхать. На царевича дракон полыхал 5 раз, на королевича — 4 раза, на простого рыцаря — З.
За первые сто лет дракона пытались прогнать 2 царевича, З королевича и 5 простых рыцарей. За второе столетие на него покушались З царевича, 2 королевича и 7 простых рыцарей. За третий век дракона беспокоили 7 царевичей, 5 королевичей и 6 простых рыцарей. За следующее столетие Сергею Михайловичу пришлось иметь дело с З царевичами, 6 королевичами и 10 простыми рыцарями. После чего дракона в конце концов оставили в покое и объявили гору, на которой он жил, заповедником для охраны редких видов животных.
Сколько человек пытались прогнать дракона за каждое из столетий в отдельности и за все 4 века вместе; сколько среди них было царевичей, сколько королевичей и сколько простых рыцарей; сколько раз дракону пришлось полыхать на них огнем в течение каждого века и за все 4 столетия вместе; сколько полыханий досталось царевичам, сколько королевичам и сколько простым рыцарям?
![]() зо Старик
Хоттабыч сдает экзамены
зо Старик
Хоттабыч сдает экзамены
Старик Хоттабыч взялся помочь своим друзьям сдать экзамены. Для того, чтобы наколдовать правильный ответ на один вопрос по географии, он должен вырвать из своей бороды 6 волосков, чтобы наколдовать правильный ответ на один вопрос по математике — 10 волосков, правильный ответ на один вопрос по русскому языку — 8 волосков.
Вольке-ибн-Алеше досталось: на экзамене по географии — З вопроса, на экзамене по математике — 5 вопросов, на экзамене по русскому языку — 2 вопроса.
Женьке досталось: на экзамене по географии — 4 вопроса, на экзамене по математике — З вопроса, на экзамене по русскому языку — 4 вопроса.
Гоге-Пилюле досталось: на экзамене по географии — 2 вопроса, на экзамене по математике — 4 вопроса, на экзамене по русскому языку — 5 вопросов.
И, наконец, самому Хоттабычу: на экзамене по географии — 5 вопросов, на экзамене по математике — 2 вопроса, на экзамене по русскому языку — З вопроса.
информационные модели
![]()
Сколько волосков пришлось вырвать Хоттабычу из своей 60роды для того, чтобы помочь каждому из своих друзей (и себе самому тоже); сколько волосков пошло на сдачу экзаменов по каждому из предметов? Посчитайте, сколько всего волосков пришлось вырвать Хоттабычу, и проверьте результат «уголком».
![]() 31 Почта
дяде Федору
31 Почта
дяде Федору
Дядя Федор, кот Матроскин и пес Шарик летом жили в Простоквашино, а папа с мамой отправляли им письма, посылки, телеграммы и бандероли, которые доставлял почтальон Печкин. Каждое письмо весило в среднем 100 г, каждая посылка — 5 кг, каждая телеграмма — 50 г, каждая бандероль — 500 г.
Дядя Федор получил 10 писем, 2 посылки, 10 телеграмм и 1 бандероль. Кот Матроскин получил 4 письма, 1 посылку, 2 телеграммы и 1 бандероль. Пес Шарик не получил ни одного письма, ни одной телеграммы, зато получил 4 посылки и 2 бандероли.
Сколько и какой почты получил каждый из трех жителей Простоквашино; сколько килограммов почты получил каждый из трех простоквашинцев; сколько весила вся доставленная Печкиным почта одного вида; какой общий груз пришлось перенести почтальону Печкину? Проверьте последнее число «уголком» .
З
![]()
Компьютерная информация и архитектура ЭЂМ
![]()
З. 1.1. Структура внутренней памяти
Основные структурные единицы памяти компьютера: бит, байт, машинное слово.
Бит. Все данные и программы, хранящиеся в памяти компьютера, имеют вид двоичного кода. Один символ из двухсимвольного алфавита несет 1 бит информации. Ячейка памяти, хранящая один двоичный знак, называется «бит». В одном бите памяти хранится один бит информации.
Битовая структура памяти определяет первое свойство памяТИ Дискретность.
Байт. Восемь расположенных поДряД битов памяти образуют байт. В одном байте памяти хранится один байт информации. Во внутренней памяти компьютера все байты пронумерованы. Нумерация начинается от нуля. Порядковый номер байта называется его адресом. В компьютере адреса обозначаются двоичным кодом. Используется также шестнадцатеричная форма обозначения адреса.
Пример 1. Компьютер имеет оперативную память 2 Кбайт. Указать адрес последнего байта оперативной памяти (десятичный, шестнадцатеричный, двоичный).
Решение. Объем оперативной памяти составляет 2048 байт. Десятичный адрес (номер) последнего байта равен
![]() Машинное слово.
Последовательность битов, которую процессор может обрабатывать как еДиное
целое, называют машинным словом. Длина машинного слова может быть разной — 8,
16, 32 бита и т. д. Адрес машинного слова в памяти компьютера равен адресу
младшего байта, входящего в это слово.
Машинное слово.
Последовательность битов, которую процессор может обрабатывать как еДиное
целое, называют машинным словом. Длина машинного слова может быть разной — 8,
16, 32 бита и т. д. Адрес машинного слова в памяти компьютера равен адресу
младшего байта, входящего в это слово.
Занесение информации в память, а также извлечение ее из памяти производится по адресам. Это свойство памяти называется адресуемостью.
![]() Пример 2. Объем
оперативной памяти компьютера равен 1 Мбайт, а адрес последнего машинного слова
— 1 048 574.
Пример 2. Объем
оперативной памяти компьютера равен 1 Мбайт, а адрес последнего машинного слова
— 1 048 574. ![]() Чему равен размер машинного слова?
Чему равен размер машинного слова?
Решение. 1 Мбайт = 1024 Кбайта — 1 048 576 байт. Так как нумерация байтов начинается с нуля, значит адрес последнего байта будет равен 1 048 575. Таким образом, последнее машинное слово включает в себя 2 байта с номерами 1 048 574 и 1 048 575. Ответ: 2 байта.
![]()
Оперативная память компьютера содержит 163 840 машинных слов, что составляет 0,625 Мбайт. Сколько битов содержит каждое машинное слово?
Объем оперативной памяти компьютера составляет 1/8 часть Мбайта. Сколько машинных слов составляют оперативную память, если одно машинное слово содержит 64 бита?
Вы работаете на компьютере с 4-байтовым машинным словом. С каким шагом меняются адреса машинных слов?
Компьютер имеет объем оперативной памяти 0,5 Кбайт. Адреса машинных слов меняются с шагом 4. Сколько машинных слов составляют оперативную память компьютера?
Компьютер имеет объем оперативной памяти 0,5 Кбайт. Адреса машинных слов меняются с шагом 2. Сколько машинных слов составляют оперативную память компьютера?
Компьютер имеет объем оперативной памяти 1 Кбайт. Адреса машинных слов меняются с шагом 2. Сколько машинных слов составляют оперативную память компьютера?
Какой объем имеет оперативная память компьютера, если 3FF — шестнадцатеричный адрес последнего байта оперативной памяти?
5 Информатика и ИКТ. Т. I
Какой объем имеет оперативная память компьютера, если FF — шестнадцатеричный адрес последнего байта оперативной памяти?
Г.Г2 10
FE — шестнадцатеричный адрес последнего машинного слова оперативной памяти компьютера, объем которой составляет 1/4 Кбайт. Найти длину машинного слова (в байтах).
ЛЕ 11
1FC — шестнадцатеричный адрес последнего машинного слова оперативной памяти компьютера, объем которой составляет 1/2 Кбайт. Найти длину машинного слова (в байтах).
ЛЕ 12
Какой объем имеет оперативная память компьютера, если FC — шестнадцатеричный адрес последнего 4-байтового машинного слова оперативной памяти?
Компьютер имеет объем оперативной памяти равный 1/2 Кбайта и содержит 128 машинных слов. Укажите адрес последнего байта и адрес последнего машинного слова памяти компьютера (в шестнадцатеричной форме).
Г.Г2 15
Компьютер имеет объем оперативной памяти равный 1 Кбайт и содержит 512 машинных слов. Укажите адрес последнего байта и адрес последнего машинного слова памяти компьютера (в шестнадцатеричной форме).
З. 1.2. Структура дисков; файлы и каталоги
![]() Внешняя память компьютера
используется для длительного хранения информации.
Внешняя память компьютера
используется для длительного хранения информации.
Устройства внешней памяти: магнитные диски и ленты, оптические (лазерные) диски, магнитооптические диски.
Дисководы — устройства чтения [записи информации на диски. Различают гибкие магнитные диски (дискеты) и жесткие магнитные диски. Жесткие магнитные диски встроены в дисковод и в отличие от дискет являются несъемными.
Структура магнитного диска: одна или несколько сторон (магнитных поверхностей), разделенных на концентрические Дорожки, каждая из которых, в свою очередь, поделена на сектора, состоящие из «клеточек» — байтов. Все секторы на одном диске имеют фиксированный размер. Вся работа по считыванию и записи данных на дисках производится только полными секторами. Полный объем памяти диска определяется формулой:
ОБЪЕМ = СТОРОНЫ х ДОРОЖКИ х СЕКТОРЫ х БАЙТЫ,
где СТОРОНЫ — количество сторон диска, ДОРОЖКИ — количество дорожек на стороне, СЕКТОРА — количество секторов на дорожке, БАЙТЫ — количество байт в секторе.
Информация на устройствах внешней памяти имеет файловую организацию. Файл — поименованная совокупность данных, хранящихся на внешнем носителе.
Файловая структура диска — это совокупность файлов на диске и взаимосвязей между ними.
Каталог — это поименованная совокупность файлов и подкаталогов (т. е. вложенных каталогов). Каталог самого верхнего уровня иерархии называется корневым. Он не вложен ни в какие другие каталоги.
Путь к файлу — это последовательность, состоящая из имен каталогов (разделенных символом «Х»), начиная от корневого и заканчивая тем, в котором непосредственно хранится файл.
Полное имя файла состоит из имени логического диска, пути к файлу и имени файла. В одном каталоге не может быть нескольких файлов и каталогов с одинаковыми именами. В разных каталогах это допустимо.
Дерево — это графическое изображение иерархической файловой структуры диска.
![]() Пример 1. Дано дерево файловой структуры диска. Заглавными
буквами обозначены имена каталогов, строчными — имена файлов.
Пример 1. Дано дерево файловой структуры диска. Заглавными
буквами обозначены имена каталогов, строчными — имена файлов.
Перечислить имена каталогов 1-го, 2-го, 3-го уровней. Указать путь к файлу letter.txt от корневого каталога. Указать путь к файлу letter1.doc от корневого каталога, а к файлу letter2.doc — от каталога WORk. Указать полные имена файлов
![]() корневой DOC1
корневой DOC1
каталог DOCUMENT letter1.doc
WORk DOC2 -я— letter2.doc
UROk
letter.txt и letter1.doc, если файловая структура хранится на диске С.
Решение. Каталоги 1-го уровня COMPUTER, WORk, UROk. Каталоги 2-го уровня — ТМ, APPLE, DOCUMENT, PRINT. Каталоги 3-го уровня — DOC1, DOC2.
![]() Путь к файлу
letter.txt от корневого каталога: \WORk\PRINT. Путь к файлу letter1.doc от
корневого каталога: путь к файлу letter2.doc от ка-
Путь к файлу
letter.txt от корневого каталога: \WORk\PRINT. Путь к файлу letter1.doc от
корневого каталога: путь к файлу letter2.doc от ка-
талога
Полные имена файлов letter.txt и letter1.doc:
![]()
![]()
Двусторонняя дискета имеет объем 1200 Кбайт. Сколько дорожек на одной стороне дискеты, если каждая дорожка содержит 15 секторов по 4096 битов?
Какой объем имеет двусторонняя дискета, если каждая сторона ее разбита на 80 дорожек по 20 секторов на дорожке? Объем каждого сектора составляет 0,5 Кбайт.
Какой объем имеет каждый сектор двусторонней дискеты емкостью 1440 Кбайт, если каждая сторона дискеты разбита на 80 дорожек по 18 секторов на дорожке?
Сколько файлов размером 100 Кбайт каждый можно разместить на дискете объемом: 1) 1,2 Мбайт; 2) 1,44 Мбайт?
В результате повреждения односторонней дискеты 10 0/0 секторов оказались дефектными, что составило 36 864 байта. Какой объем имеет дискета?
Л) 21
На скольких дискетах емкостью 1440 Кбайт можно разместить содержимое жесткого диска объемом 1 Гбайт?
Г.Г2 22
Односторонняя дискета имеет объем 180 Кбайт. Сколько дорожек на диске, если каждая из них содержит 9 секторов, а в каждом секторе размещается по 1024 символа из 16-символьного алфавита?
Л) 23
Текст, записанный с помощью 16-символьного алфавита, занимает 10 полных секторов на односторонней дискете объемом 180 Кбайт. Дискета разбита на 40 дорожек по 9 секторов. Сколько символов содержит этот текст?
Г.Г2 24
Какой объем имеет двусторонняя дискета, если каждая сторона содержит 40 дорожек по 9 секторов, а в каждом секторе размещается 512 символов из 256-символьного алфавита?
Г.Г2 25
FREND
mikle.txt МАНУkate.txt mary.txt mikle.txt
GAMES
NICOL peter.txt
Найти ошибки в файловой структуре.
Г.Г2 26
Дано дерево иерархической файловой структуры на магнитном диске. Заглавными буквами обозначены имена каталогов, строчными — имена файлов:
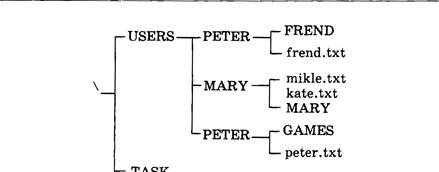
TASk
Найти ошибки в файловой структуре.
![]() 27
27
Дано дерево иерархической файловой структуры на магнитном диске. Заглавными буквами обозначены имена каталогов, строчными — имена файлов:
Перечислить каталоги 1-го, 2-го, 3-го уровней, если они есть.
Указать пути от корневого каталога к каждому из файлов.
Указаны пути от корневого каталога к некоторым файлам, хранящимся на магнитном диске. Заглавными буквами обозначены имена каталогов, строчными — имена файлов:

Отобразить файловую структуру в виде дерева.
Л) 29
Указаны пути от корневого каталога к некоторым файлам, хранящимся на магнитном диске. Заглавными буквами обозначены имена каталогов, строчными — имена файлов:

Отобразить файловую структуру в виде дерева.
![]()
Указаны пути от корневого каталога к некоторым файлам, хранящимся на магнитном диске. Заглавными буквами обозначены имена каталогов, строчными — имена файлов: \SPORT\SkI\russia.txt; \SPORT\SkI\germany.txt;
![]()
Отобразить файловую структуру в виде дерева.
З. 1.3. Представление символьной информации
![]() Для представления
текстовой (символьной) информации в компьютере используется алфавит мощностью
256 символов. Один символ из такого алфавита несет 8 битов информации, так как
2 8 256. Но 8 битов
Для представления
текстовой (символьной) информации в компьютере используется алфавит мощностью
256 символов. Один символ из такого алфавита несет 8 битов информации, так как
2 8 256. Но 8 битов ![]() = 1 байту, следовательно, Двоичный код
каждого символа в компьютерном тексте занимает 1 байт памяти.
= 1 байту, следовательно, Двоичный код
каждого символа в компьютерном тексте занимает 1 байт памяти.
Пример 1. Сколько
битов памяти компьютера займет ![]() слово «микропроцессор»?
слово «микропроцессор»?
Решение. Слово состоит из 14 букв. Каждая буква является символом компьютерного алфавита и поэтому занимает 1 байт памяти. Слово займет 14 байт = 112 битов памяти, т. к. 1 байт 8 битов.
![]() Таблица кодировки —
это таблица, в которой устанавливается соответствие между символами и их
порядковыми номерами в компьютерном алфавите.
Таблица кодировки —
это таблица, в которой устанавливается соответствие между символами и их
порядковыми номерами в компьютерном алфавите.
Все символы компьютерного алфавита пронумерованы от О до 255. Каждому номеру соответствует 8-разрядный
![]()
вый номер символа в двоичной системе счисления.
Для разных типов ЭВМ используются различные таблицы кодировки. С распространением персональных компьютеров типа IBM РС международным стандартом стала таблица кодировки под названием ASCII (American Standard Code for Information Interchange) — Американский стандартный код для информационного обмена.
Стандартными в этой таблице являются только первые 128 символов, т. е. символы с номерами от нуля (двоичный код
![]()
алфавита, цифры, знаки препинания, скобки и некоторые другие символы. Остальные 128 кодов, начиная со 128 (двоичный
![]()
дировки букв национальных алфавитов, символов псевдографики и научных символов (например, символы 2, или ±). В русских национальных кодировках в этой части таблицы размещаются символы русского алфавита.
Принцип последовательного кодирования алфавита: в кодовой таблице ASCII латинские буквы (прописные и строчные) располагаются в алфавитном порядке. Расположение цифр также упорядочено по возрастанию значений. Данное правило соблюдается и в других таблицах кодировки. Благодаря этому и в машинном представлении для символьной информации сохраняется понятие «алфавитный порядок» .
В Приложении 2 в 1-й таблице приведена стандартная часть (управляющие коды — от 00 до 31 — в данную таблицу не включены) кода ASCII. Во 2-й таблице дан фрагмент альтернативной части кода ASCII, содержащий буквы русского алфавита. Здесь в первой колонке — десятичный номер символа, во второй колонке — символ, в третьей — двоичный код.
Пример 2. Буква «i» в таблице кодировки символов имеет десятичный код 105. Что зашифровано последовательностью десятичных кодов: 108 105 110 107?
![]() Буква «5» будет иметь код 106, «К» — код
107 и т. д. Следовательно, закодировано слово «link» .
Буква «5» будет иметь код 106, «К» — код
107 и т. д. Следовательно, закодировано слово «link» .
![]() Пример З. С
помощью последовательности десятичных кодов: 99 111 109 112 117 116 101 114
зашифровано слово «computer». Какая последовательность десятичных кодов будет
соответствовать этому же слову, записанному заглавными буквами?
Пример З. С
помощью последовательности десятичных кодов: 99 111 109 112 117 116 101 114
зашифровано слово «computer». Какая последовательность десятичных кодов будет
соответствовать этому же слову, записанному заглавными буквами?
Решение. При шифровке слова не обязательно пользоваться таблицей кодировки символов. Необходимо лишь учесть, что разница между десятичным кодом строчной буквы латинского алфавита и десятичным кодом соответствующей заглавной буквы равна 32. Если букве «с» соответствует код 99, то заглавная буква «С» имеет десятичный код 67 = 99 — 32. Следовательно, слову «COMPUTER» соответствует последовательность кодов: 67 79 77 80 85 84 69 82.
![]() Текстовая информация,
хранящаяся в памяти компьютера в двоичном коде, из-за своей многозначности
неудобна для восприятия человеком. На практике внутреннее представление чаще
всего перекодируется в шестнадцатеричную форму. Шестнадцатеричный код каждого
символа — Двузначное число от 00 до FF.
Текстовая информация,
хранящаяся в памяти компьютера в двоичном коде, из-за своей многозначности
неудобна для восприятия человеком. На практике внутреннее представление чаще
всего перекодируется в шестнадцатеричную форму. Шестнадцатеричный код каждого
символа — Двузначное число от 00 до FF.
Пример 4. Последовательность двоичных кодов:
![]() слову «stop». Построить
представление этого слова.
слову «stop». Построить
представление этого слова.
Решение. Необходимо учесть, что каждая шестнадцатеричная цифра представима четырехзначным двоичным числом,
т. е. двоичному коду 01110011 будут соответствовать две шестнадцатеричные цифры 7 (0111) и З (0011). Следовательно, шестнадцатеричный код будет иметь вид: 73 74 6F 70.
![]() Пример 5. Из
последовательности слов: «окно», «кино»,
Пример 5. Из
последовательности слов: «окно», «кино», ![]() «ника», «конь»,
«ночь» выбрать слово, имеющее наибо
«ника», «конь»,
«ночь» выбрать слово, имеющее наибо![]() льшую сумму кодов символов из таблицы
кодировки ASCII.
льшую сумму кодов символов из таблицы
кодировки ASCII.
Решение. При решении этой задачи используется принцип последовательного кодирования. Буквы в кодировочной таблице располагаются в алфавитном порядке. Нет необходимости знать код каждой буквы. Сопоставим, например, слова «кино» и «ника». Они отличаются только одной буквой. Код (номер) буквы «о» больше, чем код буквы «а». Следовательно, слово «кино» имеет большую сумму кодов символов. Аналогично проанализируем остальные слова. Ответ: ночь.
![]() «1999», «2001»,
«файл», «file», «2b2d» выбрать тот, что
«1999», «2001»,
«файл», «file», «2b2d» выбрать тот, что ![]() имеет минимальную
сумму кодов символов в таблице
имеет минимальную
сумму кодов символов в таблице ![]() ASCII.
ASCII.
Решение. Согласно последовательному кодированию цифры упорядочены по возрастанию и предшествуют буквам, т. е. имеют меньшие коды. Ответ: «2001».
![]()
Текст занимает 0,25 Кбайт памяти компьютера. Сколько символов содержит этот текст?
![]() 32
32
Текст занимает полных 5 страниц. На каждой странице размещается 30 строк по 70 символов в строке. Какой объем оперативной памяти (в байтах) займет этот текст?
Свободный объем оперативной памяти компьютера 640 Кбайт. Сколько страниц книги поместится в ней, если на странице:
1) 32 строки по 64 символа в строке; 2) 64 строки по 64 символа в строке; З) 16 строк по 64 символа в строке?
.N2 34
Текст занимает полных 10 секторов на односторонней дискете объемом 180 Кбайт. Дискета разбита на 40 дорожек по 9 секторов. Сколько символов содержит текст?
Десятичный код латинской буквы «е» в таблице кодировки символов ASCII равен 101. Какая последовательность десятичных кодов будет соответствовать слову 1) file; 2) help?
.М 36
Десятичный код латинской буквы «о» в таблице кодировки символов ASCII равен 111. Что зашифровано с помощью последовательности десятичных кодов:
1) 115 112 111 114 116; 2) 109 111 117 115 101?
![]() 37
37
Г.Г2 38
С помощью последовательности десятичных кодов: 66 65 83 73 67 зашифровано слово BASIC. Какая последовательность десятичных кодов будет соответствовать этому слову, записанному строчными буквами?
Пользуясь таблицей кодировки символов ASCII, закодируйте с помощью шестнадцатеричных кодов следующий текст: 1) Norton Commander; 2) Computer IBM РС.
Пользуясь таблицей кодировки символов ASCII, расшифруйте текст, представленный в виде шестнадцатеричных кодов символов:
1) 57 69 6Е 64 6F 77 73 21) 39 35;
2) 63 6F 6D 65 21) 4F 4Е 2D 6C 69 6Е 65.
Пользуясь таблицей кодировки символов ASCII, закодируйте с помощью двоичных кодов следующие слова: 1) EXCEL; 2) Word.
ль 42
По шестнадцатеричному коду восстановить двоичный код и, пользуясь таблицей кодировки символов, расшифровать слова: 1) 42 61 73 69 63; 2) 50 61 73 63 61 6C.
ль 43
По шестнадцатеричному коду восстановить десятичный код и, пользуясь таблицей кодировки символов, расшифровать слово: 8А 8Е 8C 8F 9C 9Е 92 85 90.
![]() 44
44
Пользуясь таблицей кодировки символов, получить шестнадцатеричный код слова ИНФОРМАТИКА.
.М2 45
Сколько букв и какого алфавита содержит зашифрованный десятичными кодами текст: 128 32 139 32 148 32 128 32 130 32 136 32 146?
З. 1.4. Представление числовой информации
3.1.4.1. Целые числа
![]()
Множество целых чисел, представимых в памяти компьютера, ограничено. Диапазон значений зависит от размера ячеек памяти, используемых для их хранения. В Ь-разряДной ячейке может храниться различных целых чисел.
Пример 1. Пусть для представления целых
чисел в ![]() R компьютере используется 16-разрядная
ячейка (2 байта). Определить, каков диапазон хранимых чисел, если: а)
используются только положительные числа; б) используются как положительные так
и отрицательные числа
R компьютере используется 16-разрядная
ячейка (2 байта). Определить, каков диапазон хранимых чисел, если: а)
используются только положительные числа; б) используются как положительные так
и отрицательные числа
в равном количестве.
Решение. Всего в 16-разрядной ячейке может храниться 2 16 = 65 536 различных значений. Следовательно:
а) диапазон значений от О до 65 535 (от О до
![]() б) диапазон значений от —32 768 до 32 767 (от —2 №-1 до
б) диапазон значений от —32 768 до 32 767 (от —2 №-1 до
Чтобы получить внутреннее представление целого положительного числа N, хранящегося в К-разрядном машинном слове, необходимо:
1) перевести число N в двоичную систему счисления;
2) полученный результат дополнить слева незначащими нулями до К разрядов.
Пример 2. Получить внутреннее представление целого числа 1607 в 2-байтовой ячейке.
Решение. лг = 160710 110010001112. Внутреннее представление этого числа в ячейке будет следующим: 0000 0110 0100 0111. Шестнадцатеричная форма внутреннего представления числа получается заменой 4-х двоичных цифр одной шестнадцатеричной цифрой: 0647.
Для записи внутреннего представления целого отрицательного числа (—N) необходимо:
1) получить внутреннее представление положительного числа N;
2) получить обратный код этого числа заменой О на 1 и 1 на О; З) к полученному числу прибавить 1.
Данная форма представления целого отрицательного числа называется Дополнительным кодом. Использование дополнительного кода позволяет заменить операцию вычитания на операцию сложения уменьшаемого числа с дополнительным кодом вычитаемого.
Пример З. Получить внутреннее представление целого отрицательного числа —1607.
![]() Решение. 1)
Внутреннее представление положительного числа: 0000 0110 0100 0111 2) обратный
код:
Решение. 1)
Внутреннее представление положительного числа: 0000 0110 0100 0111 2) обратный
код:
это внутреннее двоичное представление числа —1607. Шестнадцатеричная форма: F9B9.
Двоичные разряды в ячейке памяти
нумеруются от О до К справа налево. Старший, К-й разряд во внутреннем ![]() представлении
любого положительного числа равен
представлении
любого положительного числа равен ![]() нулю, отрицательного числа — единице.
Поэтому этот разряд называется знаковым разрядом.
нулю, отрицательного числа — единице.
Поэтому этот разряд называется знаковым разрядом.
![]()
![]() 46
46
Компьютер работает только с целыми положительными числами. Каков диапазон изменения чисел, если для представления числа в памяти компьютера отводится 1 байт?
Г.Г2 47
Каков диапазон изменения целых чисел (положительных и отрицательных), если в памяти компьютера для представления целого числа отводится 1 байт?
Г.Г2 48
Компьютер работает только с целыми положительными числами. Каков диапазон изменения чисел, если для представления числа в памяти компьютера отводится 4 байта?
Г.Г2 49
Каков диапазон изменения целых чисел (положительных и отрицательных), если в памяти компьютера для представления целого числа отводится 4 байта?
![]() 50
50
Записать в двоичной и шестнадцатеричной форме внутреннее представление наибольшего положительного целого и наибольшего по абсолютной величине отрицательного целого числа, представленных в 1-байтовой ячейке памяти. Г.Г2 51
![]() 52
52
Представители племени Мульти оперируют целыми положительными числами и умеют считать только до 100. Для проведения расчетов в племени применяется калькулятор. Указать минимальную длину ячейки памяти в битах, необходимую для хранения чисел.
В «игрушечных» компьютерах С8, С1О, С12 и С16 для представления целых чисел (положительных и отрицательных) используется 8, 10, 12 и 16 битов памяти соответственно. На каком (каких) из этих компьютеров можно успешно вычислить сумму первых 32-х членов арифметической прогрессии: 2, 4, 6, 8, 10, ...7
Работа № 1
Целые числа в памяти компьютера ЗаДания (Для всех вариантов):
1. Получить двоичную форму внутреннего представления целого числа в 2-байтовой ячейке.
2. Получить шестнадцатеричную форму внутреннего представления целого числа в 2-байтовой ячейке.
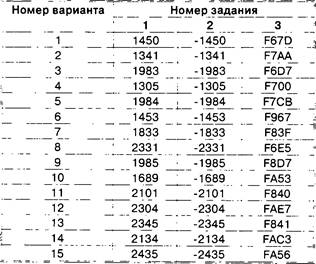
3.1.42. Вещественные числа
![]()
![]() Формат с плавающей
точкой использует представление вещественного числа R в виде произведения
мантиссы т на основание системы счисления п в некоторой целой степени р,
которую называют порядком: R = т О.
Формат с плавающей
точкой использует представление вещественного числа R в виде произведения
мантиссы т на основание системы счисления п в некоторой целой степени р,
которую называют порядком: R = т О.
Представление числа в форме с плавающей точкой неоднозначно. Например, справедливы следующие равенства:
25,324 - 2,5324 • 10 1 - 0,0025324 • 10 4 - 2532,4 • 10 -2 и т. п.
В компьютере используют нормализованное представление числа в форме с плавающей точкой. Мантисса в нормализованном представлении должна удовлетворять условию: 0,1 < т < 1 . Иначе говоря, мантисса меньше единицы и первая значащая цифра не ноль.
В памяти компьютера мантисса представляется как целое число, содержащее только значащие цифры (О целых и запятая не хранятся). Следовательно, внутреннее представление вещественного числа сводится к представлению пары целых чисел: мантиссы и порядка.
В разных типах компьютеров применяются различные варианты представления чисел в форме с плавающей точкой. Для примера рассмотрим внутреннее представление вещественного числа в 4-х байтовой ячейке памяти.
В ячейке должна содержаться следующая информация о числе: знак числа, порядок и значащие цифры мантиссы.
![]() :Е маш. порядок
:Е маш. порядок
1-й байт 2-й байт 3-й байт 4-й байт
В старшем бите 1-го байта хранится знак числа: О обозначает плюс, 1 — минус. Оставшиеся 7 битов первого байта содержат машинный поряДок. В следующих трех байтах хранятся значащие цифры мантиссы (24 разряда).
В семи двоичных разрядах помещаются двоичные числа в
![]()
изменяется в диапазоне от О до 127 (в десятичной системе счисления). Всего 128 значений. Порядок, очевидно, может быть как положительным так и отрицательным. Разумно эти 128 значений разделить поровну между положительными и отрицательными значениями порядка: от —64 до 63.
Машинный порядок смещен относительно математического и имеет только положительные значения. Смещение выбирается так, чтобы минимальному математическому значению поряДка соответствовал нуль.
ф) в рассматриваемом случае выражается формулой:
Мр = р + 64.
Полученная формула записана в десятичной системе. В двоичной системе формула имеет вид: МР2 = Р2 + 100 00002.
Для записи внутреннего представления вещественного числа необходимо:
1) перевести модуль данного числа в двоичную систему счисления с 24 значащими цифрами;
2) нормализовать двоичное число;
З) найти машинный порядок в двоичной системе счисления;
4) учитывая знак числа, выписать его представление в 4-байтовом машинном слове.
Пример 4. Записать внутреннее
представление числа ![]() 250,1875 в форме с плавающей точкой.
250,1875 в форме с плавающей точкой.
Решение
1.
Переведем его в двоичную систему счисления с 24 значащими
цифрами: 250,187510![]()
2. Запишем в форме нормализованного двоичного числа
![]()
Здесь мантисса, основание системы счисления (210 = 102) и порядок (810 — 10002) записаны в двоичной системе.
З. Вычислим машинный порядок в двоичной системе счисления: МР2 1000 + 100 0000 100 1000.
4. Запишем представление числа в 4-байтовой ячейке памяти с учетом знака числа:
![]()
Шестнадцатеричная форма: 48FA3000.
Пример 5. По шестнадцатеричной форме внутреннего представления числа в форме с плавающей точкой 09811000 восстановить само число.
Решение
1. Перейдем к двоичному представлению числа в 4-байтовой ячейке, заменив каждую шестнадцатеричную цифру 4-мя двоичными цифрами:
1100 1001 1000 0001 0001 0000 0000 0000
![]() 1 1001001 10000001
00010000 00000000
1 1001001 10000001
00010000 00000000
![]()
З. Запишем в форме нормализованного двоичного числа с плавающей точкой с учетом знака числа:
-0,100000010001000000000000 • 10![]()
4. Число в двоичной системе счисления имеет вид: -100000010,0012.
5. Переведем число в десятичную систему счисления:
-100000010,0012 ![]() - -258,12510.
- -258,12510.
![]() Диапазон
вещественных чисел значительно шире диапазона целых чисел. Положительные и
отрицательные числа расположены симметрично относительно нуля. Следовательно,
максимальное и минимальное числа равны между собой по модулю.
Диапазон
вещественных чисел значительно шире диапазона целых чисел. Положительные и
отрицательные числа расположены симметрично относительно нуля. Следовательно,
максимальное и минимальное числа равны между собой по модулю.
Наименьшее по абсолютной величине число равно нулю. Наибольшее по абсолютной величине число в форме с плавающей точкой — это число с самой большой мантиссой и самым большим порядком.
Для 4-байтового машинного слова таким числом будет:
![]()
После перевода в десятичную систему счисления получим:
![]() 2-24) • 263
2-24) • 263![]()
Множество вещественных чисел, представимых в памяти компьютера в форме с плавающей точкой, является ограниченным и дискретным. Количество вещественных чисел, точно преДставимых в памяти компьютера, вычисляется по формуле: лт = 2 t • (U — L + 1) + 1. Здесь t — количество двоичных разрядов мантиссы; U — максимальное значение математического порядка; — минимальное значение порядка. Для рассмотренного нами варианта (t = 24, U = 63, 1., = —64) получается: ДТ = 2 146 683 548.
![]()
Представить вещественное число 1) 0,005089; 2) 1234,0456 в нормализованной форме с плавающей точкой в десятичной системе счисления.
Для представления вещественного числа отводится 2 байта. Порядок занимает 7 битов. Сколько различных вещественных чисел точно представимы в памяти такого компьютера?
Минимальное значение математического порядка в десятичной системе счисления равно —1024. Чему равно смещение?
Получить шестнадцатеричную форму внутреннего представления отрицательного числа —123,125 в формате с плавающей точкой в 4-байтовой ячейке.
Для представления вещественного числа используется 2-байтовая ячейка памяти. В 1-м байте содержится знак числа и порядок, во 2-м байте — мантисса. Определить минимальное и максимальное по абсолютной величине числа, точно представимые в таком компьютере.
В «игрушечном» компьютере для представления вещественных чисел используется однобайтовая ячейка памяти (биты нумеруются от О до 7 справа налево). 7-й бит — знак числа; 5-й и 6-й биты — машинный порядок; с 4-го по О-й биты — мантисса. Определить: 1) количество точно представимых вещественных чисел; 2) 5 наименьших положительных десятичных чисел, представимых точно в таком компьютере.
Говорят, что число, превышающее максимальное значение, представимое в компьютере, вызывает переполнение. Определить для «игрушечного» компьютера (задача .N2 60), какие из следующих чисел вызовут переполнение: 0,5; 10,0; 4,3; 8,1; 7,8.
.N2 62
«Игрушечный» компьютер сохраняет значение числа, не вызывающего переполнение и не представленного точно, в виде ближайшего снизу (по абсолютной величине) точно представимого числа. Какие значения примут следующие числа в таком компьютере: 1,25; 1,6; 1,9?
.N2 63
Увидит ли разницу «игрушечный» компьютер между следующими парами чисел: 1) 1,4 и 1,5; 2) 1,6 и 1,62; З) 1,8 и 1,9?
Работа № 2
Вещественные числа в памяти компьютера
1. Получить шестнадцатеричную форму внутреннего представления числа в формате с плавающей точкой в 4-х байтовой ячейке.
2. По шестнадцатеричной форме внутреннего представления вещественного числа в 4-байтовой ячейке восстановить само число.
![]()
1 2
![]()
1
26.28125 С5ОВОООО ![]() 1-.
1-. ![]()
2 -29.625 45014000
![]()
з 91 .8125 C5EDOOOO
![]()
4 -27.375 47В7АООО
![]()
5 139.375 C5D14000
![]()
6 -26.28125 48886000
7 27.375 С7В7АООО
8 -33.75 45ОВОООО
9 29.625 08886000
45EDOOOO
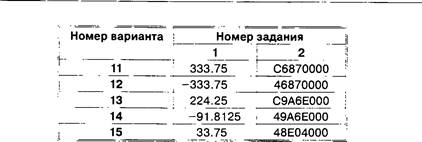
З. 1.5. Представление графической информации
3.1.5.1. Растровое представление
![]()
Компьютерная графика — раздел
информатики, предметом которого является работа на компьютере с графи![]() ческими
изображениями (рисунками, чертежами, фото
ческими
изображениями (рисунками, чертежами, фото![]() графиями,
видеокадрами и пр.).
графиями,
видеокадрами и пр.).
Пиксель наименьший элемент изображения на экране (точка на экране).
Растр — прямоугольная сетка пикселей на экране.
Разрешающая способность экрана — размер сетки растра, задаваемого в виде произведения М х N, где М — число точек по горизонтали, лт — число точек по вертикали (число строк).
ВиДеоинформачия — информация об изображении, воспроизводимом на экране компьютера, хранящаяся в компьютерной памяти.
ВиДеопажять оперативная память, хранящая видеоинформацию во время ее воспроизведения в изображение на экране.
Графический файл — файл, хранящий информацию о графическом изображении.
Число цветов, воспроизводимых на экране дисплея (К), и число битов, отводимых в видеопамяти под каждый пиксель (N), связаны формулой:
![]()
![]() Пример
1. Сколько битов видеопамяти занимает инфор-
Пример
1. Сколько битов видеопамяти занимает инфор-
![]()
![]() мация об
одном пикселе на черно-белом экране (без полутонов)?
мация об
одном пикселе на черно-белом экране (без полутонов)?
Решение. Для черно-белого изображения без полутонов К = 2. Следовательно 2 N = 2. Отсюда лт = 1 бит на пиксель.
Пример 2.
Современный монитор позволяет получать на ![]() экране 16 777 216
различных цветов. Сколько битов па
экране 16 777 216
различных цветов. Сколько битов па![]() мяти занимает 1 пиксель?
мяти занимает 1 пиксель?
Решение. Поскольку К = 16 777 216 = 2 24 , то N = 24 бита на пиксель.
Величину N называют битовой глубиной.
Страница раздел видеопамяти, вмещающий информацию об одном образе экрана (одной «картинке» на экране). В видеопамяти могут размещаться одновременно несколько страниц.
Пример З
На экране с
разрешающей способностью 640 х 200 ![]() высвечиваются только двухцветные
изображения. Какой минимальный объем видеопамяти необходим для хранения
изображения?
высвечиваются только двухцветные
изображения. Какой минимальный объем видеопамяти необходим для хранения
изображения?
Решение. Так как битовая глубина двухцветного изображения равна 1, а видеопамять, как минимум, должна вмещать одну страницу изображения, то объем видеопамяти равен
640 • 200 • 1 128 ООО битов — 16 ООО байт.
Пример 4. Рассмотрим «маленький монитор» с растровой сеткой размером 10 х 10 и черно-белым изображение ем. На рис. 3.1 приведено изображение буквы «К». Представить содержимое видеопамяти в виде битовой матрицы, в которой строки и столбцы соответствуют строкам и столбцам растровой сетки.
![]() 1
1
10
![]()
Решение
Для кодирования изображения на таком экране требуется 100 битов (1 бит на пиксель) видеопамяти. Пусть «1» обозначает закрашенный пиксель, а «О» не закрашенный. Вот как будет выглядеть такая матрица:
0000000000
0001000100
0001001000
0001010000
0001100000
0001010000
0001001000
0001000100
0000000000
0000000000
![]() Все
многообразие красок на экране получается путем смешивания трех базовых цветов:
красного, синего и зеленого. Каждый пиксель на экране состоит из трех близко
расположенных элементов, светящихся этими цветами. Цветные дисплеи,
использующие такой принцип, называются RGB
Все
многообразие красок на экране получается путем смешивания трех базовых цветов:
красного, синего и зеленого. Каждый пиксель на экране состоит из трех близко
расположенных элементов, светящихся этими цветами. Цветные дисплеи,
использующие такой принцип, называются RGB![]()
Код цвета пикселя содержит информацию о доле каждого базового цвета.
В ней наличие базового цвета обозначено единицей, а отсутствие нулем.
Двоичный код восьмицветной палитры
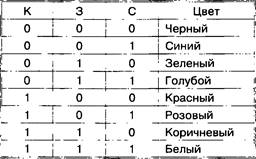
Пример 5. Из
смешения каких цветов получается розо![]() вый цвет?
вый цвет?
Решение. Глядя на таблицу, видим, что код розового цвета — 101. Это значит, что розовый цвет получается смешением красной и синей красок.
Шестнадцатицветная палитра получается
при использовании 4-разрядной кодировки пикселя: к трем битам ![]() базовых
цветов добавляется один бит интенсивности. Этот бит управляет яркостью всех
трех цветов одновременно. Например, если в 8-цветной палитре код 100 обозначает
красный цвет, то в 16-цветной палитре: 0100 красный, 1100 — ярко-красный цвет;
0110 — коричневый, 1110 — ярко-коричневый (желтый).
базовых
цветов добавляется один бит интенсивности. Этот бит управляет яркостью всех
трех цветов одновременно. Например, если в 8-цветной палитре код 100 обозначает
красный цвет, то в 16-цветной палитре: 0100 красный, 1100 — ярко-красный цвет;
0110 — коричневый, 1110 — ярко-коричневый (желтый).
Большее количество цветов получается при раздельном управлении интенсивностью базовых цветов. Причем интенсивность может иметь более двух уровней, если для кодирования каждого из базовых цветов выделять больше одного бита.
При использовании битовой глубины 8 битов/пиксель количество цветов: 2 8 — 256. Биты такого кода распределены следующим образом:
кккзззсс.
Это значит, что под красную и зеленую компоненты выделено по З бита, под синюю — 2 бита. Следовательно, красная и зеленая компоненты имеют по 2 3 — 8 уровней яркости, а синяя — 4 уровня.
![]() Пример
6
Пример
6
Решение. Нетрудно посчитать, что 256 • 256 • 256 = 16 777 216.
![]()
Г.Г2 64
Какой объем видеопамяти необходим для хранения двух
страниц изображения при условии, что разрешающая способность дисплея равна 640
х 350 пикселей, а количество используемых цветов ![]()
Г.Г2 65
Какой объем видеопамяти необходим для хранения четырех страниц изображения, если битовая глубина равна 24, а разрешающая способность дисплея — 800 х 600 пикселей?
Г.Г2 66
Объем видеопамяти равен 256 Кб, количество используемых цветов — 16. Вычислите варианты разрешающей способности дисплея при условии, что число страниц в видеопамяти может быть равно 1, 2 или 4.
![]()
Объем видеопамяти равен 1 Мб. Разрешающая способность дисплея — 800 х 600. Какое максимальное количество цветов можно использовать при условии, что видеопамять делится на две страницы?
Г•Г2 68
Объем видеопамяти равен 2 Мб, битовая глубина — 24, разрешающая способность дисплея — 640 х 480. Какое максимальное количество страниц можно использовать при этих условиях?
.М2 69
На экране дисплея необходимо отображать 2 24 (16 777 216) различных цветов. Вычислить необходимый объем одной страницы видеопамяти при различных значениях разрешающей способности дисплея (например, 640 х 480, 800 х 600, 1024 х 768, 1240 х 1024).
Битовая глубина равна 32, видеопамять делится на две страницы, разрешающая способность дисплея — 800 х 600. вычислить объем видеопамяти.
Г•Г2 71
Видеопамять имеет объем, в котором может храниться 4-цветное изображение размером ЗОО х 200. Какого размера изображение можно хранить в том же объеме видеопамяти, если оно будет использовать 16-цветную палитру?
![]() 72
72
Видеопамять имеет объем, в котором может храниться 4-цветное изображение размером 640 х 480. Какого размера изображение можно хранить в том же объеме видеопамяти, если использовать 256-цветную палитру?
Рассмотрим маленький монитор с разрешающей способностью 10 х 10 и шестнадцатицветным изображением. По двоичному коду

определить, что изображено, цвет изображения и цвет фона.
Для маленького монитора с разрешающей способностью 10 х 10 построить двоичный код изображения:
— букв алфавита, ![]() цифр,
цифр,
— геометрических фигур (квадрата, треугольника, эллипса и др.) при условии, что битовая глубина равна:
1) двум;
2) четырем.
Цвет изображения и фона выбрать самостоятельно.
Для изображения ярко-желтого зонтика (рис. 3.2) на голубом фоне построить двоичный код при условии, что битовая глубина равна:
1) двум;
2)

![]()
Разрешающая способность дисплея равна 640 х 200. Для размещения одного символа в текстовом режиме используется матрица 8 х 8 пикселей, которая называется знакоместом. Какое максимальное количество:
1) текстовых строк; 2) знакомест в строке может быть размещено на экране?
Для размещения одного символа в текстовом режиме используется матрица 8 х 8, количество текстовых строк равно 75, а знакомест в строке (см. задачу № 76) — 100. Вычислить разрешающую способность дисплея.
Битовая глубина равна 24. Сколько различных оттенков красного, зеленого и синего используется для формирования цвета?
.М2 79
На экране может быть отображено 256 цветов. Сколько различных уровней яркости принимает красная, зеленая и синяя составляющие?
.М2 80
Объем видеопамяти равен 512 Кб, разрешающая способность дисплея — 320 х 200. Сколько различных уровней яркости принимает красная, зеленая и синяя составляющие при условии, что видеопамять делится на две страницы?
Битовая глубина равна 24. Сколько различных оттенков серого цвета может быть отображено на экране?
.М2 82
Битовая глубина равна 24. Опишите несколько вариантов двоичного представления светло-серых и темно-серых оттенков.
.М2 83
На экране компьютера необходимо получить 1024 оттенка серого цвета. Какой должна быть битовая глубина?
.М2 84
Объем видеопамяти — 2 Мб, разрешающая способность дисплея равна 800 х 600. Сколько оттенков серого цвета можно получить на экране при условии, что видеопамять делится на две страницы?
.М2 85
На экране компьютера отображаются 16 цветов. Опишите двоичное представление различных оттенков зеленого и сиреневого (синий + красный) цвета.
.М2 86
Битовая глубина равна 24. Опишите двоичное представление не менее пяти различных оттенков красного и желтого (красный + зеленый) цвета.
3.1.52. Векторное представление
![]()
При векторном подходе изображение рассматривается как совокупность простых элементов: прямых линий, дуг, окружностей, эллипсов, прямоугольников, закрасок и пр., которые называются графическими примитивами. Графическая информация — это данные, однозначно определяющие все графические примитивы, составляющие рисунок.
Положение и форма
графических примитивов задаются в систеже графических координат, связанных с
экраном. Обычно начало координат расположено в верхнем левом углу экрана. Сетка
пикселей совпадает с координатной сеткой. Горизонтальная ось Х направлена слева
направо; вертикальная ось У ![]() сверху вниз.
сверху вниз.
Отрезок прямой линии однозначно определяется указанием координат его концов; окружность координатами центра и радиусом; многоугольник координатами его углов, закрашенная область — граничной линией и цветом закраски и пр.
![]() Пример 7.
Вернемся к рассмотрению изображения буквы «К» на растровой сетке 10 х 10.
Описать букву «К» последовательностью векторных команд.
Пример 7.
Вернемся к рассмотрению изображения буквы «К» на растровой сетке 10 х 10.
Описать букву «К» последовательностью векторных команд.
В векторном представлении буква «К» это три линии. Всякая линия описывается указанием координат ее концов в таком виде:
![]()
Изображение буквы «К» на рис. 3.3 описывается следующим образом:
![]()
ЛИНИЯ(5,5,8,2)
ЛИНИЯ(5,5,8,8)
10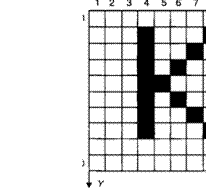
![]() Пример 8. Имеется
следующая система команд векторной графики:
Пример 8. Имеется
следующая система команд векторной графики:

центра, R — длина радиуса в шагах растровой сетки.
'! Эллипс Х1, У1, Х2, У2 Нарисовать эллипс, ограниченный прямоугольником; (Х 1, У 1) — координаты левого верхнего, а (Х2, У2) — правого нижнего угла этого прямоугольника.
|
|
правого |
|
ЦВЕТ |
Уст |
щвет рисования ановить текущий цвет рисования.
ii цвет закраски ЦВЕТновить текущий цвет закраски.
|
Уста |
|
|
|
— цвет граничной |
![]() ll Закрасить Х, У, Закрасить
произвольную замкн.ду.ю Фигуру; Х, У ЦВЕТ ГРАНИЦЫ — координаты любой точки
внутри замкнутой фигуры, ЦВЕТ ГРАНИЦЫ
ll Закрасить Х, У, Закрасить
произвольную замкн.ду.ю Фигуру; Х, У ЦВЕТ ГРАНИЦЫ — координаты любой точки
внутри замкнутой фигуры, ЦВЕТ ГРАНИЦЫ
Описать с помощью векторных команд изображение кораблика. Разрешающая способность дисплея — 64 х 48.
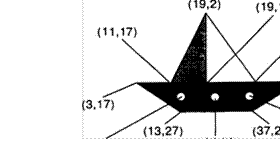
(18,22) (25,22) (32,22)
Решение
Цвет рисования Голубой Установить 3,17 линия к 47,17 линия к 37,27 линия к 13,27 Линия к 3,17
Цвет закраски Голубой
Цвет рисования Белый
Закрасить 25,22, Белый Окружность 32,22, 2
Цвет рисования Синий Цвет закраски Красный
Цвет рисования Коричневый Установить 19,2 линия к 32,17 линия к 19,17 Линия к 19,2
Закрасить 22,10, Коричневый
![]()
С помощью векторных команд, данных в примере 8, описать объекты 87 А — 87 Р. Разрешающую способность дисплея выбрать самостоятельно.
Для изображения десятичных цифр в стандарте почтового индекса (как пишут на конвертах) получить векторное и растровое представление. Размер растровой сетки выбрать самостоятельно.
87 д 87 Е 87 ж 87 з
|
|
|
|
87 и 87 к 87 л 87 м
87 н 870 87 п 87 р
Г.Г2 89
Ниже даны описания некоторых рисунков с помощью использованной в примере 8 системы векторных команд. Воспроизвести на бумаге эти рисунки. Разрешающая способность дисплея — 64 х 48.
![]() 89 А Цвет рисования Красный Цвет
закраски Желтый Окружность 16, 10, 2
89 А Цвет рисования Красный Цвет
закраски Желтый Окружность 16, 10, 2
|
Линия |
16, 23 |
|
Линия |
19, 29 |
|
Линия |
21, 29 |
|
Линия |
16, 23, 13, 29 |
|
Линия |
13, 29, 11, 29 |
|
Линия |
16, 16, 11, 12 |
|
Линия |
16, 16, 21, 12 |
.М2 89 Б
|
Окружность |
20, 10 5 |
|
Окружность |
20, 10, 10 |
|
Закрасить |
25, 15, Красный |
|
Окружность |
20, зо 5 |
|
Окружность |
20, 30, 10 |
|
Закрасить |
28, 32, Красный |
|
Цвет рисования |
Голубой |
|
Прямоугольник |
12, 5, 18, 11 |
|
Прямоугольник |
10, 1, 20, 21 |
|
Прямоугольник |
20, 9, 50, 21 |
Цвет закраски Зеленый Окружность 20, 24, З Окружность 40, 24, З
Цвет закраски Розовый
Цвет закраски Голубой
.М9 89 г
|
Установить |
30, 5 |
|
Линия к |
32, 1 |
|
Линия к |
34, 5 |
|
Линия к |
30, 5 |
|
Закрасить |
32, З, Зеленый |
|
Установить |
28, 11 |
|
Линия к |
32, 5 |
|
Линия к Линия к |
36, 11 |
|
Закрасить |
32, 8, Зеленый |
|
Установить |
26, 17 |
|
ЛИНИЯ к ЛИНИЯ к |
38, 17 |
|
Закрасить |
32, 15, Зеленый |
Цвет рисования Коричневый
Цвет закраски Коричневый
Прямоугольник 31, 17, 33, 20
Закрасить 32, 19, Коричневый
Линия к 46, 20
ЛИНИЯ к 46, 24
Линия к 44, 24
ЛИНИЯ к 44, 26
ЛИНИЯ к 46, 26
ЛИНИЯ к 46, 36
Линия к 32, 36 ЛИНИЯ к 32, 20 Цвет закраски Серый
Закрасить 38, 30, Серый
Закрасить 39, 28, Белый
Эллипс 38, 31, 40, 35
Закрасить 39, 32, Черный
Л) 89 Е
Цвет рисования Коричневый
Цвет закраски Коричневый
Закрасить 20, 28, Коричневый
|
Установить |
12, 20 |
|
Линия к |
22, 9 |
|
Линия к |
32, 20 |
|
ЛИНИЯ к |
12, 20 |
|
Цвет закраски |
Серый |
|
Закрасить |
22, 16, Серый |
|
Закрасить |
22, 16, Зеленый |
|
Прямоугольник |
14, 22, 20, 28 |
|
Закрасить |
15, 24, Зеленый |
|
Прямоугольник |
24, 22, 30, 28 |
|
Закрасить |
25, 24, Зеленый |
Цвет рисования Черный
Прямоугольник 25, 31, 30, 40 Цвет закраски Черный
Закрасить 26, 35, Черный
![]() 89 Ж
89 Ж
Цвет рисования Серый
Цвет закраски Коричневый Прямоугольник 10, 11, 35, 18
|
Линия |
15 7 |
|
Линия |
15, 9 |
|
Линия |
17, 9 |
|
Линия |
17, 2 |
|
Линия Линия к Линия |
20, 2 |
|
Эллипс |
|
|
Закрасить |
25, 15, Серый |
|
Закрасить |
18, 7, Серый |
|
Закрасить |
40, 10, Серый |
|
Эллипс |
38, 10, 42, 19 |
|
Цвет закраски |
Белый |
|
Закрасить |
40, 15, Серый |
3.1.6. Звук в памяти компьютера
Физическая природа звука — колебания в
определенном диапазоне частот, передаваемые звуковой волной через ![]() воздух
(или другую упругую среду). Процесс преобразо
воздух
(или другую упругую среду). Процесс преобразо![]() вания звуковых волн в
двоичный код в памяти компьютера:
вания звуковых волн в
двоичный код в памяти компьютера:
ток
|
звуковая волна —» МИКРОФОН——» переменный электрический |
|
АУДИОАДАПТЕР —» двоичный код —» ПАМЯТЬ КОМПЬЮТЕРА |
Процесс воспроизведения звуковой информации, сохраненной в памяти компьютера: ПАМЯТЬ КОМПЬЮТЕРА
|
двоичный код —.АУДИОАДАПТЕР |
|
переменный электрический ток —» ДИНАМИК —» звуковая волна |
Аудиоадаптер (звуковая плата) специальное устройство, подключаемое к компьютеру, предназначенное для преобразования электрических колебаний звуковой частоты в числовой двоичный код при вводе звука и для обратного преобразования (из числового кода в электрические колебания) при воспроизведении звука.
В процессе записи звука аудиоадаптер с определенным периодом измеряет амплитуду электрического тока и заносит в регистр двоичный код полученной величины. Затем полученный код из регистра переписывается в оперативную память компьютера. Качество компьютерного звука определяется характеристиками аудиоадаптера: частотой дискретизации и разрядностью.
Частота дискретизации это количество измерений входного сигнала за 1 секунду. Частота измеряется в герцах (Гц). Одно измерение за одну секунду соответствует частоте 1 Гц. 1000 измерений за 1 секунду — 1 килогерц (кГц). Характерные частоты дискретизации аудиоадаптеров: 11 кГц, 22 кГц, 44,1 кГц и др.
Звуковой файл — файл, хранящий звуковую информацию в числовой двоичной форме. Как правило, информация в звуковых файлах подвергается сжатию.
![]() Пример 1
Пример 1
Определить размер
(в байтах) цифрового аудиофайла, ![]() время звучания которого составляет 10
секунд при частоте дискретизации 22,05 кГц и разрешении 8 битов. Файл сжатию не
подвержен.
время звучания которого составляет 10
секунд при частоте дискретизации 22,05 кГц и разрешении 8 битов. Файл сжатию не
подвержен.
Решение. Формула для расчета размера (в байтах) цифрового аудиофайла (монофоническое звучание): (частота дискретизации в Гц) х (время записи в секундах) х (разрешение в битах)/8.
Таким образом, размер файла вычисляется так: 22 050 • 10 - 8 / 8 220 500 байт.
6 Информатика
н ИКТ. Т. ![]()

Г.Г2 90
Определить объем памяти для хранения цифрового аудиофайла, время звучания которого составляет две минуты при частоте дискретизации 44,1 кГц и разрешении 16 битов.
В распоряжении пользователя имеется память объемом 2,6 Мб. Необходимо записать цифровой аудиофайл с длительностью звучания 1 минута. Какой должна быть частота дискретизации и разрядность?
.М2 92
Объем свободной памяти на диске 5,25 Мб, разрядность звуковой платы — 16. Какова длительность звучания цифрового аудиофайла, записанного с частотой дискретизации 22,05 КГЦ?
ЛЕ 93
Одна минута записи цифрового аудиофайла занимает на диске 1,3 Мб, разрядность звуковой платы — 8. С какой частотой дискретизации записан звук?
.М2 94
Какой объем памяти требуется для хранения цифрового аудиофайла с записью звука высокого качества при условии, что время звучания составляет З минуты?
.М2 95
Цифровой аудиофайл содержит запись звука низкого качества (звук мрачный и приглушенный). Какова длительность звучания файла, если его объем составляет 650 Кб?
Две минуты записи цифрового аудиофайла занимают на диске 5,05 Мб. Частота дискретизации — 22 050 Гц. Какова разрядность аудиоадаптера?
Гб 97
Объем свободной памяти на диске — 0,1 Гб, разрядность звуковой платы — 16. Какова длительность звучания цифрового аудиофайла, записанного с частотой дискретизации 44 100 Гц?
3.2. Архитектура ЭВМ
![]() Архитектура ЭВМ —
описание устройства и функционирования ЭВМ без подробностей технической
реализации. В понятие архитектуры входит: описание состава основных
функциональных узлов и их информационного взаимодействия; описание спбсобов
представления информации в компьютере; описание структуры процессора и языка
машинных команд.
Архитектура ЭВМ —
описание устройства и функционирования ЭВМ без подробностей технической
реализации. В понятие архитектуры входит: описание состава основных
функциональных узлов и их информационного взаимодействия; описание спбсобов
представления информации в компьютере; описание структуры процессора и языка
машинных команд.
Машина Неймана — архитектура ЭВМ, предложенная американским ученым Джоном фон Нейманом в 1946 году. Основные принципы включают:
![]() состав устройств однопроцессорной ЭВМ
(рис. 3.4);
состав устройств однопроцессорной ЭВМ
(рис. 3.4);
![]() использование двоичной системы счисления
в машинной арифметике;
использование двоичной системы счисления
в машинной арифметике; ![]() адресуемость памяти ЭВМ; а хранение
данных и программ в общей памяти ЭВМ;
адресуемость памяти ЭВМ; а хранение
данных и программ в общей памяти ЭВМ; ![]() состав системы команд процессора.
состав системы команд процессора.
Принципы архитектуры Неймана во многом сохраняются в современных компьютерах.
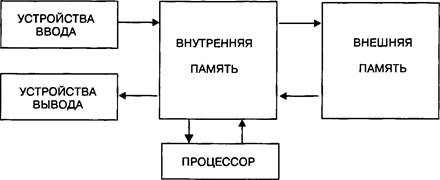
|
|
|
устройства |
|
устройства связи |
устройства хранения |
долговременного |
|
компьютера |
оперативной |
хранения |
|
с внешним миром |
информации и ее обработки Рис. 3.4 |
информации |
О способах двоичного представления информации в памяти компьютера, об использовании двоичной системы счисления см. раздел 1.5. В данном разделе рассматривается язык машинных команд компьютера. При этом не будут подробно излагаться языки «настоящих» компьютеров, а будет использована методика «учебных компьютеров».
3.2.1. Формат машинной команды
![]() Машинная программа
—последовательность машинных команд.
Машинная программа
—последовательность машинных команд.
Принцип хранимой программы (принцип Неймана): во время исполнения программа хранится в оперативной памяти вместе с данными. Каждая команда программы занимает ячейку памяти и имеет свой адрес (адрес ячейки).
![]()
![]()
В зависимости от структуры адресной части команды, процессоры делятся на трехадресные, Двухадресные, одноадресные и безадресные (стековые). На рис. 3.6 показан формат одноадресной команды; на рис. 3.7 — формат трехадресной команды.
Код операции : Адрес аргумента или результата
Что делать? Откуда взять или куда поместить?
Рис. 3.6
![]() первого
второго аргумента аргумента
первого
второго аргумента аргумента
![]()
Длина команды. Длина кода операции зависит от числа операций, входящих в систему команд компьютера. Так код операции длиной в 4 бита позволяет хранить коды до 16 (2 4 ) раз-
![]()
сформулировать простое правило определения оптимальной длины кода операции:
![]()
где К — количество команд в системе команд машинного языка, К — длина поля кода операции (в битах). Фактически во многих случаях длина поля кода операции берется с избытком, что, например, легко позволяет расширять систему команд.
Пример 1. В системе команд компьютера содержится 50 команд. Какова оптимальная длина кода операции?
Решение. Поскольку 2 5 = 32 < 50 < 64 = 2 6 , то длина кода операции должна быть не меньше 6 битов.
В трех- (двух-) адресной машине длины полей всех адресов одинаковы, поэтому общую длину команды (в битах) можно определить по формуле:
![]()
где К — длина поля кода операций, п — количество адресов в адресной части (п = 1, 2, З), а — длина поля адресной части (в битах). Очевидно, в этом случае размеры адресуемого пространства (А — количество адресуемых ячеек памяти) определяются формулой:
А = 20 .
Какова оптимальная длина поля кода операций (в битах) для компьютера, система машинных команд которого состоит из: 1) 10 команд; 2) 20 команд; З) 40 команд; 4) 80 команд?
Какое максимальное количество машинных команд может содержать система команд компьютера, если длина поля кода операции в формате его машинных команд составляет: 1) З бита; 2) 4 бита; З) 6 битов; 4) 1 байт?
Каков размер адресуемой памяти компьютера (в ячейках), если длина адресного поля равна:
1) 6 битов; 2) 1 байт; З) 12 битов; 4) 2 байта?
Какова длина адресного поля компьютера (в битах), если размер его адресуемой памяти составляет:
1) 8 ячеек; 2) 64 ячейки; З) 256 ячеек; 4) 4096 ячеек?
Какова длина машинной команды компьютера (в битах), если длина поля кода операций 4 бита и
1) длина адресной части 6 битов, процессор — двухадресный;
2) длина адресной части 1 байт, процессор — одноадресный;
З) размер адресуемой памяти 256 ячеек, процессор — одноадресный;
4) размер адресуемой памяти 16 ячеек, процессор — трехадресный?
Какова длина машинной команды (в битах), если размер адресуемой памяти составляет 1024 ячейки и
1)
2) длина поля кода операций 1 байт, процессор — трехадресный;
З) длина поля кода операций 4 бита, процессор — одноадресный;
4) процессор — одноадресный, число машинных команд в системе команд не может превышать 16?
Длина машинной команды составляет 2 байта, размер поля кода операций — 4 бита, определить:
1) размер адресуемой памяти, если процессор двухадресный;
2) размер адресуемой памяти, если процессор трехадресный;
З) количество адресов в команде, если размер адресуемой памяти 16 ячеек;
4) количество адресов в команде, если длина адресного поля составляет 6 битов.
Определить общий объем памяти компьютера (в байтах) при условии, что размер ячейки памяти равен длине команды и
1) длина поля кода операции 4 бита, длина адресного поля 4 бита, процессор — трехадресный;
2) длина поля кода операции 1 байт, длина адресного поля 1 байт, процессор — трехадресный;
З) длина поля кода операции 4 бита, размер адресуемой памяти — 64 ячейки, процессор — двухадресный;
4) длина поля кода операции 4 бита, длина адресного поля 4 бита, процессор — одноадресный.
Разработайте формат машинной команды для двухадресного процессора с числом машинных команд в системе команд не более 16 и объемом адресуемой памяти не менее 256 ячеек.
3.2.2. Язык машинных команд
В соответствии с принципами Дж. фон Неймана выделяют четыре основных типа машинных команд: арифметические и логические;
Для уяснения специфики программирования на ЯМК воспользуемся двумя «учебными компьютерами»: Счетная Машина «Малютка» и Учебный Компьютер «Нейман», описанных в учебниках по информатике, приведенных в списке дополнительной литературы. Для простоты ограничимся только целочисленной арифметикой и минимально необходимым подмножеством команд из систем машинных команд этих исполнителей.
СМ «Малютка»: процессор одноадресный, длина поля кода операции 4 бита, длина поля адресной части 1 байт, длина адресуемой ячейки памяти равна длине команды, система счисления двоично-шестнадцатеричная.
Система команд СМ «Малютка»
(шестнадцатеричное представление)

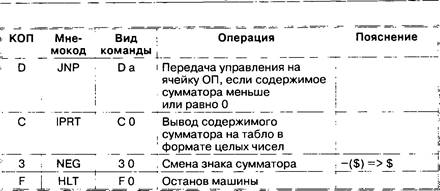
Здесь запись а и $ обозначает адрес ячейки и «адрес» сумматора. Запись (а) и ($) обозначает содержимое ячейки с адресом а и содержимое сумматора, соответственно.
УК «Нейман»: процессор — трехадресный, длина поля кода операции 1 байт, адресуем каждый байт памяти, длина ячейки памяти равна длине машинной команды, система счисления — двоично-шестнадцатеричная.
Система команд УК «Нейман»
(шестнадцатеричное представление)
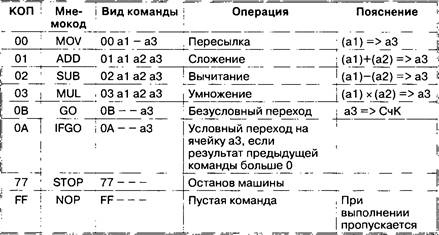
Здесь знак «—» означает, что соответствующие операнды в выполнении команды не участвуют.
Управление учебными компьютерами осуществляется посредством программы в автоматическом режиме (принцип программного управления). Самая первая команда программы располагается в ячейке с нулевым адресом. Команды выполняются в естественном порядке до тех пор, пока не встретится команда остановки или невыполнимая команда. В регистре счетчика команд (СчК) при этом содержится адрес следующей команды.
![]() Пример 1
(программа с линейной структурой). Даны значения целых чисел Ь, с, d, е.
Составить программу
Пример 1
(программа с линейной структурой). Даны значения целых чисел Ь, с, d, е.
Составить программу ![]() вычисления по формуле:
вычисления по формуле:
![]()
Решение
Сначала запишем алгоритм на алгоритмическом языке с учетом особенностей систем команд учебных компьютеров.
Алгоритм, ориентированный Алгоритм, ориентированный на СМ «Малютка» на УК «Нейман»
![]() вывод а кон
вывод а кон
вывод а кон
|
Адрес коп
|
М Комментарий 06 Программа начинается с ячейки Об №десь будет значение переменной а
• Сюда вводится значение переменной
|
|||||
![]() Программа на ЯМК СМ
«Малютка» (все адреса и коды операций даются в шестнадцатеричной системе
счисления,• память под переменные отводится перед программой).
Программа на ЯМК СМ
«Малютка» (все адреса и коды операций даются в шестнадцатеричной системе
счисления,• память под переменные отводится перед программой).

Программа на ЯМК УК «Нейман» (все адреса и коды операций даются в шестнадцатеричной системе счисления; память под переменные отводится после программы: ячейка с адресом 30 — переменная Ь, 34 с, 38 — d, ЗС — е , 40 — а , 44 — О.
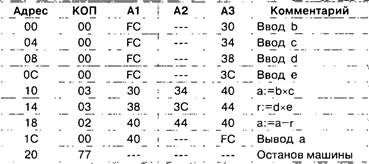
Пример 2 (программа с ветвлением). Даны целые числа
Определить z тах(х,у).
Решение
Алгоритм, ориентированный Алгоритм, ориентированный на СМ «Малютка» на УК «Нейман» алг Пример_2 алг Пример_2 цел х, у, z цел х, у, z, r нач ввод х нач ввод х ввод У ввод у
![]() r:=x—Y если
r то z:=x
r:=x—Y если
r то z:=x
О иначе z:=y кв иначе $:=х вывод z
кв кон z:=$ вывод z кон
Программа на ЯМК СМ «Малютка».
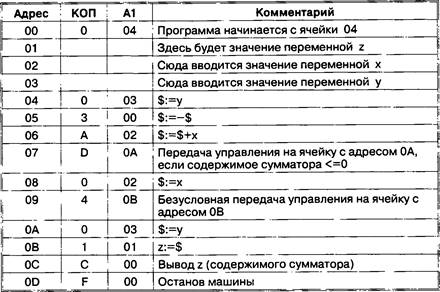
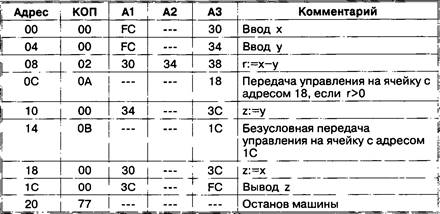
![]() Пример З (программа с циклом). Дано целое
число п.
Пример З (программа с циклом). Дано целое
число п.
![]() Вычислить = п! (п! —
Вычислить = п! (п! —![]()
Решение
Алгоритм, ориентированный Алгоритм, ориентированный на СМ «Малютка» на УК «Нейман»
|
алг Пример_З |
алг Пример_З |
|
цел п, f |
цел п, f |
|
нач ввод п |
нач ввод п повторять |
![]()
![]() повторять
повторять
до п ![]() вывод f кон
вывод f кон
вывод f кон
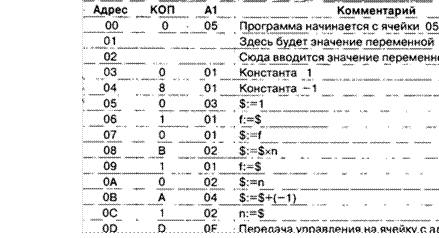 Передача управления на ячейку с адресом ОР, если содержимое
сумматора <=O
Передача управления на ячейку с адресом ОР, если содержимое
сумматора <=O
 Безусловная передача управления на ячейку с
Безусловная передача управления на ячейку с
Программа на ЯМК УК «Нейман» (распределение памяти:

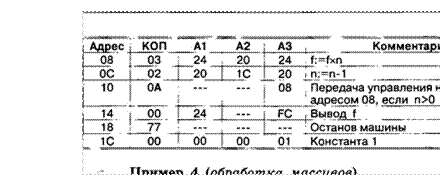 Пример 4 (обработка
массивов)
Пример 4 (обработка
массивов)
В
последовательности из п чисел найти минимальное. Решение. Для представления
исходных данных воспользуемся переменной с индексом (массивом) a[i], i![]()
![]() , п. Перебор
элементов массива в цикле можно реализовать, воспользовавшись одной из идей Дж.
фон Неймана: возможностью работы с командой как с данными (модификация
команды). Ниже используется обозначение — адрес ОП, где
, п. Перебор
элементов массива в цикле можно реализовать, воспользовавшись одной из идей Дж.
фон Неймана: возможностью работы с командой как с данными (модификация
команды). Ниже используется обозначение — адрес ОП, где
расположен элемент массива.
Алгоритм, ориентированный на СМ «Малютка»
алг Пример_4 цел п, i, r, min массив цел нач ввод п ввод a[i], i=1, 2, п min:=$
повторять
![]()
r:=$
$:=$+min если $ < О
![]()
min:=$ кв
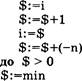
вывод min кон
Алгоритм, ориентированный на УК «Нейман»
алг Пример_4 кон цел п, i, r, min, z массив цел нач ввод п
![]()
z:=r—min если z < О то min:=r кв z:=i—n
![]()
вывод min кон

Программа на ЯМК УК «Нейман» (распределение памяти: ячейка 58 — константа 1, 5С — п, 60 — т, 64 — min, 68 —
42], 78 а[З] и т. д.).
|
Адрес |
коп |
|
Комментарий |
|
|
|
10 |
Формирование начального состояния команды по адресу 10 |
|
|
|
24 |
Формирование начального состояния команды по адресу 24 |
|
|
|
5С |
Ввод п Команда ввода текущего элемента массива (формируется и модифицируется) |
|
|
|
|
ЕС |
Вывод mim Останов машины |
|
48 |
00 |
ЕС |
70 68 04 00 01 |
Заготовка для команды ввод а[1], которая будет модифицироваться Заготовка для команды которая будет модифицироваться Константа для модификации поля адреса АЗ в команде с адресом 10 Константа для модификации поля адреса А 1 в команде с адресом 24 Константа 1 |
Передача управления на ячейку с адресом 34, если 00
. min:=r
Модификация команды с адресом 24
Передача управления на ячейку с адресом 24, если п>О
![]()

Для решения задач .N2 10 — N2 27 разработать программы на языке машинных команд для любого из описанных учебных компьютеров.
Поменять местами содержимое двух ячеек памяти (Х У).
Выполнить циклический обмен содержимого трех ячеек памяти (Х» У» Z).
![]()
Выдать на табло произведения числа, расположенного в заданной ячейке памяти, на числа 11, 12, 13, 14.
1) Для СМ «Малютка» адрес данной ячейки 01. 2) Для УК «Нейман» адрес данной ячейки — 30.
.N2 13
Пусть в четырех последовательных ячейках памяти расположены числа х, у, 10, 14 соответственно. Вычислить выражение 10х — 14у.
Вычислить значения выражений:
1) 2х 2
+ зу 2 + 35ху - 18; 2) 7х 3 + 4х + 5;![]()
![]() 5)
х 4 15х + 20.
5)
х 4 15х + 20.
Л) 15
Для заданного Х вычислить значение Х 32 , используя по возможности наименьшее количество команд и переменных.
.N2 16
Вычислить значения выражений:
2![]()
Л) 17
Вычислить значения выражений:
![]() если
если ![]() 5, если
5, если ![]()
если ![]() если
если![]()
если ![]() если
если ![]()
Пусть задано некоторое целое положительное число Х. С использованием конструкции цикла просуммировать все числа
![]()
![]()
Определить делится ли целое число Х на целое число У (Х > У), используя вычитание У из Х в цикле.
Определить наибольший общий делитель (НОД(х,у)) двух натуральных чисел с помощью алгоритма Евклида, используя очевидное свойство НОД(х,у) — НОД(х — у,у) при х > у.
Дано целое число Х и натуральное N. Вычислить значение выражения XN .
.N2 22
Числа Фибоначчи определяются по формуле
![]() — U + Un_1 (U1 — U 2 — 1), т. е. каждый
последующий
— U + Un_1 (U1 — U 2 — 1), т. е. каждый
последующий
член равен сумме двух предыдущих.
1) Определить значение числа Фибоначчи с заданным номером, 2) Найти сумму т-шсал Фиажаччи, не превьп...иаюпџж заданнот К.
Вычислить сумму числовой последовательности
![]() + (2n — 1) и убедиться, что она равна п 2
.
+ (2n — 1) и убедиться, что она равна п 2
.
Вычислить сумму числовой последовательности
 16 + . + 8(n — 1) и
убедиться, что она равна
16 + . + 8(n — 1) и
убедиться, что она равна
Отсортировать заданную последовательность чисел в возрастающем (убывающем) порядке.
![]() 26
26
Даны два отсортированных массива, объединить их в один, тоже отсортированный.
Для заданной последовательности чисел х 1 , х2 , определить их сумму и сумму квадратов:
![]()
3.2.3. Машинно-ориентированные языки (Автокод — Ассемблер)
Процесс программирования на ЯМК по ряду причин достаточно сложен:
![]() необходимо самому
распределять память под данные и постоянно помнить в какой ячейке что
находится;
необходимо самому
распределять память под данные и постоянно помнить в какой ячейке что
находится;
о иметь дело с цифровыми кодами команд, запоминать которые не очень удобно; о при модификации (исправлении) программы, добавлении (удалении) в нее команд требуется тщательно корректировать адреса передачи управления.
Программа-переводчик, которая автоматически распределяег память, распознает мнемонические обозначения команд и в конечном итоге получает готовую к исполнению программу на машинном языке, называется Ассемблер (Автокод).
Язык ассемблера естественным образом связан с ЯМК машины и поэтому называется машинно-ориентированным. В качестве примера рассмотрим Ассемблер СМ «Малютка» и Автокод УК «Нейман».
![]() Пример 1 (программа с линейной
структурой)
Пример 1 (программа с линейной
структурой)
Вычислить выражение а![]()
Решение
Программа на Ассемблере СМ «Малютка».
![]() —
резервируем в памяти одну ячейку под переменную а;
—
резервируем в памяти одну ячейку под переменную а;
В: dw 8; — резервируем в памяти ячейку под переменную Ь и заносим туда некоторое значение (например, число 8);
![]() С:
dw 10; — аналогично с; — аналогично d;
С:
dw 10; — аналогично с; — аналогично d;
— аналогично е;
|
ТЧТ; |
— начало программы; |
|
LDA |
— загрузили В в сумматор (команда О); |
|
МКЛ.,Т |
— умножили содержимое сумматора на С (команда В); |
|
STA |
— сохранили содержимое сумматора в А (1); |
|
LDA |
|
|
МКЛ.„Т |
— умножили содержимое сумматора на Е (В); |
|
NEG; |
— сменили знак содержимого сумматора (ЗОО); |
|
ADD |
— сложили содержимое сумматора со значением из А (А); |
|
STA |
— сохранили содержимое сумматора в А (1); |
|
IPRT; |
— печать содержимого сумматора (ООО); |
|
НЬТ; |
— останов машины (FOO). |
|
Программа на Автокоде УК «Нейман». |
|
|
INPUT В — ввод Ь; |
|
|
INPUT С — ввод с; |
|
|
INPUT D — ввод Ф, |
|
INPUT Е — ввод е;
![]() МТЛ, В,С,А
МТЛ, В,С,А
MUL![]()
SUB![]()
|
окјтркјт А |
— вывод а; |
|
STOP |
— останов машины, |
Как видно из приведенных текстов, распределение памяти под данные в Ассемблере СМ «Малютка» и Автокоде УК «Нейман» происходит по-разному: в Ассемблере программист сам распределяет память, указывая мнемонические имена (метки) адресов ячеек, а в Автокоде память отводится автоматически (сразу же после последней команды программы) по мере встречаемости мнемонических имен в тексте программы.
![]() Пример 2 (программа
с циклом)
Пример 2 (программа
с циклом) ![]() Вычислить f = п! (п!
Вычислить f = п! (п!![]()
Программа на Ассемблере СМ «Малютка».
![]() —
резервируем в памяти одну ячейку под переменную f;
—
резервируем в памяти одну ячейку под переменную f;
![]() — резервируем в
памяти ячейку под переменную п и заносим туда некоторое значение (например,
число 9);
— резервируем в
памяти ячейку под переменную п и заносим туда некоторое значение (например,
число 9);
|
ONE: dw 1; |
— резервируем в памяти ячейку под константу 1 ; |
|
NONE: dw -1; |
— резервируем в памяти ячейку под константу -1; |
|
ENT; |
— начало программы; |
|
LDA (ОМ); |
— загрузили константу 1 в сумматор (команда О); |
|
STA |
— сохранили содержимое сумматора в F (команда 1); |
![]() М1:
LDA — загрузили F в сумматор (О);
М1:
LDA — загрузили F в сумматор (О);
МЕЛИТ— умножили содержимое сумматора на N (В);
STA— сохранили содержимое сумматора в F
|
|
(команда 1); |
|
LDA |
— загрузили N в сумматор (О); |
|
ADD (NONE); |
— сложили содержимое сумматора с константой —1 (А); |
|
STA |
— сохранили содержимое сумматора в N (1); |
|
JNP M2; |
— передаем управление на метку М2, если содержимое сумматора меньше или равно О (D); |
|
ејмр M1•, |
— передаем управление на метку М 1 (4); |
|
М2: LDA |
— загрузили F в сумматор (О); |
|
IPRT; |
— вывод содержимого сумматора (СОО); — останов машины. |
Программа на Автокоде УК «Нейман». пчртјт N — ввод п;
![]()
IFGO Ы — передача управления на метку L1, если п > О;
OUTPUT ![]() — вывод f;
— вывод f;
STOP — останов машины.
Отметим, что
1) для констант в Ассемблере используются мнемонические имена, а в Автокоде специальное обозначение (<число>);
2) обозначение адресов для передачи управления и в Ассемблере и в Автокоде производится с помощью меток; в свою очередь, используя метки как имена переменных, можно работать с командами как с данными (см. пример 4 из предыдущего пункта).
Если синтаксических ошибок не обнаружено, то начинается второй этап работы транслятора — перекодировка программы в машинные коды. Результатом этой работы является машинный код (программы на ЯМК).
А теперь опишем алгоритм, по которому работает транслятор с Ассемблера (Автокода) после завершения синтаксической отладки.
1) Распределение
памяти. Память должна быть выделена под данные и под команды программы.
Ассемблер сначала (начиная с нулевой ячейки) выделяет память под данные, затем
располагает команды программы. Автокод поступает наоборот: в начале памяти
располагает команды программы, затем ![]() данные, т. е. константы и переменные.
Переменные и константы располагаются в памяти в той последовательности, в
которой они встречаются в тексте программы.
данные, т. е. константы и переменные.
Переменные и константы располагаются в памяти в той последовательности, в
которой они встречаются в тексте программы.
![]()
2) Перекодировка команд. Каждая команда на Ассемблере (Автокоде) переводится в соответствующую команду на машинном языке. При этом мнемонический код заменяется на код операции, а переменные и константы — на их машинные адреса. Константы переводятся в двоичную систему и записываются в отведенные для них ячейки.
В качестве примера рассмотрим трансляцию программы, умножающей 2 на 2.
Программа на Ассемблере СМ Программа на Автокоде УК
« Малютках « Нейман »
DVA: dw 002 МТЛ,![]()
![]() OUTPUT
Х
OUTPUT
Х
ENT УГОР
LDA (DVA)
Мш,Т (DVA)
STA (Х)
IPRT
Результат трансляция программы с Ассемблера на ЯМК.
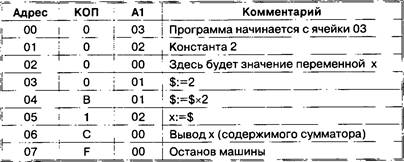
Результат трансляции программы с Автокода на ЯМК.
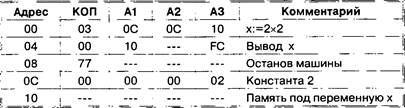

Г•Г2 28
Оттранслировать с Ассемблера на ЯМК:
![]()
![]() 1)
А: dw 0032) ONE: dw 001 3) N: dw 020
1)
А: dw 0032) ONE: dw 001 3) N: dw 020
|
В: dw 004 |
ZERO: dw 000 Х: dw 005 |
|
ONE: dw 001 |
![]() ENT SIGN:
ds 1ENT
ENT SIGN:
ds 1ENT
|
MULT (А) |
|
LDA (ONE) |
|
STA (1) |
|
STA (С) |
|
NEG |
|
М1: LDA (1) |
|
LDA (В) |
|
STA (SIGN) |
|
MULT (1) |
![]() LDA (А)
LDA (А)![]() ENT LDA
(ONE)
ENT LDA
(ONE)
|
MULT (В) |
|
LDA (Х) |
|
IPRT |
|
ADD (С) |
|
епчр М1 |
|
LDA (ONE) |
|
STA (С) |
|
LDA (ONE) |
|
ADD (1) |
![]() IPRT STA
(SIGN)
IPRT STA
(SIGN) ![]() STA (1)
STA (1)
НИГлир м2 NEG
М1: NEG ADD (N) епчр МЗ JNp М2 јмр М2 лир м1 мез: LDA (ZERO) М2: НИГ
|
STA
(SIGN) М2: LDA (SIGN) IPRT Н1„Т Оттранслировать с Автокода на ЯМК: |
|
|
|
1) пчртјт А 2) INPUT Х |
|
3) INPUT N |
|
пчртјт в МОх,' |
|
МОх,' |
|
МКЛ, |
|
Ы: ADD 1, |
|
МЕШ |
|
МЕШ |
|
ADD C,R,C SUB |
|
OUTPUT Х |
|
OUTPUT С IFGO L2 |
|
SUB |
|
УГОР МОГ |
|
IFGO Ы УГОР |
![]() И: МолТ
И: МолТ![]()
![]() Ы: OUTPUT SIGN STOP
Ы: OUTPUT SIGN STOP
.М2 зо
Записать программы решения задач 10-25 из предыдущего раздела на Ассемблере (Автокоде), оттранслировать полученные программы на ЯМК и сравнить результаты с программами на ЯМК, написанными ранее «вручную» .
![]()
![]()
![]() Алгоритм — понятное
и точное предписание исполнителю выполнить конечную последовательность команд,
приводящую от исходных данных к искомому результату.
Алгоритм — понятное
и точное предписание исполнителю выполнить конечную последовательность команд,
приводящую от исходных данных к искомому результату.
Исполнитель алгоритма — это тот объект или субъект, для управления которым составлен алгоритм.
Система команд исполнителя (СКИ) — это вся совокупность команд, которые исполнитель умеет выполнять.
Свойства алгоритма: понятность, точность, конечность.
Понятность: алгоритм составляется только из команд, входящих в ОКИ.
Точность: каждая команда алгоритма управления определяет однозначное действие исполнителя.
Конечность (или результативность): выполнение алгоритма должно приводить к результату за конечное число шагов.
Среда исполнителя — это обстановка, в которой функционирует исполнитель.
Определенная последовательность действий исполнителя всегда применяется к некоторым исходным данным. Например: для приготовления блюда по кулинарному рецепту нужны соответствующие продукты (данные). Для решения математической задачи (решение квадратного уравнения) нужны исходные числовые данные (коэффициенты уравнения).
Полный набор данных — это необходимый и достаточный набор данных для решения поставленной задачи (получения искомого результата).
![]()
Назвать исполнителей следующих видов работы: уборка мусора во дворе, перевозка пассажиров, выдача заработной платы, прием экзаменов, сдача экзаменов, обучение детей в школе. Попробуйте сформулировать СКИ для каждого из этих исполнителей.
4.
![]()
Г.Г2 2
Придумать своего исполнителя и описать его по схеме: среда, СКИ (как отдаются, как выполняются, «НЕ МОГУ»).
Описать исполнителя «Графопостроитель», который с помощью «пера» строит в декартовой системе координат изображение на бумаге с нанесенной масштабной сеткой.
Описать систему команд исполнителя «Геометр», который мог бы выполнять геометрические построения с помощью циркуля и линейки.
По каналу навстречу друг другу движутся два корабля. Канал узкий, и кораблям в нем не разойтись. В канале есть бухта, в которой помещается лишь один корабль. Описать команды исполнителя «автоматический диспетчер», который осуществляет проводку кораблей через канал. Придумать удобную символическую запись для каждой команды. Составить программу действий диспетчера.
Г.Г2 6
Определить полный набор данных для решения следующих задач обработки информации:
1) вычисление стоимости покупок в магазине;
2) вычисление суммы сдачи от данных вами продавцу денег;
З) определение времени показа по телевизору интересующего вас фильма;
4) вычисление площади треугольника;
5) определение времени падения кирпича с крыши дома; 6) определение месячной платы за расход электроэнергии; 7) перевод русского текста на итальянский язык; 8) перевод итальянского текста на русский язык.
Г.Г2 7
Сформулируйте алгоритмы обработки информации для заданий из предыдущей задачи, если исполнителем являетесь вы сами. Какие команды при этом вы должны уметь выполнять?
![]()
4.2.1. Машина Поста
![]() СреДа — бесконечная
информационная лента, разделенная на позиции (клетки). В каждой клетке может
либо стоять метка (будем обозначать ее жирной точкой: о) либо — пусто. Вдоль
ленты движется каретка. Она мо-
СреДа — бесконечная
информационная лента, разделенная на позиции (клетки). В каждой клетке может
либо стоять метка (будем обозначать ее жирной точкой: о) либо — пусто. Вдоль
ленты движется каретка. Она мо-
жет передвигаться шагами; один шаг смещение на одну клетку вправо или влево. Клетку, у которой установлена каретка будем называть текущей.
лента

![]()
Назначение исполнителя: преобразование записи на информационной ленте.
Данные: определенная расстановка меток в позициях информационной ленты.
Действия исполнителя: с помощью каретки машина Поста может:
— распознать, клетка пустая или помеченная;
— стереть метку в текущей клетке;
— поставить метку в пустую текущую клетку.
Система команд исполнителя: (везде буква п обозначает номер текущей команды):


1. «НЕ ПОНИМАЮ» — если исполнителю отдается команда, не входящая в его СКИ;
2. «НЕ МОГУ» — если исполнитель должен стереть метку из пустой секции или поставить метку в заполненную секцию.
Пример 1. Начальное состояние (Н.с.) информационной ленты:
![]()
![]()
17
![]()
По этой программе исполнитель добавляет метку справа от данной.
Результат — конечное состояние (Юс.):
![]()
![]()
![]()
Выполнить на машине Поста программу:

Нарисовать начальное и конечное состояния информационной ленты.
Выполнить на машине Поста программу:

Нарисовать начальное и конечное состояния информационной ленты.
![]()
Выполнить на машине Поста программу:

Нарисовать начальное и конечное состояния информационной ленты.
Какую задачу решает исполнитель в задаче № З? Написать свой вариант программы, решающей ту же задачу.
Что произойдет при выполнении исполнителем программы из задачи № З, если начальное состояние информационной ленты и каретки имеет вид:
![]()
Составить программу перевода информационной ленты машины Поста из начального состояния в конечное:

Составить программу перевода информационный ленты машины Поста из начального состояния в конечное:

1. Выполнить на машине Поста программу:
![]()
4.

2. Какую задачу решает исполнитель по этой программе?
З. Что произойдет, если начальное состояние информационной ленты имеет вид:
нас.![]()
На информационной ленте машины Поста помечены метками N клеток подряд. Каретка располагается под самой левой помеченной клеткой. Какой вид будет иметь информационная лента после окончания работы исполнителя по программе?
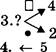
.М2 10
На информационной ленте на расстоянии 5 клеток расположены две метки. Каретка находится под правой помеченной клеткоЙ. Какой вид будет иметь лента после окончания работы машины по программе?
![]()
З
4
н.с.![]()
В задачах с N2 11 по N2 17 считается, что N расположенных подряд меток обозначают число N (непозиционная система счисления с основанием 1).
Написать для машины Поста программу сложения двух чисел, записанных на ленте и расположенных через одну пустую клетку друг от друга. Начальное положение каретки под пустой клеткой, отделяющей числа.
ЛЕ 12
Написать для машины Поста программу вычитания двух чисел, разделенных одной пустой клеткой. Уменьшаемое не меньше вычитаемого. Начальное положение каретки под пустой клеткой, отделяющей уменьшаемое от вычитаемого.
![]()
Указание: стирать метки по одной у каждого числа, пока у вычитаемого не кончатся все метки.
Используя программу вычитания, проверить:
1) что получится, если уменьшаемое равно вычитаемому? 2) что получится, если уменьшаемое меньше вычитаемого?
Написать для машины Поста программу деления числа, записанного метками, на 2. Исходное число должно делиться на 2 без остатка.
Указания: стереть каждую вторую метку; уплотнить оставшиеся метки.
Используя программу деления числа на 2:
1) проверить, что получится для числа 2;
2) модифицировать программу с учетом числа 2.
Указания: справа от пустой клетки поставить метку, а слева стирать по две метки до тех пор, пока слева остаются метки.
На информационной ленте машины Поста на расстоянии в лт клеток друг от друга расположены две помеченные метками клетки. Начальное положение каретки — под левой из помеченных клеток. Какую работу выполнит машина Поста по программе?
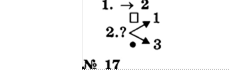
Написать для машины Поста программу умножения на 2 числа, записанного метками на ленте.
Указания: через одну пустую клетку поставить две метки, а из исходного числа стереть одну и т. д.
Написать программу для игры в Баше с машиной Поста. На информационной ленте 21 помеченная секция. За один ход каждый играющий может стереть 1, 2, З или 4 кружочка, идущих подряд. Побеждает тот, кто стирает последний кружок. Начальное положение каретки — под самой левой из помеченных секций.
Выигрышная стратегия: стирать столько кружочков, чтобы в сумме со стертыми противником за один ход их было пять.
Написать для машины Поста программу, проверяющую делится ли записанное кружочками число на 5.
.N2 ЗА
На информационной ленте машины Поста помечена 2N—1 секция. Составить программу отыскания средней помеченной секции и стирания из нее кружочка.
На информационной ленте машины Поста расположены два массива помеченных секций. Написать программу стирания кружочков, расположенных в большем массиве.
4.2.2. «Умный мячик»
![]() Среда: линейка
длиной 14 см, вдоль которой прыгает «умный мячик». Над каждым делением линейки
может находиться буква или знак «*» , который обозначает невидимую букву (см.
рис. 4.2).
Среда: линейка
длиной 14 см, вдоль которой прыгает «умный мячик». Над каждым делением линейки
может находиться буква или знак «*» , который обозначает невидимую букву (см.
рис. 4.2).
Назначение исполнителя: собирать слова из букв, расположенных вдоль линейки.
— перемещение вдоль линейки;
— чтение (копирование) буквы в текущей позиции; — сравнение буквы в текущей позиции с заданной. Система команД исполнителя:
1. + число движение вправо на указанное число единиц ! — число движение влево на указанное число единиц взять копию буквы, над которой находится мячик
4. конец собирания слова
|
6. ПОКА НЕ |
выполнение действий, указанных в скобках, до |
|
буква |
тех пор, пока буква, на которую указывает мячик, |
|
(действия) |
не совпадет&фуквой, указанной в команде |
5.
![]()
![]()
![]() ?буква проверка буквы и выбор
действий; если буква, (действие1, над которой находится мячик, совпадает с
действие2) буквой, указанной в команде, то выполняется
?буква проверка буквы и выбор
действий; если буква, (действие1, над которой находится мячик, совпадает с
действие2) буквой, указанной в команде, то выполняется ![]() действие1,
действие1, ![]() а при несовпадении —
действие2
а при несовпадении —
действие2
7. ЭТО имя описание вспомогательного
алгоритма, действия_вспо- обращение к нему — указать в основной могательного![]() программе имя алгоритма
программе имя алгоритма ![]() КОНЕЦ
КОНЕЦ![]()
Реакция исполнителя:
1) «НЕ ПОНИМАЮ» — на команду, не входящую в СКИ или записанную с ошибкой; на обращение к неописанному вспомогательному алгоритму;
2) «НЕ МОГУ» — при выходе исполнителя за деления О или 14; при попытке взять букву в позиции, где буквы нет.
![]() Пример 1.
Начальное расположение мячика и расстановка букв вдоль линейки представлены на
рисунке 4.2.
Пример 1.
Начальное расположение мячика и расстановка букв вдоль линейки представлены на
рисунке 4.2.

![]()
Составить с помощью «умного мячика» слово горизонт. Решение. Программа, решающая поставленную задачу:
![]()
Решение
Вариант 1![]()
Вариант 2: -3! +1! +1! -1! +7! -4! -3! ПОКА НЕ ш(+1)!.
Вариант З: ЭТО алг ПОКА НЕ КОНЕЦ
—3! +1! +1! алг +7! -4! алг ПОКА НЕ ш (+1)!.
![]()
|
к |
р |
|
Т |
о |
з |
н |
и |
м |
|
![]()
Начальное положение «умного мячика» и расположение букв представлены на рис. 4.3. Что получится после выполнения «умным мячиком» программы:
1) -3! -2! +3! -1! +4! +2! -2! -51. •
Л'2 19
Начальное положение «умного мячика» и расположение букв представлены на рис. 4.3. Напишите для исполнителя программу, по которой он сможет собрать слово городок.
Г.Г2 20
Начальное положение «умного мячика» и расположение букв представлены на рис. 4.3. Напишите для исполнителя программу, по которой он сможет собрать слово карниз.
Начальное положение «умного мячика» и расположение букв представлены на рис. 4.3. Напишите для исполнителя программу, по которой он сможет собрать слово агроном.

Рис. 4.4
![]() 22
22
![]() . -11! +1!, -5! -6! +1!). ?
. -11! +1!, -5! -6! +1!). ?
Начальное положение «умного мячика» и расположение букв представлены на рис. 4.4. Под одной из «*» спрятана буква с. Напишите для исполнителя программу, по которой он сможет собрать слово носорог.
Г.Г2 24
Начальное положение «умного мячика» и расположение букв представлены на рис. 4.4. Под одной из «*» спрятана буква ш. Напишите для исполнителя программу, по которой он сможет собрать слово карандаш.
![]() 25
25
Начальное положение «умного мячика» и расположение букв представлены на рис. 4.4. Под «*» спрятаны буквы м и л. Напишите для исполнителя программу, по которой он сможет собрать слово алгоритм.
Г.Г2 26
Начальное положение «умного мячика» и расположение букв представлены на рис. 4.4. Под «*» спрятаны буквы м и я. Напишите для исполнителя программу, по которой он сможет собрать слово армия.

![]()
.N2 27
Начальное положение «умного мячика» и расположение букв представлены на рис. 4.5. Выбрать алгоритм, с помощью которого «умный мячик» соберет слово алгоритм, если под одной из «*» находится буква о.
1) -3! +12! -9! +1 +2! -4! +7! -4! -4!).
2) -3! +12! -9! +1 -2! +3! -4!) +7! -4! -4!.
4) -3! +12! -9! +1 -22, +2! +7! -4! 5) -3! +12! -9! +1 -2, +3! -4!) +7! -4!
.N2 28
Начальное положение «умного мячика» и расположение букв представлены на рис. 4.5. Под одной из «*» находится буква
![]() 29
29
Расположение букв представлено на рис. 4.5. Под одной из «*» спрятана буква о. Указать начальное положение мячика (в см), если после исполнения алгоритма —3 ?о(! —1l, +2! —3!) +5! +1!. будет собрано слово огни.
Начальное положение «умного мячика» и расположение букв представлены на рис. 4.5. Под «*» спрятаны буквы п и ц. Написать программу для «умного мячика», с помощью которой он соберет слово процессор.
.N2 31
Начальное положение «умного мячика» и расположение букв представлены на рис. 4.5. Под одной из «*» спрятана буква о. Какое слово соберет исполнитель после выполнения алгоритма: ПОКА НЕ 0(+1) ! ПОКА НЕ р(—1) ! +3!. ?
.N2 32
Начальное положение «умного мячика» и расположение букв представлены на рис. 4.5. Под одной из «*» спрятана буква о.
7 Информатика
и ИКТ. Т. ![]()
Написать для исполнителя программу, по которой можно собрать слово мрамор.
Начальное положение «умного мячика» и расположение букв представлены на
рис. 4.5. Под одной из «*» спрятана буква о. Какое слово соберет исполнитель
после исполнения программы: -4! алг ПОКА НЕ ! алг ПОКА НЕ с(+1) ![]() ЭТО алг +5 +2!) КОНЕЦ ?
ЭТО алг +5 +2!) КОНЕЦ ?
ЛЕ 34
Начальное положение «умного мячика» и расположение букв представлены на рис. 4.5. Под одной из «*» скрывается буква о. Написать программу, по которой исполнитель соберет слово информатика.
Начальное положение «умного мячика» и расположение букв представлены на рис. 4.5. Написать программу, по которой исполнитель соберет слово математика.
Начальное положение «умного мячика» и расположение букв представлены на рис. 4.5. Под одной из «*» спрятана буква ш. Написать программу, по которой «умный мячик» составит ;финиш;финал.
После выполнения алгоритма:
-5 алг -2 +1!) +5! -7 алг -1! -2! ![]() ЭТО
алг ! +1 +5!, +3! +2!) КОНЕЦ будет собрано финиш;финал. Выбрать вариант
начального положения «умного мячика» и расположения букв, если под одной из «*»
спрятана буква а, а под другой — и.
ЭТО
алг ! +1 +5!, +3! +2!) КОНЕЦ будет собрано финиш;финал. Выбрать вариант
начального положения «умного мячика» и расположения букв, если под одной из «*»
спрятана буква а, а под другой — и.
1)
2)
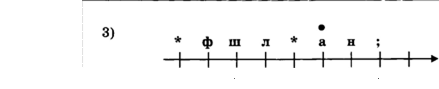
4)
5) 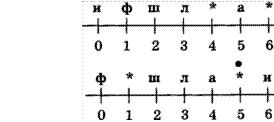
Придумать не менее З заданий для «умного мячика», решения которых реализуются с помощью линейного алгоритма.
Придумать не менее З заданий для «умного мячика», решения которых реализуются с помощью алгоритма с ветвлениями.
Придумать не менее З заданий для «умного мячика», решения которых реализуются с помощью циклического алгоритма.
Придумать не менее З заданий для «умного мячика», решения которых реализуются с помощью алгоритма с ветвлением и циклического алгоритма.
Придумать не менее З заданий для «умного мячика», решения которых реализуются с помощью вспомогательного алгоритма.
![]()
Придумать не менее З заданий для «умного мячика», решения которых реализуются с помощью вспомогательного алгоритма, в котором могут быть ветвления или цикл ПОКА-НЕ.
4.2.3. Графический исполнитель (Г РИС) [1]
![]() Среда: лист
(страница экрана) для рисования. На лист нанесена прямоугольная сетка. Г РИС
располагается в узлах сетки и может иметь одно из четырех направлений: вверх,
вниз, налево, направо.
Среда: лист
(страница экрана) для рисования. На лист нанесена прямоугольная сетка. Г РИС
располагается в узлах сетки и может иметь одно из четырех направлений: вверх,
вниз, налево, направо.
Назначение исполнителя: получение рисунков, составленных из вертикальных и горизонтальных отрезков.
Данные: исполнитель работает «в обстановке». Исходными данными являются положение исполнителя на поле и его направление. Результатом полученный рисунок.
Действия исполнителя: перемещение вдоль линий сетки с рисованием или без; поворот; проверка условия выхода на край поля.
Система команд исполнителя:
![]()
1.
Шаг![]() Перемещение ГРИС на один шаг
Перемещение ГРИС на один шаг ![]() вперед с рисов_анием линии.
вперед с рисов_анием линии.
![]()
2.
![]()
![]() Поворот Поворот на 90 0 против
часовой
Поворот Поворот на 90 0 против
часовой ![]() стрелки .
стрелки .![]()
![]()
![]()
![]()
![]()
![]()
|
4. |
Сделай |
Вызов вспомогательного |
|
|
имя вспомогательного алго- |
алгоритма. |
![]()
|
5. |
Пока <условие>, повторять |
Цикл. Варианты условий: |
|
|
нц |
«впереди край» или «впереди не |
|
|
<тело цикла> |
край». Тело цикла повторяет |
![]() кц
кц![]() выполнение пока условие
выполнение пока условие ![]() истинно.
истинно.
![]()
6. Если
<условие> Ветвление. Серия_1 то <серия_1> выполняется, если
условие, иначе <серия_2> записанное после слова «если» ![]()
![]() кв истинно. В противном случае
кв истинно. В противном случае ![]() выполняется серия 2.
выполняется серия 2.
![]()
Формат описания основной программы:
программа имя (заголовок основной программы} нач
<тело программы> кон
Формат описания вспомогательного алгоритма ( процедуры ): процедура имя {заголовок вспомогательного алгоритма} нач
<тело процедуры> кон
Реакция исполнителя:
1) «НЕ МОГУ» — исполнитель достиг края листа и не может выполнить следующую команду.
2) «НЕ ПОНИМАЮ» исполнителю отдается команда, не входящая в СКИ или не описанная с помощью вспомогательного алгоритма.
![]() Пример 1. Программа рисования буквы Т.
Начальное положение исполнителя: в левом конце горизонтального
Пример 1. Программа рисования буквы Т.
Начальное положение исполнителя: в левом конце горизонтального ![]() отрезка,
направление направо.
отрезка,
направление направо.
Пример 2. Составить программу решения предыдущей задачи с использованием вспомогательного алгоритма.
Решение. Рисунок состоит из двух прямых отрезков длиной 4 шага. Рисование отрезка оформим в виде про-
цедуры «ПРЯМАЯ».
|
процедура ПРЯМАЯ |
программа Т |
|
нач |
нач |
|
шаг |
сделай ПРЯМАЯ |
|
шаг |
поворот |
|
шаг |
поворот |
|
шаг |
прыжок |
|
кон |
прыжок поворот сделай ПРЯМАЯ кон |
Пример З. Нарисовать прямоугольную рамку вдоль края поля. Исходное положение Г РИС: в левом верхнем углу, направление вниз.
|
программа Рамка |
процедура ЛИНИЯ |
|
|
нач |
|
нач |
|
|
сделай ЛИНИЯ |
пока впереДи не край, повторять |
|
|
поворот |
нц |
|
|
сделай ЛИНИЯ |
шаг |
|
|
поворот |
кц |
|
кон |
сделай ЛИНИЯ поворот сделай ЛИНИЯ |
кон |
![]()
ЛР2 39
Выбрать из перечисленных фигур и букв те, которые может нарисовать исполнитель Г РИС: прямоугольник, треугольник, пятиконечную звезду, квадрат, буквы Н, Х, З, Р, М, Л .
«М 40
Составить для исполнителя программу, с помощью которой можно нарисовать: 1) прямоугольник; 2) квадрат.
Л) 41
Составить для исполнителя программу, с помощью которой можно написать буквы:
Используя в качестве вспомогательных алгоритмов программы из задачи 41, помогите исполнителю написать слова:
1) ПЕРО; 2) ПОРОГ; 3) БОР; 4) БЕРЕГ;
5) ПЕРЕЦ; 6) БОРЕЦ; 7) ГЕРБ; 8) ГОРЕЦ.
.М2 43
Используя вспомогательные алгоритмы, нарисовать:
 3)
3) 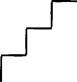
1) 2)
программа похоД программа похоД
нач нач
пока впереди не край, повторять пока впереди не край, повторять
нц нц
прыжок прыжок
кц поворот
поворот прыжок
пока впереди не край, повторять поворот
нц поворот
прыжок поворот
кц кц
кон кон
.М2 45
Составить программу, переводящуло исполнителя в угол поля из любого исходного положения.
![]() 46
46
Составить программу рисования прямоугольной рамки вдоль края листа, исходя из любого начального состояния исполнителя.
.М2 47
Составить программу, переводящую исполнителя из нижнего левого угла в верхний правый угол.
Расчертить все поле горизонтальными пунктирными линиями.
![]() 49
49
Нарисовать квадраты во всех четырех углах поля.
.М2 50
Расчертить все поле в клетку со стороной, равной шагу исполнителя.
![]()
Нарисовать орнамент, состоящий из квадратов по краю поля. Сторона квадрата и расстояние между двумя соседними квадратами равны одному шагу ГРИС.
![]() 52
52
Нарисовать орнамент, изображенный на рис. 4.6.

Рис. 4.6
Г.С2 ПА
Придумайте не менее трех заданий для графического исполнителя, в которых необходимо использовать вспомогательные алгоритмы.
Г.С2 12А
Придумайте не менее трех заданий для графического исполнителя, в которых наряду с вспомогательными алгоритмами необходимо использовать алгоритмы с ветвлениями и/или циклами.
4.2.4. ЛОГО — Черепашка
![]() Среда: лист (экран
компьютера), по которому может двигаться черепашка. В начале сеанса черепашка
находится в центре листа. Черепашка рисует хвостом. Если хвост опущен, то при
движении черепашка рисует, если поднят — не рисует.
Среда: лист (экран
компьютера), по которому может двигаться черепашка. В начале сеанса черепашка
находится в центре листа. Черепашка рисует хвостом. Если хвост опущен, то при
движении черепашка рисует, если поднят — не рисует.
Назначение исполнителя: получение рисунков, составленных из отрезков прямых и закрашенных областей.
Данные: исполнитель работает с числовыми значениями длины перемещения, угла поворота, номера цвета.
Действия исполнителя: перемещение по экрану с рисованием или без; повороты; управление цветом; закраска замкнутых областей.
|
<число> — движение вперед на шагов (FD <число>); — движение назад на шагов (ВК <число>); перемещение черепашки в центр — поворот налево на указанное (LT <число>); — поворот направо на |
|
Система команД исполнителя:
![]()
1. Команды FORWARD перемещения: указанное число
ВАСК <число> указанное число НОМЕ — листа.
![]()
|
|
LEPI' число RIGHT указа |
|
|
|
|
З. |
Команды |
PU — поднять хвост; |
|
|
изменения состояния: |
PD — опустить хвост. |
|
|
Команды |
SETBG <число> — установить цвет рабочего |
|
|
работы |
поля (фона); |
|
|
с цветом: |
SETC <число> — установить цвет черепахпки и ее хвоста. Нумерация цветов: О — прозрачный 8 — черный белый 9 — светло-серый голубой 10 — светло-голубой З — фиолетовый 11 — розовый 4 — красный 12— светло-красный 5 — синий 13 — светло-синий 6 — коричневый 14 — желтый зеленый 15 — светло-зеленый FILL — команда заливки замкнутой области текущим цветом черепап:жи. |
|
5. |
Команда |
REPEAT <число повторений> |
|
|
повторения: |
«повторяющиеся действия>]; Например, нарисовать квадрат со стороной 40 шагов можно по команде REPEAT 4 [FD 40 RT 90]. |
Команды<число> поворотов:градусов
|
|
IF <условие> выполнено]. |
6. Неполное[что делать, если условие ветвление:
|
7. |
Полное |
IFEISE <условие> [что делать, если условие |
|
|
ветвление: |
выполнено] [что делать, если условие не выполнено]. |
8. Описание ТО <имя> <параметры> — заголовок вспомогатель- вспомогательного алгоритма (процедуры), ного алгоритма: параметры могут отсутствовать;
END — конец вспомогательного алгоритма.
9. Команда МАКЕ “ <имя переменной> <выражение>. присваивания Например: МАКЕ 5; переменной: МАКЕ + 5.
10. Операция READCHAR
I чтения символа Например: МАКЕ READCHAR. с клавиатуры:
11. Команда RG. очистки экрана:
Реакция исполнителя:
«НЕ ПОНИМАЮ» — отдается команда, не входящая в СКИ или не описанная с помощью вспомогательного алгоритма.
Пример 1. Нарисовать на экране два квадрата — большой и
маленький. ТО SQ![]()
REPEAT 4 [FD RT 901 — вспомогательный алгоритм, с по-
ENDмощью которого можно нарисовать квадрат с любой стороной.
![]() Вариант 1: SQ 60 LT
90 PU FD 50 PD SQ 20. Вариант 2: SQ 20 RT 90 РТ-Ј FD 60 PD SQ 60. Вариант З: ТО
SQ2 .•k2
Вариант 1: SQ 60 LT
90 PU FD 50 PD SQ 20. Вариант 2: SQ 20 RT 90 РТ-Ј FD 60 PD SQ 60. Вариант З: ТО
SQ2 .•k2
— это описание новой коман-
RT 90 РТ-Ј FDды исполнителя, с помо-
SQ![]() щью которой можно нариENDсовать сразу два
квадрата.
щью которой можно нариENDсовать сразу два
квадрата.
Обращение к новой команде имеет вид : SQ2 60 20.
Пример 2. Нарисовать квадрат красного цвета. Для решения задачи воспользуемся процедурой SQ.
ТО CSQ ![]()
![]() рисуем
квадрат со стороной :dl
рисуем
квадрат со стороной :dl
RT 45 PU FD :dl / 2 Р D — не оставляя следа,
входим внутрь квадрата
SETC 4 меняем цвет черепашки на красный закрашиваем квадрат
![]() /
2 LT 45 возвращаем черепашку
/
2 LT 45 возвращаем черепашку
в исходное положение
SETC 1 — устанавливаем цвет черепашки белым END
Пример З. Процедура, вызывающая сама себя, называется рекурсивной. Рассмотрим пример рекурсивной процедуры, рисующей квадрат.
ТО SQ![]()
FD RT 90 — нарисовать сторону и повернуться направо на 900
END
Это пример бесконечной рекурсии. Чтобы прекратить выполнение программы, надо нажать клавиши CTRL+BREAk.
![]() Пример 4. Пример управляемой рекурсии —
рисование
Пример 4. Пример управляемой рекурсии —
рисование ![]() квадратной спирали.
квадратной спирали.
• ТО А![]()
FD RT 90
IF < 80 [А + 5]
END
![]()
![]() 53
53
Нарисовать в тетради результат выполнения следующих последовательностей команд, обозначив схематически на чертеже начальное и конечное положение черепашки:
1) FD ЗО RT ЗО FD 60;
2) FD 40 LT 90 FD 40 LT 90 FD 40.
Л) 54
Дополнить последовательность команд из задачи М 53 (пункт 2) так, чтобы получился полный квадрат.
![]() 55
55
Получить на экране квадрат. Сколько вариантов решения вы нашли? Записать каждый в тетради.
Л) 56
Нарисовать на экране «конверт» (квадрат с диагоналями).
![]() 57
57
Нарисовать на экране равносторонний треугольник (все стороны равны, углы равны 600).
.М2 58
Программным путем измерить в черепашьих шагах длину и ширину экрана. Что происходит, если черепашка вышла за край листа?
Можно ли в процедуре рисования квадрата
ТО SQ
FD 60 RT 90
FD 60 RT 90
FD 60 RT 90
FD 60 RT 90
END
использовать другие команды? Нарисовать в тетради, что получится, если выполнить подряд все варианты. Проверить на компьютере.
Определить новую команду STEP и с ее помощью описать команду рисования лесенки.
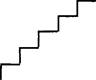

ЛЕ 62
Написать программы для рисования следующих рисунков:
П У Н К Т И Р
![]()

.N2 63
Описать новую команду для рисования фигуры:
Используя новую команду из задачи N2 63, написать программу для рисования «забора» .
![]()
Оформить решение задачи Г•Г2 64 в виде новой команды и с ее помощью составить программу рисования следующей фигуры:

Что нарисует черепашка по команде REPEAT З [FD 20 RT 360 / 3] '?
.М2 67
.М2 68
Написать процедуру рисования правильного ЛТ -угольника со стороной А.
Выполнить ее для лт — 6, 8, 9, 10, 12, 36. На что похожи последние фигуры?
N2 69
Написать программы для получения следующих рисунков:
Г.Г2 70 Что нарисует черепашка по команде REPEAT 4 [TR RT 90], где
ТО TR
REPEAT З [FD 40 RT 120] END ?
![]()
Написать процедуры для рисования «лепестков» разной формы:
1) квадратных;
2) пятиугольных; З) круглых.
ЛЕ 72
Используя процедуры из задачи № 71, написать программы, рисующие цветы с разным количеством лепестков различной формы.
Нарисовать три равносторонних треугольника. Первый треугольник закрасить в красный, второй — в синий, третий в зеленый цвет.
Изменить программы из задачи № 69 так, чтобы каждая фигура была закрашена в свой цвет.
![]() 75
75
Написать программу рисования на экране шахматной доски.
Нарисовать на экране:
1) 2)

Описать необходимые процедуры и составить программу для рисования пенсне.
Используя процедуры рисования полуокружностей, нарисовать следующие картинки:
ВОЛНА
![]()
ПРУЖИНА
![]()
ПЕРО
![]() 79
79
Используя процедуру рисования пера, нарисовать цветок из пяти лепестков и раскрасить его в красный цвет.
Описать необходимые процедуры и, используя их, нарисовать:
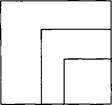 2)
2) 
Используя только одну вспомогательную процедуру, нарисовать на одной линии правильный треугольник, квадрат и шестиугольник.
Нарисовать:
1) пирамидку из трех квадратов; 2) снеговика; З) елочку.
Нарисовать три рядом стоящие елочки, используя процедуру для рисования фигур переменного размера.
Нарисовать в тетради результат работы процедуры
ТО А
FD 50 RT 90
END.
.N2 85
По какой траектории будет двигаться черепашка, если угол поворота в процедуре А (из задачи № 84) изменить с 90 0 на 500 ? Сначала нарисовать в тетради, а потом проверить на компьютере.
Написать рекурсивные процедуры рисования:
1) разворачивающейся квадратной спирали (спираль рисуется изнутри наружу);
2) сворачивающейся квадратной спирали (спираль рисуется снаружи внутрь);
З) разворачивающейся прямоугольной спирали; 4) сворачивающейся прямоугольной спирали.
.N2 87
Написать рекурсивные процедуры рисования: 1) раскручивающейся круглой спирали; 2) скручивающейся круглой спирали.
.N2 88
Используя операцию ввода символа с клавиатуры, напишите программу имитации простейшего художника. Система команд художника: продвижение на 20 шагов, поворот направо и налево на 900 . Нарисовать с помощью художника простой рисунок.
Творческие задачи и проекты
Разработать систему команд исполнителя — художник, который может рисовать не только прямые отрезки, но и дуги, может изменять цвет пера. Написать программу, имитирующую исполнителя художник.
Разработать систему команд робота, умеющего писать почтовые индексы. Написать программу, имитирующую работу робота.
![]() Величина это
отдельный информационный объект, который имеет имя, значение и тип.
Величина это
отдельный информационный объект, который имеет имя, значение и тип.
Исполнителем алгоритмов работы с величинами может быть человек или специальное техническое устройство, например компьютер. Такой исполнитель должен обладать памятью для хранения величин.
Величины бывают постоянными и переменными.
Постоянная величина (константа) не изменяет своего значения в ходе выполнения алгоритма. Константа может обозначаться собственным значением (числа 10, 3.5) или символическим именем (число п).
Переменная величина может изменять значение в ходе выполнения алгоритма. Переменная всегда обозначается символическим именем (Х, А, R5 и т. п.).
Тип величины определяет множество значений, которые может принимать величина, и множество действий, которые можно выполнять с этой величиной. Основные типы величин: целый, вещественный, символьный, логический.
Команда присваивания — команда исполнителя, в результате которой переменная получает новое значение. Формат команды:
«(имя переменной>:=<выражение>
Исполнение команды присваивания происходит в таком порядке: сначала вычисляется <выражение>, затем полученное значение присваивается переменной.
Пример 1. Пусть переменная А имела значение 6. Какое значение получит переменная А после выполнения команды: А.— 2 х А — 1.
Решение. Вычисление выражения 2 х А — 1 при А — 6 даст число 11. Значит новое значение переменной А будет равно 11.
Пример 2.
Написать последовательность команд присваивания, в результате выполнения
которых переменные ![]() А и В поменяются значениями.
А и В поменяются значениями.
Решение. Для решения этой задачи потребуется еще одна дополнительная переменная С. В следующей таблице приведен алгоритм и трассировочная таблица исполнения алгоритма для начальных значений А = З, В = 7.
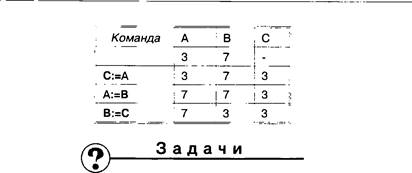
Определить конечные значения переменных Х и У в результате выполнения следующих алгоритмов:
Написать алгоритм вычисления по формуле:
![]()
учитывая следующие ограничения: 1) пользоваться можно только операциями сложения, вычитания и умножения; 2) каждое выражение может содержать только одну арифметическую операцию.
Пользуясь ограничениями предыдущей задачи, написать
наиболее короткие алгоритмы вычисления: ![]() х10.
х10.
![]()
Постараться использовать минимальное число дополнительных переменных. Выполнить трассировку алгоритмов для
Записать алгоритм циклического перемещения влево значений между переменными А, В, С. Схема циклического перемещения:
![]()
Записать алгоритм циклического перемещения вправо значений между переменными А, В, С, D. Схема перемещения:
![]()
В дальнейшем будет предполагаться, что исполнителем алгоритмов работы с величинами является компьютер. Любой алгоритм может быть построен из команд присваивания, ввода, вывода, ветвления и цикла.
Команда ввода команда, по которой значения переменных задаются через устройства ввода (например, клавиатуру).
Пример: ввод А — ввод значения переменной А с клавиату-
ры компьютера.
Команда вывода — команда, по которой значение величины отражается на устройстве вывода компьютера (например, на экране дисплея).
Пример: вывод Х — значение переменной Х выводится на
экран.
Команда ветвления — разделяет алгоритм на два пути в зависимости от некоторого условия, затем исполнение алгоритма выходит на общее продолжение. Ветвление бывает полное и неполное. Описание ветвления в блок-схемах и на Алгоритмическом языке:
Полное ветвление Неполное ветвление
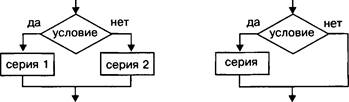
если <условие> если <условие> то <серия 1> то <серия> иначе «(серия 2> кв
Здесь под серией понимается одна или несколько последовательных команд; кв конец ветвления.
Команда цикла обеспечивает повторное выполнение последовательности команд (тела цикла) по некоторому условию.
Цикл с предусловием — цикл, выполнение которого повторяется, пока истинно условие цикла:
![]() пока
<условие>, повторять ни,
пока
<условие>, повторять ни,
<тело цикло кц
Цикл с параметром повторное выполнение тела цикла, пока целочисленный параметр пробегает множество всех значений от начального (In) до конечного (П):
![]() для i от In до Ik,
повторять нц
для i от In до Ik,
повторять нц
<тело цикла> кц
Пример З. Даны две простые дроби. Составить алгоритм получения дроби, являющейся результатом их деления.
Решение. В алгебраической форме решение задачи выглядит следующим образом:
![]()
Исходными данными являются четыре целые величины: а, Ь, с, d. Результат два целых числа т и п.
вывод
” Числитель= , ![]() вывод ” Знаменатель— , п кон
вывод ” Знаменатель— , п кон
Обратите внимание, что для вывода текста (любой символьной последовательности) его следует записать в кавычках в команде вывод.
Пример 4. Даны три вещественных числа А, В, С. Найти наибольшее среди них.
Решение. Сначала определяется большее среди двух значений А и В, затем большее между найденным значением и величиной С. Алгоритм имеет структуру двух последовательных ветвлений.
![]() Пример 5. Дано целое
положительное число ЛУ . Вычислить факториал этого числа: Л! — 1 • 2
• З
Пример 5. Дано целое
положительное число ЛУ . Вычислить факториал этого числа: Л! — 1 • 2
• З
Решение. Задача решается с помощью циклического алгоритма. Составим два варианта алгоритма: с применением цикла с предусловием и цикла с параметром.
алг Факториал 1 алг Факториал 2 ![]() цел р, N,
R нач ввод N нач ввод N
цел р, N,
R нач ввод N нач ввод N
![]() для
R от 1 до N повторять пока RSN, повторять нц нц
для
R от 1 до N повторять пока RSN, повторять нц нц ![]() кц
вывод
кц
вывод ![]() , кц кон вывод ” Факториал— ,
, кц кон вывод ” Факториал— , ![]()
кон
![]()
Составить алгоритм вычисления площади треугольника со сторонами а, Ь, с (а, Ь, с — вещественные положительные числа).
Длины сторон первого прямоугольника а и Ь, его площадь в 6 раз меньше площади второго прямоугольника. Найти длину стороны второго прямоугольника, если длина одной из его сторон равна с.
Длина стороны треугольника равна а, периметр равен р, длины двух других сторон равны между собой. Найти эти длины.
Периметр треугольника равен р, длина одной стороны равна а, другой — Ь. Найти длину третьей стороны.
![]() 10
10
Найти площадь поверхности куба со стороной а.
Построить графики функций у(х), заданных следующими алгоритмами:
|
то у 1/(х х х) |
|
|
|
иначе |
иначе |
|
|
если х S 2 то у х х х |
если х < 1
|
|
|
иначе у 4 |
иначе у |
1/(х — 0.5) |
|
кв |
кв |
|
|
кв |
кв |
|
Написать алгоритм нахождения максимального среди четырех целых чисел.
.М2 13
Написать алгоритм проверки условия: имеются ли среди трех целых чисел два положительных значения?
.М2 14
Написать алгоритм проверки условия: могут ли три данных числа быть длинами сторон треугольника?
.М2 15
Написать алгоритм проверки условия: лежит ли данная точка с координатами (х, у) в первой четверти координатной плоскости?
Лё 16
Проверить принадлежность числа х интервалам [а, Ь] или
Проверить, является ли четырехугольник со сторонами а, Ь, с, d ромбом.
Определить, является ли треугольник со сторонами а, Ь, ![]() равнобедренным.
равнобедренным.
Определить, является ли треугольник со сторонами а, Ь, ![]() равносторонним.
равносторонним.
.N2 20
Среди чисел а, Ь, с определить количество отрицательных.
.N2 21
Среди чисел а, Ь, с определить количество положительных. .М2 22
Числа а и Ь — катеты одного треугольника, с и d — катеты другого. Определить, являются ли эти треугольники равновеликими.
![]() 24
24
Определить значение целочисленной переменной S после выполнения алгоритмов:
а) 128 ![]() для i от 1
до 4 повторять для i от 1 до 2 повторять
для i от 1
до 4 повторять для i от 1 до 2 повторять
нц нц для .j от 2 до З повторять
![]()
кц ![]()
кц кц
.N2 25
Определить значение целочисленной переменной S после выполнения алгоритмов:
![]() - 1 б) для
i от 1 до З повторять для i от 1 до З повторять нц
- 1 б) для
i от 1 до З повторять для i от 1 до З повторять нц
ни, для .i от 2 до 2 повторять
![]()
![]() нц
нц
кц кц кц
26
|
пока i < З, повторять |
пока i 1, повторять |
|
нц |
нц |
![]()
![]() Определить
значение переменной S после выполнения алгоритмов:
Определить
значение переменной S после выполнения алгоритмов:
![]()
кц кц
.М2 27
Определить значение переменной S после выполнения алгоритмов:
|
пока i < .Ј, повторять |
пока а + Ь < 10, повторять |
|
нц |
нц
|
|
кц |
кц |
![]()

Последовательно вводятся целых чисел. Найти сумму всех положительных среди них.
Последовательно вводятся лт целых чисел. Найти количество отрицательных среди них.
Последовательно вводятся целых чисел. Определить каких среди них чисел больше: положительных или отрицатель-
ных.
.N2 33
Последовательно вводятся лт целых чисел. Найти максимальное из них. Л) 34
Последовательно вводятся лт целых чисел. Найти минимальное из положительных значений.
Последовательно вводятся лт целых чисел. Сосчитать сколько из них совпадают с первым числом.
.М2 36
Последовательно вводятся лт целых чисел. Найти разницу между наибольшим и наименьшим из них.
Последовательно вводятся ЛУ целых чисел. Найти среднее арифметическое этих чисел.
Л) 38
Найти наибольший общий делитель двух чисел А и В (алгоритм Евклида).
Л) 39
.М2 40
Найти первое из чисел 1, 1/2, 1/3, 1/4 и т. д., меньшее заданного числа А.
Найти сумму чисел 1, 1/2, 1/3, 1/4 и т. д., больших заданного числа А.
Л) 42
Леспромхоз ведет заготовку деловой древесины. Ее первоначальный объем на территории леспромхоза был равен Р м з . Ежегодный прирост составляет КУО . Годовой план заготовки древесины — Т мз . Какой объем деловой древесины на данной территории будет через год, через два и т. д., пока этот объем не станет меньше минимального значения В мз ?
![]()
Данный раздел содержит большой практический материал для начального изучения программирования. Задачи ориентированы, главным образом, на использование процедурных языков программирования, из которых в настоящее время наиболее распространенными являются Паскаль, Бейсик и СИ. Чаще всего именно эти языки изучаются на уроках информатики.
С точки зрения авторов, наиболее подходящим языком для первоначального освоения программирования является язык Паскаль. Как известно, автор Паскаля Н. Вирт создавал его прежде всего как учебный язык. Позднее фирмой Borland была разработана система программирования Турбо-Паскаль, расширившая область применения языка и развившая сам язык программирования. Современные версии Турбо-Паскаля достаточно широко распространены в компьютерных классах учебных заведений.
Предлагаемые в данном разделе задачи могут решаться с использованием любого языка программирования. Однако весь пояснительный материал и примеры программ приведены на Паскале. Таким образом, помимо задач, раздел содержит краткий справочник по программированию на Паскале. Описание языка не является полным. За более подробными сведениями о Паскале следует обращаться к специальной литературе.
Некоторые тематические разделы поделены на части, отличающиеся уровнем сложности задач. Эти части обозначены буквами А, В и
т. д. по возрастанию сложности.
4.4.1. Программирование линейных алгоритмов
![]() Программы с линейной
структурой составляются из операторов присваивания, ввода, вывода, обращения к
процедурам. Оператор присваивания можно назвать основным в любом языке
программирования.
Программы с линейной
структурой составляются из операторов присваивания, ввода, вывода, обращения к
процедурам. Оператор присваивания можно назвать основным в любом языке
программирования.
Оператор присваивания:
<переменная> <выражение>
Оператор выполняется следующим образом. Вычисляется значение <выражения>, после чего <переменная> получает вычисленное значение. При этом тип выражения должен быть совместим с типом переменной.
Примеры оператора присваивания:
![]() (А>В) апа (C<-D) .
(А>В) апа (C<-D) .
Выражение может включать в себя константы, переменные, знаки операций, функции, скобки. В результате вычисления выражения получается значение определенного типа.
Тип выражения определяется типом полученного значения.
Арифметическое выражение выражение числового типа (целого или вещественного). Идентификатор целого типа: integer, вещественного типа: real.
языках
![]()
Арифметические операции бывают унарными и бинарными. К унарным относится операция изменения знака. Ее формат: — <величина>.
В следующей таблице представлены бинарные арифметические операции Паскаля. А и В обозначают операнды, для типов величин использованы обозначения: I — целый, R — вещественный.
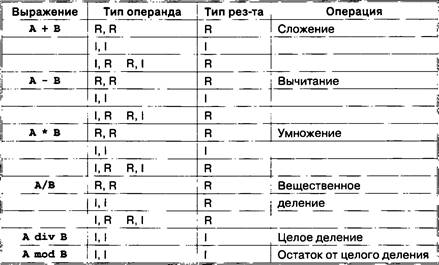
Стандартные математические функции Паскаля представлены в следующей таблице:
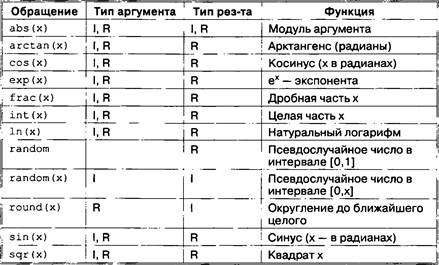

Возведение положительного числа в вещественную степень следует производить, используя следующее математическое тождество: х у = е! х . На Паскале это записывается так: ехр (у*1п (х) )
Пример 1. Записать математические выражения в виде арифметических выражений на Паскале.
Математическое выражение Выражение на Паскале
![]() (Abs (х) -Abs (у) )
/
(Abs (х) -Abs (у) )
/
(1+Abs (х * у) )
Ln (Abs ( (y—Sqrt (Abs (х) ) ) * (х- у / (z+Sqr (x) /4 ) ) ) )
Ввод данных с клавиатуры производится путем обращения к стандартным процедурам:
Read (список ввода>) ReadLn «список ввода>)
Элементы списка ввода — идентификаторы переменных. Вводимые значения отражаются на экране. При выполнении оператора пользователь набирает на клавиатуре соответствующую последовательность значений, разделяя их пробелами.
Вывод данных на экран производится путем обращения к стандартным процедурам:
Rri te (список вывода>) Wri te2n (<спксок вывода>) Элементы списка вывода константы, переменные, выражения, форматы вывода.
Структура программы на Паскале:
Program <Имя программы>;
языках
![]()
Procedure (Function) <раздел описания подпрограмм>; Begin
<раздел операторов> End .
Для любой программы обязательным является лишь раздел операторов. Все программные объекты (константы, переменные, типы и пр.) должны быть описаны в соответствующих разделах описаний.
Здесь и в дальнейшем служебные слова Паскаля будут выделяться полужирным шрифтом. Служебными называются слова, значения которых в языке однозначно определены.
Пример 2.
Скорость первого автомобиля км/ч, второ![]() го — км/ч, расстояние между ними s км.
Какое рас
го — км/ч, расстояние между ними s км.
Какое рас![]() стояние будет между ними через t ч, если
автомобили движутся в разные стороны?
стояние будет между ними через t ч, если
автомобили движутся в разные стороны?
Решение. Согласно условию задачи искомое расстояние s 1 = s + (и + V2)t (если автомобили изначально двигались в противоположные стороны) или s2 = l(V1 + V2)t — .sl (если автомобили первоначально двигались навстречу друг другу).
Программа организует ввод исходных данных, вычисление искомых величин по формулам и вывод их на экран. Все величины в программе вещественного типа.
Program Car;
Var V1, V2, Т, S , S1, S2 : Rea1;
Write ( '
Введите скорости автомобилей, расстояние между ними и время движения :![]()
ReadLn (V1, '\72, S , Т) ;
![]()
Пример З. Выполнить вычисление по формуле:
![]()
![]()
Решение
Write ( ' Введите значения переменных Т, К, М, 2,![]()
ReadLn (Т, К, М, Ь, х, У) ; z : ![]() т
* т-К*К) / ( sqr (Sqr (М) ) -Ехр (5*Ln (Ы ) ) ) + Sqrt (Abs ( (Sqrt (Х) + У) /
(12-Abs (Х) ) + 4 ) ) ; WriteLn ( ' Значение выражения :
т
* т-К*К) / ( sqr (Sqr (М) ) -Ехр (5*Ln (Ы ) ) ) + Sqrt (Abs ( (Sqrt (Х) + У) /
(12-Abs (Х) ) + 4 ) ) ; WriteLn ( ' Значение выражения : ![]() End .
End .
![]() Логические
выражения в результате вычисления принимают логические значения true или false.
Операндами логического выражения могут быть логические константы, переменные
логического типа, отношения. Идентификатор логического типа в Паскале: boolean.
Логические
выражения в результате вычисления принимают логические значения true или false.
Операндами логического выражения могут быть логические константы, переменные
логического типа, отношения. Идентификатор логического типа в Паскале: boolean.
Логические операции. В Паскале имеются 4 логические операции: отрицание — NOT, логическое умножение — AND, логическое сложение — 0R, исключающее «или» — XOR. Результаты логических операций для различных значений операндов приведены в таблице. Использованы обозначения: Т — Пие, — false.
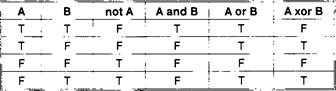
Приоритеты логических операций:
1) not; 2) and; 4) xor.
Примеры логических выражений:
1) True•, 2) Fa1se; 3) А>В; 4) (А=В) апа![]()
Операции отношений (— <>, ![]() <,
>) имеют более низкий приоритет, чем логические операции, поэтому их следует
заключать в скобки при использовании по отношению к ним логических операций.
<,
>) имеют более низкий приоритет, чем логические операции, поэтому их следует
заключать в скобки при использовании по отношению к ним логических операций.
![]() Пример 4. Составить
программу, по которой выведется значение true, если точка с заданными координатами
(х, у) лежит внутри заштрихованной области (рис. 4.7), и false в противном
случае.
Пример 4. Составить
программу, по которой выведется значение true, если точка с заданными координатами
(х, у) лежит внутри заштрихованной области (рис. 4.7), и false в противном
случае.
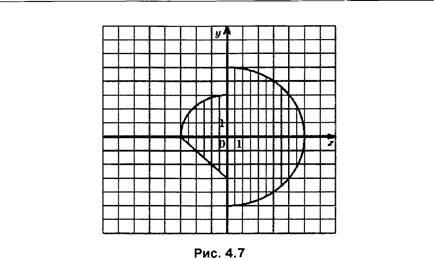
Решение. Рассматриваемая область состоит из двух частей, каждая из которых описывается системой неравенств.
1-я часть: х О; х2 + у2 9.,![]()
2-я часть: х О; х 2 + у 2 25.
Точка с координатами (х, у) лежит в заштрихованной области, если она принадлежит 1-й или 2-й части.
Программа вводит координаты точки, вычисляет логическое выражение, определяющее принадлежность точки области и выводит полученную логическую величину на экран.
Program Point ;
Write ( ' Введите Х: ' ) ; Readln (Х) ;
Write Введите У : ' ) ; ReadLn (У) ;
WriteLn ( '
Точка лежит в заданной области? ' ![]() End .
End .
![]()
Вычислить значения выражений по формулам 1 - 26 (все переменные имеют действительный тип):
![]() -2
-2 ![]()

![]() 13
13 ![]()
cos x
![]() + 16x •
cos(xy) - 2;
+ 16x •
cos(xy) - 2; ![]()
![]() 15
15
1
2ctg(3x) — ![]() 12x2 + 7x — 5
12x2 + 7x — 5
Y N
17 x .![]()
x cos x ![]()
3
![]() 2
2
N 19 e x
ln cos x
![]() 21 2ctg(3x)
-
21 2ctg(3x)
-![]()
![]() 23 3 x
23 3 x![]()
Ne 25 X - IOsin x +
cos(x — y); ![]() x
2 -8x + 12
x
2 -8x + 12
14
— cos x + sin(2xy);
![]()
18 sin Vx + 1 — sin
I + Sin N! X I 20
cos(12y —4)
![]()
4
24 x — 10 sin x + l x — x51 ;
I + Sin2 (X y)
26
![]()
Alli'OPHTMH3a1.4Hfl H nporpaMMH1)0BaHHe
![]()
3 5
Ng6 x- X ![]() x
x ![]()
3 5
N 8(1 - tg x)ctgx + cos(x — y);
![]() + 18xy2.
+ 18xy2.
N 12 ![]()
Вычислить периметр и площадь прямоугольного треугольника по заданным длинам двух катетов а и Ь.
Заданы координаты трех вершин треугольника (хр У1), (х2, У2), (хз, уз). Найти его периметр и площадь.
![]() 29
29
Вычислить длину окружности и площадь круга одного и того же заданного радиуса R.
![]() зо Найти
произведение цифр заданного четырехзначного числа.
зо Найти
произведение цифр заданного четырехзначного числа.
Даны два числа. Найти среднее арифметическое кубов этих чисел и среднее геометрическое модулей этих чисел.
Вычислить расстояние между двумя точками с заданными координатами (хр У1) и (х2, У2).
Г•Г2 34
Дана длина ребра куба. Найти площадь грани, площадь полной поверхности и объем этого куба.
.М2 35
Дана сторона равностороннего треугольника. Найти площадь этого треугольника, его высоты, радиусы вписанной и описанной окружностей.
.М2 36
Известна длина окружности. Найти площадь круга, ограниченного этой окружностью.
![]() 37
37
Найти площадь кольца, внутренний радиус которого равен r, а внешний R (R > r).
.М2 38
Треугольник задан величинами своих углов и радиусом описанной окружности. Найти стороны треугольника.
8 1/4
Информатика и ИКТ. Т. ![]()
Найти площадь равнобедренной трапеции с основаниями а и Ь и углом а при большем основании а.
Вычислить корни квадратного уравнения ах 2 + bx + с = О, заданного коэффициентами а, Ь и с (предполагается, что а О и что дискриминант уравнения неотрицателен).
Дано действительное число х. Не пользуясь никакими другими арифметическими операциями, кроме умножения, сложения и вычитания, вычислить за минимальное число операций значение выражения
2х4 3х3
+ 4х2![]()
Дано х. Получить значения выражений —2х + 3х 2 — 4х 3 и
1 + 2х + 3х 2 + 4х 3 . Позаботиться об экономии операций.
Л) 43
Найти площадь треугольника, две стороны которого равны а и Ь, а угол между этими сторонами равен у.
Дано а. Не используя никаких функций и никаких операций, кроме умножения, получить а 8 за три операции; а 10 и а 16 за четыре операции.
Л) 45
Найти сумму членов арифметической прогрессии, если известны ее первый член, знаменатель и число членов прогрессии.
![]() 46
46
Найти все углы треугольника со сторонами а, Ь, с. Предусмотреть в программе перевод радианной меры угла в градусы, минуты и секунды.
Л) 47
Три сопротивления Щ, R,z, R3 соединены параллельно. Найдите сопротивление соединения.
Л) 48
Составить программу для вычисления пути, пройденного лодкой, если ее скорость в стоячей воде км/ч, скорость течения реки и км/ч, время движения по озеру t1 ч, а против течения реки — t2 ч.
ль 49
Текущее показание электронных часов: т часов (О т 23), п мин (О п 59), К с (О К 59). Какое время будут показывать часы через р ч q мин r с?
ль 50
Полторы кошки за полтора часа съедают полторы мышки. Сколько мышек съедят Х кошек за У часов?
Составить программу вычисления объема цилиндра и конуса, которые имеют одинаковую высоту Н и одинаковый радиус основания R.
ль 52
Ввести любой символ и определить его порядковый номер, а также указать предыдущий и последующий символы.
Дана величина А, выражающая объем информации в байтах. Перевести А в более крупные единицы измерения информаЦИИ.
ль 54
1) сумма двух первых цифр заданного четырехзначного числа равна сумме двух его последних цифр;
2) сумма цифр данного трехзначного числа N является четным числом;
З) точка с координатами (х, у) принадлежит части плоскости, лежащей между прямыми х = т, х = п (т < п);
4) квадрат заданного трехзначного числа равен кубу суммы цифр этого числа;
5) целое число N является четным двузначным числом;
6) треугольник со сторонами а, Ь, с является равносторонним;
7) треугольник со сторонами а, Ь, с является равнобедренным;
8) среди чисел а, Ь, с есть хотя бы одна пара взаимно противоположных чисел;
9) числа а и Ь выражают длины катетов одного прямоугольного треугольника, а с и d — другого. Эти треугольники являются подобными;
10) даны три стороны одного и три стороны другого треугольника. Эти треугольники равновеликие, т. е. имеют равные площади;
11) данная
тройка натуральных чисел а, Ь, с является тройкой Пифагора, т. е. с2 ![]()
12) все цифры данного четырехзначного числа N различны;
13) данные числа х, у являются координатами точки, лежащей в первой координатной четверти;
14) (х 1 , ур и (х 2, 6.12) координаты левой верхней и правой нижней вершин прямоугольника; точка А(х, у) лежит внутри этого прямоугольника или на одной из его сторон;
15) число с является средним арифметическим чисел а и Ь;
16) натуральное число „'V является точным квадратом;
1 7) цифры данного четырехзначного числа N образуют строго возрастающую последовательность;
18) цифры данного трехзначного числа N являются членами арифметической прогрессии;
19)
20) данные числа с и d являются соответственно квадратом и кубом числа а;
21) цифра М входит в десятичную запись четырехзначного числа N;
22) данное четырехзначное число читается одинаково слева направо и справа налево;
23) сумма двух натуральных чисел кратна 2;
24) произведение натуральных чисел а и Ь кратно числу с;
25) сумма двух действительных чисел а и Ь является целым числом, т. е. дробная часть суммы равна нулю;
26) данное натуральное число а кратно числу Ь, но не кратно числу с.
Составить программу, которая печатает true, если точка с координатами (х, у) принадлежит заштрихованной области, и false в противном случае:
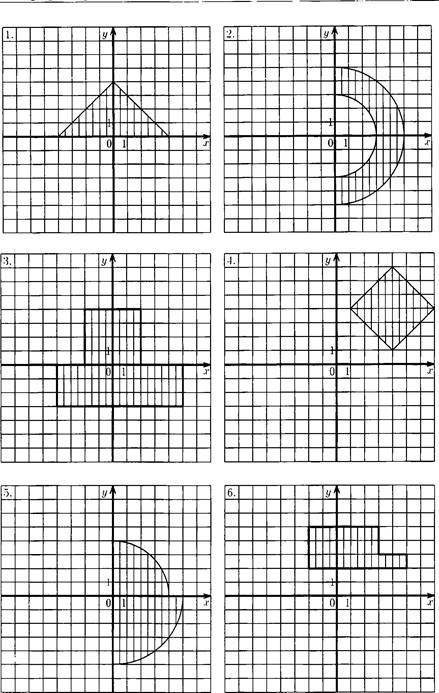
8 Информатика и ИКТ. Т. I
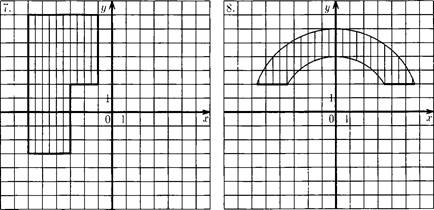
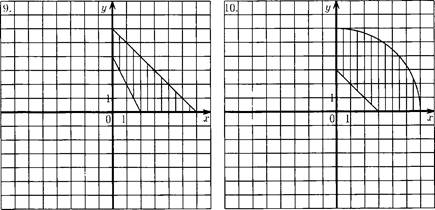
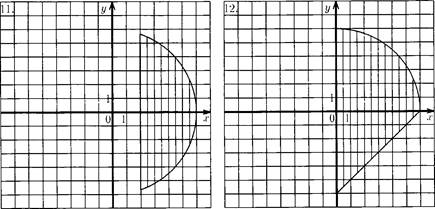
![]() 4·4· IIP()IpaMMHPOB8HHe Ha 3
4·4· IIP()IpaMMHPOB8HHe Ha 3
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
丨 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
丨丨 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
丨 |
龞 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
丨 |
|
|
|
嶓 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
丨丨 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
丨丨 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
丨丨 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
丨 |
丨 |
龞 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
丨 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
龘 |
丨 |
|
丨 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
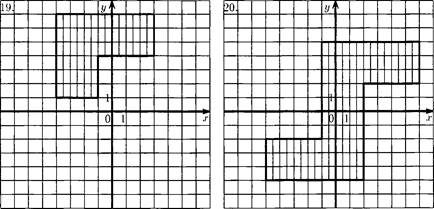
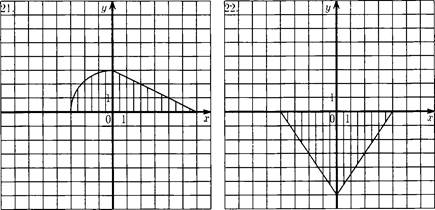
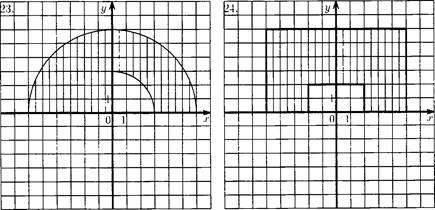
4.42. Программирование ветвящихся алгоритмов
![]() Для программирования
ветвящихся алгоритмов применяются условный оператор (оператор ветвления) и
оператор выбора.
Для программирования
ветвящихся алгоритмов применяются условный оператор (оператор ветвления) и
оператор выбора.
Условный оператор имеет следующий формат:
Xf «(логическое выражение> Тћеп <операшор![]()
Else <оператор 2>;
Операторы 1 и 2 могут быть простыми или составными. Если логическое выражение, выступающее в качестве условия ветвления, принимает значение False, то выполняется оператор 2, если 1'rue — оператор 1.
Неполная форма условного оператора:
Xf <логическое выражение> Then <операшор>;
![]() Пример 1.
Из трех данных вещественных чисел Х, У, Z
Пример 1.
Из трех данных вещественных чисел Х, У, Z ![]() выбрать наибольшее.
выбрать наибольшее.
Решение 1. Используем алгоритм с вложенными полными ветвлениями. Program МахЗ_1 ;
![]()
Тћеп Xf Then МАХ : E1se МАХ
WriteLn ( ' Максимальное МАХ)
End .
Решение 2. Используем алгоритм с последовательными неполными ветвлениями и сложными логическими выражениями.
Program Мах З 2;
Begin Write Введите Х, У, Z' ) ; ReadLn (Х,![]()
Xf апа Тћеп![]()
Xf апа Тћеп![]()
If апа Then![]()
Пример 2. Дано действительное число а. Вычислить f(a), если
![]() О при х О, х2 х при
О х S 1, х2 — sin пх 2 при других х.
О при х О, х2 х при
О х S 1, х2 — sin пх 2 при других х.
Решение. Алгоритм имеет вложенную ветвящуюся структу-
Program Formula;
WriteLn ( ' введите действительное число . • ; ReadLn (Х) ;
![]()
Тћеп F•.![]()
Else If X<=1 Then F: =sqr (Х) -Х
WriteLn ( ' Значеюте ФУНК.ЩШ (х) гри
х — , Х, ' равно ' ![]() End.
End.
![]()
Даны две точки А(хр У1) и в(х2, У2). Составить алгоритм, определяющий, которая из точек находится ближе к началу координат.
Даны два угла треугольника (в градусах). Определить, существует ли такой треугольник. Если да, то будет ли он прямоугольным.
Даны действительные числа х и у, не равные друг другу. Меньшее из этих двух чисел заменить половиной их суммы, а большее — их удвоенным произведением.
На плоскости ХОУ задана своими координатами точка А. Указать, где она расположена: на какой оси или в каком координатном угле.
Даны целые числа т, п. Если числа не равны, то заменить каждое из них одним и тем же числом, равным большему из исходных, а если равны, то заменить числа нулями.
Дано трехзначное число N. Проверить, будет ли сумма его цифр четным числом.
Определить, равен ли квадрат заданного трехзначного числа кубу суммы цифр этого числа.
Определить, является ли целое число N четным двузначным числом.
Определить, является ли треугольник со сторонами а, Ь, с равносторонним.
Л) 11
Определить, является ли треугольник со сторонами а, Ь, с равнобедренным.
Л) 12
Определить, имеется ли среди чисел а, Ь, с хотя бы одна пара взаимно противоположных чисел.
Подсчитать количество положительных чисел среди чисел а,
Л) 15
Подсчитать количество целых чисел среди чисел а, Ь, с.
Л) 16
Определить, делителем каких чисел а, Ь, с является число К.
Услуги телефонной сети оплачиваются по следующему правилу: за разговоры до А минут в месяц оплачиваются В руб., а разговоры сверх установленной нормы оплачиваются из расчета С руб. в минуту. Написать программу, вычисляющую плату за пользование телефоном для введенного времени разговоров за месяц.
Л) 18
Даны три стороны одного и три стороны другого треугольника. Определить, будут ли эти треугольники равновеликими,
т. е. имеют ли они равные площади.
![]()
Программа-льстец. На экране появляется вопрос «Кто ты: мальчик или девочка? Введи Д или М». В зависимости от ответа на экране должен появиться текст «Мне нравятся девочки!» или «Мне нравятся мальчики!» .
Г.Г2 20
Грузовой автомобиль выехал из одного города в другой со скоростью !..'1 км/ч. Через t ч в этом же направлении выехал легковой автомобиль со скоростью км/ч. Составить программу, определяющую, догонит ли легковой автомобиль грузовой через t1 ч после своего выезда.
Перераспределить значения переменных х и у так, чтобы в х оказалось большее из этих значений, а в у — меньшее.
.М 22
Определить правильность даты, введенной с клавиатуры (число — от 1 до 31, месяц — от 1 до 12). Если введены некорректные данные, то сообщить об этом.
.М 23
Составить программу, определяющую результат гадания на ромашке — «любит — не любит» , взяв за исходное данное количество лепестков п.
Л) 24
Написать программу нахождения суммы большего и меньшего из З чисел.
![]() 25
25
Определить, является ли треугольник со сторонами а, Ь, с прямоугольным. Если нет, то вычислить больший угол.
![]() 26
26
Найти max{min(a, Ь), min(c, d)}.
Г.Г2 27
Даны три числа а, Ь, с. Определить, какое из них равно d. Если ни одно не равно d, то найти max(d—a, d—b, d—c).
Г.Г2 28
Даны четыре точки АД х 1 , Щ), А2(Х2, У2), Аз(хз, уз), ААх 4 , у 4). Определить, будут ли они вершинами параллелограмма.
![]()
Даны три точки А(хр Щ), в(х2, У2) и С(хз, уз). Определить, будут ли они расположены на одной прямой. Если нет, то вычислить АВС.
Даны действительные числа а, Ь, с. Удвоить эти числа, если a<b<c, и заменить их абсолютными значениями, если это не так.
На оси ОХ расположены три точки а, Ь, с. Определить, какая из точек Ь, с расположена ближе к а.
![]() 32
32
Даны три положительных числа а, Ь, с. Проверить, могут ли они быть длинами сторон треугольника. Если да, то вычислить площадь этого треугольника.
Написать программу решения уравнения ах 3 + Ьх О для произвольных а, Ь.
Г.Г2 34
Даны числа х, у, 2. Найти значение выражения:
тах 2 (х, у, 2) —2 х • min (х, у, 2) sin2x + тах(х, у, г) / min(x, у, г)
![]() 36
36
Дано число х. Напечатать в порядке возрастания числа: sin х, cos х, ln х. Если при каком-либо х некоторые из выражений не имеют смысла, вывести сообщение об этом и сравнивать значения только тех, которые имеют смысл.
![]() 37
37
Заданы размеры А, В прямоугольного отверстия и размеры Х, У, Z кирпича. Определить, пройдет ли кирпич через отверстие.
Составить программу, осуществляющую перевод величин из радианной меры в градусную или наоборот. Программа должна запрашивать, какой перевод нужно осуществить, и выполнять указанное действие.
Два прямоугольника, расположенные в первом квадранте, со сторонами, параллельными осям координат, заданы координатами своих левого верхнего и правого нижнего углов. Для первого прямоугольника это точки (хр ур и (х2, О), для второго (хз, уз), (х 4 , О). Составить программу, определяющую, пересекаются ли данные прямоугольники, и вычисляющую площадь общей части, если они пересекаются.
В небоскребе лт этажей и всего один подъезд; на каждом этаже по З квартиры; лифт может останавливаться только на нечетных этажах. Человек садится в лифт и набирает номер нужной ему квартиры М. На какой этаж должен доставить лифт пассажира?
Написать программу, которая по заданным трем числам определяет, является ли сумма каких-либо двух из них положительной.
![]() 42
42
Составить программу, которая проверяла бы, не приводит ли суммирование двух целых чисел А и В к переполнению (т. е. к результату большему, чем 32 767). Если будет переполнение, то сообщить об этом, иначе вывести сумму этих чисел.
в
Даны действительные числа а, Ь, с (а > О). Полностью исследовать биквадратное уравнение ах 4 + bx 2 + с = О, т. е. если действительных корней нет, то должно быть выдано сообщение об этом, иначе найти действительные корни, сообщив, сколько из них являются различными.
Дана точка А(х, у). Определить, принадлежит ли она треугольнику с вершинами в точках (х 1 , Щ), (х 2 , У2), (х з, уз).
Написать программу, определяющую, будут ли прямые А 1 х + ВIУ + С 1 = О и А2Х + В2У + С2 = О перпендикулярны. Если нет, то найти угол между ними.
![]()
Если сумма трех попарно различных действительных чисел Х, У, Z меньше единицы, то наименьшее из этих трех чисел заменить полусуммой двух других; в противном случае заменить меньшее из Х, У полусуммой двух оставшихся значений.
Написать программу решения системы линейных уравнений
02 х + Ь? у =c2.
Даны три положительных числа. Определить, можно ли построить треугольник с длинами сторон, равным этим числам. Если можно, то ответить на вопрос, является ли он остроугольным.
Найти координаты точек пересечения прямой у — Кх + Ь и окружности радиуса R с центром в начале координат. В каких координатных четвертях находятся точки пересечения? Если точек пересечения нет или прямая касается окружности, выдать соответствующее сообщение.
Заданы координаты вершин прямоугольника: (хр У1), (х2, У2), (хз, уз), (х 4 , у 4). Определить площадь части прямоугольника, расположенной в 1-й координатной четверти.
В задачах 52 — 61 для данного х вычислить значения
функций:
![]() Л) 52 Л)
53
Л) 52 Л)
53
![]() х — 3х + 9, если
х — 3х + 9, если
если х
![]() .N2 54 ЛЕ
55
.N2 54 ЛЕ
55
О,
![]() если
если
![]() Л) 56 ЛЕ
57
Л) 56 ЛЕ
57
—3х + 9, если х 7;
если х > 7.
![]() ЛЕ 58 Л)
59
ЛЕ 58 Л)
59
![]() 2
2
х , если О S х З;
4, если х > З или
+ 3х + 9, если х 2 З;
, если х < З.
если х 1;
, если
если ![]()
, если![]()
![]()
если![]()

А 2 : оператор 2>;
End ;
Здесь К — выражение-селектор, которое может иметь только простой порядковый тип (целый, символьный, логический). А АЛТ — константы того же типа, что и селектор, выполняющие роль меток ветвей. Исполнение оператора начинается с вычисления выражения К, полученное значение сравнивается с константами (метками) и выполняется соответствующий оператор. Если ни одна из меток не совпала со значением К, то выполняется оператор после слова else.
Возможно использование неполного оператора выбора без ветви else. Метки ветвей также могут быть заданы списком или интервалом.
![]() Пример З. В
старояпонском календаре был принят двенадцатилетний цикл. Годы внутри цикла
носили назва
Пример З. В
старояпонском календаре был принят двенадцатилетний цикл. Годы внутри цикла
носили назва![]() ния животных: крысы, коровы, тигра,
зайца, дракона, змеи, лошади, овцы, обезьяны, петуха, собаки и свиньи. Написать
программу, которая по номеру года определяет его название в старояпонском
календаре, если известно, что 1996 г. был годом крысы началом очередного цикла.
Решение
ния животных: крысы, коровы, тигра,
зайца, дракона, змеи, лошади, овцы, обезьяны, петуха, собаки и свиньи. Написать
программу, которая по номеру года определяет его название в старояпонском
календаре, если известно, что 1996 г. был годом крысы началом очередного цикла.
Решение
Поскольку цикл является двенадцатилетним, поставим в соответствие название года остатку от деления номера этого года на 12. При этом учтем, что остаток от деления 1996 на 12 равен 4.
Program Goroskop;
Саве Year mod 12 of
0 WriteLn ( ' Год Обезьяны' ) ;
З : WriteLn ( ' Год свиньи ' ) ; 4 : WriteLn ( ' Год Крысы ' ) ; 5 : WriteLn ( ' Год Коровы ' ) ; б : WriteLn ( ' Год Тигра ' ) ; 7 • WriteLn ( ' Год Зайца ' ) ;
8 . WriteLn ( ' Год дракона ' ) ;
9 : WriteLn ( ' Год Змеи ' ) ; 10 : WriteLn ( ' Год Лошади ' ) ;
![]() Пример 4. Найти
наибольшее из двух действительных
Пример 4. Найти
наибольшее из двух действительных ![]() чисел, используя оператор выбора.
чисел, используя оператор выбора.
Решение. Здесь селектором является логическая величина.
Program Maximum;
Write ( ' Введите два неравных числа : ReadLn (Х, У) ;
Сазе Х>У
of true : Мах :![]()
false : Мах :![]()
WriteLn ( ' Максимальное из двух есть ' Мах : 12 : 6)
![]() Пример 5.
Преобразовать символ, если он является строчной русской буквой, в заглавную
букву. Предпола
Пример 5.
Преобразовать символ, если он является строчной русской буквой, в заглавную
букву. Предпола![]() гается использование альтернативной
кодировки ASCII.
гается использование альтернативной
кодировки ASCII.
Решение. Так как в альтернативной системе кодировки ASCII строчные русские буквы идут не подряд, а с некоторым разрывом, то в данном случае, в зависимости от того, в какую часть таблицы попадает введенная буква, используется та или иная формула.
Program UpCase;
Begin Write ( ' Введите символ : ReadLn (С) ;
![]()
WriteLn (С) End .
В этой программе в качестве меток использованы интервалы (диапазоны) значений символьных величин.
![]()
Написать программу, которая по номеру дня недели (натуральному числу от 1 до 7) выдает в качестве результата количество уроков в вашем классе в этот день.
Написать программу, позволяющую по последней цифре числа определить последнюю цифру его квадрата.
Составить программу, которая по заданным году и номеру месяца т определяет количество дней в этом месяце.
.М2 65
Для каждой введенной цифры (0—9) вывести соответствующее ей название на английском языке (О — zero, 1 — опе, 2 —
![]()
.М2 66
Составить программу, которая по данному числу (1—12) выводит название соответствующего ему месяца.
.М2 67
Составить программу, позволяющую получить словесное описание школьных отметок (1 — плохо, 2 — неудовлетворительно, З — удовлетворительно, 4 — хорошо, 5 — отлично).
.М2 69
Пусть элементами круга являются радиус (первый элемент), диаметр (второй элемент) и длина окружности (третий элемент). Составить программу, которая по номеру элемента запрашивала бы его соответствующее значение и вычисляла бы площадь круга.
.М2 70
Пусть элементами прямоугольного равнобедренного треугольника являются:
из
![]()
1) катет а;
2) гипотенуза Ь;
З) высота, опущенная из вершины прямого угла на гипотенузу h;
4) площадь S.
Составить программу, которая по заданному номеру и значению соответствующего элемента вычисляла бы значение всех остальных элементов треугольника.
Написать программу, которая по номеру месяца выдает название следующего за ним месяца (при т = 1 получаем февраль, 4 — май).
.М2 72
Написать программу, которая бы по введенному номеру времени года (1 — зима, 2 — весна, З — лето, 4 — осень) выдавала соответствующие этому времени года месяцы, количество дней в каждом из месяцев.
Для целого числа К от 1 до 99 напечатать фразу «Мне К лет», учитывая при этом, что при некоторых значениях К слово «лет» надо заменить на слово «год» или «года» . Например, 11 лет, 22 года, 51 год.
.М2 74
Написать программу, которая бы по введенному номеру единицы измерения (1 —дециметр, 2 — километр, З — метр, 4 — миллиметр, 5 — сантиметр) и длине отрезка 1., выдавала бы соответствующее значение длины отрезка в метрах.
Написать программу, которая по вводимому числу от 1 до 11 (номеру класса) выдает соответствующее сообщение «Привет, К-классник». Например, если К 1, «Привет, первоклассник»; при К = 4: «Привет, четвероклассник».
Написать программу, которая по данному натуральному числу от 1 до 12 (номеру месяца) выдает все приходящиеся на этот месяц праздничные дни (например, если введено число 1, то: 1 января — Новый год, 7 января — Рождество).
![]() 77
77
Дано натуральное число N. Если оно делится на 4, вывести на экран ответ лт = 4k (где К — соответствующее частное); если
![]()
остаток от деления на 4 равен 1, N = 4k + 1; если остаток
от деления на 4 равен 2, = 4k + 2; если остаток от деления на 4 равен З, N= 4k
+ З. Например, 12![]()
.N2 78
Имеется пронумерованный список деталей: 1) шуруп; 2) гайка; З) винт; 4) гвоздь; 5) болт. Составить программу, которая по номеру детали выводит на экран ее название.
![]() 79
79
Составить программу, позволяющую по последней цифре данного числа определить последнюю цифру куба этого числа.
Составить программу, которая для любого натурального числа печатает количество цифр в записи этого числа.
Даны два действительных положительных числа х и у. Арифметические действия над числами пронумерованы (1 — сложение, 2 — вычитание, З — умножение, 4 — деление). Составить программу, которая по введенному номеру выполняет то или иное действие над числами.
Написать программу, которая бы по введенному номеру
единицы измерения (1 килограмм, 2 — миллиграмм, З ![]() грамм, 4 — тонна, 5 —
центнер) и массе М выдавала бы соответствующее значение массы в килограммах.
грамм, 4 — тонна, 5 —
центнер) и массе М выдавала бы соответствующее значение массы в килограммах.
Пусть элементами равностороннего треугольника являются: 1) сторона а; 2) площадь S; З) высота h; 4) радиус вписанной окружности r; 5) радиус описанной окружности R
Составить программу, которая по заданному номеру и значению соответствующего элемента вычисляла бы значение всех остальных элементов треугольника.
Составить программу для определения подходящего возраста кандидатуры для вступления в брак, используя следующее соображение: возраст девушки равен половине возраста мужчины плюс 7, возраст мужчины определяется соответственно как удвоенный возраст девушки минус 14.
Найти произведение цифр заданного К-значного числа.
![]()
Составить программу, которая читает натуральное число N в десятичном представлении (N 10000), а на выходе выдает это же число в десятичном представлении и на естественном языке. Например, 7 семь; 204 двести четыре; 52 пятьдесят два.
4.4.3. Программирование циклических алгоритмов
![]() Цикл многократное
повторение последовательности действий по некоторому условию. Известны три типа
циклических алгоритмических структур: цикл с предусловием, цикл с постусловием
и цикл с параметром. В Паскале существуют операторы, реализующие все три типа
циклов.
Цикл многократное
повторение последовательности действий по некоторому условию. Известны три типа
циклических алгоритмических структур: цикл с предусловием, цикл с постусловием
и цикл с параметром. В Паскале существуют операторы, реализующие все три типа
циклов.
Цикл с предусловием (цикл-пока) наиболее универсальная циклическая структура. Реализуется оператором while. Формат оператора:
Whi1e <логическое выражение> Do <тело цикла>
Пока значение логического выражения true, выполняется тело цикла. Тело цикла может быть простым или составным оператором.
Цикл с постусловием (цикл-до) имеет формат:
Repeat <тело цикла> Unti1 <логическое выражение>
Повторяется выполнение тела цикла. Цикл заканчивается, когда логическое выражение принимает значение true. Тело цикла с постусловием выполняется хотя бы один раз. Использования begin и end для ограничения составного тела цикла не требуется.
Цикл с параметром имеет два варианта записи:
2) For 1 п downto 1 К Do <тело цикла> .
Здесь I — параметр
цикла — простая переменная порядкового типа ; ![]() выражение того же
типа, определяющее начальное значение параметра; п — выражение того же типа,
определяющее конечное значение параметра;
выражение того же
типа, определяющее начальное значение параметра; п — выражение того же типа,
определяющее конечное значение параметра;
«(тело цикла> может быть простым или составным оператором.
Цикл повторяется, пока значение параметра лежит в интервале между In и П. Причем эти выражения вычисляются только один раз в начале выполнения цикла.
В первом варианте при каждом повторении
цикла значение параметра изменяется на следующее значение в данном типе (для
целого типа увеличивается на 1). Во втором варианте при каждом повторении цикла
значение параметра изменяется на предыдущее значение в данном типе (для целого
типа ![]() уменьшается на 1).
уменьшается на 1).
Пример 1. Вычислить сумму натурального ряда чисел от
![]()
Решение. Программа будет состоять из трех частей, в которых повторяется решение этой задачи с использованием операторов цикла while, repeat и for.
Program Natur ;
Write ![]() ReadLn (N)
;
ReadLn (N)
; ![]() цикл с предусловием} а : = 1 ; Sumna:=O;
цикл с предусловием} а : = 1 ; Sumna:=O;
Sumna : =Summa+a;
![]()
(Цикл с постусловием) а : = 1 ; Summa:=O;
Sumna : =Surnma+ а;
![]()
WriteLn (' Результат второго сутлирования:' , Surna) ; (Цикл с параметром)
![]()
Eor а : - 1 to N Do Summa![]()
WriteLn ( ' Результат третьего суммирования: ' , Surna) End .
Очевидно, что все три результата будут одинаковыми.
Пример 2. Функцию у = их можно вычислить как предельное значение последовательности, определяемой рекуррентной формулой:
![]() (ук_1 + х/ук_ 1)/2 для К 1,2,...
(ук_1 + х/ук_ 1)/2 для К 1,2,...
Начальное значение уо задается
произвольно. За приближенное с точностью Е значение корня берется первое ук,
для которого выполняется условие: — ук_1![]()
Решение. Для вычисления значений числовой последовательности достаточно двух простых переменных, в которых на каждом шаге будут храниться последнее и предпоследнее значения: ук и ук_1. Обозначим эти переменные Anew и Aold. При программировании этой задачи нельзя использовать цикл с параметром, т. к. неизвестно заранее число повторений цикла. Воспользуемся циклом с предусловием.
Var Х, eps, A01d, Anew : Rea1; К: integer; Begin
Write ( ' Введите число Epsi10n ' ) ; ReadLn (eps) ;
Write ( ' Введите значение Х ' ) ; ReadLn (Х) ;
A01d:=X; Anew:= (A01d + X/A01d) / 2 ;
While abs (Anew-A01d) >=eps Do
Begin A01d : = Anew;
Anew:= (A01d + X/A01d) / 2;
WriteLn ( ' Корень квадратный , Х, ' ) = ' , Anew) End .
Пример З. На интервале [2; п] найти натуральное число с максимальной суммой делителей.
Алгоритм будет содержать два вложенных цикла. Исполнение вложенных циклов происходит так: для каждого значения параметра внешнего цикла происходит полная «прокрутка» внутреннего цикла.
Program Sum_Del ;
Begin Write ( ' Введите число N: ' ) ; ReadLn (N) ;
Sum Мах: = 1; Ch:=1; ( начальные значения величин }
For I :=2 to N Do ( ВНеШНИЙ цикл : перебор чисел}
Sum![]()
(Внутренний цикл : поиск делителей}
Тћеп Sum : =Sum + К; (Суплмрование делителей)
![]() Выбор максимальной суммы делителей)
Выбор максимальной суммы делителей)
If Sum ![]() 'ItenBeginSun Мах : =
Sun,• СЮ. :
'ItenBeginSun Мах : =
Sun,• СЮ. : ![]() End; fNriteLn ( ' Максимальную
сумму делителей
End; fNriteLn ( ' Максимальную
сумму делителей ![]() Sum Мах, имеет число
Sum Мах, имеет число ![]() End .
End .
![]()
Имеется серия измерений элементов треугольника. Группы элементов пронумерованы. В серии в произвольном порядке могут встречаться такие группы элементов треугольника:
[3 основание и высота; а две стороны и угол между ними (угол задан в радианах); а три стороны.
Начав тренировки, спортсмен в первый день пробежал 10 км. Каждый день он увеличивал дневную норму на 10 % нормы предыдущего дня. Какой суммарный путь пробежит спортсмен за 7 дней?
Одноклеточная амеба каждые З часа делится на 2 клетки. Определить, сколько амеб будет через З, 6, 9, 12, . , 24 часа.
Около стены наклонно стоит палка длиной х м. Один ее конец находится на расстоянии у м от стены. Определить значение угла а между палкой и полом для значений х = К м и у, изменяющегося от 2 до З м с шагом h м.
У гусей и кроликов вместе 64 лапы. Сколько могло быть кроликов и гусей (указать все сочетания, которые возможны)?
Составить алгоритм решения задачи: сколько можно купить
быков, коров и телят, платя за быка 10 руб., за корову ![]() 5 руб., а за теленка
0,5 руб., если на 100 руб. надо купить 100 голов скота?
5 руб., а за теленка
0,5 руб., если на 100 руб. надо купить 100 голов скота?
Доказать (путем перебора возможных значений), что для любых величин А, В, С типа Boolean следующие пары логических выражений имеют одинаковые значения (эквивалентны):
1) А OR В и В OR А;
2) А AND В и В AND А;
3) (А OR В) OR С и А OR (В OR С);
4) (А AND В) AND С и А AND (В AND С);
5) А AND (А OR В) и А;
6) А OR (А AND В) и А;
7) А AND (В OR С) и (А AND В) OR (А AND С); 8) А OR (В AND С) и (А OR В) AND (А OR С).
Составить программу для проверки утверждения: «Результатами вычислений по формуле х 2 + х + 17 при О х 15 являются простые числа». Все результаты вывести на экран.
Составить программу для проверки утверждения: «Результатами вычислений по формуле х 2 + х + 41 при О х 40 являются простые числа». Все результаты вывести на экран.
Л) 10
Ь = 2m•n, с = т 2 + п 2 (т, п — натуральные, 1 < т < К,
![]() — данное число).
Результат вывести на экран в виде таблицы из пяти столбцов: т, п, а, Ь, с.
— данное число).
Результат вывести на экран в виде таблицы из пяти столбцов: т, п, а, Ь, с.
.N2 11
Покупатель должен заплатить в кассу S руб. У него имеются 1, 2, 5, 10, 50, 100, 500 руб. Сколько купюр разного достоинСТВа отдаст покупатель, если он начинает платить с самых крупных?
Ежемесячная стипендия студента составляет А руб., а расходы на проживание превышают стипендию и составляют В руб. в месяц. Рост цен ежемесячно увеличивает расходы на З % . Составьте программу расчета необходимой суммы денег, которую надо единовременно попросить у родителей, чтобы можно было прожить учебный год (10 месяцев), используя толысо эти деньги и стипендию.
9 Информатика и ИКТ. Т. I
Составить программу, которая печатает таблицу умножения и сложения натуральных чисел в десятичной системе счисления.
Составить программу, которая печатает таблицу умножения и сложения натуральных чисел в шестнадцатеричной системе счисления.
ЛЬ 15
Найти сумму всех п-значных чисел (1 п 4).
|
Найти сумму всех п-значных чисел, кратных К (1 ЛЬ 17 Покажите, что для всех п = 1, 2, З, ..., лт (12 + 25 + + п5) + (17+ 27 + + Ю) = 2 (1 + 2 + |
п 4). + п |
ХРУСТ • ГРОХОТ = РРРРРРРРРРР.
Составить программу, которая запрашивает пароль (например, четырехзначное число) до тех пор, пока он не будет правильно введен.
Задачи ЛЬ 20 — N2 43 решить двумя способами: с использованием цикла с параметром и одного из двух других типов цикла. Л) 20
Дано натуральное число N. Вычислить:
![]()
![]() Дано натуральное число N. Вычислить: 1 1 1
sin 1 sin1 + sin2 sin1 + sin2 + ... + sinN
Дано натуральное число N. Вычислить: 1 1 1
sin 1 sin1 + sin2 sin1 + sin2 + ... + sinN
Дано натуральное число N. Вычислить произведение первых лт сомножителей

Л) 23
Дано натуральное число N. Вычислить:
cos1 cos1 + cos2 COS1 + COS2 + + cosN sin1 sin1 + sin2 Sin1 + Sin2 + . . . + sinN
Л) 24
Дано действительное число х. Вычислить:
з 5 7 9 11 13
![]()
![]() 25
25
Даны натуральное п, действительное х. Вычислить:
S = sin х + sin sinx + ... + sin sin...sin х
![]()
п раз
![]() 26
26
Даны действительное число а, натуральное число п. Вычислить:
![]()
Г.Г2 27
Даны действительное число а, натуральное число п. Вычислить:
Р = а(а — п)(а — 2n) • ![]()
Даны действительное число а, натуральное число п. Вычис-
лить:
![]()
![]() 29
29
Дано действительное х. Вычислить:
(х - - 7) • • (х -63)
(х — 2)(х — —8) • . . . • (х —64)
.ТЧђ ЗО
Вычислить:
(1 + sinO,1)(1 + sin02) • . . . (1 + sin10).
Даны натуральное п, действительное х. Вычислить:
Дано натуральное п. Вычислить:
![]()
.N2 33
Дано натуральное число п. Вычислить:
![]() , где п>2.
, где п>2.
Дано натуральное число п. Вычислить:
![]()
.N2 35
Дано натуральное число п. Вычислить:
![]()
![]() 36
36
Дано натуральное число п. Вычислить:
![]()
Определить f40![]()
![]() 38
38
Дано натуральное п. Вычислить: у =![]()
.N2 39
Дано натуральное п. Вычислить: у = 2 • 4 - 6 •![]()
Вычислить: у =cosx + cosx 2
+ cosx 3 +![]() + COS Х
+ COS Х ![]()
Вычислить:
у = sin1 + sin1,1 + sin 12 + . . . + sin2.
Даны натуральные числа п и К. Вычислить:
![]()
Дано натуральное п. Вычислить:
![]()
![]()
В задачах N2 44 — N2 55 дан числовой ряд и малая величина е = 10-3 . С точностью Е найти сумму ряда, общий член которого задан формулой:
![]()
![]() (2п)!
(2п)!
Х 54![]()
В задачах .М2 56 — N2 65 найти наименьший номер элемента последовательности, для которого выполняется условие
![]() < е. Вывести на экран этот номер и все элементы а.,
< е. Вывести на экран этот номер и все элементы а.,
,
п, если Е = ![]()
![]()
![]()
![]() о 56 ап =arctg ап
о 56 ап =arctg ап
![]() 2 57 а
2 57 а
![]() 2 58 ап
2 58 ап
![]() 2 62 а
2 62 а
Оп п) п
![]() 2 64 ап
2 64 ап ![]()
![]() 2 65 ап
2 65 ап![]()
![]()
В задачах N2 66 — Л) 69 найти наименьший
номер элемента последовательности, для которого выполняется условие М. Вывести
на экран этот номер и все элементы Ч, где — ![]() п, если Е = 10-3 .
п, если Е = 10-3 .
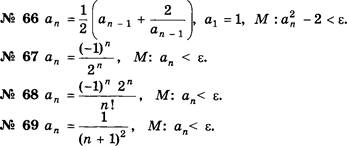
В задачах ЛЬ 70 — Л) 95 составить программу вычисления значений функции F(x) на отрезке [а; Ь] с шагом h. Результат представить в виде таблицы, первый столбец которой — значения аргумента, второй — соответствующие значения функции.
![]() 70 (х) = х — sin х.
70 (х) = х — sin х.
![]() 72 Ах) = 2cosx — 1.
72 Ах) = 2cosx — 1. ![]() 74 ах) =ctg х + 1.
74 ах) =ctg х + 1.
![]() 76 F(x) = х • sin х.
76 F(x) = х • sin х.
![]() 78 ах) = х • cos— + 2.
78 ах) = х • cos— + 2.
х
![]() 80 ах) = х • cos 2 х.
80 ах) = х • cos 2 х.
![]() 82 F(x) =cosx + ctg х.
82 F(x) =cosx + ctg х.
|
Г.Г2 84 Ах)
= tg |
+ 2cosx. |
|
М 86 ах) = |
х |
|
2 |
4 |
![]() 2
2 ![]()
х • sin![]()
Г.Г2 90 F(x) = sin х —cos(2x).
Г.Г2 92 F(x) = — cos(2x).
![]() 94 ах) = sinx + 0,5cos х.
94 ах) = sinx + 0,5cos х.
М 71 Ах) = sin 2 х.
Г.Г2 73 ах) = tg х.
Г.Г2 75 Ах) — - sinx — cos х.
Г.Г2 77 Ах) = sin— + 2.
х
Г.Г2 79 F(x) =2 sin 2 х + 1.
![]() 81 Ах) = sinx + tg х.
81 Ах) = sinx + tg х.
Г.Г2 83 ах) =![]()
![]() 85 ах) =ctg — + — sin х.
85 ах) =ctg — + — sin х.
Г.Г2 87 Ах) = 2cos х + 0,5.
1х
Г.Г2 89 Ах) = -с![]()
24
1
![]() 91 7 sin 2 х ——cos х. 2
91 7 sin 2 х ——cos х. 2
Г.Г2 93 F(x) = tg(2x) — З.
х
![]() 95 ах) =
95 ах) =![]()
cos х
ЗаДачи на работу с целыми числами
![]() 96
96
Дано натуральное число п. Найти сумму первой и последней цифры этого числа.
.М2 97
Дано натуральное число п. Переставить местами первую и последнюю цифры этого числа.
![]() 98
98
Даны два натуральных числа т и п (т 9999, п 9999). Проверить, есть ли в записи числа т цифры, одинаковые с цифрами в записи числа п.
![]() 99
99
Дано натуральное число п. Проверить, есть ли в записи числа три одинаковые цифры (п 9999).
Л) 100
Дано натуральное число п 99. Дописать к нему цифру К в конец и в начало.
Даны натуральные числа п, К. Проверить, есть ли в записи числа п к цифра т.
Л) 102
Среди всех п-значных чисел указать те, сумма цифр которых равна данному числу К.
![]() 103
103
Составьте программу, которая по номеру дня в невисокосном году выводит число и месяц в общепринятой форме (например, 33-й день года — 2 февраля).
Г.Г2 104
Найти наибольшую и наименьшую цифры в записи данного натурального числа.
Произведение п первых нечетных чисел равно р. Сколько сомножителей взято? Если введенное р не является указанным произведением, сообщить об этом.
Найти на отрезке [п; т] натуральное число, имеющее наибольшее количество делителей.
![]()
Задумано некоторое число х (х < 100). Известны числа К, т, п — остатки от деления этого числа на З, 5, 7. Найти х.
Дано натуральное число п. Проверить, будут ли все цифры числа различными.
Найти все целые корни уравнения ах з + bx 2 + сх + d = О, где а, Ь, с и d — заданные целые числа, причем а * О и d О.
Замечание: целыми корнями могут быть только положительные и отрицательные делители коэффициента d.
.N2 110
Дано натуральное число п. Поменять порядок следования цифр в этом числе на обратный или сообщить, что это невозможно в силу переполнения.
Найти все делители натурального числа п.
.N2 112
Натуральное число М называется совершенным, если оно равно сумме всех своих делителей, включая единицу, но исключая себя. Напечатать все совершенные числа, меньшие заданного числа N.
Натуральные числа а, Ь, с называются числами Пифагора, если выполняется условие а 2 + b2 = с 2 . Напечатать все числа Пифагора, меньшие N.
Дано натуральное число п. Среди чисел 1, . , п найти такие, запись которых совпадает с последними цифрами записи их квадратов (например, 6 2 = 36, 25 2 = 625).
.N2 115
Заданы три натуральных числа А, В, С, которые обозначают число, месяц и год. Найти порядковый номер даты, начиная отсчет с начала года.
.N2 116
Долгожитель (возраст не менее 100 лет) обнаружил однажды, что если к сумме квадратов цифр его возраста прибавить число дня его рождения, то как раз получится его возраст. Сколько лет долгожителю?
.м 117
Дано целое п > 2. Напечатать все простые числа из диапазона
Даны натуральные числа п, т. Найти все натуральные числа, меньшие п, квадрат суммы цифр которых равен т.
Найти натуральное число в диапазоне от 1 до п с максимальной суммой делителей.
.М2 120
Даны натуральные числа р и q. Получить все делители числа q, взаимно простые с р.
Для заданных натуральных п и К определить, равно ли число п сумме К-х степеней своих цифр.
Найти все двузначные числа, сумма квадратов цифр которых кратна М.
Найти все натуральные числа, не превосходящие заданного п, которые делятся на каждую из своих цифр.
Задано натуральное число п. Найти количество натуральных чисел, не превышающих п и не делящихся ни на одно из чисел 2, З, 5.
Пусть Л — п-й член последовательности, определяемой следующим образом:
Покажите, ![]() что 2
что 2
Последовательность Хэмминга образуют натуральные числа, не имеющие других простых делителей, кроме 2, З и 5. Найти:
1) первые лт элементов этой последовательности;
2) сумму первых лт элементов;
З) N-ii элемент по заданному номеру N;
4) первый элемент, больший данного числа М, а также номер этого элемента в последовательности;
5) сумму всех элементов с номера N по номер М.
.М2 127
Игрок А объявляет двузначное число от 01 до 99. Игрок В меняет местами его цифры и полученное число прибавляет к сумме его цифр. Полученный результат он объявляет игроку А. Игрок А проделывает с этим числом ту же процедуру, и так они продолжают поступать поочередно, объявляя числа. От суммы чисел берется остаток от деления на 100, поэтому объявляются лишь двузначные числа. Какие числа может объявить игрок А на начальном шаге, чтобы игрок В в некоторый момент объявил число 00?
в
.М2 128
Дано натуральное К. Напечатать К-ю цифру последовательности 12345678910111213..., в которой выписаны подряд все натуральные числа.
.М2 129
.М2 130
Составить программу перевода натурального числа из десятичной системы счисления в двоичную.
.М2 131
Составить программу перевода данного натурального числа п в шестнадцатеричную систему счисления.
.М2 132
Дано натуральное число п. Переставить его цифры так, чтобы образовалось максимальное число, записанное теми же цифрами.
.М2 133
Дано натуральное число п. Переставить его цифры так, чтобы образовалось наименьшее число, записанное теми же цифрами.
.М2 134
Для записи римскими цифрами используются символы 1, V, Х, L, С, D, М, обозначающие соответственно числа 1, 5, 10, 50, 100, 500, 1000. Составить программу, которая запись любого данного числа п (п 3999) арабскими цифрами переводила бы в запись римскими цифрами.
.М2 135
Используя все цифры от 1 до 9 по одному разу в различных комбинациях и операции сложения и вычитания, получить в сумме 100.
.М2 136
Используя все цифры от 1 до 9 по одному разу и операции сложения и вычитания, получить в сумме 100, при условии, что цифры появляются в возрастающем или убывающем порядке.
Например,
123 - 45 - 67 + 89 - 100, 98 - 76 + 54 + з +21 - 100.
Палиндромы
Палиндром это сочетания символов, которые читаются одинаково туда и обратно. Элементом палиндрома может быть буква (например, КОК, ПОП, А РОЗА УПАЛА НА ЛАПУ АЗОРА), цифра (4884, 121) или слово (STRAP 0N — N0 PARTS).
.М2 137
.М2 138
Найдите целые числа, которые при возведении в квадрат дают палиндромы, например, 26 2 = 676.
.М2 139
Найдите целые числа-палиндромы, которые при возведении в квадрат также дают палиндромы (22 2 = 484).
.М2 140
Найдите целые числа, которые при возведении в З, или 4, или 5 степень дают палиндромы, например, 11 3 = 1331.
.М2 141
Дано натуральное число п. Если это не палиндром, реверсируйте его цифры и сложите исходное число с числом, полученным в результате реверсирования. Если сумма не палиндром, то повторите те же действия и выполняйте их до тех пор, пока не получите палиндром. Например для исходного числа 78 это выглядит так:
![]() - 165; 165 + 561 - 726;
- 165; 165 + 561 - 726;
726 + 627 - 1353; 1353 + 3531 - 4884.
4.4.4. Работа с массивами
![]() Массив упорядоченный
набор однотипных значений компонент массива. Тип компонент называется базовым
типом массива.
Массив упорядоченный
набор однотипных значений компонент массива. Тип компонент называется базовым
типом массива.
В Паскале массив рассматривается как переменная структурированного типа. Массиву присваивается имя, посредством которого можно ссылаться на него, как на единое целое, а также на любую из его компонент.
Переменная с индексом — идентификатор компоненты массива. Формат записи:
<имя массива>[<индекс>], где индекс может быть выражением порядкового типа.
Описание массива определяет имя, размер массива и базовый тип. Формат описания в разделе переменных:
Var <имя массива> : Array [<тип индекса>] 0f Фазовый тип>
Чаще всего в качестве типа индекса используется интервальный целый тип.
Линейный (одномерный) массив — массив, у которого элементы — простые переменные. В одномерных массивах хранятся значения линейных таблиц. Примеры описания одномерных массивов:
Ввод и вывод массива производится поэлементно. Обычно для этого используется цикл с параметром, где в качестве параметра применяется индексная переменная.
Пример 1. В программе вводится десять значений
целочисленного массива А и выводятся значения веществен![]() ного массива В,
содержащего 50 элементов. Соответствующие фрагменты программы:
ного массива В,
содержащего 50 элементов. Соответствующие фрагменты программы:
Var А : Array г 1 . . 10] of integer; В : Array[1 . . 501 0f rea1;
Begin Write А , i , ' ' ) ; ReadLn (A[i] ) End;
For - 1 to 50 Do
Begin WriteLn
( ' в [ ' ![]() В [1] ) End; End .
В [1] ) End; End .
Пример 2. Заполнить случайными числами из диапазона [О, 1] вещественный линейный массив из чисел.
Найти максимальное значение и его индекс (первый, если таких значений несколько).
Решение. Поскольку размер массива в программе должен быть однозначно задан, определим лт в разделе констант, например, N = 20. При изменении размера массива достаточно будет отредактировать в программе лишь описание константы N.
Var Х: Array [1 :N] of rea1; К: integer; та х : rea1; Ктах: integer; Begin
E'or К to Do х [К] :=random; (Заполнение случайн . числами тах : [1) ; Ктах {ИНИЦИаЛИЗаЦИЯ вычисляемых переменных }
E'or К : to N Do Поиск максимального значения
If х [К] >тах Then Begin тах : [К) ; Ктах:=К End;
End .
Пример З. Дан целочисленный линейный массив. Отсортировать его элементы в порядке возрастания значений.
![]()
Опишем массив на максимальный размер (например, 100), а фактический размер N определим вводом.
Var N, 1, З, Р : integer; А: Array [ 1 . . 100] of integer; Begin Write (' Введите число элементов : ; ReadLn (N) ; For to N Do
Begin Write (' Введите А [ ' , 1, ] ReadLn (А [ 1] ) End;
For = ![]() Begin For Ј:=1 to N—I Do
Begin For Ј:=1 to N—I Do
Begin А[Ј]
![]() А [3+1] End
А [3+1] End
For : —1 - to
N Do Write (А [1) , ![]() End .
End .
Тест: N = 10; элементы массива: 1, 2, 2, 2, -1, 1, о, 34, з, з.
Ответ: -1, о, 1, 1, 2, 2, 2, з, з, 34![]()

Линейные массивы
Дан массив натуральных чисел. Найти сумму элементов, кратных данному К.
В целочисленной последовательности есть нулевые элементы. Создать массив из номеров этих элементов.
Дана последовательность целых чисел ар а,г, ..., а . Выяснить, какое число встречается раньше — положительное или отрицательное.
![]() Дана последовательность действительных чисел ар аг, ..., а
Выяснить, будет ли она возрастающей.
Дана последовательность действительных чисел ар аг, ..., а
Выяснить, будет ли она возрастающей.
Дана последовательность натуральных чисел ар а,г, ... , а
Со ![]() здать массив из четных чисел этой
последовательности. Если таких чисел нет, то вывести сообщение об этом факте.
здать массив из четных чисел этой
последовательности. Если таких чисел нет, то вывести сообщение об этом факте.
Дана последовательность чисел Ч, а,г, . . ., а . Указать наименьшую длину числовой оси, содержащую все эти числа.
Дана последовательность действительных чисел Ч, 02 , . . ., а . Заменить все ее члены, большие данного Z, этим числом. Подсчитать количество замен.
Последовательность действительных чисел оканчивается нулем. Найти количество членов этой последовательности.
Дан массив действительных чисел, размерность которого N. Подсчитать, сколько в нем отрицательных, положительных и нулевых элементов.
Даны действительные числа Ч, 02 , а . Поменять местами наибольший и наименьший элементы.
Даны целые числа ар Ч, ..., а . Вывести на печать только те числа, для которых выполняется а. i.
Даны натуральные числа ар Ч, а . Указать те, у которых остаток от деления на М равен 1., (О 1., < М — 1).
В заданном одномерном массиве поменять местами соседние элементы, стоящие на четных местах, с элементами, стоящими на нечетных.
При поступлении в вуз абитуриенты, получившие двойку на первом экзамене, ко второму не допускаются. В массиве A[nl записаны оценки экзаменующихся, полученные на первом экзамене. Подсчитать, сколько человек не допущено ко второму экзамену.
Дана последовательность чисел, среди которых имеется один нуль. Вывести на печать все числа до нуля включительно.
В одномерном массиве размещены: в первых элементах значения аргумента, в следующих — соответствующие им значения функции. Напечатать элементы этого массива в виде двух параллельных столбцов (аргументы и значения функции).
Пригодность детали оценивается по размеру В, который должен соответствовать интервалу (А — 5, А + 5). Определить, имеются ли в партии из лт деталей бракованные. Если да, то подсчитать их количество, иначе выдать отрицательный ответ.
ль 18
У вас есть доллары. Вы хотите обменять их на рубли. Есть информация о стоимости купли-продажи в банках города. В городе лт банков. Составьте программу, определяющую, какой банк выбрать, чтобы выгодно обменять доллары на рубли.
Дан целочисленный массив с количеством элементов п. Напечатать те его элементы, индексы которых являются степенями двойки (1, 2, 4, 8, 16, ...).
![]() 20
20
Дан одномерный массив A[Nl. Найти тах@2 , а4 , . . . , аи) + min@1 , аз , . . . , аи + 1).
Дана последовательность действительных чисел Ч, а,г, . .., а п. Указать те ее элементы, которые принадлежат отрезку [с, Щ.
![]() 22
22
Дана последовательность целых положительных чисел. Найти произведение только тех чисел, которые больше заданного числа М. Если таких нет, то выдать сообщение об этом.
.М2 23
Последовательность ар а,г, ..., а состоит из нулей и единиц. Поставить в начало этой последовательности нули, а затем единицы.
.М2 24
Даны действительные числа ар Ч, .. ., а п. Среди них есть
положительные и отрицательные. Заменить нулями те числа, которые по модулю
больше максимального числа ![]() ал > тах , а,г, .
ал > тах , а,г, .![]()
![]() Даны действительные числа
ар Ч, .. ., тах(а1 + а
Даны действительные числа
ар Ч, .. ., тах(а1 + а
![]() 26
26
В последовательности действительных чисел ар а,г, ..., ап есть только положительные и отрицательные элементы. Вычислить произведение отрицательных элементов Р 1 и произведение положительных элементов Р 2. Сравнить модуль Р 2 с модулем Р 1 , указать, какое из произведений по модулю больше.
Дан массив действительных чисел. Среди них есть равные. Найти первый максимальный элемент массива и заменить его нулем.
.М2 28
Дана последовательность действительных чисел ![]() а
Вставить действительное число Ь в нее так, чтобы последовательность осталась
неубывающей.
а
Вставить действительное число Ь в нее так, чтобы последовательность осталась
неубывающей.
![]() 29
29
Даны целые положительные числа ар Ч, ..., а . Найти среди них те, которые являются квадратами некоторого числа т.
![]()
Дана последовательность целых чисел ар а,г, ..., а .
Образовать новую последовательность, выбросив из исходной те члены, которые
равны ![]()
У прилавка магазина выстроилась очередь из п покупателей.
Время обслуживания Г-го покупателя равно t. (i —![]()
Определить время С. пребывания Г-го покупателя в очереди.
![]() 32
32
Секретный замок для сейфа состоит из 10 расположенных в ряд ячеек, в которые надо вставить игральные кубики. Но дверь открывается только в том случае, когда в любых трех соседних ячейках сумма точек на передних гранях кубиков равна 10 (игральный кубик имеет на каждой грани от 1 до 6 точек). Напишите программу, которая разгадывает код замка при условии, что два кубика уже вставлены в ячейки.
.N2 33
В массиве целых чисел с количеством элементов п найти наиболее часто встречающееся число. Если таких чисел несколько, то определить наименьшее из них.
![]() 34
34
Каждый солнечный день улитка, сидящая на дереве, поднимается вверх на 2 см, а каждый пасмурный день опускается вниз на 1 см. В начале наблюдения улитка находилась в А см от земли на В-метровом дереве. Имеется 30-элементный массив, содержащий сведения о том, был ли соответствующий день наблюдения пасмурным или солнечным. Написать программу, определяющую местоположение улитки к концу 30-го дня наблюдения.
Дан целочисленный массив с количеством элементов п. «Сожмите» массив, выбросив из него каждый второй элемент. Примечание. Дополнительный массив не использовать.
.N2 36
Задан массив, содержащий несколько нулевых элементов. Сжать его, выбросив эти элементы.
.N2 37
Задан массив с количеством элементов N. Сформируйте два массива: в первый включите элементы исходного массива с четными номерами, а во второй — с нечетными.
![]()
Дана последовательность целых чисел ар Ч, ..., а . Указать пары чисел ар а., таких, что а. + а. = т.
Даны целые числа ар Ч, ..., а . Наименьший член этой последовательности заменить целой частью среднего арифметического всех членов, остальные члены оставить без изменения. Если в последовательности несколько наименьших членов, то заменить последний по порядку.
Даны целые числа ар Ч, ..., а![]() , ь п. Преобразовать
последовательность br, Ь, , ь п по правилу: если а. О, то Ь. увеличить в 10
раз, иначе bi заменить нулем (i =
, ь п. Преобразовать
последовательность br, Ь, , ь п по правилу: если а. О, то Ь. увеличить в 10
раз, иначе bi заменить нулем (i =![]()
Даны действительные числа а 1 , Ч, а п. Требуется умножить все члены последовательности а] , а,г, ..., а на квадрат ее наименьшего члена, если а» О, и на квадрат ее наибольшего члена, если а» < О (1 S k S п).
![]() 42
42
Даны координаты п точек на плоскости: (Х 1 , У1), ..., (хп, Уп) (п 30). Найти номера пары точек, расстояние между которыми наибольшее (считать, что такая пара единственная).
Дана последовательность из п различных целых чисел. Найти сумму ее членов, расположенных между максимальным и минимальным значениями (в сумму включить и оба этих числа).
![]() 44
44
Японская радиокомпания провела опрос ЛУ радиослушателей по вопросу: «Какое животное вы связываете с Японией и японцами?» Составить программу получения К наиболее часто встречающихся ответов и их долей (в процентах).
Э.Г2 45
Дан массив, состоящий из п натуральных чисел. Образовать новый массив, элементами которого будут элементы исходного, оканчивающиеся на цифру К.
Дан массив целых чисел. Найти в этом массиве минимальный элемент т и максимальный элемент М. Получить в порядке возрастания все целые числа из интервала (т; М), которые не входят в данный массив.
языках
![]()
![]() 47
47
Дано действительное число х и массив А[п]. В массиве найти два члена, среднее арифметическое которых ближе всего к х.
Даны две последовательности ар а,р, . . . , а 1, ![]() т
(т п). В каждой из них члены различны. Верно ли, что все члены второй
последовательности входят в первую последовательность?
т
(т п). В каждой из них члены различны. Верно ли, что все члены второй
последовательности входят в первую последовательность?
Напишите программу, входными данными которой является возраст п человек. Программа подсчитывает количество людей, возраст которых находится в интервале 10 лет, а именно:
<..> человек имеет возраст в диапазоне 0—10 лет,
<..> человек имеет возраст в диапазоне 10—20 лет,
![]()
в
В одномерном массиве все отрицательные элементы переместить в начало массива, а остальные — в конец с сохранением порядка следования. Дополнительный массив заводить не разрешается.
В одномерном массиве с четным количеством элементов (2N) находятся координаты точек плоскости. Они располагаются в следующем порядке: хр Щ, х,г, у,г, хз, уз, х п, уп. Определить минимальный радиус круга с центром в начале координат, который содержит все точки.
![]() 52
52
В одномерном массиве с четным количеством элементов (2N) находятся координаты N точек плоскости. Они располагаются в следующем порядке: хр Щ, х,г, у,г, хз, уз, х п, уп. Определить кольцо с центром в начале координат, которое содержит все точки.
В одномерном массиве с четным количеством элементов (2N)
находятся координаты N точек плоскости. Они располагаются в следующем порядке:
хр Щ, .x,p, у,г, хз, уз, ..., ![]() целые). Определить номера точек, которые
могут являться вершинами квадрата.
целые). Определить номера точек, которые
могут являться вершинами квадрата.
![]()
Л) 54
В одномерном массиве с четным количеством элементов (2N) находятся координаты лт точек плоскости. Они располагаются в следующем порядке: х 1 , Щ, х 2 , 612 , хз, уз, ..., хп, уп. Определить номера точек, которые могут являться вершинами равнобедренного треугольника.
Л) 55
Задан целочисленный массив размерности N. Есть ли среди элементов массива простые числа? Если да, то вывести номера этих элементов.
.N2 56
Дана последовательность целых чисел. Найти количество различных чисел в этой последовательности.
.N2 57
Дан массив из п четырехзначных натуральных чисел. Вывести на экран только те, у которых сумма первых двух цифр равна сумме двух последних.
.N2 58
Даны две последовательности целых чисел ар Ч, ..., а и Ь
![]()
![]() Ь . Все члены
последовательностей — различные числа. Найти, сколько членов первой
последовательности совпадают с членами второй последовательности.
Ь . Все члены
последовательностей — различные числа. Найти, сколько членов первой
последовательности совпадают с членами второй последовательности.
Дан целочисленный массив A[nl, среди элементов есть одинаковые. Создать массив из различных элементов А[п].
.N2 60
На плоскости п точек заданы своими координатами и также дана окружность радиуса R с центром в начале координат. Указать множество всех треугольников с вершинами в заданных точках, пересекающихся с окружностью; множество всех треугольников, содержащихся внутри окружности.
.N2 61
В одномерном массиве с четным количеством элементов (2N) находятся координаты лт точек плоскости. Они располагаются в следующем порядке: х 1 , У] , х 2 , 612 , хз, уз, ..., х п, уп. Найти номера самых удаленных друг от друга точек и наименее удаленных друг от друга точек.
.N2 62
В одномерном массиве с четным количеством элементов (2N) находятся координаты лт точек плоскости. Они располагаются в следующем порядке: хр ур ху 612 , хз, уз, ..., х п, уп. Определить три точки, которые являются вершинами треугольни-
язьпсах
![]()
ка, для которого разность числа точек вне его и внутри является минимальной.
Сортировка массивов ЛЕ 63
Заданы два одномерных массива с различным количеством элементов и натуральное число К. Объединить их в один массив, включив второй массив между К-м и (К+1)-м элементами первого, не используя дополнительный массив.
.М2 64
Даны две последовательности
![]() 1 2
1 2![]()
Образовать из них новую последовательность чисел так, чтобы она тоже была неубывающей. Примечание. Дополнительный массив не использовать.
Сортировка выбором. Дана последовательность чисел Ч, а,г, ![]() ,
а п. Требуется переставить элементы так, чтобы они были расположены по
убыванию. Для этого в массиве, начиная с первого, выбирается наибольший элемент
и ставится на первое место, а первый — на место наибольшего. Затем, начиная со
второго, эта процедура повторяется. Написать алгоритм сортировки выбором.
,
а п. Требуется переставить элементы так, чтобы они были расположены по
убыванию. Для этого в массиве, начиная с первого, выбирается наибольший элемент
и ставится на первое место, а первый — на место наибольшего. Затем, начиная со
второго, эта процедура повторяется. Написать алгоритм сортировки выбором.
.М2 66
Сортировка обменами. Дана последовательность чисел ар Ч, ![]() а
п. Требуется переставить числа в порядке возрастания. Для этого сравниваются
два соседних числа а. и Ч +1. Если
а
п. Требуется переставить числа в порядке возрастания. Для этого сравниваются
два соседних числа а. и Ч +1. Если ![]() 1, то делается перестановка. Так
продолжается до тех пор, пока все элементы не окажутся расположенными в порядке
возрастания. Составить алгоритм сортировки, подсчитывая при этом количество
перестановок.
1, то делается перестановка. Так
продолжается до тех пор, пока все элементы не окажутся расположенными в порядке
возрастания. Составить алгоритм сортировки, подсчитывая при этом количество
перестановок.
![]() Сортировка
вставками. Дана последовательность чисел Ч, а п. Требуется переставить числа в
порядке возрастания. Делается это следующим образом. Пусть ар а,г, ..., al
Сортировка
вставками. Дана последовательность чисел Ч, а п. Требуется переставить числа в
порядке возрастания. Делается это следующим образом. Пусть ар а,г, ..., al ![]() упорядоченная
последовательность, т. е.
упорядоченная
последовательность, т. е. ![]()
рется следующее число и вставляется в последовательность так, чтобы новая последовательность была также возрастающей. Процесс производится до тех пор, пока все элементы от i+1 до п не будут перебраны.
Сортировка Шелла. Дан массив п действительных чисел. Требуется упорядочить его по возрастанию. Делается это следующим образом: сравниваются два соседних элемента а. и ан 1. Если а. 1, то эти элементы продвигаются на один эле-
![]()
![]()
мент вперед. Если а. > а. , то
производится перестановка этих элементов, затем они сдвигаются на один элемент
назад. Составить алгоритм такой сортировки. ![]() 69
69
Пусть даны неубывающая последовательность действительных
чисел ![]() ... S а и действительные числа b1 b2
< ...S < ь т. Требуется указать те места, на которые нужно вставлять
элементы последовательности [71 , b2 , ь т в первую последовательность так,
чтобы новая последовательность оставалась возрастающей.
... S а и действительные числа b1 b2
< ...S < ь т. Требуется указать те места, на которые нужно вставлять
элементы последовательности [71 , b2 , ь т в первую последовательность так,
чтобы новая последовательность оставалась возрастающей.
Даны дроби ![]() — натуральные). Составить
— натуральные). Составить
программу, которая приводит эти дроби к общему знаменателю и упорядочивает их в порядке возрастания.
Алгоритм фон Неймана. Упорядочить массив ар Ч, ..., а по неубыванию с помощью алгоритма сортировки слияниями:
![]() каждая пара соседних
элементов сливается в одну группу из двух элементов (последняя группа может
состоять из одного элемента); а каждая пара соседних двухэлементных групп
сливается в одну четырехэлементную группу и т. д.
каждая пара соседних
элементов сливается в одну группу из двух элементов (последняя группа может
состоять из одного элемента); а каждая пара соседних двухэлементных групп
сливается в одну четырехэлементную группу и т. д.
При каждом слиянии новая укрупненная группа упорядочивается.
Двумерный массив структура данных,
хранящая прямоугольную матрицу. В матрице каждый элемент ![]() определяется
номером строки и номером столбца, на пересечении которых он расположен.
определяется
номером строки и номером столбца, на пересечении которых он расположен.
В Паскале двумерный массив рассматривается как массив, элементы которого есть линейные массивы. Два следующих описания двумерных массивов тождественны:
Чаще пользуются вторым способом описания. Элементы двумерного массива идентифицируются переменными с двумя индексами. Например: М[З, 5]. Обычно первый индекс связывают с номером строки, второй — с номером столбца матрицы.
Пример 4. Сформировать матрицу Пифагора (таблицу умножения в матричной форме) и вывести ее на экран.
Решение. Значения элементов матрицы Пифагора вычисляются следующим образом:
Вычисления и вывод матрицы производятся в двух вложенных циклах. Вывод на экран организуем в виде прямоугольной таблицы.
Program Pifagor ;
Begin For —
![]()
![]()
WriteLn (Производит перевод печати на новую строку) End End.
![]() Пример 5. Заполнить
матрицу порядка п по следующе
Пример 5. Заполнить
матрицу порядка п по следующе![]() му образцу:
му образцу:
2 1 2 п—З ![]()
З 2 1 п—2
Решение. Идея алгоритма основана на двух свойствах этой матрицы: она симметрична относительно главной диагонали, т. е. = и элементы верхнего треугольника матрицы вычисляются по формуле = е..т — I + 1. Программа составлена для п=1О.
Program Mas iv ;
Begin Write (' Введите порядок матрицы: ' ) ; ReadLn (N) ; For : = 1 to Do Вложенные циклы. Внутренний цикл — )
For : = to Do переменной длины.
Происходит перебор)
For : 1 to Do
Write (A [ I, ![]() End End.
End End.
![]()
Двумерные массивы






Дано действительное число х. Получить квадратную матрицу порядка п+1:
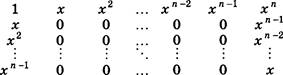
.М2 86
Даны действительные числа а 1 , [12 , ..., а . Получить квадратную матрицу порядка п:
![]()
![]()
![]()
![]() а
а
|
.М2 87 Получить матрицу: |
|
|
|
|
|
1 |
2 |
з |
|
10 |
|
о |
1 |
2 |
|
9 |
|
о |
о |
1 |
|
8 |
|
о .М2 88 Получить матрицу: |
о |
о |
|
1 |
|
1 |
о |
|
1 |
|
|
о |
1 |
1 |
|
|
1 о![]() о 1
о 1
.М2 89
Составить программу, которая заполняет квадратную матрицу порядка п натуральными числами 1, 2, З, , п 2 , записывая их в нее «по спирали».
Например, для п 5 получаем следующую матрицу:
1 ![]()
|
16 |
17 18 19 6 |
|
15 |
24 25 20 7 |
|
14 |
23 22 21 8 |
|
13 |
12 11 10 9 |
Дана действительная квадратная матрица порядка 2n. Получить новую матрицу, переставляя ее блоки размера п х п по часовой стрелке, начиная с блока в левом верхнем углу.
.М2 91
Дана действительная квадратная матрица порядка 2n. Получить новую матрицу, переставляя ее блоки размера п х п крест-накрест.
Дан линейный массив хр х,г, ..., х л, х . Получить действительную квадратную матрицу порядка п:

Дан линейный массив хр х,г, .. ., х , х п. Получить действительную квадратную матрицу порядка п:

![]() (п 1)n 1 (п
(п 1)n 1 (п 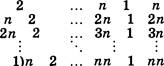 1)n
2
1)n
2
Получить квадратную матрицу порядка п:

Магическим квадратом порядка п называется квадратная матрица размера п х п, составленная из чисел 1, 2, . .. , п 2 так, что суммы по каждому столбцу, каждой строке и каждой из двух больших диагоналей равны между собой. Построить такой квадрат.
Пример магического квадрата порядка З:
![]()
Вычислить сумму и число положительных элементов матрицы A[N, N], находящихся над главной диагональю.
Дана вещественная матрица А размера п х т. Определить К — количество «особых» элементов массива А, считая его элемент особым, если он больше суммы остальных элементов его столбца.
Задана квадратная матрица. Переставить строку с максимальным элементом на главной диагонали со строкой с заданным номером т.
.М2 100
Дана матрица B[N, М]. Найти в каждой строке матрицы максимальный и минимальный элементы и поменять их с первым и последним элементом строки соответственно.
Дана целая квадратная матрица п-го порядка. Определить, является ли она магическим квадратом, т. е. такой, в которой суммы элементов во всех строках и столбцах одинаковы.
.М2 102
Элемент матрицы назовем седловой точкой, если он является наименьшим в своей строке и одновременно наибольшим в своем столбце или, наоборот, является наибольшим в своей строке и наименьшим в своем столбце. Для заданной целой матрицы размером п х т напечатать индексы всех ее седловых точек.
Дана вещественная матрица размером п х т. Переставляя ее строки и столбцы, добиться того, чтобы наибольший элемент (или один из них) оказался в верхнем левом углу.
Определить, является ли заданная целая квадратная матрица п-го порядка симметричной (относительно главной диагонали).
Дана целочисленная квадратная матрица. Найти в каждой строке наибольший элемент и поменять его местами с элементом главной диагонали.
.М9 106
Упорядочить по возрастанию элементы каждой строки матрицы размером п х т.
.М2 107
Задана матрица размером п х т. Найти максимальный по модулю элемент матрицы. Переставить строки и столбцы матрицы таким образом, чтобы максимальный по модулю элемент был расположен на пересечении К-й строки и К-го столбца.
Л) 108
Дана квадратная матрица A[N, N]. Записать на место отрицательных элементов матрицы нули, а на место положительных единицы. Вывести на печать нижнюю треугольную матрицу в общепринятом виде.
.М2 109
Дана действительная матрица размером п х т, все элементы которой различны. В каждой строке выбирается элемент с наименьшим значением, затем среди этих чисел выбирается наибольшее. Указать индексы элемента с найденным значением.
Дана действительная квадратная матрица порядка N (N ![]() нечетное),
все элементы которой различны. Найти наибольший элемент среди стоящих на
главной и побочной диагоналях и поменять его местами с элементом, стоящим на
пересечении этих диагоналей.
нечетное),
все элементы которой различны. Найти наибольший элемент среди стоящих на
главной и побочной диагоналях и поменять его местами с элементом, стоящим на
пересечении этих диагоналей.
.М2 111
Для заданной квадратной матрицы сформировать одномерный массив из ее диагональных элементов. Найти след матрицы, суммируя элементы одномерного массива. Преобразовать исходную матрицу по правилу: четные строки разделить на полученное значение, нечетные оставить без изменения.
Л) 112
Задана квадратная матрица. Получить транспонированную матрицу, т. е. матрицу, где столбцы и строки меняются местами.
.М2 113
Квадратная матрица, симметричная относительно главной диагонали, задана верхним треугольником в виде одномерного массива. Восстановить исходную матрицу и напечатать по строкам.
Л) 114
Задана матрица порядка п и число К, Разделить элементы К-й строки на диагональный элемент, расположенный в этой строке.
Л) 115
Для целочисленной квадратной матрицы найти число элементов, кратных К, и наибольший из полученных результатов.
Л) 116
Найти наибольший и наименьший элементы прямоугольной матрицы и поменять их местами.
ЛЕ 117
Дана прямоугольная матрица. Найти строку с наибольшей и наименьшей суммой элементов. Вывести на печать найденные строки и суммы их элементов.
Л) 118
Л) 119
В данной действительной квадратной матрице порядка п найти наибольший по модулю элемент. Получить квадратную матрицу порядка п — 1 путем отбрасывания из исходной матрицы строки и столбца, на пересечении которых расположен элемент с найденным значением.
.N2 120
Дана действительная квадратная матрица порядка п. Преобразовать матрицу по правилу: строку с номером п сделать столбцом с номером п, а столбец с номером п — строкой с номером п.
.N2 121
Пусть дана действительная матрица размером п х т. Требуется преобразовать матрицу: поэлементно вычесть последнюю строку из всех строк, кроме последней.
Определить номера тех строк целочисленной матрицы A[N, К], которые совпадают с массивом ЦК]. Если таких строк нет, выдать соответствующее сообщение.
.М2 123
Определить наименьший элемент каждой четной строки матрицы А[М, Nl.
.М2 124
Расположить столбцы матрицы ЦМ, Nl в порядке возрастания элементов К-ой строки (1 К М).
Л) 125
Определить номера строк матрицы ЩМ, М, хотя бы один элемент КОТОРЫХ равен с, и элементы этих строк умножить на d.
Л) 126
Матрица A[N, М] (М кратно 4) разделена по вертикали на две половины. Определить сумму элементов каждого столбца левой половины и сумму элементов каждого четного столбца правой половины матрицы А.
Л) 127
.М2 128
«Тестирование коллектива». Пусть целочисленная матрица размером п х т содержит информацию об учениках некоторого класса из п человек. В первом столбце проставлена масса (кг), во втором — рост (см), в третьем — успеваемость (средний балл) и т. д. (используйте свои дополнительные показатели). Ученик называется среднестатистическим по К-му параметру (уникальным по К-му параметру), если на нем достигается минимум (максимум) модуля разности среднего арифметического чисел из К-го столбца и значения К-го параметра этого ученика. Ученик называется самым уникальным (самым средним), если он уникален (является среднестатистическим) по самому большому количеству параметров. По данной матрице определить самых уникальных учеников и самых средних.
4.4.5. Подпрограммы
![]() Подпрограмма
— программа, реализующая вспомогательный алгоритм. Основная программа
программа, реализующая основной алгоритм решения задачи и содержащая в себе
обращения к подпрограммам. В Паскале существуют два типа подпрограмм:
подпрограммы-функции и подпрограммы-процедуры. Используемые в программе
нестандартные подпрограммы должны быть описаны в разделе описания подпрограмм.
Подпрограмма
— программа, реализующая вспомогательный алгоритм. Основная программа
программа, реализующая основной алгоритм решения задачи и содержащая в себе
обращения к подпрограммам. В Паскале существуют два типа подпрограмм:
подпрограммы-функции и подпрограммы-процедуры. Используемые в программе
нестандартные подпрограммы должны быть описаны в разделе описания подпрограмм.
Подпрограмма-функция имеет следующий формат описания:
Eunction <имя функции> «параметры—аргументы>) :
<тип функции>;
![]()
Тип функции может быть только простым типом (в Турбо-Паскале исключением из этого правила является тип string). Блок содержит локальные для функции описания и раздел операторов. Обращение к функции является операндом в выражении.
Подпрограмма-процедура имеет следующий формат описания:
В качестве результата процедура может возвращать в вызывающую программу множество простых или структурированных величин или не возвращать никаких значений. Среди параметров процедуры указываются как аргументы, так и результаты. Параметры-результаты должны быть обязательно параметрами-переменными (описанными после служебного слова Var). Обращение к процедуре отдельный оператор.
Обмен данными между вызывающей программой и подпрограммой может происходить не только через параметры, но и через глобальные переменные.
Пример 1. Вычислить разность двух простых дробей:
![]() натуральные числа). Результат по-
натуральные числа). Результат по-
лучить в виде простой несократимой дроби e/f.
Решение. Следует вычислить числитель и знаменатель по правилам вычитания дробей, и сократить их на наибольший общий делитель (НОД). Вычисление НОД двух чисел оформим в виде подпрограммы, используя известный в математике алгоритм Евклида.
Составим два варианта программы решения этой задачи: с подпрограммой-функцией и подпрограммой-процедурой.
Решение 1
Program Sub1 ;
Function Nod (M,N: integer) : integer; Описание
функции ![]()
Begin ![]() вычисления НОД}
вычисления НОД}
While![]() двух натуральных чисел
двух натуральных чисел
If Then
М: =M-N ![]() по алгоритму Евклида
по алгоритму Евклида ![]() Else
Else![]()
Nod:![]()
End ;
ReadLn (А, В, С, Р) ;
(Основная программа вычитания ![]() дробей
и сокращения результата
дробей
и сокращения результата ![]()
![]() Then
WriteLn (Е) Обращение к функции
Then
WriteLn (Е) Обращение к функции ![]()
Else Begin производится дважды ![]()
![]() div Nod (Abs (Е) ;
div Nod (Abs (Е) ; ![]() div Nod (Abs (Е) , Е) ; WriteLn ( '
Ответ:
div Nod (Abs (Е) , Е) ; WriteLn ( '
Ответ: ![]()
Решение 2
Program Sub2 ;
Var А, В, С, D, G, Е, Е : integer,•
Begin Whi1e
M<>N Do Процедура вычисления НОД ![]() If Then М: =M-N (двух
натуральных чисел
If Then М: =M-N (двух
натуральных чисел ![]()
E1se N:
=N-M; по алгоритму Евклида ![]()
End,•
ReadLn (А, В, С, Т ; (Основная
программа ![]()
![]() Обращение к процедуре
Обращение к процедуре ![]() происходит
один раз
происходит
один раз
![]() Then
WriteLn (Е) (Результат получается
Then
WriteLn (Е) (Результат получается ![]()
E1se
Begin (в переменной (З ![]()
Nod(abs
Е,![]()
WriteLn ( ' Ответ: '
End End.
10 Информатика
н ИКТ. Т. ![]()
Пример 2. Составить рекурсивную подпрограмму-функцик) вычисления факториала целого положительного числа.
Решение. Рекурсивной называется подпрограмма, которая в своем описании содержит обращение к самой себе. Функцию N! рекурсивно можно определить, исходя из следующей формулы:
![]() 1, при лт =
О;
1, при лт =
О;
(N-1)! • N, при > О.
Описание функции на Паскале:
If N=O Тћеп
factoria1 :![]()
Пример З. В целочисленной матрице размером 10 х 10 произвести сортировку чисел в строках по возрастанию значений. Первоначально заполнить матрицу целыми случайными числами в диапазоне от О до 100.
Const![]()
Var А: Array[1 . .N] of Vector;
Var
: integer; одномерного массива![]()
E'or to N-1 Do to N-i Do
If Тћеп
Begin х
[ ј ] ![]() Х [ј+1] End;
Х [ј+1] End;
Eor К: = 1
E'or К:![]()
![]() Заполнение матрицы случайными числами) to
N Do Eor 1 to N Do
Заполнение матрицы случайными числами) to
N Do Eor 1 to N Do ![]() random (100) ; to N Do SortVek (А [К) ) ;
{ Сортировка строк)
random (100) ; to N Do SortVek (А [К) ) ;
{ Сортировка строк)
![]()
For К N Do { Вывод отсортированной матрицы)
Begin WriteLn;
Епа
![]()
Во всех задачах этого раздела использовать поДпрограммы
Треугольник задан координатами своих вершин. Составить программу вычисления его площади.
Составить программу нахождения наибольшего общего делителя и наименьшего общего кратного двух натуральных чисел
![]() нока, в) =
нока, в) =
НОД(А, В)
Составить программу нахождения наибольшего общего делителя четырех натуральных чисел.
Составить программу нахождения наименьшего общего кратного трех натуральных чисел.
Написать программу нахождения суммы большего и меньшего из З чисел.
Вычислить площадь правильного шестиугольника со стороной а, используя подпрограмму вычисления площади треугольника.
На плоскости заданы своими координатами п точек. Составить программу, определяющую между какими из пар точек самое большое расстояние. Указание. Координаты точек занести в массив.
Проверить, являются ли данные три числа взаимно простыми.
![]()
Написать программу вычисления суммы факториалов всех нечетных чисел от 1 до 9.
Даны две дроби — и — (а, Ь, с, d — натуральные числа). Составить программу:
1) деления дроби на дробь;
2) умножения дроби на дробь; З) сложения этих дробей.
Ответ должен быть несократимой дробью.
На плоскости заданы своими координатами п точек. Создать матрицу, элементами которой являются расстояние между каждой парой точек.
Даны числа х, у, г, t — длины сторон четырехугольника. Вычислить его площадь, если угол между сторонами длиной х и у — прямой.
Сформировать массив X[N], N-ii член которого определяется 1
формулой X(N) = ![]()
Составить программу вычисления суммы факториалов всех четных чисел от т до п.
Заменить отрицательные элементы линейного массива их модулями, не пользуясь стандартной функцией вычисления модуля. Подсчитать количество произведенных замен.
Дан массив A[N]. Сформировать массив Щ М], элементами которого являются большие из двух рядом стоящих в массиве А чисел. (Например, массив А состоит из элементов 1, З, 5, —2,
О, 4, О. Элементами массива В будут З, 5, 4, О.)
ль 17
Дан массив „4[N] (N — четное). Сформировать массив В[М], элементами которого являются средние арифметические двух рядом стоящих в массиве А чисел. (Например, массив А состоит из элементов 1, З, 5, —2, О, 4, О, З. Элементами массива В будут 2; 1,5; 2; 1,5.)
![]()
Дано простое число. Составить функцию, которая будет находить следующее за ним простое число.
Составить функцию для нахождения наименьшего нечетного натурального делителя К (К 1) любого заданного натурального числа п.
![]() 20
20
Дано натуральное число дт . Составить программу формирования массива, элементами которого являются цифры числа дт .
Составить программу, определяющую, в каком из данных двух чисел больше цифр.
![]() 22
22
Заменить данное натуральное число на число, которое получается из исходного записью его цифр в обратном порядке (например, дано число 156, нужно получить 651).
Даны натуральные числа К и п. Составить программу формирования массива А, элементами которого являются числа, сумма цифр которых равна и которые не больше п.
![]() 24
24
Даны три квадратных матрицы А, В, С п-го порядка. Вывести на печать ту из них, норма которой наименьшая. Нормой матрицы считать максимум из абсолютных величин ее элементов.
![]() 25
25
Два натуральных числа называются «дружественными», если каждое из них равно сумме всех делителей (кроме его самого) другого (например, числа 220 и 284). Найти все пары «дружественных чисел», которые не больше данного числа п.
![]() 26
26
Два простых числа называются «близнецами», если они отличаются друг от друга на 2 (например, 41 и 43). Напечатать все пары «близнецов» из отрезка [п, 2n], где п — заданное натуральное число, большее 2.
![]() 27
27
Написать программу вычисления суммы
![]()
![]()
для заданного числа п. Дробь — должна быть несократимой ф, q — натуральные).
Г.Г2 28
1
Написать программу
вычисления суммы 1 + — + — + + ![]() для заданного числа п. Результат
представить в виде несократимой дроби 2 ф, q — натуральные).
для заданного числа п. Результат
представить в виде несократимой дроби 2 ф, q — натуральные).
Г.Г2 29
Натуральное число, в записи которого п цифр, называется числом Амстронга, если сумма его цифр, возведенная в степень п, равна самому числу. Найти все такие числа от 1 до К.
.М2 зо
Написать программу, которая находит и выводит на печать все четырехзначные числа вида abcd, для которых выполняется:
а) а, Ь, с, d — разные цифры; б) ab — cd = а + Ь + с + d.
Найти все простые натуральные числа, не превосходящие п, двоичная запись которых представляет собой палиндром,
т. е. читается одинаково слева направо и справа налево.
.М2 32
Найти все натуральные п-значные числа, цифры в которых образуют строго возрастающую последовательность (например, 1234, 5789).
.М2 33
Найти все натуральные числа, не превосходящие заданного п, которые делятся на каждую из своих цифр.
.М2 34
Составить программу для нахождения чисел из интервала [т; п], имеющих наибольшее количество делителей.
.М2 35
1
Для последовательности ![]() составить
составить
программу печати К-го члена в виде обыкновенной несократиз 19
мой
дроби. Например, а,-к ![]() •
•
10
Дано натуральное число п. Выяснить, можно ли представить п в виде произведения трех последовательных натуральных чисел.
287
![]()
Г.Г2 37
На части катушки с автобусными билетами номера шестизначные. Составить программу, определяющую количество счастливых билетов на катушке, если меньший номер билета — N, больший — М (билет является счастливым, если сумма первых трех его цифр равна сумме последних трех).
Г.Г2 38
Написать программу, вычисляющую сумму п-значных чисел, содержащих только нечетные цифры. Определить, сколько четных цифр в найденной сумме.
Из заданного числа вычли сумму его цифр. Из результата вновь вычли сумму его цифр и т. д, Через сколько таких действий получится нуль?
Г.Г2 40
Составить программу разложения данного натурального числа
на простые множители. Например, 200 = 2 3 • 5 2![]()
Л) 41
Дано натуральное число п. Найти все меньшие п числа Мерсена. (Простое число называется числом Мерсена, если оно может быть представлено в виде 22 — 1, где р — тоже простое число. Например, 31 = 2 5 — 1 — число Мерсена.)
Г.Г2 42
Дано четное число п > 2. Проверить для него гипотезу Гольдбаха: каждое четное п представляется в виде суммы двух простых чисел.
в Г.Г2 43
Реализовать набор подпрограмм для выполнения следующих
операций над обыкновенными дробями вида — (Р — целое, Q — натуральное):
а) сложение; б) вычитание; в) умножение; г) деление;
д) сокращение дроби;
е) возведение дроби в степень п (п — натуральное);
ж) функции, реализующие операции отношения (равно, не равно, больше или равно, меньше или равно, больше, меньше).
1) Дан массив А — массив обыкновенных дробей. Найти сумму всех дробей, ответ представить в виде несократимой дроби. Вычислить среднее арифметическое всех дробей, ответ представить в виде несократимой дроби.
2) Дан массив А — массив обыкновенных дробей. Отсортировать его в порядке возрастания.
.М2 44
Реализовать набор подпрограмм для выполнения следующих операций над векторами:
а) сложение; б) вычитание; в) скалярное умножение векторов; г) умножение вектора на число; д) нахождение длины вектора.
1) Дан массив А — массив векторов. Отсортировать его в порядке убывания длин векторов.
2) С помощью датчика случайных чисел сгенерировать 2N целых чисел. N пар этих чисел задают N точек координатной плоскости. Вывести номера тройки точек, которые являются координатами вершин треугольника с наибольшим углом.
.М2 45
Реализовать набор подпрограмм для выполнения следующих операций над натуральными числами в Р-ичной системе счисления (2 Р 9):
а) сложение; б) вычитание; в) умножение; г) деление;
е) перевод из Р-ичной системы счисления в десятичную;
ж) функция проверки правильности записи числа в Р-ичной системе счисления;
з) функции, реализующие операции отношения (равно, не равно, больше или равно, меньше или равно, больше, меньше).
1) Возвести число в степень (основание и показатель степени записаны в Р-ичной системе счисления). Ответ выдать в Р-ичной и десятичной системах счисления.
2) Дан массив А — массив чисел, записанных в Р-ичной системе счисления. Отсортировать его в порядке убывания. Ответ выдать в Р-ичной и десятичной системах счисления.
.М2 46
Реализовать набор подпрограмм для выполнения следующих операций над натуральными числами в шестнадцатеричной системе счисления:
а) сложение; б) вычитание; в) умножение; г) деление;
д) перевод из двоичной системы счисления в шестнадцатеричную;
е) перевод из шестнадцатеричной системы счисления в десятичную;
ж) функция проверки правильности записи числа в шестнадцатеричной системе счисления;
з) функции, реализующие операции отношения (равно, не равно, больше или равно, меньше или равно, больше, меньше).
1) Возвести число в степень (основание и показатель степени записаны в шестнадцатеричной системе счисления). Ответ выдать в шестнадцатеричной и десятичной системах счисления.
2) Дан массив А — массив чисел, записанных в шестнадцатеричной системе счисления. Отсортировать его в порядке убывания. Ответ выдать в шестнадцатеричной и десятичной системах счисления.
Рекурсивные подпрограммы Л) 47 Найдите сумму цифр заданного натурального числа.
ль 48
Подсчитать количество цифр в заданном натуральном числе.
Л) 49
.М2 50
Описать рекурсивную логическую функцию Simm(S, i, ј), проверяющую, является ли симметричной часть строки S, начинающаяся i-M и заканчивающаяся ј-м ее элементами.
Составить программу вычисления НОД двух натуральных чисел.
.М2 52
Составить программу нахождения числа, которое образуется из данного натурального числа при записи его цифр в обратном порядке. Например, для числа 1234 получаем ответ 4321.
.М2 53
Составить программу перевода данного натурального числа в р-ичную систему счисления (2 S р 9).
.М2 54
Дана символьная строка, представляющая собой запись натурального числа в р-ичной системе счисления (2 р 9). Составить программу перевода этого числа в десятичную систему счисления.
.М2 55
Составить программу вычисления суммы: 1! + 2! + З! + + п! (п 15).
Примечание. Тип результата значения функции — LongInt.
Составить программу вычисления суммы:
![]() четное).
четное).
Примечание. Тип результата значения функции — LongInt.
4.4.6. Обработка строк
![]() Строка —
упорядоченная последовательность символов. Строковый тип данных
структурированный тип в Турбо-Паскале. Каждый символ строковой величины
занимает 1 байт памяти (код ASCII). Количество символов в строке называется ее
длиной. Длина строки может лежать в диапазоне от О до 255.
Строка —
упорядоченная последовательность символов. Строковый тип данных
структурированный тип в Турбо-Паскале. Каждый символ строковой величины
занимает 1 байт памяти (код ASCII). Количество символов в строке называется ее
длиной. Длина строки может лежать в диапазоне от О до 255.
Строковая константа последовательность символов, заключенных в апострофы. Например: ' это строковая константа' , ' 272' . Два следующих друг за другом апострофа(' ' ) обозначают пустую строку, т. е. строку с нулевой длиной.
Var <идентификатор> : string [ <макспиальная длина строки>] .
Например: Var Name: string [20) .
В описании строки можно не указывать длину. Например: Var slovo: string. В таком случае подразумевается, что она равна максимальной величине 255.
Элементы строки
идентифицируются именем строки с индексом, заключенным в квадратные скобки.
Например: N [5) , ![]() s10vo [ К+1) . Первый символ строки имеет
номер 1. Индекс может быть положительной константой, переменной, выражением
целого типа. Значение индекса не должно выходить за границы описания.
s10vo [ К+1) . Первый символ строки имеет
номер 1. Индекс может быть положительной константой, переменной, выражением
целого типа. Значение индекса не должно выходить за границы описания.
Тип string и стандартный тип char совместимы. Строки и символы могут употребляться в одних и тех же выражениях.
Операции над строками.
Операция сцепления (конкатенации) (+) применяется для соединения нескольких строк в одну результирующую строку. Сцеплять можно как строковые константы, так и переменные.
Пример: ' Мама ' +' мыла ' +' раму ' . В результате получится строка: ' Мама мыла раму ' . Длина результирующей строки не должна превышать 255.
![]()
извести сравнение двух строк, в результате чего получается логическое значение (true или false). Операция отношения имеет приоритет более низкий, чем операция сцепления. Сравнение строк производится слева направо до первого несовпадающего символа, и та строка считается больше, в которой первый несовпадающий символ имеет больший номер в таблице символьной кодировки. Если строки имеют различную длину, но в общей части символы совпадают, считается, что более короткая строка меньше, чем более длинная. Строки равны, если они полностью совпадают по длине и содержат одни и те же символы.
![]() Пример 1
Пример 1
Выражение ![]() Результат
Результат
'True1'<'True2' True
|
|
True |
|
True |
|
|
'Cat'='Cat' |
True |
'
Функция Copy(S, Рог, N) выделяет из строки S подстроку длиной лт символов, начиная с позиции Рот Здесь ЛУ и Рог — целочисленные выражения.
![]() Пример 2
Пример 2
Значение S Д Выражени ат ' Мама мыла раму ' Сору ( S , 6, 4) ' мыла ' |
||||||
|
' Маша ела кашу ' Сорус, 1,8) |
' Маша ела ' |
|||||
Функция Concat(S1, S2, SN) выполняет сцепление (конкатенацию) строк „-91 , Sz, . , SN в одну строку.
![]() Пример З
Пример З
|
Выражение Concat (' Маша ' |
Результат |
|
' Маша ела кашу |
Функция Length(S) определяет текущую длину строки S.
Результат — значение целого типа.
![]() Пример 4
Пример 4
|
Значение S 'test—5'
|
Length ( S ) Length ( S ) |
|
Функция Pos(S1, S2) обнаруживает первое появление в строке S2 подстроки ..S1 . Результат — целое число, равное номеру позиции, где находится первый символ подстроки S1. Если в S2 подстроки S1 не обнаружено, то результат равен О.
Пример 5

Процедура Delete(S, Рог, N) ![]() удаление
N символов из строки S , начиная с позиции Рог.
удаление
N символов из строки S , начиная с позиции Рог.
Пример 6

Процедура Insert(S1, S2, Рог) — вставка строки S1 в строку
ь.» , начиная с позиции Рог.
Пример 7

Пример 8. Из данной символьной строки выбрать все цифры и сформировать другую строку из этих цифр, сохранив их последовательность.
Решение. Идея алгоритма состоит в
следующем: просматриваются все символы исходной строки и проверяется
принадлежность каждого символьному интервалу от ' 0 ' до ' 9 ' . Если «да», то
такой символ присоединяется к строке![]()
Program Stroki ;
Var S 1 , S 2 : string;
Write ( ' Введите исходную строку: ReadLn (S1) ;

Тест:
Введите исходную строку: df56ghf789yt6u8k88w Результат: 567896888
![]()
Дана строка, заканчивающаяся точкой. Подсчитать, сколько в ней слов.
Дана строка, содержащая английский текст. Найти количество слов, начинающихся с буквы Ь.
Дана строка. Подсчитать в ней количество вхождений букв г,
Дана строка. Определить, сколько в ней символов * ,![]()
Дана строка, содержащая текст. Найти длину самого короткого слова и самого длинного слова.
Дана строка символов, среди которых есть двоеточие (:). Определить, сколько символов ему предшествует.
Дана строка, содержащая текст, заканчивающийся точкой. Вывести на экран слова, содержащие три буквы.
Дана строка. Преобразовать ее, удалив каждый символ * и повторив каждый символ, отличный от *.
Дана строка. Определить, сколько раз входит в нее группа букв abc.
![]()
Дана строка. Подсчитать количество букв К в последнем ее слове.
Дана строка. Подсчитать, сколько различных символов встречаются в ней. Вывести их на экран.
Дана строка. Подсчитать самую длинную последовательность подряд идущих букв а.
Дана строка символов, среди которых есть одна открывающая и одна закрывающая скобка. Вывести на экран все символы, расположенные внутри этих скобок.
Имеется строка, содержащая буквы латинского алфавита и цифры. Вывести на экран длину наибольшей последовательности цифр, идущих подряд.
Дан набор слов, разделенных точкой с запятой (;). Набор заканчивается двоеточием С). Определить, сколько в нем слов, заканчивающихся буквой а.
Дана строка. Указать те слова, которые содержат хотя бы одну букву К.
Дана строка. Найти в ней те слова, которые начинаются и оканчиваются одной и той же буквой.
.М2 18
В строке заменить все двоеточия точкой с запятой (;). Подсчитать количество замен.
В строке удалить символ двоеточие и подсчитать количество удаленных символов.
![]() 20
20
В строке между словами вставить вместо пробела запятую и пробел .
Удалить часть символьной строки, заключенной в скобки (вместе со скобками).

В строке имеется одна точка с запятой (;). Подсчитать количество символов до точки с запятой и после нее.
![]() 24
24
Дана строка из п символов. Преобразовать ее, заменив все двоеточия (:), встречающиеся среди первых п/2 символов, на пробелы и заменив точками все восклицательные знаки, встречающиеся среди символов, стоящих после п/2 символов.
![]() 25
25
Строка содержит одно слово. Проверить, будет ли оно читаться одинаково справа налево и слева направо (т. е. является ли оно палиндромом).
![]() 26
26
В записке слова зашифрованы — каждое из них записано наоборот. Расшифровать сообщение.
Проверить, одинаковое ли число открывающих и закрывающих скобок в данной строке.
Строка, содержащая произвольный русский текст, состоит не более чем из 200 символов. Написать, какие буквы и сколько раз встречаются в этом тексте. Ответ должен приводиться в грамматически правильной форме: например: а — 25 раз, к — З раза и т. д.
![]() 29
29
Упорядочить данный массив английских слов по алфавиту.
Г.Г2 зо
Даны две строки А и В. Составьте программу, проверяющую, можно ли из букв, входящих в А, составить В (буквы можно использовать не более одного раза и можно переставлять).
Например, А: ИНТЕГРАЛ; В: АГЕНТ — составить можно; В: ГРАФ —нельзя.
Строка содержит произвольный русский текст. Проверить, каких букв в нем больше: гласных или согласных.
Двумерный массив п х т содержит некоторые буквы русского алфавита, расположенные в произвольном порядке. Написать программу, проверяющую, можно ли из этих букв соста-
![]()
вить данное слово S. Каждая буква массива используется не более одного раза.
.М2 33
Результаты вступительных экзаменов в вуз представлены в виде списка из 1V строк, в каждой строке которого записаны фамилия студента и отметки по каждому из М экзаменов. Определить количество абитуриентов, сдавших вступительные экзамены только на «отлично» .
.М2 34
Составить программу преобразования натуральных чисел, записанных в римской нумерации, в десятичную систему счисления.
.М2 35
Из заданной символьной строки выбрать те символы, которые встречаются в ней только один раз, в том порядке, в котором они встречаются в тексте.
.М2 36
В строковом массиве хранятся фамилии и инициалы учеников класса. Требуется напечатать список класса с указанием для каждого ученика количества его однофамильцев.
.М2 37
Дано число в двоичной системе счисления. Проверить правильность ввода этого числа (в его записи должны быть только символы О и 1). Если число введено неверно, повторить ввод. При правильном вводе перевести число в десятичную систему счисления.
Дана строка, содержащая текст, записанный строчными русскими буквами. Получить в другой строке тот же текст, записанный заглавными буквами.
Дана строка, содержащая произвольный текст. Выяснить, чего в нем больше: русских букв или цифр.
.М2 40
Дана строка, содержащая текст на русском языке. Выяснить, входит ли данное слово в указанный текст, и если да, то сколысо раз.
«М 41
Дана строка, содержащая текст на русском языке. В предложениях некоторые из слов записаны подряд несколько раз (предложение заканчивается точкой или знаком восклицания). По-
языках
![]()
лучить в новой строке отредактированный текст, в котором удалены подряд идущие вхождения слов в предложениях.
Л) 42
Дана строка, содержащая текст, набранный заглавными русскими буквами. Провести частотный анализ текста, т. е. указать (в процентах), сколько раз встречается та или иная буква.
Л) 43
Дана строка, содержащая текст на русском языке. Определить, сколько раз встречается в ней самое длинное слово.
.N2 44
Дана строка, содержащая произвольный текст. Проверить, правильно ли в нем расставлены круглые скобки (т. е. находится ли правее каждой открывающей скобки закрывающая, и левее закрывающей — открывающая).
.N2 45
Дана строка, содержащая текст на русском языке. Составить в алфавитном порядке список всех слов, встречающихся в этом тексте.
.N2 46
Дана строка, содержащая текст на русском языке. Определить, сколько раз встречается в нем самое короткое слово.
.N2 47
Дана строка, содержащая текст на русском языке и некоторые два слова. Определить, сколько раз они входят в текст и сколько раз они входят непосредственно друг за другом,
.N2 48
Дана строка, содержащая текст на русском языке. Выбрать из него только те символы, которые встречаются в нем только один раз, в том порядке, в котором они встречаются в тексте.
.N2 49
Дана строка, содержащая текст и арифметические выражения вида а О Ь, где О — один из знаков -е, —, * , /. Выписать все арифметические выражения и вычислить их значения.
.N2 50
Дана строка, содержащая текст на русском языке, и некоторая буква. Найти слово, в котором указанная буква встречается наибольшее количество раз. Л) 51
Дана строка, содержащая текст на русском языке, и НеКОТОрая буква. Подсчитать, сколько слов начинается с указанной буквы.
![]()
.М2 52
Дана строка, содержащая текст на русском языке. Найти слово, встречающееся в каждом предложении, или сообщить, что такого слова нет.
.М2 53
Дана строка, содержащая текст, включающий русские и английские слова. Подсчитать, каких букв в тексте больше — русских или латинских.
.М2 54
Дана строка, содержащая текст. Сколько слов в тексте? Сколько цифр в тексте?
.М2 55
Дана строка, содержащая текст, включающий русские и английские слова. Получить новую строку, заменив в исходной все заглавные буквы строчными и наоборот.
Л) 56
Дана строка, содержащая зашифрованный русский текст. Каждая буква заменяется на следующую за ней (буква я заменяется на а). Получить в новом файле расшифровку данного текста.
.М2 57
Даны две строки f1 и f2. Строка f1 содержит произвольный текст. Слова в тексте разделены пробелами и знаками препинания. Строка f2 содержит не более 30 слов, которые разделены запятыми. Эти слова образуют пары: каждое второе является синонимом первого. Заменить в строке f1 те слова, которые можно, их синонимами. Результат поместить в новую строку.
.М2 58
Дана строка. Удалить из нее все лишние пробелы, оставив между словами не более одного. Результат поместить в новую строку.
Дана строка и некоторое слово. Напечатать те предложения строки, которые содержат данное слово.
Дана строка. Напечатать в алфавитном порядке все слова из данной строки, имеющие заданную длину п.
.М2 61
Дана строка, содержащая текст на русском языке. Подсчитать количество слов, начинающихся и заканчивающихся на одну и ту же букву.
Приложение 1
![]()
Количество информации в сообщении об одном из
N равновероятных событий: i — logzN
1 0,00000 17 4,08746 33 5,04439 49 5,61471 2 1 ,ooooo 18 4, 16993 34 5,08746 50 5,64386 з 1 ,58496 19 4,24793 35 5,12928 51 5,67243 4 2,00000 20 4,32193 36 5, 16993 52 5,70044
5 2,32193 21 4,39232 37 5,20945 53 5,72792
6 2,58496 22 4,45943 38 5,24793 54 5,75489
7 2,80735 23 4,52356 39 5,28540 55 5,78136
8 3,00000 24 4,58496 , 40 5,32193 56 5,80735
9 3,16993 25 4,64386 41 5,35755 57 5,83289
10 3,32193 26 42 5,39232 58 5,85798
, 11 3,45943 27 4,75489 43 5,42626 59 5,88264
12 3,58496 28 4,80735 44 5,45943 60 5,90689
13 3,70044 29 4,85798 45 5,49185 61 5,93074
14 3,80735 30 4,90689 46 5,52356 62 5,95420
15 3,90689 31 4,95420 47 5,55459 63 5,97728
32 5,00000 48 5,58496 64 6,00000
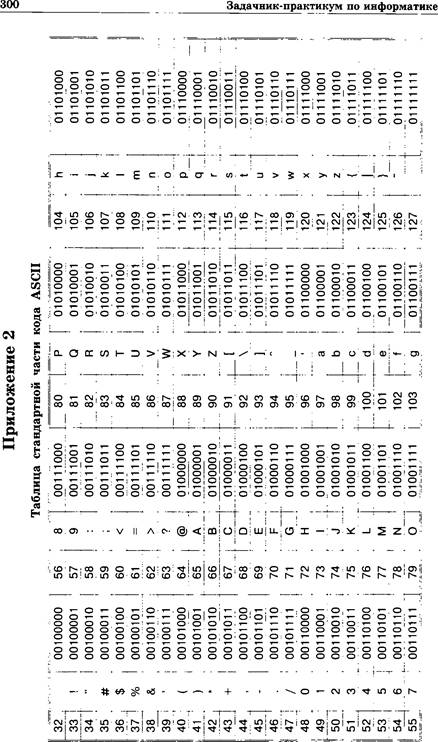
|
138 K 10001010 154 b 1001 1010 139 月 10001011 155 나 10011011
|
|||||||||||
|
140 M |
|||||||||||
|
|
10011 101 |
||||||||||
|
1001 1 110 |
|||||||||||
|
143 n 100011 1 1 159 q 1001 1 1 1 1 |
|||||||||||
![]()
ло
![]()
N2 4 lot si.
![]() 8
Цаля — яблоко, баля — груша, каля солнышко.
8
Цаля — яблоко, баля — груша, каля солнышко.
1.2
N2 27 Просто.
![]() З 1 бит; N2 4 2 бита; ЛЕ 5 1 бит; N9 6 О
бит; 7 2 бита; N2 8 З бита; 9 4 бита; N2 10 7 битов; N2 11 128; ЛЬ 12 64; Л) 13
16; ЛЬ 14 8; .М2 15 2,80735 бита; .М 16 3,58496 бита;
З 1 бит; N2 4 2 бита; ЛЕ 5 1 бит; N9 6 О
бит; 7 2 бита; N2 8 З бита; 9 4 бита; N2 10 7 битов; N2 11 128; ЛЬ 12 64; Л) 13
16; ЛЬ 14 8; .М2 15 2,80735 бита; .М 16 3,58496 бита; ![]() 17 4,90689 бита; N2
18 13,09671 бита; Л) 19 З бита; Л) 20 120 битов; Л) 21 400 и 420 битов; 22 36
битов; Л) 23 740 битов; 24 4 буквы; N2 25 2 бита; 26 16 символов; ЛЬ 27 256
символов; 28 131 072 символа; Л) 29 1,5 Кбайта; N2 30 0,1875 Кбайта; 31 10 500
байтов; 32 4 символа; Л) 33 65 символов; N2 34 2 символа; ЛЕ 35 8 и 4 символа,•
N2 36 32 и 4 символа; N2 37 З • 10 23 битов; № 38 6,64386 бита.
17 4,90689 бита; N2
18 13,09671 бита; Л) 19 З бита; Л) 20 120 битов; Л) 21 400 и 420 битов; 22 36
битов; Л) 23 740 битов; 24 4 буквы; N2 25 2 бита; 26 16 символов; ЛЬ 27 256
символов; 28 131 072 символа; Л) 29 1,5 Кбайта; N2 30 0,1875 Кбайта; 31 10 500
байтов; 32 4 символа; Л) 33 65 символов; N2 34 2 символа; ЛЕ 35 8 и 4 символа,•
N2 36 32 и 4 символа; N2 37 З • 10 23 битов; № 38 6,64386 бита.
1.4
2 бита.
З бита.
4 карандаша.
32 пары.
1 бит.
2; 2,32193; 4,32193 бита.
16 банок. 24 шара.
Л) 15 5 битов.
Л) 1 3500; 4; 19; 1996.
![]() 6 1997.
6 1997.
ЛЕ 12 1) 253411 - 2 . 104 + 5 . 10 3 + 3 . 10 2 + 4 - 10 + 1; 25341 0 — 2 . 84 + 5 . 83 + З . 82 + 4 - 8 + 1.
8
![]() 15 1) 3419 - 28010, 3418 -
22510.
15 1) 3419 - 28010, 3418 -
22510.
Л) 18 Минимальное основание системы счисления З.
ЛЬ 21 Во всех системах счисления
с нечетным основанием. ![]() 2 22
2 22![]()
ЛЕ 23 2) 1210 - 1103; 52410 - 2011023; 7610 - 22113;
.М2 25 2) 0,58510 = 0,1000112; 0,33310 - 0,0101012;
0,121310 = 0,0001112; 0,45310 - 0,0111002. ЛЬ 33 1) 6065; 125; 0,51620; 0,7704.
1 зоз
2 34 1) 6D1•, 7FC1; О,6А; О,Е6А.
.N2 35 1) 42,358; 52,718; 43,78.
36 1) 10101110; 0,011100101; 10100,000010101; 0,010101. 2 46 1) 111; 2) 210; 3) 112; 4) 2.
48 1) 3723; 2) 7153; 3) 100225; 4) 77540.
49 1) 10000; 2) D450; 3) ВЗ2Е; 4) F79.
.N2 50 1) 11010012; 2) АЕ5416•, 3) 105; 4) 1222023.
2 51 Да, в системе счисления с основанием 9.
![]() 2 52
2 52
53 р - 82357.
![]() 2 55 В шестеричной
системе счисления.
2 55 В шестеричной
системе счисления.
2 57 В восьмеричной системе счисления.
2 58 В пятеричной системе счисления.
2 59 В шестеричной системе счисления.
2 61 Пятая цифра слева 316.
2 62 б) Наименьшее — 1008 ; наибольшее 7778.
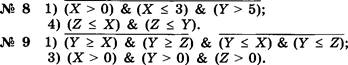
.N2 10 1) (Х > 0) х., (У > 0) х., (Z > 0).
.N2 11 1) (Х > 10) 10) 10)
10) (Z 10) х., (Х 10) (У S 10) > 10).
- 22 = 8, х., 8, х».
.N2 23
2 24 х., -.t1 8, & х., 23).
29 4,5,8 — всегда истинны; 1,2,3,6,7 — ложны, если ложно заключение.
.N2 ЗО 5) (А х., В) х., С О,
А — Спортсмен
некорректен по отношению ![]() сопернику;
сопернику;
В — Спортсмен некорректен к судье;
![]() Спортсмен принимает допинг;
Спортсмен принимает допинг;
D — Спортсмен подлежит дисквалификации.
![]() 2 39 Иванов участвовал в преступлении.
2 39 Иванов участвовал в преступлении.
![]() 40 В кино пойдут Вика и Сергей.
40 В кино пойдут Вика и Сергей.
![]() 2 41 Будет ясная погода без дождя, но с
ветром.
2 41 Будет ясная погода без дождя, но с
ветром.
![]() 2 42 Сергей — 1-е место, Леонид — 2-е
место,
2 42 Сергей — 1-е место, Леонид — 2-е
место,
Виктор 3-е место, Роман — 4-е
место. ![]() о 43 Сосуд финикийский и
изготовлен в V веке.
о 43 Сосуд финикийский и
изготовлен в V веке.
![]()
Ответы к разделу 3.1
N2 1 32 бита; N2 2 16384 машинных слова; N2 З с шагом 2; N2 4 с шагом 4; N2 5 128 машинных слов; N2 6 256 машинных слов; N2 7 512 машинных слов; N2 8 1 Кбайт; N2 9 256 байт; N2 10 2 байта; 4 байта; N2 12 256 байт; N2 13 512 байт; N2 14 адрес последнего байта 1FF, адрес последнего машинного слова — 1FC; N2 15 адрес последнего байта — 3FF, адрес последнего машинного слова 3FE; 16 80 дорожек; Г.Г2 17 1600 Кбайт; N2 18 512 байт; N2 19 1) 12 файлов; 2) 14 файлов; N2 20 360 Кбайт; N2 21 729 дискет; N2 22 40 дорожек; N2 23 10240 символов; N2 24 360 Кбайт; N2 31 256 символов; Л) 32 10500 байт; N233 1) 320 страниц; 2) 160 страниц; З) 640 страниц; N2 34 5120 символов; Г•Г2 35 1) 102 105 108 101; 2) 104 101 108 112; Г.Г2 36 1) sport; 2) mouse•, 37 73 78 70 79 82 77 65 84 73 79 78; Л) 38 98 97 115 105 99; Л) 39 1) 4Е 6F 72 74 6F 6Е 20 43 6F 61) 61) 61 6Е 64 65 72; 2) 43 6F 61) 70 75 74 65 72 20 49 42 41) 20 50
43; Л) 40 1) Windows-95; 2) come-ON-line; Г.Г2 41 1) 01000101
01110010 01100100; 42 1) 01000010 01100001 01110011
01101001 01100011; Basic; 2) 01010000 01100001 01110011
01100011 01100001 01101100; Pascal; Л) 43 138 142 140 143
156 158 146 133 144; КОМПЬЮТЕР; Г.Г2 44 88 81) 94 8Е 90 8C 80 92 88 8А 80; 45 7 букв русского алфавита; N2 46; от О до 255; Г.Г2 47 от -128 до 127; Г.Г2 48 от о до 2 32 - 1; N2 49 от —2 31 до 2 31 1; N2 50 двоичное и шестнадцатеричное представления
![]()
теричное представления отрицательного числа: 10000000 и 80; N2 51 двоичное и шестнадцатеричное представления положи-
![]()
шестнадцатеричное представления отрицательного числа: 1000 0000 0000 0000 и 8000; Л) 52 7 битов; 53 C12 и C16;
Г.Г2 54 1) 0,5089 • 10 -2 ; 2) 0,12340456 • 10 4 ;
ЛЕ 55 32769 чисел; ![]() 56 52 цифры; ЛЕ 59 О и (1 - 2 -8 ) • 2 63
; N2 60 1) 129; 2) 0,125; 0,1328125; 0,140625; 0,1484375; 0,15625; Г.Г2
61 10,0; 4,3; 8,1; 7,8; ЛЕ 62 1,25; 1,5625; 1,875; 63 1) да; 2) нет; 3) да.
56 52 цифры; ЛЕ 59 О и (1 - 2 -8 ) • 2 63
; N2 60 1) 129; 2) 0,125; 0,1328125; 0,140625; 0,1484375; 0,15625; Г.Г2
61 10,0; 4,3; 8,1; 7,8; ЛЕ 62 1,25; 1,5625; 1,875; 63 1) да; 2) нет; 3) да.
![]() 64 218,75 Кб.
64 218,75 Кб.
Г.Г2 65 5,5 Мб.
![]() 66.
66.
Одна страница — 830 х 630; две страницы 650 х 400; четыре страницы 420 х 310.
![]() 67 256.
67 256.
N2 68 Две страницы.
3.1
![]()
Г.Г2 69
|
Разрешающая Размер одной страницы способность видеопамяти |
|
|
800 х 600 1024х 768 1240 х 1024 |
|
Г.Г2 70 3,66 Мб.
![]() 2 71 200 х 150 или ЗОО х 100. Г.Г2 72 320
х 240.
2 71 200 х 150 или ЗОО х 100. Г.Г2 72 320
х 240.
![]() 73 На белом фоне
изображен коричневый домик с ярко-желтой крышей.
73 На белом фоне
изображен коричневый домик с ярко-желтой крышей.
![]() 2 76 25 строк и 80 знакомест в строке.
2 76 25 строк и 80 знакомест в строке.
![]() 77 800 х 600.
77 800 х 600.
![]() 2 78 256 оттенков
красного, 256 оттенков зеленого и 256 оттенков синего.
2 78 256 оттенков
красного, 256 оттенков зеленого и 256 оттенков синего.
![]() 2
79 Красная — 8, зеленая синяя 4.
2
79 Красная — 8, зеленая синяя 4.
![]() 81 256.
81 256.
![]() 2 82 Светло-серые оттенки
2 82 Светло-серые оттенки

Темно-серые оттенки

N2 83 Как минимум — 30 (по 10 битов для каждого основного цвета).
Л) 84 1024 оттенка (битовая глубина равна 32).
Л) 85 Оттенки зеленого
![]()
Оттенки сиреневого
![]()
 Интенсивность Зеленый Синий
Интенсивность Зеленый Синий
![]() 86 Оттенки красного
86 Оттенки красного

Оттенки желтого
![]()
Красный Зеленый Синий ![]()
![]()
001 1 1 100 00001 1 11 00000000
![]()
001 1001 1 0001 1010 00000000
![]()
 2 1 8
2 1 8
![]()
![]() 92 124,8 секунды.
92 124,8 секунды.
ЛЕ 93 22,05 КГЦ.
![]() 94 Высокое качество
звучания достигается при частоте дискретизации 44,1 кГц и разрядности
аудиоадаптера, равной 16. Требуемый объем памяти 15,1 Мб.
94 Высокое качество
звучания достигается при частоте дискретизации 44,1 кГц и разрядности
аудиоадаптера, равной 16. Требуемый объем памяти 15,1 Мб.
![]() 95 Для мрачного и приглушенного звука
характерны следующие параметры: частота дискретизации
95 Для мрачного и приглушенного звука
характерны следующие параметры: частота дискретизации ![]() 11 кГц, разрядность
аудиоадаптера — 8. Длительность звучания равна 60,5 с. N2 96 16 битов.
11 кГц, разрядность
аудиоадаптера — 8. Длительность звучания равна 60,5 с. N2 96 16 битов.
![]() 97 20,3 минуты.
97 20,3 минуты.
3.2
![]()
1) ![]()
1) 8; 2) 16; 3) 64; 4) 256. 0 3 64; 2) 256; 3) 4096; 4) 65536.
0 4 1) з; 2) 6; 3) 8; 4) 12.
0 5 1) 16; 2) 12; 3) 12; 4) 16.
2 6 1) 26; 2) 38; 3) 14; 4) 14.
2 7 64 ячейки; 2) 16 ячеек; З) З адреса;
4) 2 адреса. .N2 8 1) 32; 2) 1024; 3) 128; 4) 16.
![]()
Ответы к работе № 1
![]() Номер варианта
Номер варианта
1 0000 0101 1010 1010 FA56 -2435
0000 0101 001 1 1 101 Г-АСЗ
F841
![]() 4 0000 0101 0001 1001 РАЕ
7 0000 01 11 1 100 0000 6-840
4 0000 0101 0001 1001 РАЕ
7 0000 01 11 1 100 0000 6-840
6 0000 0101 1010 1101 БА 53 -1689
0000 011 1 0010 1001 Г-8О7 -1985
F83F -1833
10 Г-967 -1453
ПС В
6700 Г-6О7
77АА F67D
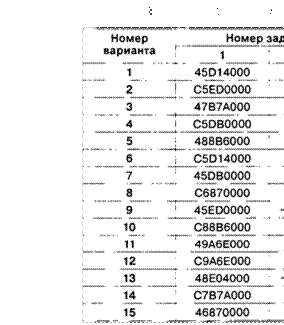
![]()
Литература для дополнительного чтения
1. Вирт Н. Алгоритмы и структуры данных. М.: Мир, 1989.
2. Глушков В. М. Основы безбумажной информатики. М.: Наука, 1987.
З. Гейн А. Г., Сенокосов АИ. Информатика: Учеб. для 8—9 кл. шк. с углуб. изуч. информатики. М.: Просвещение, 1995.
4. Гейн А. Г., Сенокосов А. И., Шолохович В. Ф. Информатика. Учебник для 7—9 классов. М.: Дрофа, 1998.
5. Горячев А. В. и др. Информатика в играх и задачах: Учебник-тетрадь в 4 частях. М.: Баллас, 1995—1997.
6. Информатика: Энциклопедический словарь для начинающих / Под ред. Д. А. Поспелова. М.: Педагогика-Пресс, 1994.
7. Иенсен Е., Вирт Н. Паскаль: руководство для пользователей и описание языка. М.: Мир, 1982.
8. Касаткин В. Н. Информация, алгоритмы, ЭВМ. М.: Просвещение, 1991.
9. Кнут Д. Искусство программирования для ЭВМ. М.: Мир. 1976.
10. Кушниренко А. Г., Лебедев Г. В., Скворень Р. А. Основы информатики и вычислительной техники. М.: Просвещение, 1992.
11. Мнеян М. Г. Физические принципы работы ЭВМ. М.: Просвещение, 1987.
12. Первин Ю. А. и др. Информационная культура (комплект учебных пособий). М.: Дрофа, 1995—1998.
13. Перегудов Ф. И., Тарасенко Ф. П. Введение в системный анализ. М.: Высшая школа, 1989.
14. Першиков В. И., Савинков В. М. Толковый словарь по информатике. М.: Финансы и статистика. 1995.
15. Словарь школьной информатики / Сост. А П. Ершов / Математический энциклопедический словарь. М.: Советская энциклопедия, 1988.
16. Семакин И. Г., Залогова Л. А, Русаков С. В., Шестакова Л. В. Информатика. Базовый курс для 7—9 кл. М.: Лаборатория Базовых Знаний, 1998.
17. Семакин И. Г. Информатика, Беседы об информации, компьютерах и программах. В 2-х частях. Пермь: Изд-во ПГУ, 1996—1997.
18. Семакин И. Г., Шестаков А. П. Лекции по программированию. Пермь: изд-во ПГУ, 1998.
19. Хьюз Дж., Мичтом Дж. Структурный подход к программированию. М.: Мир, 1980.
Учебное издание
ИНФОРМАТИКА И ИКТ.
ЗАДАЧНИК-ПРАКТИКУМ
В двух томах том 1
Ведущий редактор О. Полежаева
Редактор Е. Костомарова
Художник С. Инфантэ
Технический редактор Е. Денюкова Компьютерная верстка: В. Носенко
Подписано в печать 29.08.11. Формат 60х 90/16.
Усл. печ. л. 19,5. Тираж 5500 экз. Заказ № 4137003
Издательство «БИНОМ. Лаборатория знаний»
125167, Москва, проезд Аэропорта, д. З Телефон: (499) 157-5272 e-mail: binom@Lbz.ru, http://www.Lbz.ru При участии ООО « Эмпреза » .
Отпечатано в ОАО «Первая Образцовая типография» Филиал «Нюкполиграф»
603950, г.Нюкний Новгород, ГПС-123, ул. Варварская, 32.
[1] Исполнитель ГРИС аналогичен исполнителям Кенгуренок, Чертежник, реализованным на компьютере.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.