Поделиться
Информатика_и_ИКТ._9кл._Урок№25.docx
Урок 25. Алгоритмическая конструкция «следование» Планируемые образовательные результаты:
предметные – представление об алгоритмической конструкции «следование»;
умение исполнять линейный алгоритм для формального исполнителя с заданной
системой команд; умение составлять простые (короткие) линейные алгоритмы для
формального исполнителя с заданной системой команд;
метапредметные – умение выделять линейные алгоритмы в
различных процессах; понимание ограниченности возможностей
линейных алгоритмов;
личностные – алгоритмическое мышление, необходимое для
профессиональной деятельности в современном обществе.
Решаемые учебные задачи:
1) обобщить представления об алгоритмической конструкции «следование»;
2) получить навыки выполнения линейных алгоритмов для различных формальных исполнителей;
3) получить навыки разработки линейных алгоритмов для различных формальных исполнителей с заданной системой команд.
Основные понятия, рассматриваемые на уроке:
алгоритм;
следование;
линейный алгоритм;
блок-схема;
таблица значений переменных.
Используемые на уроке средства ИКТ:
персональный компьютер (ПК) учителя, мультимедийный
проектор, экран;
ПК учащихся.
Электронные образовательные ресурсы
презентация «Основные алгоритмические конструкции.
Следование» из электронного приложения к учебнику; демонстрация
«Режимы работы программы "Конструктор алгоритмов"» (sc.edu.ru);
71
программа "Конструктор
алгоритмов"(sc.edu.ru);
модуль для коллективной работы «Линейные алгоритмы» (sc.edu.ru).
Особенности изложения содержания темы урока
По ходу изложения нового материала решается множество задач в
рабочей тетради или из учебника.
Практическая работа по составлению блок-схем алгоритмов на компьютере может быть организована на основе программы «Конструктор алгоритмов». Инструкция по работе с этой средой представлена в презентации ««Режимы работы программы "Конструктор алгоритмов"».
Ответы и решения к заданиям в РТ
№ 123. а) 113.
б) 1) 142; 2) 142; 3) 4113232.
в) 1) 315151532525352444.
2) 3353531515145454252524.
При наличии времени п. в) можно выполнить в среде КуМир. На рисунке (здесь и далее) положение Робота после исполнения алгоритма.
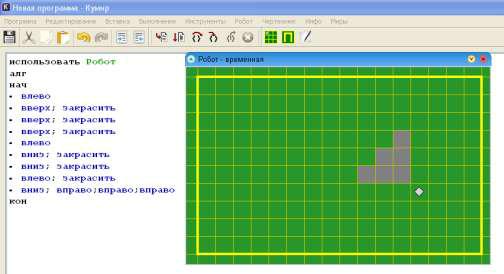
№ 124 (стр. 75)
а)
|
a |
b |
|
9 |
- |
|
|
4 |
|
|
40 |
|
5 |
|
|
б) |
|
|
a |
b |
|
123 |
- |
|
|
12 |
|
|
5 |
72
127
250
в)
|
a |
|
b |
|
|
951 |
|
- |
|
|
|
|
60 |
|
|
95 |
|
|
|
|
5 |
|
|
|
|
65 |
|
|
|
|
г) |
|
|
|
|
a |
|
b |
|
|
336 |
|
- |
|
|
|
|
8 |
|
|
42 |
|
|
|
|
|
|
2 |
|
|
д) |
|
|
|
|
a |
|
b |
|
|
10 |
|
- |
|
|
|
|
20 |
|
|
|
|
30 |
|
|
20 |
|
|
|
|
|
|
50 |
|
|
№ 125. |
|||
|
a |
|
b |
|
|
x |
|
- |
|
|
|
|
2x+5 |
|
|
x+2x+5=20 |
|
|
|
Ответ: х = 5.
№ 126.
D:=A
A:=B
B:=C
C:=D
№ 127. Ответ: a = 7, b = -2.
№ 128. Результат работы алгоритма – сумма цифр трѐхзначного числа.
|
x |
|
125 |
248 |
|
789 |
|
||
|
a |
|
1 |
2 |
|
7 |
|
||
|
b |
|
2 |
4 |
|
8 |
|
||
|
c |
|
5 |
8 |
|
9 |
|
||
|
s |
|
8 |
14 |
|
24 |
|
||
|
|
|
№ 129. |
|
|
|
|
|
|
|
a1 |
a2 |
a3 |
|
a4 |
|
y |
||
73
|
1/x |
- |
- |
- |
- |
|
|
1/x2 |
- |
- |
- |
|
|
|
1/x3 |
- |
- |
|
|
|
|
1/x4 |
- |
|
|
|
|
|
1/x + 1/x2 |
|
|
|
|
|
1/x + 1/x2 + 1/x3 |
1/x + 1/x2 + 1/x3
+ 1/x4
Ответ: Формула: y = 1/x + 1/x2 + 1/x3 + 1/x4
№ 130. Опечатки в условии. См. по №5 на стр. 145 учебника.
|
Алгоритм |
x:= 1 |
x:= 2 |
x |
|
y:=2*x |
2 |
4 |
2x |
|
y:=y+3 |
5 |
7 |
2x+3 |
|
y:=y*x |
5 |
14 |
(2x + 3)x |
|
y:=y+4 |
9 |
18 |
(2x + 3)x+4 |
|
y:=y*x |
9 |
36 |
((2x + 3)x+4)x |
|
5 |
14 |
41 |
((2x + 3)x+4)x+5 |
Ответ: y = ((2x + 3)x+4)x+5.
№ 131.
Алгоритм h := tfh * 24 m := h * 60 c := m * 60
|
tfh |
1 |
2 |
1/2 |
|
h |
24 |
48 |
12 |
|
m |
1440 |
2880 |
720 |
|
c |
86400 |
172800 |
43200 |
№ 132. Ответ: y = x*7*500*3*28*25,4/10/100/1000.
Домашнее задание. §3.4.1; вопросы и задания 1–9 к параграфу; №3 – можно в среде КуМир. Дополнительное задание: работа с модулем «Линейные алгоритмы».
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
