Инструкционная карта занятия Тема: Случайная дискретная величина.

Инструкционная карта занятия

Тема: Вычисление среднего арифметического, математического ожидания и дисперсии случайной дискретной величины.

Цели: 

 Сформировать навык нахождения числовых характеристик дискретной случайной величины;

 Развивать логическое мышление, память, внимание и самостоятельность.

Теоретическая часть.

Простая средняя арифметическая — Равна отношению суммы индивидуальных значений признака к количеству признаков в совокупности

Пример 1. Бригада из 6 рабочих получает в месяц 3 3,2 3,3 3,5 3,8 3,1 тыс. руб.

Найти среднюю заработную плату. Решение: 

(3 + 3,2 + 3,3 +3,5 + 3,8 + 3,1) / 6 = 3,32 тыс. руб.

Взвешенная средняя арифметическая — равна отношению (суммы произведений значения признака к частоте повторения данного признака) к (сумме частот всех признаков). Используется, когда варианты исследуемой совокупности встречаются неодинаковое количество раз.

Представим это в виде следующей формулы:

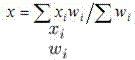§        — цена за единицу продукции;

§        — количество (объем) продукции;

Пример 2. Найти среднюю заработную плату рабочих цеха за месяц

Средняя заработная плата может быть получена путем деления общей суммы заработной платы на общее число рабочих:

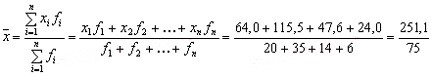
Ответ: 3,35 тыс.руб.

Математическим ожиданием дискретной случайной величины называ-ется сумма произведений ее возможных значений на соответствующие им вероятности:

М(Х) = х1р1 + х2р2 + … + х_пр_п .

Пример 3. Найти математическое ожидание дискретной случайной величины, зная закон ее распределения: 

Решение: По формуле  находим математическое ожидание:

M (X) = 5*0,2 + 4*0,5 + 3*0,3 = 3,3.

Дисперсией (рассеянием) дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

D (X) = M [X - M (X)]².

Пример 4. Найти дисперсию случайной величины X, которая задана следующим законом распределения: 

Решение: По формуле  находим математическое ожидание:

M (X) = 1*0,3 + 2*0,5 + 5*0,2 = 2,3.

Записываем все возможные значения квадрата отклонения: [X₁ - M (X)]² = (1 - 2,3)² = 1,69;

[X₂ - M (X)]² = (2 - 2,3)² = 0,09; [X₃ - M (X)]² = (5 - 2,3)² = 7,29.

Тогда закон распределения квадрата отклонения имеет следующий вид: 

По формуле  находим дисперсию:

D (X) = 1,69*0,3 + 0,09*0,5 + 7,29*0,2 = 2,01.

Практическая часть.

1.  Задан закон распределения случайной величины Х (в первой строке таблицы указаны возможные значения величины Х, а во второй строке указаны вероятности p этих возможных значений). Найти:

1.      математическое ожидание,  

2.      дисперсию,  

3.      построить многоугольник распределения.

1.1                                                                                           

2.  Рассчитать средний возраст студентов в группе из 20 человек: